Integrability and Dynamic Behavior of a Piezoelectro-Magnetic Circular Rod

Abstract

The present work strives to explore some qualitative analysis for the governing equation describing the dynamic response of a piezoelectro-magnetic circular rod. As a result of the integrability study of the governed equation, which furnishes valuable insights into its structure, solutions, and applications in various fields, we apply the well-known Ablowitz–Ramani–Segur (ARS) algorithm to prove the non-integrability of the governed equation in a Painlevé sense. The qualitative theory for planar integrable systems is applied to study the bifurcation of the solutions based on the values of rod material properties. Some new solutions for the governing equation are presented and they are categorized into solitary and double periodic functions. We display a 3D representation of the solutions in addition to investigating the influence of wave velocity on the obtained solution for the particular material of the rod.

1. Introduction

Recent research has focused more on magneto–electro–elastic materials due to their unique properties and wide range of energy conversions. These materials are novel in that they combine phases of piezoelectric and piezomagnetic properties. Consequently, it is possible to convert energy from one form of electric, magnetic, or elastic materials to another using this mixture. Furthermore, there are reciprocal reactions between these materials with respect to mechanical and magnetoelectric loadings. To put it another way, they are capable of creating both electric and magnetic fields when exposed under mechanical stress and can deform when subjected to external magnetic electric forces. These kinds of materials can be used in many engineering applications, including controllers, actuators, and sensors, because of these qualities.

In recent years, there has been an increased amount of research conducted on these specific piezoelectro-magnetic materials. Their best-known feature is their cross-coupling between magnetization and electric polarization, which opens up new avenues for the development of useful electrical devices. From a historical perspective, BaTiO${}_3$-NiFe${}_2$O${}_4$ combined with trace amounts of cobalt and manganese formed the basis for one of the earliest sintered magneto-electric composites. The electro–magnetic coupling impact of a CoFe${}_2$O${}_4$ matrix reinforced by BaTiO${}_3$ fibers was investigated by Van Run et al. [1]. They demonstrated that, in these piezoelectric–piezomagnetic composites, a notable electromagnetic coupling effect occurs in such piezoelectro-magnetic structure. According to Boomgaard et al. [2], the magneto–electric coupling effect might be seen in a mix of piezoelectric and piezomagnetic phases. Wu and Huang [3] provided an analytical technique to explore the electro–magnetic coupling impact via the eigen-strain relation in conjunction with the Mori–Tanaka model. The impact of imperfect mechanical, electrical, and magnetic contact conditions as well as the spatial fiber distribution on the electromagnetic effective coefficients was examined by Espinosa-almeyda et al. [4]. The asymptotic homogenization approach was used to calculate these electromagnetic coefficients. Sobhy [5] investigated the impacts of the boundary conditions, electric and magnetic potential, and thermal load on the bending of nanocomposite doubly curved shallow shells integrated with piezoelectro-magnetic layers. The impact of PZT-7A piezoelectric interphase on the piezoelectro-magnetic characteristics of a CoFe${}_2$O${}_4$ piezomagnetic matrix reinforced by carbon fibers was illustrated by Haghgoo et al. [6] based on a simplified unit cell micromechanical approach. In accordance with the modified couple stress theory and the first-order theory, Hong et al. [7] elucidated static bending and wave propagation in functionally graded porous piezoelectro-magnetic beams. To investigate the dissipated behavior of anti-plane surface waves, namely Love waves, in a homogeneous piezoelectro-magnetic structure, an analytical technique has been proposed by Chaki et al. [8]. Many recent papers in the literature have focused on the behavior of piezoelectro-magnetic composites (see, e.g., Refs. [9,10,11,12,13,14]).

It is well known that the governing equations for these types of problems are always nonlinear partial differential equations. This has become a significant topic of research over the last decades and approached from different aspects, including detecting integrability and finding solutions. Soliton solutions are one of the important aspects of nonlinear equations [15,16,17,18]. There are diverse methods for solving them, such as Lie symmetry analysis [19,20], the bilinear formalism method, the first integral method [21], the bifurcation theory [22,23,24,25,26], the direct method of the Hirota and the linear superposition principle [27], and a combination of the complete discriminate method and bifurcation theory [28]. The Painlevé analysis is a powerful approach employed to detect the integrability of both ordinary and partial differential equations [29]. ARS is the algorithm used to detect the Painlevé integrability for partial differential equations [30] and it has been successfully applied in several works (see, e.g., [31,32,33,34,35,36,37,38,39]).

Our study strives to analyze the dynamic behavior of a piezoelectro-magnetic infinite circular rod under variations in wave velocity and wave number. We suppose that the rod is made of the BaTiO${}_3$-CoFe${}_2$O${}_4$. The governing equation is formulated based on the three-dimensional elasticity theory. Painlevé analysis is performed to detect the integrability of Equation (8) by following the well-known ARS algorithm. Thanks to the bifurcation theory, novel wave solutions for the governing equation are revealed. The phase portrait for different values of bifurcation constraints is introduced. We restrict ourselves to constructing bounded and real solutions. A 3D graphic representation of the solutions is shown. Finally, we illustrate the impact of wave velocity on the solutions.

This work is organized as follows: The governing equation is formulated in Section 2. The integrability of the governed equation is examined using the singularity analysis in Section 2. Section 4 includes the application of bifurcation analysis to the traveling wave system corresponding to the present governing equation. Some new solutions, which are categorized into solitary and periodic, to the motion equation are delivered in Section 5. Based on certain values of the material of the rod, we illustrate a 3D representation of solitary and periodic solutions and study the impact of wave velocity on some of the solutions, as illustrated in Section 6. A summary of the obtained results is given in Section 7.

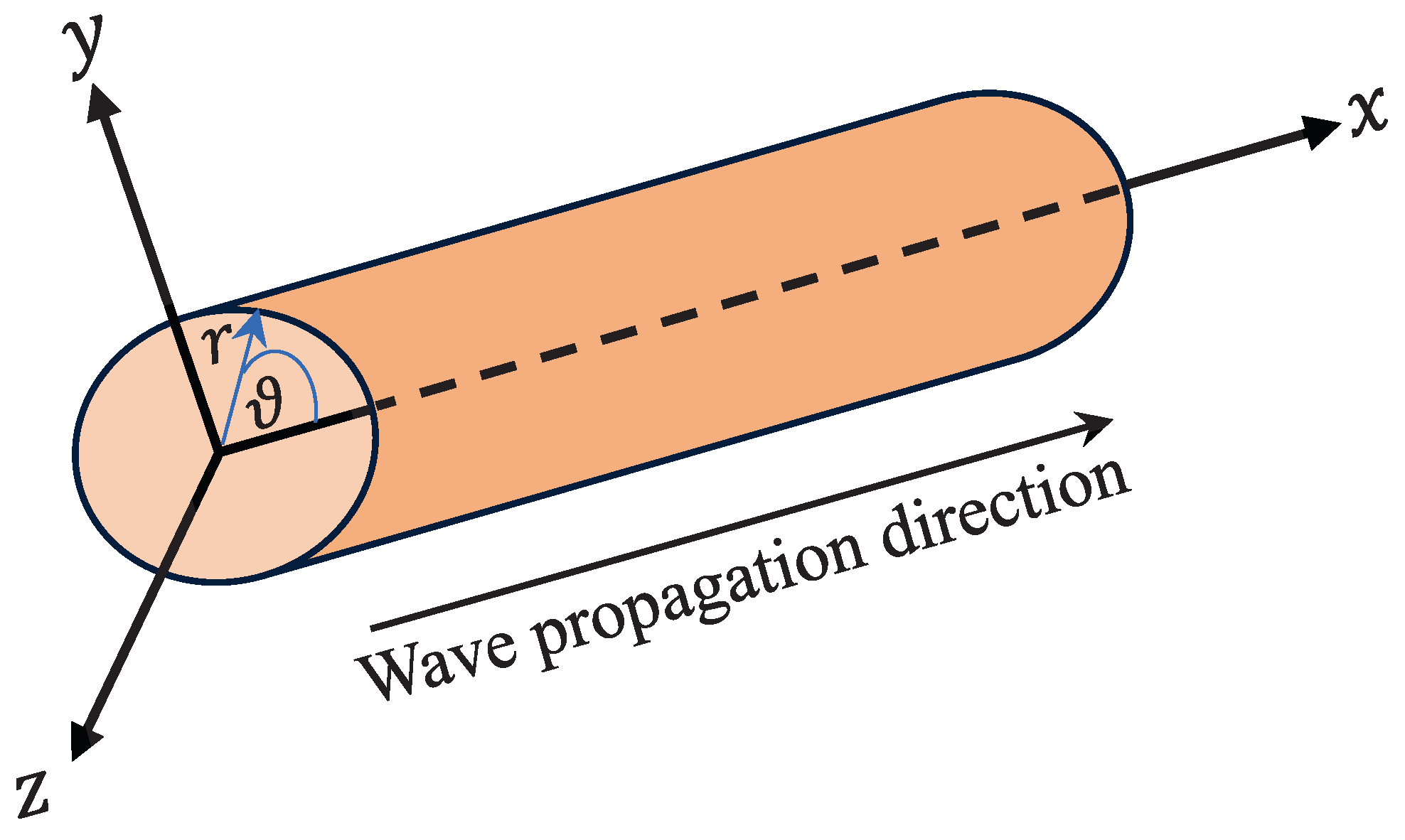
2. Formulation of the Problem

Consider a homogeneous circular rod with a constant cross section having radius a, which is made of a piezoelectro-magnetic (PEM) material. To describe the deformation of the presented PEM rod, the cylindrical coordinate system $(r,\vartheta ,x)$ is used, as shown in Figure 1, where $\vartheta \in [0,2\pi ]$. In this analysis, the waves are assumed to propagate along the rod’s direction. For this purpose, the ensuing assumptions are made:

• The deformation of the rod occurs in axial symmetry; this means that the circumferential displacement $u_{\vartheta }=0$ and $\partial /\partial \vartheta =0$.
• The following relationship between the longitudinal and radial displacements is valid [40]:

  $$u_r=-r\nu {\partial }_x{u}_x,$$

  (1)

  where $\nu$ is Poisson’s ratio and ${\partial }_k^j=\frac{{\partial }^j}{\partial k^j}$, $k=r,x,t$; $j=1,2,3,...$.
• The rod is assumed to be thin; therefore, the problem is considered one-dimensional. Accordingly, the extended tractions on the rod’s lateral boundary must vanish (${\sigma }_{rr}={\sigma }_{r\vartheta }={\sigma }_{rx}=D_{rr}=B_{rr}=0$). This leads to

  $$\begin{array}{l}{ϵ}_{rx}={ϵ}_{\vartheta x}={\mathcal{E}}_{rr}={\mathcal{E}}_{\vartheta \vartheta }=0,\\ {\mathcal{H}}_{rr}={\mathcal{H}}_{\vartheta \vartheta }=D_{\vartheta \vartheta }=B_{\vartheta \vartheta }=0,\end{array}$$

  (2)

  where ${\sigma }_{ij}$ and ${ϵ}_{ij}$ are, respectively, the stress and strain tensors; $D_{ii}$ and $B_{ii}$ stand for the electric displacement and magnetic induction, respectively; ${\mathcal{E}}_{ii}$ and ${\mathcal{H}}_{ii}$ are, respectively, the electric and magnetic fields.

According to the 3D elasticity theory and based on the above assumptions, the motion equations can be expressed as

$$-\frac{{\sigma }_{\vartheta \vartheta }}{r}=\rho {\partial }_t^2{u}_r,{\partial }_x{\sigma }_{xx}=\rho {\partial }_t^2{u}_x,{\partial }_x{D}_{xx}=0,{\partial }_x{B}_{xx}=0,$$

(3)

where the normal stresses, electric displacement $D_{xx}$, and magnetic induction $B_{xx}$ of the transversely isotropic PEM rod are defined as

$$\begin{array}{c}\left\{\begin{array}{c}{\sigma }_{rr}\\ {\sigma }_{\vartheta \vartheta }\\ {\sigma }_{xx}\end{array}\right\}=\left[\begin{array}{ccc}{S}_{11}& S_{12}& S_{13}\\ S_{12}& S_{11}& S_{13}\\ S_{13}& S_{13}& S_{33}\end{array}\right]\left\{\begin{array}{c}{ϵ}_{rr}\\ {ϵ}_{\vartheta \vartheta }\\ {ϵ}_{xx}\end{array}\right\}-\left\{\begin{array}{c}{\eta }_{31}\\ {\eta }_{31}\\ {\eta }_{33}\end{array}\right\}{\mathcal{E}}_{xx}-\left\{\begin{array}{c}{\beta }_{31}\\ {\beta }_{31}\\ {\beta }_{33}\end{array}\right\}{\mathcal{H}}_{xx},\hfill \\ D_{xx}={\eta }_{31}({ϵ}_{rr}+{ϵ}_{\vartheta \vartheta })+{\eta }_{33}{ϵ}_{xx}+b_{33}{\mathcal{E}}_{xx}+c_{33}{\mathcal{H}}_{xx},\hfill \\ B_{xx}={\beta }_{31}({ϵ}_{rr}+{ϵ}_{\vartheta \vartheta })+{\beta }_{33}{ϵ}_{xx}+c_{33}{\mathcal{E}}_{xx}+d_{33}{\mathcal{H}}_{xx},\hfill \end{array}$$

(4)

where $S_{ij}$, ${\eta }_{ij}$, $b_{ij}$, ${\beta }_{ij}$, $d_{ij}$, and $c_{ij}$ stand for the elastic, piezoelectric, dielectric, piezomagnetic, magnetic, and electromagnetic coefficients, respectively. Since ${\sigma }_{rr}=0$, one has ${ϵ}_{rr}=\frac{1}{S_{11}}({\eta }_{31}{\mathcal{E}}_{xx}+{\beta }_{31}{\mathcal{H}}_{xx}-S_{12}{ϵ}_{\vartheta \vartheta }-S_{13}{ϵ}_{xx})$.

The non-zero strains, electric and magnetic fields are expressed as

$$\begin{array}{l}{ϵ}_{\vartheta \vartheta }=\frac{u_r}{r},{ϵ}_{xx}={\partial }_x{u}_x+\frac{1}{2}{\left({\partial }_x{u}_x\right)}^2,\\ {\mathcal{E}}_{xx}=-{\partial }_x\mathrm{\Phi },{\mathcal{H}}_{xx}=-{\partial }_x\mathrm{\Psi },\end{array}$$

(5)

where $\mathrm{\Phi }$ and $\mathrm{\Psi }$ are the electric and magnetic potentials, respectively. Inserting Equations (4) and (5) into Equation (3) results in the equations of motion in terms of $u_x$, $\mathrm{\Phi }$, and $\mathrm{\Psi }$ as

$$\begin{array}{l}{b}_1{\partial }_x^2\mathrm{\Phi }+b_2{\partial }_x^2\mathrm{\Psi }-b_3\nu {\partial }_x^{2}u=-b_4{\partial }_x{ϵ}_{xx}+\frac{1}{2}\nu \rho a^2{\partial }_t^2{\partial }_x^{2}u,\\ c_1{\partial }_x^2\mathrm{\Phi }+c_2{\partial }_x^2\mathrm{\Psi }-b_4\nu {\partial }_x^{2}u=-c_4{\partial }_x{ϵ}_{xx}+\rho {\partial }_t^{2}u,\\ d_1{\partial }_x^2\mathrm{\Phi }+d_2{\partial }_x^2\mathrm{\Psi }+b_1\nu {\partial }_x^{2}u=c_1{\partial }_x{ϵ}_{xx},\\ d_2{\partial }_x^2\mathrm{\Phi }+e_2{\partial }_x^2\mathrm{\Psi }+b_2\nu {\partial }_x^{2}u=c_2{\partial }_x{ϵ}_{xx},\end{array}$$

(6)

where $u=u_x$ and

$$\begin{array}{l}{b}_1=\frac{{\eta }_{31}}{S_{11}}(S_{11}-S_{12}),b_2=\frac{{\beta }_{31}}{S_{11}}(S_{11}-S_{12}),b_3=\frac{1}{S_{11}}(S_{11}^2-S_{12}^2),\\ b_4=\frac{S_{13}}{S_{11}}(S_{11}-S_{12}),c_1={\eta }_{33}-\frac{S_{13}}{S_{11}}{\eta }_{31},c_2={\beta }_{33}-\frac{S_{13}}{S_{11}}{\beta }_{31},\\ c_4=S_{33}-\frac{S_{13}^2}{S_{11}},d_1=b_{33}+\frac{{\eta }_{31}^2}{S_{11}},d_2=c_{33}+\frac{{\eta }_{31}}{S_{11}}{\beta }_{31},\\ e_2=d_{33}+\frac{{\beta }_{31}^2}{S_{11}}.\end{array}$$

(7)

Solving the first, third, and fourth equations of Equation (6) for u, $\mathrm{\Phi }$, and $\mathrm{\Psi }$ and then substituting them into the second equation of Equation (6) leads to the following standard nonlinear wave equation (for more details, see Appendix A):

$${\partial }_t^{2}q-c_0^2{\partial }_x^{2}q=\frac{c_0^2}{2}{\partial }_x^2(q^2+N{\partial }_t^{2}q),$$

(8)

where $q={\partial }_{x}u$ and the coefficient $c_0$ represents the linear longitudinal wave velocity and N stands for the the dispersion coefficient, which are defined in Appendix A. Equation (8) is the nonlinear wave equation with respect to the axial displacement gradient of the PEM rod having lateral dispersion resulting from Poisson’s impact. Note that, if $c_0=0$, there are no waves to propagate. While, if $N=0$, there is no lateral dispersion for the longitudinal waves.

3. Painlevé Analysis

We endeavor to detect the integrability of Equation (8) by following the well-known ARS algorithm. So, we introduce the next definition.

Definition 1

(Painlevé integrability [29]). A nonlinear partial differential equation has a Painlevé property if its solution around a movable singular manifold is single-valued.

The integrability of Equation (8) is checked by performing the ARS algorithm, which is briefly presented in Appendix B, to have a self-contained article. We achieve the singularity analysis for Equation (8) by looking for the dependent variable Laurent series q in the non-characteristic singular manifold neighborhood of $\tau (x,t)$ satisfying ${\tau }_x\ne 0,{\tau }_t\ne 0$ in the form

$$q(x,t)=\tau {(x,t)}^p\sum _{i=0}^{\infty }{q}_i(x,t)\tau {(x,t)}^i,$$

(9)

where $q_0(x,t)\ne 0$ and p is the negative integer that needs to be determined. To investigate the dominant behavior of the solution, we take into account the first term (9), i.e.,

$$q(x,t)=q_0(x,t)\tau {(x,t)}^p.$$

(10)

Inserting the last expression into Equation (8) and balancing the most dominant, we find $p=-2$. To determine $q_0(x,t)$, the coefficient of the leading order term in the Laurent series (9), we insert (9) with $p=-2$ into Equation (8) and, comparing the coefficient of ${\tau }^{-6}$, which is the leading term in the resulting equation, we obtain the leading behavior term coefficient in the form

$$q_0(x,t)=-6N{\tau }_t^2.$$

(11)

The calculation of resonances, which are the powers of f at which free functions can occur in the Laurent series (9), is what we will be doing in the second step. The resonances r are possibly determined by plugging the next expansion

$$q(x,t)=q_0(x,t)\tau {(x,t)}^{-2}+q_r(x,t){\tau }^{r-2},$$

(12)

into Equation (8), and computing the coefficient of $f^{r-6}$, we obtain

$$c_0^{2}N{q}_r(x,t){\tau }_x^2{\varphi }_t^2(r+1)(r-4)(r-5)(r-6)=0.$$

(13)

Hence, $q_r(x,t)$ is an arbitrary function if $r=-1,4,5,6$, which are the required resonances. Note that resonance $r=-1$ is the only acceptable negative resonance that always refers to the singular manifold arbitrariness $\tau (x,t)$.

Finally, we investigate whether there are enough free functions at these resonances without the necessity of movable critical singular manifolds. Thus, the dependent variable q is expanded as

$$q(x,t)=\tau {(x,t)}^{-2}\sum _{i=0}^6{q}_i(x,t)\tau {(x,t)}^i.$$

(14)

By inserting the expression (14) into Equation (8) and computing the coefficients of different powers $\tau (x,t)$, we can prove that the Laurent series (9) does not have a sufficient number of arbitrary functions. This proves that the solution of Equation (8) is not free from movable critical singular manifolds. Hence, Equation (8) fails to possess the Painlevé property and this proves the next theorem.

Theorem 1.

The governing equation of the PEM circular rod does not have a Painlevé property.

4. Bifurcation Analysis

Based on Theorem 1, the non-integrability of the governing equation in a Painlevé sense motivates us to search for particular solutions to Equation (8). One of the most significant particular solutions is the traveling wave solution. The wave solution for Equation (8) is postulated:

$$q(x,t)=\psi \left(\xi \right),\xi =k(x-\omega t),$$

(15)

where $\xi$ is the wave variable, k is the wave number, and $\omega$ is the wave velocity. Equation (8) is transformed into an ordinary differential equation as

$$k^2{\psi }^{\prime \prime \prime \prime }-\frac{2({\omega }^2-c_0^2)}{N{c}_0^2{\omega }^2}{\psi }^{″}+\frac{1}{N{\omega }^2}{\left({\psi }^2\right)}^{″}=0,$$

(16)

where the primes indicate a derivative with respect to $\xi$. Integrating the last equation twice with respect to $\xi$ and ignoring the constants of integration imply

$${\psi }^{″}-2f\psi +3g{\psi }^2=0,$$

(17)

where

$$f=\frac{{\omega }^2-c_0^2}{N{c}_0^2{\omega }^2{k}^2},g=\frac{1}{3N{\omega }^2{k}^2}$$

(18)

are presented for the sake of simplicity. We rewrite Equation (17) as

$${\psi }^{\prime }=y,y^{\prime }=2f\psi -3g{\psi }^2.$$

(19)

System (19) is a conservative system because $\mathrm{div}({\psi }^{\prime },y^{\prime })=0$ and a Hamiltonian because they are considered a Hamilton equation for the Hamiltonian

$$H=\frac{1}{2}{y}^2-f{\psi }^2+g{\psi }^3.$$

(20)

Due to the Hamiltonian H not depending explicitly on $\xi$, which is equivalent to the time in Hamiltonian mechanics, it is itself a first integral or it is sometimes named a conserved quantity [41,42], i.e.,

$$\frac{1}{2}{y}^2-f{\psi }^2+g{\psi }^3=h,$$

(21)

where h is an arbitrary parameter. Thus, the issue of discovering a solution for Equation (8) is equivalent to finding a solution for the equation of motion of a particle in one dimension. This equivalent is beneficial in determining the interval of real solutions. A one-dimension differential form

$$\frac{d\psi }{\sqrt{T_3\left(\psi \right)}}=d\xi ,$$

(22)

is obtained by setting $y={\psi }^{\prime }$ into Equation (21) and splitting the variables, where

$$T_3\left(\psi \right)=2[h+f{\psi }^2-g{\psi }^3].$$

(23)

The integration of both sides of (22) requires the determination of the range of the parameters $h,f,$ and g. There are two different methods to find the required range. They are a complete discriminate system for the polynomial $T_3\left(\psi \right)$ [43] and bifurcation analysis [41]. The most significant of them is bifurcation analysis because it provides a classification of solutions without finding them based on phase orbits, and also enables us to construct all possible wave propagations.

We initiate the calculation of the equilibrium points for the system (19) in order to investigate the phase portrait. These points are obtained by setting ${\psi }^{\prime }=0=y^{\prime }$. Hence, the system (19) has two equilibrium points $O=(0,0),Q=(\frac{2f}{3g},0)$. The classification of them is determined by computing the Jacobian matrix eigenvalues at the equilibrium points for the system (19). These eigenvalues are ${\lambda }_{1,2}=\pm \sqrt{-\det J(x_0,0)}$, where det$J(x_0,0)=-2f+6g{x}_0$ is the determinate of the Jacobi matrix calculated at the equilibrium point $(x_0,0)$. Following [44], the equilibrium point $(x_0,0)$ is either saddle if $\det J(x_0,0)<0$ or center if $\det J(x_0,0)>0$ or $\det J(x_0,0)=0$. In addition, the Poincaré index for the equilibrium point is zero [44]. Thus, we have the following cases:

(a)

If $f>0$, then points O and Q are saddle and centre, respectively. The phase portrait for this case is described in Figure 2a,b for $g>0$ and $g<0$, respectively.

(b)

If $f<0$, point O is centre while Q is a saddle point. The phase portrait for this case is depicted by Figure 3a,b for $g>0$ and $g<0$, respectively.

The phase plane orbits are parameterized by one parameter h, i.e.,

$${\mathcal{C}}_h=\{(\psi ,y)\in {\mathbb{R}}^2:y^2=T_3\left(\psi \right)\}.$$

(24)

Hence, to describe the phase plane orbits, the value of h is computed at the equilibria, i.e.,

$$h_0=H\left(O\right)=0,h_1=H\left(Q\right)=\frac{-4f^3}{27g^2}.$$

(25)

We summarize the description of the phase plane displayed in Figure 2a in the next theorem:

Theorem 2.

For $(f,g)\in {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}$, system (19) owns the following:

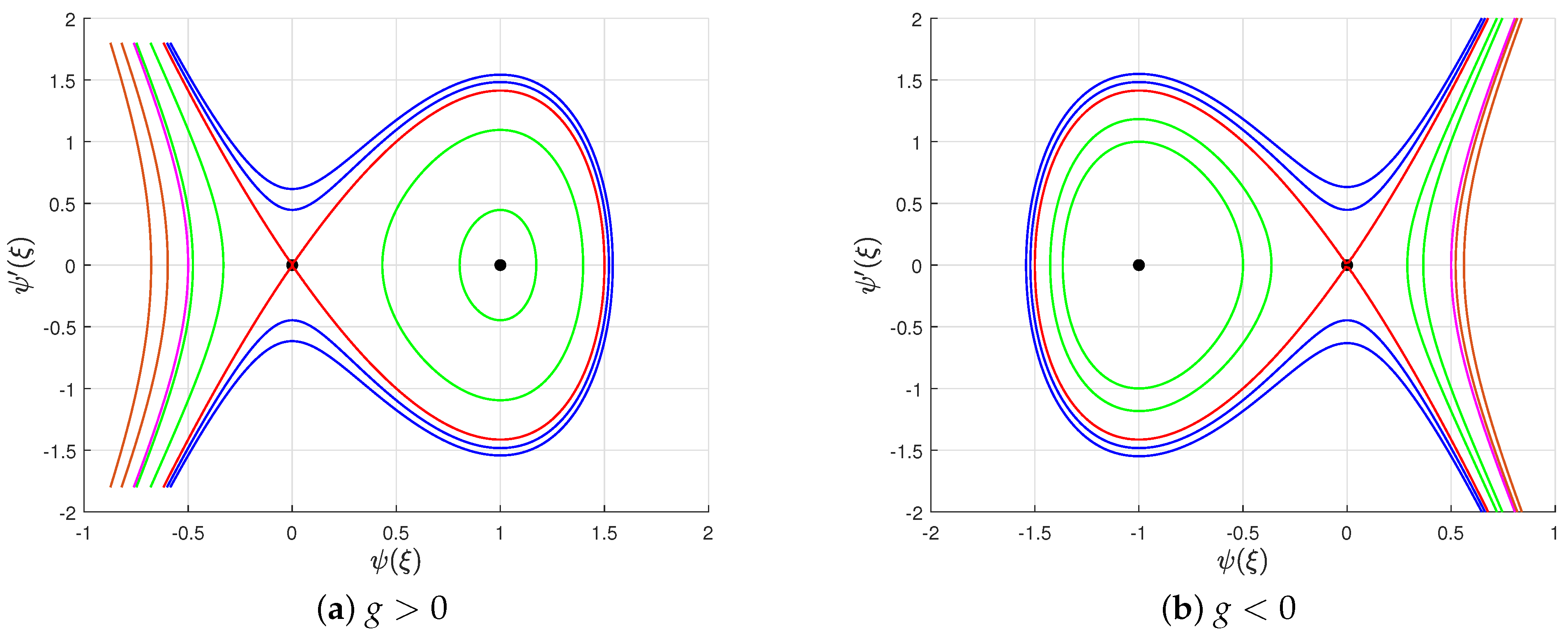
(a) 

Unbounded orbits’ family ${\mathcal{C}}_{\left\{h_1\right\}\cup ]0,\infty [\cup ]-\infty ,h_1[}$ in pink, blue, and brown, respectively.

(b) 

Two green orbits’ families ${\mathcal{C}}_{]h_1,0[}$. One of them is periodic around the center point Q and placed inside the homoclinic orbit ${\mathcal{C}}_{\left\{0\right\}}$ in red, while the other one is unbounded and appears outside the homoclinic orbit in red.

Likewise, the other phase portrait delivered by Figure 2b and Figure 3a,b can be depicted.

Based on the bifurcation analysis, we introduce the next theorem.

Theorem 3.

Let us postulate that Equation (8) has a solution in the form (15). Then, it is one of the following:

(a) 

A periodic solution if $(f,g,h)\in ({\mathbb{R}}^{+}\times {\mathbb{R}}^{+}\times ]h_1,0\left[\right)\cup ({\mathbb{R}}^{+}\times {\mathbb{R}}^{-}\times ]h_1,0\left[\right)\cup ({\mathbb{R}}^{-}{\mathbb{R}}^{+}\times ]0,$$h_1\left[\right)\cup \left(\right]{\mathbb{R}}^{-}\times {\mathbb{R}}^{-}\times ]h_1,0\left[\right).$

(b) 

A solitary solution if $(f,g,h)\in ({\mathbb{R}}^{+}\times {\mathbb{R}}^{+}\times \left\{0\right\})\cup ({\mathbb{R}}^{+}\times {\mathbb{R}}^{-}\times \left\{0\right\})\cup ({\mathbb{R}}^{-}\times {\mathbb{R}}^{+}\times \left\{h_1\right\}\cup ({\mathbb{R}}^{-}\times {\mathbb{R}}^{-}\times \left\{h_1\right\})$.

(c) 

Otherwise, it is unbounded.

It is evident that Theorem 3 supplies the conditions of the presence of periodic solutions and solitary solutions for Equation (8). This is one of the significant benefits of the utilization of bifurcation theory.

5. Solution Construction

Based on the bifurcation constrains on the parameters $f,g,$ and h, as outlined in Theorem 3, we can integrate both sides of Equation (22) along possible intervals of real wave propagation. In other words, for fixed values of the two parameters $f,g$ and distinct values of the parameters h, the solutions will be found.

 Case I:

For $f>0,g>0$, we consider the next different values of h:

• When $h\in ]h_1,0[$, there are two orbit families in green for the system (19). A single orbit of this family intersects the $\psi -$ axis at three points. Hence, the polynomial $T_3\left(\psi \right)$ has three real roots, namely, ${\psi }_i,i=1,2,3$ with ${\psi }_1<{\psi }_2<{\psi }_3$, i.e., it takes the form $T_3\left(\psi \right)=2g({\psi }_1-\psi )(\psi -{\psi }_2)(\psi -{\psi }_3)$. The interval of real wave propagation is $\psi \in ]-\infty ,{\psi }_1[\cup ]{\psi }_2,{\psi }_3[$. Assuming $\psi \left(0\right)={\psi }_3$, the integration of both sides of Equation (22) gives

  $$\begin{array}{l}q(x,t)={\psi }_3-({\psi }_3-{\psi }_2){\mathrm{sn}}^2\left(\sqrt{\frac{g({\psi }_3-{\psi }_1)}{2}}\xi ,\sqrt{\frac{{\psi }_3-{\psi }_2}{{\psi }_3-{\psi }_1}}\right),\\ 0<\xi <\sqrt{\frac{2}{g({\psi }_3-{\psi }_1)}}K\left(\sqrt{\frac{{\psi }_3-{\psi }_2}{{\psi }_3-{\psi }_1}}\right),\end{array}$$

  (26)

  where $K\left(k\right)$ denotes the first type of complete elliptic integrals [45]. This solution is periodic solution with period $\frac{4\sqrt{2}}{\sqrt{g({\psi }_3-{\psi }_1)}}K\left(\sqrt{\frac{{\psi }_3-{\psi }_2}{{\psi }_3-{\psi }_1}}\right)$. From another side, if we consider $\psi \in ]-\infty ,{\psi }_1[$, we assume $\psi \left(0\right)={\psi }_1$, and consequently, the integration of both sides produces the solution

  $$\begin{array}{l}q(x,t)={\psi }_3+({\psi }_1-{\psi }_3){\mathrm{ns}}^2\left(\sqrt{\frac{g({\psi }_3-{\psi }_1)}{2}}\xi ,\sqrt{\frac{{\psi }_3-{\psi }_2}{{\psi }_3-{\psi }_1}}\right),\\ 0<\xi <\sqrt{\frac{2}{g({\psi }_3-{\psi }_1)}}K\left(\sqrt{\frac{{\psi }_3-{\psi }_2}{{\psi }_3-{\psi }_1}}\right).\end{array}$$

  (27)
• When $h=\left\{0\right\}$, the Hamilton system (19) has a homoclinic orbit in red, which connect the saddle point O to itself. Such orbits prove the existence of a solitary wave solution for Equation (8). For this case, the polynomial $T_3\left(\psi \right)$ has one simple root $\psi =\frac{f}{g}$ while the other is double at the origin, i.e., it has the form $T_3\left(\psi \right)=2g{\psi }^2(\frac{f}{g}-\psi )$. The intervals of real propagation are $\psi \in ]-\infty ,0[\cup ]0,\frac{f}{g}[$. There are two possible choices for real wave propagation. First, we assume $\psi \left(0\right)=\frac{f}{g}$, and consequently, the integration of both sides of Equation (22) gives the solution

  $$q(x,t)=\frac{f}{g}{\sec \mathrm{h}}^2\left(\sqrt{\frac{f}{2}}\xi \right),$$

  (28)

  which is the soliton solution for Equation (8).
• When $h\in {\mathbb{R}}^{+}\cup \left\{h_1\right\}\cup ]-\infty ,h_1[$, there are two unbounded orbit families for system (19) in blue and brown in addition to a single orbit in pink. All these orbits cut the $\psi -$ axis at exactly one point. Therefore, the polynomial $T_3\left(\psi \right)$ has one real root and two complex conjugate roots, namely, ${\psi }_4,{\psi }_5,$ and ${\psi }_5^{*}$, where ${}^{*}$ refers to the complex conjugate. Hence, $T_3\left(\psi \right)=2g({\psi }_4-\psi )(\psi -{\psi }_5)(\psi -{\psi }_5^{*})$ and the interval of real wave propagation is $\psi \in ]-\infty ,{\psi }_4[$. We integrate Equation (22) along the interval of real wave propagation and obtain

  $$q(x,t)={\psi }_4+A-\frac{2A}{\mathrm{cn}\left(\sqrt{2gA}\xi ,\sqrt{\frac{A-\mathrm{Re}{\psi }_5+{\psi }_4}{2A}}\right)+1},$$

  (29)

  where $A^2={\mathrm{Im}}^2{\psi }_5+{({\psi }_4-\mathrm{Re}{\psi }_5)}^2$.

 Case II:

For the case $f>0,g<0$, the solution of Equation (8) can be constructed according to the values of the parameter h.

• When $h\in ]h_1,0[$, the polynomial (23) has three real roots, $r_1,r_2,$ and $r_3$, where $r_1<r_2<r_3$. Thus, it reads as $T_3\left(\psi \right)=-2g(\psi -r_1)(\psi -r_2)(\psi -r_3)$. The interval of real wave propagation is $\psi \in ]r_1,r_2[$. Assuming $\psi \left(0\right)=r_1$ and integrating both sides of Equation (22), we obtain

  $$\begin{array}{l}q(x,t)=r_1+(r_2-r_1){\mathrm{sn}}^2\left(\sqrt{\frac{-g}{2}(r_3-r_1)}\xi ,\sqrt{\frac{r_2-r_1}{r_3-r_1}}\right),\\ 0<\xi <\frac{-2}{g(r_3-r_1)}K\left(\sqrt{\frac{r_2-r_1}{r_3-r_1}}\right).\end{array}$$

  (30)
  The periodic solution (30) is new. It has a period $2\sqrt{\frac{2}{-g(r_3-r_1)}}K\left(\sqrt{\frac{r_2-r_1}{r_3-r_1}}\right)$.
• If $h\in \left\{0\right\}$, the polynomial has three real roots: one of them is not simple and the others are simple, i.e., the polynomial (23) reads as $T_3\left(\psi \right)=-2g{\psi }^2(\psi -\frac{f}{g})$. The interval of the real solution is $\psi \in ]\frac{f}{g},0[$. Postulating $\psi \left(0\right)=\frac{f}{g}$, the integration of both sides of Equation (22) implies

  $$q(x,t)=\frac{-f}{g}{sinh}^2\left(\sqrt{\frac{-g}{2}}\xi \right),$$

  (31)

  which is a new solitary wave solution.
• If $h\in \left\{h_1\right\}\cup {\mathbb{R}}^{+}\cup ]-\infty ,h_1[$, the polynomial (23) has one real root $r_4$ and two conjugate complex roots $r_5$ and $r_5^{*}$. Therefore, it is written as $T_3\left(\psi \right)=-2g(\psi -r_4)(\psi -r_5)(\psi -r_5^{*})$. Assuming $\psi \in ]r_4,\infty [$, the integration of both sides of Equation (22) provides

  $$\begin{array}{l}q(x,t)=-B+r_4+\frac{2B}{1+\mathrm{cn}\left(\sqrt{-2Bg}\xi ,\sqrt{\frac{B+Re.r_5-r_4}{2B}}\right)},\\ 0<\xi <\frac{2}{\sqrt{-2gB}}K\left(\sqrt{\frac{B+Re.r_5-r_4}{2B}}\right),\end{array}$$

  (32)

  where $B^2={(Re.r_5-r_4)}^2+I{m}^2{r}_5$. Solution (32) is a new solution for Equation (8).

 Case III:

The two cases in which $f<0,g>0$ and $f<0,g<0$ provide the same solutions as in the two cases I and II but with different values of the roots of the polynomial $T_3\left(\psi \right)$.

It can be demonstrated that the obtained solutions are consistent by studying their degeneracy through the transmission between phase orbits. Let us clarify the following:

(a)

If $h\to 0$, the family of periodic orbits in green will be reduced to the homoclinic orbit in red, as illustrated by Figure 2a. Consequently, the periodic solution corresponding to this family will also degenerate to a solitary solution corresponding to the homoclinic orbit. Thus, we have ${\psi }_1={\psi }_2=0$ and ${\psi }_3=\frac{f}{g}$, and solution (26) becomes

$$q(x,t)=\frac{f}{g}-\frac{f}{g}{tanh}^2\left(\sqrt{\frac{f}{2}}\xi \right)=\frac{f}{g}{\mathrm{sech}}^2\left(\sqrt{\frac{f}{2}}\xi \right),$$

(33)

which is in agreement with solution (28).

(b)

On the other hand, when h tends to zero, the family of unbounded orbits in blue will reduce to the homoclinic orbit, and consequently, solution (29) must be transformed into solution (28). Let us outline that. When $h\to 0$, we find ${\psi }_5={\psi }_5^{*}=0$ and ${\psi }_4=\frac{f}{g}$, and consequently, solution (29) becomes

$$q(x,t)=\frac{2f}{g}\left(1-\frac{1}{cosh\left(\sqrt{2f}\xi \right)+1}\right)=\frac{f}{g}{\mathrm{sech}}^2\left(\sqrt{\frac{f}{g}}\xi \right),$$

(34)

which is identical to solution (28).

6. Results and Discussion

In the current section, various numerical investigations are presented to explain the dynamic behavior of the piezoelectro-magnetic infinite circular rod under various values of wave velocity. It is assumed that the rod is made of the BaTiO${}_3$-CoFe${}_2$O${}_4$, with a radius $a=0.05$ cm [46], Poisson’s ratio $\nu =0.3451$ [46], and density $\rho =5550$ kg/m${}^3$ [46]. The other mechanical and electromagnetic properties are presented in

Table 1. Material properties of the BaTiO${}_3$-CoFe${}_2$O${}_4$ rod [46].

Coefficient	Value	Unit
$S_{11}$	225	GPa
$S_{12}$	125	GPa
$S_{13}$	124	GPa
$S_{33}$	216	GPa
$S_{44}$	44	GPa
${\eta }_{31}$	−2.2	C/m${}^2$
${\eta }_{33}$	9.3	C/m${}^2$
${\beta }_{31}$	290.2	N A/m
${\beta }_{33}$	350	N A/m
$b_{11}$	5.64	${10}^{-9}$C${}^2$ N/m${}^2$
$b_{33}$	6.35	${10}^{-9}$C${}^2$ N/m${}^2$
$c_{11}$	0	${10}^{-12}$ N s/(V C)
$c_{33}$	0	${10}^{-12}$ N s/(V C)
$d_{11}$	2.97	${10}^{-4}$ Ns${}^2$/C${}^2$
$d_{33}$	0.835	${10}^{-4}$ Ns${}^2$/C${}^2$

. We find that $c_0=5144.679524$ and $N=1.124780021\times {10}^{-11}$. Assuming the wave number $k=10$, wave velocity $\omega =1.1c_0=5659.148$, and the radius of the rod is $a=0.05$, we obtain $f=5.829746604$, $g=9.253566030$, and $h_1=-0.3427891010$. Due to $f>0,g>0$, the solution for Equation (8) can be constructed by utilizing case I, and moreover, the solution can be constructed based on the value of the parameter h. Let us clarify that the following applies for some possible values of the parameter h.

• If $h=-0.1713945505\in [-h_1,0]$, Equation (8) has a periodic solution in the form of Equation (26), which has the form

  $$q(x,t)=0.5737306702-0.3637306700{\mathrm{sn}}^2{(103823.4694t-18.34613249x,0.7071067813)}^2.$$

  (35)
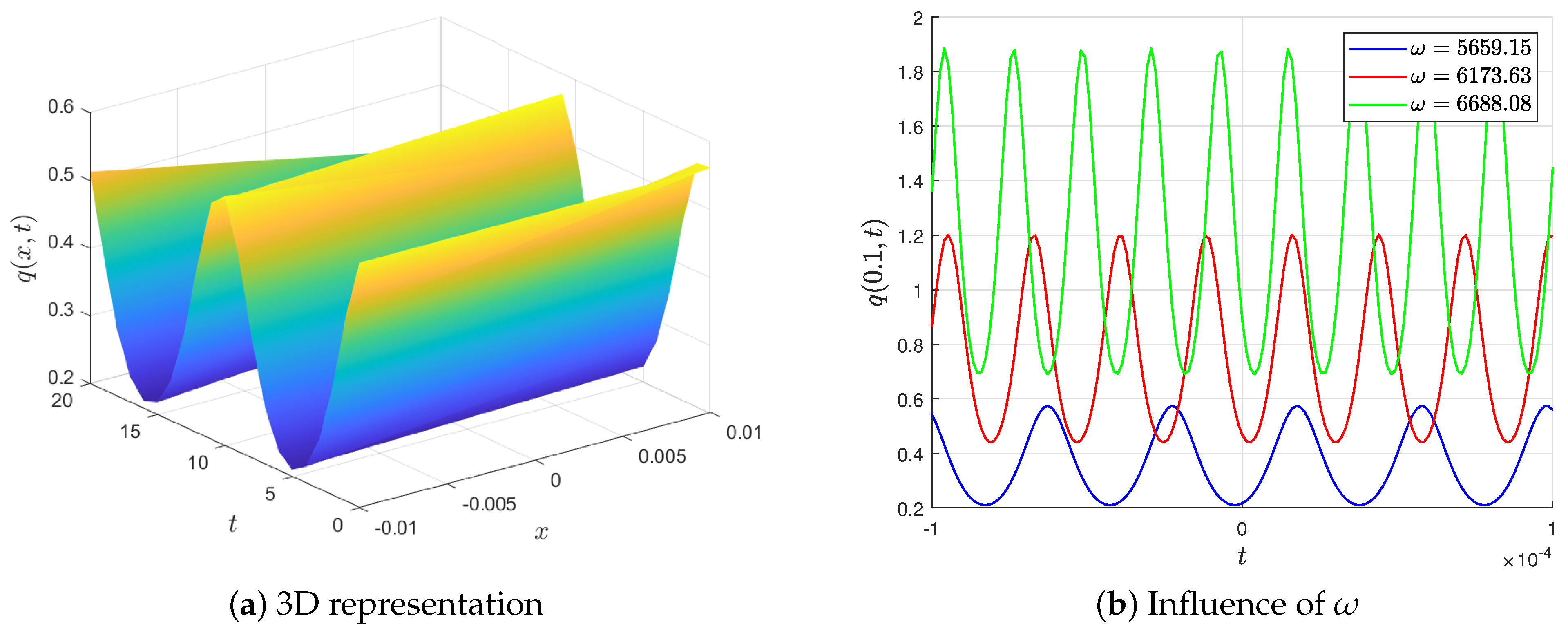
  This solution is clarified by Figure 4a. Now, we study the effect of the wave velocity $\omega$ on the periodic solution (26) by allowing $\omega$ to take distinct values and the other parameters to be unchanged. It is obvious that, as the wave velocity $\omega$ grows, the amplitude of the periodic solution increases and the width of the solution decreases.
• If $h=0$, then the solitary solution (28) for Equation (8) has the form

  $$q(x,t)=1.320000002{\sec \mathrm{h}}^2(139854.8539t-22.65363878x).$$

  (36)
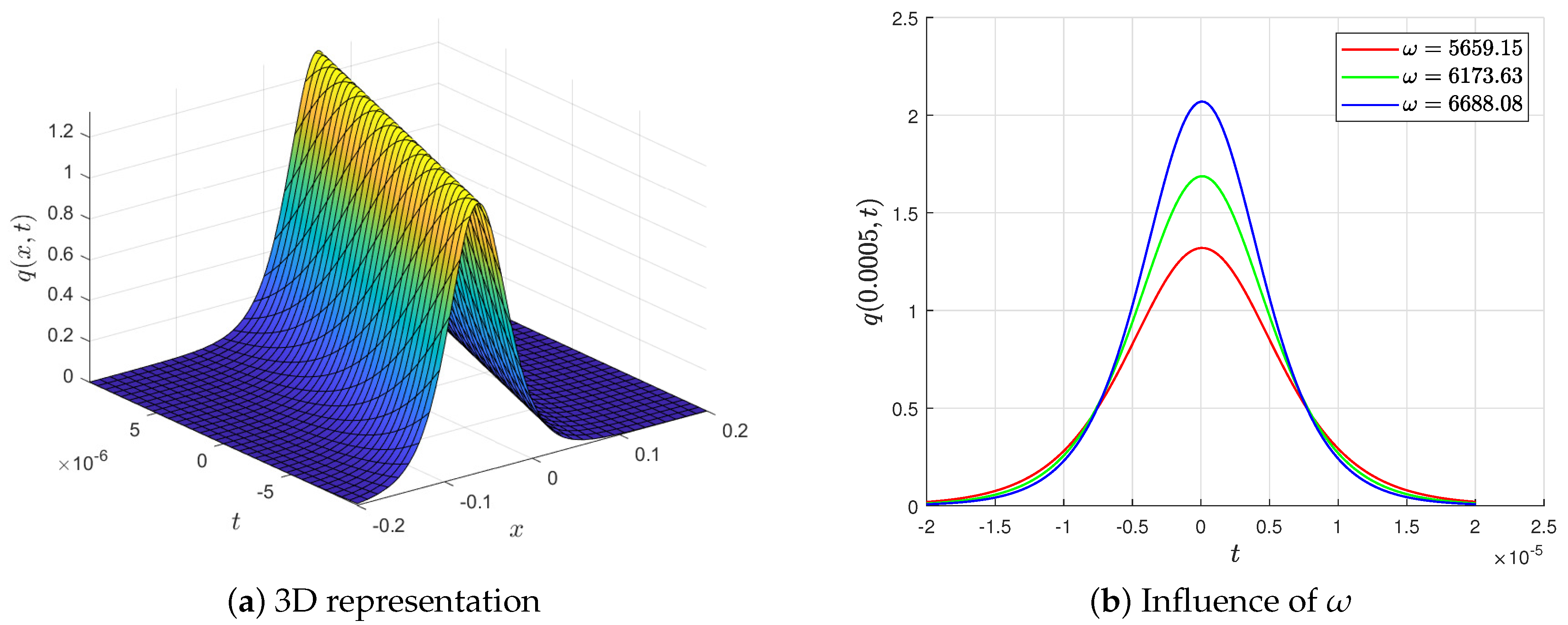
  Figure 5a illustrates the 3D representation of solution (36). Figure 5b outlines the effects of the wave velocity $\omega$ on solution (28) for different values of $\omega$ while the others remain fixed on the plane $x=0.0005$. It is obvious that the curves are symmetric about the line $t=0$. The amplitude of the solution increases as the value of the wave velocity grows.

We also investigate the influence of the other parameters on the obtained solutions but it is very tiny.

7. Conclusions

The current work is interested in studying some qualitative analyses of a motion equation describing the behavior of a piezoelectro-magnetic circular rod. In accordance with the three-dimensional elasticity theory, the motion equation has been established. We have shown the motion equation is non-integrable in a Painlevé sense by using the well-known ARS algorithm. As a result of its non-integrability, the search for semi-analytical solutions or numerical solutions is instructed. Therefore, we seek particular solutions, like traveling wave solutions, which can be used to explain the physical interpretations of the phenomenon. The qualitative theory of planar integrable systems has been applied to study the bifurcation of the solutions based on the material properties of the rod. The employment of the bifurcation theory encloses multiple benefits. Let us elucidate them:

(a)

The bifurcation theory has enabled us to prove Theorem 3, which provided the constraints on the parameters classifying the types of the solutions before constructing them.

(b)

Determining the intervals of real solutions, which are sometimes named the intervals of real wave propagation, is significant because it implies that there are different types of solutions that are completely different from mathematical and physical points of view. For clarification, when $(f,g,h)\in {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}\times ]h_1,0[$, we have two solutions (26) and (29) that are periodic and unbounded. The two solutions are obtained with the same conditions on the parameters $f,g$, and h but with different intervals of real solutions. Hence, the interval of real solutions is significant.

We have introduced some new solutions that have been classified into double periodic solutions and solitary solutions, depending on the phase plane orbit. Taking into account the material constants of the rod, 3D representations of periodic and solitary solutions have been displayed. It is well-known that wave velocity enables us to compute the speed at which a wave travels through a medium. The magnitude of the wave velocity is the distance that the wave travels in a given time. This is of considerable importance for the propagation of information and other demonstrations of wave motion in science and engineering. Therefore, it is significant to study the influence of the wave velocity on the obtained solutions that represent the wave propagation in the rod. As the wave velocity increased while the other parameters were unchanged, it has been noticed on the plane $x=0.1$ that the amplitude and the width of the periodic solution increased and decreased, respectively. That is to say, the waves with a bigger amplitude would have a narrower width due to the dispersion feature in the nonlinear waves. Also, the amplitude of the solitary solution on the plane $x=0.0005$ decreased with the growing wave velocity. The effects of the other parameters on the solutions are very tiny so can be ignored.