Modified Block Bootstrap Testing for Persistence Change in Infinite Variance Observations
Abstract
:1. Introduction
2. Materials and Methods
3. Results
4. Block Bootstrap Approximation
5. Numerical Results
5.1. Properties of the Tests under the H1, H0, and Near-Unit Root
5.2. Properties of the Tests under the H10 and H01
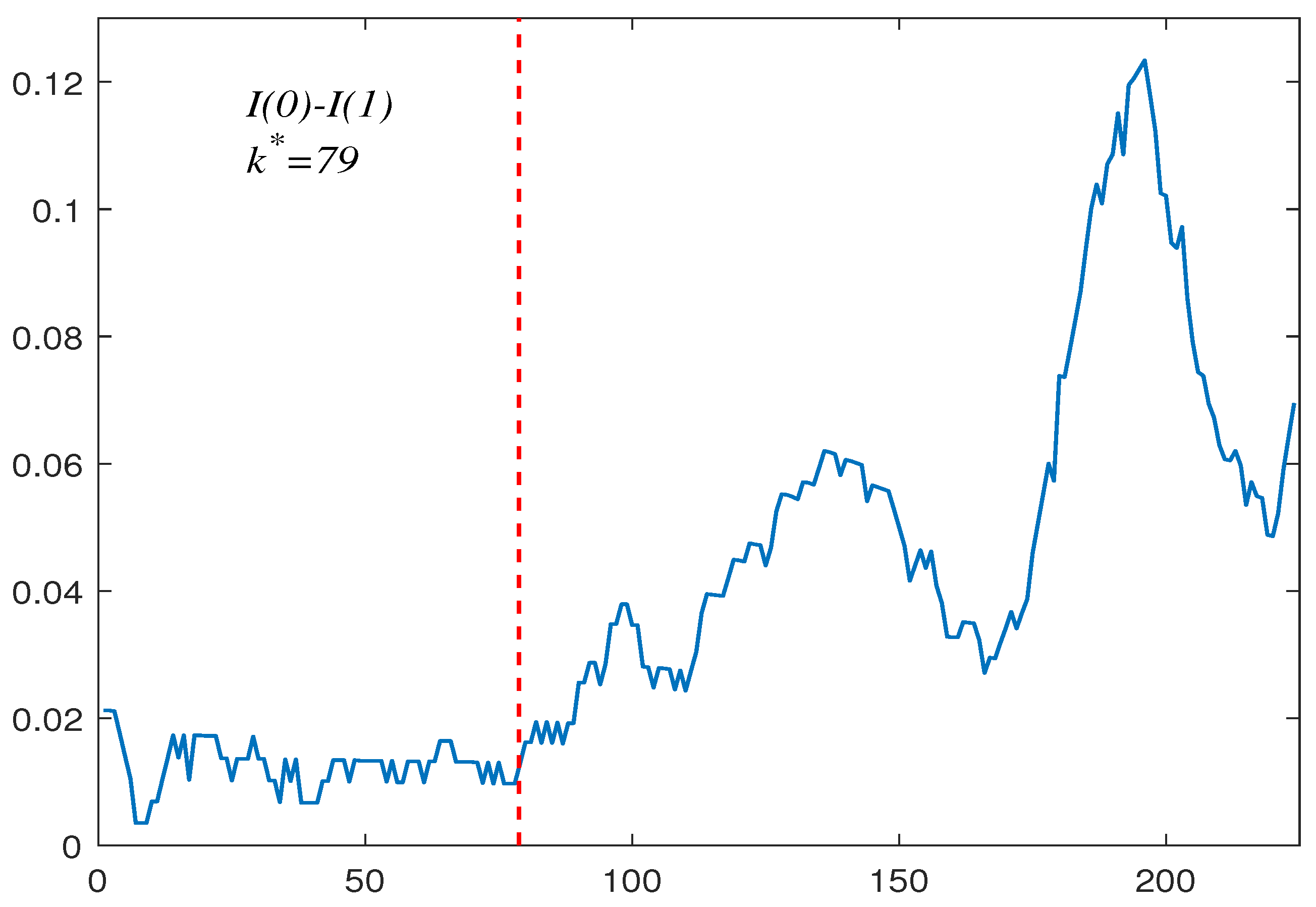
6. Empirical Applications
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Busetti, F.; Taylor, A.R. Tests of stationarity against a change in persistence. J. Econom. 2004, 123, 33–66. [Google Scholar] [CrossRef]
- Chen, W.; Huang, Z.; Yi, Y. Is there a structural change in the persistence of wti–brent oil price spreads in the post-2010 period? Econ. Model. 2015, 50, 64–71. [Google Scholar] [CrossRef]
- Belaire-Franch, J. A note on the evidence of inflation persistence around the world. Empir. Econ. 2019, 56, 1477–1487. [Google Scholar] [CrossRef]
- Sibbertsen, P.; Willert, J. Testing for a break in persistence under long-range dependencies and mean shifts. Stat. Pap. 2012, 53, 357–370. [Google Scholar] [CrossRef]
- Kim, J.Y. Detection of change in persistence of a linear time series. J. Econom. 2000, 95, 97–116. [Google Scholar] [CrossRef]
- Leybourne, S.; Kim, T.H.; Taylor, A.R. Detecting multiple changes in persistence. Stud. Nonlinear Dyn. Econom. 2007, 11. [Google Scholar] [CrossRef]
- Leybourne, S.; Taylor, R.; Kim, T.H. Cusum of squares-based tests for a change in persistence. J. Time Ser. Anal. 2007, 28, 408–433. [Google Scholar] [CrossRef]
- Cerqueti, R.; Costantini, M.; Gutierrez, L.; Westerlund, J. Panel stationary tests against changes in persistence. Stat. Pap. 2019, 60, 1079–1100. [Google Scholar] [CrossRef]
- Kejriwal, M. A robust sequential procedure for estimating the number of structural changes in persistence. Oxf. Bull. Econ. Stat. 2020, 82, 669–685. [Google Scholar] [CrossRef]
- Hao, J.; Si, Z. Spurious regression between long memory series due to mis-specified structural break. Commun.-Stat.-Simul. Comput. 2018, 47, 692–711. [Google Scholar]
- Hao, J.; Si, Z.; Jinsuo, Z. Modified tests for change point in variance in the possible presence of mean breaks. J. Stat. Comput. Simul. 2018, 88, 2651–2667. [Google Scholar]
- Wingert, S.; Mboya, M.P.; Sibbertsen, P. Distinguishing between breaks in the mean and breaks in persistence under long memory. Econ. Lett. 2020, 193, 1093338. [Google Scholar] [CrossRef]
- Grote, C. Issues in Nonlinear Cointegration, Structural Breaks and Changes in Persistence. Ph.D. Thesis, Leibniz Universität Hannover, Hannover, Germany, 2020. [Google Scholar]
- Mittnik, S.; Rachev, S.; Paolella, M. Stable paretian modeling in finance: Some empirical and theoretical aspects. In A Practical Guide to Heavy Tails; Birkhäuser: Boston, MA, USA, 1998; pp. 79–110. [Google Scholar]
- Han, S.; Tian, Z. Bootstrap testing for changes in persistence with heavy-tailed innovations. Commun. Stat. Theory Methods 2007, 36, 2289–2299. [Google Scholar] [CrossRef]
- Qin, R.; Liu, Y. Block bootstrap testing for changes in persistence with heavy-tailed innovations. Commun. Stat. Theory Methods 2018, 47, 1104–1116. [Google Scholar] [CrossRef]
- Chen, Z.; Tian, Z.; Zhao, C. Monitoring persistence change in infinite variance observations. J. Korean Stat. Soc. 2012, 41, 61–73. [Google Scholar] [CrossRef]
- Yang, Y.; Jin, H. Ratio tests for persistence change with heavy tailed observations. J. Netw. 2014, 9, 1409. [Google Scholar] [CrossRef]
- Hao, J.; Si, Z.; Jinsuo, Z. Spurious regression due to the neglected of non-stationary volatility. Comput. Stat. 2017, 32, 1065–1081. [Google Scholar]
- Hao, J.; Jinsuo, Z.; Si, Z. The spurious regression of AR(p) infinite variance series in presence of structural break. Comput. Stat. Data Anal. 2013, 67, 25–40. [Google Scholar]
- Wang, D. Monitoring persistence change in heavy-tailed observations. Symmetry 2021, 13, 936. [Google Scholar] [CrossRef]
- Chan, N.H.; Zhang, R.M. Inference for nearly nonstationary processes under strong dependence with infinite variance. Stat. Sin. 2009, 19, 925–947. [Google Scholar]
- Cheng, Y.; Hui, Y.; McAleer, M.; Wong, W.K. Spurious relationships for nearly non-stationary series. J. Risk Financ. Manag. 2021, 14, 366. [Google Scholar] [CrossRef]
- Paparoditis, E.; Politis, D.N. Residual-based block bootstrap for unit root testing. Econometrica 2003, 71, 813–855. [Google Scholar] [CrossRef]
- Chan, N.H.; Wei, C.Z. Asymptotic inference for nearly nonstationary AR(1) processes. Ann. Stat. 1987, 15, 1050–1063. [Google Scholar] [CrossRef]
- Leybourne, S.J.; Kim, T.H.; Robert Taylor, A. Regression-based tests for a change in persistence. Oxf. Bull. Econ. Stat. 2006, 68, 595–621. [Google Scholar] [CrossRef]
- Phillips, P.C.; Solo, V. Asymptotics for linear processes. Ann. Stat. 1992, 20, 971–1001. [Google Scholar] [CrossRef]
- Ibragimov, I.A. Some limit theorems for stationary processes. Theory Probab. Appl. 1962, 7, 349–382. [Google Scholar] [CrossRef]
- Resnick, S.I. Point processes, regular variation and weak convergence. Adv. Appl. Probab. 1986, 18, 66–138. [Google Scholar] [CrossRef]
- Chan, N.H. Inference for near-integrated time series with infinite variance. J. Am. Assoc. 1990, 85, 1069–1074. [Google Scholar] [CrossRef]
- Mandelbrot, B. The variation of some other speculative prices. J. Bus. 1967, 40, 393–413. [Google Scholar] [CrossRef]
- Arcones, M.A.; Giné, E. The bootstrap of the mean with arbitrary bootstrap sample size. Ann. IHP Probab. Stat. 1989, 25, 457–481. [Google Scholar]
- Chen, Z.; Jin, Z.; Tian, Z.; Qi, P. Bootstrap testing multiple changes in persistence for a heavy-tailed sequence. Comput. Stat. Data Anal. 2012, 56, 2303–2316. [Google Scholar] [CrossRef]
- John, P.N. Numerical calculation of stable densities and distribution functions. Commun. Stat. Stoch. Model. 1997, 13, 759–774. [Google Scholar]
- Cherstvy, A.G.; Vinod, D.; Aghion, E.; Chechkin, A.V.; Metzler, R. Time averaging, ageing and delay analysis of financial time series. New J. Phys. 2017, 19, 063045. [Google Scholar] [CrossRef]
- Yu, Z.; Gao, H.; Cong, X.; Wu, N.; Song, H.H. A Survey on Cyber-Physical Systems Security. IEEE Internet Things J. 2023, 10, 21670–21686. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Knight, K. Limit theory for autoregressive-parameter estimates in an infinite-variance random walk. Can. J. Stat. 1989, 17, 261–278. [Google Scholar] [CrossRef]
- Amemiya, T. Regression analysis when the dependent variable is truncated normal. Econom. Econom. Soc. 1973, 41, 997–1016. [Google Scholar] [CrossRef]

| Q | Q | Q | Q | Q | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) Empirical Size | 0.0543 | 0.0480 | 0.0433 | 0.0503 | 0.0527 | 0.0487 | 0.0513 | 0.0443 | 0.0527 | 0.0437 | |
| (b) Power Values | |||||||||||
| 0.9517 | 0.7413 | 0.8653 | 0.5717 | 0.7507 | 0.4043 | 0.5907 | 0.2933 | 0.3923 | 0.0010 | ||
| 0.9170 | 0.6690 | 0.8133 | 0.5147 | 0.6943 | 0.3633 | 0.5307 | 0.2280 | 0.3637 | 0.0003 | ||
| 0.8247 | 0.5273 | 0.7170 | 0.3927 | 0.6003 | 0.2660 | 0.4480 | 0.1757 | 0.3060 | 0.0003 | ||
| 0.9977 | 0.9170 | 0.9750 | 0.7977 | 0.9167 | 0.6570 | 0.7843 | 0.4387 | 0.4957 | 0.0023 | ||
| 0.9910 | 0.8730 | 0.9567 | 0.7420 | 0.8727 | 0.5667 | 0.7177 | 0.3923 | 0.4270 | 0.0017 | ||
| 0.9400 | 0.7410 | 0.8860 | 0.5900 | 0.7777 | 0.4397 | 0.6160 | 0.3083 | 0.3763 | 0.0010 | ||
| 0.9973 | 0.9273 | 0.9860 | 0.8250 | 0.9597 | 0.6723 | 0.8603 | 0.4833 | 0.5407 | 0.0153 | ||
| 0.9860 | 0.8557 | 0.9707 | 0.7413 | 0.9127 | 0.5777 | 0.7793 | 0.4103 | 0.4667 | 0.0090 | ||
| 0.9280 | 0.6757 | 0.8793 | 0.5823 | 0.8027 | 0.4430 | 0.6443 | 0.2957 | 0.4057 | 0.0023 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 0.0043 | 0 | 0.0140 | 0 | 0.0310 | 0.0003 |
| 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0010 | 0.0013 | 0.0013 | 0.0047 | |
| 0.9 | 0.0050 | 0 | 0.0047 | 0 | 0.0063 | 0.0037 | 0.0093 | 0.0050 | 0.0057 | 0.0167 | |
| 1.0 | 0.0543 | 0.0473 | 0.0433 | 0.0530 | 0.0527 | 0.0443 | 0.0513 | 0.0480 | 0.0527 | 0.0473 | |
| 0.6 | 0 | 0 | 0 | 0 | 0 | 0.0017 | 0 | 0.0080 | 0.0007 | 0.0593 | 0 |
| 0.5 | 0 | 0 | 0.0040 | 0 | 0.0603 | 0 | 0.2043 | 0.0010 | 0.5140 | 0.0007 | |
| 0.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0023 | 0.0020 | 0.0100 | 0.0083 | |
| 1.0 | 0.0507 | 0.0263 | 0.0443 | 0.0180 | 0.0423 | 0.0227 | 0.0503 | 0.0467 | 0.0527 | 0.0403 | |
| −0.6 | 0 | 0 | 0 | 0 | 0 | 0.0053 | 0 | 0.0237 | 0.0003 | 0.0493 | 0.0017 |
| 0.5 | 0 | 0 | 0.0043 | 0 | 0.0287 | 0 | 0.0467 | 0 | 0.0040 | 0.0030 | |
| 0.9 | 0.0170 | 0 | 0.0147 | 0 | 0.0163 | 0.0003 | 0.0150 | 0.0020 | 0.0177 | 0.0083 | |
| 1.0 | 0.0540 | 0.0517 | 0.0550 | 0.0537 | 0.0527 | 0.0240 | 0.0570 | 0.0277 | 0.0450 | 0.0440 | |
| 0 | 1 | 0.0787 | 0.0367 | 0.0647 | 0.0343 | 0.0710 | 0.0430 | 0.0550 | 0.0487 | 0.0387 | 0.0463 |
| 3 | 0.0967 | 0.0153 | 0.0777 | 0.0160 | 0.0697 | 0.0297 | 0.0553 | 0.0303 | 0.0273 | 0.0320 | |
| 5 | 0.0983 | 0.0077 | 0.0727 | 0.0067 | 0.0592 | 0.0190 | 0.0380 | 0.0213 | 0.0237 | 0.0327 | |
| 0.6 | 1 | 0.0607 | 0.0053 | 0.0467 | 0.0050 | 0.0510 | 0.0133 | 0.0547 | 0.0157 | 0.0637 | 0.0287 |
| 3 | 0.0803 | 0.0003 | 0.0503 | 0.0007 | 0.0457 | 0.0033 | 0.0487 | 0.0097 | 0.0540 | 0.0203 | |
| 5 | 0.0480 | 0 | 0.0280 | 0 | 0.0313 | 0.0013 | 0.0373 | 0.0067 | 0.0417 | 0.0240 | |
| −0.6 | 1 | 0.0747 | 0.0293 | 0.0943 | 0.0330 | 0.0853 | 0.0163 | 0.0710 | 0.0233 | 0.0537 | 0.0353 |
| 3 | 0.1193 | 0.0137 | 0.1263 | 0.0210 | 0.0900 | 0.0077 | 0.0853 | 0.0167 | 0.0567 | 0.0250 | |
| 5 | 0.1203 | 0.0093 | 0.1127 | 0.0113 | 0.0907 | 0.0040 | 0.0870 | 0.0107 | 0.0433 | 0.0223 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0.0030 | 0 | 0.0107 | 0.0003 | 0.0273 | 0.0007 |
| 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0003 | 0.0003 | 0.0037 | |
| 0.9 | 0 | 0 | 0.0013 | 0 | 0.0043 | 0.0007 | 0.0073 | 0.0033 | 0.0033 | 0.0110 | |
| 1.0 | 0.0557 | 0.0470 | 0.0463 | 0.0587 | 0.0407 | 0.0583 | 0.0497 | 0.0453 | 0.0457 | 0.0507 | |
| 0.6 | 0 | 0 | 0 | 0 | 0 | 0.0017 | 0 | 0.0080 | 0 | 0.0480 | 0.0003 |
| 0.5 | 0 | 0 | 0.0063 | 0 | 0.0760 | 0 | 0.2173 | 0 | 0.5233 | 0.0003 | |
| 0.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0007 | 0.0003 | 0.0050 | 0.0070 | |
| 1.0 | 0.0537 | 0.0370 | 0.0473 | 0.0277 | 0.0413 | 0.0323 | 0.0560 | 0.0470 | 0.0517 | 0.0490 | |
| −0.6 | 0 | 0 | 0 | 0 | 0 | 0.0040 | 0 | 0.0113 | 0.0007 | 0.0307 | 0.0010 |
| 0.5 | 0 | 0 | 0.0060 | 0 | 0.0243 | 0 | 0.0580 | 0 | 0.0030 | 0.0020 | |
| 0.9 | 0.0010 | 0 | 0.0047 | 0 | 0.0083 | 0.0003 | 0.0113 | 0.0017 | 0.0077 | 0.0090 | |
| 1.0 | 0.0553 | 0.0517 | 0.0563 | 0.0433 | 0.0537 | 0.0453 | 0.0560 | 0.0270 | 0.0447 | 0.0473 | |
| 0 | 1 | 0.0820 | 0.0323 | 0.0647 | 0.0353 | 0.0593 | 0.0507 | 0.0527 | 0.0380 | 0.0347 | 0.0493 |
| 3 | 0.0987 | 0.0143 | 0.0823 | 0.0157 | 0.0690 | 0.0267 | 0.0507 | 0.0310 | 0.0350 | 0.0470 | |
| 5 | 0.1053 | 0.0077 | 0.0763 | 0.0057 | 0.0720 | 0.0157 | 0.0413 | 0.0220 | 0.0190 | 0.0340 | |
| 0.6 | 1 | 0.0733 | 0.0180 | 0.0550 | 0.0077 | 0.0503 | 0.0117 | 0.0597 | 0.0193 | 0.0570 | 0.0313 |
| 3 | 0.0837 | 0.0013 | 0.0550 | 0 | 0.0517 | 0.0030 | 0.0523 | 0.0097 | 0.0593 | 0.0223 | |
| 5 | 0.0670 | 0 | 0.0370 | 0 | 0.0363 | 0.0007 | 0.0490 | 0.0060 | 0.0550 | 0.0183 | |
| −0.6 | 1 | 0.0850 | 0.0370 | 0.0830 | 0.0430 | 0.0737 | 0.0373 | 0.0690 | 0.0200 | 0.0490 | 0.0337 |
| 3 | 0.1187 | 0.0147 | 0.1200 | 0.0227 | 0.1010 | 0.0147 | 0.0943 | 0.0147 | 0.0487 | 0.0290 | |
| 5 | 0.1207 | 0.0070 | 0.1153 | 0.0160 | 0.0890 | 0.0043 | 0.0857 | 0.0117 | 0.0400 | 0.0227 | |
| 0 | 0.3 | 0.3 | 0.9517 | 0 | 0.8653 | 0 | 0.7507 | 0 | 0.6010 | 0 | 0.3923 | 0.0027 |
| 0.5 | 0.9170 | 0 | 0.8133 | 0 | 0.6943 | 0 | 0.5307 | 0.0007 | 0.3637 | 0.0030 | ||
| 0.7 | 0.8247 | 0 | 0.7170 | 0 | 0.6003 | 0 | 0.4480 | 0.0013 | 0.3193 | 0.0073 | ||
| 0.5 | 0.3 | 0.9977 | 0 | 0.9750 | 0 | 0.9167 | 0 | 0.7843 | 0 | 0.4957 | 0.0047 | |
| 0.5 | 0.9910 | 0 | 0.9567 | 0 | 0.8727 | 0 | 0.7177 | 0.0007 | 0.4390 | 0.0067 | ||
| 0.7 | 0.9400 | 0 | 0.8860 | 0 | 0.7827 | 0 | 0.6160 | 0.0017 | 0.3817 | 0.0087 | ||
| 0.7 | 0.3 | 0.9973 | 0 | 0.9907 | 0 | 0.9597 | 0 | 0.8603 | 0 | 0.5557 | 0.0080 | |
| 0.5 | 0.9860 | 0 | 0.9707 | 0 | 0.9127 | 0 | 0.7793 | 0.0007 | 0.4820 | 0.0083 | ||
| 0.7 | 0.9280 | 0 | 0.8793 | 0 | 0.8060 | 0.0003 | 0.6443 | 0.0030 | 0.4097 | 0.0107 | ||
| 0.6 | 0.3 | 0.3 | 0.5710 | 0 | 0.4923 | 0 | 0.4953 | 0 | 0.5487 | 0 | 0.6380 | 0.0023 |
| 0.5 | 0.5637 | 0 | 0.4947 | 0 | 0.5323 | 0 | 0.6337 | 0.0007 | 0.7150 | 0.0013 | ||
| 0.7 | 0.5437 | 0 | 0.4483 | 0 | 0.4503 | 0 | 0.5470 | 0.0003 | 0.6643 | 0.0020 | ||
| 0.5 | 0.3 | 0.8507 | 0 | 0.7693 | 0 | 0.7457 | 0 | 0.7347 | 0.0003 | 0.6463 | 0.0047 | |
| 0.5 | 0.8287 | 0 | 0.7290 | 0 | 0.7353 | 0 | 0.7497 | 0.0007 | 0.7000 | 0.0063 | ||
| 0.7 | 0.7520 | 0 | 0.6437 | 0 | 0.6317 | 0 | 0.6423 | 0.0020 | 0.6340 | 0.0063 | ||
| 0.7 | 0.3 | 0.8663 | 0 | 0.8067 | 0 | 0.7600 | 0 | 0.7430 | 0.0003 | 0.6177 | 0.0067 | |
| 0.5 | 0.8227 | 0 | 0.7207 | 0 | 0.6887 | 0 | 0.6617 | 0.0017 | 0.5940 | 0.0067 | ||
| 0.7 | 0.7303 | 0 | 0.6343 | 0 | 0.5740 | 0 | 0.5537 | 0.0020 | 0.5067 | 0.0137 | ||
| −0.6 | 0.3 | 0.3 | 0.9867 | 0 | 0.9420 | 0 | 0.8710 | 0 | 0.7827 | 0 | 0.6127 | 0.0023 |
| 0.5 | 0.9593 | 0 | 0.9067 | 0 | 0.8173 | 0 | 0.6867 | 0 | 0.4093 | 0.0017 | ||
| 0.7 | 0.8883 | 0 | 0.8100 | 0 | 0.6680 | 0 | 0.5193 | 0 | 0.3640 | 0.0043 | ||
| 0.5 | 0.3 | 0.9993 | 0 | 0.9903 | 0 | 0.9557 | 0 | 0.8803 | 0 | 0.6103 | 0.0040 | |
| 0.5 | 0.9963 | 0 | 0.9793 | 0 | 0.9043 | 0 | 0.7607 | 0 | 0.4693 | 0.0033 | ||
| 0.7 | 0.9677 | 0 | 0.9170 | 0 | 0.7907 | 0 | 0.6303 | 0.0007 | 0.3990 | 0.0047 | ||
| 0.7 | 0.3 | 0.9993 | 0 | 0.9940 | 0 | 0.9633 | 0 | 0.8703 | 0 | 0.5747 | 0.0033 | |
| 0.5 | 0.9957 | 0 | 0.9813 | 0 | 0.8983 | 0 | 0.7483 | 0 | 0.4750 | 0.0050 | ||
| 0.7 | 0.9573 | 0 | 0.9247 | 0 | 0.7837 | 0 | 0.6143 | 0.0007 | 0.3913 | 0.0080 | ||
| 0 | 0.3 | 0.3 | 0.9920 | 0 | 0.9217 | 0 | 0.8327 | 0 | 0.6577 | 0 | 0.4313 | 0.0017 |
| 0.5 | 0.9803 | 0 | 0.9073 | 0 | 0.7797 | 0 | 0.6040 | 0 | 0.3983 | 0.0030 | ||
| 0.7 | 0.9357 | 0 | 0.8263 | 0 | 0.7060 | 0 | 0.5520 | 0.0007 | 0.3457 | 0.0047 | ||
| 0.5 | 0.3 | 1 | 0 | 0.9870 | 0 | 0.9563 | 0 | 0.8573 | 0 | 0.5637 | 0.0030 | |
| 0.5 | 0.9990 | 0 | 0.9823 | 0 | 0.9237 | 0 | 0.7860 | 0.0007 | 0.4890 | 0.0067 | ||
| 0.7 | 0.9907 | 0 | 0.9570 | 0 | 0.8720 | 0 | 0.6993 | 0.0010 | 0.4280 | 0.0063 | ||
| 0.7 | 0.3 | 1 | 0 | 0.9990 | 0 | 0.9797 | 0 | 0.9230 | 0 | 0.6180 | 0.0023 | |
| 0.5 | 1 | 0 | 0.9927 | 0 | 0.9537 | 0 | 0.8567 | 0 | 0.5393 | 0.0060 | ||
| 0.7 | 0.9877 | 0 | 0.9633 | 0 | 0.8980 | 0.0007 | 0.7550 | 0.0007 | 0.4627 | 0.0107 | ||
| 0.6 | 0.3 | 0.3 | 0.7213 | 0 | 0.6367 | 0 | 0.5947 | 0 | 0.6173 | 0 | 0.6917 | 0.0020 |
| 0.5 | 0.7253 | 0 | 0.6310 | 0 | 0.6350 | 0 | 0.7010 | 0 | 0.7487 | 0.0017 | ||
| 0.7 | 0.6963 | 0 | 0.5963 | 0 | 0.5887 | 0 | 0.6267 | 0 | 0.7187 | 0.0030 | ||
| 0.5 | 0.3 | 0.9427 | 0 | 0.8863 | 0 | 0.8350 | 0 | 0.8013 | 0 | 0.6810 | 0.0053 | |
| 0.5 | 0.9397 | 0 | 0.8593 | 0 | 0.8223 | 0 | 0.8137 | 0 | 0.7363 | 0.0053 | ||
| 0.7 | 0.8967 | 0 | 0.7960 | 0 | 0.7743 | 0 | 0.7053 | 0 | 0.6927 | 0.0043 | ||
| 0.7 | 0.3 | 0.9693 | 0 | 0.9170 | 0 | 0.8490 | 0 | 0.8177 | 0 | 0.6667 | 0.0053 | |
| 0.5 | 0.9393 | 0 | 0.8720 | 0 | 0.8013 | 0 | 0.7557 | 0 | 0.6413 | 0.0060 | ||
| 0.7 | 0.8887 | 0 | 0.7880 | 0 | 0.7027 | 0 | 0.6490 | 0.0003 | 0.5513 | 0.0097 | ||
| −0.6 | 0.3 | 0.3 | 0.9993 | 0 | 0.9820 | 0 | 0.9190 | 0 | 0.8440 | 0 | 0.6530 | 0 |
| 0.5 | 0.9950 | 0 | 0.9597 | 0 | 0.8873 | 0 | 0.7367 | 0 | 0.4600 | 0.0020 | ||
| 0.7 | 0.9583 | 0 | 0.9067 | 0 | 0.7660 | 0 | 0.6250 | 0 | 0.3983 | 0.0037 | ||
| 0.5 | 0.3 | 1 | 0 | 0.9987 | 0 | 0.9793 | 0 | 0.9023 | 0 | 0.6710 | 0.0007 | |
| 0.5 | 1 | 0 | 0.9957 | 0 | 0.9397 | 0 | 0.8127 | 0 | 0.5087 | 0.0037 | ||
| 0.7 | 0.9953 | 0 | 0.9747 | 0 | 0.8743 | 0 | 0.7107 | 0 | 0.4563 | 0.0057 | ||
| 0.7 | 0.3 | 1 | 0 | 0.9987 | 0 | 0.9807 | 0 | 0.9143 | 0 | 0.6290 | 0.0017 | |
| 0.5 | 1 | 0 | 0.9953 | 0 | 0.9337 | 0 | 0.8033 | 0 | 0.5123 | 0.0037 | ||
| 0.7 | 0.9967 | 0 | 0.9720 | 0 | 0.8637 | 0 | 0.7013 | 0 | 0.4497 | 0.0050 | ||
| 0.3 | 0.3 | 0.3352 | 0.0869 | 0.3357 | 0.1005 | 0.3539 | 0.1363 | 0.3910 | 0.1909 | 0.4335 | 0.2344 |
| 0.5 | 0.3698 | 0.1386 | 0.3639 | 0.1390 | 0.3648 | 0.1501 | 0.3904 | 0.1869 | 0.4276 | 0.2272 | |
| 0.7 | 0.4097 | 0.1895 | 0.3996 | 0.1817 | 0.3849 | 0.1731 | 0.3697 | 0.1661 | 0.3608 | 0.1719 | |
| 0.5 | 0.3 | 0.5335 | 0.0841 | 0.5277 | 0.0891 | 0.5263 | 0.1087 | 0.5279 | 0.1350 | 0.5217 | 0.1578 |
| 0.5 | 0.5538 | 0.1093 | 0.5393 | 0.1094 | 0.5378 | 0.1206 | 0.5246 | 0.1377 | 0.5200 | 0.1589 | |
| 0.7 | 0.5708 | 0.1436 | 0.5564 | 0.1441 | 0.5359 | 0.1487 | 0.5115 | 0.1577 | 0.4737 | 0.1765 | |
| 0.7 | 0.3 | 0.7185 | 0.0557 | 0.7103 | 0.0618 | 0.6941 | 0.0973 | 0.6831 | 0.1194 | 0.6498 | 0.1749 |
| 0.5 | 0.7201 | 0.0732 | 0.7102 | 0.0867 | 0.6963 | 0.1071 | 0.6815 | 0.1317 | 0.6533 | 0.1748 | |
| 0.7 | 0.7188 | 0.1059 | 0.7062 | 0.1215 | 0.6937 | 0.1397 | 0.6642 | 0.1736 | 0.6294 | 0.2082 | |
| 0.3 | 0.3 | 0.3332 | 0.0794 | 0.3528 | 0.1086 | 0.3868 | 0.1539 | 0.4450 | 0.2166 | 0.5106 | 0.2814 |
| 0.5 | 0.3462 | 0.1042 | 0.3674 | 0.1345 | 0.3971 | 0.1700 | 0.4511 | 0.2273 | 0.5089 | 0.2844 | |
| 0.7 | 0.3702 | 0.1493 | 0.3882 | 0.1678 | 0.4101 | 0.1901 | 0.4525 | 0.2300 | 0.5051 | 0.2831 | |
| 0.5 | 0.3 | 0.5177 | 0.0898 | 0.5312 | 0.1153 | 0.5605 | 0.1430 | 0.5886 | 0.1805 | 0.6184 | 0.2152 |
| 0.5 | 0.5134 | 0.1134 | 0.5219 | 0.1297 | 0.5473 | 0.1540 | 0.5766 | 0.1843 | 0.5975 | 0.2131 | |
| 0.7 | 0.5055 | 0.1457 | 0.5193 | 0.1534 | 0.5366 | 0.1655 | 0.5643 | 0.1874 | 0.5747 | 0.2126 | |
| 0.7 | 0.3 | 0.7028 | 0.0894 | 0.7088 | 0.1068 | 0.7036 | 0.1358 | 0.7081 | 0.1548 | 0.6871 | 0.1900 |
| 0.5 | 0.6797 | 0.1273 | 0.6876 | 0.1365 | 0.6812 | 0.1595 | 0.6798 | 0.1774 | 0.6594 | 0.2073 | |
| 0.7 | 0.6415 | 0.1773 | 0.6408 | 0.1858 | 0.6407 | 0.1980 | 0.6392 | 0.2078 | 0.6276 | 0.2226 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Jin, H.; Su, M. Modified Block Bootstrap Testing for Persistence Change in Infinite Variance Observations. Mathematics 2024, 12, 258. https://doi.org/10.3390/math12020258
Zhang S, Jin H, Su M. Modified Block Bootstrap Testing for Persistence Change in Infinite Variance Observations. Mathematics. 2024; 12(2):258. https://doi.org/10.3390/math12020258
Chicago/Turabian StyleZhang, Si, Hao Jin, and Menglin Su. 2024. "Modified Block Bootstrap Testing for Persistence Change in Infinite Variance Observations" Mathematics 12, no. 2: 258. https://doi.org/10.3390/math12020258
APA StyleZhang, S., Jin, H., & Su, M. (2024). Modified Block Bootstrap Testing for Persistence Change in Infinite Variance Observations. Mathematics, 12(2), 258. https://doi.org/10.3390/math12020258




