Predicting Critical Path of Labor Dispute Resolution in Legal Domain by Machine Learning Models Based on SHapley Additive exPlanations and Soft Voting Strategy

Abstract

The labor dispute is one of the most common civil disputes. It can be resolved in the order of the following steps, which include mediation in arbitration, arbitration award, first-instance mediation, first-instance judgment, and second-instance judgment. The process can cease at any step when it is successfully resolved. In recent years, due to the increasing rights awareness of employees, the number of labor disputes has been rising annually. However, resolving labor disputes is time-consuming and labor-intensive, which brings a heavy burden to employees and dispute resolution institutions. Using artificial intelligence algorithms to identify and predict the critical path of labor dispute resolution is helpful for saving resources and improving the efficiency of, and reducing the cost of dispute resolution. In this study, a machine learning approach based on Shapley Additive exPlanations (SHAP) and a soft voting strategy is applied to predict the critical path of labor dispute resolution. We name our approach LDMLSV (stands for Labor Dispute Machine Learning based on SHapley additive exPlanations and Voting). This approach employs three machine learning models (Random Forest, Extra Trees, and CatBoost) and then integrates them using a soft voting strategy. Additionally, SHAP is used to explain the model and analyze the feature contribution. Based on the ranking of feature importance obtained from SHAP and an incremental feature selection method, we obtained an optimal feature subset comprising 33 features. The LDMLSV achieves an accuracy of 0.90 on this optimal feature subset. Therefore, the proposed approach is a highly effective method for predicting the critical path of labor dispute resolution.

1. Introduction

With the increasing awareness of labor rights among employees, the number of labor disputes in China has been showing a year-on-year increase [1]. The large volume of labor dispute cases imposes a heavy burden on both employees and dispute resolution institutions. Labor disputes can be resolved through both non-litigation and litigation methods. Specifically, employees can sequentially utilize five methods (mediation in arbitration, arbitration awards, first-instance mediation, first-instance judgments, and second-instance judgments) to resolve disputes until achieving a satisfactory outcome [2]. In practice, however, we do not know which critical path should be taken with the case in advance. Hence, this may take a lot of time and resources and can lead to protracted legal disputes. Predicting the optimal critical path of resolving labor disputes assists employees and dispute resolution institutions in making appropriate decisions. Hence, it may expedite the dispute resolution process, save dispute resolution resources, and reduce dispute-related costs, thereby alleviating the burden on both the dispute resolution institutions and employees.

The introduction of Artificial Intelligence (AI) techniques has brought new opportunities to the legal domain. It can help legal professionals escape from repetitive tasks (e.g., legal judgment prediction [3,4,5], legal question answering [6,7,8], and legal case retrieval [9,10,11]) and then have time to focus on more valuable things. Dispute resolution, being a crucial component of the legal domain, has obtained considerable attention from researchers regarding how artificial intelligence can be utilized to address issues related to disputes, such as predicting dispute occurrences, dispute resolution methods, and dispute resolution outcomes. Chou et al. [12] proposed an integrated method of a Support Vector Machine, Artificial Neural Network, and decision tree C5.0 to predict the occurrence of disputes at the initiation stage of Public–Private Partnership projects, achieving an accuracy of 84.33%. Ayhan et al. [13] used majority voting technology to predict the occurrence of disputes, and the accuracy rate reached 91.11%, which proved the effectiveness of machine learning technology in the early prediction of the occurrence of disputes. Tsurel et al. [14] used XGBoost to predict the outcome of e-commerce disputes, determining whether the buyer or seller would prevail, which can achieve an accuracy of 86%.

In the prediction of dispute resolution methods, there have also been some research studies conducted. Lokanan [15] used a machine learning algorithm to resolve financial fraud disputes, treating disciplinary hearings as a binary classification problem between settlement and contested hearings. They achieved 99% accuracy using the Gradient Boosting classifier for prediction. Chou et al. [16] proposed a hybrid artificial intelligence system that combines fuzzy logic, a fast and messy genetic algorithm, and support vector machines. This system treats project dispute resolution as a five-class classification problem, encompassing mediation, arbitration, litigation, negotiation, and administrative appeals, achieving an accuracy of 77.04%. Ayhan et al. [17] proposed an approach for the resolution of construction project disputes as a six-class classification problem, with input variables encompassing factors influencing dispute resolution. The output variables included six dispute resolution methods: litigation, arbitration, dispute review boards, mediation, senior executive appraisal, and negotiation. They conducted attribute reduction using the Chi-square test and employed an ensemble classifier, achieving an accuracy of 89.44% through ten-fold cross-validation. However, to the best of our knowledge, there is no prediction model for labor dispute resolution methods, and the need for an AI method of predicting labor dispute resolution is becoming increasingly apparent.

In this study, we introduce a prediction model called LDMLSV (stands for Labor Dispute Machine Learning based on SHapley additive exPlanations and Voting). LDMLSV focuses on utilizing machine learning algorithms to predict the critical path of resolving labor disputes. We obtained 1255 legal documents from the court and arbitration committee in the Yuhu district of Xiangtan city of China, which include legal documents of mediation in arbitration, arbitration awards, first-instance mediation, first-instance judgments, and second-instance judgments. The resolution of labor disputes progresses sequentially through mediation in arbitration, arbitration awards, first-instance mediation, first-instance judgments, and second-instance judgments. The process can cease at any step when it is successfully resolved. Consequently, this forms five paths of labor dispute resolutions of lengths 1, 2, 3, 4, and 5. Because each stage cannot be skipped, these five paths can be distinguished by predicting only the last step. Therefore, we can consider the predictive problem of labor dispute resolution paths as a five-class classification problem for predicting the ultimate resolution method. Firstly, we compared the classification performance of 10 machine learning algorithms under multiple sample-balancing methods. Leveraging classifiers with an accuracy greater than 0.85, an ensemble method based on a soft voting strategy was used to predict the critical path for labor dispute resolution. Secondly, we applied a post hoc explanation method called SHapley Additive exPlanations (SHAP) [18,19], and importance scores for all features were computed to reveal the decision logic behind the model. Then, Incremental Feature Selection (IFS) [20] and Jackknife cross-validation were employed to select optimal features. The predictive outcomes of the optimal feature subset were compared with the original dataset on the soft voting classifier.

The main contributions of this work are listed in the following bullet points.

• This work provides a more effective and efficient way to predict the critical path of labor dispute resolution. This prediction helps judges, lawyers, and relevant stakeholders gain a better understanding of possible case development trends, enabling them to make wiser decisions.
• Predicting the critical path of labor dispute resolution aids in seeking effective solutions, significantly reducing both the time and costs associated with legal procedures.
• LDMLSV also aids in better resource allocation within the judicial system. It can assist courts in managing caseloads more effectively, prioritizing cases that might have a greater impact, thereby enhancing judicial efficiency and fairness.
• Overall, the contribution of predicting the critical path to labor dispute resolution lies in providing a tool and method that can facilitate a more efficient and equitable resolution of labor disputes within the judiciary, while optimizing resource utilization.

The organization of this work is as follows: Section 2 introduces the data sources, methods of data preprocessing, model framework, and machine learning interpretation tools. Section 3 presents the results, while Section 4 discusses these findings. Section 5 summarizes the primary discoveries of this work and outlines important directions for future endeavors.

2. Materials and Methods

2.1. Dataset Description

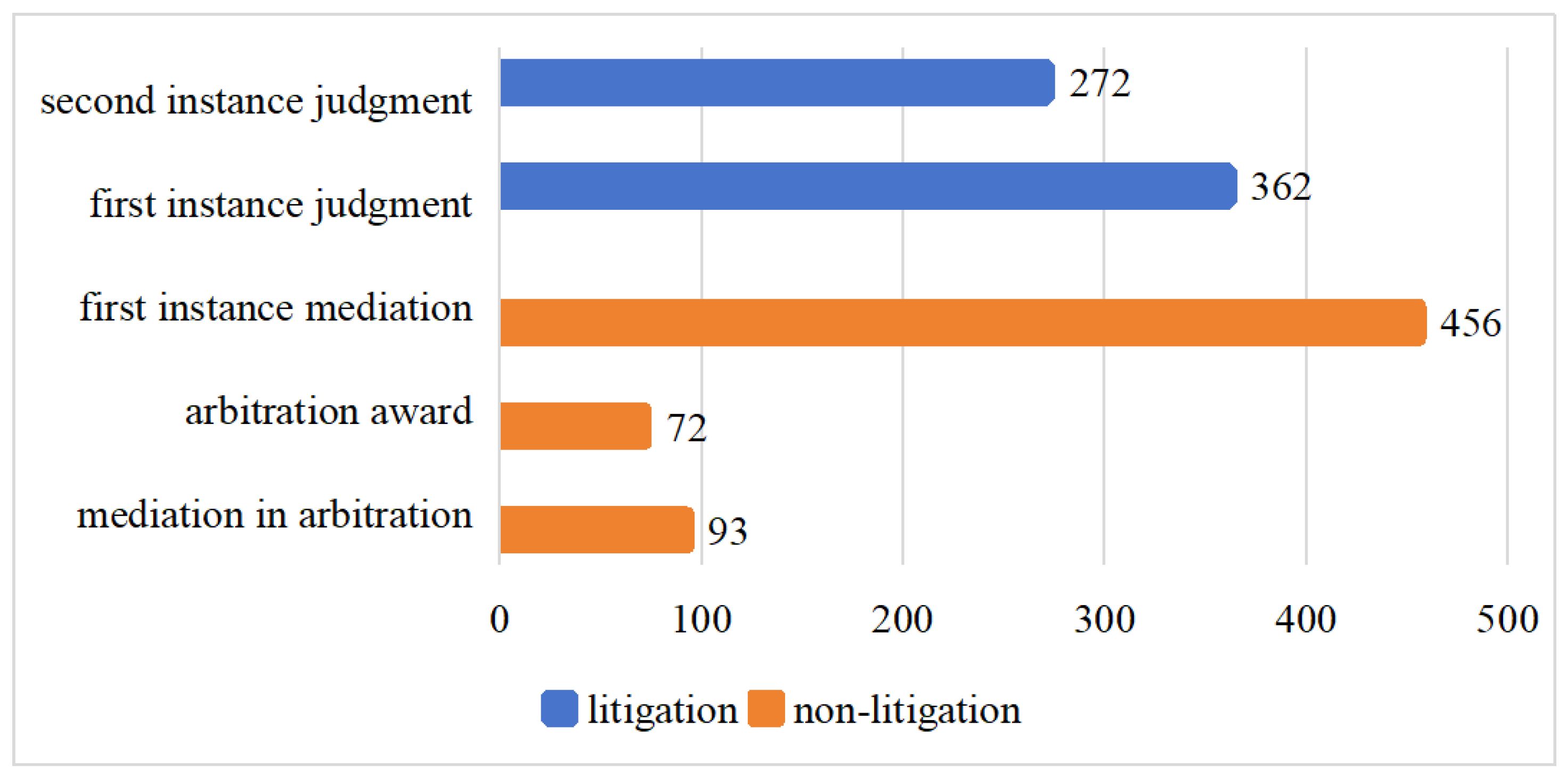
The labor dispute dataset consists of 1255 legal documents from the court and arbitration committee spanning from 2014 to 2022 in the Yuhu district of Xiangtan city of China, as illustrated in Figure 1. Among these documents, there are 93 documents of mediation in arbitration, 72 documents of arbitration awards, 456 documents of first-instance mediation, 362 documents of first-instance judgment, and 272 documents of second-instance judgment. For each piece of data, they were assigned 57 attributes as characteristics (see Appendix A 

Table A1. Attributes of labor disputes.

Attributes	Description	Attributes	Description
Employee’s Age	Age in years	Nursing Care Expenses	1 = yes, 0 = no
Sex	0 = female,1 = male	Transportation Expenses/Travel Expenses	1 = yes, 0 = no
Salary/Wage	1 = yes, 0 = no	Non_Compete Agreement Breach Penalty	1 = yes, 0 = no
Overtime Pay	1 = yes, 0 = no	Bonus	1 = yes, 0 = no
Performance Pay	1 = yes, 0 = no	Termination of Employment	1 = yes, 0 = no
Annual Leave Pay	1 = yes, 0 = no	Lawsuit Amount	total amount
Double Pay	1 = yes, 0 = no	Signing Employment Contract	1 = yes, 0 = no
Rest Day Pay	1 = yes, 0 = no	No Employment Contract	1 = yes, 0 = no
Leave with Pay	1 = yes, 0 = no	Nonexistent Employment Relationship	1 = yes, 0 = no
Sick Leave Pay	1 = yes, 0 = no	Unpaid Wages	1 = yes, 0 = no
Social Insurance	1 = yes, 0 = no	Bank Card	1 = yes, 0 = no
Pension Insurance	1 = yes, 0 = no	Attendance Record	1 = yes, 0 = no
Medical Insurance	1 = yes, 0 = no	Work Documents	1 = yes, 0 = no
Work Injury Insurance	1 = yes, 0 = no	Social Insurance Contribution	1 = yes, 0 = no
Maternity Insurance	1 = yes, 0 = no	Work Injury Insurance Contribution	1 = yes, 0 = no
Unemployment Insurance	1 = yes, 0 = no	Medical Insurance Contribution	1 = yes, 0 = no
Housing Fund	1 = yes, 0 = no	Pension Insurance Contribution	1 = yes, 0 = no
Confirmation of Illegal Termination	1 = yes, 0 = no	Maternity Insurance Contribution	1 = yes, 0 = no
Confirmation of Termination	1 = yes, 0 = no	Unemployment Insurance Non_Contribution	1 = yes, 0 = no
Confirmation of Employment	1 = yes, 0 = no	Unpaid Medical Insurance Contribution	1 = yes, 0 = no
Confirmation of Existence of Employment	1 = yes, 0 = no	Unpaid Pension Insurance Contribution	1 = yes, 0 = no
Economic Compensation	1 = yes, 0 = no	Unpaid Maternity Insurance Contribution	1 = yes, 0 = no
Compensation	1 = yes, 0 = no	Unpaid Social Insurance Contribution	1 = yes, 0 = no
Lump Sum Disability Allowance	1 = yes, 0 = no	Statute of Limitations Expired	1 = yes, 0 = no
Lump Sum Disability Employment Allowance	1 = yes, 0 = no	Employment Relationship Terminated	1 = yes, 0 = no
Lump Sum Work Injury Medical Allowance	1 = yes, 0 = no	Business Difficulty	1 = yes, 0 = no
Meal Allowance	1 = yes, 0 = no	Job Transfer	1 = yes, 0 = no
Medical Expenses	1 = yes, 0 = no	Hospitalization	1 = yes, 0 = no
Unpaid Work Injury Insurance Contribution	1 = yes, 0 = no

for details).

2.2. Data Preprocessing

2.2.1. Corpus Annotation

For the 1255 cases, the BRAT Rapid Annotation Tool (BRAT, version 1.3) [21] was used to annotate all attributes. BRAT is an annotation software that supports Chinese and can be downloaded from https://github.com/nlplab/brat/releases/tag/v1.3p1 (accessed on 12 August 2023). After annotation, attributes were transformed into numerical representations suitable for machine learning, as described in Table A1 of Appendix A, while the five methods of dispute resolution or the five critical paths of labor dispute resolution were encoded as 0, 1, 2, 3, 4.

2.2.2. Feature Scaling

For each case, there are 57 attributes assigned. Compared with other attributes, attributes like employees’ ages and lawsuit amounts exhibit significantly larger variations. They would impact the effectiveness of model training. Normalization can help map all data to a similar range, which is crucial for unstructured data that contain highly diverse values. MinMaxScaler normalization has proven to be very effective for processing high-dimensional data. MinMaxScaler is a type of normalization that scales all labor dispute features to values between 0 and 1 through the following formula:

$$v\prime =\frac{v-v_{\min }}{v_{\max }-v_{\min }},$$

(1)

where $v_{\min }$ and $v_{\max }$ represent the minimum and maximum value of the considered feature, respectively.

2.2.3. Oversampling for Dataset

As can be seen from Figure 1, the labor dispute dataset is highly unbalanced, with more than six times as many first-instance mediations as arbitration awards. To enhance predictive performance and alleviate the impact of sample imbalance, we opted for the KMeansSMOTE [22] oversampling method to balance samples, comparing it against three other oversampling techniques: Synthetic Minority Over-sampling Technique (SMOTE) [23], Adaptive Synthetic Sampling (ADASYN) [24], and Support Vector Machine Synthetic Minority Over-sampling Technique (SVMSMOTE) [25]. Figure 2 illustrates the sample distribution before and after KMeansSMOTE when selecting an automatic sampling strategy.

2.3. Model Architecture

In this study, we apply a machine learning approach named LDMLSV, based on SHAP and a soft voting strategy, to predict the critical path of labor dispute resolution. Figure 3 illustrates the entire workflow.

2.3.1. Base Classifiers and Hyperparameter Tuning

Here, ten classifiers serve as base classifiers, namely: Gaussian Naive Bayes, (GaussianNB) [26], Support Vector Machine (SVM) [27], Decision tree (DT) [28], K-nearest neighbors (KNN) [29], Random Forest (RF) [30], Logistic Regression (LR) [31], multilayer perceptrons (MLPs) [32], Extra Trees (ET) [33], extreme gradient boosting (Xgboost) [34], and Categorical gradient Boosting (CatBoost) [35]. Then, we randomly selected 80% of the dataset for training and 20% for testing. Hyperparameters were selected using GridSearchCV with 10-fold cross-validation on the training set. Finally, we used the soft voting strategy to integrate three classifiers with prediction accuracies exceeding 0.85.

2.3.2. Soft Voting Strategy

Ensemble learners utilize two or more classifiers to create a model that can provide more accurate predictions. A voting classifier is a type of ensemble learner commonly used for classification problems [36]. The voting classifier can employ two strategies: hard voting and soft voting. In contrast to hard voting, soft voting predicts the output class based on the probabilities assigned to classes by the classifiers. The soft voting strategy can consider additional information about prediction probabilities, thereby generating more accurate predictions. Equation (2) provides the definition:

$$\widehat{y}=\arg \max (\frac{1}{m}{\displaystyle \sum _{j=1}^m{p}_{0j}},\frac{1}{m}{\displaystyle \sum _{j=1}^m{p}_{1j}}\dots \frac{1}{m}{\displaystyle \sum _{j=1}^m{p}_{ij}}\dots \frac{1}{m}{\displaystyle \sum _{j=1}^m{p}_{nj}}),$$

(2)

where i is the value of class encoding, n + 1 is the number of class, m is the number of classifiers, and $p_{ij}$ represents the probability that the j-th classifier predicts the i-th class. Figure 4 provides an illustration of soft voting.

2.3.3. Explainable Artificial Intelligence Methods Based SHAP

Shapley Values [18], introduced by Shapley in 1953, are a concept from game theory used to measure a fair distribution of rewards among a group based on players’ contributions to a particular outcome. In 2017, Lundberg and Lee [19] extended this game theory concept into the explainable artificial intelligence and introduced SHAP. The introduction of SHAP has been beneficial for transitioning machine learning models from black-box models to glass-box models, enhancing their interpretability. In SHAP, the machine learning model is viewed as the set of game rules, and the input features are considered as potential players. The SHAP values can be calculated as follows:

$${\varphi }_i={\displaystyle \sum _{S\subseteq F\backslash \left\{x_i\right\}}\frac{\left|S\right|!(p-|S|-1)!}{\left|p\right|!}}\left[f_{S\cup \left\{x_i\right\}}(x_{S\cup \left\{x_i\right\}})-f_S(x_S)\right],$$

(3)

where $F=\{x_1,x_2\cdots x_p\}$, $p$ is the number of features. $F\backslash \left\{x_i\right\}$ denotes the removal of $x_i$ from $F$. Specifically, the marginal contribution of $x_i$ is the average value of $f_{S\cup \left\{x_i\right\}}(x_{S\cup \left\{x_i\right\}})-f_S(x_S)$ after iterating through $S\subseteq F\backslash \left\{x_i\right\}$.

2.3.4. The Optimal Feature Set Obtained from SHAP

An ordered feature ranking, denoted as $A$ like Equation (4), can be obtained according to SHAP values. The more important the feature, the smaller its corresponding index $t$ is.

$$A=\{f_1^{\prime },f_2^{\prime }\cdots f_t^{\prime }\cdots f_N^{\prime }\},$$

(4)

To determine the optimal feature set in $A$, we construct $N$ feature sets by incrementally adding one feature at a time, following the Incremental Feature Selection (IFS) method proposed by Huang et al. [20], as shown in Equation (5):

$$S_t=\{f_1^{\prime },f_2^{\prime }\cdots f_t^{\prime }\}(1\le t\le N),$$

(5)

For $N$ feature sets, predictors are used in turn, and an IFS table containing the number of features and feature performance is obtained by calculating Matthews Correlation Coefficient (MCC) of Jackknife cross-validation. The subset corresponding to the highest MCC is the optimal feature set we are looking for.

3. Results

3.1. Performance Evaluation Metrics

The prediction of critical paths of labor dispute resolution can be considered as a five-class classification problem, and we evaluated the performance using four metrics: accuracy, precision, recall, and F1-score.

$$Accuracy=\frac{TP+TN}{TP+FP+TN+FN},$$

(6)

$$Precision=\frac{TP}{TP+FP},$$

(7)

$$Recall=\frac{TP}{TP+FN},$$

(8)

$$F1-score=\frac{2\cdot \mathrm{Pr}ecision\cdot \mathrm{Re}call}{\mathrm{Pr}ecision+\mathrm{Re}call}$$

(9)

where TP stands for True Positives, TN stands for True Negatives, FP stands for False Positives, and FN stands for False Negatives.

3.2. Comparison and Evaluation of Base Classifiers and Soft Voting Classifier

3.2.1. The Experimental Results of Hyperparameter Tuning

Hyperparameter optimization is a crucial step in improving model generalization, reducing overfitting, and enhancing the classification performance. In this study, GridSearchCV with 10-fold cross-validation was employed to obtain the optimal hyperparameter values for the base models.

Table 1. Best hyperparameters of base classifiers after Grid Search when selecting the KMeansSMOTE sample balancing method.

Base Classifier	Hyperparameters	Search Range and Step Count	Best Value for the Hyperparameters
GaussianNB	default
SVM	C	[1, 10, 100, 1000]	1000
	kernel	[‘linear’, ‘rbf’]	‘rbf’
	gamma	(0.1, 0.9, 0.1)	0.5
DT	criterion	[‘gini’, ‘entropy’]	gini
	max_depth	(10, 100, 5)	20
	min_samples_leaf	(2, 11, 1)	2
	min_samples_split	(2, 11, 1)	5
KNN	n_neighbors	(3, 10, 1)	3
RF	max_depth	(10, 100, 5)	15
	n_estimators	(10, 200, 10)	90
LR	C	[10, 100, 1000]	10
	penalty	[‘l1’, ‘l2’]	‘l2’
	l1_ratio	[0.01, 0.02, 0.03]	0.01
MLPs	solver	[‘lbfgs’, ‘sgd’, ‘adam’]	‘adam’
	hidden_layer_sizes	[(100, ), (200, )]	(100, )
	max_iter	[300, 400, 500]	300
ET	max_depth	(10, 100, 10)	30
	n_estimators	(10, 200, 10)	100
	min_samples_leaf	(1, 11, 1)	1
XGBoost	max_depth	(2, 10, 1)	5
	n_estimators	(10,100,10)	70
	learning_rate	[0.1, 0.01, 0.05]	0.1
CatBoost	depth	[4, 6, 10]	4
	learning_rate	[0.03, 0.05, 0.1]	0.03

provides a list of hyperparameter tuning values for the base classifiers when employing the KMeansSMOTE sample balancing method.

3.2.2. Comparison between Base Classifiers and the Soft Voting Classifier

In this study, four oversampling methods were employed to balance the samples. Evaluation of ten base classifiers was conducted using the test set, and those with an accuracy exceeding 0.85 were selected to be integrated into a soft voting classifier, as depicted in

Table 2. The performance of all models on the test set.

Classifiers	Oversampling Technique	Accuracy	Precision	Recall	F1-Score
GaussianNB	SMOTE	0.29	0.49	0.29	0.22
	ADASYN	0.28	0.42	0.28	0.22
	KMeansSMOTE	0.28	0.44	0.28	0.23
	SVMSMOTE	0.38	0.54	0.38	0.34
SVM	SMOTE	0.75	0.76	0.75	0.75
	ADASYN	0.69	0.70	0.69	0.69
	KMeansSMOTE	0.85	0.85	0.85	0.85
	SVMSMOTE	0.83	0.84	0.83	0.83
DT	SMOTE	0.69	0.70	0.69	0.69
	ADASYN	0.69	0.69	0.69	0.69
	KMeansSMOTE	0.80	0.81	0.80	0.80
	SVMSMOTE	0.72	0.73	0.72	0.72
KNN	SMOTE	0.75	0.76	0.75	0.75
	ADASYN	0.69	0.71	0.69	0.69
	KMeansSMOTE	0.83	0.83	0.83	0.83
	SVMSMOTE	0.77	0.77	0.77	0.77
RF	SMOTE	0.81	0.81	0.81	0.81
	ADASYN	0.81	0.82	0.81	0.81
	KMeansSMOTE	0.87	0.88	0.87	0.87
	SVMSMOTE	0.85	0.86	0.85	0.85
LR	SMOTE	0.66	0.67	0.66	0.66
	ADASYN	0.57	0.60	0.57	0.57
	KMeansSMOTE	0.79	0.80	0.79	0.79
	SVMSMOTE	0.73	0.74	0.73	0.73
MLPs	SMOTE	0.77	0.77	0.77	0.77
	ADASYN	0.71	0.72	0.71	0.71
	KMeansSMOTE	0.84	0.85	0.84	0.84
	SVMSMOTE	0.83	0.83	0.83	0.83
ET	SMOTE	0.80	0.80	0.80	0.80
	ADASYN	0.78	0.79	0.78	0.78
	KMeansSMOTE	0.86	0.87	0.86	0.86
	SVMSMOTE	0.84	0.84	0.84	0.84
XGBoost	SMOTE	0.80	0.80	0.80	0.80
	ADASYN	0.74	0.75	0.74	0.74
	KMeansSMOTE	0.87	0.88	0.87	0.87
	SVMSMOTE	0.84	0.84	0.84	0.83
CatBoost	SMOTE	0.79	0.79	0.79	0.79
	ADASYN	0.78	0.79	0.78	0.78
	KMeansSMOTE	0.86	0.86	0.86	0.86
	SVMSMOTE	0.84	0.84	0.84	0.84
VotingClassifier (RF + ET + XGBoost)	KMeansSMOTE	0.88	0.88	0.88	0.88
VotingClassifier (RF + ET + CatBoost)	KMeansSMOTE	0.89	0.89	0.89	0.89

. Under the KMeansSMOTE oversampling method, the ensemble soft voting classifier comprising RF, ET, and CatBoost exhibited the best predictive performance, achieving an accuracy of 0.89. For all performance evaluation metrics, including accuracy, precision, recall, and F1-score, the soft voting classifier based on RF, ET, and CatBoost outperformed individual classifiers. Additionally, the soft voting classifier based on RF, ET, and CatBoost surpassed the soft voting classifier based on RF, ET, and XGBoost, as well as other classifier ensembles, across all evaluated performance metrics.

Since the prediction of critical paths of labor dispute resolution is a multi-classification problem, it is crucial to avoid situations where the overall prediction is good while the certain categories are poor.

Table 3. The predictive outcomes among five dispute resolution paths.

Classifier	Accuracy	Class	Classification Report
			Precision	Recall	F1-Score	Support
VotingClassifier (RF + ET + CatBoost)	0.89	0	0.95	0.87	0.91	99
		1	0.96	0.91	0.93	106
		2	0.80	0.89	0.85	83
		3	0.89	0.83	0.86	81
		4	0.83	0.93	0.88	88

Note: Class 0: Mediation in arbitration, Class 1: Arbitration awards, Class 2: First-instance mediation, class 3: First-instance judgments, class 4: Second-instance judgments, Support: The number of samples for each class.

presents the predictive results for each class. The results indicate that the soft voting classifier exhibits similar performance across these five dispute resolution paths, with F1-scores all surpassing 0.8. The soft voting classifier demonstrates excellent performance in predicting the critical path of labor dispute resolution.

Different oversampling steps can significantly impact the final classification results. We kept classes 2, 3, and 4 fixed at the maximum class count, and then adjusted the ratios of minority classes 0 and 1.

Table 4. Analysis of F1-score Sensitivity of KMeansSMOTE to Different Sampling Strategies.

Classifier	Class	Sampling_Strategy (Ratios)
		Unadjusted	0.25	0.5	0.75	1
VotingClassifier (RF + ET + CatBoost)	0	0.48	0.64	0.82	0.92	0.91
	1	0.35	0.75	0.86	0.91	0.93
	2	0.90	0.92	0.89	0.90	0.85
	3	0.88	0.89	0.87	0.86	0.86
	4	0.85	0.83	0.90	0.87	0.88

Note: Class 0: Mediation in arbitration, Class 1: Arbitration awards, Class 2: First-instance mediation, class 3: First-instance judgments, class 4: Second-instance judgments, Support: The number of samples for each class.

presents the results of the soft voting classifier for both the unadjusted ratio and selected ratios of 0.25, 0.5, and 1. From the results, it is evident that as the sampling ratio increases, there is an upward trend in the predictive outcomes for the minority classes.

3.3. Model Interpretation Based on SHAP

Compared to other classifiers, the soft voting classifier based on RF, ET, and CatBoost demonstrates superior performance. In this study, SHAP is employed to interpret and analyze the predictions of these four models, thereby deducing the crucial features influencing the models. RF, ET, and CatBoost utilize TreeExplainer for analysis, and the VotingClassifier employs a KernelExplainer. To obtain a global importance chart of features, a summary plot is employed to visualize features’ importance. Figure 5 illustrates the top 20 most important features for each of these four classifiers. The features are arranged from top to bottom, with each row representing a specific feature. For each base classifier, different colors are used to denote the contribution of that feature to various categories. Given that VotingClassifier is an amalgamation of individual classifiers, the overall contribution is considered instead of categorical distinctions.

3.4. The optimal Feature Set Based on SHAP

SHAP, in addition to explaining the model, can also be utilized for feature selection. Appendix A 

Table A2. Average absolute SHAP values for the soft voting classifier.

Feature Name	The Mean Absolute Value of the SHAP Values	Feature Name	The Mean Absolute Value of the SHAP Values
No Employment Contract	0.648959414	Confirmation of Existence of Employment	0.01059931
Lawsuit Amount	0.346669272	Lump Sum Work Injury Medical Allowance	0.009847109
Unpaid Social Insurance Contribution	0.199835268	Housing Fund	0.009541126
Employee’s Age	0.119818414	Medical Insurance	0.009512734
Unpaid Maternity Insurance Contribution	0.09492057	Lump Sum Disability Allowance	0.009292651
Double Pay	0.092609688	Transportation Expenses/Travel Expenses	0.009145641
Economic Compensation	0.083888036	Work Injury Insurance	0.009010271
Salary	0.081995194	Confirmation of Illegal Termination	0.008964941
Unpaid Wages	0.068425982	Confirmation of Termination	0.008838653
Employment Relationship Terminated	0.061327811	Leave with Pay	0.008766349
Unpaid Medical Insurance Contribution	0.055390951	Medical Expenses	0.008750366
Unemployment Insurance	0.050822899	Medical Insurance Contribution	0.008611888
Sex	0.048811927	Confirmation of Employment	0.008502667
Unpaid Pension Insurance Contribution	0.03665694	Bank Card	0.008446629
Signing Employment Contract	0.030486727	Maternity Insurance	0.008412141
Compensation	0.022131219	Social Insurance Contribution	0.008378908
Nonexistent Employment Relationship	0.021548357	Work Documents	0.008348484
Overtime Pay	0.01748199	Rest Day Pay	0.00826537
Social Insurance	0.016962045	Lump Sum Disability Employment Allowance	0.008150623
Termination of Employment	0.016126691	Pension Insurance Contribution	0.007965058
Pension Insurance	0.015367977	Performance Pay	0.007916206
Statute of Limitations Expired	0.01400964	Maternity Insurance Contribution	0.007723693
Annual Leave Pay	0.012883244	Business Difficulty	0.007714222
Bonus	0.012705845	Attendance Record	0.007689007
Unemployment Insurance Non-Contribution	0.011474051	Meal Allowance	0.007536683
Unpaid Work Injury Insurance Contribution	0.011242743	Sick Leave Pay	0
Hospitalization	0.011026164	Job Transfer	0
Work Injury Insurance Contribution	0.010891424	Non-Compete Agreement Breach Penalty	0
Nursing Care Expenses	0.010741868

presents the SHAP results of the soft voting classifier. Based on this importance ranking, we employed IFS to construct 57 feature subsets. Furthermore, we conducted jackknife cross-validation on the training set and computed the MCC. Through this calculation, we determine that the optimal feature set is the one containing the top 33 features sorted by SHAP feature importance, as shown in Figure 6. When the number of features is 33, the highest MCC is 0.8540.

Retraining the soft voting classifier with the optimal feature subset achieves an accuracy of 0.90. From

Table 5. Comparison of soft voting classifiers trained on different feature dimensions.

Methods	Features Number	Accuracy	Precision	Recall	F1-score
VotingClassifier (RF + ET + CatBoost)	57	0.89	0.89	0.89	0.89
SHAP + VotingClassifier (RF + ET + CatBoost)	33	0.90	0.90	0.90	0.90

, it can be seen that the soft voting classifier performs better on the optimal feature subset containing 33 features compared with the results on the original dataset containing 57 features. Despite the reduction in the number of features, the performance of the model is improved. This demonstrates that SHAP is an efficient method for dimensionality reduction and eliminating redundancy.

3.5. Comparison with Other Methods

Research regarding the use of artificial intelligence to predict dispute resolution methods is still limited. Here, we apply two additional models, each predicting different types of dispute resolution methods, to the problem of labor dispute resolutions and compare their performance. Lokanan [15] utilized a Gradient Boosting classifier to predict resolution methods for financial fraud disputes, while Ayhan et al. [17] integrated decision tree C4.5, Naïve Bayes, and Multilayer Perceptron into a majority voting classifier to predict resolution methods for construction project disputes. We compare these two approaches with LDMLSV on our dataset.

Table 6. Comparison with previous research.

Methods	Accuracy	Precision	Recall	F1-score
Lokanan [15]	0.77	0.77	0.77	0.76
Ayhan et al. [17]	0.74	0.75	0.74	0.74
LDMLSV (ours)	0.90	0.90	0.90	0.90

presents the results of the comparison. The experimental results demonstrate that LDMLSV is better suited for our problem.

4. Discussion

An increasing body of research suggests that utilizing artificial intelligence algorithms to identify and predict critical paths in labor dispute resolutions contributes to efficiency improvements, resource conservation, and cost reduction in this domain. This study introduces a method combining a SHAP-based analysis and soft voting for predicting critical paths in labor dispute resolutions. Given the highly imbalanced nature of labor dispute samples, we opted for the KMeansSMOTE oversampling method and compared it with SMOTE, SVMSMOTE, and ADASYN. The results indicate that, except for the Gaussian Naive Bayes classifier, the performance of other classifiers under KMeansSMOTE oversampling outperformed the results from the other three oversampling methods. This can be attributed to KMeansSMOTE’s initial clustering of samples using K-means, followed by SMOTE oversampling within each cluster. This method pays more attention to samples near the boundaries between different classes, facilitating more accurate synthetic sample generation while reducing noise introduction compared to other oversampling methods.

Comparing base classifiers and the soft voting classifier, RF, ET, XGBoost, and CatBoost achieved accuracies exceeding 0.85. We integrated classifiers with accuracies above 0.85 using a soft voting strategy. A comparison was made between the soft voting classifier integrating RF, ET, and XGBoost and the soft voting classifier integrating RF, ET, and CatBoost, revealing superior performance in predicting critical paths in labor disputes for the RF, ET, and CatBoost ensemble. Additionally, the ensemble of RF, ET, XGBoost, and CatBoost using a soft voting strategy did not perform as well as the RF, ET, and CatBoost ensemble.

SHAP, based on the Shapley values from cooperative game theory, offers more precise and stable explanations for models by mathematically measuring the contribution of each feature to predictions. Analyzing the results of four models—RF, ET, CatBoost, and the soft voting classifier—provided insights into the contributions of features to the outcomes. Across these models, No Employment Contract showed the highest contribution to outcomes, followed by the amount of the lawsuit. Comparing the top 20 important features across the four models revealed that 17 features were consistently present: Compensation, Double Pay, Economic Compensation, Employee’s Age, Employment Relationship Terminated, Lawsuit Amount, No Employment Contract, Overtime Pay, Sex, Salary, Signing Employment Contract, Unemployment Insurance, Unpaid Medical Insurance Contribution, Unpaid Pension Insurance Contribution, Unpaid Social Insurance Contribution, Unpaid Wages, and Unpaid Maternity Insurance Contribution. The presence of these 17 features suggests their crucial role in characterizing labor dispute cases.

SHAP not only provides a comprehensive assessment of feature importance and explains the contributions of model features but also guides feature engineering and model improvement. Hence, employing an incremental feature selection method based on the SHAP importance rankings from the voting classifier, we obtained the optimal subset containing the top 33 features. Despite reducing the features from 57 to 33, the accuracy reached 0.90. This indicates that SHAP can identify features with minimal or negative impact on the model, accurately eliminating those that do not contribute or may even harm the model’s predictive capability. This enhances model simplicity and generalizability.

5. Conclusions

This paper applies an ensemble soft voting method based on RF, ET, and CatBoost for predicting critical paths in labor dispute resolutions. Addressing sample imbalance using KMeansSMOTE utilizes SHAP and incremental feature selection to obtain the optimal feature subset.

The results indicate that the predictive performance based on SHAP feature selection and the soft voting strategy outperforms individual algorithms significantly. The ensemble model achieves an accuracy and F1-score of 0.90, demonstrating strong competitiveness compared with previous proposed models. Additionally, balancing the data using KMeansSMOTE contributed to enhancing the prediction of the model for individual classes. SHAP’s explanation of the model also aids in understanding the underlying logic behind the predictions. LDMLSV offers logical, reliable, and practical judgments, alleviating pressure on judges and boosting confidence among laborers.

While the proposed model has yielded encouraging findings, its application in civil dispute resolution requires further research. In this study, we considered only a few oversampling techniques. In future work, we aim to explore undersampling, as well as hybrid sampling methods, to expand our sample set. Furthermore, the labor dispute attributes were manually selected. Future attempts will involve utilizing natural language processing methods for text representation, developing various types of ensemble models, among other approaches, to further improve the model and enhance its predictive performance.