Dimensional Synthesis of the Compliant Mechanism Using the Parametric Fuzzy Form of the Freudenstein Equation
Abstract
1. Introduction
1.1. Synthesis Methods of CMs
1.2. Dimensional Synthesis of CMs
1.3. Region-Based Approach for Dimensional Synthesis of CMs
1.4. Paper Structure
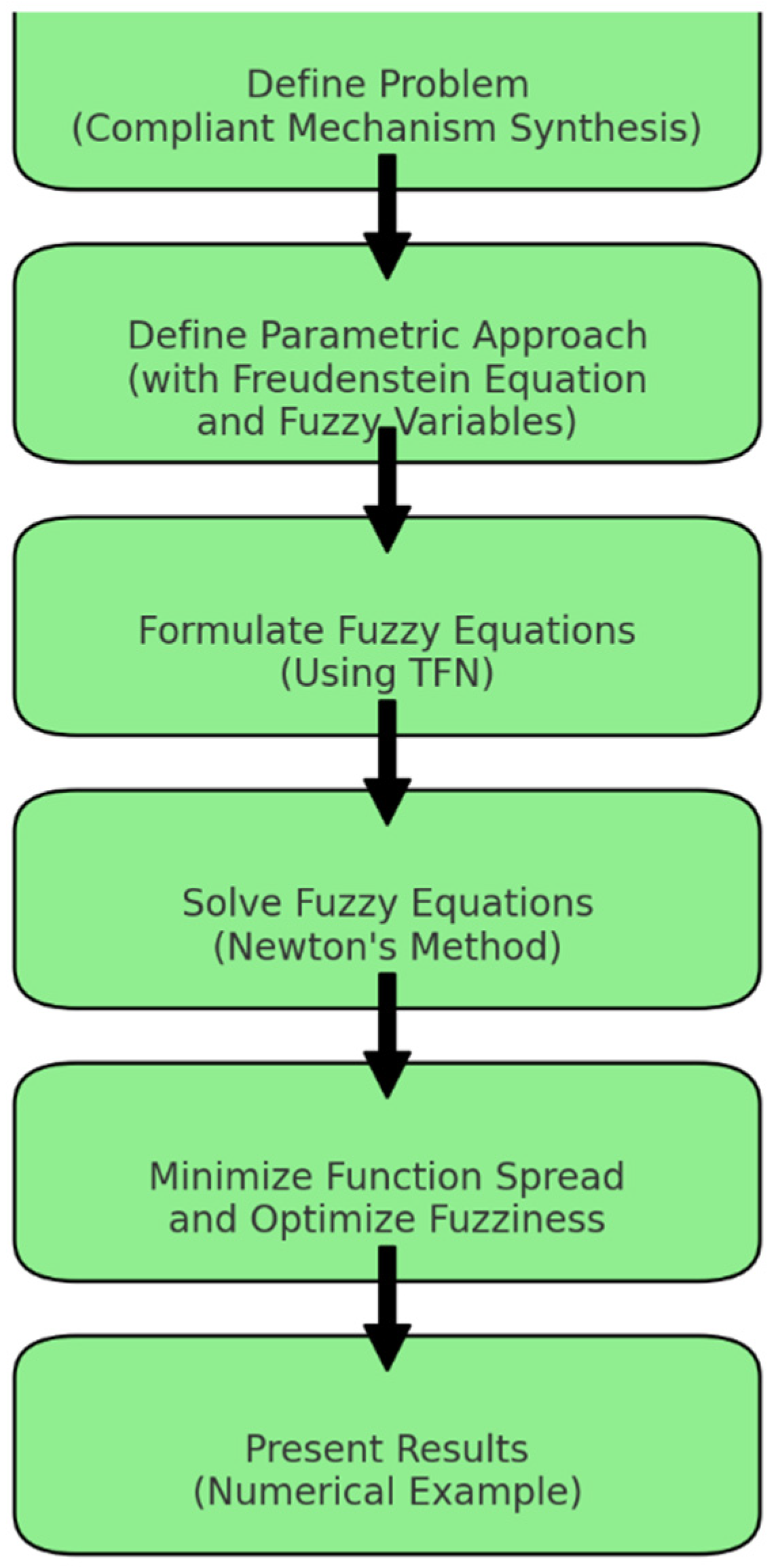
2. Methodology
2.1. Parametric Approach of Fuzzy Equations for Dimensional Synthesis of CMs
2.2. Variability of Fuzzy Functions Generation for Dimensional Synthesis of CMs
3. Function-Generation Synthesis of the CMs
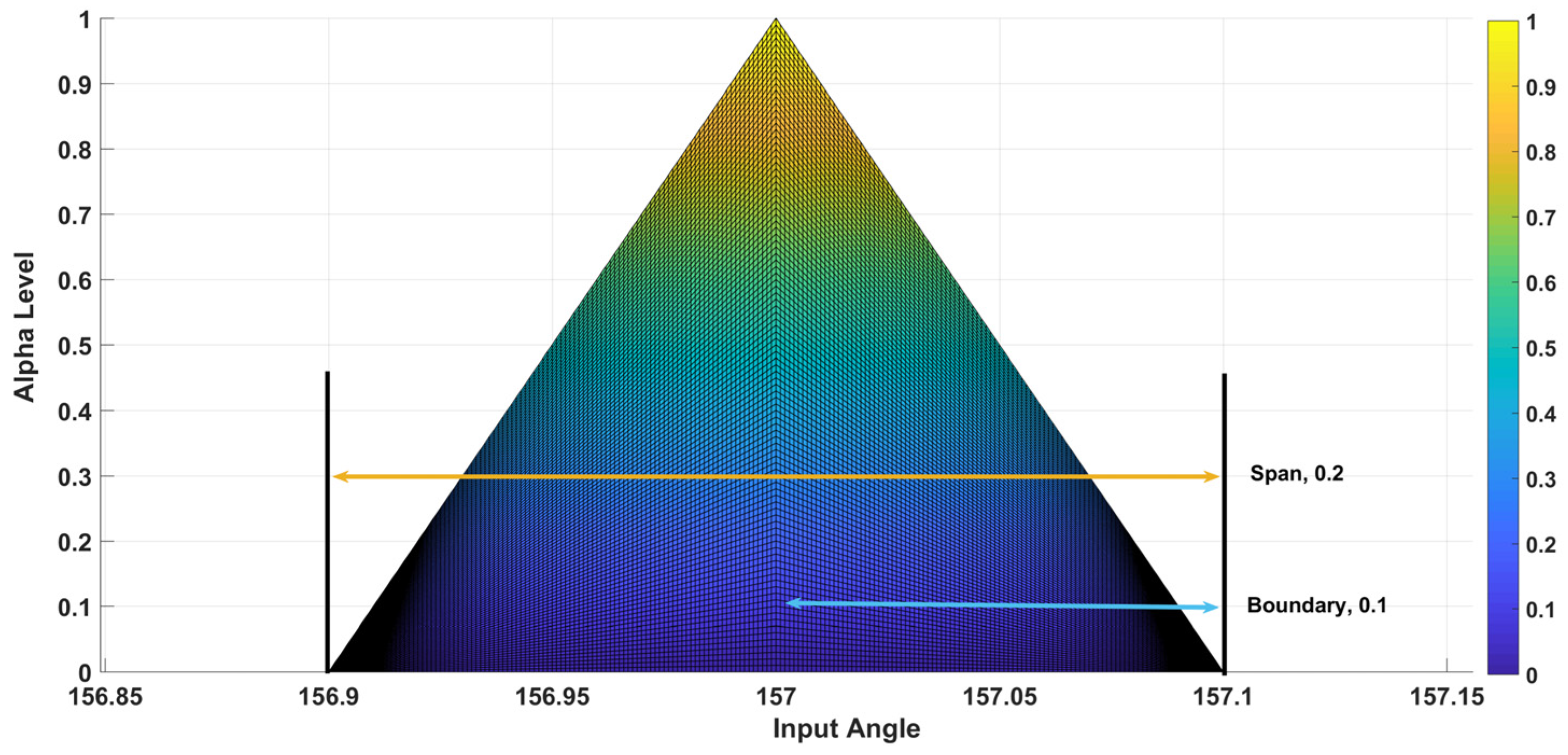
3.1. Triangular Fuzzy Number (TFN)
3.2. The TFN of the CMs
3.3. The Fuzzy Freudenstein’s Equation
4. Parametric Form and Newton’s Method
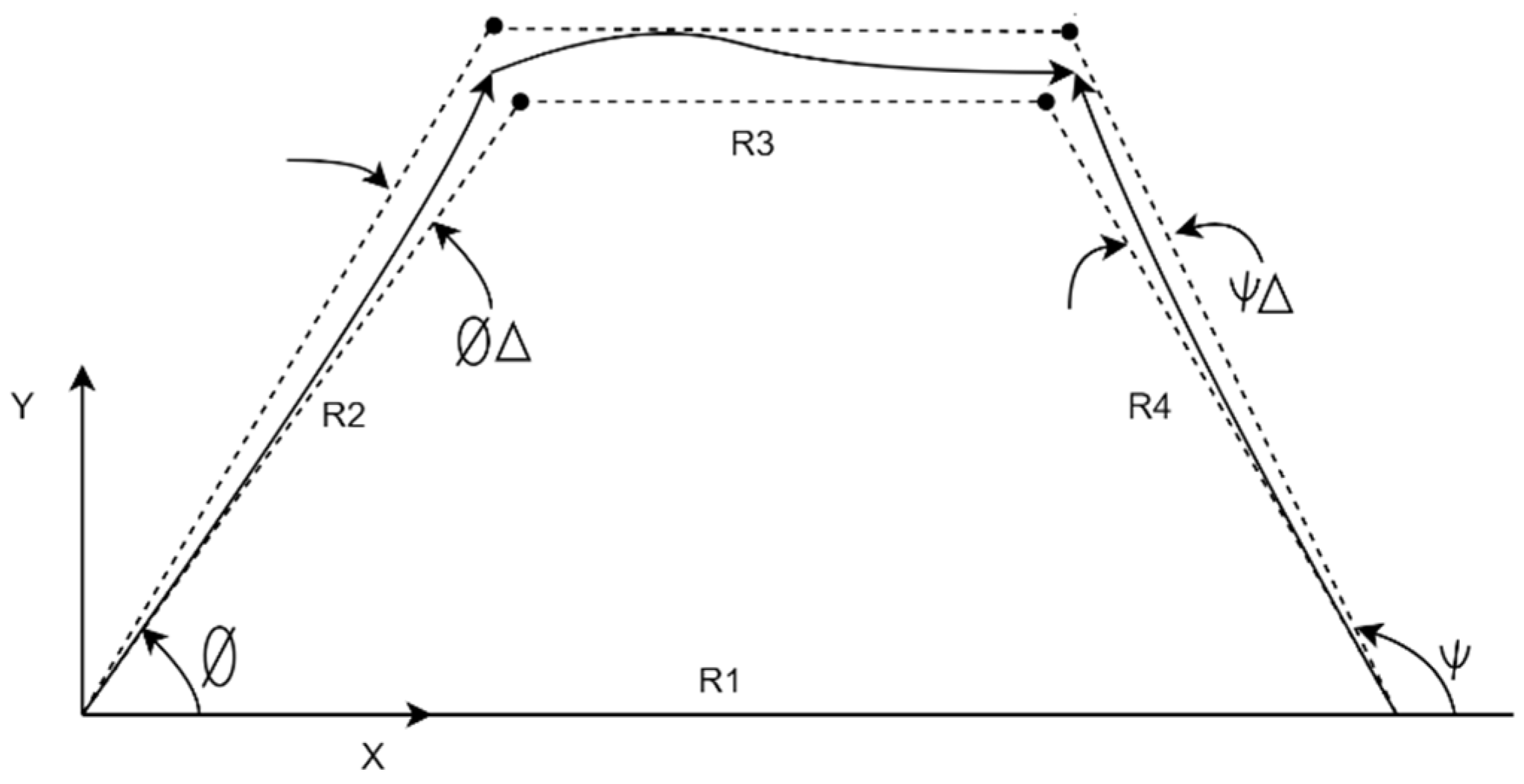
4.1. Parametric Form
4.2. Newton Method
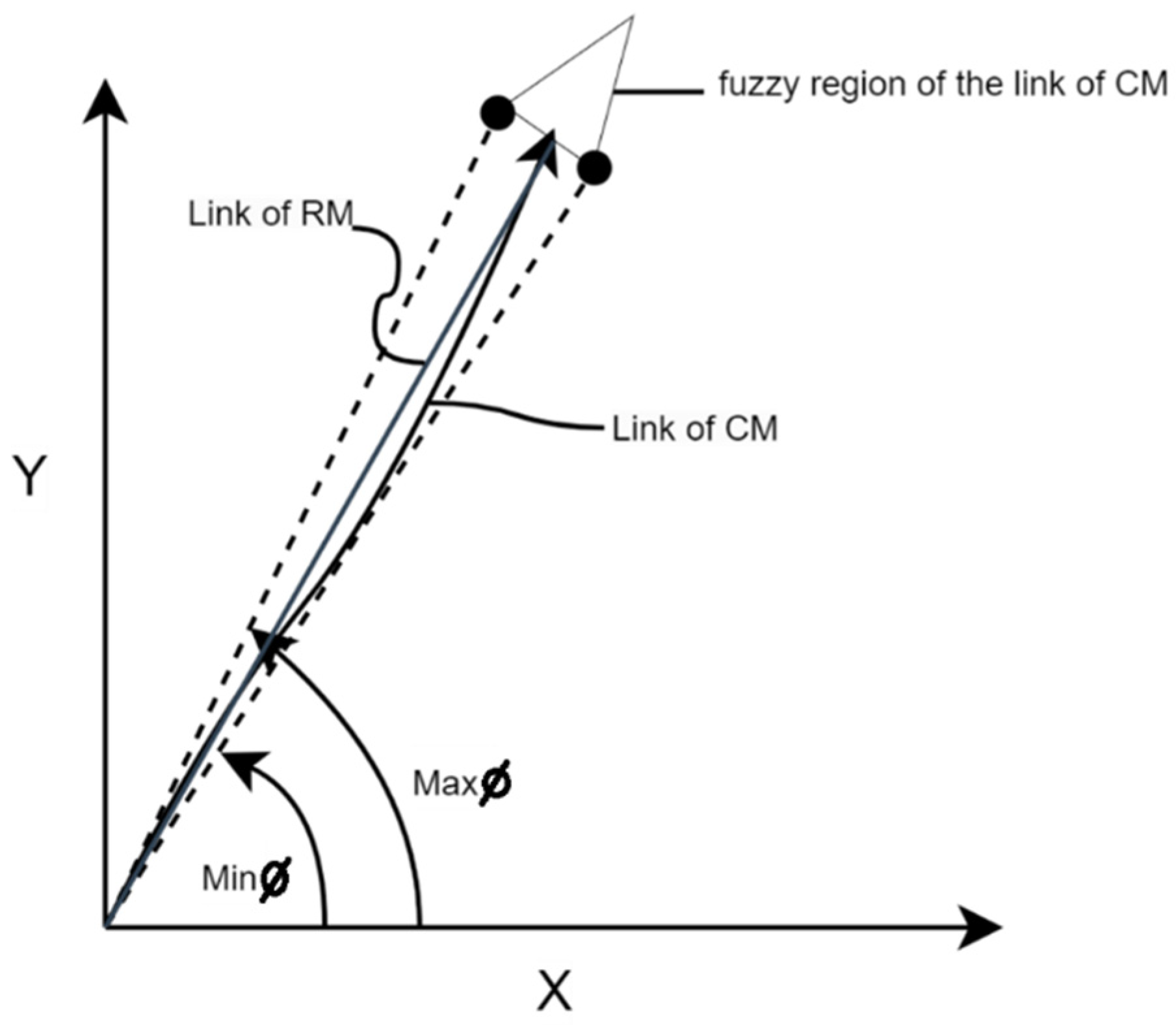
4.3. Fuzzy Lengths for CMs
4.4. Fuzzy Optimization
4.4.1. Inputs
4.4.2. Output
4.4.3. Fuzzy Rules
4.4.4. Defuzzification and Methods
5. Numerical Examples
5.1. Example 1
5.2. Example 2
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Howell, L.L. Compliant Mechanisms. In 21st Century Kinematics; McCarthy, J.M., Ed.; Springer: London, UK, 2013; pp. 189–216. [Google Scholar]
- Kota, S.; Lu, K.-J.; Kreiner, Z.; Trease, B.; Arenas, J.; Geiger, J. Design and Application of Compliant Mechanisms for Surgical Tools. J. Biomech. Eng. 2005, 127, 981–989. [Google Scholar] [CrossRef] [PubMed]
- Lobontiu, N. Compliant Mechanisms: Design of Flexure Hinges, 1st ed.; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar] [CrossRef]
- Bamberg, E. Principles of Rapid Machine Design; Massachusetts Institute of Technology: Cambridge, MA, USA, 2000; Available online: https://cir.nii.ac.jp/crid/1573105975363153536 (accessed on 23 September 2024).
- Howell, L.L.; Midha, A. A Method for the Design of Compliant Mechanisms with Small-Length Flexural Pivots. J. Mech. Des. 1994, 116, 280–290. [Google Scholar] [CrossRef]
- Su, H.-J.; McCarthy, J.M. Synthesis of Bistable Compliant Four-Bar Mechanisms Using Polynomial Homotopy. J. Mech. Des. 2006, 129, 1094–1098. [Google Scholar] [CrossRef]
- Hopkins, J.B.; Culpepper, M.L. Synthesis of multi-degree of freedom, parallel flexure system concepts via Freedom and Constraint Topology (FACT)–Part I: Principles. Precis. Eng. 2010, 34, 259–270. [Google Scholar] [CrossRef]
- Chiou, S.-J.; Sridhar, K. Automated conceptual design of mechanisms. Mech. Mach. Theory 1999, 34, 467–495. [Google Scholar] [CrossRef]
- Krishnan, G.; Kim, C.; Kota, S. An Intrinsic Geometric Framework for the Building Block Synthesis of Single Point Compliant Mechanisms. J. Mech. Robot. 2010, 3, 011001. [Google Scholar] [CrossRef]
- Kim, C. Design Strategies for the Topology Synthesis of Dual Input-Single Output Compliant Mechanisms. J. Mech. Robot. 2009, 1, 041002. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer: Berlin/Heidelberg, Germany, 2013; Available online: https://books.google.com/books?id=ZCjsCAAAQBAJ (accessed on 23 September 2024).
- Saxena, A.; Ananthasuresh, G.K. Topology Synthesis of Compliant Mechanisms for Nonlinear Force-Deflection and Curved Path Specifications. J. Mech. Des. 1999, 123, 33–42. [Google Scholar] [CrossRef]
- Frecker, M.I.; Ananthasuresh, G.K.; Nishiwaki, S.; Kikuchi, N.; Kota, S. Topological Synthesis of Compliant Mechanisms Using Multi-Criteria Optimization. J. Mech. Des. 1997, 119, 238–245. [Google Scholar] [CrossRef]
- Pedersen, C.B.W.; Buhl, T.; Sigmund, O. Topology synthesis of large-displacement compliant mechanisms. Int. J. Numer. Methods Eng. 2001, 50, 2683–2705. [Google Scholar] [CrossRef]
- Hernández, A.; Muñoyerro, A.; Urízar, M.; Altuzarra, O. Kinematic Analysis of a Tendon-Driven Hybrid Rigid–Flexible Four-Bar; Application to Optimum Dimensional Synthesis. Mathematics 2023, 11, 4215. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Asady, B. Newton’s method for solving fuzzy nonlinear equations. Appl. Math. Comput. 2004, 159, 349–356. [Google Scholar] [CrossRef]
- Todorov, T.S. Synthesis of four-bar mechanisms by Freudenstein–Chebyshev. Mech. Mach. Theory 2002, 37, 1505–1512. [Google Scholar] [CrossRef]
- Tanaka, H.; Watada, J. Possibilistic linear systems and their application to the linear regression model. Fuzzy Sets Syst. 1988, 27, 275–289. [Google Scholar] [CrossRef]
- Chukhrova, N.; Johannssen, A. Fuzzy regression analysis: Systematic review and bibliography. Appl. Soft Comput. 2019, 84, 105708. [Google Scholar] [CrossRef]
- Nasrabadi, M.M.; Nasrabadi, E. A mathematical-programming approach to fuzzy linear regression analysis. Appl. Math. Comput. 2004, 155, 873–881. [Google Scholar] [CrossRef]
- Kao, C.; Chyu, C.-L. A fuzzy linear regression model with better explanatory power. Fuzzy Sets Syst. 2002, 126, 401–409. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y. A systematic approach to optimizing value for fuzzy linear regression with symmetric triangular fuzzy numbers. Math Probl. Eng. 2013, 2013, 210164. [Google Scholar] [CrossRef]
- Chen, L.-H.; Nien, S.-H. A new approach to formulate fuzzy regression models. Appl. Soft Comput. 2020, 86, 105915. [Google Scholar] [CrossRef]
- Mwangi, J.K.; Muvengei, O.M.; Oduori, M.F. Review of the Application of Genetic Algorithm and Precision Points in Optimisation of the Four-bar Mechanism. In Proceedings of the Sustainable Research and Innovation Conference, Pretoria, South Africa, 22–24 June 2022; pp. 203–212. [Google Scholar]
- Ross, T.J. Fuzzy Logic with Engineering Applications; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Shrestha, R.R.; Bárdossy, A.; Nestmann, F. Analysis and propagation of uncertainties due to the stage–discharge relationship: A fuzzy set approach. Hydrol. Sci. J. 2007, 52, 595–610. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]


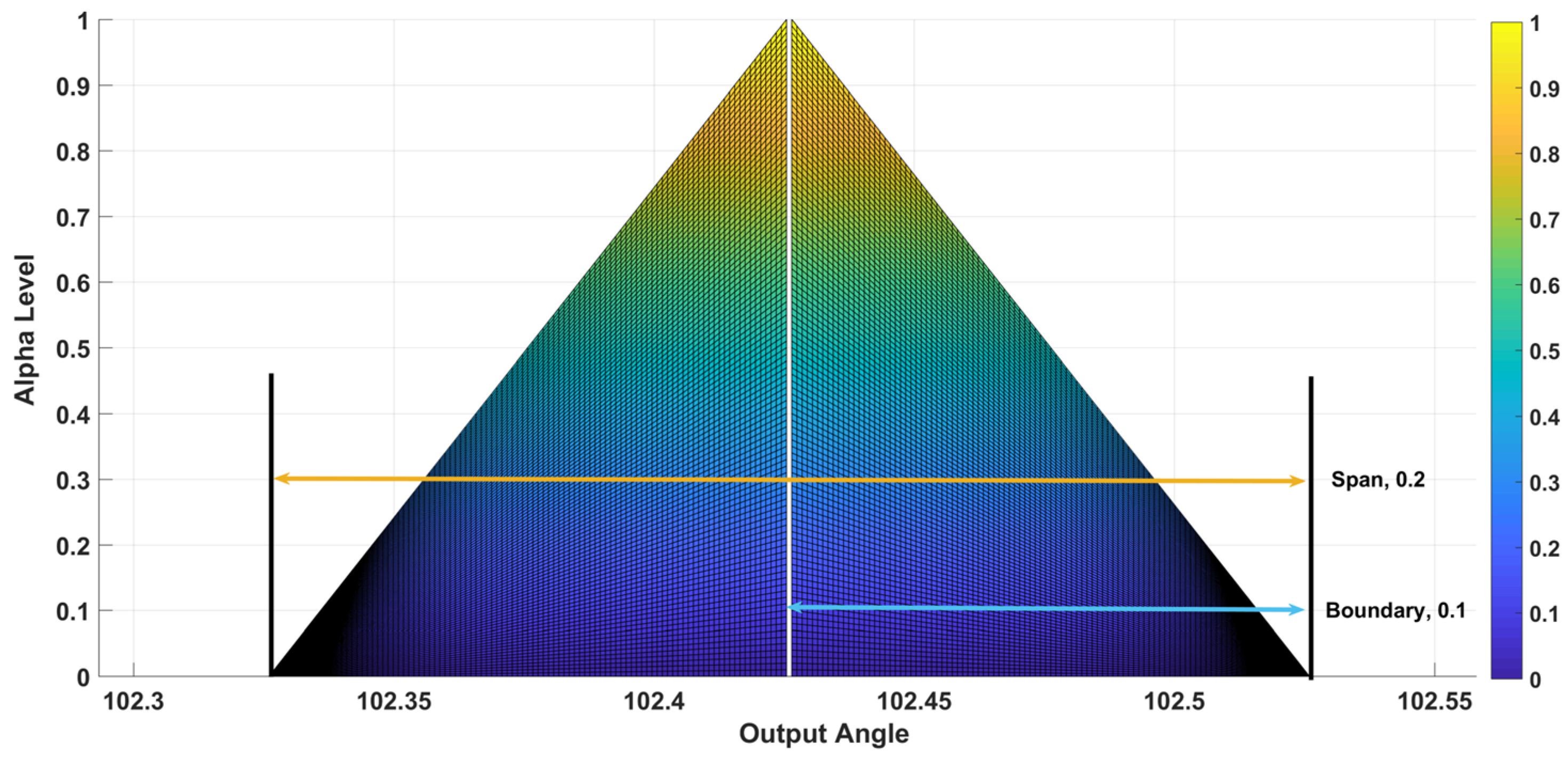
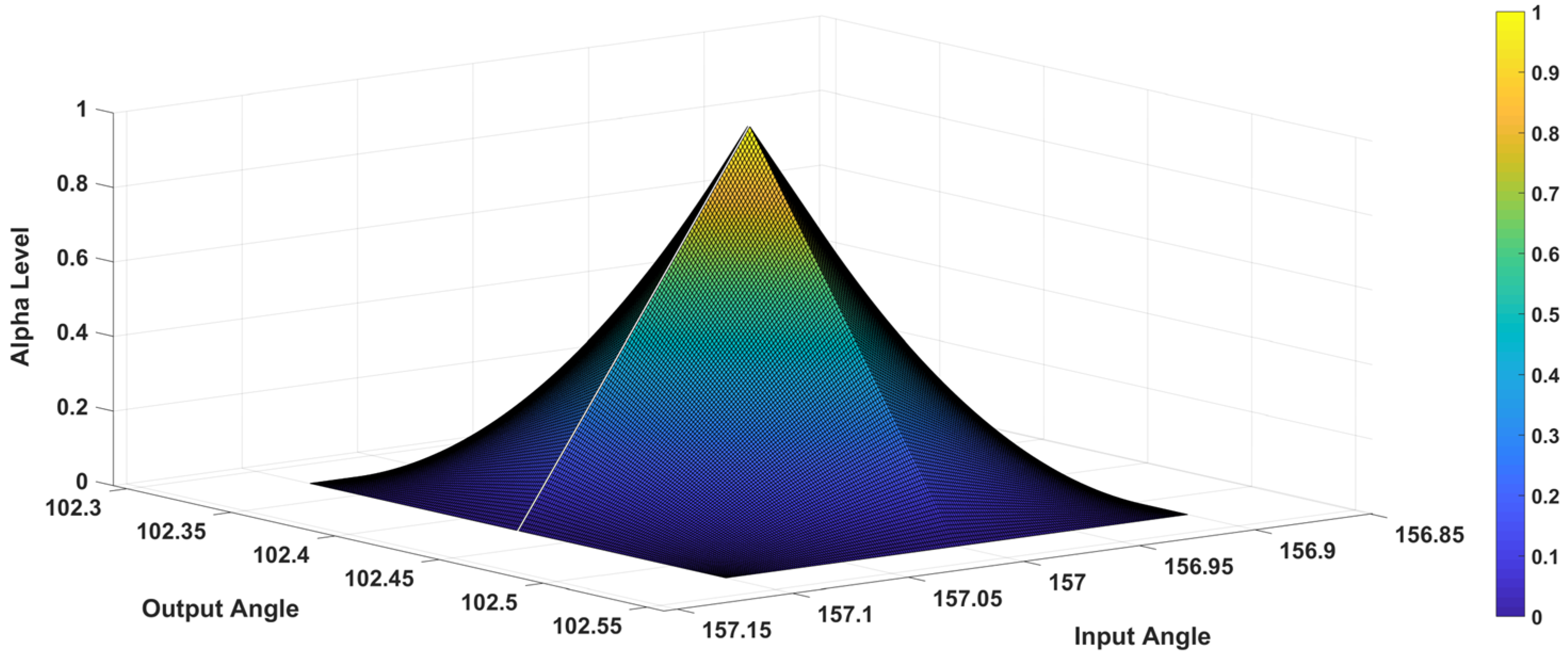

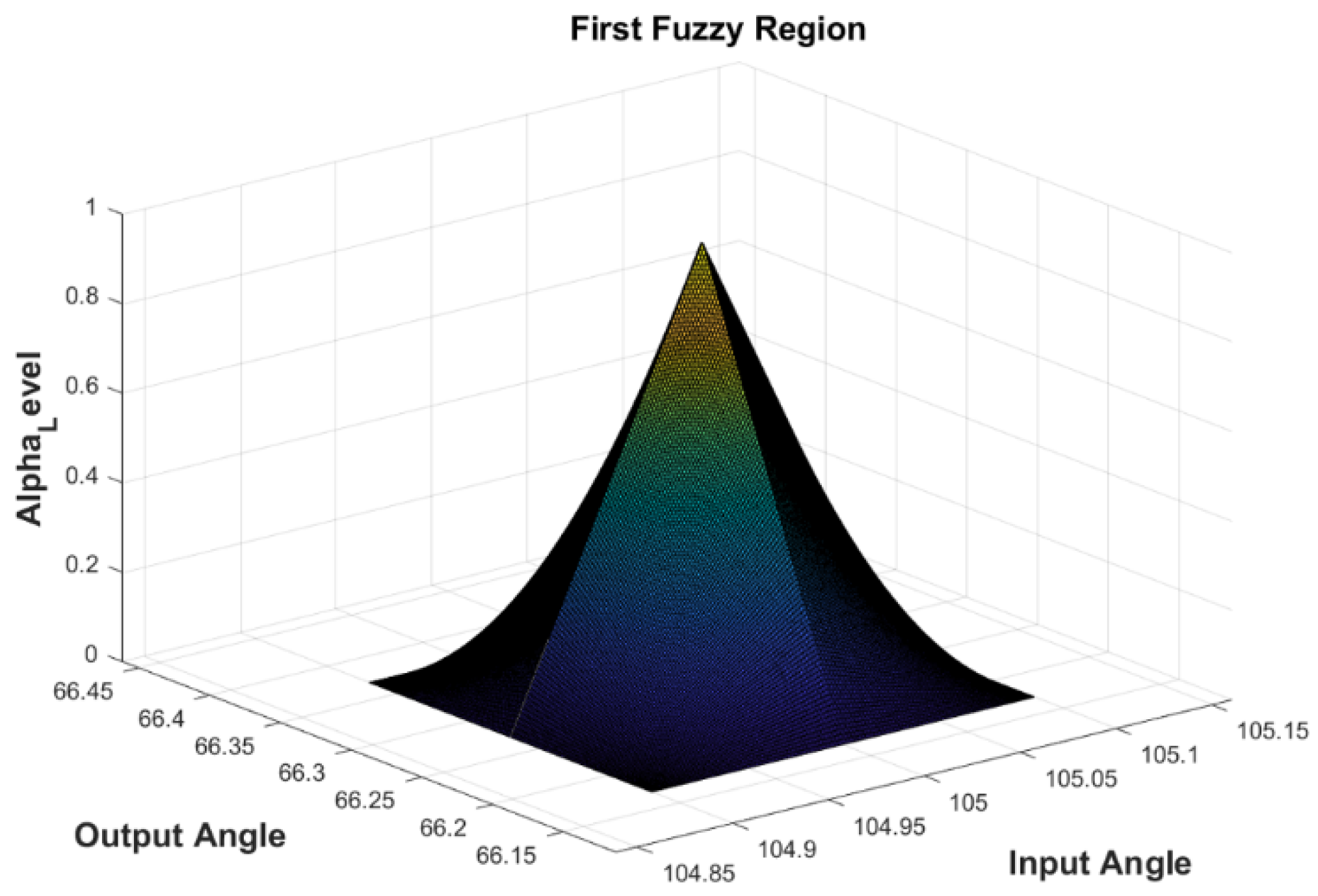
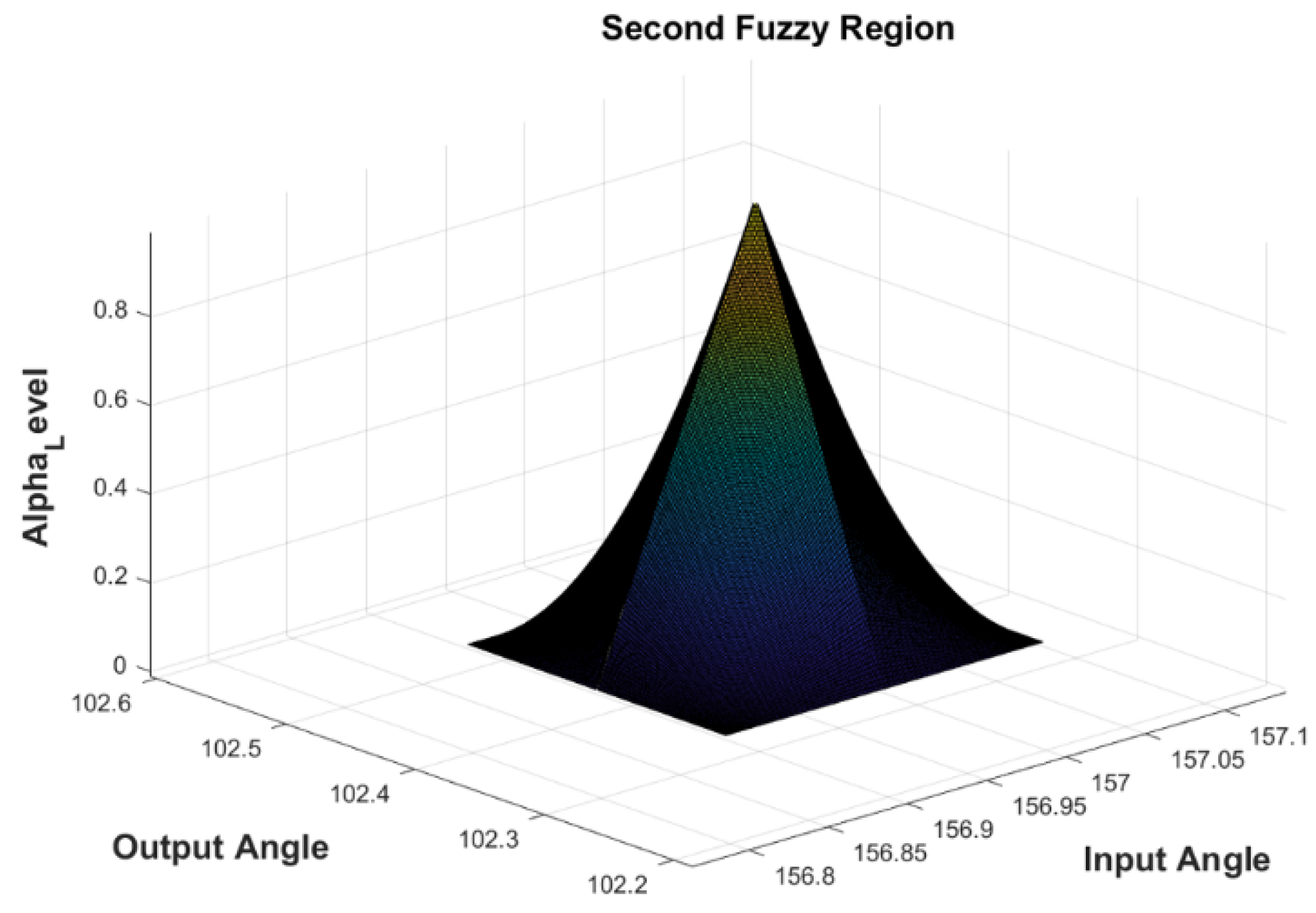
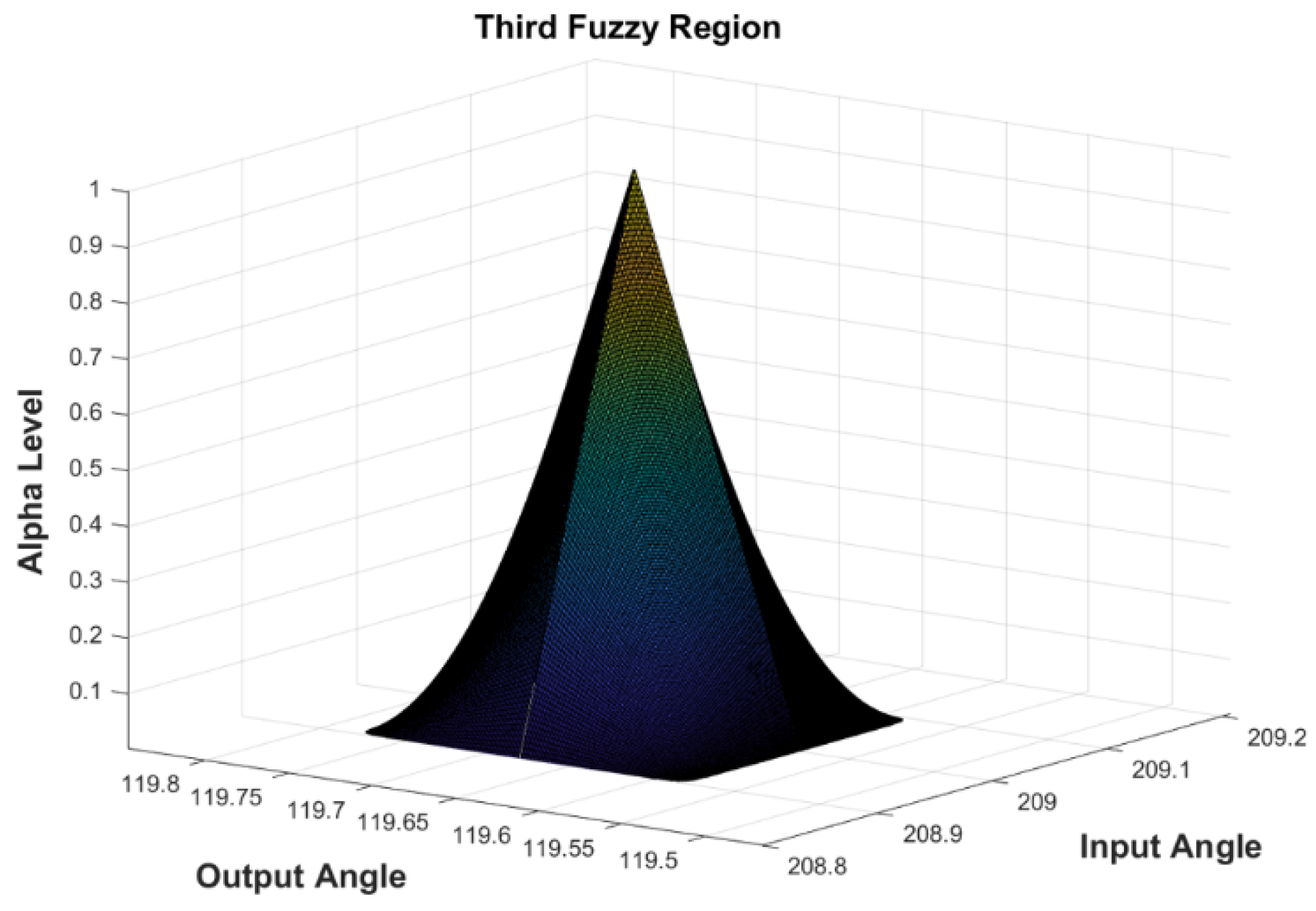
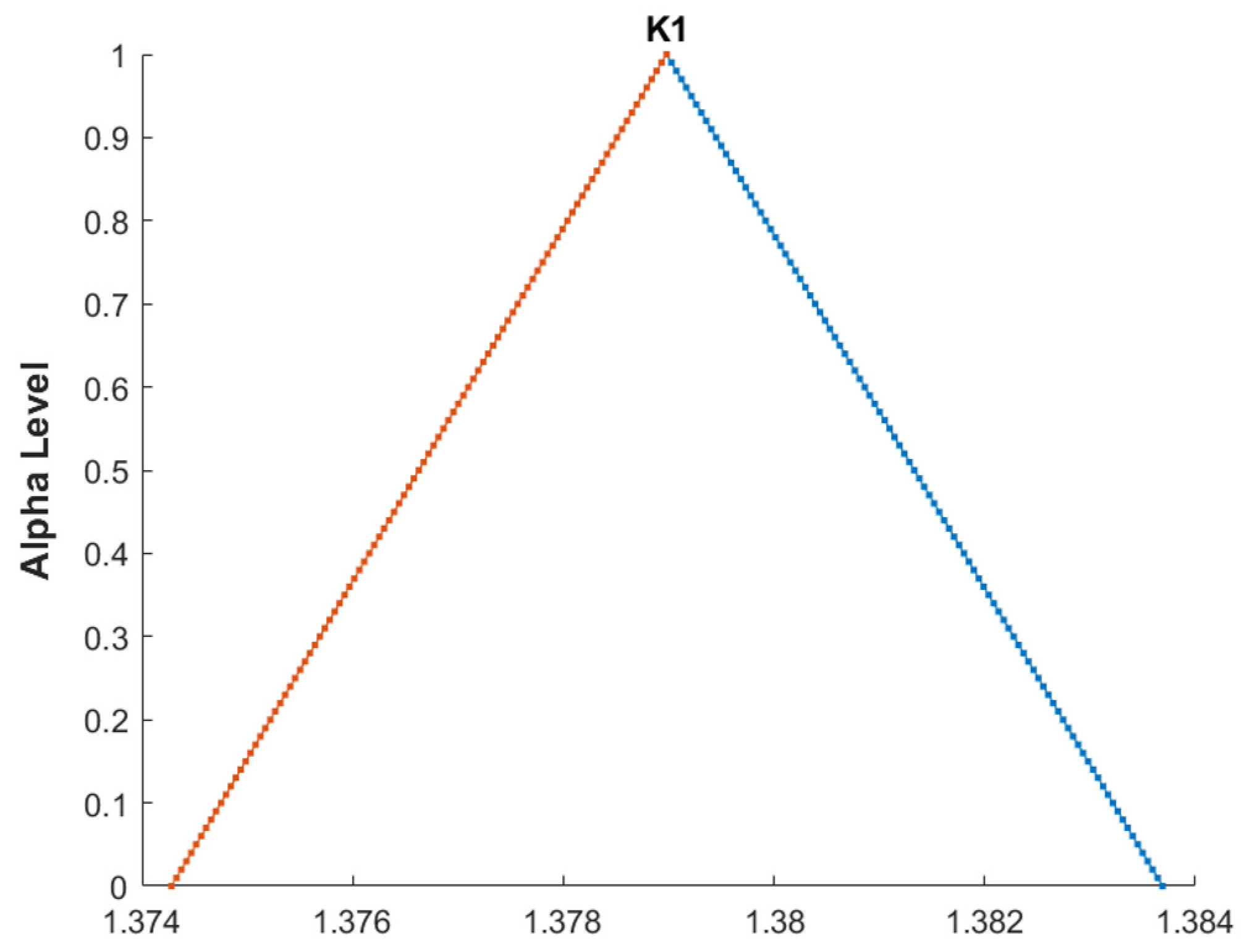
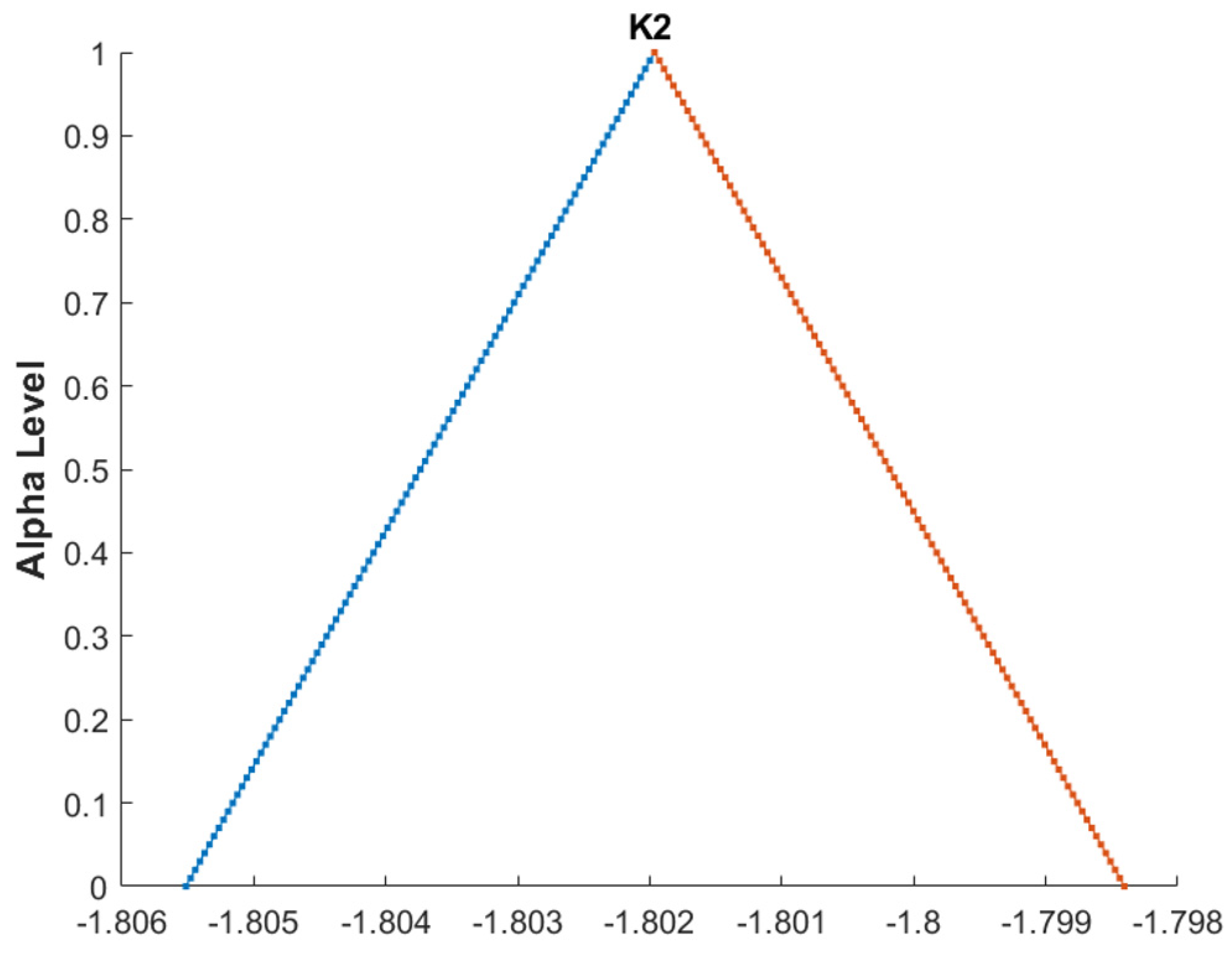
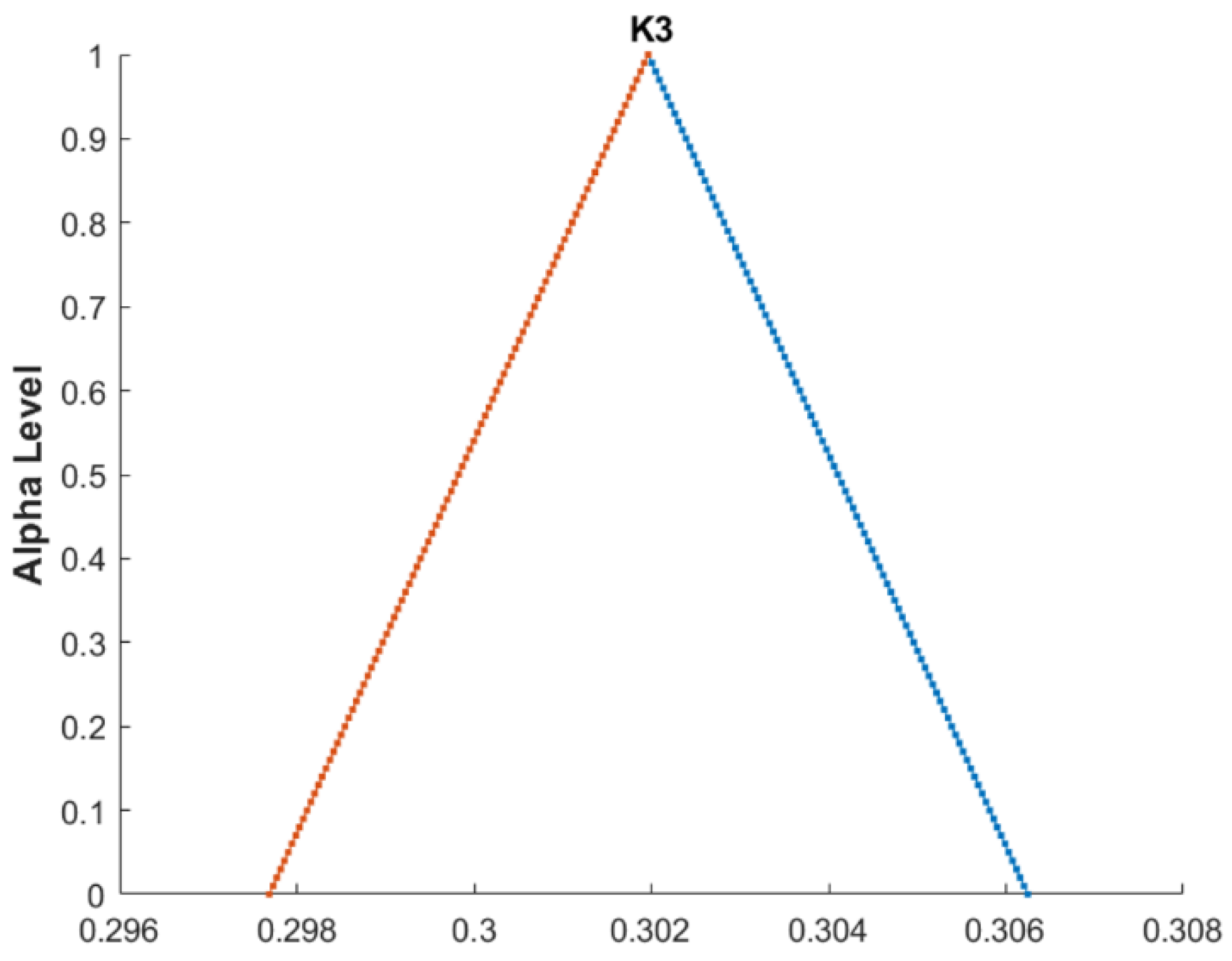
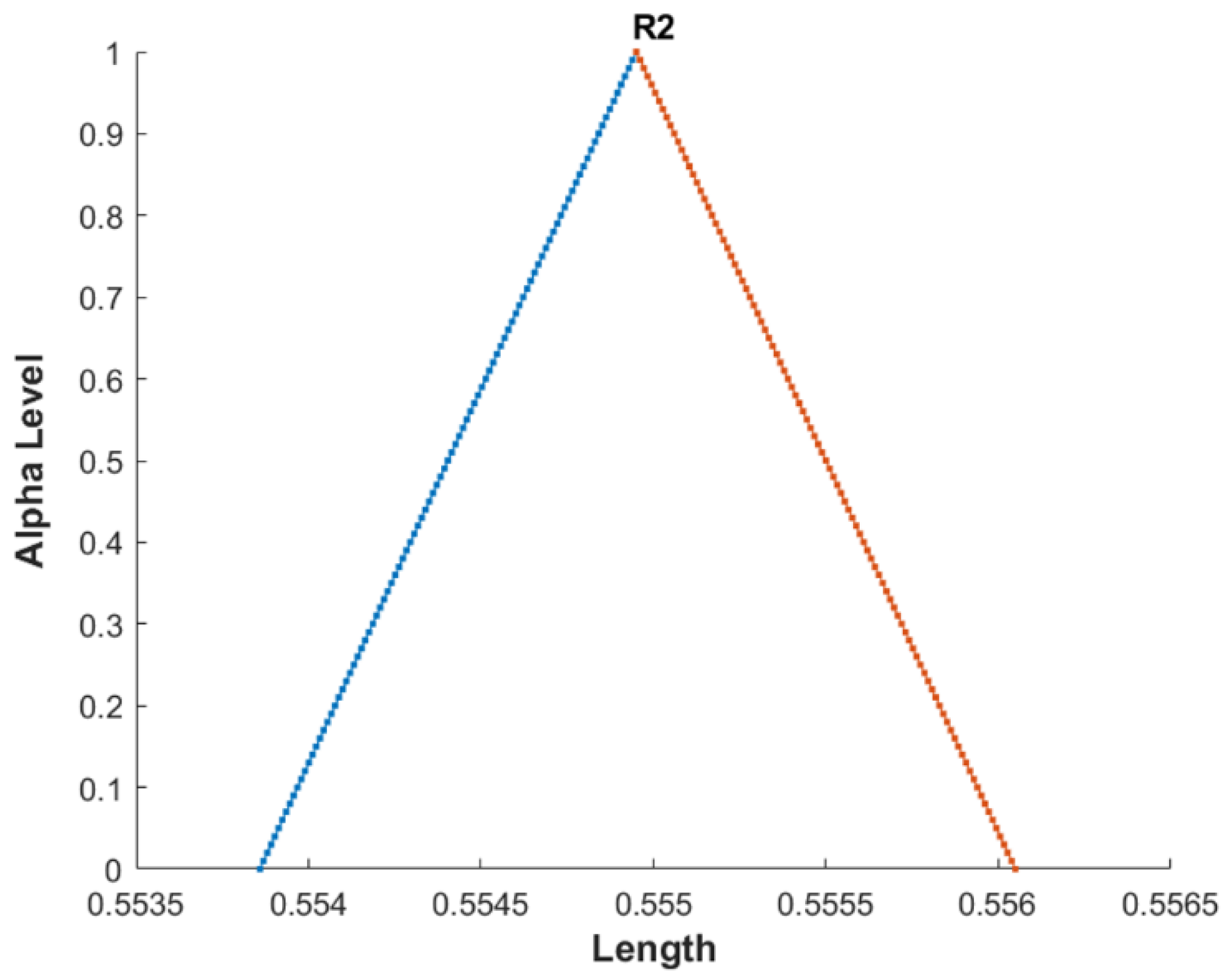
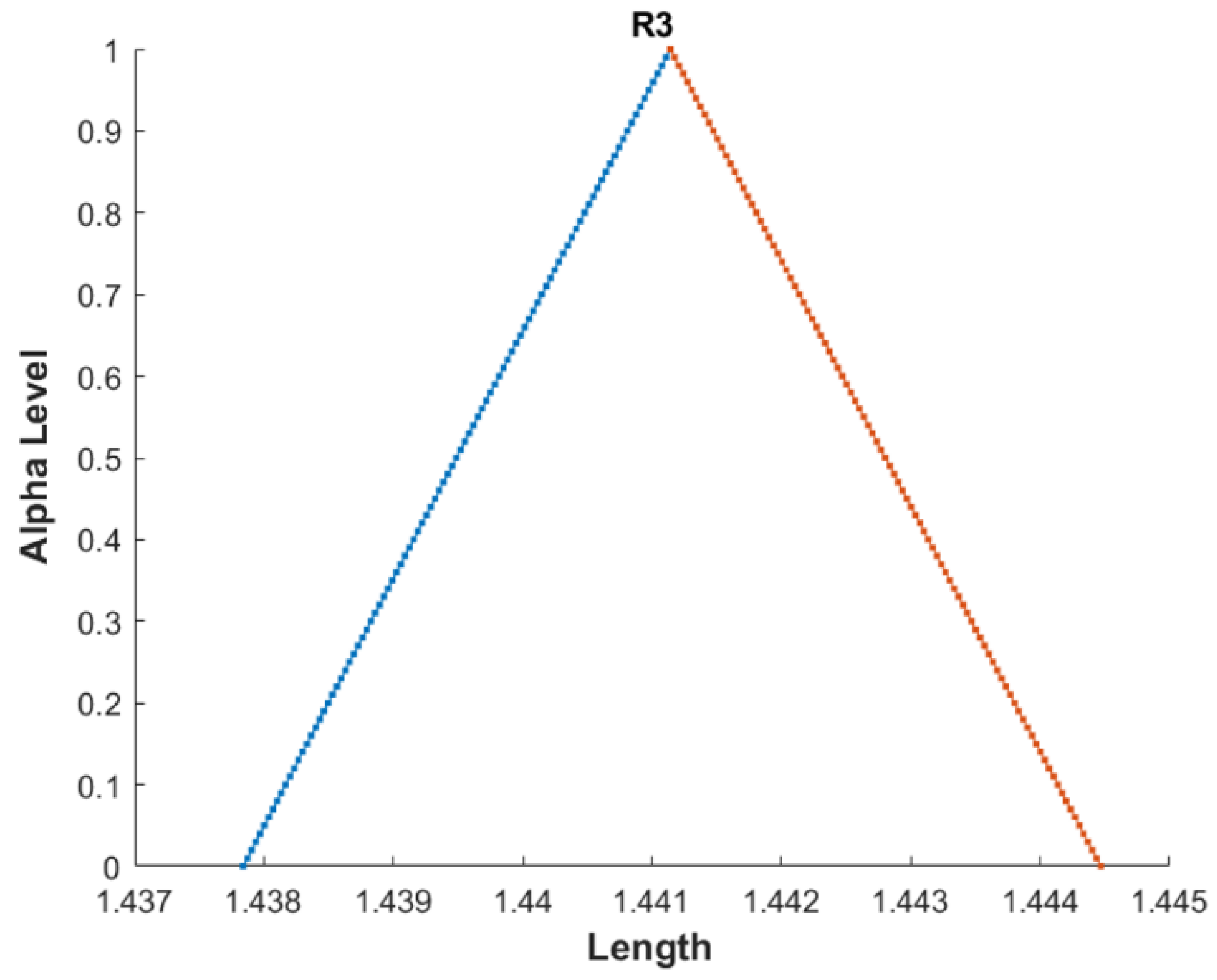
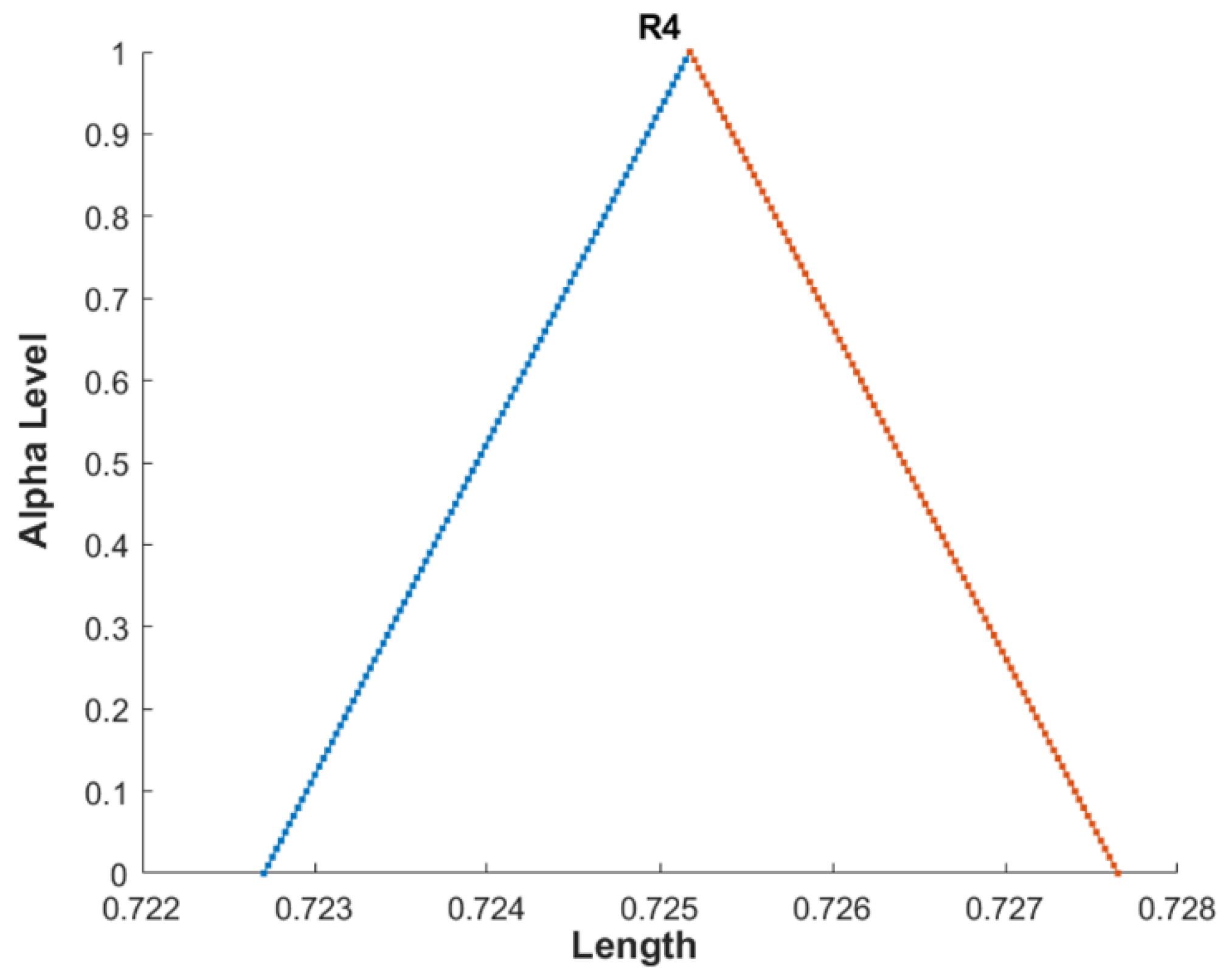
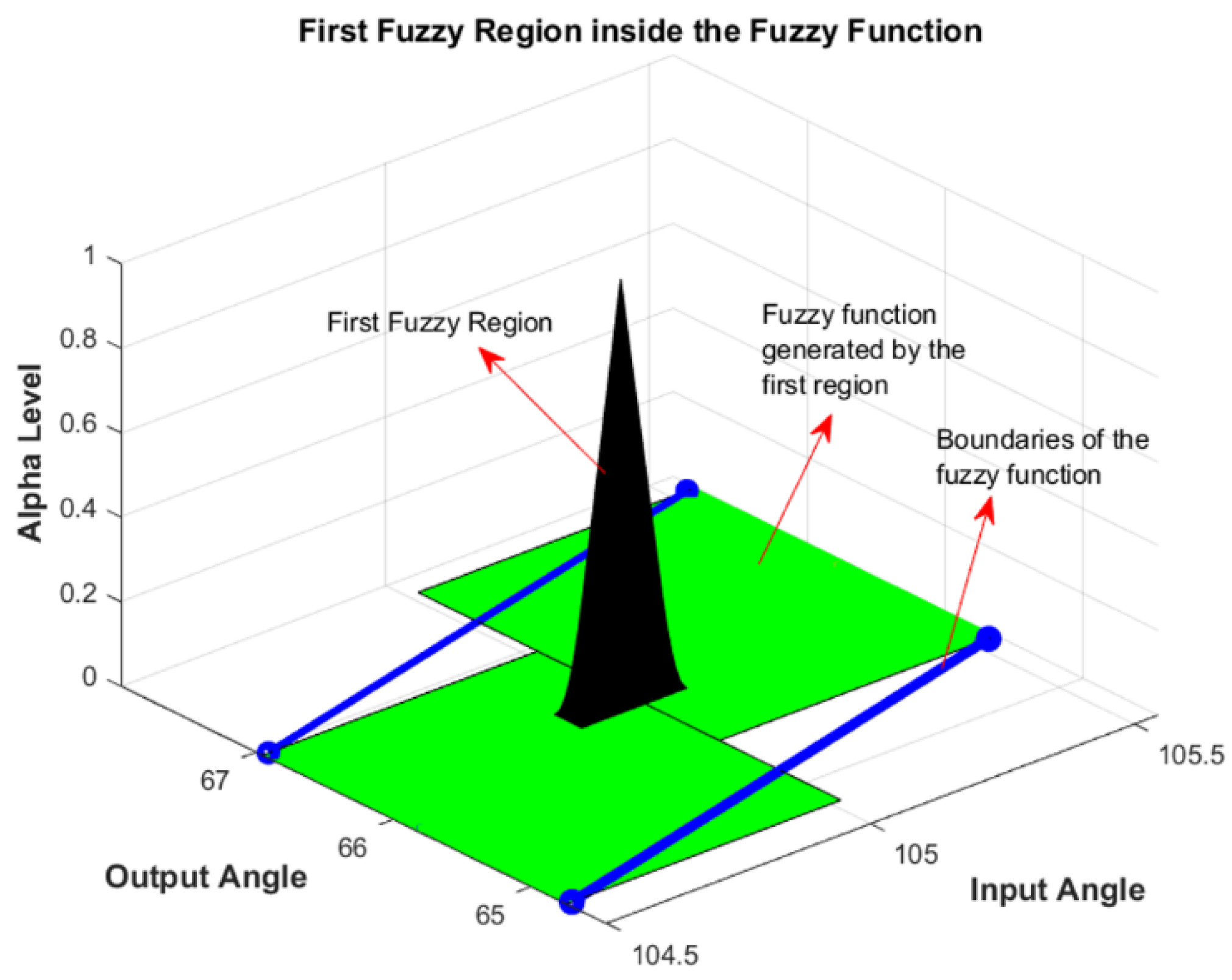
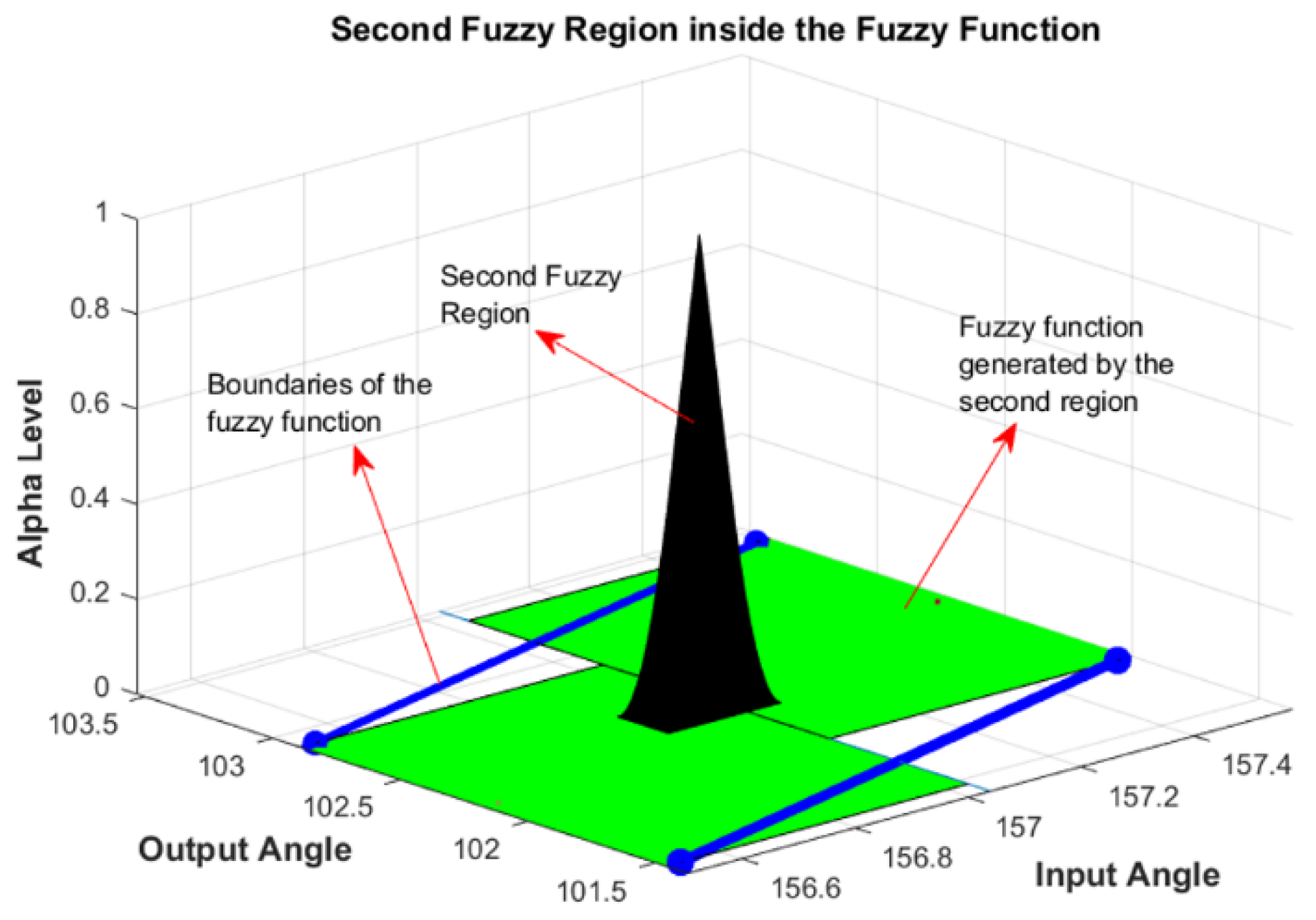
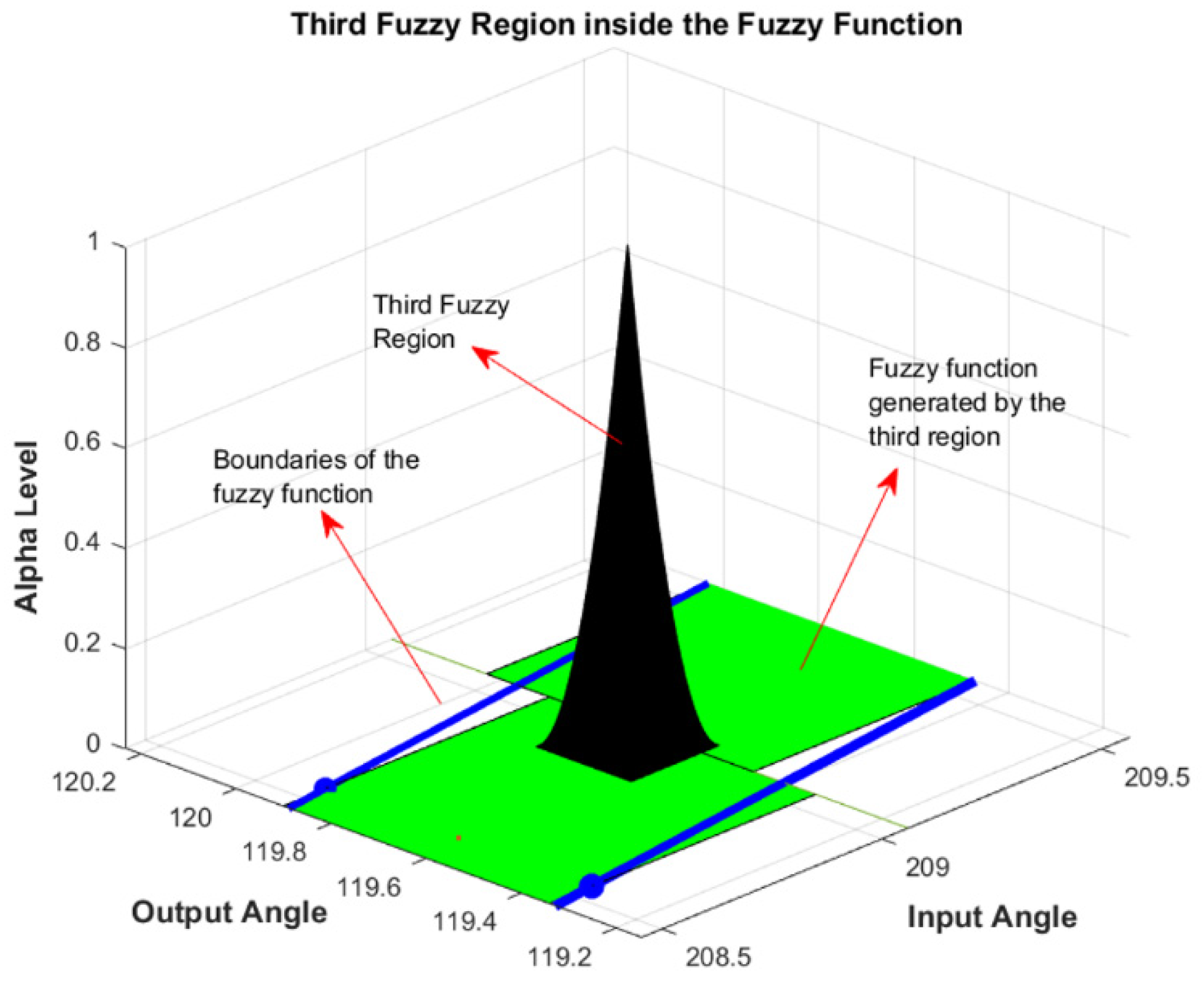
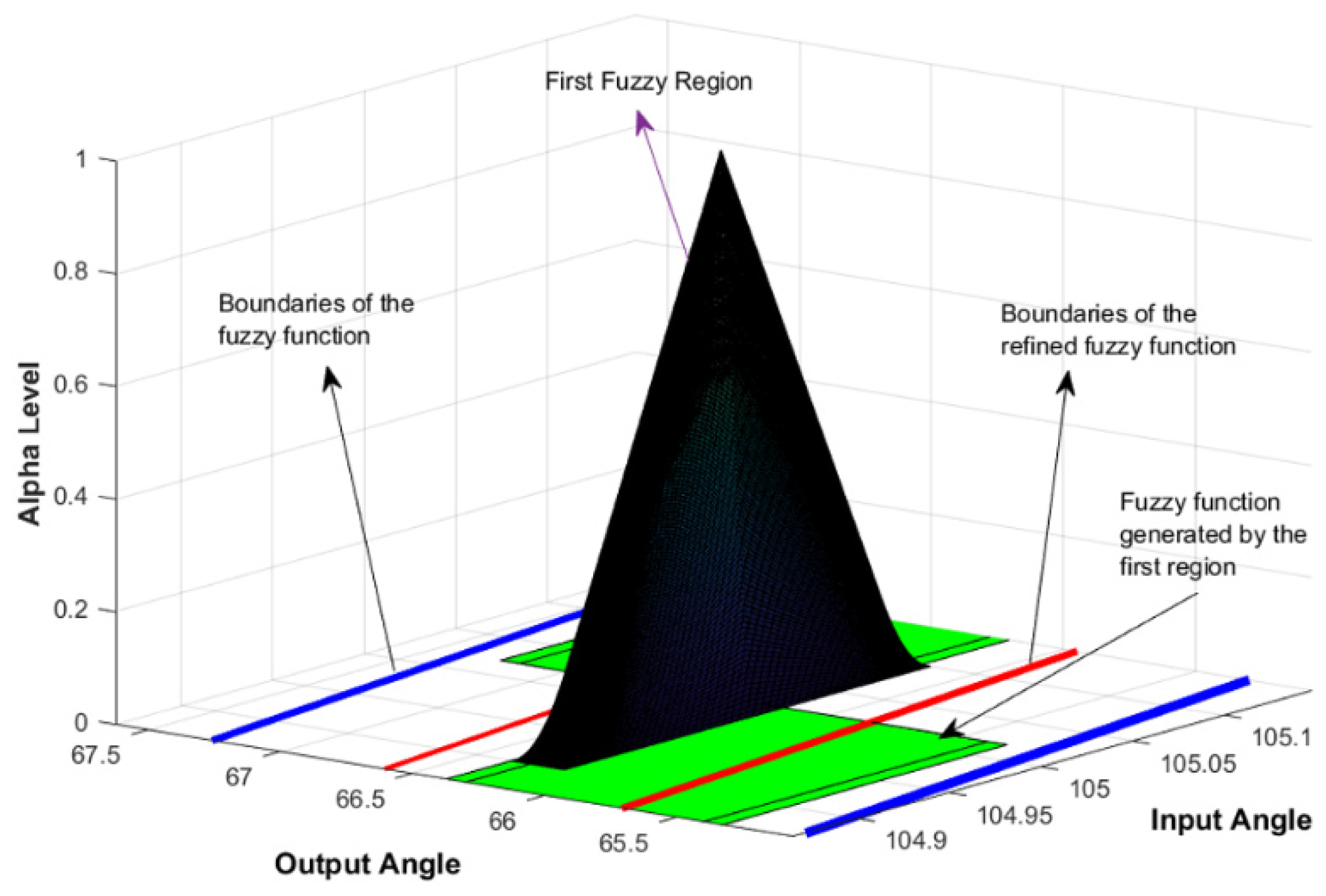

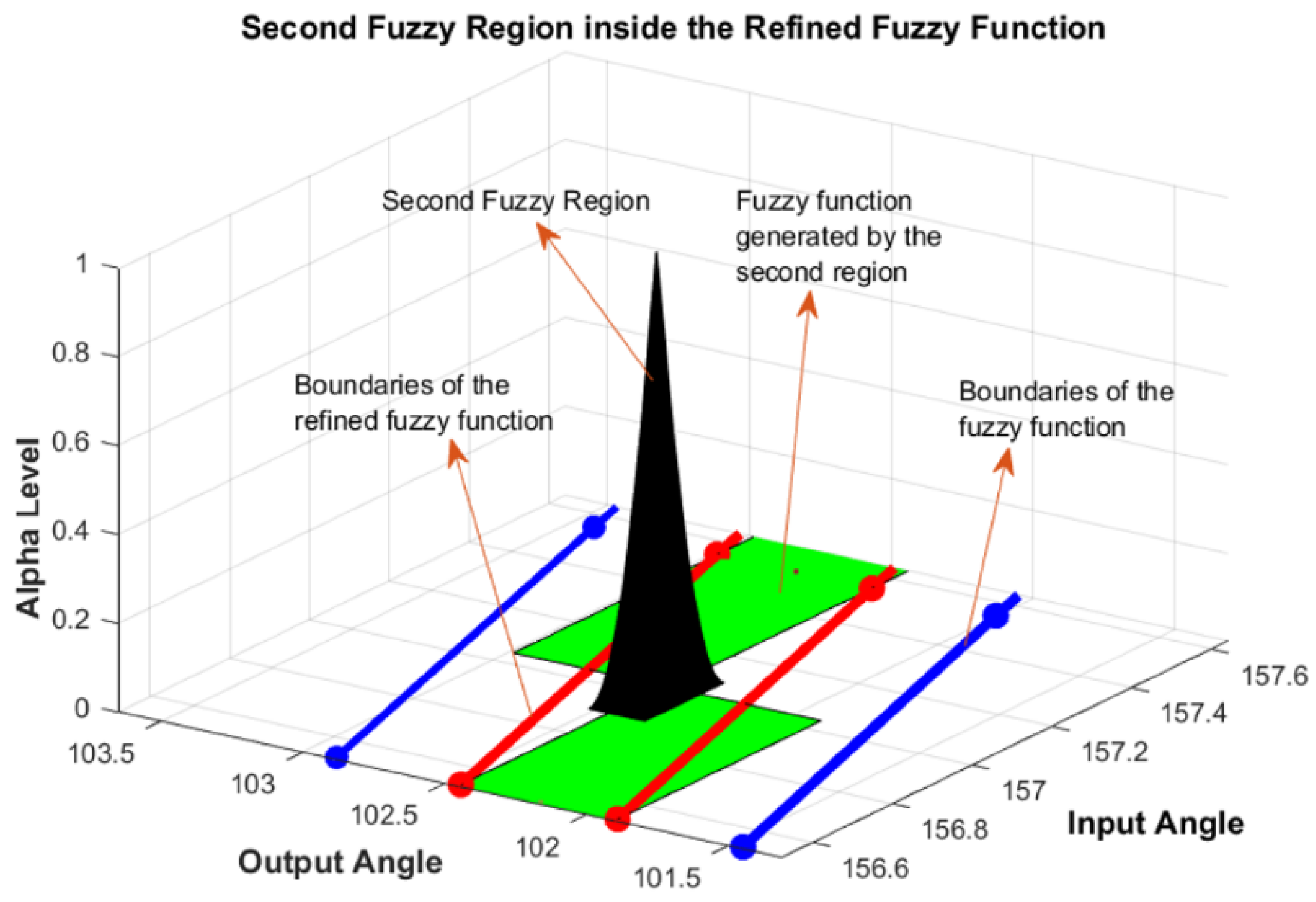
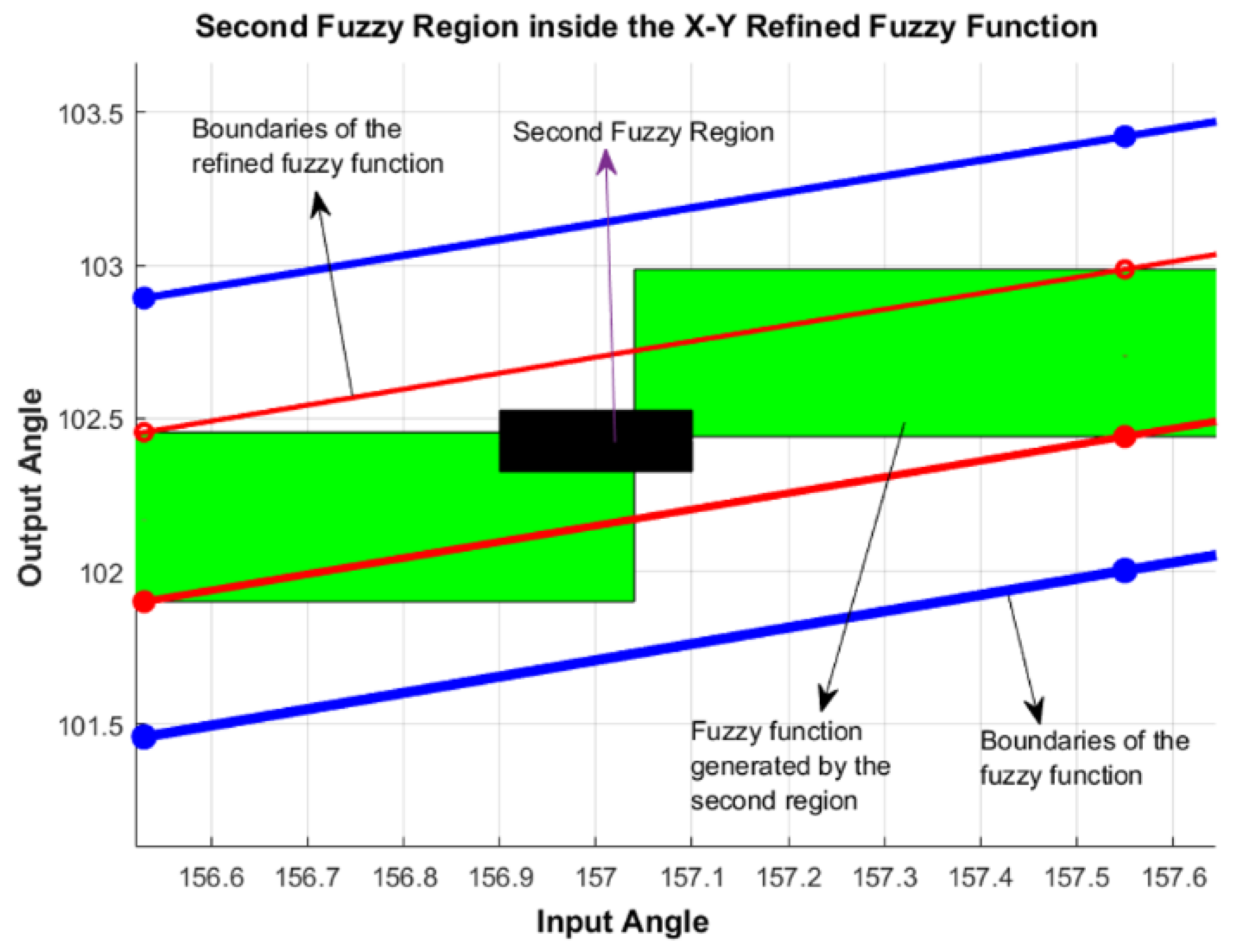
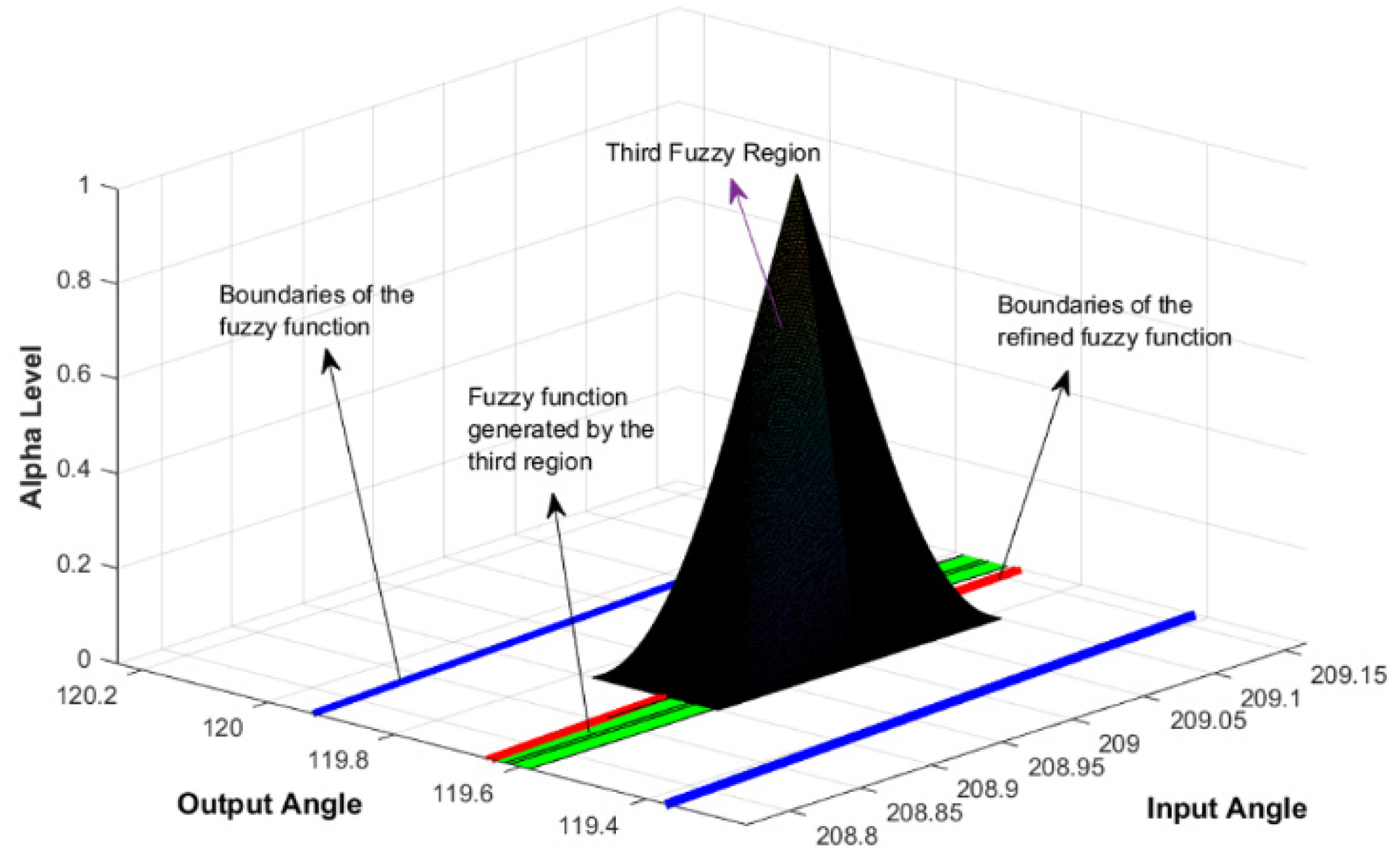
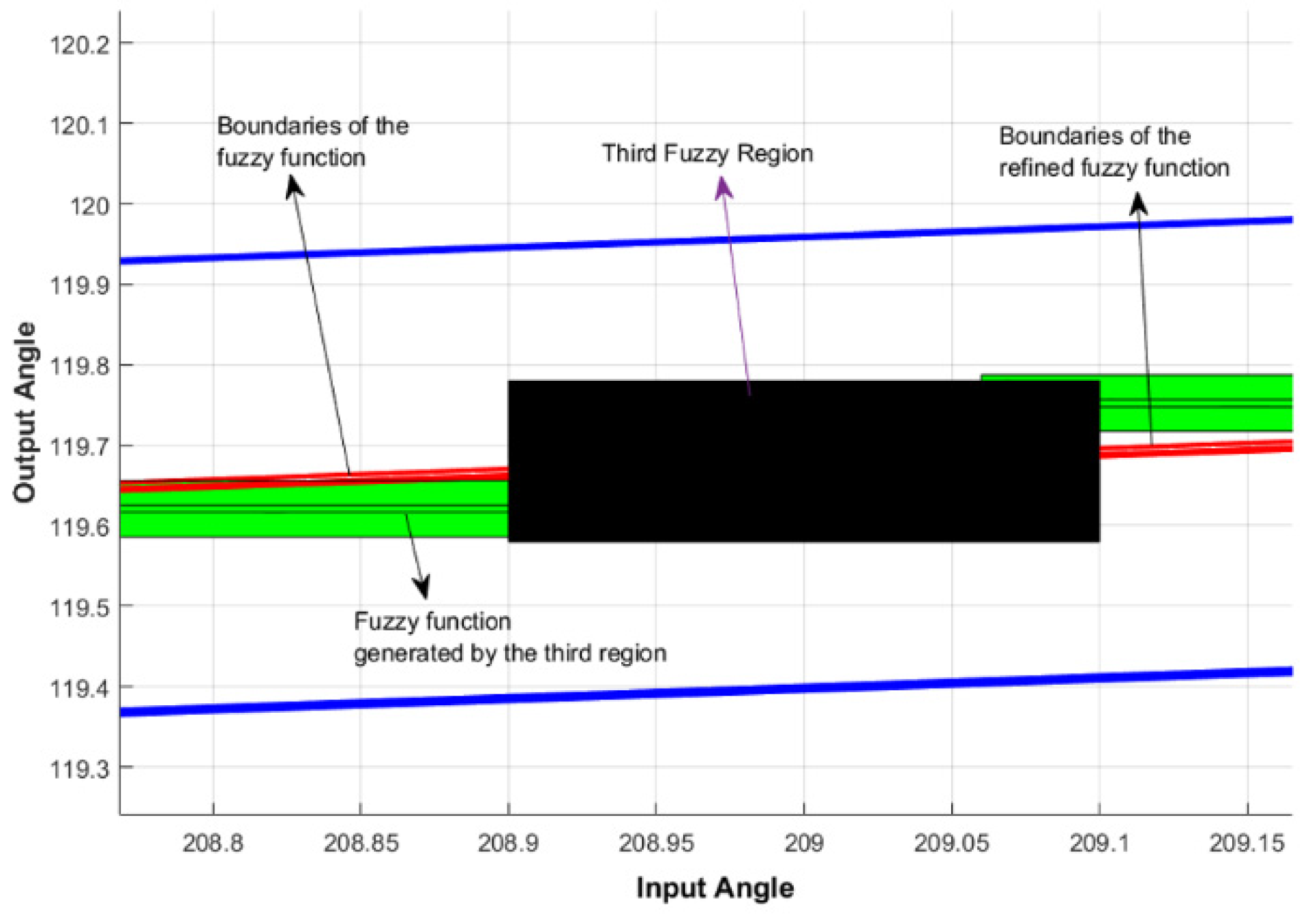
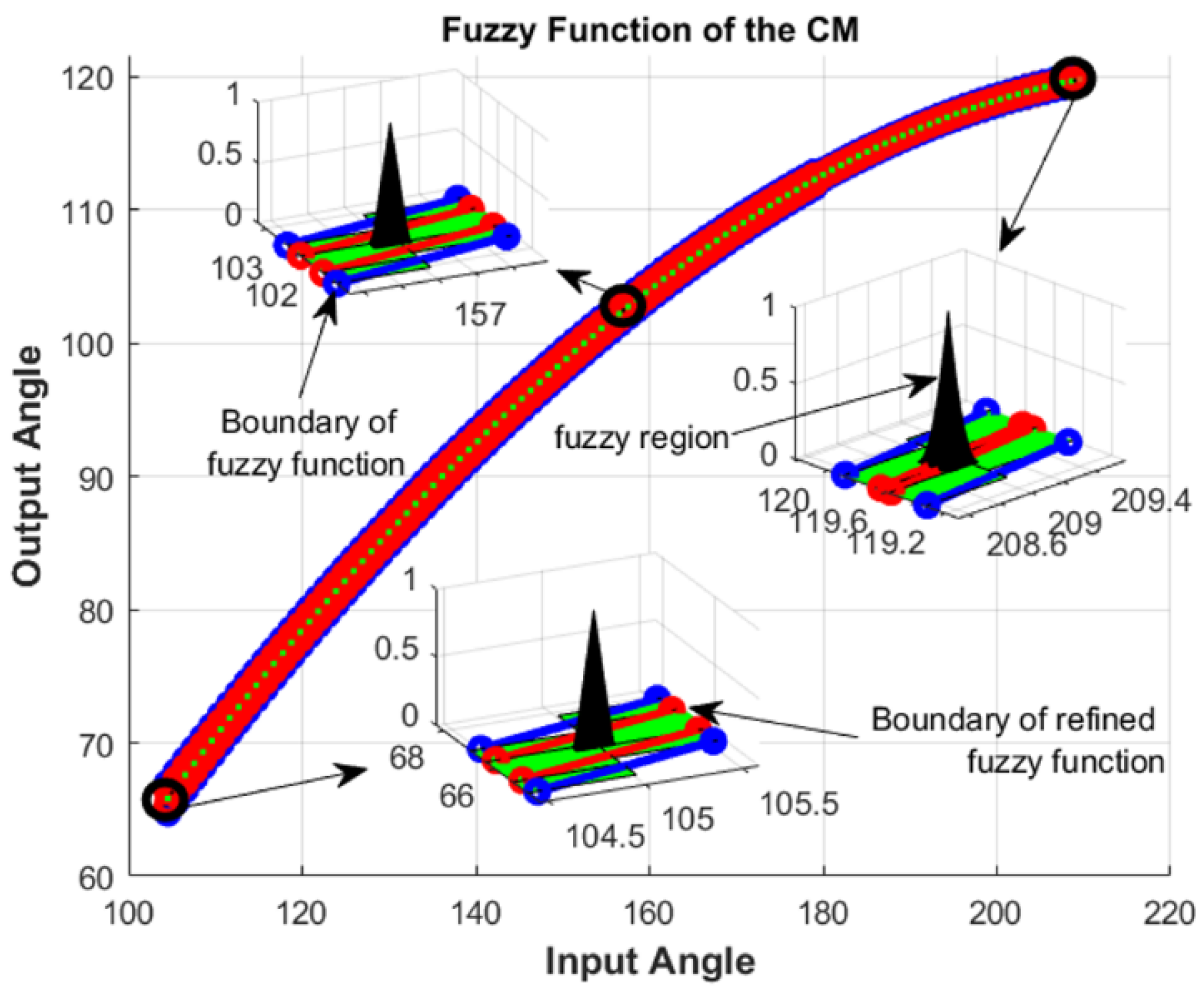
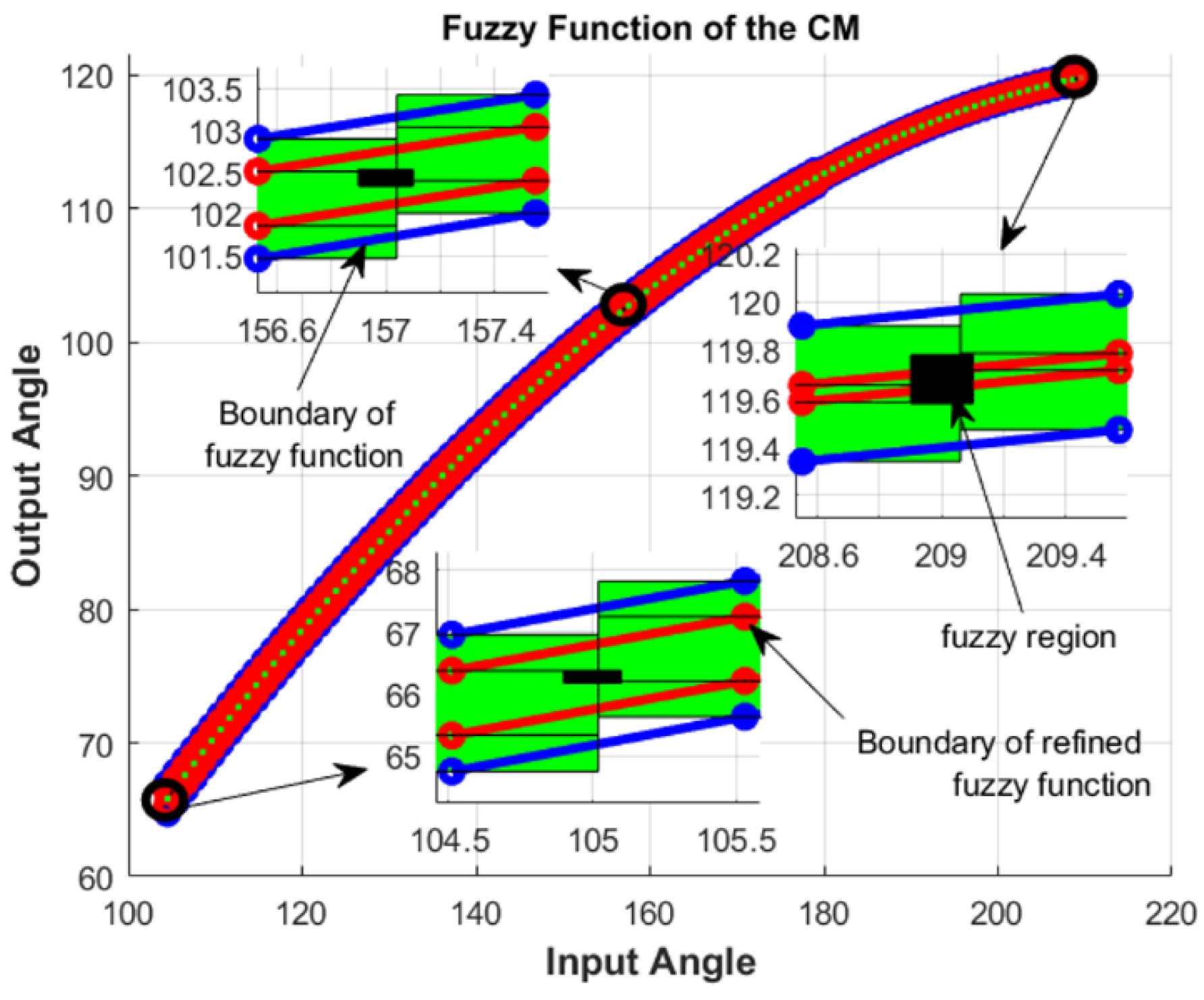
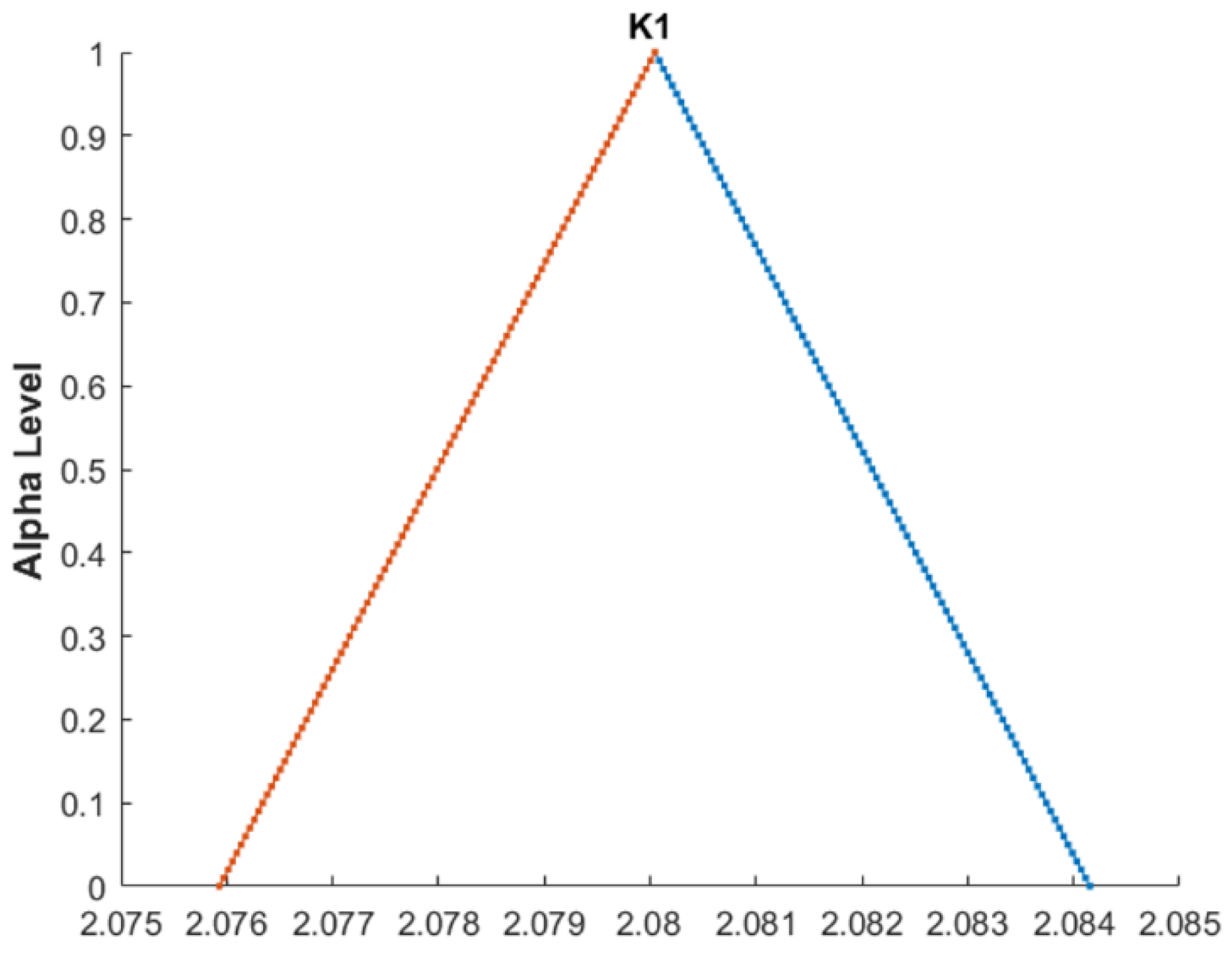


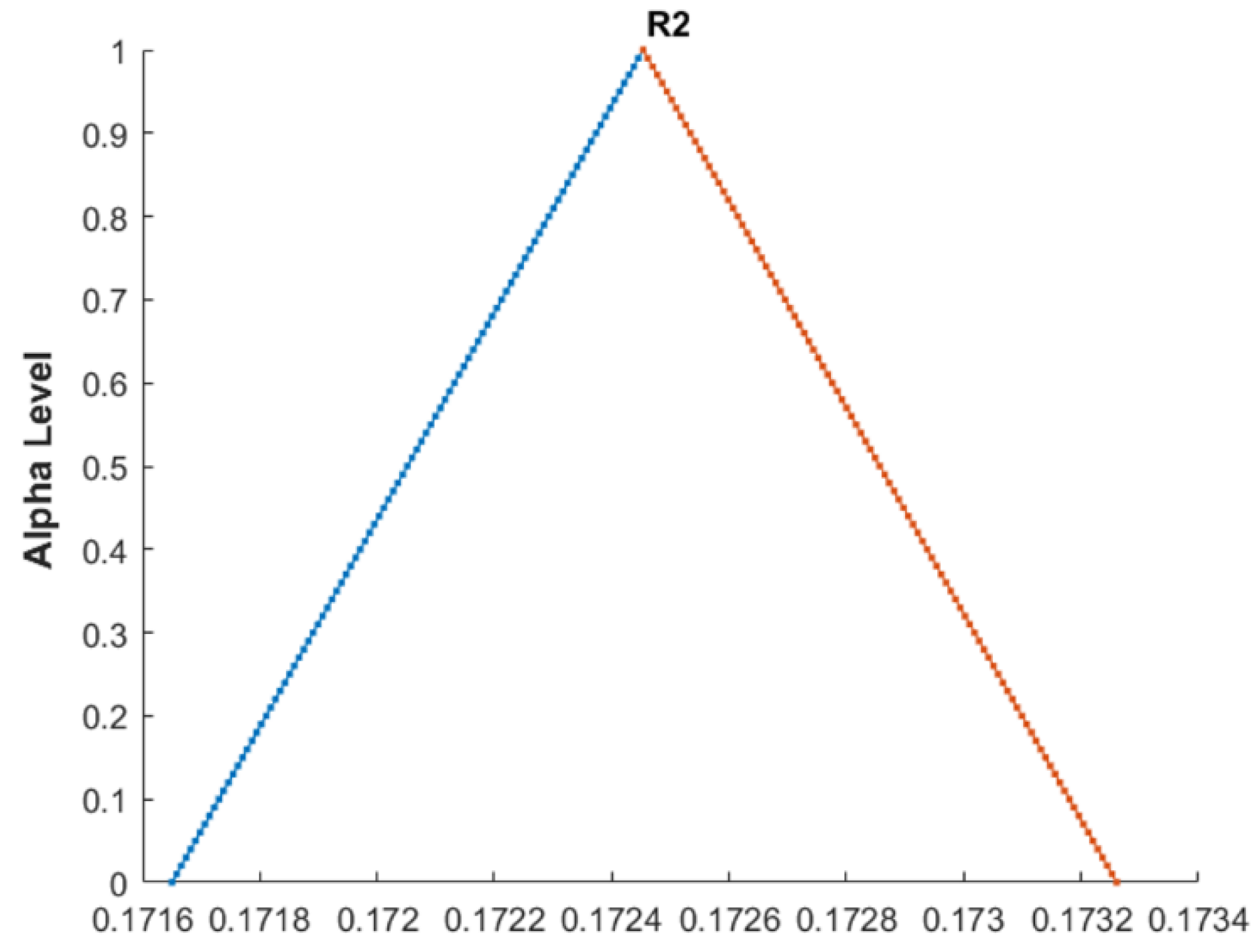
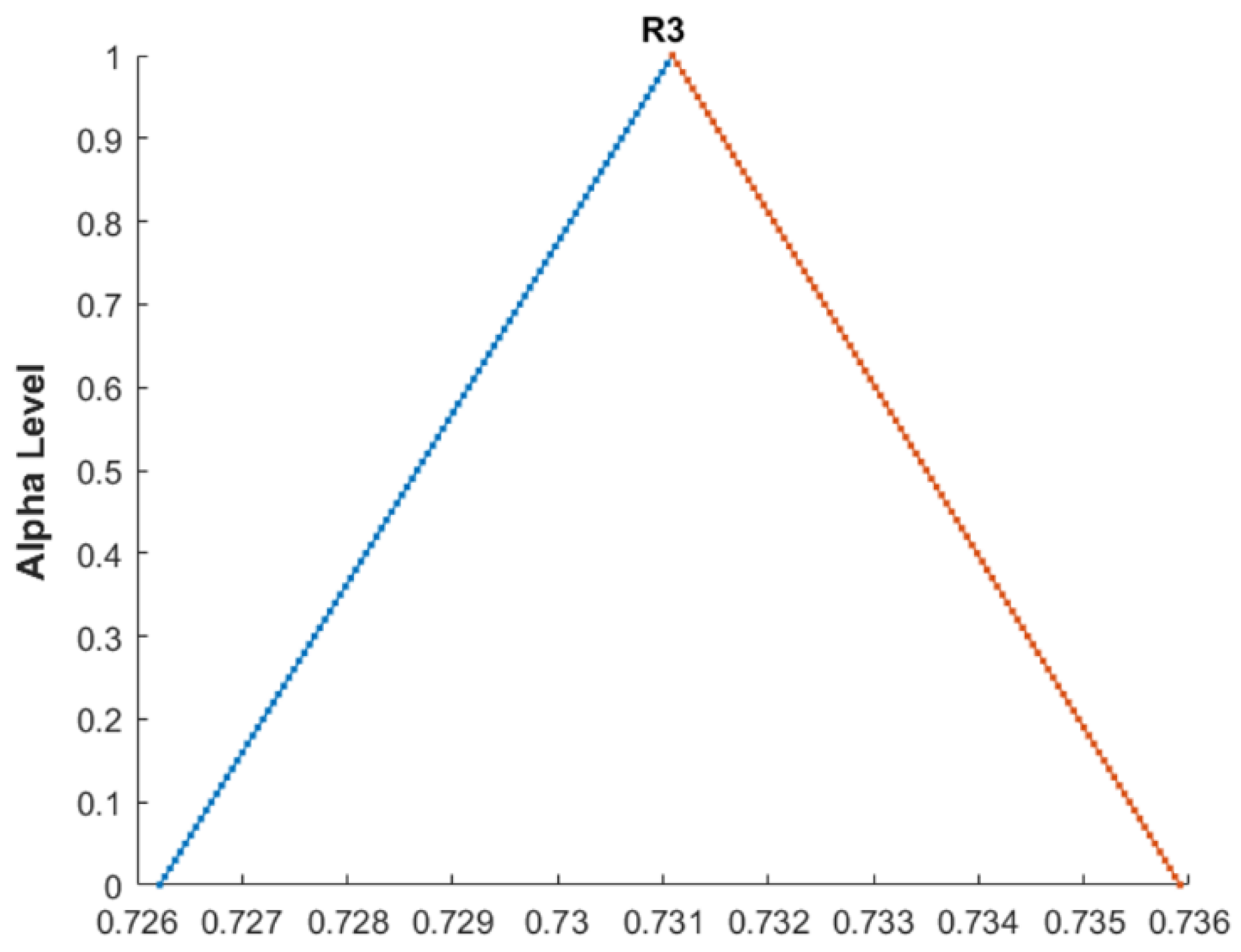

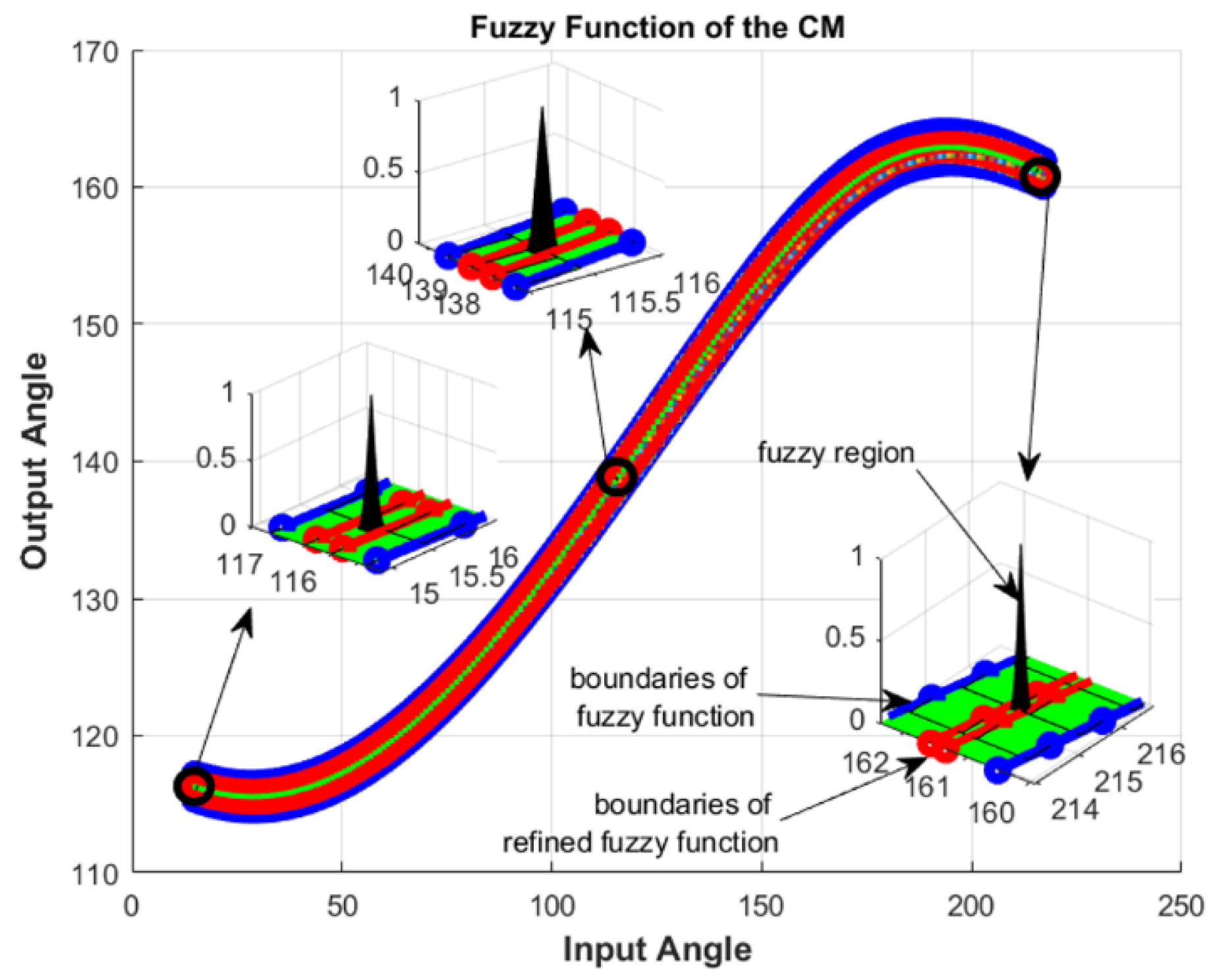
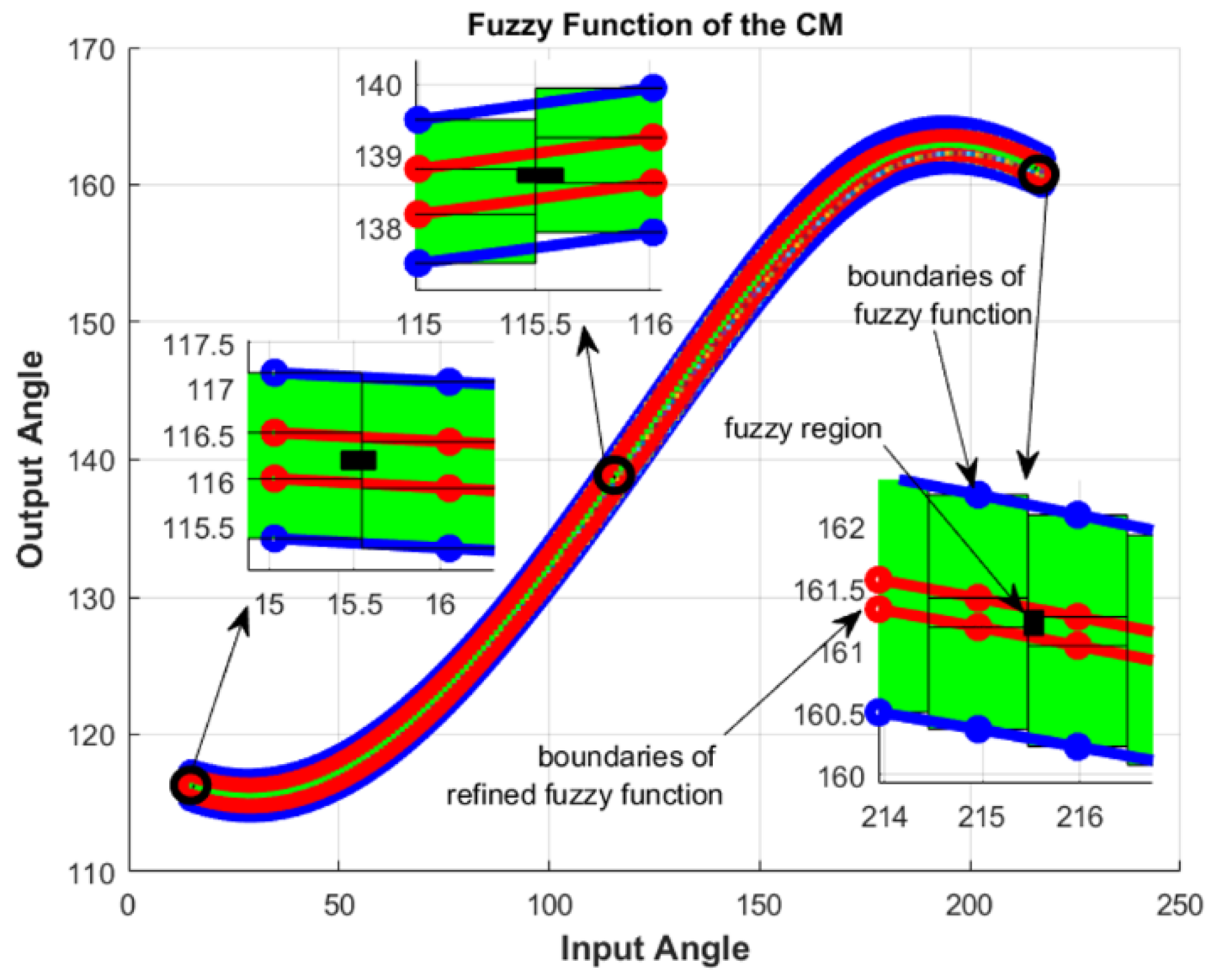
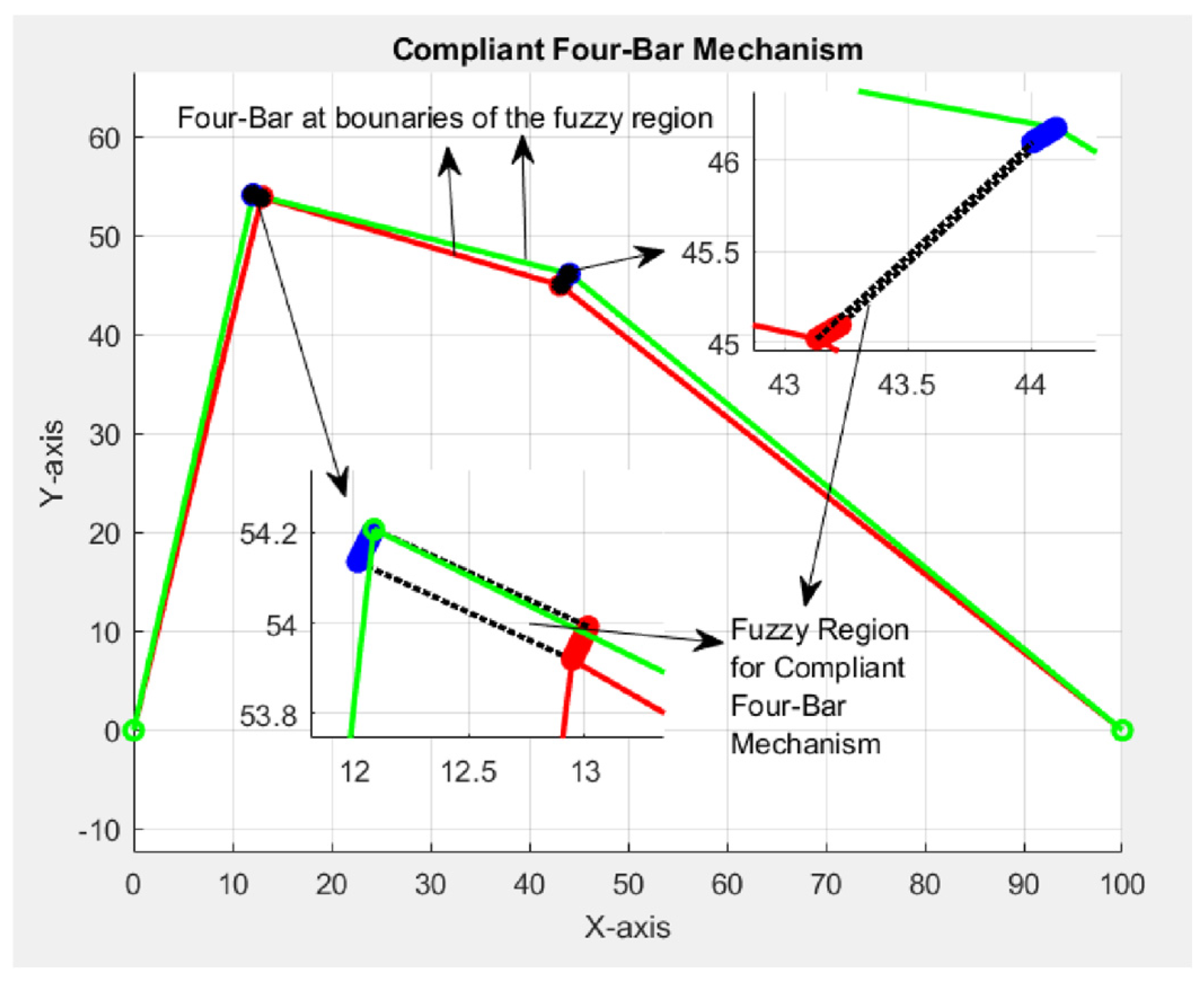
| Comparison Metric | Genetic Algorithms (GAs) | Fuzzy Function Approach |
|---|---|---|
| Population Initialization | Rely on random sampling, which may lead to poor representation of the search space. Uniform or biased sampling can be used to improve initial population distribution [24]. | Not required, as fuzzy function approach naturally incorporates variability and uncertainty into the design. |
| Infeasibility and Illegal Solutions | May produce infeasible or illegal solutions during the search process, requiring penalty functions or repair techniques to correct [24]. | Fuzzy function approach inherently accommodates a range of possible solutions due to fuzzy variable definitions, reducing the chance of infeasibility. |
| Sensitivity to Parameters | Highly sensitive to choices like population size, mutation rate, and crossover rate, leading to potential issues with nonconvergence or suboptimal results [24]. | Less sensitive to such parameters because it operates within a tolerance range of solutions, making it more adaptable to changes. |
| Robustness to Uncertainty | Limited robustness, as GAs optimize for specific parameters. Small variations in input conditions or link lengths can degrade performance [24]. | Designed to be robust to uncertainty in link lengths, input angles, and forces. Fuzzy synthesis accounts for variations, making the mechanism more adaptable to real-world conditions. |
| Optimization Efficiency | Require careful tuning of genetic operators to achieve global optima, which can take time and multiple generations. Convergence can be slow in complex design spaces [24]. | Faster in scenarios involving uncertainty, as it does not need to evolve a population. Instead, it optimizes within a fuzzy range of solutions. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhindi, A.; Chew, M.-S. Dimensional Synthesis of the Compliant Mechanism Using the Parametric Fuzzy Form of the Freudenstein Equation. Mathematics 2024, 12, 3170. https://doi.org/10.3390/math12203170
Alhindi A, Chew M-S. Dimensional Synthesis of the Compliant Mechanism Using the Parametric Fuzzy Form of the Freudenstein Equation. Mathematics. 2024; 12(20):3170. https://doi.org/10.3390/math12203170
Chicago/Turabian StyleAlhindi, Ahmed, and Meng-Sang Chew. 2024. "Dimensional Synthesis of the Compliant Mechanism Using the Parametric Fuzzy Form of the Freudenstein Equation" Mathematics 12, no. 20: 3170. https://doi.org/10.3390/math12203170
APA StyleAlhindi, A., & Chew, M.-S. (2024). Dimensional Synthesis of the Compliant Mechanism Using the Parametric Fuzzy Form of the Freudenstein Equation. Mathematics, 12(20), 3170. https://doi.org/10.3390/math12203170






