A Morley Type Triangular Finite Element with High Convergence for the Biharmonic Problem
Abstract
1. Introduction
2. The Model Problem and Some Preliminaries
3. Convergence Theorems
- (H1)
- , , ,
- (H2)
- , is continuous at the interior vertices and zero at the vertices on ,
- (H3)
- , ,
- (H4)
- , , ,
4. A New Morley Type Element with High Convergence
- K is a triangle.
- .
- The degrees of freedom are given by ,
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meleshko, V. Selected topics in the history of the two-dimensional biharmonic problem. Appl. Mech. Rev. 2003, 56, 33–85. [Google Scholar] [CrossRef]
- Ushakov, A.L. Analysis of the problem for the biharmonic equation. J. Comput. Eng. Math. 2022, 9, 43–58. [Google Scholar] [CrossRef]
- Argyris, J.; Balmer, H.; Doltsinis, J.S.; Dunne, P.; Haase, M.; Kleiber, M.; Malejannakis, G.; Mlejnek, H.P.; Müller, M.; Scharpf, D. Finite element method—The natural approach. Comput. Methods Appl. Mech. Eng. 1979, 17, 1–106. [Google Scholar] [CrossRef]
- Bell, K. A refined triangular plate bending finite element. Int. J. Numer. Methods Eng. 1969, 1, 101–122. [Google Scholar] [CrossRef]
- Bogner, F. The generation of interelement compatible stiffness and mass matrices by the use of interpolation formulae. In Proceedings of the Conference on Matrix Methods in Structural Mechanics, Wright Patterson Air Force Base, OH, USA, 26–28 October 1965. [Google Scholar]
- Clough, R. Finite element stiffness matrices for analysis of plates in bending. In Proceedings of the 1st Conference on Matrix Methods in Structural Mechanics, Wright-Patterson Air Force Base, OH, USA, 26–28 October 1965. [Google Scholar]
- Zienkiewicz, O.; Taylor, R.; Too, J. Reduced integration technique in general analysis of plates and shells. Int. J. Numer. Methods Eng. 1971, 3, 275–290. [Google Scholar] [CrossRef]
- De Veubeke, B.F. A conforming finite element for plate bending. Int. J. Solids Struct. 1968, 4, 95–108. [Google Scholar] [CrossRef]
- Lascaux, P.; Lesaint, P. Some nonconforming finite elements for the plate bending problem. Rev. Fr. d’Autom. Inform. Rech. Opér. Anal. Numér. 1975, 9, 9–53. [Google Scholar] [CrossRef][Green Version]
- Morley, L. The triangular equilibrium element in the solution of plate bending problems. Aeronaut. Q. 1968, 19, 149–169. [Google Scholar] [CrossRef]
- Adak, D.; Mora, D.; Silgado, A. A Morley-type virtual element approximation for a wind-driven ocean circulation model on polygonal meshes. J. Comput. Appl. Math. 2023, 425, 115026. [Google Scholar] [CrossRef]
- De Veubeke, B.F. Variational principles and the patch test. Int. J. Numer. Methods Eng. 1974, 8, 783–801. [Google Scholar] [CrossRef]
- Adini, A.; Clough, R.W. Analysis of Plate Bending by the Finite Element Method; University of California: Berkeley, CA, USA, 1960. [Google Scholar]
- Shi, Z. On the convergence of the incomplete biquadratic nonconforming plate element. Math. Numer. Sin. 1986, 8, 53–62. [Google Scholar]
- Hu, J.; Huang, Y.; Zhang, S. The lowest order differentiable finite element on rectangular grids. SIAM J. Numer. Anal. 2011, 49, 1350–1368. [Google Scholar] [CrossRef]
- Park, C.; Sheen, D. A quadrilateral Morley element for biharmonic equations. Numer. Math. 2013, 124, 395–413. [Google Scholar] [CrossRef]
- Shi, D.; Yang, H. Superconvergent estimates of conforming finite element method for nonlinear time-dependent Joule heating equations. Numer. Methods Partial. Differ. Equ. 2018, 34, 336–356. [Google Scholar] [CrossRef]
- Luo, P.; Lin, Q. Accuracy analysis of the Adini element for biharmonic equation. Acta Math. Sin. 2004, 20, 135–146. [Google Scholar] [CrossRef]
- Mao, S.; Shi, Z.c. High accuracy analysis of two nonconforming plate elements. Numer. Math. 2009, 111, 407–443. [Google Scholar] [CrossRef]
- Zhao, J.; Mao, S.; Zhang, B.; Wang, F. The interior penalty virtual element method for the biharmonic problem. Math. Comput. 2023, 92, 1543–1574. [Google Scholar] [CrossRef]
- Sun, M.; Song, S.; Liu, Z. A nonconforming scheme with high accuracy for the plate bending problem. Comput. Math. Appl. 2014, 68, 1083–1092. [Google Scholar] [CrossRef]
- Gao, B.; Zhang, S.; Wang, M. A note on the nonconforming finite elements for elliptic problems. J. Comput. Math. 2011, 29, 215–226. [Google Scholar]
- Chen, H.; Chen, S.; Qiao, Z. C0-nonconforming tetrahedral and cuboid elements for the three-dimensional fourth order elliptic problem. Numer. Math. 2013, 124, 99–119. [Google Scholar] [CrossRef]
- Chen, H.; Chen, S.; Qiao, Z.H. C0-nonconforming triangular prism elements for the three-dimensional fourth order elliptic problem. J. Sci. Comput. 2013, 55, 645–658. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, S.; Zhang, B. The nonconforming virtual element method for plate bending problems. Math. Models Methods Appl. Sci. 2016, 26, 1671–1687. [Google Scholar] [CrossRef]
- Antonietti, P.F.; Manzini, G.; Verani, M. The fully nonconforming virtual element method for biharmonic problems. Math. Models Methods Appl. Sci. 2018, 28, 387–407. [Google Scholar] [CrossRef]
- Carstensen, C.; Khot, R.; Pani, A.K. Nonconforming virtual elements for the biharmonic equation with Morley degrees of freedom on polygonal meshes. SIAM J. Numer. Anal. 2023, 61, 2460–2484. [Google Scholar] [CrossRef]
- Grisvard, P. Singularities in Boundary Value Problems; Recherches en Mathématiques Appliquées [Research in Applied Mathematics]; Masson: Paris, France; Springer: Berlin/Heidelberg, Germany, 1992; Volume 22, pp. xiv+199. [Google Scholar]
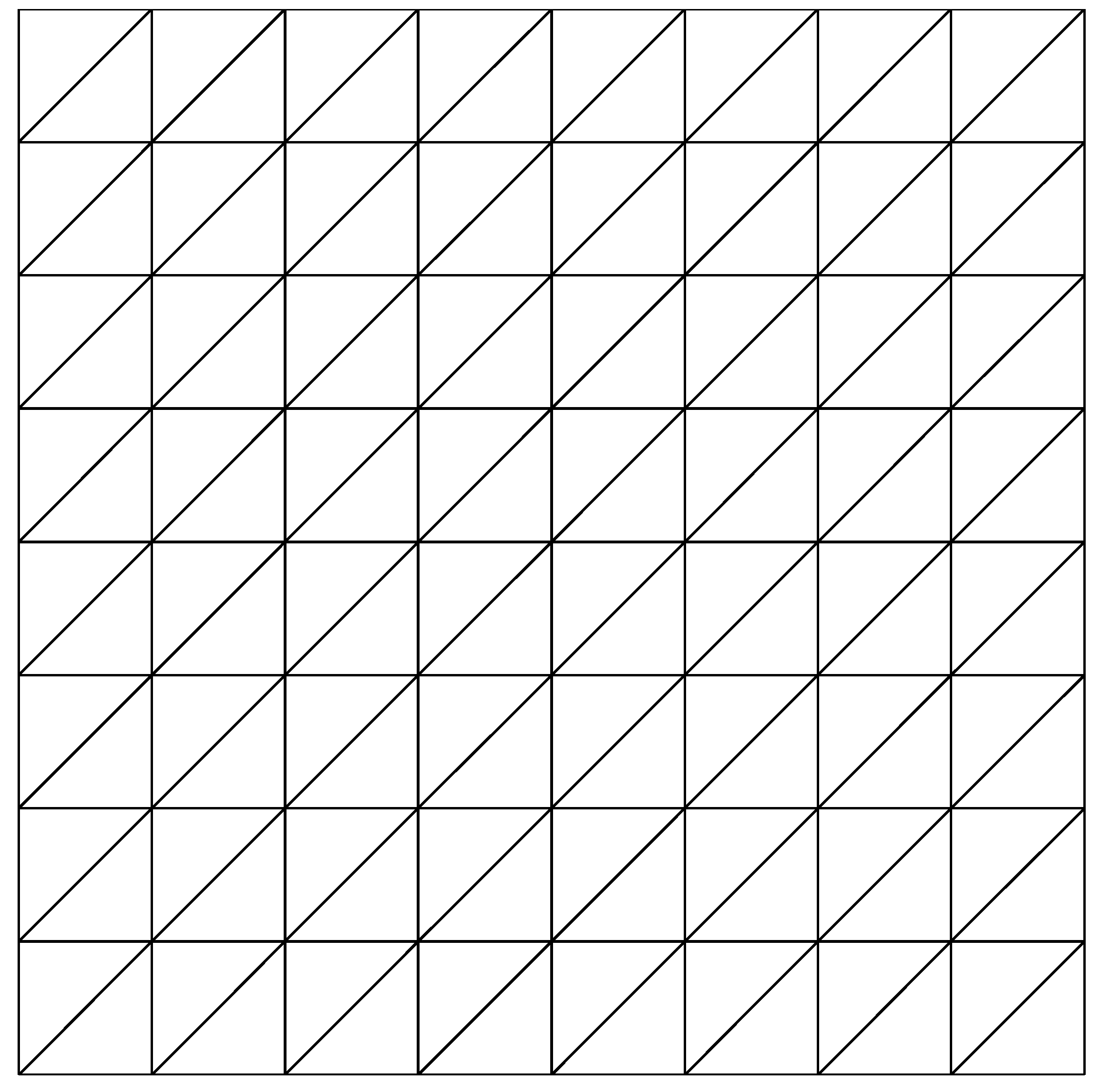
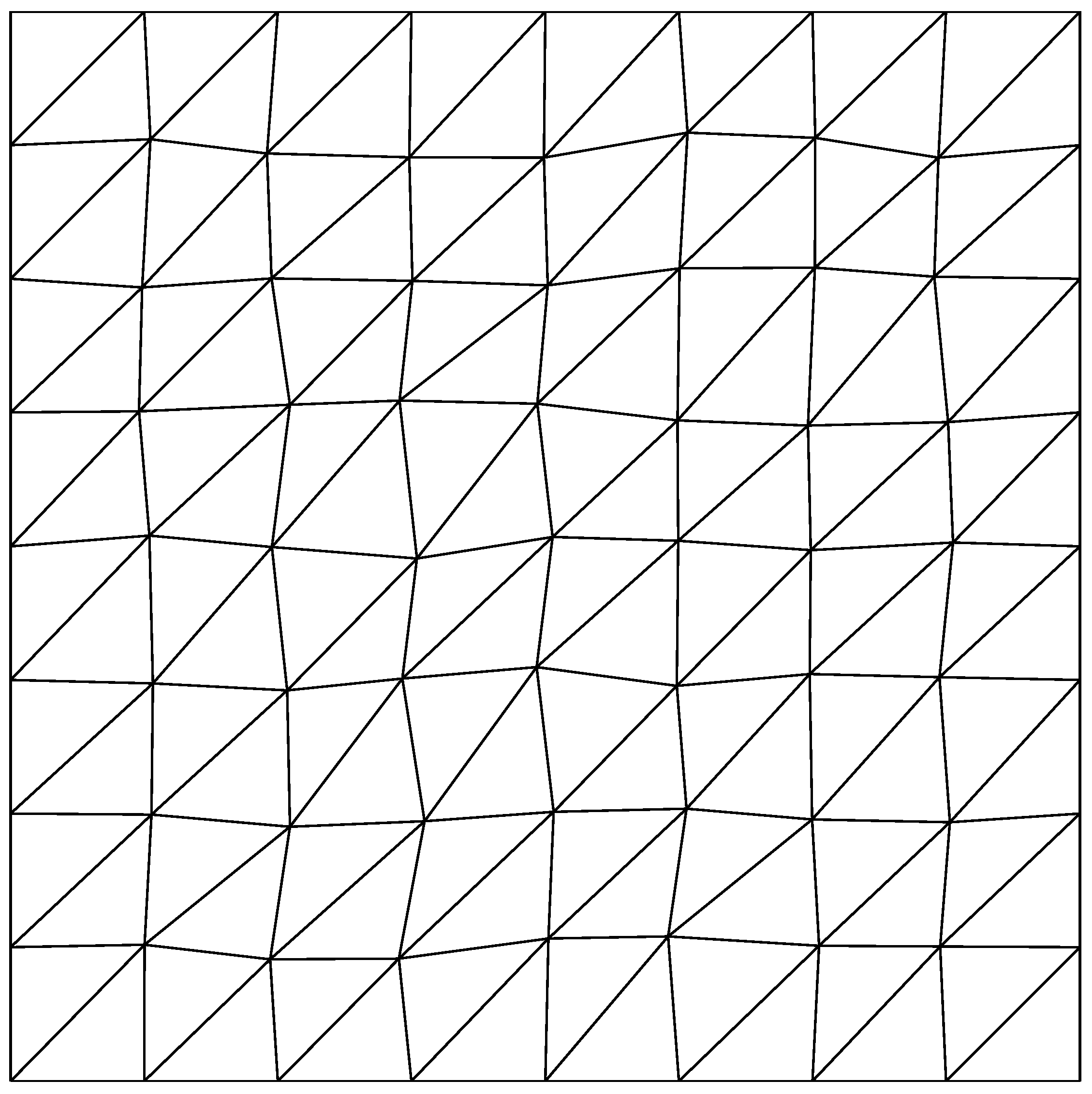
| n | ||||||
|---|---|---|---|---|---|---|
| Value | Order | Value | Order | Value | Order | |
| 4 | 0.0030 | - | 0.0504 | - | 1.4953 | - |
| 8 | 3.6927 | 0.0072 | 2.8074 | 0.3935 | 1.9260 | |
| 16 | 3.7706 | 0.0010 | 2.8480 | 0.1016 | 1.9535 | |
| 32 | 3.8811 | 2.9206 | 0.0258 | 1.9775 | ||
| 64 | 3.9463 | 2.9661 | 0.0065 | 1.9889 | ||
| 128 | 4.0611 | 2.9848 | 0.0016 | 2.0224 |
| n | ||||||
|---|---|---|---|---|---|---|
| Value | Order | Value | Order | Value | Order | |
| 4 | 0.0033 | - | 0.0547 | - | 1.5881 | - |
| 8 | 3.6929 | 0.0077 | 2.8286 | 0.4098 | 1.9543 | |
| 16 | 3.8453 | 0.0010 | 2.9449 | 0.1049 | 1.9659 | |
| 32 | 3.8654 | 2.8556 | 0.0268 | 1.9687 | ||
| 64 | 3.9518 | 2.9681 | 0.0068 | 1.9786 | ||
| 128 | 3.9750 | 2.9850 | 0.0017 | 2.0000 |
| n | ||||||
|---|---|---|---|---|---|---|
| Value | Order | Value | Order | Value | Order | |
| 4 | 0.0057 | - | 0.0978 | - | 2.8488 | - |
| 8 | 3.8169 | 0.0121 | 3.0148 | 0.6773 | 2.0725 | |
| 16 | 3.1592 | 0.0024 | 2.3339 | 0.2463 | 1.4594 | |
| 32 | 3.7039 | 2.7463 | 0.0668 | 1.8825 | ||
| 64 | 3.8472 | 2.8794 | 0.0173 | 1.9491 | ||
| 128 | 3.9413 | 2.9421 | 0.0044 | 1.9752 |
| n | ||||||
|---|---|---|---|---|---|---|
| Value | Order | Value | Order | Value | Order | |
| 4 | 0.0050 | - | 0.0902 | - | 2.7398 | - |
| 8 | 3.5334 | 0.0127 | 2.8283 | 0.6970 | 1.9748 | |
| 16 | 3.2359 | 0.0025 | 2.3448 | 0.2482 | 1.4897 | |
| 32 | 3.6685 | 2.7598 | 0.0685 | 1.8579 | ||
| 64 | 3.8501 | 2.8829 | 0.0177 | 1.9524 | ||
| 128 | 3.9368 | 2.9417 | 0.0045 | 1.9758 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, Y.; Yang, S. A Morley Type Triangular Finite Element with High Convergence for the Biharmonic Problem. Mathematics 2024, 12, 3199. https://doi.org/10.3390/math12203199
Bao Y, Yang S. A Morley Type Triangular Finite Element with High Convergence for the Biharmonic Problem. Mathematics. 2024; 12(20):3199. https://doi.org/10.3390/math12203199
Chicago/Turabian StyleBao, Yuan, and Sibo Yang. 2024. "A Morley Type Triangular Finite Element with High Convergence for the Biharmonic Problem" Mathematics 12, no. 20: 3199. https://doi.org/10.3390/math12203199
APA StyleBao, Y., & Yang, S. (2024). A Morley Type Triangular Finite Element with High Convergence for the Biharmonic Problem. Mathematics, 12(20), 3199. https://doi.org/10.3390/math12203199






