A Novel Normal Contact Stiffness Model of Bi-Fractal Surface Joints
Abstract
:1. Introduction
2. Normal Contact Stiffness Modeling of Bi-Fractal Surface Joint
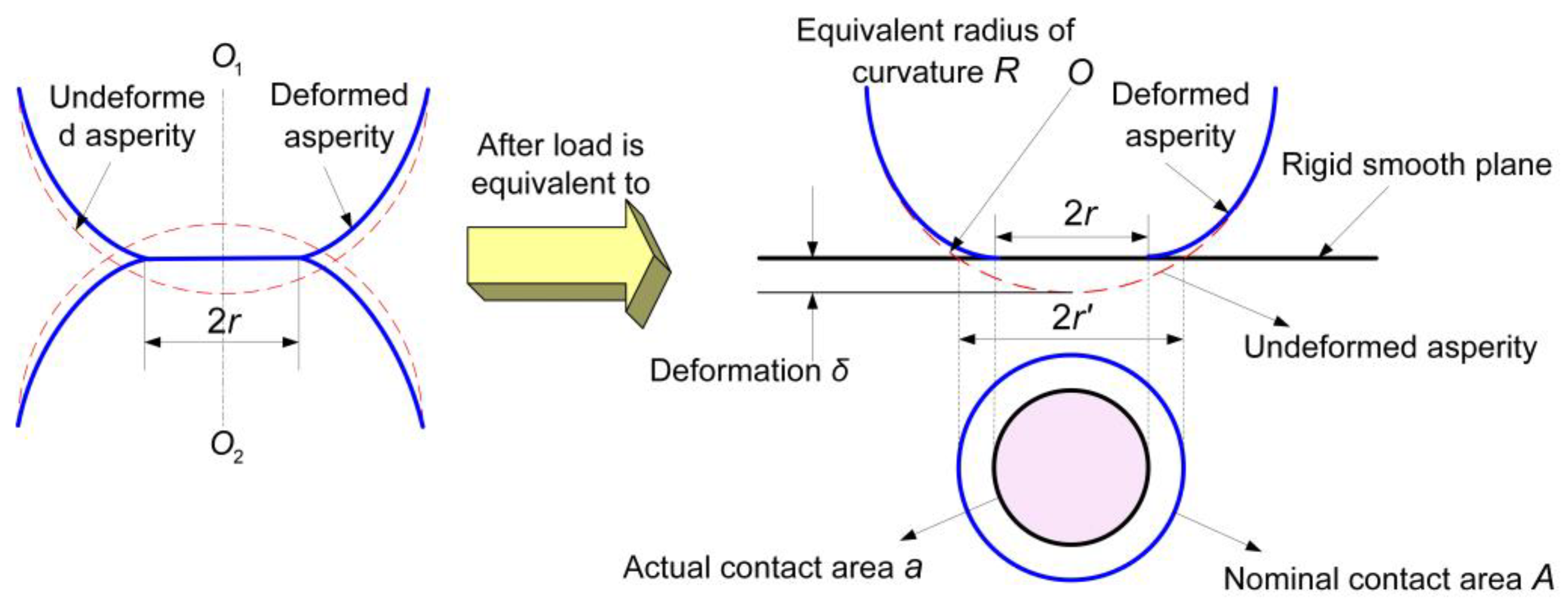
2.1. Single Asperity Contact Analysis
2.1.1. Elastic Contact
2.1.2. Plastic Contact
2.1.3. Elastoplastic Contact
2.2. Bi-Fractal Surface Contact Analysis
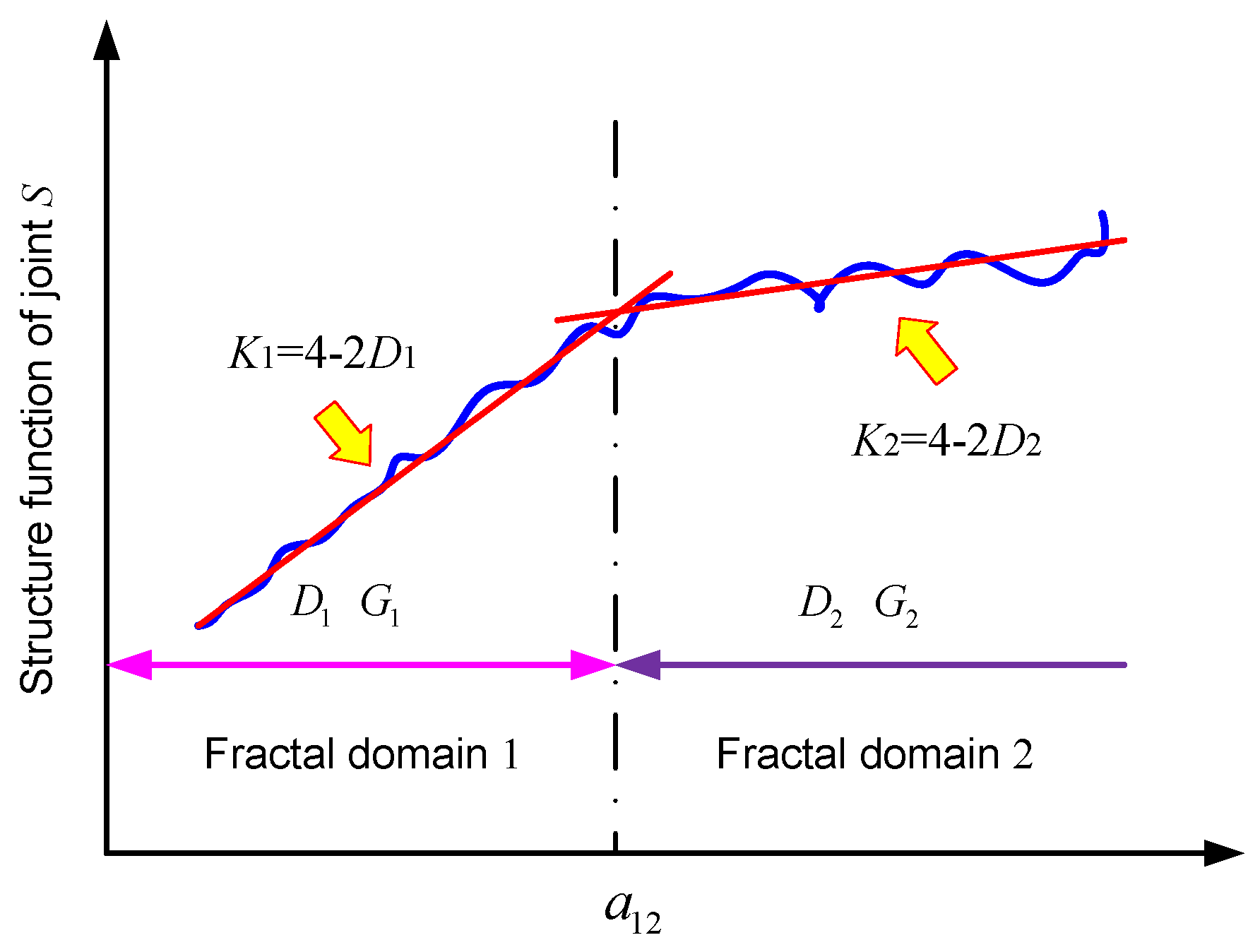
2.2.1. Contact Mechanics of Bi-Fractal Surfaces
2.2.2. Area Density Distribution Function
2.3. Contact Stiffness of the Entire Joint
2.3.1. Total Real Contact Area
2.3.2. Total Normal Load
- (1)
- If the maximum contact area of a single asperity is larger than the elastic critical contact area, that is , the total normal load of the bi-fractal surface joint is calculated as follows:Substituting Equations (7), (11), (20), (23) and (24) into Equation (27), we can obtain
- (2)
- If the maximum contact area of a single asperity is larger than the plastic critical contact area and smaller than the elastic critical contact area, that is , the total normal load of the bi-fractal surface joint is expressed as follows:Substituting Equations (11), (20), (23), and (24) into Equation (29), we obtain the following:
- (3)
- If the maximum contact area of a single asperity is smaller than the plastic critical contact area, that is , the total normal load of the bi-fractal surface joint is expressed as follows:Substituting Equations (11), (23) and (24) into Equation (31), we obtain the following:
2.3.3. Total Normal Contact Stiffness
- (1)
- If the maximum contact area of a single asperity is larger than the elastic critical contact area, that is , the total normal contact stiffness of the bi-fractal surface joint is as follows:Substituting Equations (8), (21) and (24) into Equation (33), we obtain the following:
- (2)
- If the maximum contact area of a single asperity is larger than the plastic critical contact area and smaller than the elastic critical contact area, that is , the total normal contact stiffness of the bi-fractal surface joint is as follows:Substituting Equations (21) and (24) into Equation (35), we obtain the following:
- (3)
- If the maximum contact area of a single asperity is smaller than the plastic critical contact area, that is , due to the asperities of bi-fractal surface joint are all plastic, we can draw a conclusion that the total normal contact stiffness of the bi-fractal surface joint is zero.
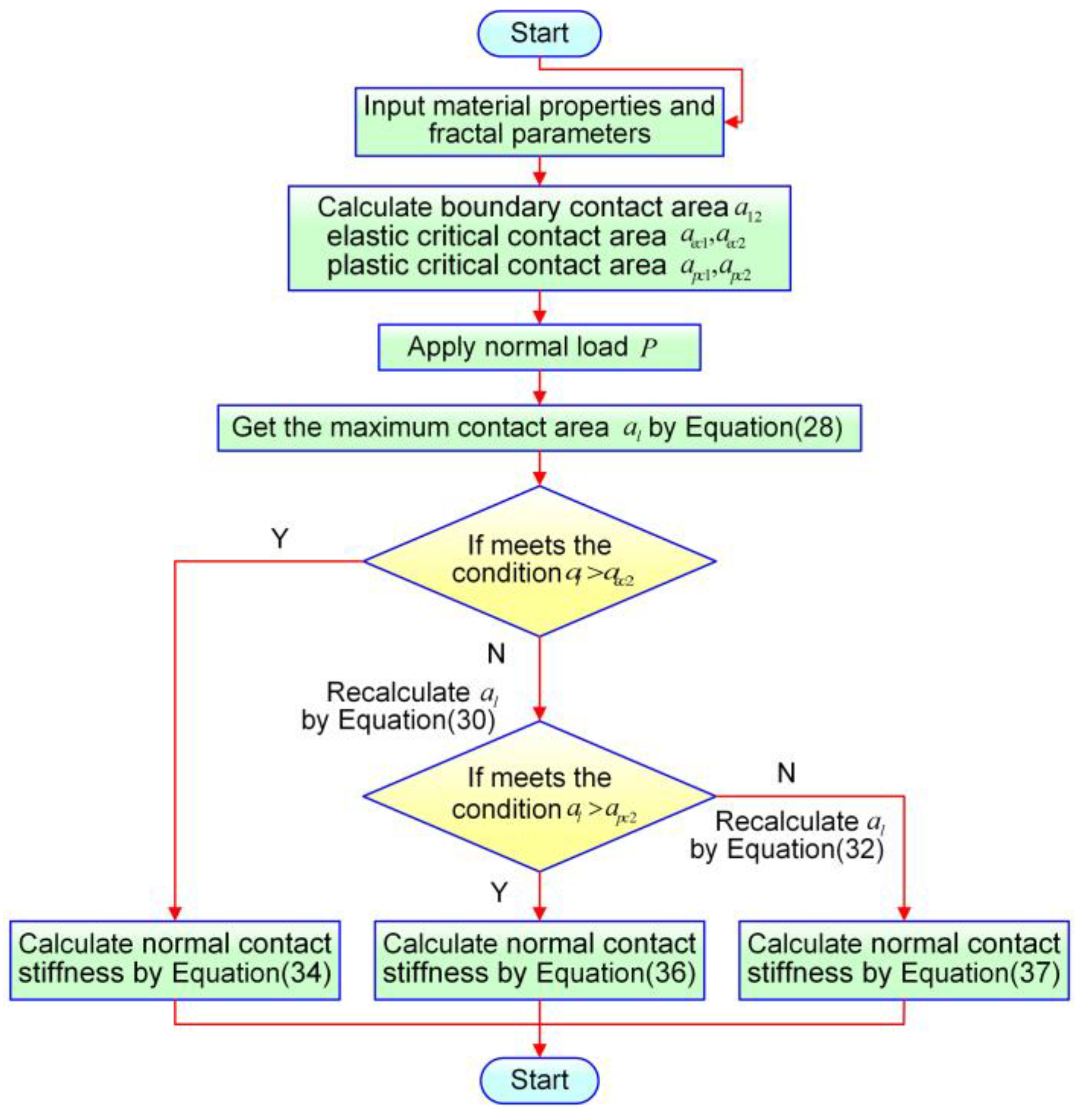
3. Simulation Analysis of Normal Contact Stiffness
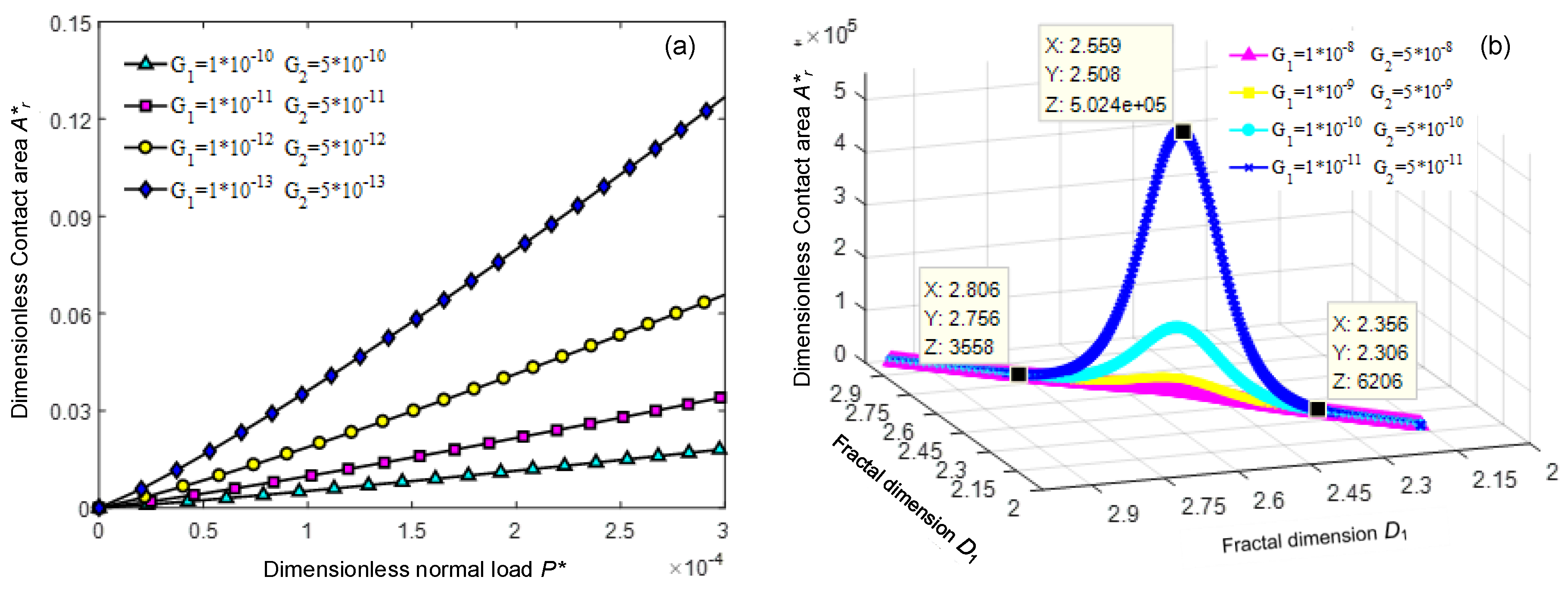
3.1. Real Contact Area
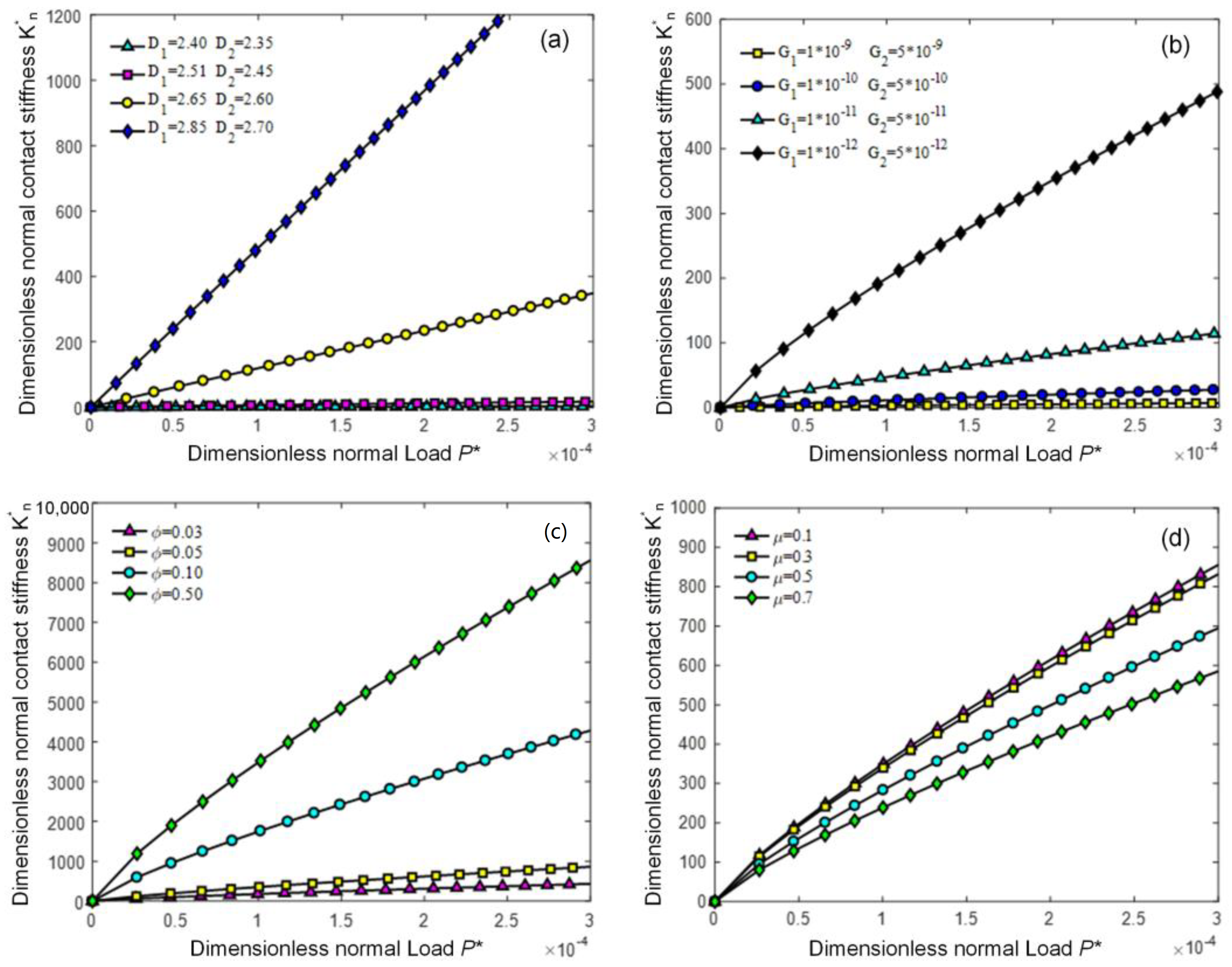
3.2. Normal Contact Stiffness
4. Validity Verification of Model
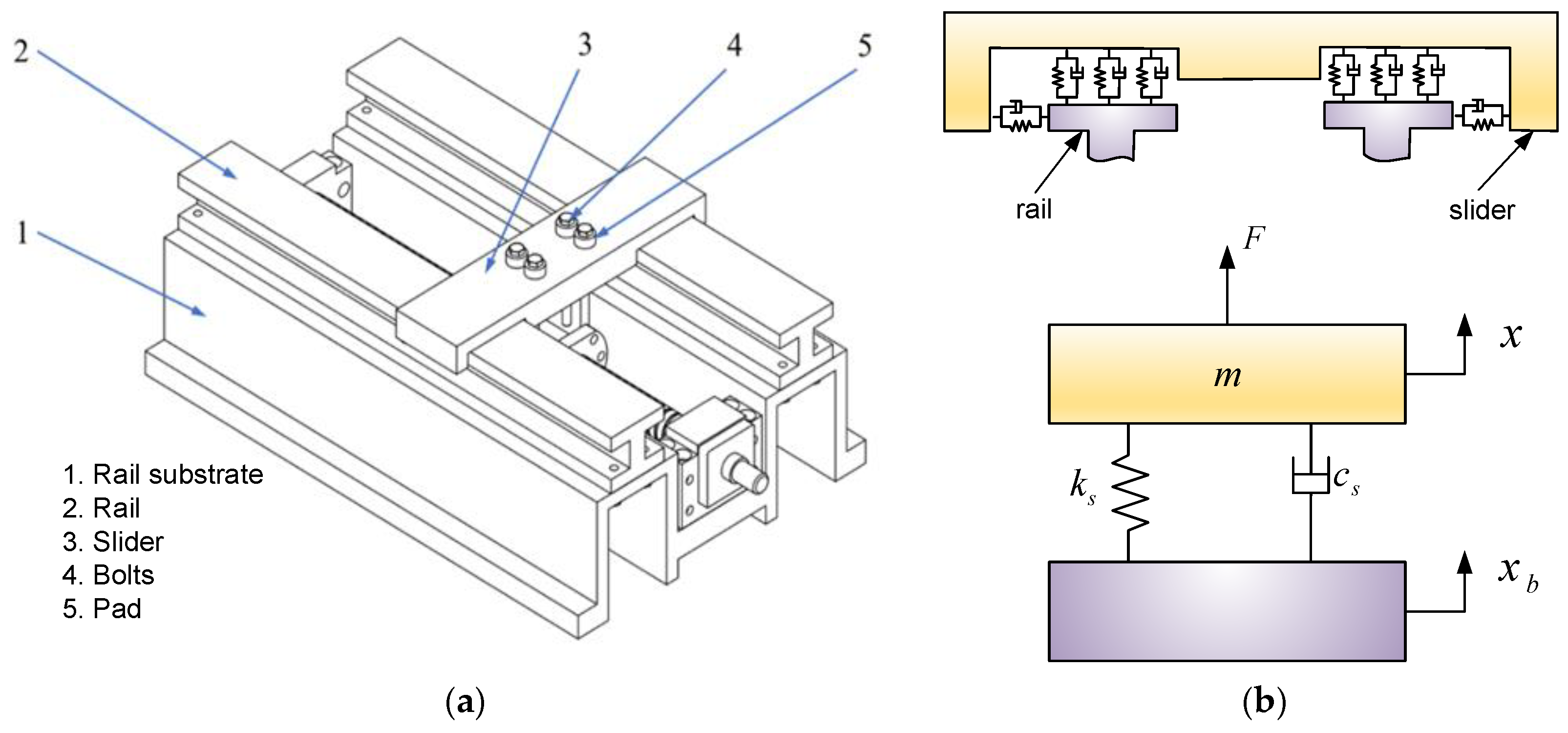
4.1. Experimental Equipment and Principle
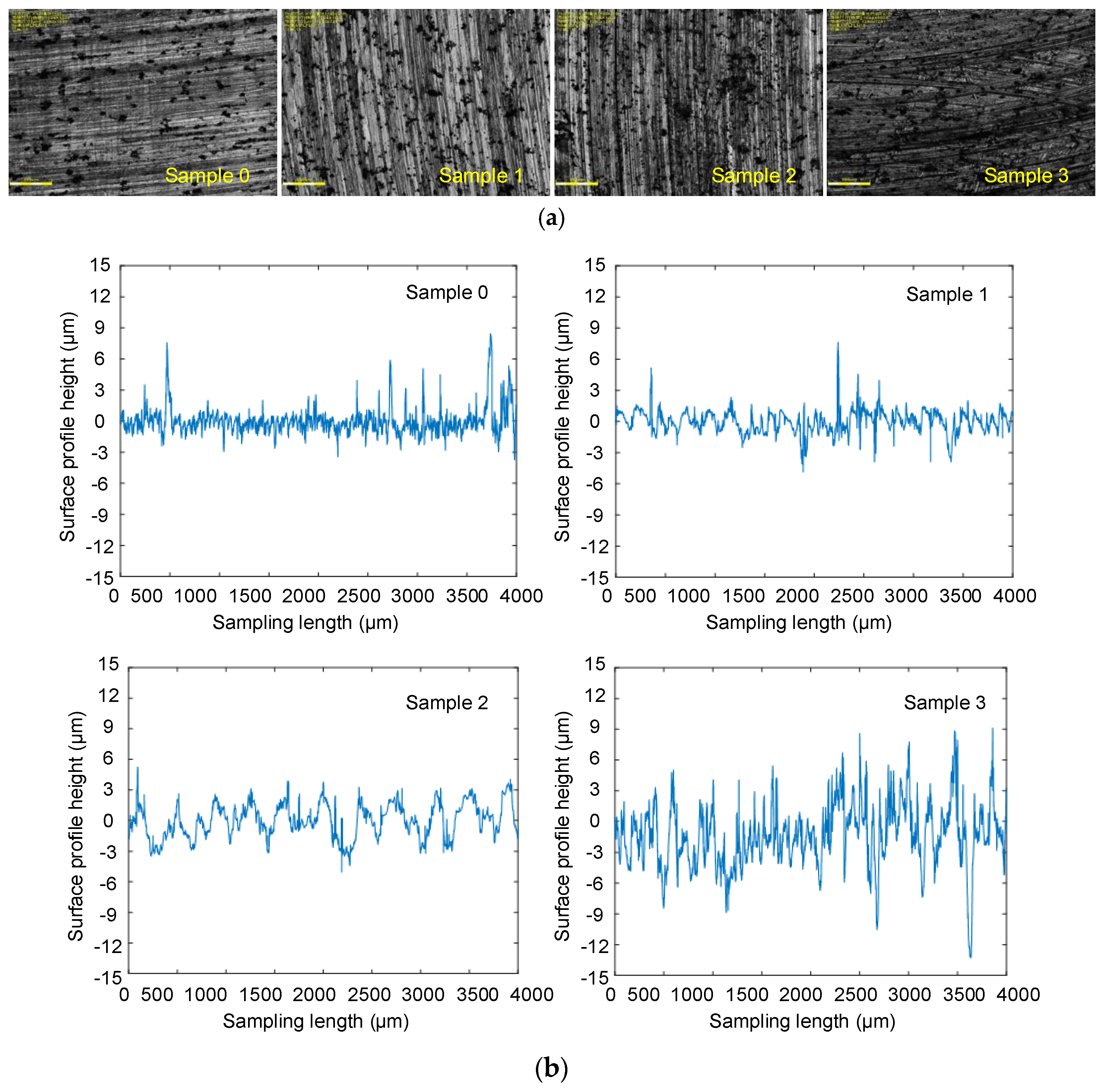
4.2. Solution of Surface Fractal Parameters
4.3. Dynamic Characteristics Identification Experiment
5. Conclusions
- (1)
- Fractal dimension and scaling parameter are the main factors affecting the topography of the bi-fractal surface. The roughness of the bi-fractal surface decreases with the increase in the fractal dimension and the decrease in the scaling parameters.
- (2)
- The true contact area of the bi-fractal surface joint increases linearly with an increase in the normal load, increases first and then decreases with an increase in the fractal dimension, and monotonously increases with a decrease in the scaling parameter.
- (3)
- The normal contact stiffness of the bi-fractal surface joint is affected by fractal parameters, material properties, friction factor, and applied loads. The normal contact stiffness of the joint increases with an increase in the normal load. When the normal load is constant, the increase in the fractal dimension and the material properties are beneficial for increasing the joint contact stiffness of the joint. A reduction in the scaling parameter and friction factor increases the normal contact stiffness of the joint.
- (4)
- By comparing the traditional fractal model with the proposed model, it can be found that the bi-fractal model is more accurate in characterizing the true fractal features of the rough surface of the joint, so the theoretical calculation of this normal contact stiffness of the joint is more consistent with the experimental results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, P.; Liu, J.; Gong, H.; Xue, F. A novel calculation method for torsional stiffness of flange-spigot structure in aeroengine rotors. Tribol. Int. 2024, 195, 109601. [Google Scholar] [CrossRef]
- Pan, W.; Sun, Y.; Li, X.; Song, H.; Guo, J. Contact mechanics modeling of fractal surface with complex multi-stage actual loading deformation. Appl. Math. Model. 2024, 128, 58–81. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Wu, S. A complete deterministic model of point contact mixed lubrication coupling dual-mode effects of surface fractal characteristics. Int. J. Non-Linear Mech. 2024, 161, 104669. [Google Scholar] [CrossRef]
- Sun, Z.; Chen, S.; Tang, J.; Hu, Z.; Tao, X.; Wang, Q.; Yang, S.; Jiang, P. New deterministic model for calculating mesh stiffness and damping of rough-surface gears considering elastic–plastic contact and energy-dissipation mechanism. Mech. Syst. Signal Process. 2024, 216, 111502. [Google Scholar] [CrossRef]
- Shen, F.; Li, Y.-H.; Ke, L.-L. A novel fractal contact model based on size distribution law. Int. J. Mech. Sci. 2023, 249, 108255. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, C.; Wang, L.; Wang, P. A rail corrugation evaluation method using fractal characterization based on structure function method. Wear 2022, 506-507, 204454. [Google Scholar] [CrossRef]
- Xiao, H.; Sun, Y.; Chen, Z. Fractal modeling of normal contact stiffness for rough surface contact considering the elastic–plastic deformation. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 11. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Wu, S. Multi-stage contact model between fractal rough surfaces based on multi-scale asperity deformation. Appl. Math. Model. 2022, 109, 229–250. [Google Scholar] [CrossRef]
- Zhao, Z.; Han, H.; Wang, P.; Ma, H.; Zhang, S.; Yang, Y. An improved model for meshing characteristics analysis of spur gears considering fractal surface contact and friction. Mech. Mach. Theory 2021, 158, 104219. [Google Scholar] [CrossRef]
- Pan, W.; Li, X.; Wang, L.; Guo, N.; Mu, J. A normal contact stiffness fractal prediction model of dry-friction rough surface and experimental verification. Eur. J. Mech. A/Solids 2017, 66, 94–102. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, M.; Song, X.; Wei, N. A modeling method for predicting the precision loss of the preload double-nut ball screw induced by raceway wear based on fractal theory. Wear 2021, 486-487, 204065. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhou, Z.; Huang, K.; Cheng, Z.; Han, G. An improved fractal model for tangential contact damping of high contact ratio gear considering friction effect. Chaos. Solitons Fractals 2021, 153, 111510. [Google Scholar] [CrossRef]
- Guan, D.; Jing, L.; Hilton, H.H.; Gong, J.; Yang, Z. Tangential contact analysis of spherical pump based on fractal theory. Tribol. Int. 2018, 119, 531–538. [Google Scholar] [CrossRef]
- Guan, D.; Jing, L.; Gong, J.; Shen, H.; Hilton, H.H. Normal contact analysis for spherical pump based on fractal theory. Tribol. Int. 2018, 124, 117–123. [Google Scholar] [CrossRef]
- Liu, J.; Ma, C.; Wang, S.; Wang, S.; Yang, B. Contact stiffness of spindle-tool holder based on fractal theory and multi-scale contact mechanics model. Mech. Syst. Signal Process. 2019, 119, 363–379. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Q.-A.; Mo, J.; Xiang, Z.; Wang, Q.; Zhai, C.; Zhu, S. Analysis of contact characteristics and dynamic response of joint interface with surface micro-grooved texture based on fractal theory. Mech. Syst. Signal Process. 2024, 218, 111553. [Google Scholar] [CrossRef]
- Bhushan, B.; Majumdar, A. Elastic-plastic contact model for bifractal surfaces. Wear 1992, 153, 53–64. [Google Scholar] [CrossRef]
- Borri, C.; Paggi, M. Topology simulation and contact mechanics of bifractal rough surfaces, Proceedings of the Institution of Mechanical Engineers. Part J J. Eng. Tribol. 2016, 230, 1345–1358. [Google Scholar] [CrossRef]
- Borri, C.; Paggi, M. Topological characterization of antireflective and hydrophobic rough surfaces: Are random process theory and fractal modeling applicable? J. Phys. D Appl. Phys. 2015, 48, 045301. [Google Scholar] [CrossRef]
- Hu, S.; Huang, W.; Shi, X.; Peng, Z.; Liu, X. Bi-fractal feature of bi-Gaussian stratified surfaces. Tribol. Int. 2019, 134, 427–434. [Google Scholar] [CrossRef]
- Meng, F.; Xia, H.; Zhang, X.; Wang, J.; Jin, Y. Study on nonlinear dynamic characteristics of gear system with 3D anisotropic rough tooth surface based on fractal theory. Int. J. Non-Linear Mech. 2023, 150, 104366. [Google Scholar] [CrossRef]
- Komvopoulos, K.; Ye, N. Three-dimensional contact analysis of elastic-plastic layered media with fractal surface topographies. J. Tribol. 2001, 123, 632–640. [Google Scholar] [CrossRef]
- Pan, W.; Li, X.; Wang, L.; Mu, J.; Yang, Z. A loading fractal prediction model developed for dry-friction rough joint surfaces considering elastic–plastic contact. Acta Mech. 2018, 229, 2149–2162. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Liu, M.; Wu, S. Analytical description of the wear process using a multi-stage contact fractal approach. Wear 2024, 549, 205364. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-plastic contact analysis of a sphere and a rigid flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Tian, H.; Zhong, X.; Zhao, C.; Zhao, X. One loading model of joint interface considering elastoplastic and variation of hardness with surface depth. J. Mech. Eng. 2015, 51, 90–104. [Google Scholar] [CrossRef]
- Čelič, D.; Boltežar, M. The influence of the coordinate reduction on the identification of the joint dynamic properties. Mech. Syst. Signal Process. 2009, 23, 1260–1271. [Google Scholar] [CrossRef]
- Liao, J.; Zhang, J.; Feng, P.; Yu, D.; Wu, Z. Identification of contact stiffness of shrink-fit tool-holder joint based on fractal theory. Int. J. Adv. Manuf. Technol. 2017, 90, 2173–2184. [Google Scholar] [CrossRef]
- Wu, J. Characterization of fractal surfaces. Wear 2000, 239, 36–47. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, K.; Zhang, C.; Zhao, Y.; Tian, Y. A stiffness model of a joint surface with inclination based on fractal theory. Precis. Eng. 2020, 62, 47–61. [Google Scholar] [CrossRef]
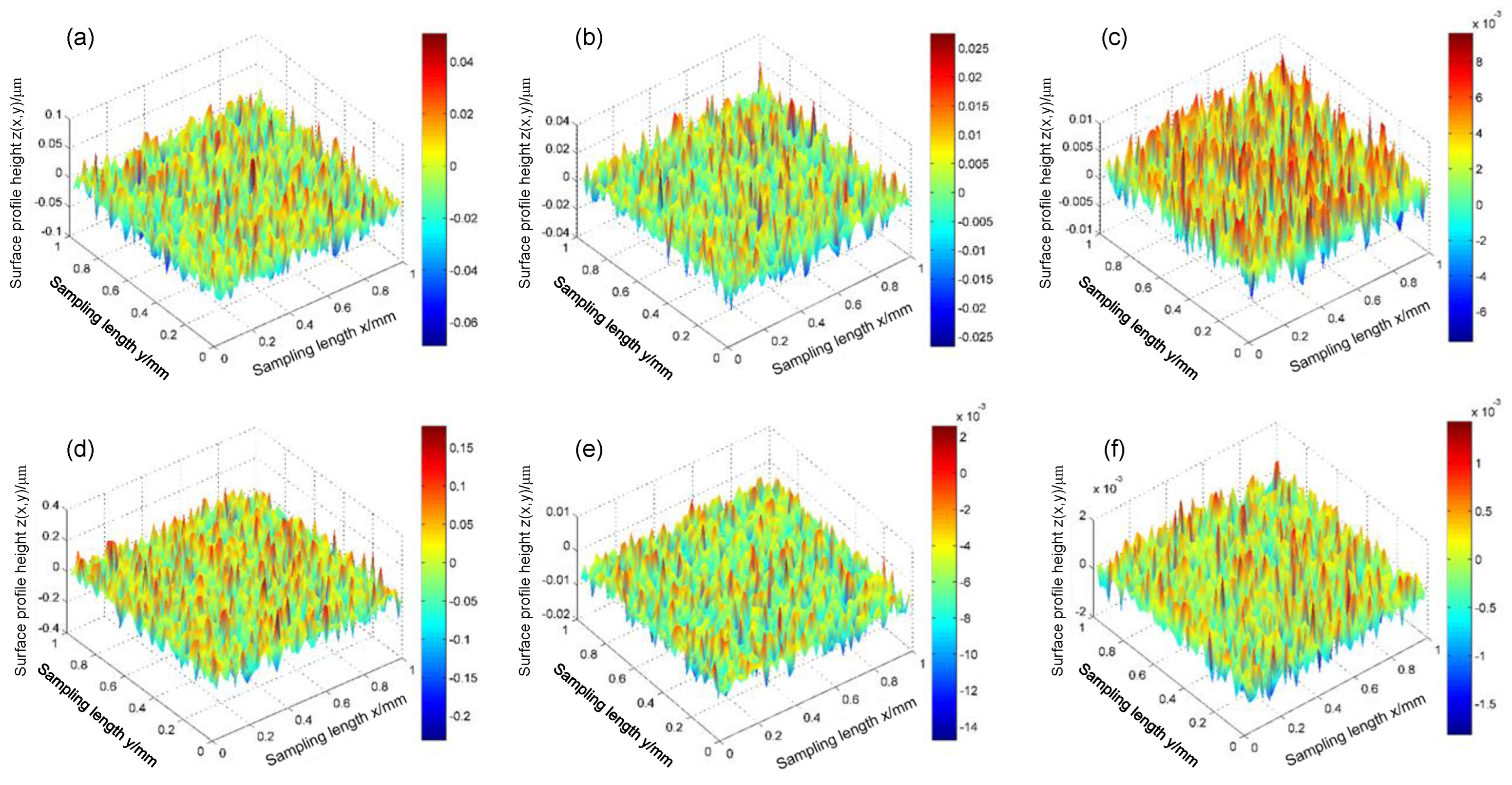

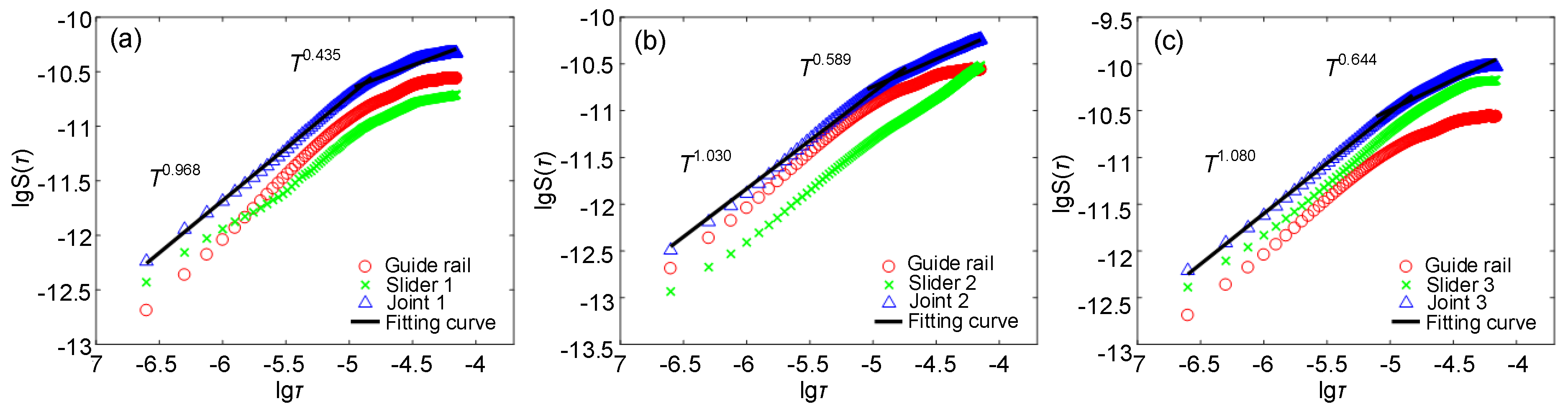
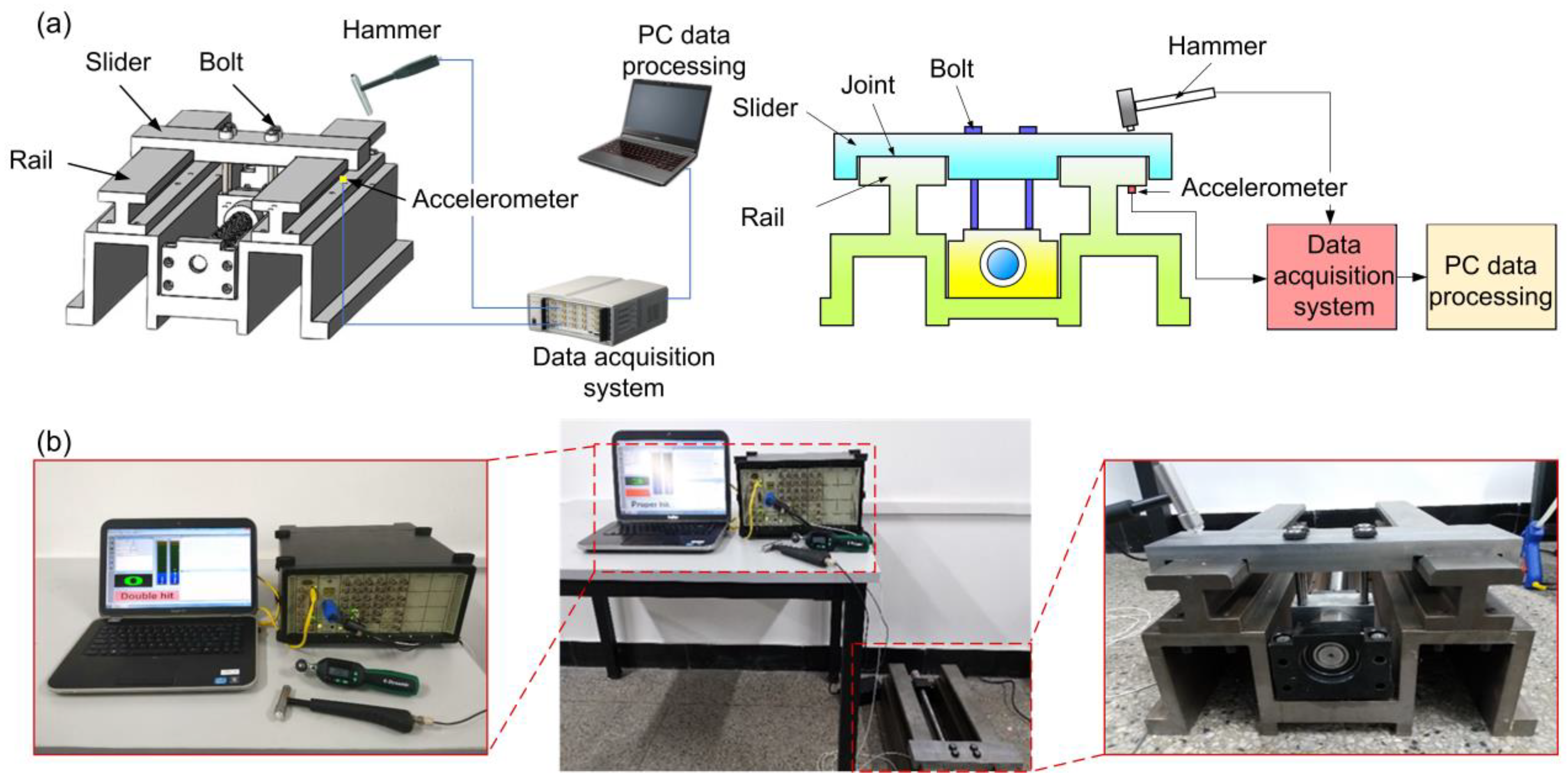
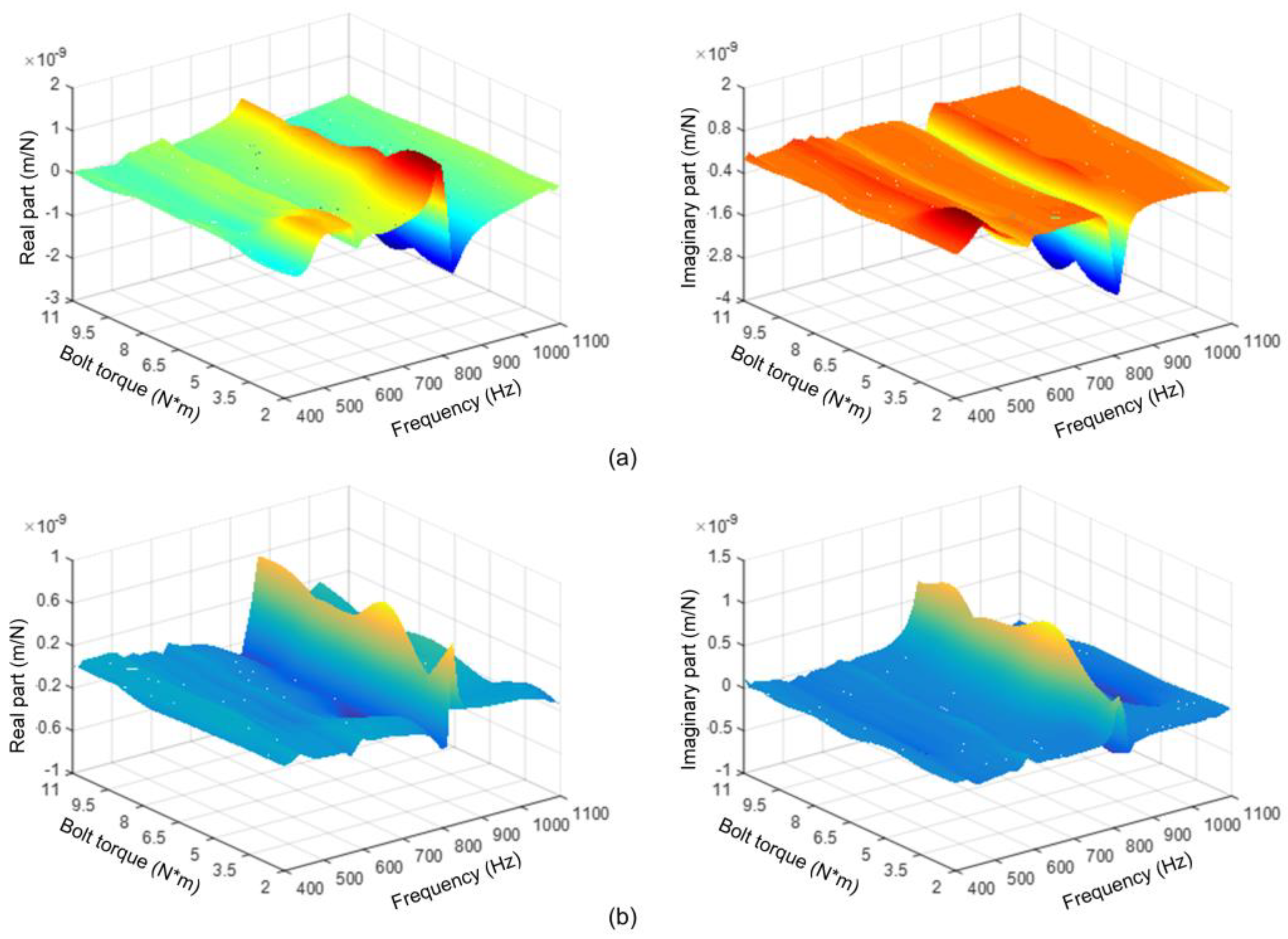

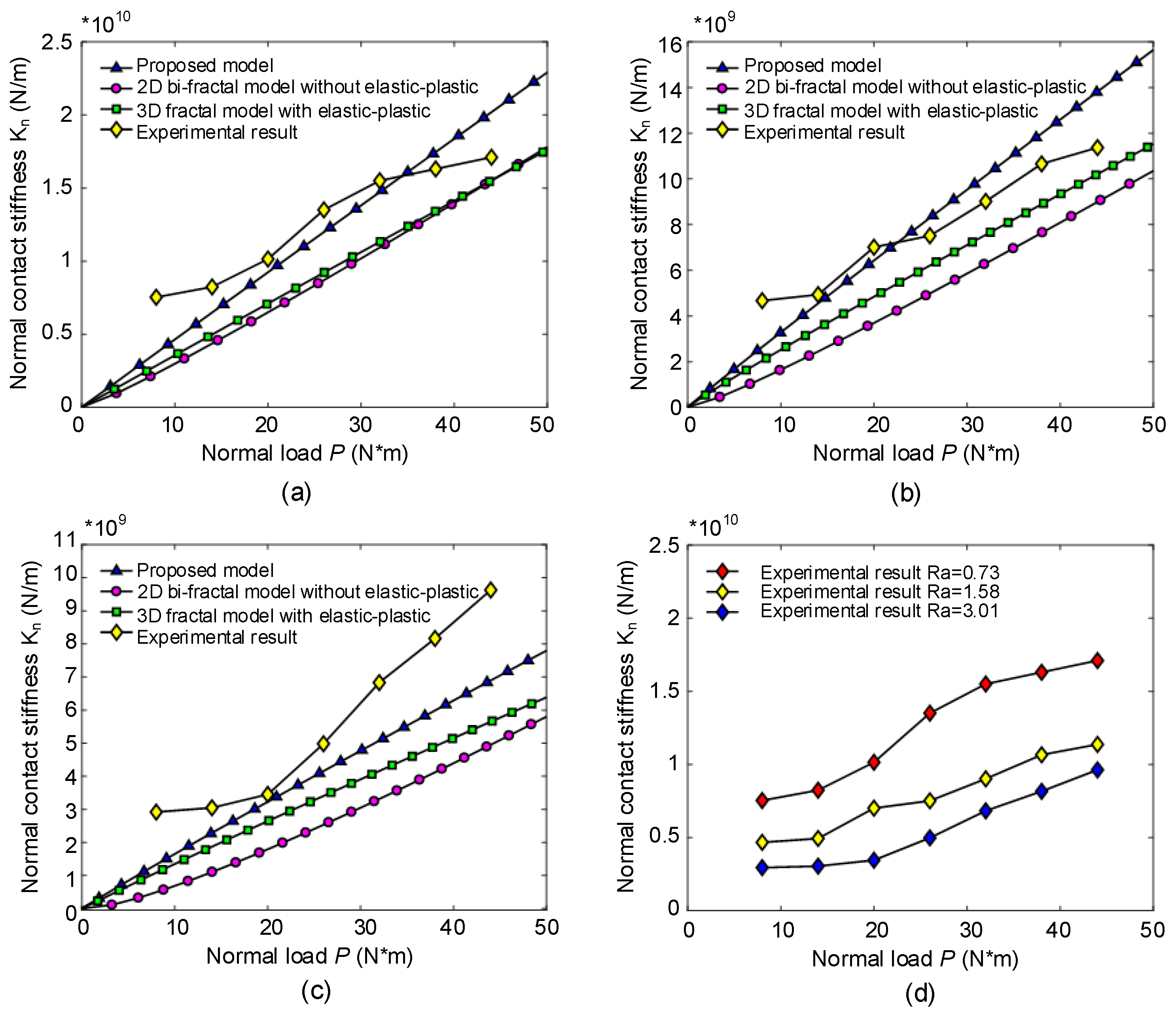
| Joint Number | Fractal Dimension | Scaling Parameter |
|---|---|---|
| 1 | 2.5162 | 5.9058 × 10−7 |
| 2.7828 | 1.1811 × 10−6 | |
| 2 | 2.4853 | 3.7237 × 10−7 |
| 2.7054 | 8.9543 × 10−7 | |
| 3 | 2.4613 | 6.4363 × 10−7 |
| 2.6779 | 1.3073 × 10−6 |
| Normal Load ) | Experimental Results N/m) | Theoretical Results N/m) | Error (%) |
|---|---|---|---|
| 8 | 0.7740 | 0.3802 | 50.9 |
| 14 | 0.8240 | 0.6626 | 19.6 |
| 20 | 1.0150 | 0.9439 | 7.0 |
| 26 | 1.3510 | 1.2244 | 9.4 |
| 32 | 1.5504 | 1.5035 | 3.0 |
| 38 | 1.6305 | 1.7837 | 9.4 |
| 44 | 1.7107 | 2.0627 | 20.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, P.; Zhu, L.; Cao, X. A Novel Normal Contact Stiffness Model of Bi-Fractal Surface Joints. Mathematics 2024, 12, 3232. https://doi.org/10.3390/math12203232
Xue P, Zhu L, Cao X. A Novel Normal Contact Stiffness Model of Bi-Fractal Surface Joints. Mathematics. 2024; 12(20):3232. https://doi.org/10.3390/math12203232
Chicago/Turabian StyleXue, Pengsheng, Lida Zhu, and Xiangang Cao. 2024. "A Novel Normal Contact Stiffness Model of Bi-Fractal Surface Joints" Mathematics 12, no. 20: 3232. https://doi.org/10.3390/math12203232
APA StyleXue, P., Zhu, L., & Cao, X. (2024). A Novel Normal Contact Stiffness Model of Bi-Fractal Surface Joints. Mathematics, 12(20), 3232. https://doi.org/10.3390/math12203232





