Modeling the Dynamics of Prosthetic Fingers for the Development of Predictive Control Algorithms
Abstract
:1. Introduction
2. Aim
- Low computational cost;
- Stability;
- Managing future information that may be known;
- Accurately managing the finger position in a determined and predefined trajectory;
- Reducing the power consumption with respect to those in the literature since human-embedded prosthetic hands are powered by a battery.
3. Materials and Methods
3.1. The Prosthetic Hand
3.2. Linear Identification Process
- First, the main system parameters (input and output) must be determined. The input power to the finger motor is established as a system input. The position of the kinematic chain is established as the system output;
- Second, an input signal must be applied to the system to excite it, which must fulfill a series of properties [22]. Theoretically, the white noise signal could drive the system at any frequency. However, since white noise is a complex signal, an equivalent signal is proposed that complies with the properties established in [22]. That work establishes the required properties and characteristics for an experiment to provide adequate data for a correct system identification. Based on previous experimentation, a pseudo-random signal is selected for identification purposes;
- Finally, knowing the system features, a battery of tests to be applied is determined. As gravity acts on the system and produces a constant steering force on all the elements of the kinematic chain of the finger, some tests have been designed in order to assess its effect.
- Palm up;
- Palm down;
- Palm perpendicular to the ground.
- u(t) is the input, the control action on the system at time t;
- y(t) is the output, the value of the system measurements at time t;
- (t) is the noise of the system at time (t);
- A(z), B(z), and C(z) are the following polynomials of order na, nb, and nc, respectively:
- Output error (OE);
- Prediction Error Method (PEM);
- The Multivariable Output Error State Space Method (N4SID);
- Auto-Regressive Exogenous (ARX).
- VLS is the function of the residual by least squares;
- n is the order of the system (i.e., the number of parameters of the model);
- N is the number of samples of the identification sequence (normally N >> n);
- is the error;
- the polynomial A(z) contains the poles of the system;
- the polynomial B(z) contains the zeros of the system.
3.2.1. Output Error
3.2.2. Prediction Error Method
3.2.3. N4SID
3.2.4. Auto Regressive eXogenous ARX
3.3. Generalized Predictive Control GPC
- The prediction model (CARIMA);
- The cost index;
- The optimization tool;
- The application of the moving horizon.
4. Results
4.1. Identification
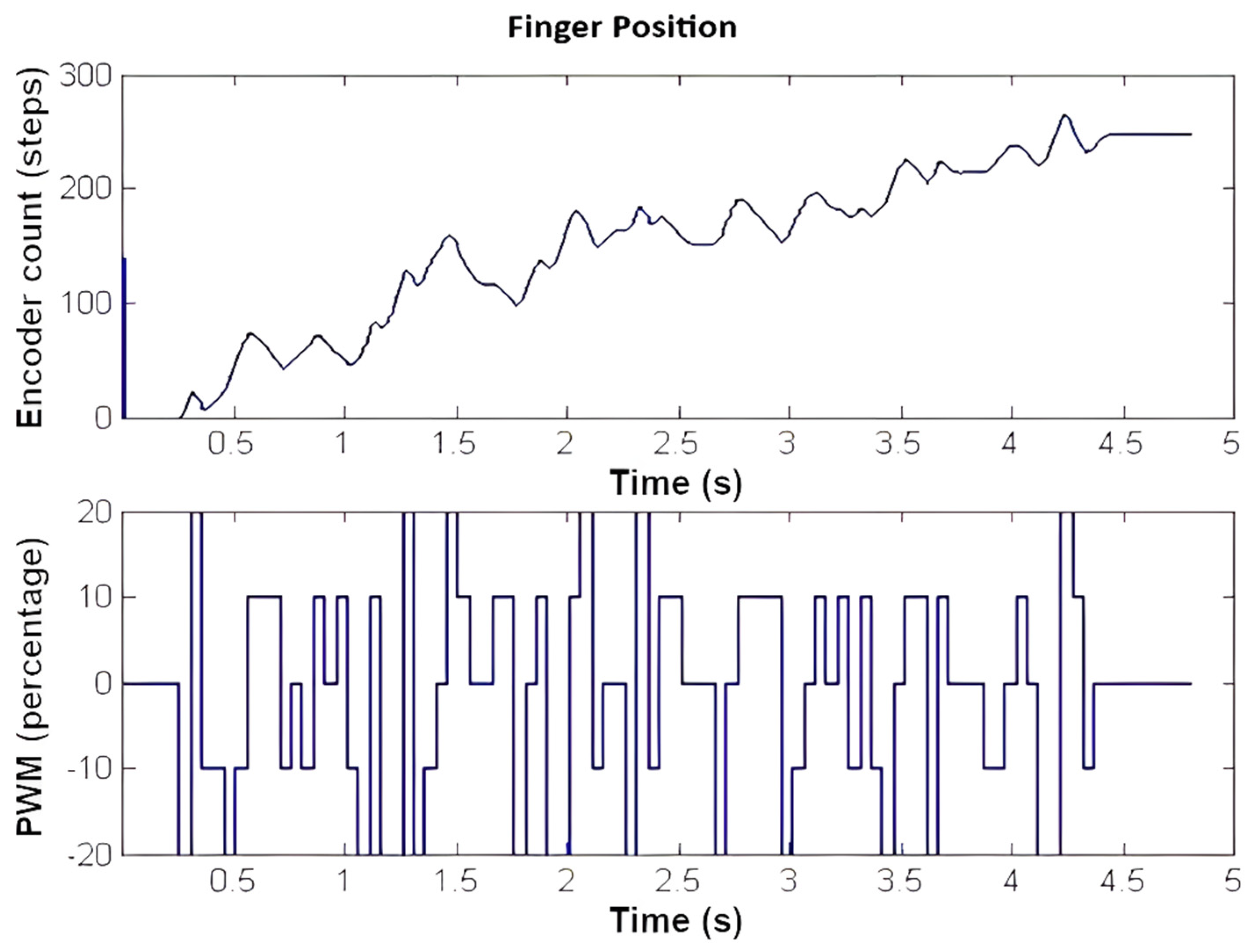
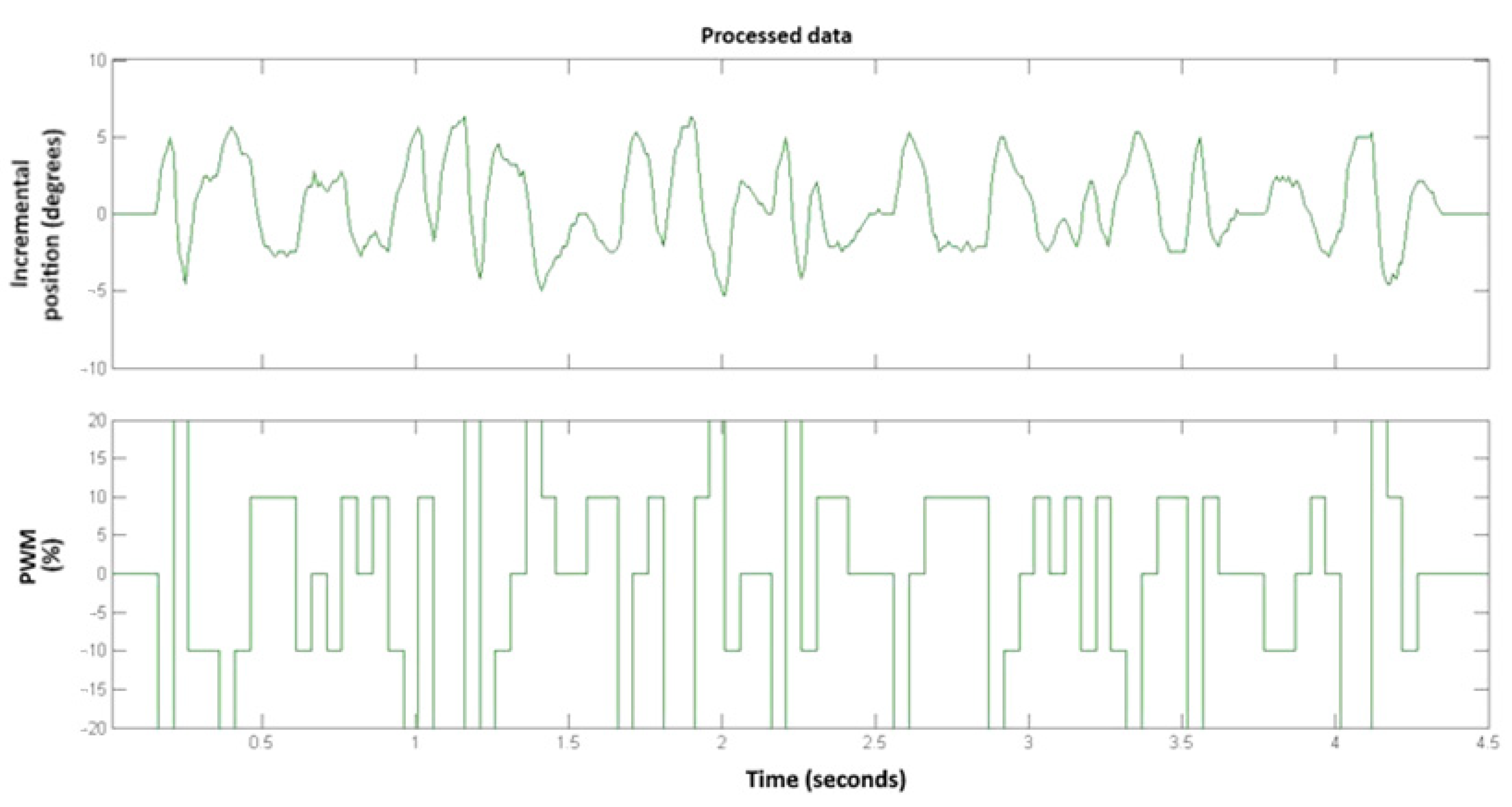
4.1.1. Tests
4.1.2. Identification Results
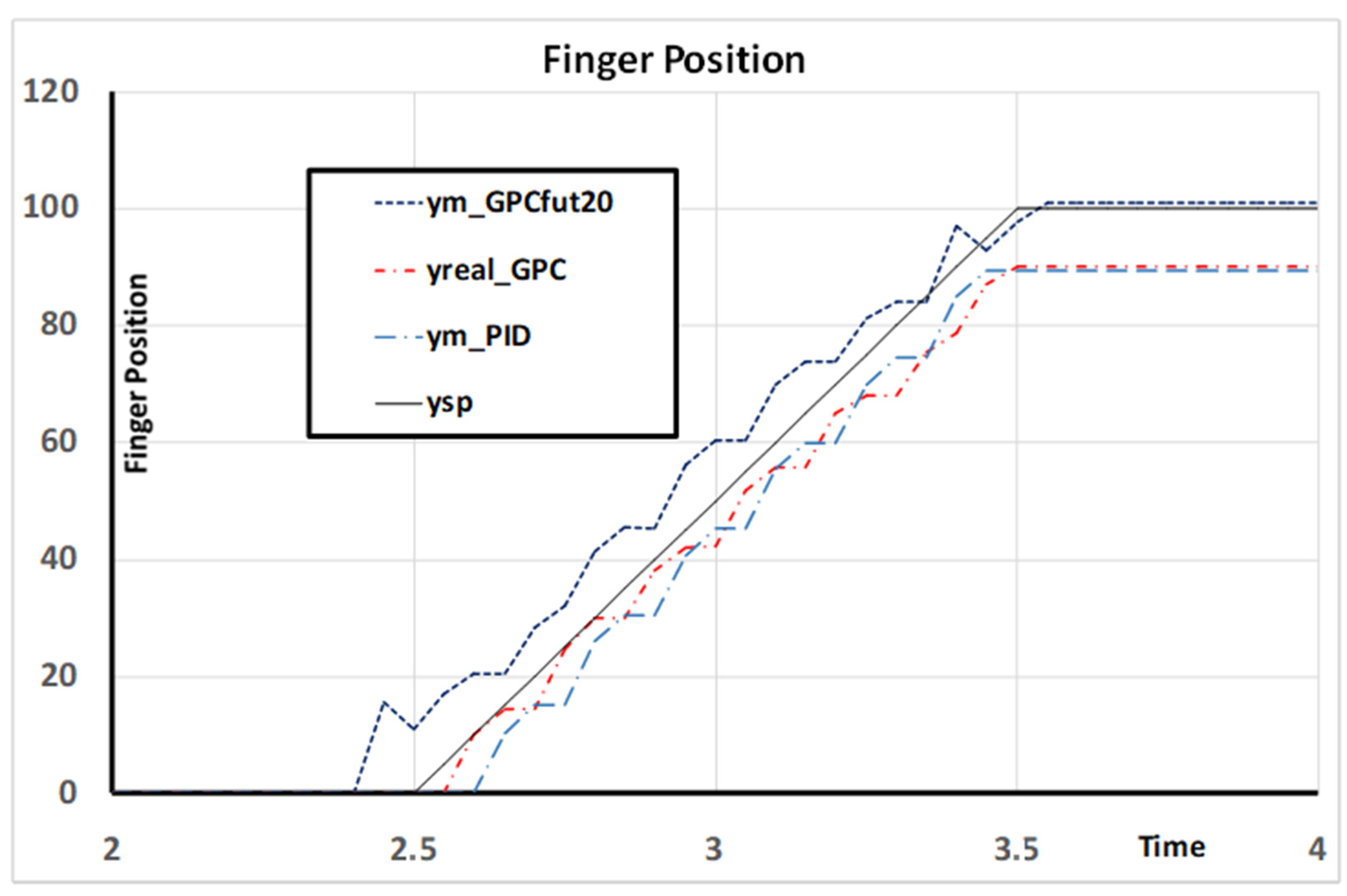
4.2. Control
- is the vector of increase in future control actions;
- N1, N2 is the prediction horizon (samples);
- Nu corresponds to the control horizon (samples);
- is the predicted response of the system;
- is the vector of future set points;
- α, λ are the weights of the contributions.
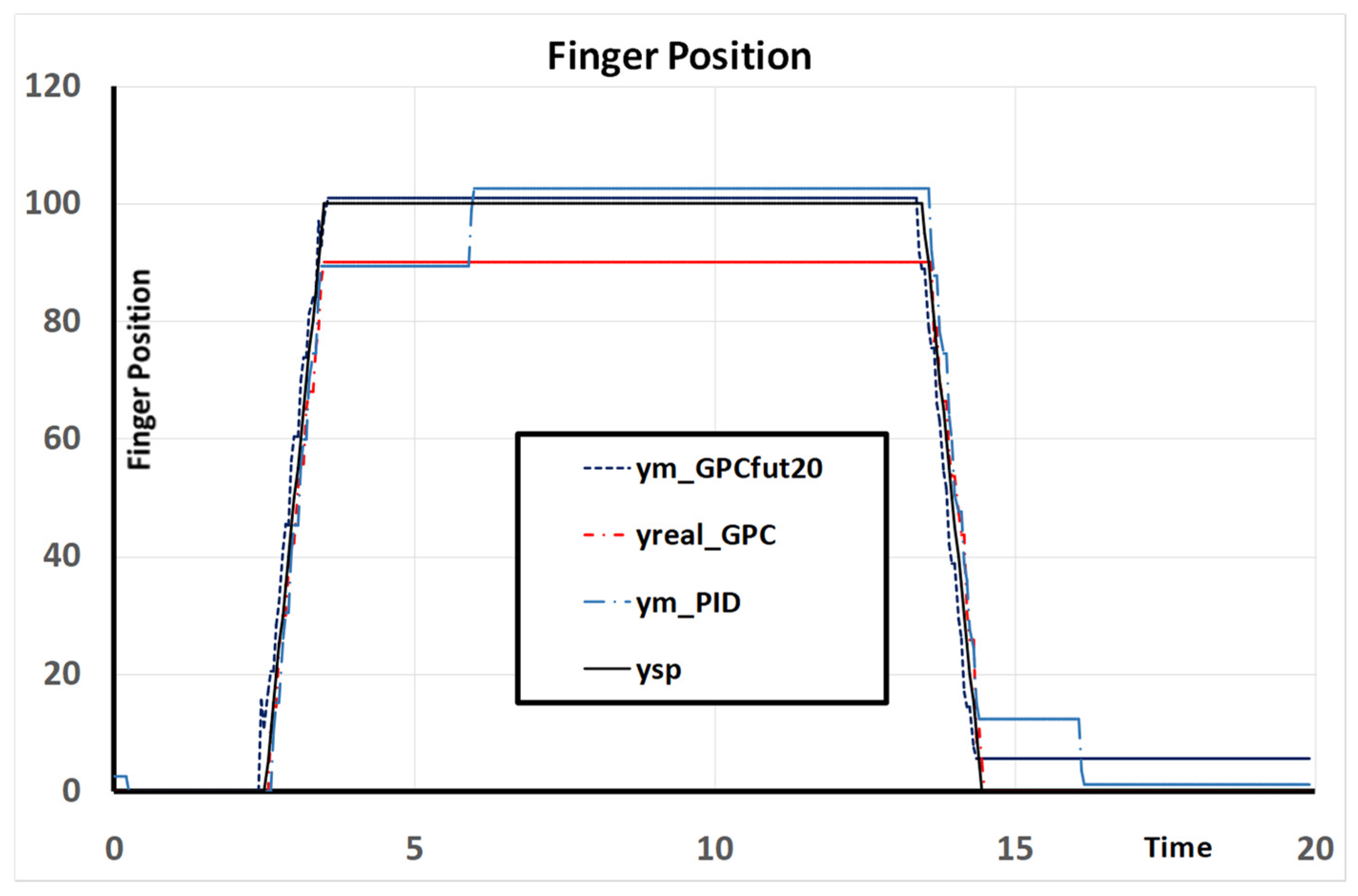
- Start from rest;
- Beginning at 2.5 s and ending at 3.5 s, increase the set point value from 0 to 100;
- Beginning at 13.4 s and ending at 14.4 s, with the linear decrease to 0.
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weir, R.F. Design of artificial arms and hands for prosthetic applications. In Standard Handbook of Biomedical Engineering and Design; Kutz, M., Ed.; McGraw-Hill: New York, NY, USA, 2003; Chapter 32. [Google Scholar]
- Atkins, D.J.; Heard, D.C.Y.; Donovan, W.H. Epidemiologic overview of individuals with upper-limb loss and their reported research priorities. J. Prosthet. Orthot. 1996, 8, 2–11. [Google Scholar] [CrossRef]
- Yang, D.; Jiang, L.; Huang, Q.; Liu, R.Q.; Liu, H. Experimental study of an EMG-controlled 5-DOF anthropomorphic prosthetic hand for motion restoration. J. Intell. Robot. Syst. 2014, 76, 427–441. [Google Scholar] [CrossRef]
- Vergara, M.; Sancho-Brú, J.L.; Gracia-Ibáñez, V.; Pérez-González, A. An introductory study of common grasps used by adults during performance of activities of daily living. J. Hand Ther. 2014, 27, 225–234. [Google Scholar] [CrossRef] [PubMed]
- Blana, D.; Kyriacou, T.; Lambrecht, J.M.; Chadwick, E.K. Feasibility of using combined EMG and kinematic signals for prosthesis control: A simulation study using a virtual reality environment. J. Electromyogr. Kinesiol. 2016, 29, 21–27. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, M.; Nathan-Roberts, D. Understanding Prosthetic Abandonment. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2019, 63, 1644–1648. [Google Scholar] [CrossRef]
- Smail, L.C.; Neal, C.; Wilkins, C.; Packham, T.L. Comfort and function remain key factors in upper limb prosthetic abandonment: Findings of a scoping review. Disabil. Rehabil. Assist. Technol. 2020, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Al-Owaidi, N.; Mora, M.C.; Ventura, S. Analysis on the Rejection and Device Passivity Problems with Myoelectric Prosthetic Hand Control. In Proceedings of the 28th World Multi-Conference on Systemics, Cybernetics and Informatics; Callaos, N., Gaile-Sarkane, E., Lace, N., Sánchez, B., Savoie, M., Eds.; International Institute of Informatics and Cybernetics: Winter Garden, FL, USA, 2024; pp. 10–17. [Google Scholar]
- Chaplot, L.; Houshmand, S.; Martinez, K.B.; Andersen, J.; Rouhani, H. Optimizing Sensor Placement and Machine Learning Techniques for Accurate Hand Gesture Classification. Electronics 2024, 13, 3072. [Google Scholar] [CrossRef]
- Sahoo, J.P.; Sahoo, G.K.; Mohapatra, N.R. Hand Gesture Recognition Based on Surface EMG Using Feature Fusion and Machine Learning Approaches. In Proceedings of the 3rd International Conference on Artificial Intelligence for Internet of Things (AIIoT), Vellore, India, 3–4 May 2024. [Google Scholar]
- Kadavath, M.R.K.; Nasor, M.; Imran, A. Enhanced Hand Gesture Recognition with Surface Electromyogram and Machine Learning. Sensors 2024, 24, 5231. [Google Scholar] [CrossRef] [PubMed]
- Mora, M.C.; García-Ortiz, J.V.; Cerdá-Boluda, J. sEMG-Based Robust Recognition of Grasping Postures with a Machine Learning Approach for Low-Cost Hand Control. Sensors 2024, 24, 2063. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhang, Z. Hand Gesture Recognition using sEMG Signals Based on Support Vector Machine. In Proceedings of the 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019. [Google Scholar]
- Starke, J.; Weiner, P.; Crell, M.; Asfour, T. Semi-autonomous control of prosthetic hands based on multimodal sensing, human grasp demonstration and user intention. Robotics Aut. Syst. 2022, 154, 104123. [Google Scholar] [CrossRef]
- Zhang, W.; White, M.; Zahabi, M.; Winslow, A.T.; Zhang, F.; Huang, H.; Kaber, D. Cognitive workload in conventional direct control vs. pattern recognition control of an upper-limb prosthesis. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 2335–2340. [Google Scholar]
- Zhang, T.; Jiang, L.; Fan, S.; Wu, X.; Feng, W. Development and experimental evaluation of multi-fingered robot hand with adaptive impedance control for unknown environment grasping. Robotica 2016, 34, 1168–1185. [Google Scholar] [CrossRef]
- Lee, D.H.; Park, J.H.; Park, S.W.; Baeg, M.H.; Bae, J.H. KITECH-Hand: A Highly Dexterous and Modularized Robotic Hand. IEEE/ASME Trans. Mechatron. 2017, 22, 876–887. [Google Scholar] [CrossRef]
- Clarke, D.W.; Mothadi, C.; Tuffs, P.S. Generalized predictive control-Part, I. The basic algorithm. Automatica 1987, 23, 137–148. [Google Scholar] [CrossRef]
- Clarke, D.W.; Mothadi, C.; Tuffs, P.S. Generalized predictive control-Part II. Extension and interpretation. Automatica 1987, 23, 149–160. [Google Scholar] [CrossRef]
- Clarke, D.W.; Mothadi, C. Properties of generalized predictive control. Automatica 1989, 25, 859–875. [Google Scholar] [CrossRef]
- Andrés, F.J.; Pérez-González, A.C.; Rubert, J.; Fuentes, B. Sospedra, Comparison of grasping performance of tendon and linkage transmission systems in an electric-powered low-cost hand prosthesis. ASME J. Mech. Robot. 2019, 11, 1–14. [Google Scholar] [CrossRef]
- Söderström, T.; Stoica, P. System Identification; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- García-Ortíz, J.V.; Mora, M.C.; Pérez-González, A.; Cantero-Ramis, J.A. PACMAR—Plataforma Automática de Control de Manos Antromorfas y Robóticas (PACMAR). Conference paper. In Proceedings of the VIII Reunión del Capítulo Español de la Sociedad Europea de Biomecánica (ESB), Castellón, Spain, 22–23 November 2018. [Google Scholar]
- Zhu, Y.; Backx, T. Identification of Multivariable Industrial Processes for Simulation, Diagnosis and Control; Springer-Verlag: London, UK, 1993. [Google Scholar]
- Van Overschee, P.; De Moor, B. Subspace algorithms for the identification of combined deterministic-stochastic systems. Automatica 1994, 30, 75–93. [Google Scholar] [CrossRef]
- Van den Boom, T.; Klompstra, M.; Damen, A. System identification for Hoo-robust control. In Proceedings of the 9th IFACIIFORS Symposium on Identification and System Parameter Estimation, Budapest, Hungary, 8–12 July 1991; pp. 1431–1436. [Google Scholar]
- Bachx, T. Identification of an Industrial Process: A Markov Parameter Approach. Ph.D. Dissertation, Electrical Engineering Department, Eindhoven University of Technology, Eindhoven, The Netherlands, 1987. [Google Scholar]
- Bach, A.C.P.M.; Damen, A.A.H. Identification of industrial MIMO processes for fixed controllers-part 1 and part 2. J. A 1989, 30. 3–12 and 33–43. [Google Scholar]



| Identification Algorithm | Id Data | Validation Data |
|---|---|---|
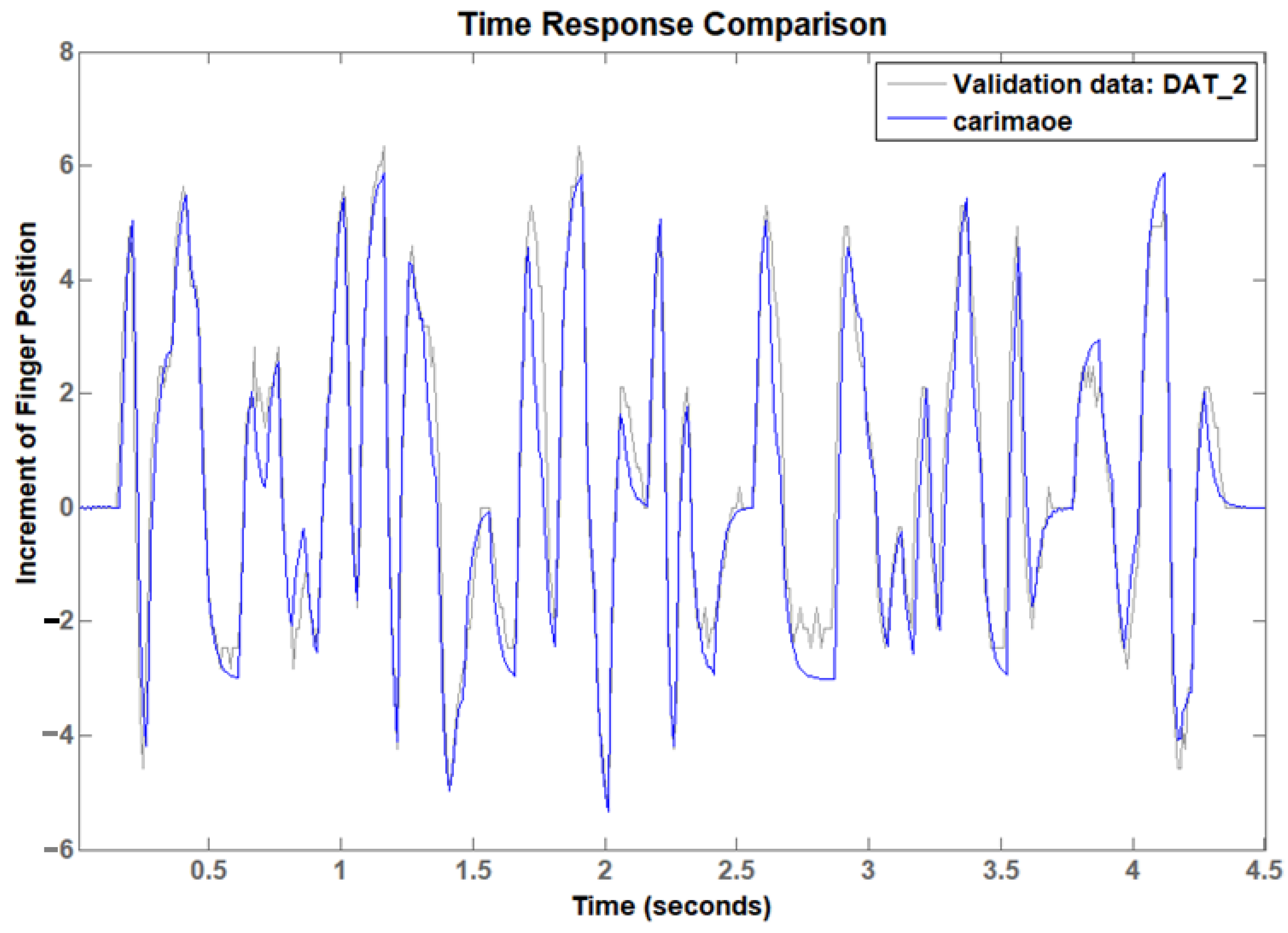
| OE (output error) | 71.22% | 58.76% |
| ARX | 70.37% | 70.30% |
| PEM | 70.54% | 66.64% |
| N4SID | 70.87% | 65.10% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Ortíz, J.V.; Mora, M.C.; Cerdá-Boluda, J. Modeling the Dynamics of Prosthetic Fingers for the Development of Predictive Control Algorithms. Mathematics 2024, 12, 3236. https://doi.org/10.3390/math12203236
García-Ortíz JV, Mora MC, Cerdá-Boluda J. Modeling the Dynamics of Prosthetic Fingers for the Development of Predictive Control Algorithms. Mathematics. 2024; 12(20):3236. https://doi.org/10.3390/math12203236
Chicago/Turabian StyleGarcía-Ortíz, José Vicente, Marta C. Mora, and Joaquín Cerdá-Boluda. 2024. "Modeling the Dynamics of Prosthetic Fingers for the Development of Predictive Control Algorithms" Mathematics 12, no. 20: 3236. https://doi.org/10.3390/math12203236
APA StyleGarcía-Ortíz, J. V., Mora, M. C., & Cerdá-Boluda, J. (2024). Modeling the Dynamics of Prosthetic Fingers for the Development of Predictive Control Algorithms. Mathematics, 12(20), 3236. https://doi.org/10.3390/math12203236









