AI-Powered Approaches for Hypersurface Reconstruction in Multidimensional Spaces
Abstract
1. Introduction
2. Methods for Surface Reconstruction
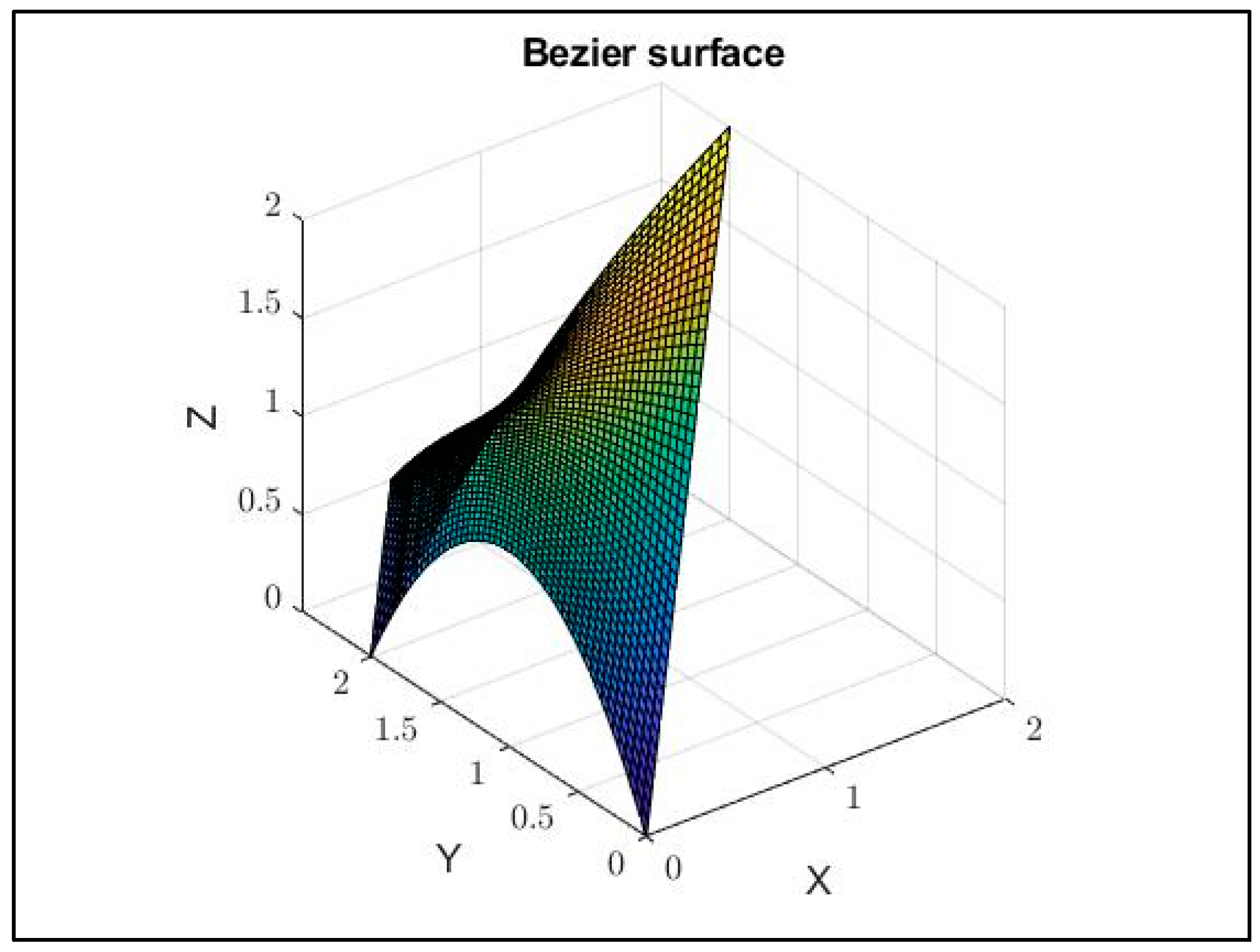
2.1. Bézier Curves
2.2. k-Nearest Neighbors Method
- Form a training dataset containing points from the known part of the surface;
- For each point that needs to be approximated (i.e., for the missing parts of the surface), find the -nearest points from the training set;
- For each unknown point, use the values (coordinates) of the -nearest neighbors to calculate its position within the same coordinate system.
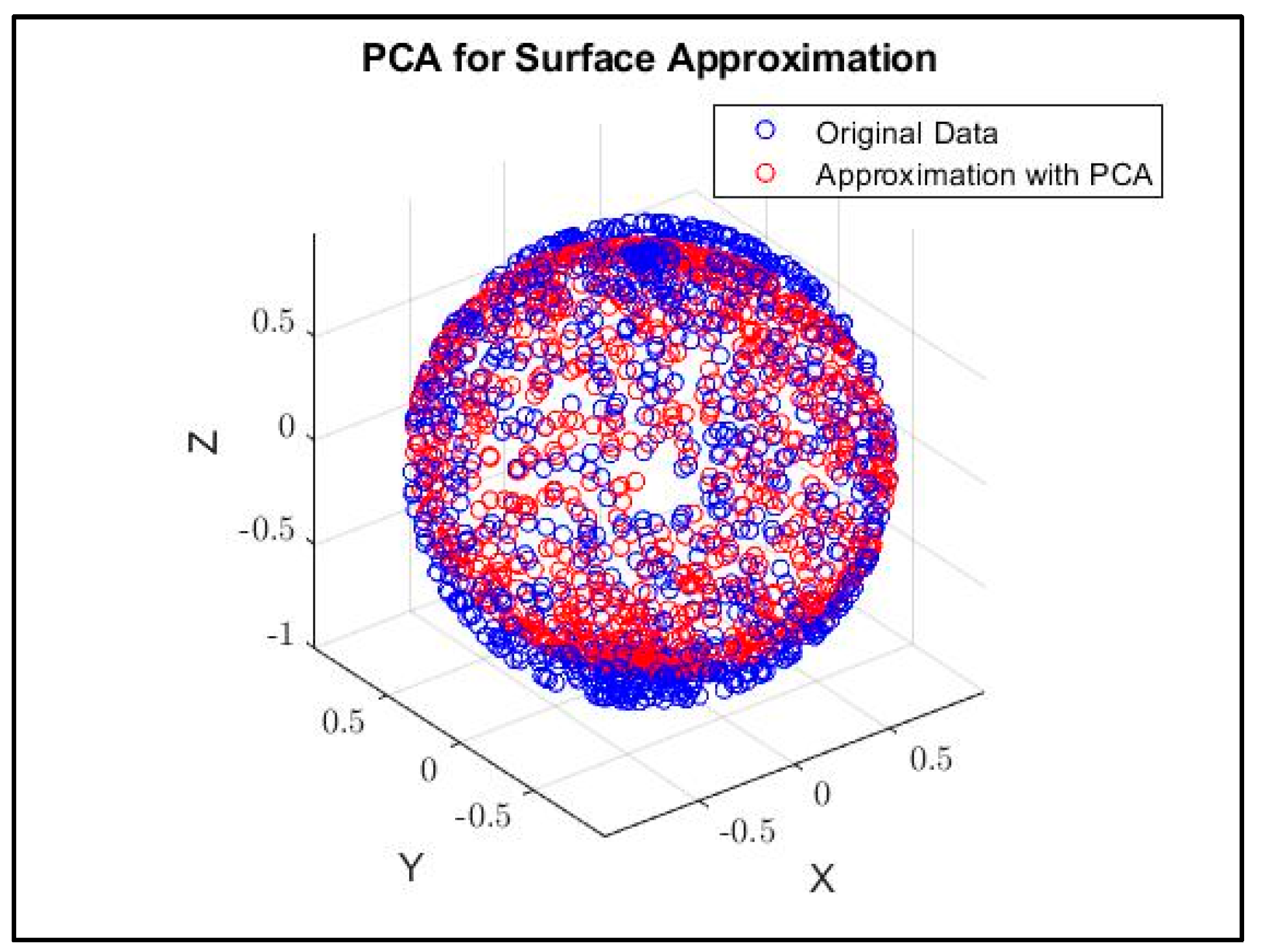
2.3. Principal Component Analysis
- In the first step of the calculations, the data (represented as matrix ) are standardized—this is the standardization process known from statistics, where the mean value is set to zero.
- In the second step, we calculate the covariance matrix as follows:where is the number of observations, and is the transpose of matrix .
- The eigenvalues measure the variance of each principal component, and the eigenvectors determine the directions of these components. They are calculated using the equation:
- Next, the principal components are selected, and dimensionality reduction is achieved by projecting the data onto the new space defined by the selected eigenvectors. The transformation is performed according to the following matrix equation:where is the matrix of eigenvectors corresponding to the largest eigenvalues, and represents the projected data.
2.4. Markov Random Fields and Conditional Random Fields
2.5. Artificial Neural Networks
3. Method for Reconstructing Hypersurfaces in a Multidimensional Euclidean Space
3.1. Representation of Hypersurface
3.2. The Main Parameters in the Algorithm for Reconstructing Hypersurfaces
- Points for training the corresponding ANN (70% of the sample size);
- Points for independent testing (15%);
- Points for determining the validity of the training (15%).
| Step 1: Generate a 3D surface. |
| Define the ranges for and . |
| Create the coordinate grid: |
| . |
| Calculate the coordinates: |
| . |
| Step 2: Convert the matrices into vectors. |
| Step 3: Remove of the points. |
| Generate a random permutation of indices: |
| Select the first indices: |
| Remove these points from the training set: |
| Step 4: Select random points from the remaining . |
| Generate a permutation for points: |
| Extract these points for training, validation, and testing: |
| Step 5: Split the data into three parts. |
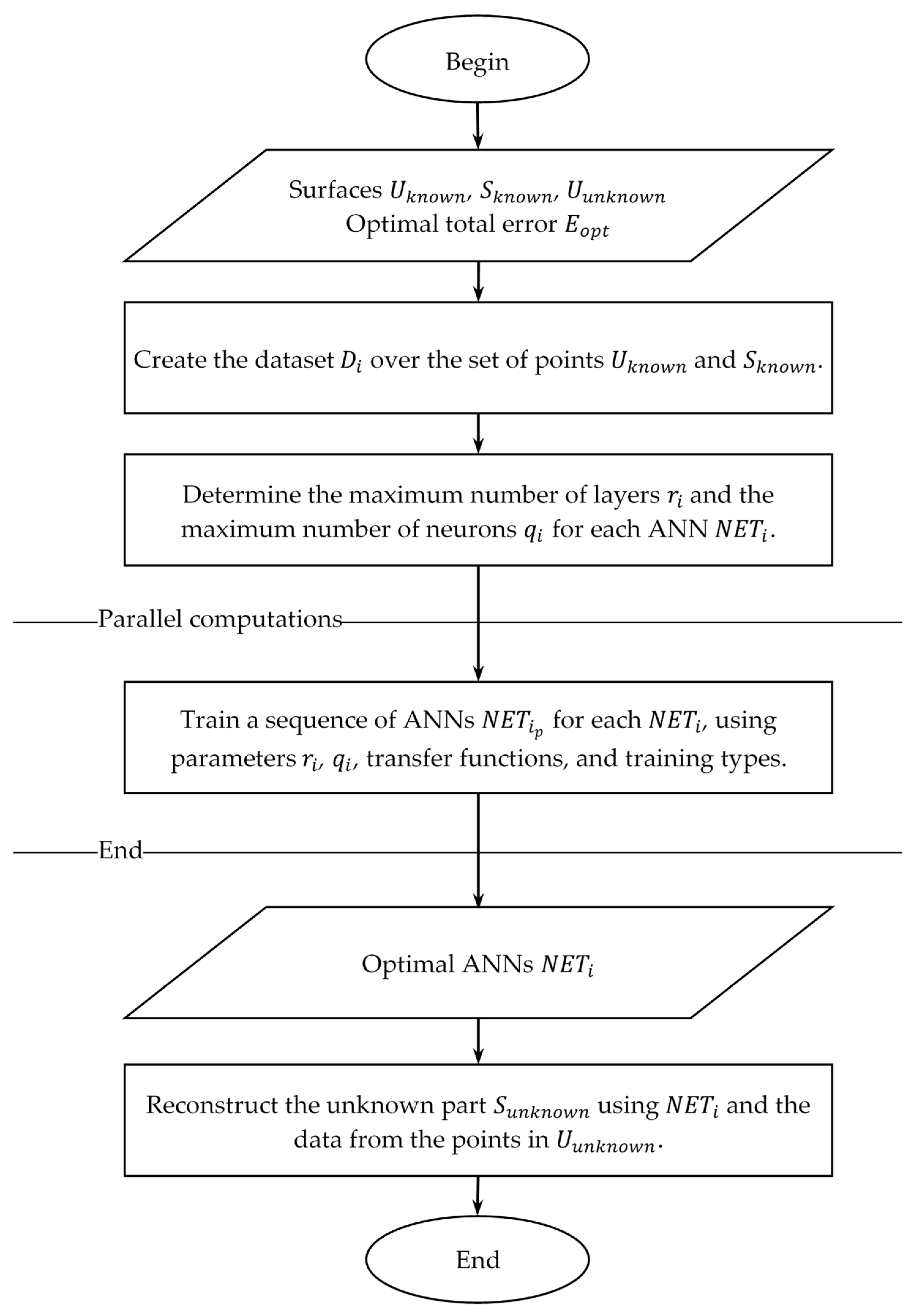
3.3. Algorithm for Reconstructing Hypersurfaces
- Step 1: Determine a set of points from and , on which the dataset will be created.
- Step 2: Determine a set of points from , for which the coordinates of . will be approximated.
- Step 3: Set an optimal total error , defined by the user, that the ANNs must satisfy.
- Step 4: Create the dataset on the set of points and .
- Step 5: Determine the maximum number of layers and the maximum number of neurons for each ANN .
- Step 6: Create a set of ANNs for each coordinate and select the optimal ANN .
- Step 7: Reconstruct the unknown part through approximation using the created ANNs and the data for points from .
- Initially create several ANNs with different numbers of neurons and neuron layers within the intervals and , respectively.
- Sort the search intervals based on the effectiveness of the created ANNs.
- Sequentially explore the intervals to find an optimal ANN.
3.4. Application of the Reconstruction Algorithm on 2D Surfaces in
- Sphere , where ;
- Right helicoid , where ;
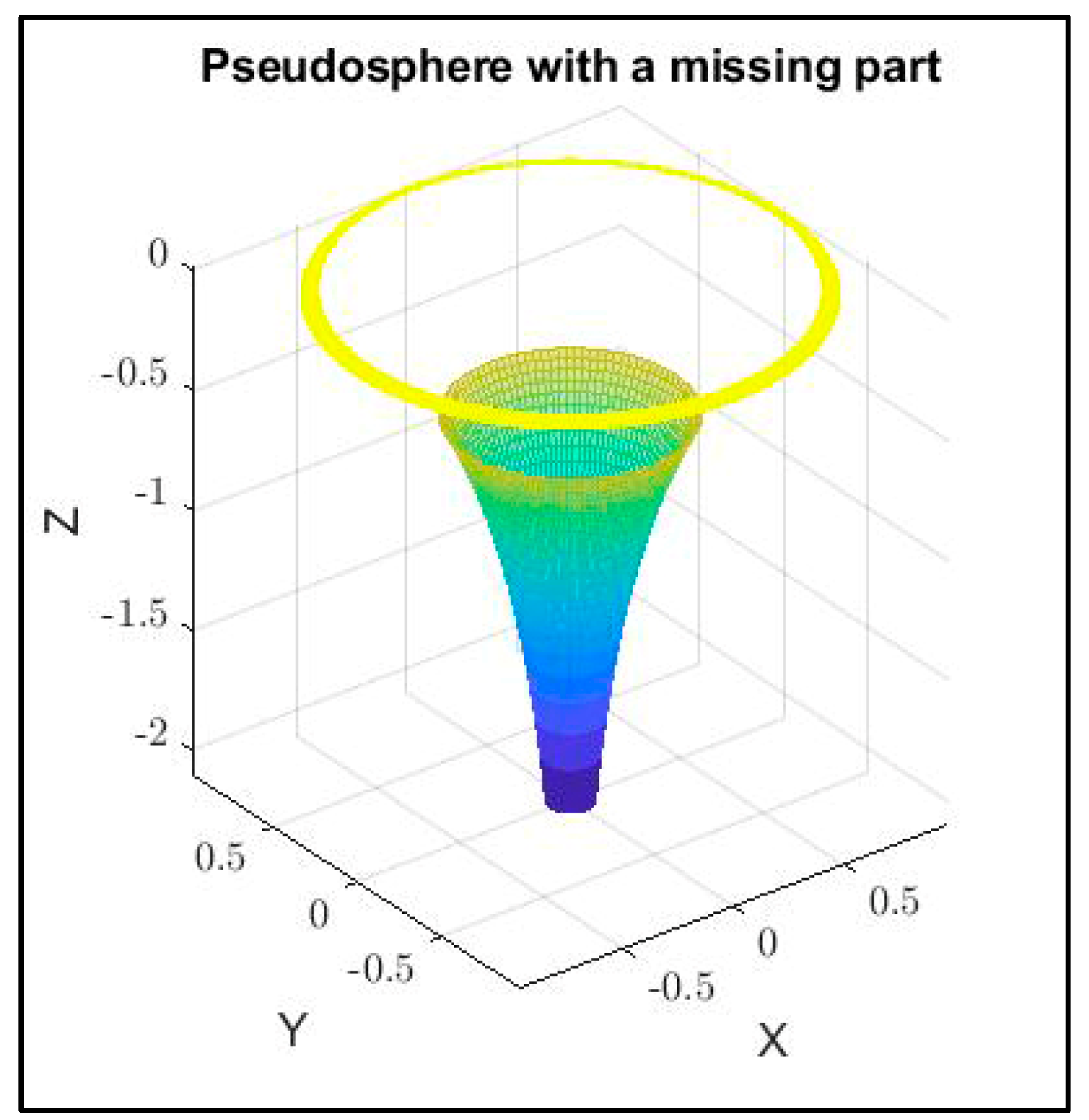
- Pseudosphere , where .
- Points for training the corresponding ANN (70% of the sample size);
- Points for independent testing (15%);
- Points for determining the validity of the training (15%).
4. Experiments
- With a dataset of 500 points from and the corresponding , the total root mean square error () of the set of ANNs was , and with 1000 points, the was .
- With 500 records in the training dataset, due to inaccuracies in the ANNs approximating the coordinates and , and despite the error in the ANN for the coordinate being zero (since it approximates a constant), the reconstructed part failed to “connect” smoothly with the known surface .
- With 1000 records in the training dataset, the ANNs successfully reconstructed the missing detail.
4.1. Reconstruction of a Sphere
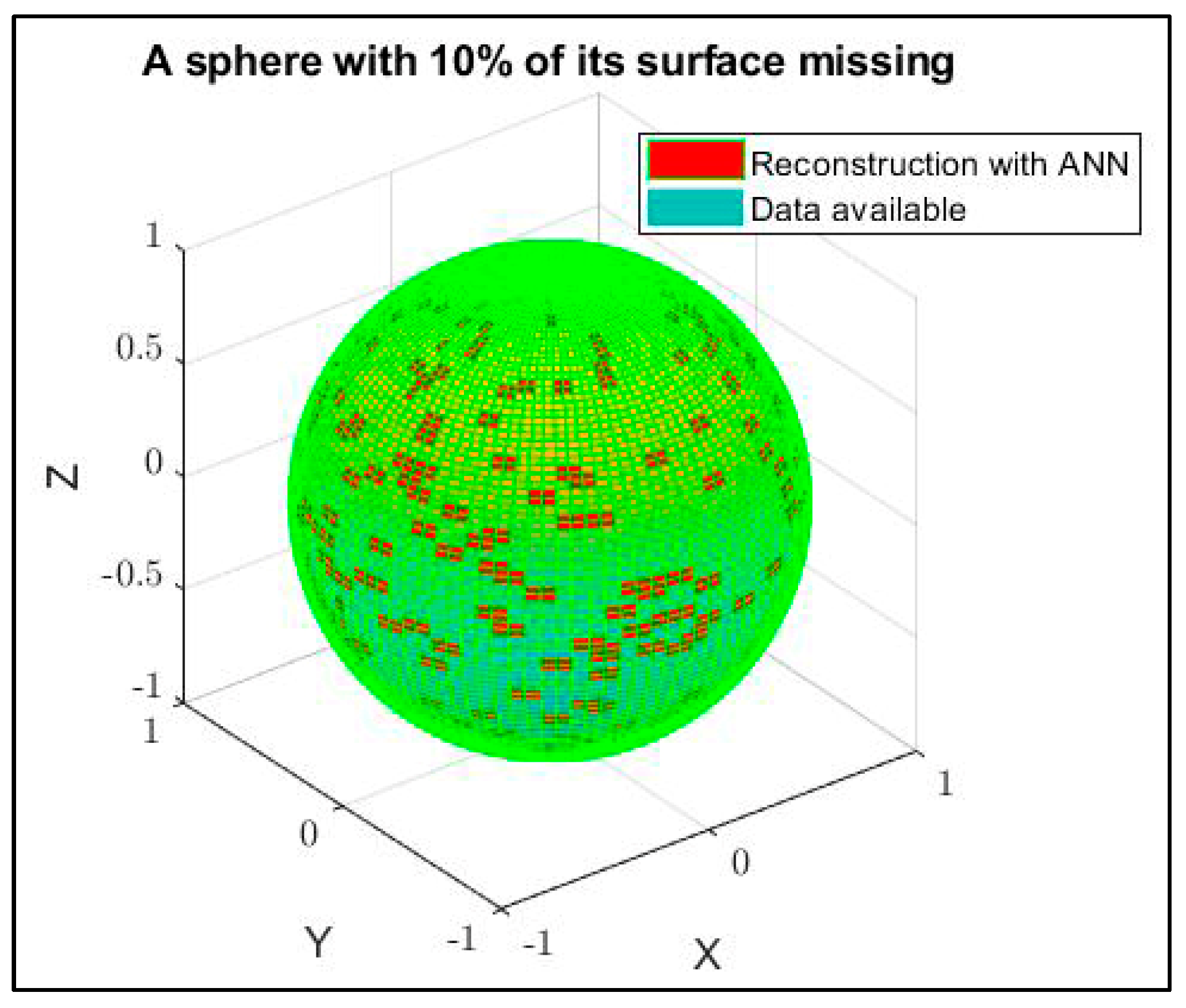
4.1.1. Reconstruction of a Whole Missing Piece of the Sphere
4.1.2. Reconstruction of Multiple Missing Small Pieces of the Sphere
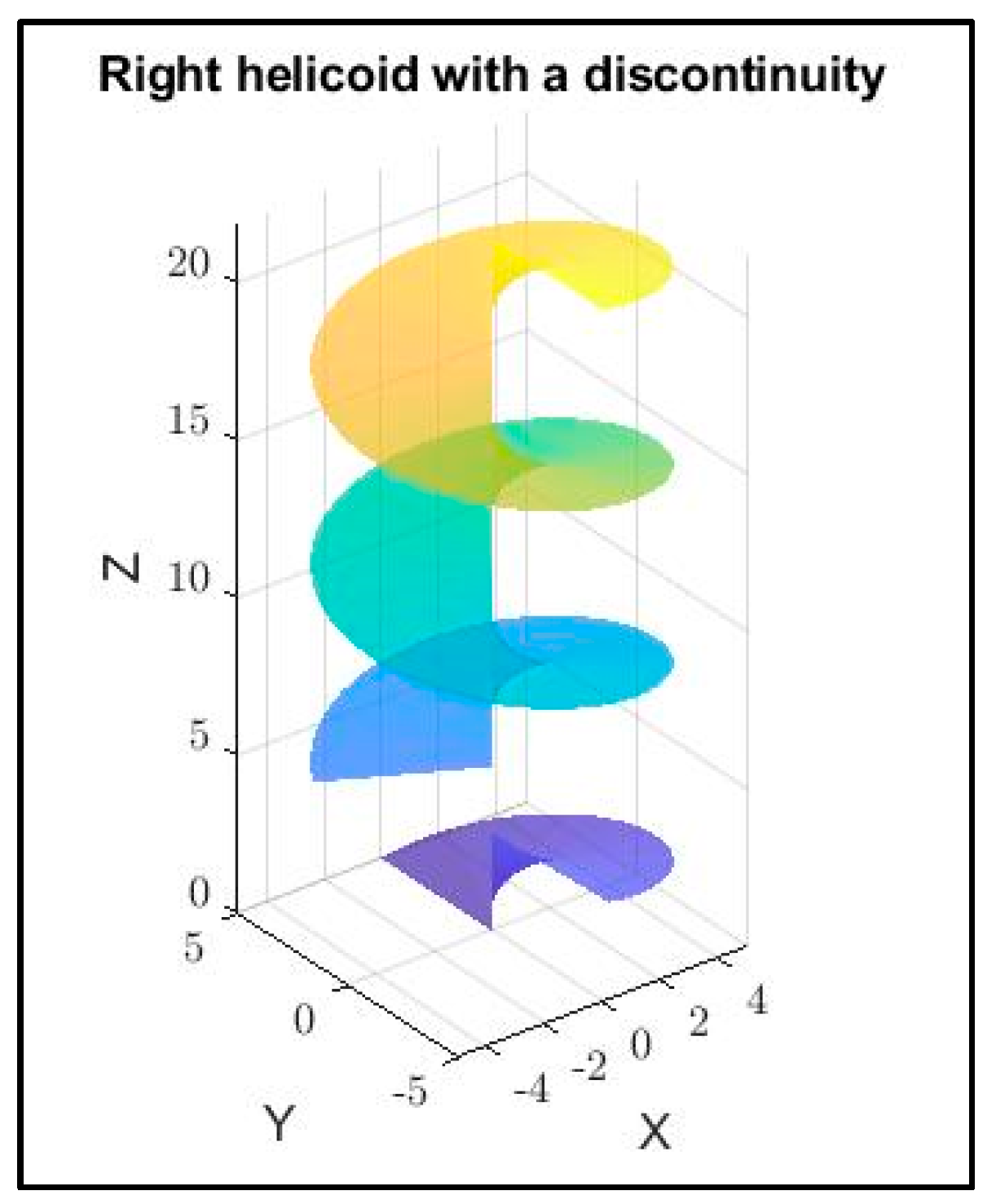
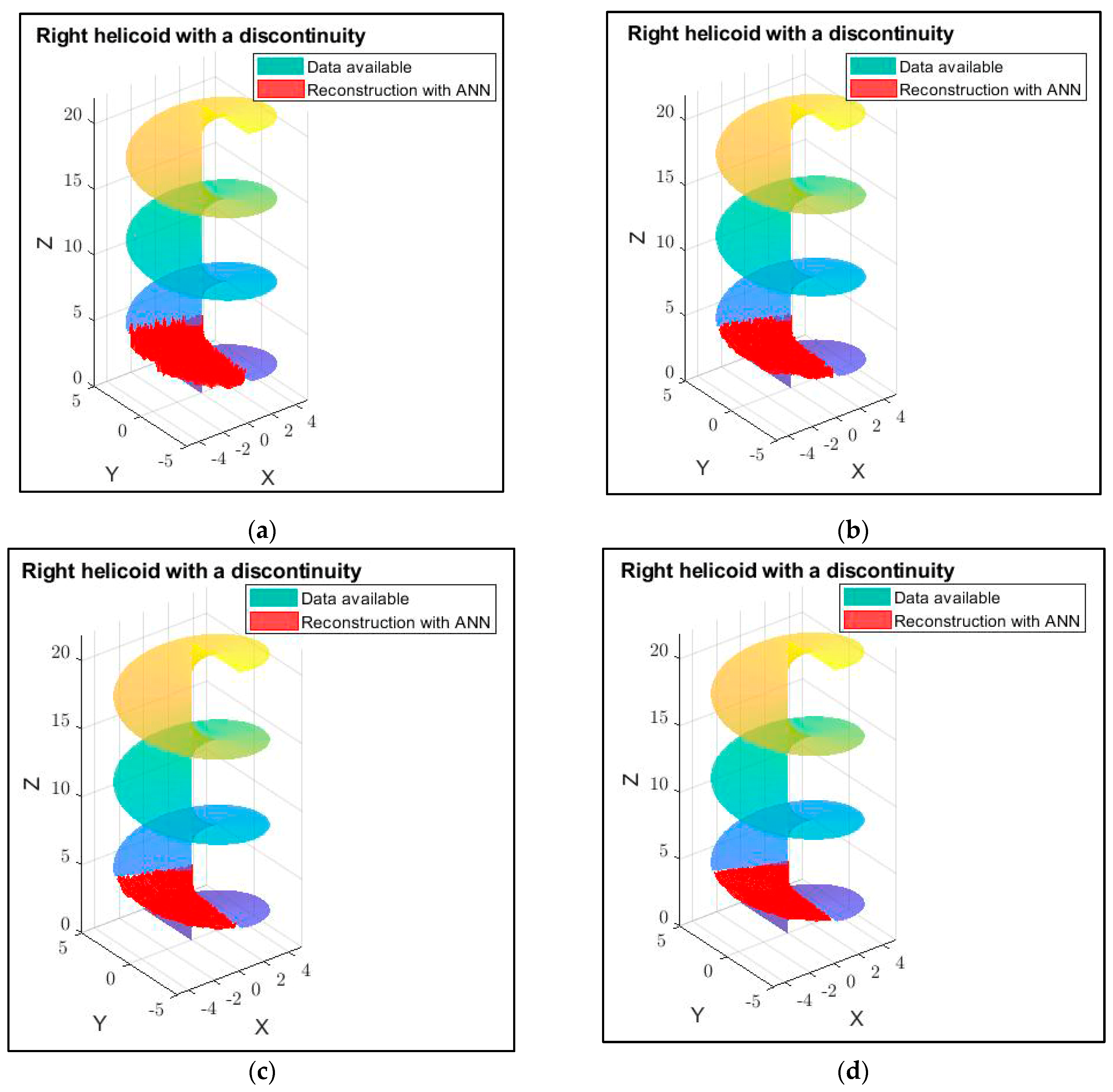
4.2. Reconstruction of a Right Helicoid
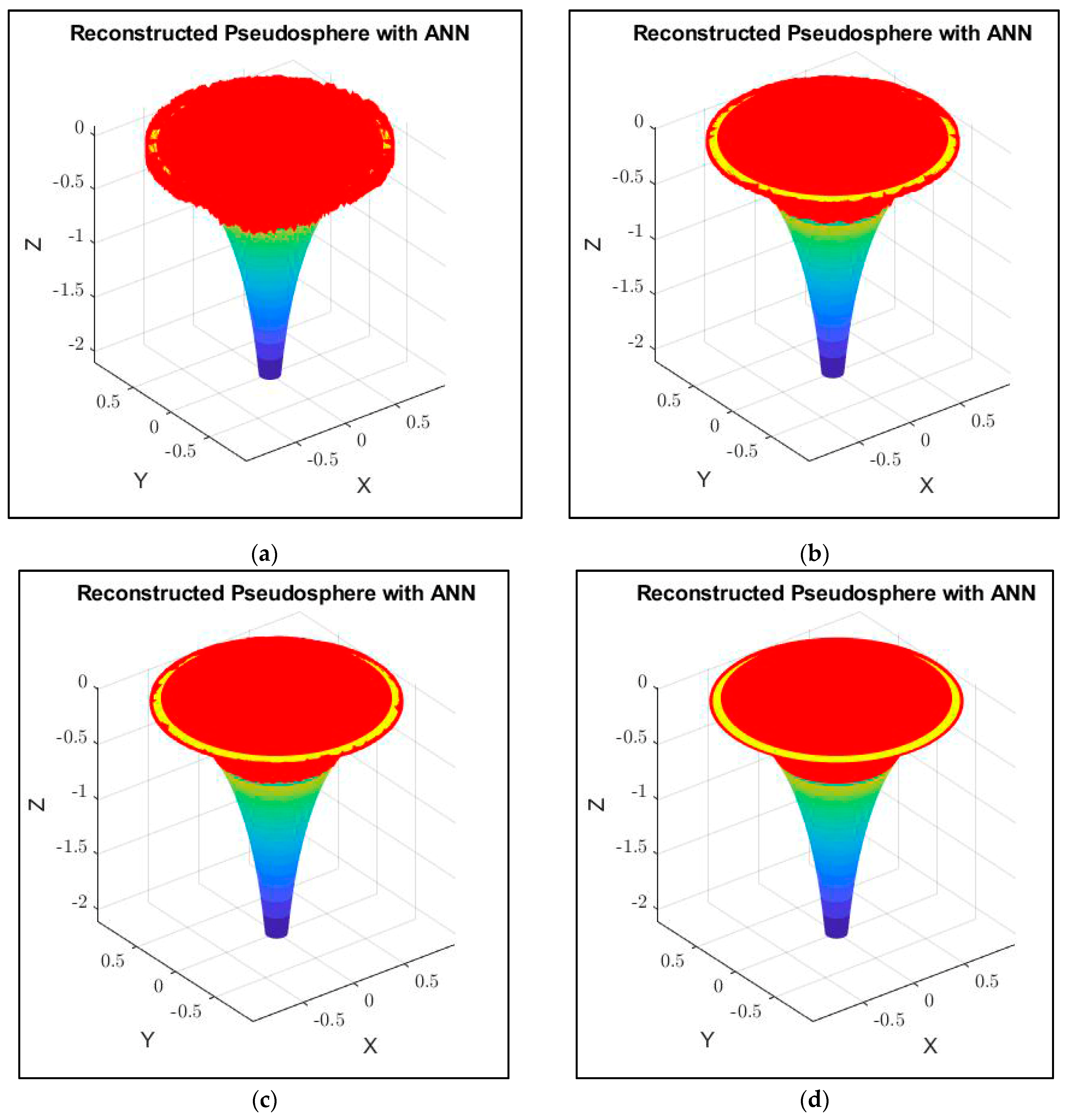
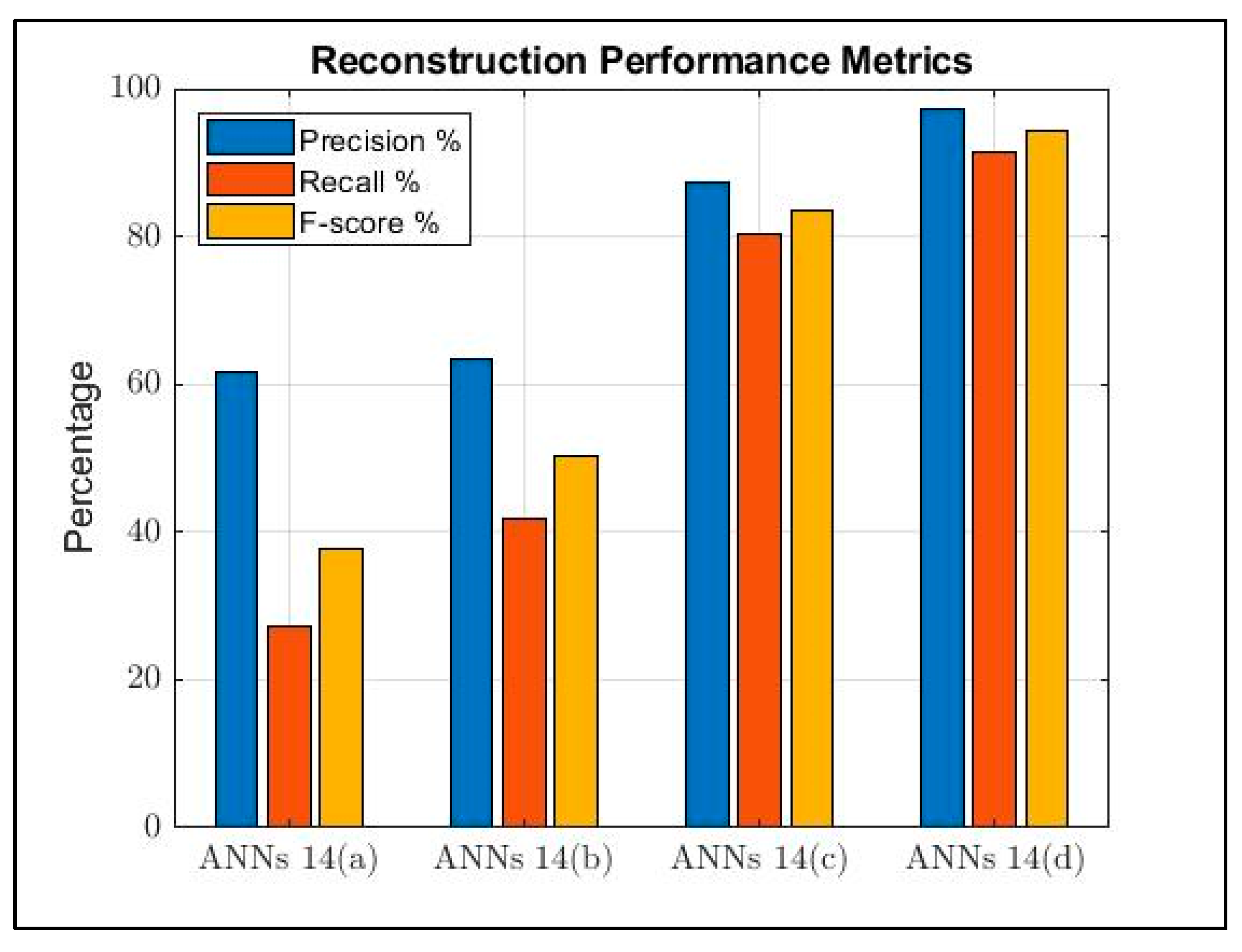
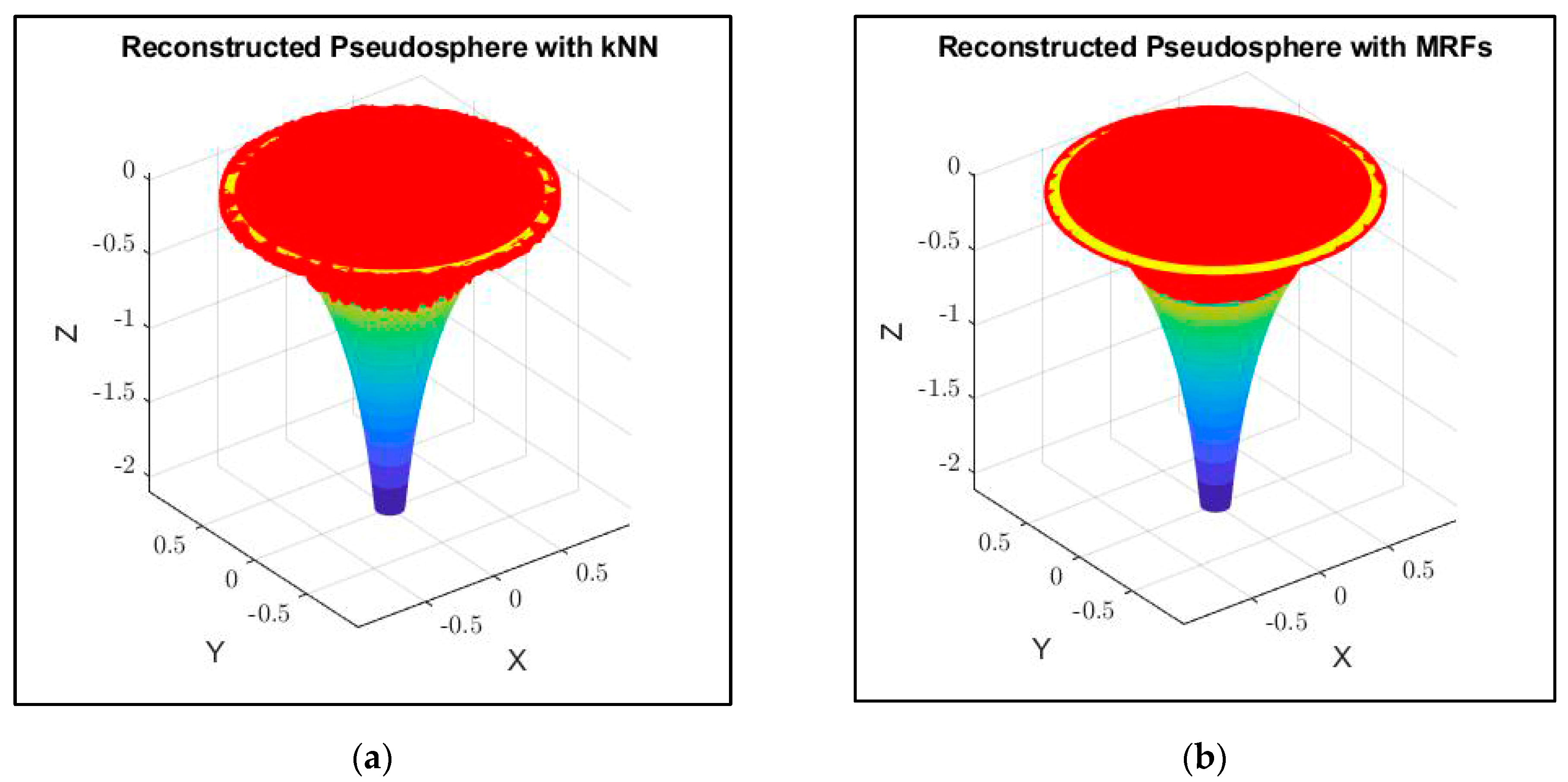
4.3. Reconstruction of a Pseudosphere
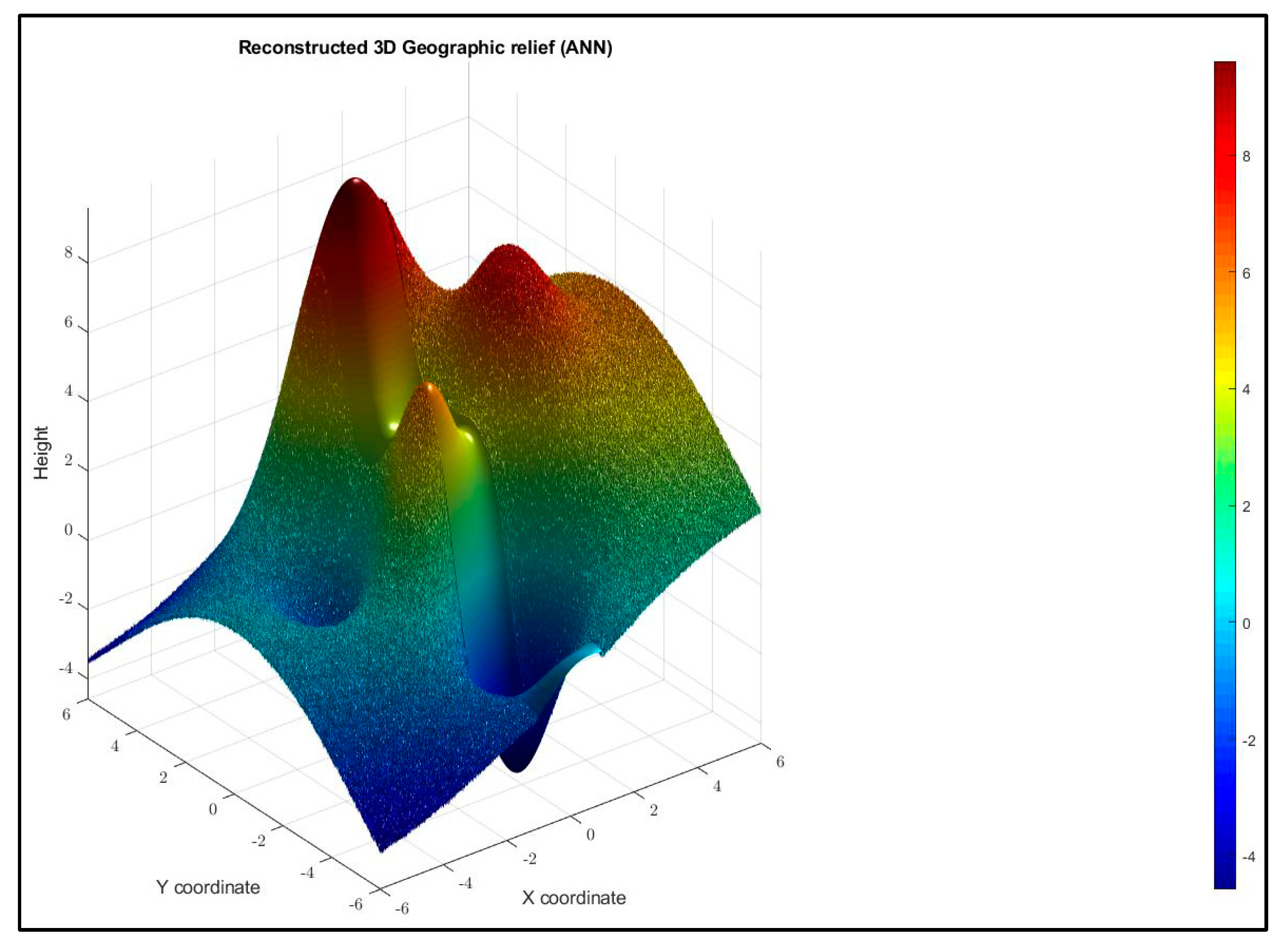
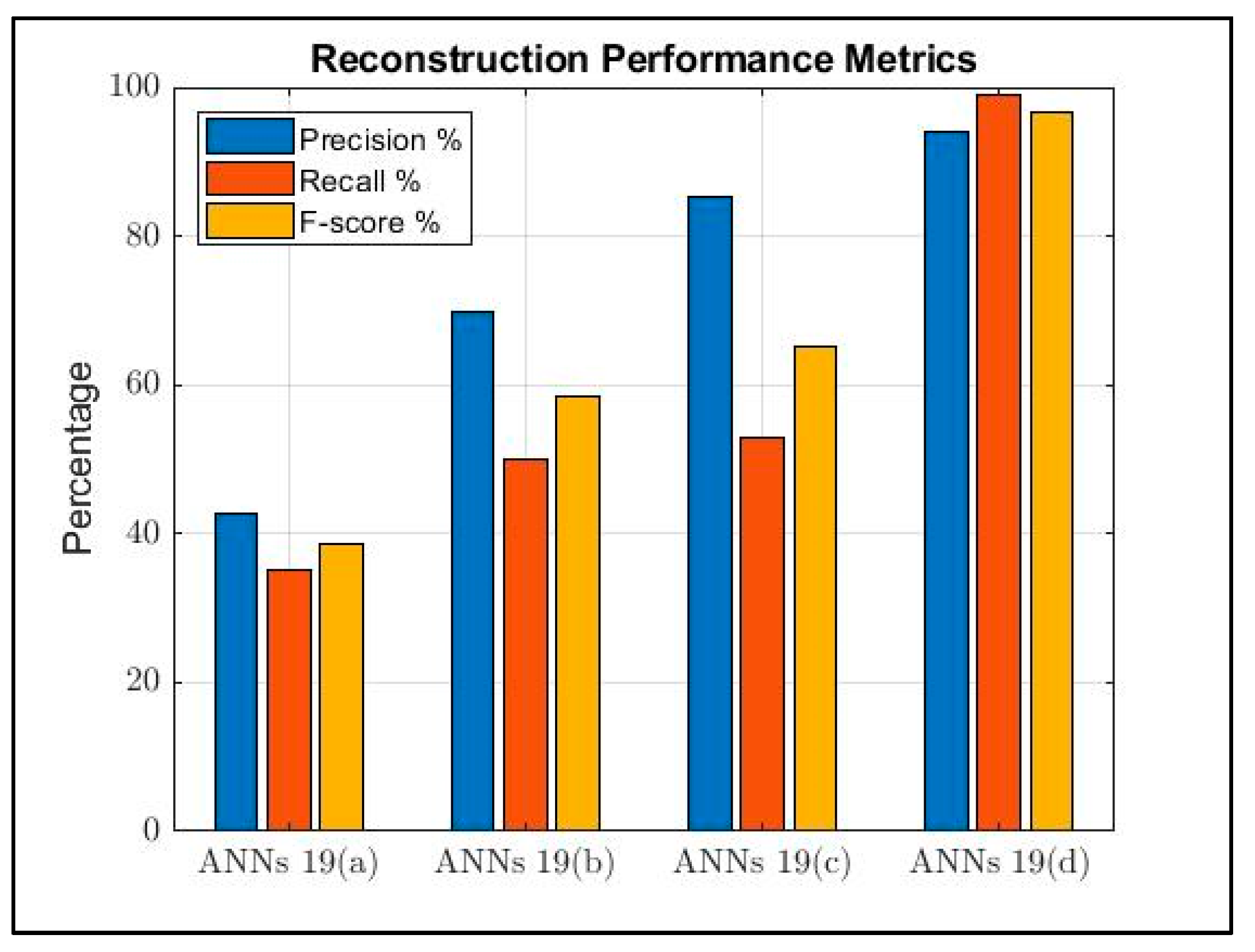
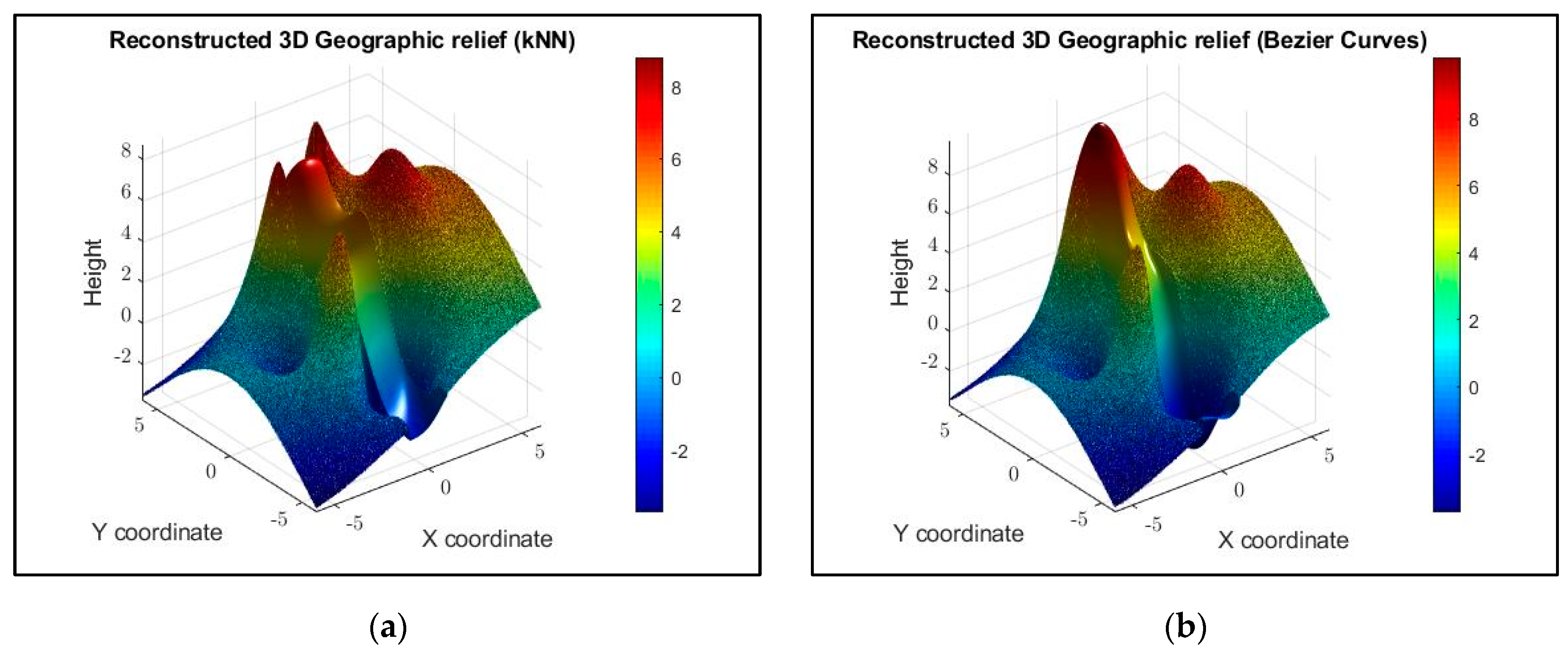
4.4. Reconstruction of Simulated Geographical Terrain
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sukumar, N.; Srivastava, A. Exact imposition of boundary conditions with distance functions in physics-informed deep neural networks. Comput. Methods Appl. Mech. Eng. 2022, 389, 114333. [Google Scholar] [CrossRef]
- Claudi, F.; Branco, T. Differential geometry methods for constructing manifold-targeted recurrent neural networks. Neural Comput. 2022, 34, 1790–1811. [Google Scholar] [CrossRef] [PubMed]
- Benfenati, A.; Marta, A. A singular Riemannian geometry approach to Deep Neural Networks I. Theoretical foundations. Neural Netw. 2023, 158, 331–343. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, S.H.; Sany, M.R.; Ahamed, M.H.; Das, S.K.; Badal, F.R.; Das, P.; Tasneem, Z.; Hasan, M.; Islam, R.; Ali, F.; et al. A State-of-the-Art Computer Vision Adopting Non-Euclidean Deep-Learning Models. Int. J. Intell. Syst. 2023, 2023, 8674641. [Google Scholar] [CrossRef]
- Mantovan, L.; Nanni, L. The computerization of archaeology: Survey on artificial intelligence techniques. SN Comput. Sci. 2020, 1, 267. [Google Scholar] [CrossRef]
- Gualandi, M.L.; Gattiglia, G.; Anichini, F. An open system for collection and automatic recognition of pottery through neural network algorithms. Heritage 2021, 4, 140–159. [Google Scholar] [CrossRef]
- Jamil, A.H.; Yakub, F.; Azizan, A.; Roslan, S.A.; Zaki, S.A.; Ahmad, S.A. A review on Deep Learning application for detection of archaeological structures. J. Adv. Res. Appl. Sci. Eng. Technol. 2022, 26, 7–14. [Google Scholar] [CrossRef]
- Barceló, J.A.; Del Castillo, F.; Kayikci, D.; Urbistondo, B. Neural networks for archaeological classification and typology: An overview. PCA Eur. J. Post-Class. Archaeol. 2022, 12, 7–32. [Google Scholar]
- Hlad, M.; Veselka, B.; Steadman, D.W.; Herregods, B.; Elskens, M.; Annaert, R.; Boudin, M.; Capuzzo, G.; Dalle, S.; De Mulder, G.; et al. Revisiting metric sex estimation of burnt human remains via supervised learning using a reference collection of modern identified cremated individuals (Knoxville, USA). Am. J. Phys. Anthropol. 2021, 175, 777–793. [Google Scholar] [CrossRef]
- Siozos, P.; Hausmann, N.; Holst, M.; Anglos, D. Application of laser-induced breakdown spectroscopy and neural networks on archaeological human bones for the discrimination of distinct individuals. J. Archaeol. Sci. Rep. 2021, 35, 102769. [Google Scholar] [CrossRef]
- Tuan, H.N.A.; Hai, N.D.X.; Thinh, N.T. Shape Prediction of Nasal Bones by Digital 2D-Photogrammetry of the Nose Based on Convolution and Back-Propagation Neural Network. Comput. Math. Methods Med. 2022, 2022, 5938493. [Google Scholar] [CrossRef] [PubMed]
- Martos, R.; Ibáñez, O.; Mesejo, P. Artificial intelligence in forensic anthropology: State of the art and Skeleton-ID project. Methodol. Technol. Adv. Death Investig. 2024, 83–153. [Google Scholar] [CrossRef]
- Jenny, B.; Heitzler, M.; Singh, D.; Farmakis-Serebryakova, M.; Liu, J.C.; Hurni, L. Cartographic relief shading with neural networks. IEEE Trans. Vis. Comput. Graph. 2020, 27, 1225–1235. [Google Scholar] [CrossRef] [PubMed]
- Hillier, M.; Wellmann, F.; Brodaric, B.; de Kemp, E.; Schetselaar, E. Three-dimensional structural geological modeling using graph neural networks. Math. Geosci. 2021, 53, 1725–1749. [Google Scholar] [CrossRef]
- He, S.; Cai, H.; Liu, S.; Xie, J.; Hu, X. Recovering 3D basement relief using gravity data through convolutional neural networks. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022611. [Google Scholar] [CrossRef]
- Chen, M.; Qian, Z.; Boers, N.; Jakeman, A.J.; Kettner, A.J.; Brandt, M.; Kwan, M.-P.; Batty, M.; Li, W.; Zhu, R.; et al. Iterative integration of deep learning in hybrid Earth surface system modelling. Nat. Rev. Earth Environ. 2023, 4, 568–581. [Google Scholar] [CrossRef]
- Thurnhofer-Hemsi, K.; Lopez-Rubio, E.; Roe-Vellve, N.; Molina-Cabello, M.A. Multiobjective optimization of deep neural networks with combinations of Lp-norm cost functions for 3D medical image super-resolution. Integr. Comput.-Aided Eng. 2020, 27, 233–251. [Google Scholar] [CrossRef]
- Nauwelaers, N.; Matthews, H.; Fan, Y.; Croquet, B.; Hoskens, H.; Mahdi, S.; El Sergani, A.; Gong, S.; Xu, T.; Bronstein, M.; et al. Exploring palatal and dental shape variation with 3D shape analysis and geometric deep learning. Orthod. Craniofacial Res. 2021, 24, 134–143. [Google Scholar] [CrossRef]
- Bai, Q.; Xu, T.; Huang, J.; Pérez-Sánchez, H. Geometric deep learning methods and applications in 3D structure-based drug design. Drug Discov. Today 2024, 29, 104024. [Google Scholar] [CrossRef]
- Deng, B.; Lewis, J.P.; Jeruzalski, T.; Pons-Moll, G.; Hinton, G.; Norouzi, M.; Tagliasacchi, A. Nasa neural articulated shape approximation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer International Publishing: New York, NY, USA, 2020. Part VII 16. pp. 612–628. [Google Scholar] [CrossRef]
- Williams, F.; Trager, M.; Bruna, J.; Zorin, D. Neural splines: Fitting 3d surfaces with infinitely-wide neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 9949–9958. [Google Scholar]
- Tewari, A.; Thies, J.; Mildenhall, B.; Srinivasan, P.; Tretschk, E.; Yifan, W.; Lassner, C.; Sitzmann, V.; Martin-Brualla, R.; Lombardi, S.; et al. Advances in neural rendering. Comput. Graph. Forum 2022, 41, 703–735. [Google Scholar] [CrossRef]
- Hilbig, A.; Vogt, L.; Holtzhausen, S.; Paetzold, K. Enhancing three-dimensional convolutional neural network-based geometric feature recognition for adaptive additive manufacturing: A signed distance field data approach. J. Comput. Des. Eng. 2023, 10, 992–1009. [Google Scholar] [CrossRef]
- Cao, W.; Robinson, T.; Hua, Y.; Boussuge, F.; Colligan, A.R.; Pan, W. Graph representation of 3D CAD models for machining feature recognition with deep learning. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Online, 17–19 August 2020; p. 84003. [Google Scholar] [CrossRef]
- Hong, R.; Zhang, L.; Lifton, J.; Daynes, S.; Wei, J.; Feih, S.; Lu, W.F. Artificial neural network-based geometry compensation to improve the printing accuracy of selective laser melting fabricated sub-millimetre overhang trusses. Addit. Manuf. 2021, 37, 101594. [Google Scholar] [CrossRef]
- Fu, X.; Peddireddy, D.; Aggarwal, V.; Jun, M.B.G. Improved dexel representation: A 3-d cnn geometry descriptor for manufacturing cad. IEEE Trans. Ind. Inform. 2021, 18, 5882–5892. [Google Scholar] [CrossRef]
- Fan, L.; Ji, D.; Lin, P. Arbitrary surface data patching method based on geometric convolutional neural network. Neural Comput. Appl. 2023, 35, 8763–8774. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Jin, J.; Kong, Z.; Yue, X. MVGCN: Multi-view graph convolutional neural network for surface defect identification using three-dimensional point cloud. J. Manuf. Sci. Eng. 2023, 145, 031004. [Google Scholar] [CrossRef]
- Zhang, T.; Xiao, M.; Zou, Y.B.; Xiao, J.D.; Chen, S.Y. Robotic curved surface tracking with a neural network for angle identification and constant force control based on reinforcement learning. Int. J. Precis. Eng. Manuf. 2020, 21, 869–882. [Google Scholar] [CrossRef]
- Vulpi, F.; Milella, A.; Marani, R.; Reina, G. Recurrent and convolutional neural networks for deep terrain classification by autonomous robots. J. Terramech. 2021, 96, 119–131. [Google Scholar] [CrossRef]
- Vincent, J.A.; Schwager, M. Reachable polyhedral marching (rpm): A safety verification algorithm for robotic systems with deep neural network components. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 9029–9035. [Google Scholar] [CrossRef]
- Tang, Y.; Zhao, C.; Wang, J.; Zhang, C.; Sun, Q.; Zheng, W.X.; Du, W.; Qian, F.; Kurths, J. Perception and navigation in autonomous systems in the era of learning: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9604–9624. [Google Scholar] [CrossRef]
- Mancinelli, C.; Nazzaro, G.; Pellacini, F.; Puppo, E. b/surf: Interactive Bézier splines on surface meshes. IEEE Trans. Vis. Comput. Graph. 2022, 29, 3419–3435. [Google Scholar] [CrossRef]
- Li, F.; Hu, G.; Abbas, M.; Miura, K.T. The generalized H-Bézier model: Geometric continuity conditions and applications to curve and surface modeling. Mathematics 2020, 8, 924. [Google Scholar] [CrossRef]
- Ammad, M.; Misro, M.Y. Construction of local shape adjustable surfaces using quintic trigonometric Bézier curve. Symmetry 2020, 12, 1205. [Google Scholar] [CrossRef]
- Ameer, M.; Abbas, M.; Shafiq, M.; Nazir, T.; Birhanu, A. Generalized Bézier-like model and its applications to curve and surface modeling. PLoS ONE 2024, 19, e0303340. [Google Scholar] [CrossRef] [PubMed]
- Mahdaoui, A.; Sbai, E.H. 3D Point Cloud Simplification Based on k-Nearest Neighbor and Clustering. Adv. Multimed. 2020, 2020, 8825205. [Google Scholar] [CrossRef]
- Boumedine, A.Y.; Bentaieb, S.; Ouamri, A. An improved KNN classifier for 3D face recognition based on SURF descriptors. J. Appl. Secur. Res. 2023, 18, 808–826. [Google Scholar] [CrossRef]
- Kumar, P.; Jain, N.K. Surface roughness prediction in micro-plasma transferred arc metal additive manufacturing process using K-nearest neighbors algorithm. Int. J. Adv. Manuf. Technol. 2022, 119, 2985–2997. [Google Scholar] [CrossRef]
- Banerjee, A.; Gajewicz-Skretna, A.; Roy, K. A machine learning q-RASPR approach for efficient predictions of the specific surface area of perovskites. Mol. Inform. 2023, 42, e2200261. [Google Scholar] [CrossRef]
- Greenacre, M.; Groenen, P.J.; Hastie, T.; d’Enza, A.I.; Markos, A.; Tuzhilina, E. Principal component analysis. Nat. Rev. Methods Primers 2022, 2, 433–459. [Google Scholar] [CrossRef]
- Hasan, B.M.S.; Abdulazeez, A.M. A review of principal component analysis algorithm for dimensionality reduction. J. Soft Comput. Data Min. 2021, 2, 20–30. [Google Scholar] [CrossRef]
- Yang, L.; Cheng, J.C.; Wang, Q. Semi-automated generation of parametric BIM for steel structures based on terrestrial laser scanning data. Autom. Constr. 2020, 112, 103037. [Google Scholar] [CrossRef]
- Panwar, V.; Sharma, D.K.; Kumar, K.P.; Jain, A.; Thakar, C. Experimental investigations and optimization of surface roughness in turning of en 36 alloy steel using response surface methodology and genetic algorithm. Mater. Today Proc. 2021, 46, 6474–6481. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Mu, X.; Hou, T.; Xu, J.; Di Renzo, M.; Al-Dhahir, N. Reconfigurable intelligent surfaces: Principles and opportunities. IEEE Commun. Surv. Tutor. 2021, 23, 1546–1577. [Google Scholar] [CrossRef]
- Pfeiffer, J.; Rutzinger, M.; Spötl, C. Terrestrial laser scanning for 3D mapping of an alpine ice cave. Photogramm. Rec. 2023, 38, 6–21. [Google Scholar] [CrossRef] [PubMed]
- Hristopulos, D.T. Random Fields for Spatial Data Modeling; Springer: Dordrecht, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Chi, Y.; Wu, Z.; Liao, K.; Ren, Y. Handling missing data in large-scale MODIS AOD products using a two-step model. Remote Sens. 2020, 12, 3786. [Google Scholar] [CrossRef]
- Kang, S.H.; Choi, Y.; Choi, J.Y. Restoration of missing patterns on satellite infrared sea surface temperature images due to cloud coverage using deep generative inpainting network. J. Mar. Sci. Eng. 2021, 9, 310. [Google Scholar] [CrossRef]
- Žukovič, M.; Hristopulos, D.T. Spatial data modeling by means of Gibbs–Markov random fields based on a generalized planar rotator model. Phys. A Stat. Mech. Its Appl. 2023, 612, 128509. [Google Scholar] [CrossRef]
- Lu, Q.; Jiang, T. Pixon-based image denoising with Markov random fields. Pattern Recognit. 2001, 34, 2029–2039. [Google Scholar] [CrossRef]
- Gleich, D.; Datcu, M. Wavelet-based despeckling of SAR images using Gauss–Markov random fields. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4127–4143. [Google Scholar] [CrossRef]
- Pleschberger, M.; Schrunner, S.; Pilz, J. An explicit solution for image restoration using Markov random fields. J. Signal Process. Syst. 2020, 92, 257–267. [Google Scholar] [CrossRef]
- Aires, F. Surface water maps de-noising and missing-data filling using determinist spatial filters based on several a priori information. Remote Sens. Environ. 2020, 237, 111481. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, Z.; Zhang, Y.; Guan, Q. Building extraction from high spatial resolution remote sensing images via multiscale-aware and segmentation-prior conditional random fields. Remote Sens. 2020, 12, 3983. [Google Scholar] [CrossRef]
- Ou-Yang, J.Y.; Liu, Y.; Yao, K.; Yang, C.J.; Niu, H.F. Model updating of slope stability analysis using 3D conditional random fields. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 04021034. [Google Scholar] [CrossRef]
- Li, R.; Chen, X. An efficient interactive multi-label segmentation tool for 2D and 3D medical images using fully connected conditional random field. Comput. Methods Programs Biomed. 2022, 213, 106534. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Shi, C.; Sun, X. Analysis of surface deformation characteristics in pipe jacking construction based on the theory of a stratum cross-correlation conditional random field. Comput. Geotech. 2023, 162, 105668. [Google Scholar] [CrossRef]
- Hoffmann, L.F.S.; Bizarria, F.C.P.; Bizarria, J.W.P. Detection of liner surface defects in solid rocket motors using multilayer perceptron neural networks. Polym. Test. 2020, 88, 106559. [Google Scholar] [CrossRef]
- Xiao, G.; Xing, J.; Zhang, Y. Surface roughness prediction model of GH4169 superalloy abrasive belt grinding based on multilayer perceptron (MLP). Procedia Manuf. 2021, 54, 269–273. [Google Scholar] [CrossRef]
- Sharma, R.; Kim, M.; Gupta, A. Motor imagery classification in brain-machine interface with machine learning algorithms: Classical approach to multi-layer perceptron model. Biomed. Signal Process. Control 2022, 71, 103101. [Google Scholar] [CrossRef]
- Yan, J.; Zeng, S.; Tian, B.; Cao, Y.; Yang, W.; Zhu, F. Relationship between highway geometric characteristics and accident risk: A multilayer perceptron model (MLP) approach. Sustainability 2023, 15, 1893. [Google Scholar] [CrossRef]
- Wang, S.; Xia, X.; Ye, L.; Yang, B. Automatic detection and classification of steel surface defect using deep convolutional neural networks. Metals 2021, 11, 388. [Google Scholar] [CrossRef]
- Cruz, R.S.; Lebrat, L.; Bourgeat, P.; Fookes, C.; Fripp, J.; Salvado, O. Deepcsr: A 3d deep learning approach for cortical surface reconstruction. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Virtual, 5–9 January 2021; pp. 806–815. [Google Scholar]
- Nguyen, H.; Wang, Y.; Wang, Z. Single-shot 3D shape reconstruction using structured light and deep convolutional neural networks. Sensors 2020, 20, 3718. [Google Scholar] [CrossRef]
- Boulch, A.; Marlet, R. Poco: Point convolution for surface reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 6302–6314. [Google Scholar]
- Huang, Z.; Wen, Y.; Wang, Z.; Ren, J.; Jia, K. Surface reconstruction from point clouds: A survey and a benchmark. IEEE Trans. Pattern Anal. Mach. Intell. 2024. [Google Scholar] [CrossRef]
- Yotov, K.; Hadzhikolev, E.; Hadzhikoleva, S.; Cheresharov, S. Finding the optimal topology of an approximating neural network. Mathematics 2023, 11, 217. [Google Scholar] [CrossRef]
- Yotov, K.; Hadzhikolev, E.; Hadzhikoleva, S.; Milev, M. Artificial Neural Networks for Approximation of 2-Parameter Surfaces in 3D Euclidean Space. In Proceedings of the 50th International Conference “Applications of Mathematics in Engineering and Economics”, Sozopol, Bulgaria, 7–13 June 2024. [Google Scholar]
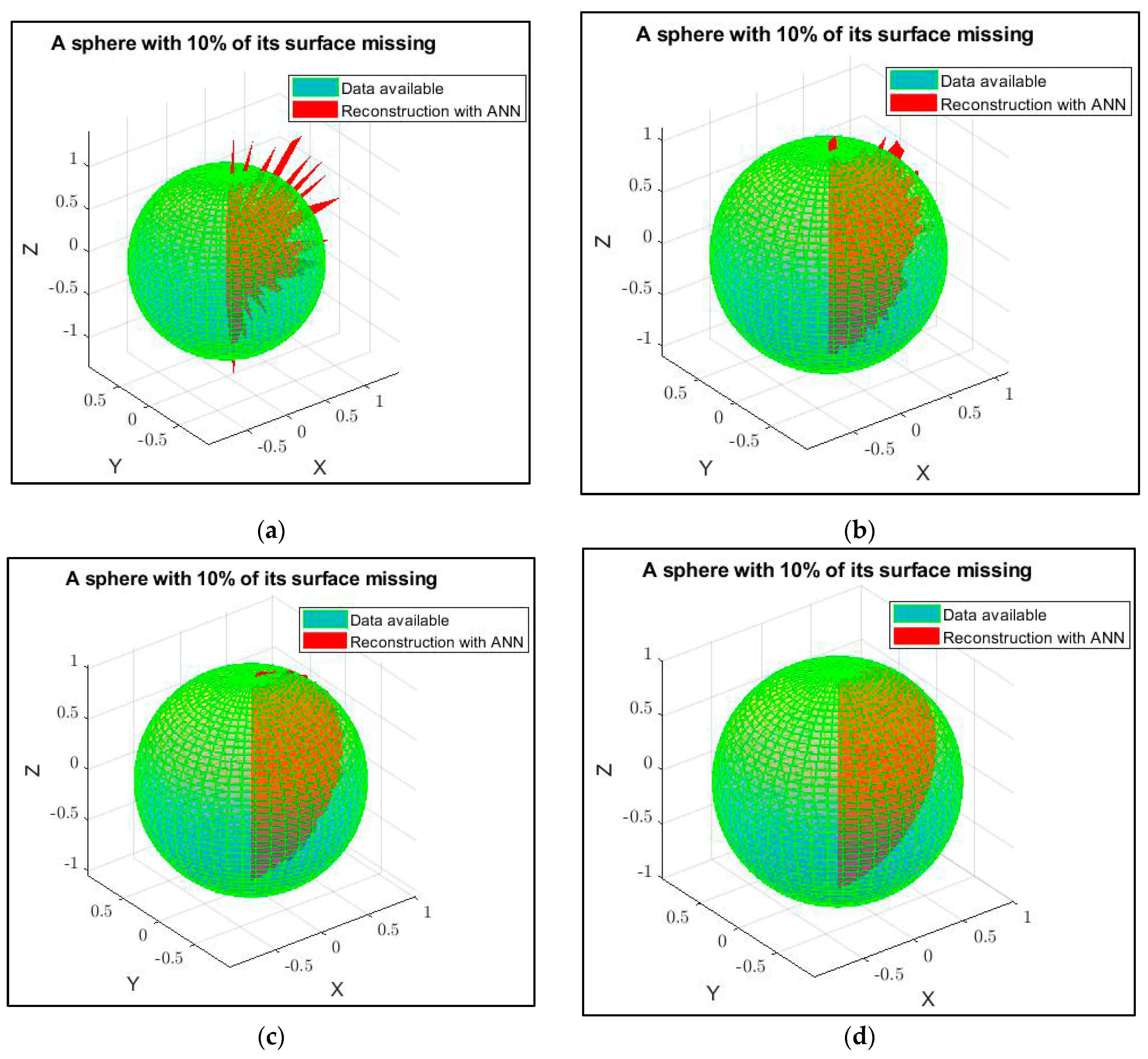
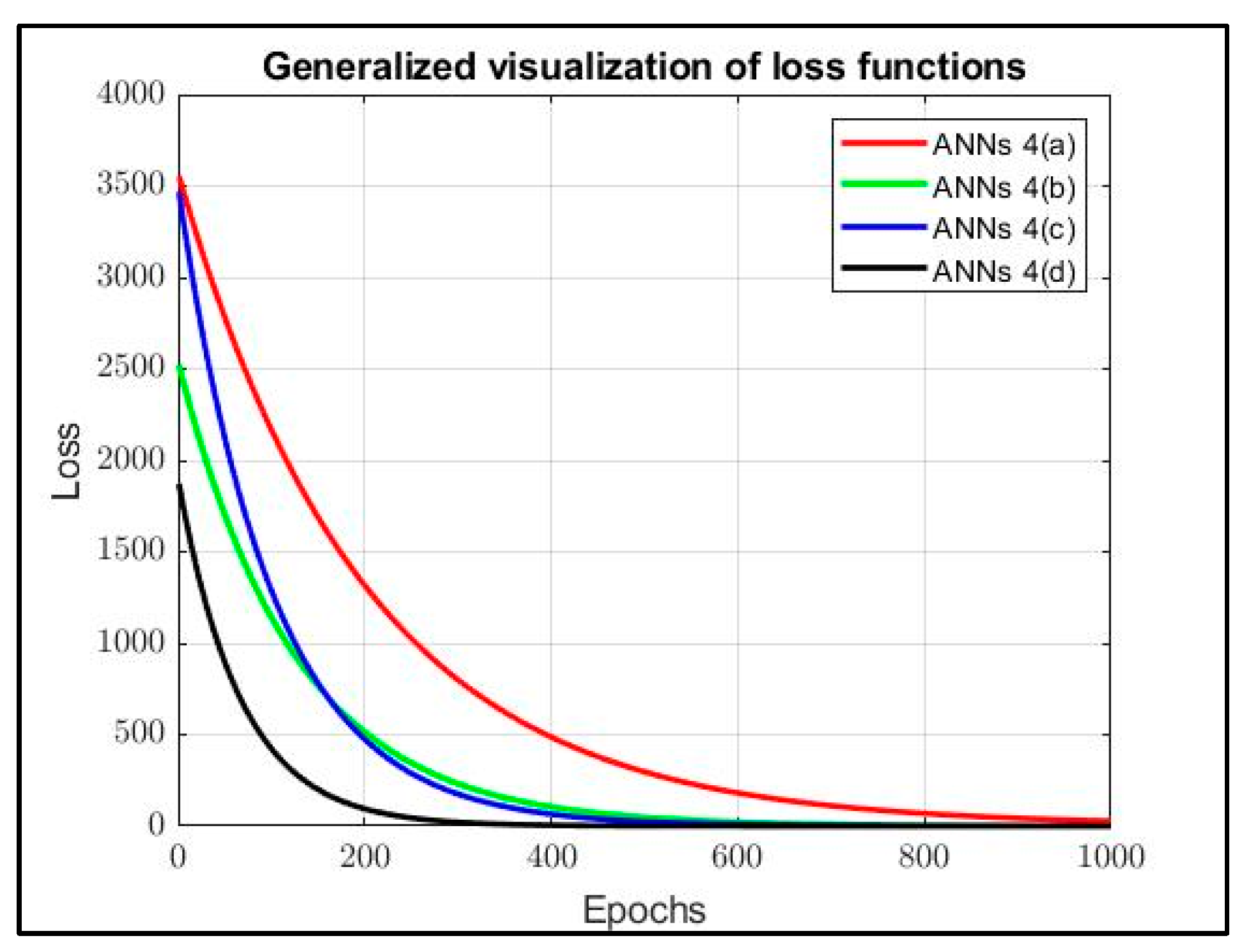
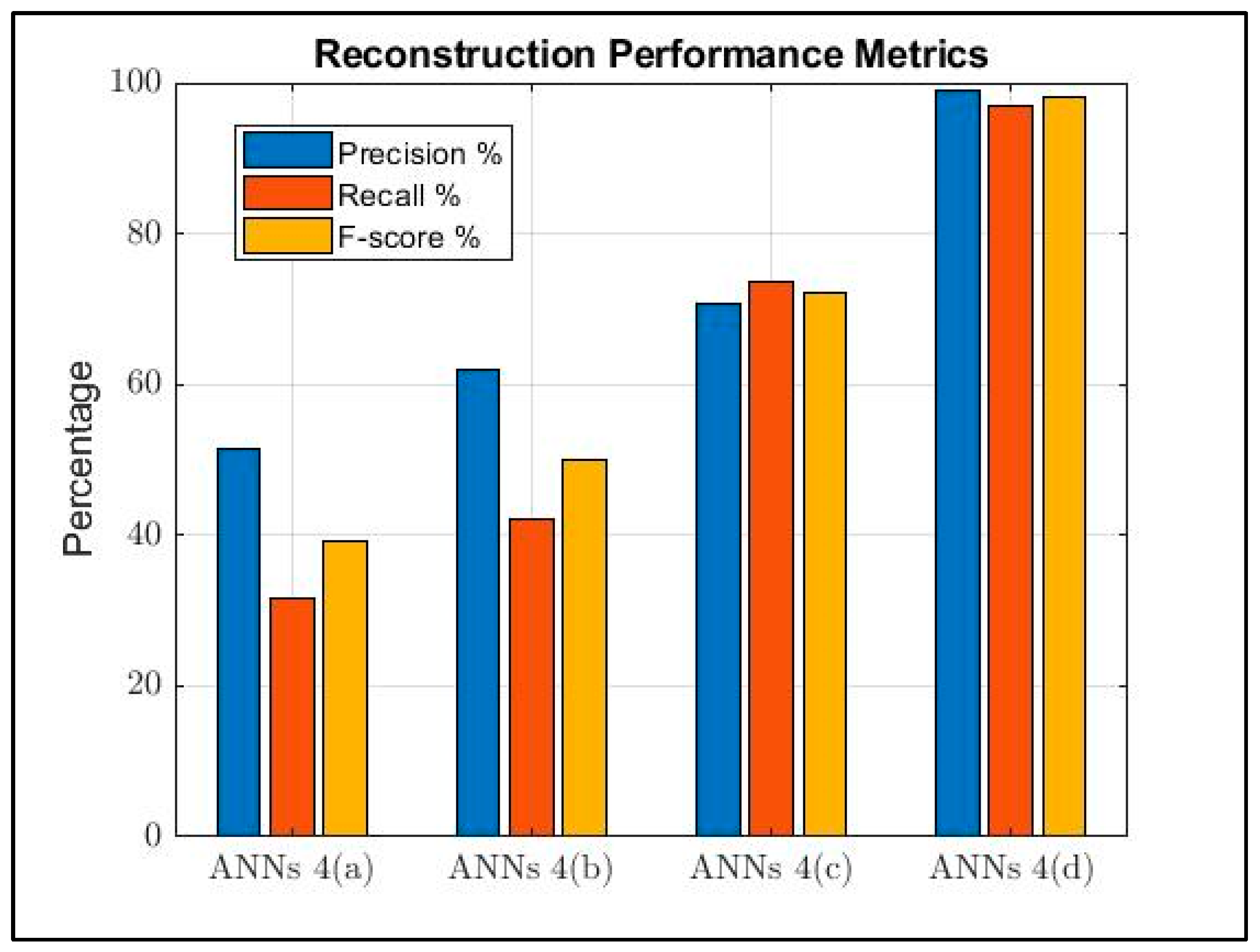






| ANNs | RMSE | Reconstruction Accuracy [%] | Similarity Percentage [%] | F-Score [%] |
|---|---|---|---|---|
| 4(a) | 3.56 | 31.67 | −78 | 39.24 |
| 4(b) | 2.3 | 42 | −15 | 50.05 |
| 4(c) | 0.3 | 73.67 | 85 | 72.1 |
| 4(d) | 10−5 | 97 | 99.99 | 97.8 |
| ANNs | RMSE | Reconstruction Accuracy [%] | Similarity Percentage [%] | F-Score [%] |
|---|---|---|---|---|
| 9(a) | 1.49 | 36 | 92.55 | 35.59 |
| 9(b) | 0.8 | 52.54 | 96 | 55.64 |
| 9(c) | 0.2 | 68.6 | 99 | 80.39 |
| 9(d) | 0.0016 | 91.3 | 99.9920 | 92 |
| ANNs | RMSE | Reconstruction Accuracy [%] | Similarity Percentage [%] | F-Score [%] |
|---|---|---|---|---|
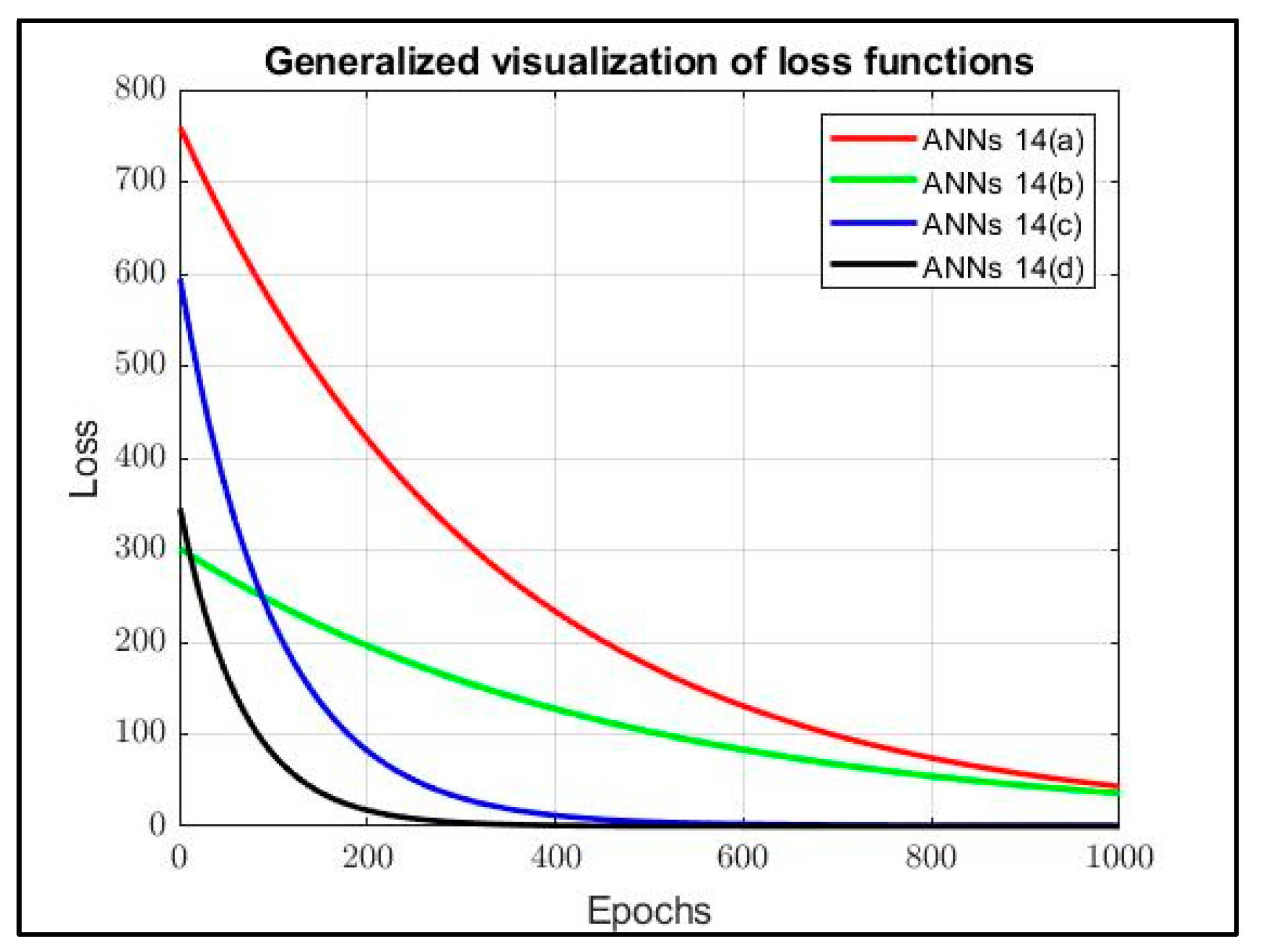
| 14(a) | 5.56 | 27.2 | −178 | 37.77 |
| 14(b) | 2.07 | 41.76 | −40 | 50.33 |
| 14(c) | 0.8 | 80.2 | 90 | 83.59 |
| 14(d) | 1.32 × 10−4 | 91.34 | 99.991 | 94.23 |
| Meтoд | RMSE | Reconstruction Accuracy [%] | Similarity Percentage [%] |
|---|---|---|---|
| KNN | 2.17 | 43.76 | −48 |
| MRFs | 0.73 | 79.2 | 87.46 |
| ANNs | RMSE | Reconstruction Accuracy [%] | Similarity Percentage [%] | F-Score [%] |
|---|---|---|---|---|
| 19(a) | 3251.27 | 35.05 | −4.054 × 104 | 38.54 |
| 19(b) | 568.49 | 50.1 | −7 × 104 | 58.35 |
| 19(c) | 0.8 | 52.8 | 90 | 65.20 |
| 19(d) | 3.72 × 10−4 | 99.05 | 99.9 | 96.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yotov, K.; Hadzhikolev, E.; Hadzhikoleva, S.; Milev, M. AI-Powered Approaches for Hypersurface Reconstruction in Multidimensional Spaces. Mathematics 2024, 12, 3285. https://doi.org/10.3390/math12203285
Yotov K, Hadzhikolev E, Hadzhikoleva S, Milev M. AI-Powered Approaches for Hypersurface Reconstruction in Multidimensional Spaces. Mathematics. 2024; 12(20):3285. https://doi.org/10.3390/math12203285
Chicago/Turabian StyleYotov, Kostadin, Emil Hadzhikolev, Stanka Hadzhikoleva, and Mariyan Milev. 2024. "AI-Powered Approaches for Hypersurface Reconstruction in Multidimensional Spaces" Mathematics 12, no. 20: 3285. https://doi.org/10.3390/math12203285
APA StyleYotov, K., Hadzhikolev, E., Hadzhikoleva, S., & Milev, M. (2024). AI-Powered Approaches for Hypersurface Reconstruction in Multidimensional Spaces. Mathematics, 12(20), 3285. https://doi.org/10.3390/math12203285






