A Time Series Synthetic Control Causal Evaluation of the UK’s Mini-Budget Policy on Stock Market
Abstract
:1. Introduction
2. Preliminaries of Causal Analysis
2.1. Notations
2.2. Causal Framework
2.3. The Conventional Synthetic Control Method
3. The Modified Synthetic Control Method
3.1. Form of the Modified Synthetic Control Method
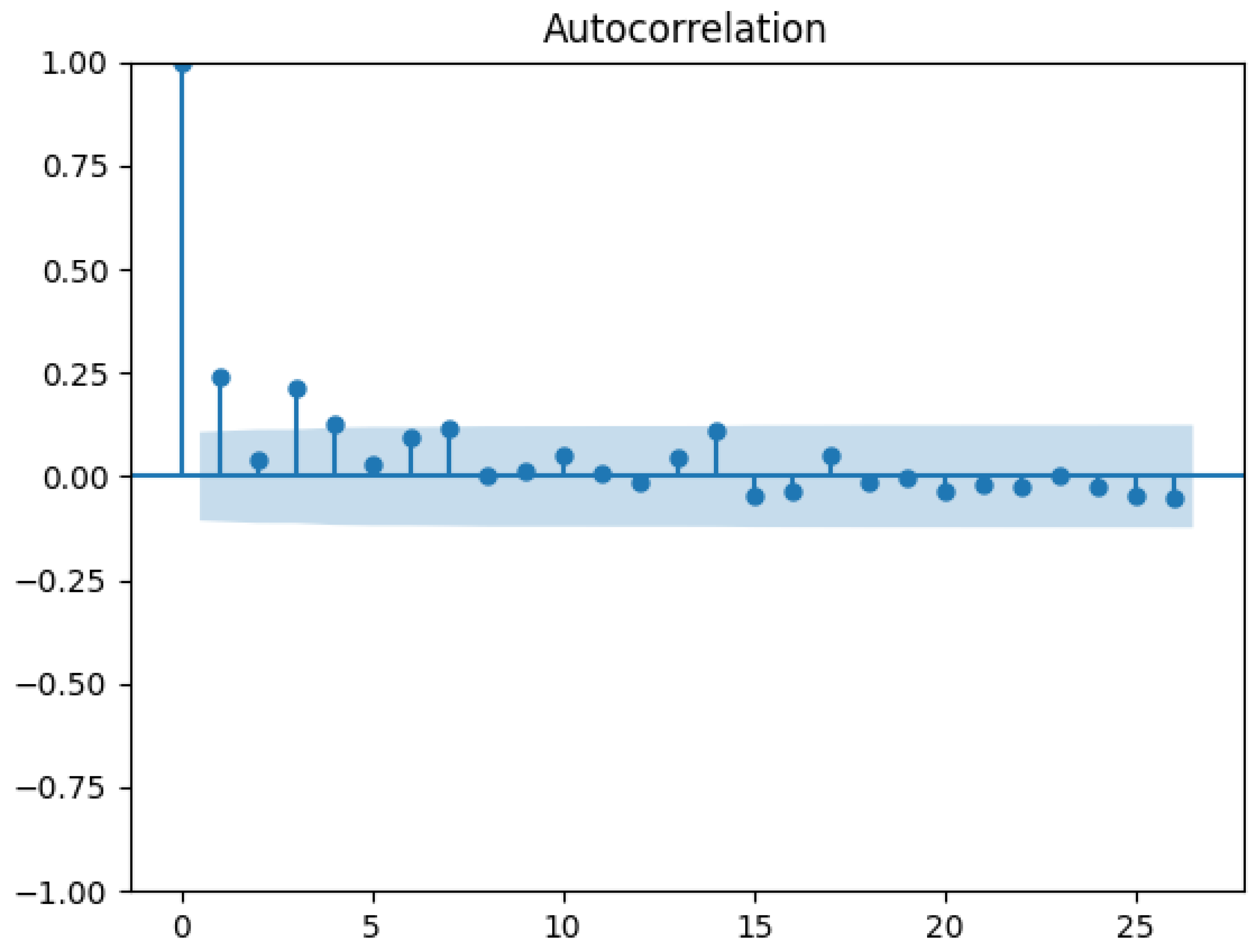
3.2. Consistency of the Modified Synthetic Control Method
4. Evaluating the Mini-Budget Policy on UK Stock Market: An Empirical Study
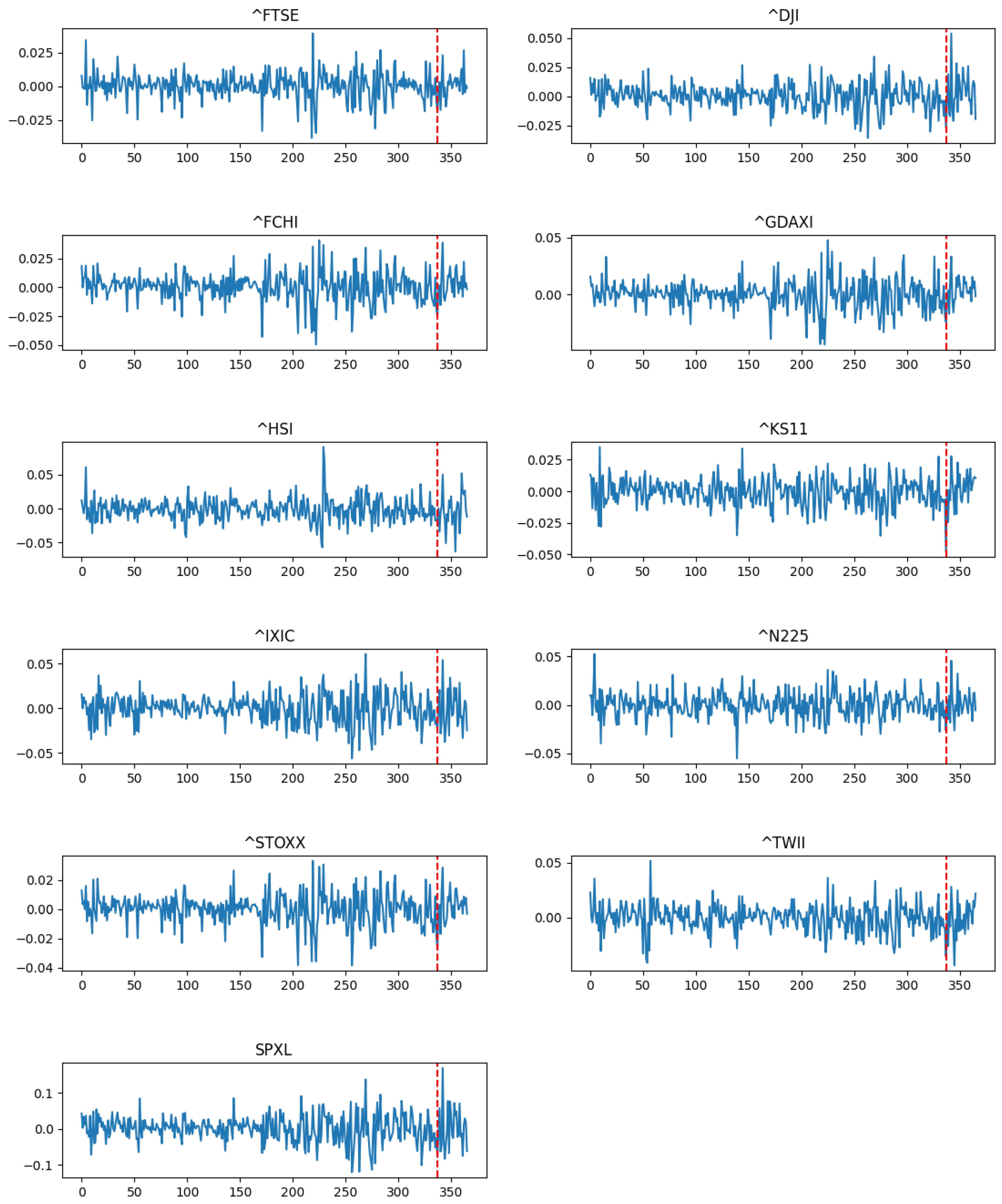
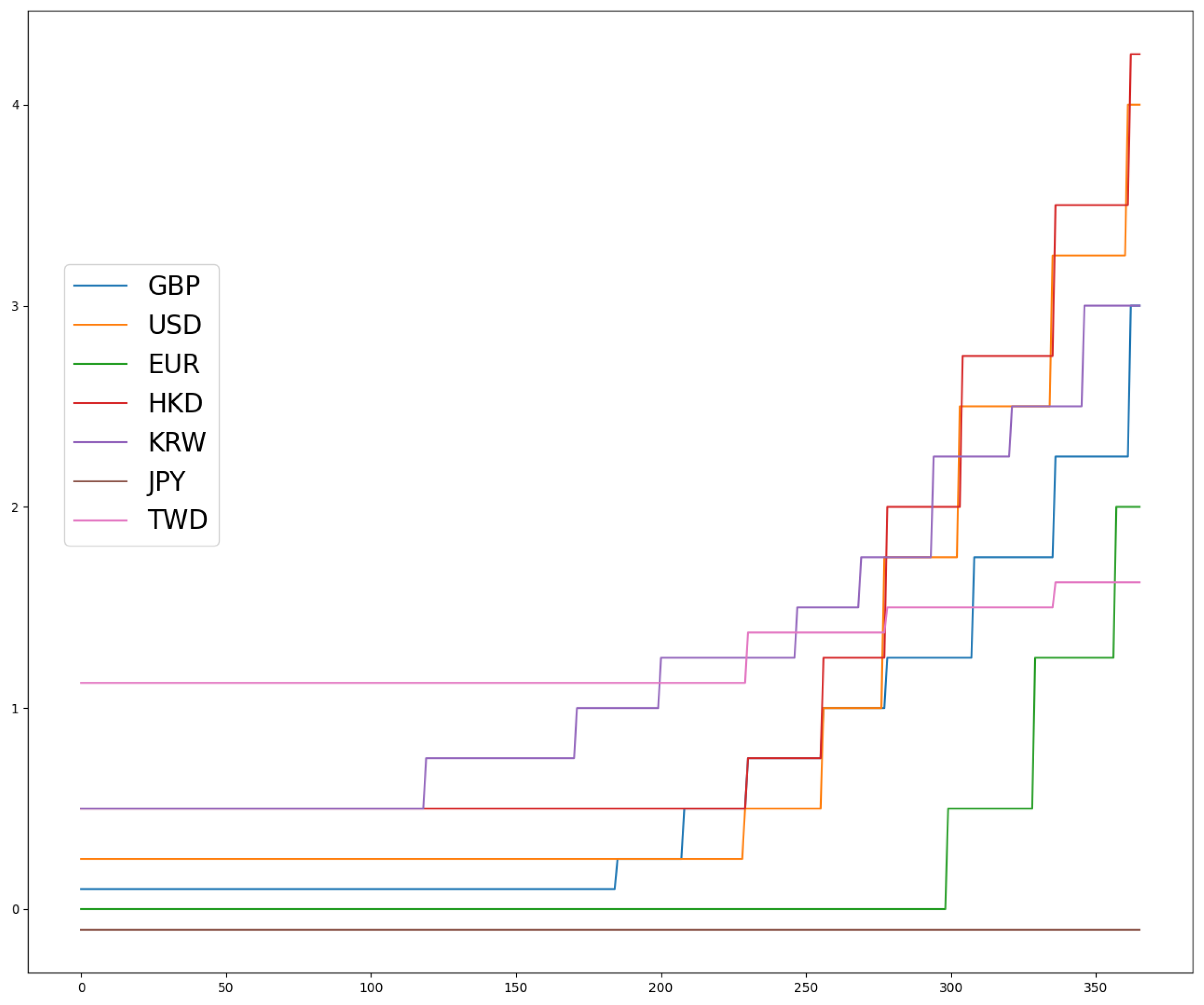
4.1. Data
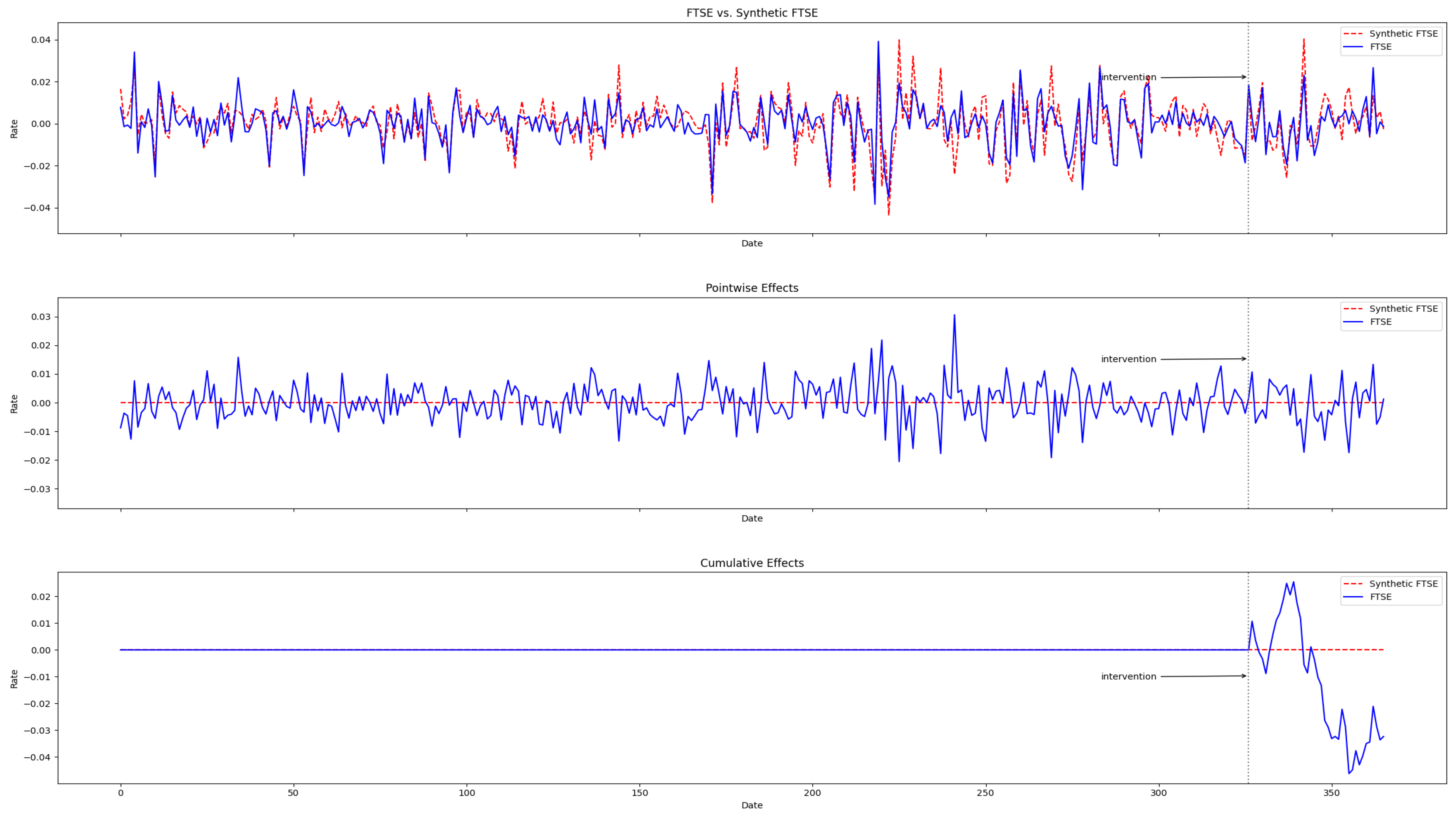
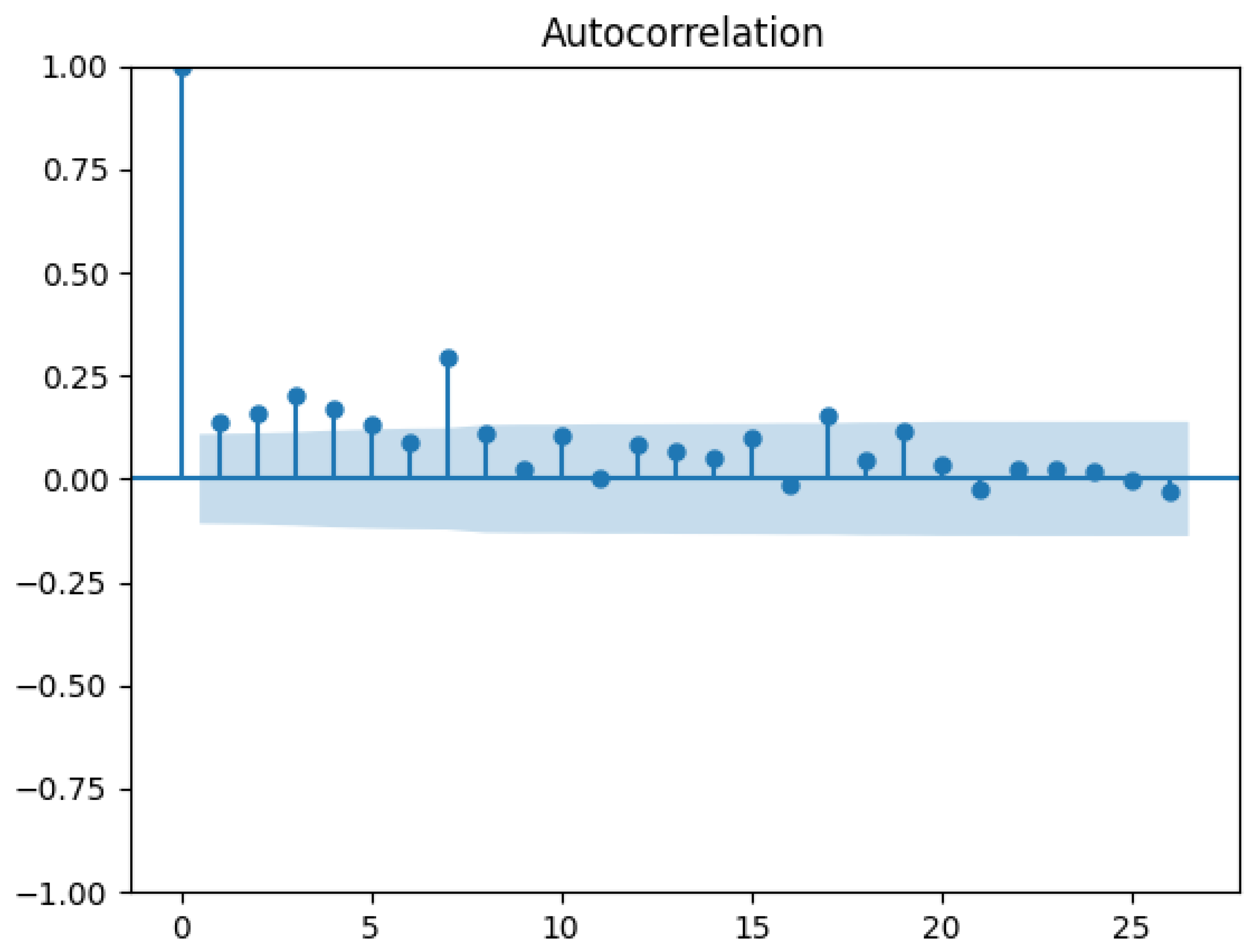
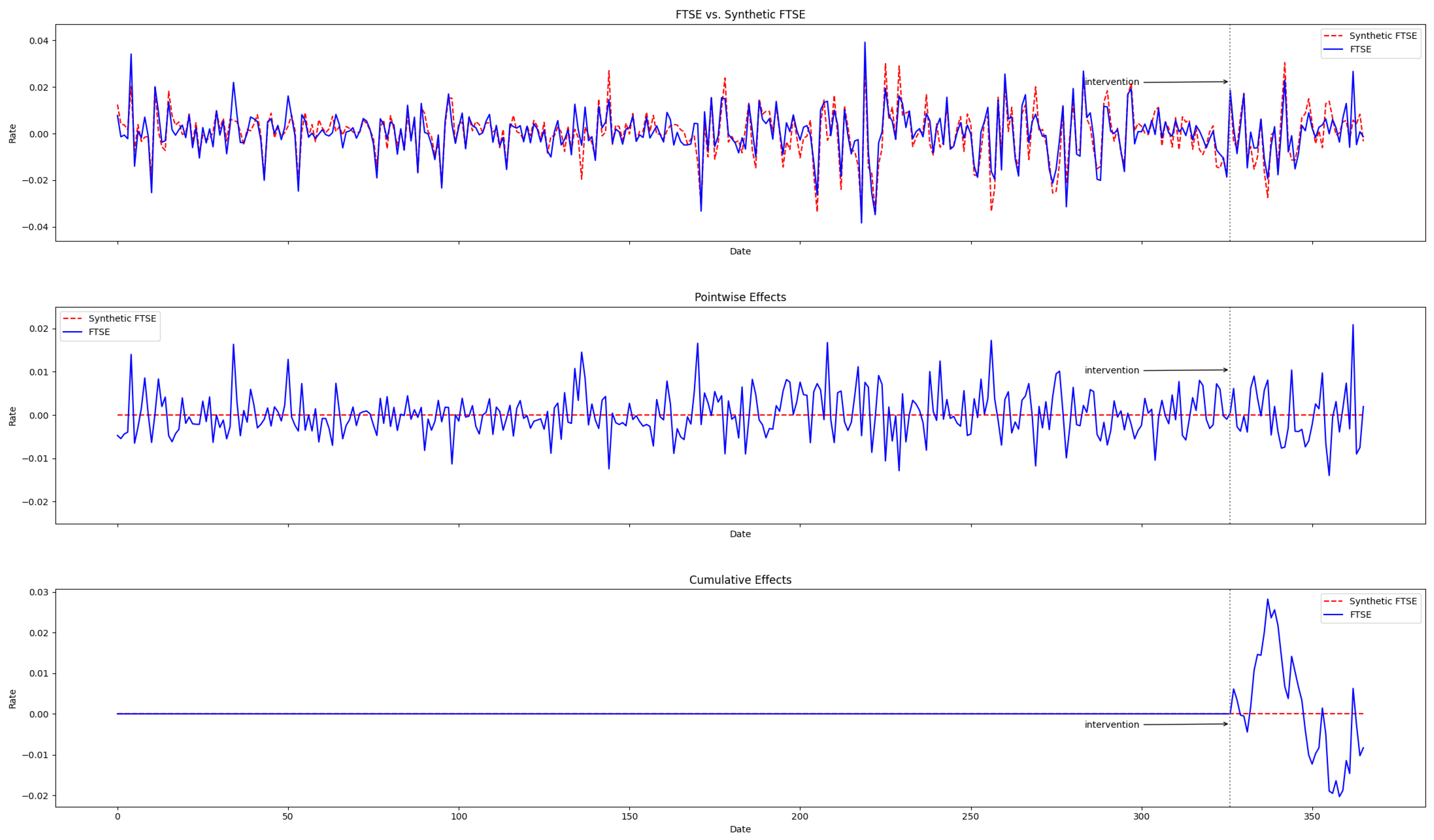
4.2. Evaluating the Causal Effect of the Mini-Budget by Conventional Synthetic Control
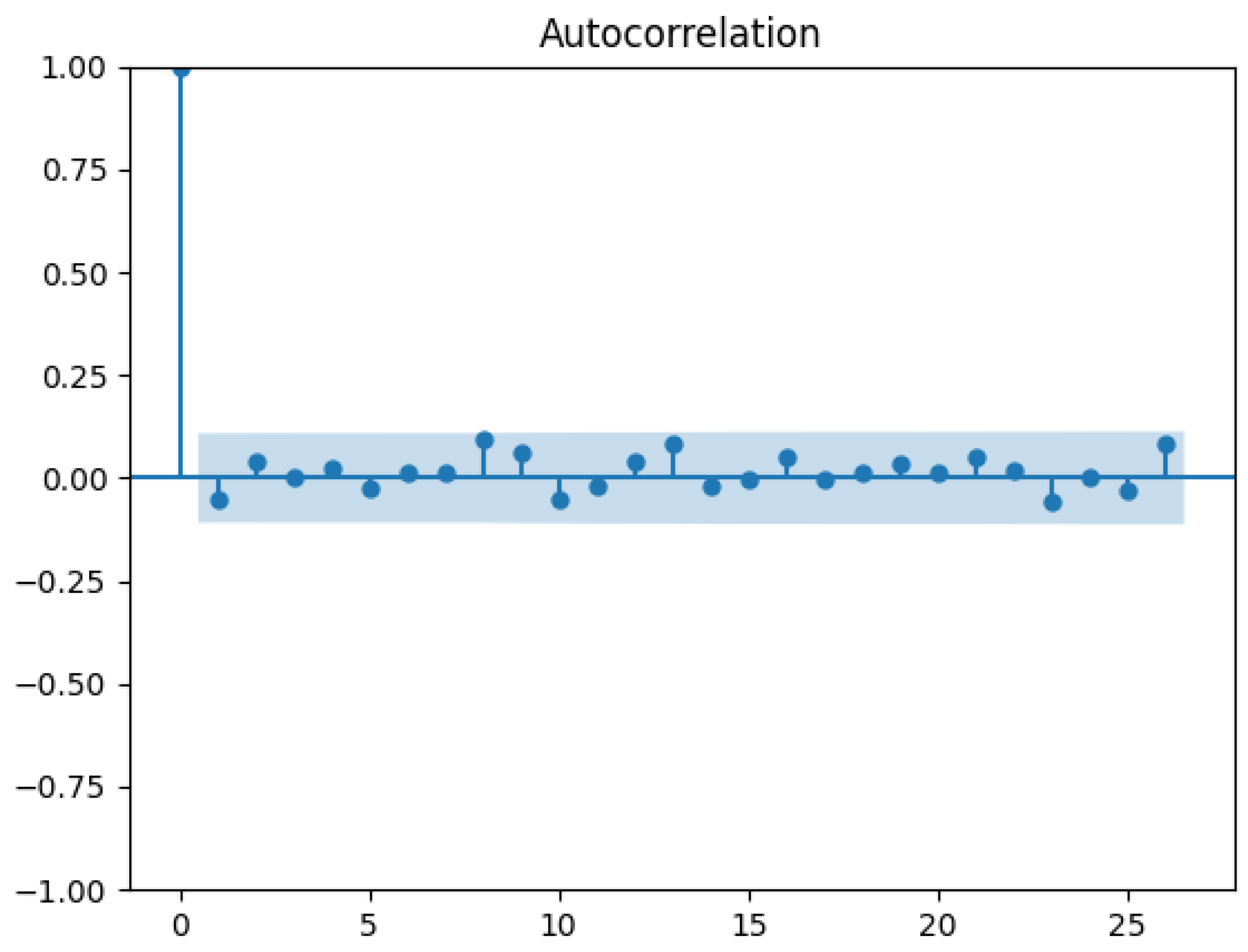
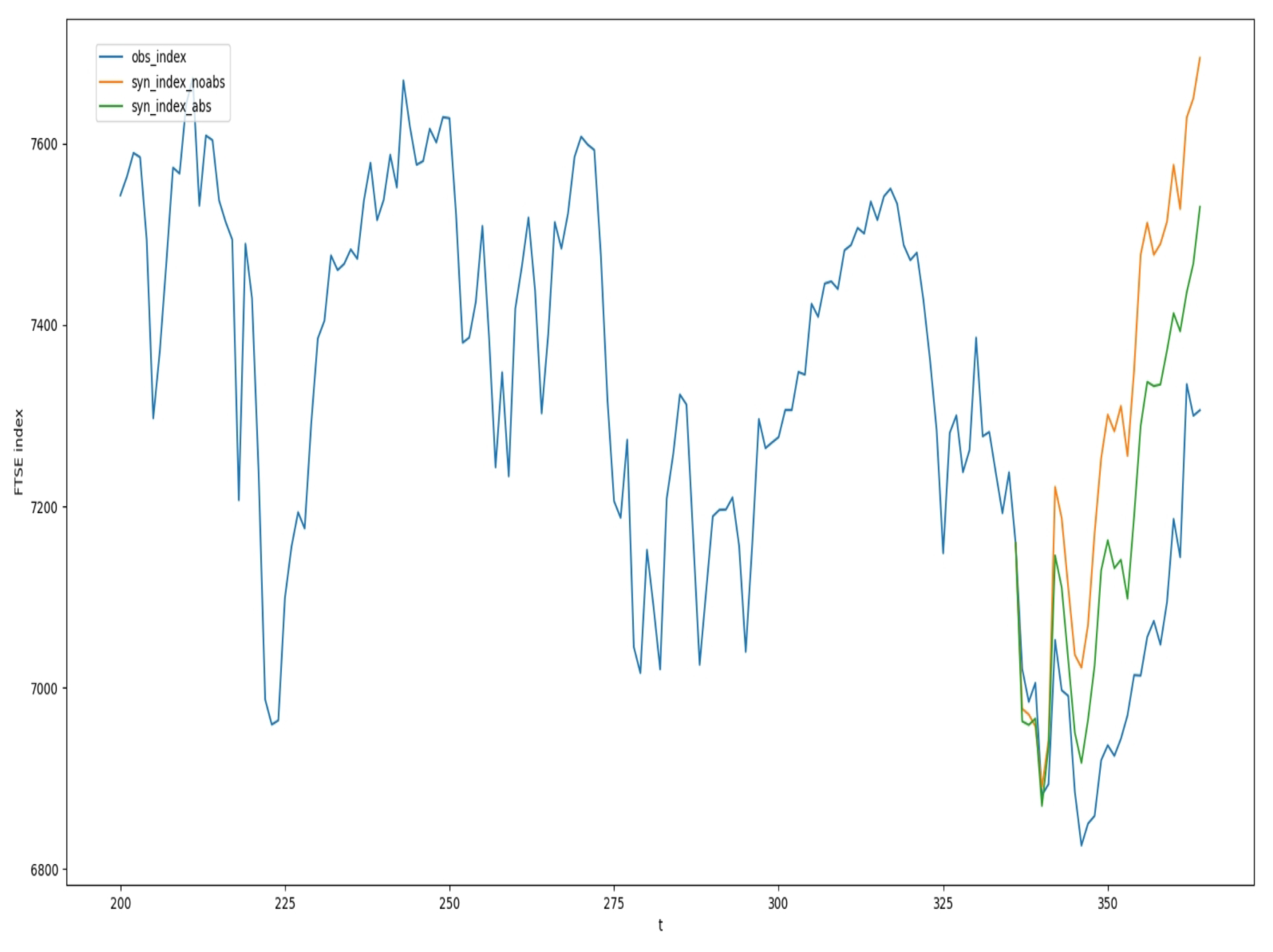
4.3. Evaluating the Causal Effect of Mini-Budget by the Modified Synthetic Control
4.4. Evaluating the Causal Effect of the Mini-Budget by Synthetic Difference in Difference
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Abadie, A.; Diamond, A.; Hainmueller, J. Synthetic control methods for comparative case studies: Estimating the effect of California’s tobacco control program. J. Am. Stat. Assoc. 2010, 105, 493–505. [Google Scholar] [CrossRef]
- Künzel, S.R.; Sekhon, J.S.; Bickel, P.J.; Yu, B. Metalearners for estimating heterogeneous treatment effects using machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 4156–4165. [Google Scholar] [CrossRef] [PubMed]
- Wager, S.; Athey, S. Estimation and inference of heterogeneous treatment effects using random forests. J. Am. Stat. Assoc. 2018, 113, 1228–1242. [Google Scholar] [CrossRef]
- Esposti, M.D.; Spreckelsen, T.; Gasparrini, A.; Wiebe, D.J.; Bonander, C.; Yakubovich, A.R.; Humphreys, D.K. Can synthetic controls improve causal inference in interrupted time series evaluations of public health interventions? Int. J. Epidemiol. 2020, 49, 2010–2020. [Google Scholar] [CrossRef]
- Chernozhukov, V.; Wüthrich, K.; Zhu, Y. An exact and robust conformal inference method for counterfactual and synthetic controls. J. Am. Stat. Assoc. 2021, 116, 1849–1864. [Google Scholar] [CrossRef]
- Athey, S.; Imbens, G.W. The state of applied econometrics: Causality and policy evaluation. J. Econ. Perspect. 2017, 31, 3–32. [Google Scholar] [CrossRef]
- Splawa-Neyman, J.; Dabrowska, D.M.; Speed, T.P. On the Application of Probability Theory to Agricultural Experiments. Essay on Principles. Section 9. Statist. Sci. 1990, 5, 465–472. [Google Scholar] [CrossRef]
- Rubin, D.B. Estimating causal effects of treatments in randomized and nonrandomized studies. J. Educ. Psychol. 1974, 66, 688. [Google Scholar] [CrossRef]
- Rubin, D.B. Causal inference using potential outcomes: Design, modeling, decisions. J. Am. Stat. Assoc. 2005, 100, 322–331. [Google Scholar] [CrossRef]
- Rosenbaum, P.R.; Rubin, D.B. The central role of the propensity score in observational studies for causal effects. Biometrika 1983, 70, 41–55. [Google Scholar] [CrossRef]
- Ben-Michael, E.; Feller, A.; Rothstein, J. The augmented synthetic control method. J. Am. Stat. Assoc. 2021, 116, 1789–1803. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Variation of Certain Speculative Prices. J. Bus. 1963, 36, 394–419. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Ding, Z. Some Properties of Absolute Return: An Alternative Measure of Risk. Ann. Econ. Stat. 1995, 67–91. [Google Scholar] [CrossRef]
- Abadie, A. Using synthetic controls: Feasibility, data requirements, and methodological aspects. J. Econ. Lit. 2021, 59, 391–425. [Google Scholar] [CrossRef]
- Moraffah, R.; Sheth, P.; Karami, M.; Bhattacharya, A.; Wang, Q.; Tahir, A.; Raglin, A.; Liu, H. Causal inference for time series analysis: Problems, methods and evaluation. Knowl. Inf. Syst. 2021, 63, 3041–3085. [Google Scholar] [CrossRef]
- Arkhangelsky, D.; Athey, S.; Hirshberg, D.A.; Imbens, G.W.; Wager, S. Synthetic difference in differences. Am. Econ. Rev. 2021, 111, 4088–4118. [Google Scholar] [CrossRef]
- Bowers, J.; Fredrickson, M.M.; Panagopoulos, C. Reasoning about interference between units: A general framework. Political Anal. 2013, 21, 97–124. [Google Scholar] [CrossRef]
- Abadie, A. Semiparametric difference in differences estimators. Rev. Econ. Stud. 2005, 72, 1–19. [Google Scholar] [CrossRef]
- Callaway, B.; Sant’Anna, P.H.C. Difference-in-differences with multiple time periods. J. Econom. 2021, 225, 200–230. [Google Scholar] [CrossRef]
- Card, D.; Krueger, A.B. Minimum Wages and Employment: A Case Study of the Fast Food Industry in New Jersey and Pennsylvania. Am. Econ. Rev. 1994, 84, 772–793. [Google Scholar]
- Bertrand, M.; Duflo, E.; Mullainathan, S. How much should we trust differences-in-differences estimates? Q. J. Econ. 2004, 119, 249–275. [Google Scholar] [CrossRef]
- Merlevede, F.; Peligrad, M.; Rio, E. Bernstein inequality and moderate deviations under strong mixing conditions. In High Dimensional Probability V: The Luminy Volume; Institute of Mathematical Statistics: Beachwood, OH, USA, 2009; Volume 5, pp. 273–292. [Google Scholar]


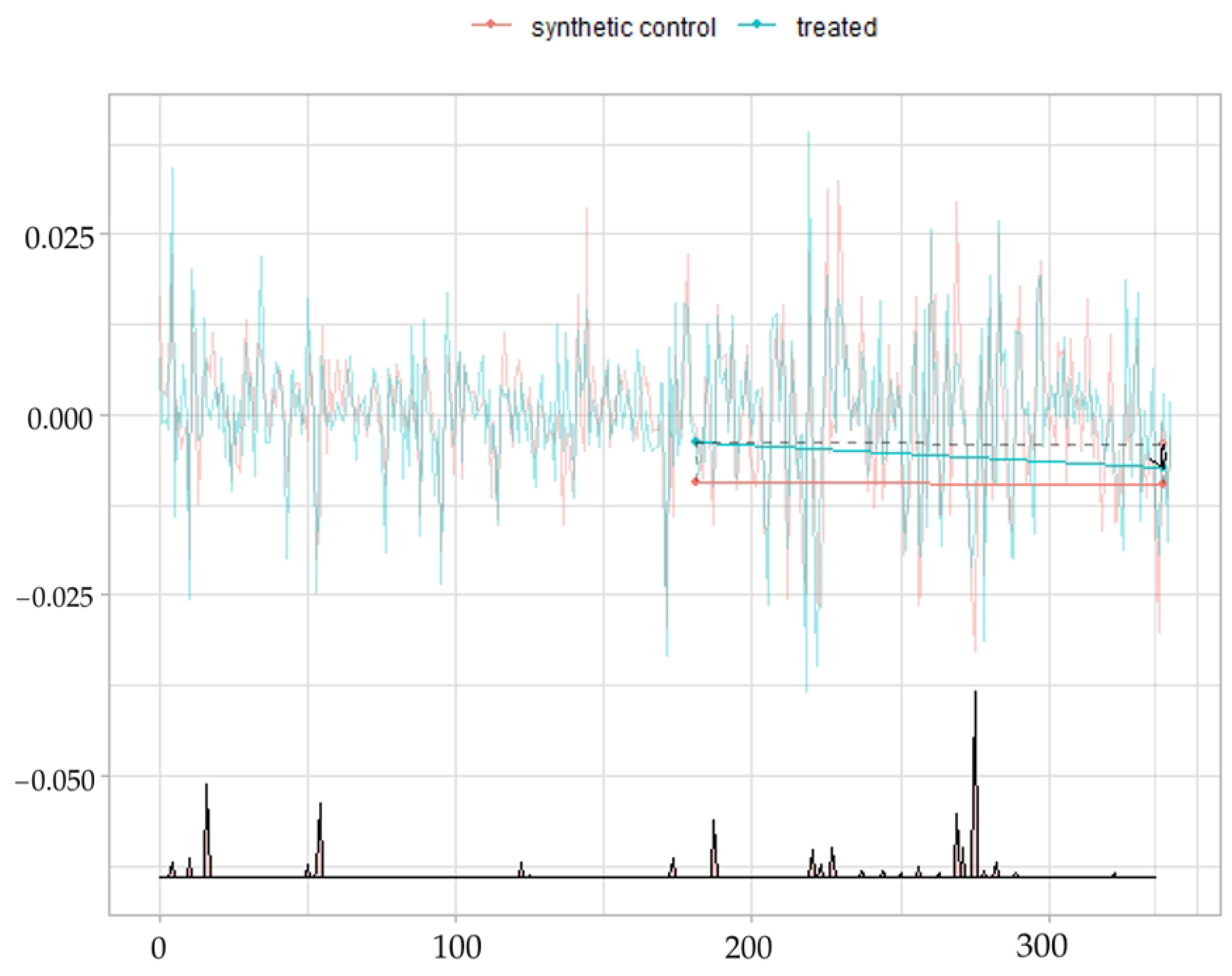
| Unit Weights | Period Weights | ||
|---|---|---|---|
| Name | Weight | Time | Weight |
| FCHI | 0.124 | 4 | 0.020 |
| STOXX | 0.126 | 10 | 0.027 |
| GDAXI | 0.121 | 16 | 0.127 |
| KS11 | 0.103 | 50 | 0.018 |
| DJI | 0.107 | 54 | 0.100 |
| TWII | 0.101 | 122 | 0.022 |
| N225 | 0.102 | 173 | 0.027 |
| HSI | 0.099 | 187 | 0.078 |
| IXIC | 0.078 | 220 | 0.037 |
| 223 | 0.017 | ||
| 227 | 0.041 | ||
| 269 | 0.087 | ||
| 271 | 0.040 | ||
| 275 | 0.253 | ||
| 282 | 0.020 | ||
| Conventional SC | Modified SC | SDID | |
|---|---|---|---|
| Average causal effect | −0.00608 | −0.00431 | −0.00329 |
| Stand error | 0.00317 | 0.00156 | 0.00175 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Lu, Z. A Time Series Synthetic Control Causal Evaluation of the UK’s Mini-Budget Policy on Stock Market. Mathematics 2024, 12, 3301. https://doi.org/10.3390/math12203301
Zhang Y, Lu Z. A Time Series Synthetic Control Causal Evaluation of the UK’s Mini-Budget Policy on Stock Market. Mathematics. 2024; 12(20):3301. https://doi.org/10.3390/math12203301
Chicago/Turabian StyleZhang, Yan, and Zudi Lu. 2024. "A Time Series Synthetic Control Causal Evaluation of the UK’s Mini-Budget Policy on Stock Market" Mathematics 12, no. 20: 3301. https://doi.org/10.3390/math12203301
APA StyleZhang, Y., & Lu, Z. (2024). A Time Series Synthetic Control Causal Evaluation of the UK’s Mini-Budget Policy on Stock Market. Mathematics, 12(20), 3301. https://doi.org/10.3390/math12203301






