Variational Bayesian EM Algorithm for Quantile Regression in Linear Mixed Effects Models
Abstract
1. Introduction
2. Model Assumptions
3. Variational Bayesian EM Algorithm
| Algorithm 1: Variational Bayesian EM Algorithm |
| 1: Variational Bayesian parameter initialization , . and do 4: E-step: Update Variational Bayesian parameters 10: 11: 12: 13: 14: 17: M-step is the solution to the equation 19: is the solution to the equation 20: Update , 21: end while |
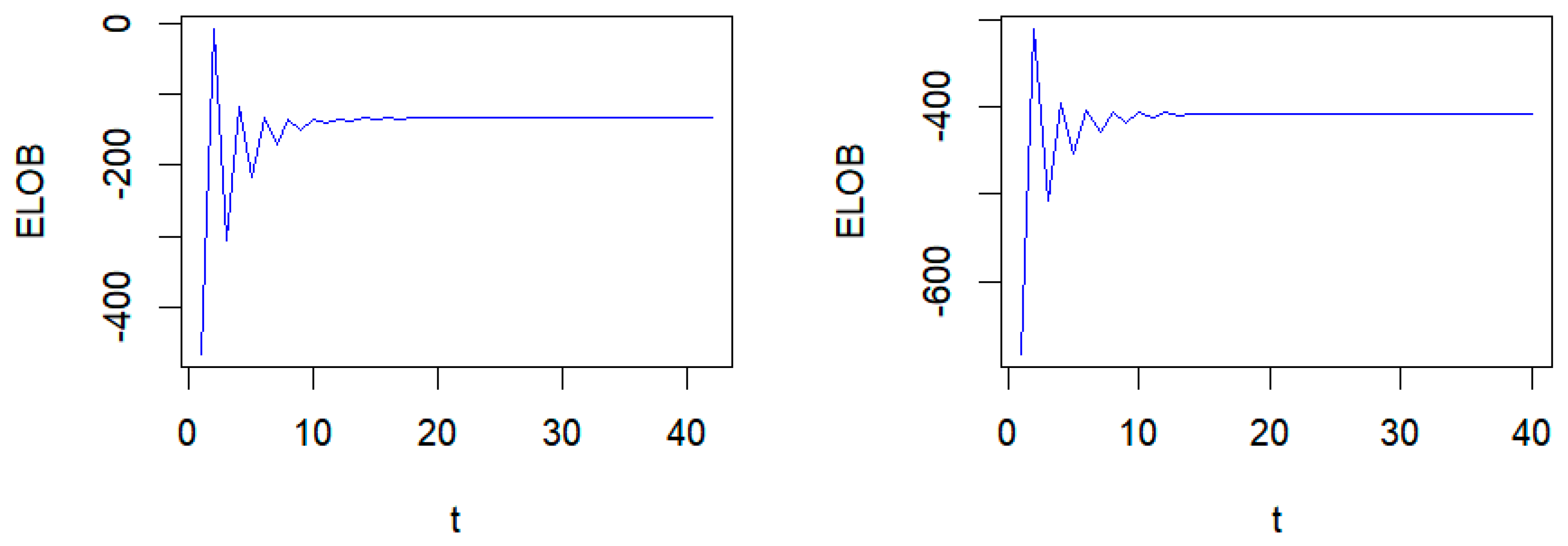
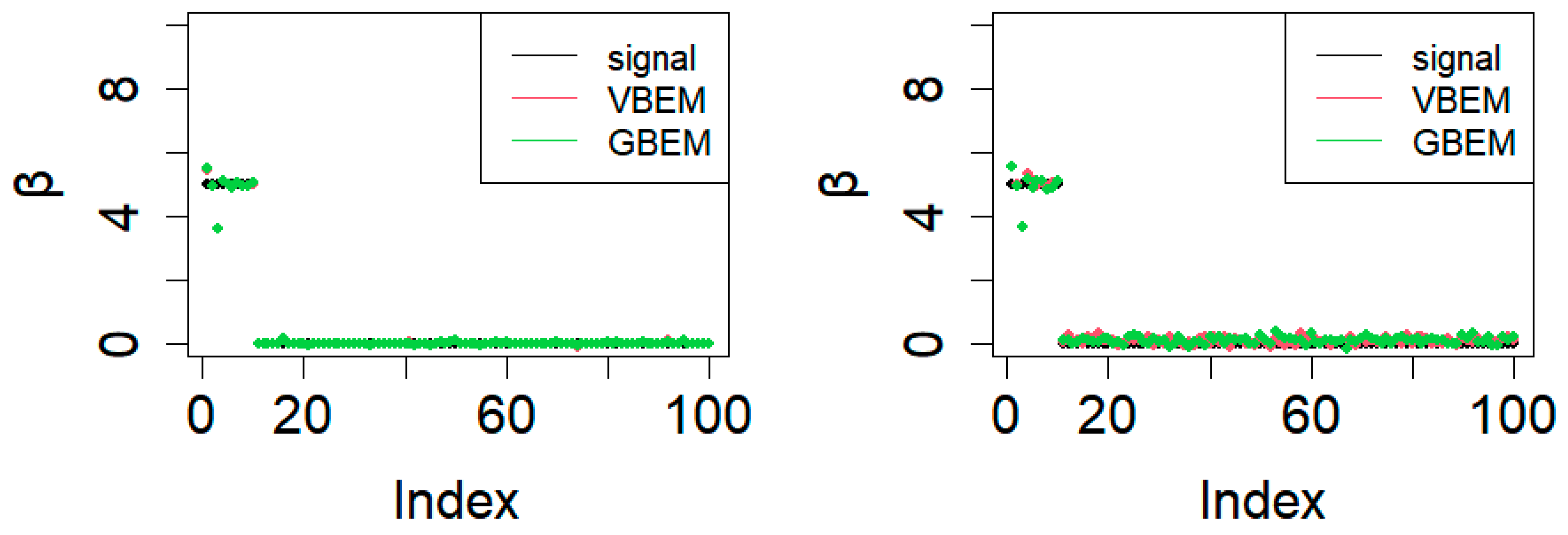
4. Simulation Study
5. Real Data Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Giraud, C. Introduction to High-Dimensional Statistics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2021. [Google Scholar]
- Koenker, R. Quantile regression for longitudinal data. J. Multivar. Anal. 2004, 91, 74–89. [Google Scholar] [CrossRef]
- Yu, K.; Moyeed, R.A. Bayesian quantile regression. Stat. Probab. Lett. 2001, 54, 437–447. [Google Scholar] [CrossRef]
- Luo, Y.; Lian, H.; Tian, M. Bayesian quantile regression for longitudinal data models. J. Stat. Comput. Simul. 2012, 82, 1635–1649. [Google Scholar] [CrossRef]
- Sriram, K.; Shi, P.; Ghosh, P. A Bayesian Semiparametric Quantile Regression Model for Longitudinal Data with Application to Insurance Company Costs. IIM Bangalore Res. Pap. 2011, 355. [Google Scholar] [CrossRef]
- Chen, C.W.S.; Dunson, D.B.; Reed, C.; Yu, K. Bayesian variable selection in quantile regression. Stat. Its Interface 2013, 6, 261–274. [Google Scholar] [CrossRef]
- Alhamzawi, R.; Yu, K.; Benoit, D.F. Bayesian adaptive Lasso quantile regression. Stat. Model. 2012, 12, 279–297. [Google Scholar] [CrossRef]
- Li, Q.; Lin, N.; Xi, R. Bayesian regularized quantile regression. Bayesian Anal. 2010, 5, 533–556. [Google Scholar] [CrossRef]
- Ji, Y.; Shi, H. Bayesian variable selection in linear quantile mixed models for longitudinal data with application to macular degeneration. PLoS ONE 2020, 15, e0241197. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Wang, J.; Liang, F. A Variational Bayesian algorithm for Bayesian variable selection. arXiv 2016, arXiv:1602.07640. [Google Scholar]
- Neville, S.E. Elaborate Distribution Semiparametric Regression via Mean Field Variational Bayesian Bayes. Ph.D. Thesis, University of Wollongong, Wollongong, Australia, 2013. [Google Scholar]
- Lim, D.; Park, B.; Nott, D.; Wang, X.; Choi, T. Sparse signal shrinkage and outlier detection in high-dimensional quantile regression with Variational Bayesian Bayes. Stat. Its Interface 2020, 13, 237–249. [Google Scholar] [CrossRef]
- Ray, K.; Szabó, B. Variational Bayesian Bayes for high-dimensional linear regression with sparse priors. J. Am. Stat. Assoc. 2022, 117, 1270–1281. [Google Scholar] [CrossRef]
- Ray, K.; Szabó, B.; Clara, G. Spike and slab Variational Bayesian Bayes for high dimensional logistic regression. arXiv 2010, arXiv:2010.11665. [Google Scholar]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational Bayesian inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Dai, D.; Tang, A.; Ye, J. High-Dimensional variable selection for quantile regression based on variational method. Mathematics 2023, 11, 2232. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Y.; Cheng, W. Variational inference on a Bayesian adaptive lasso Tobit quantile regression model. Stat 2023, 12, e563. [Google Scholar] [CrossRef]
- Li, X.; Tuerde, M.; Hu, X. Variational Bayesian Inference for Quantile Regression Models with Nonignorable Missing Data. Mathematics 2023, 11, 3926. [Google Scholar] [CrossRef]
- Bai, R.; Ghosh, M. On the beta prime prior for scale parameters in high-dimensional bayesian regression models. Stat. Sin. 2021, 31, 843–865. [Google Scholar] [CrossRef]
- Kozumi, H.; Kobayashi, G. Gibbs sampling methods for Bayesian quantile regression. J. Stat. Comput. Simul. 2011, 81, 1565–1578. [Google Scholar] [CrossRef]
- Hahn, P.R.; Carvalho, C.M. Decoupling shrinkage and selection in bayesian linear models: A posterior summary perspective. J. Am. Stat. Assoc. 2015, 110, 435–448. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Eisen, M.B.; Spellman, P.T.; Brown, P.O.; Botstein, D. Cluster analysis and display of genome-wide expression patterns. Proc. Natl. Acad. Sci. USA 1998, 95, 14863–14868. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhou, J.; Qu, A. Penalized generalized estimating equations for high-dimensional longitudinal data analysis. Biometrics 2011, 68, 353–360. [Google Scholar] [CrossRef] [PubMed]
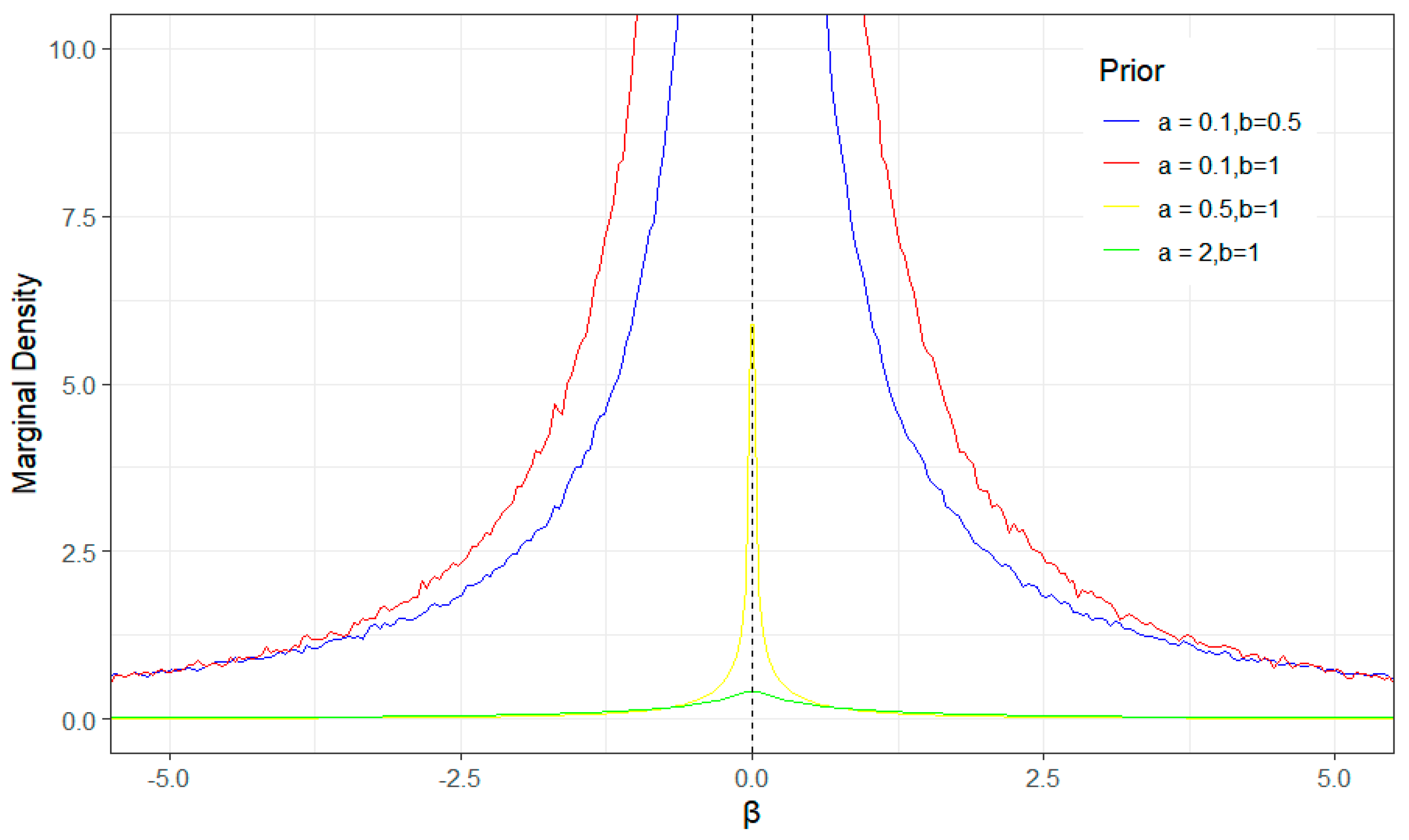
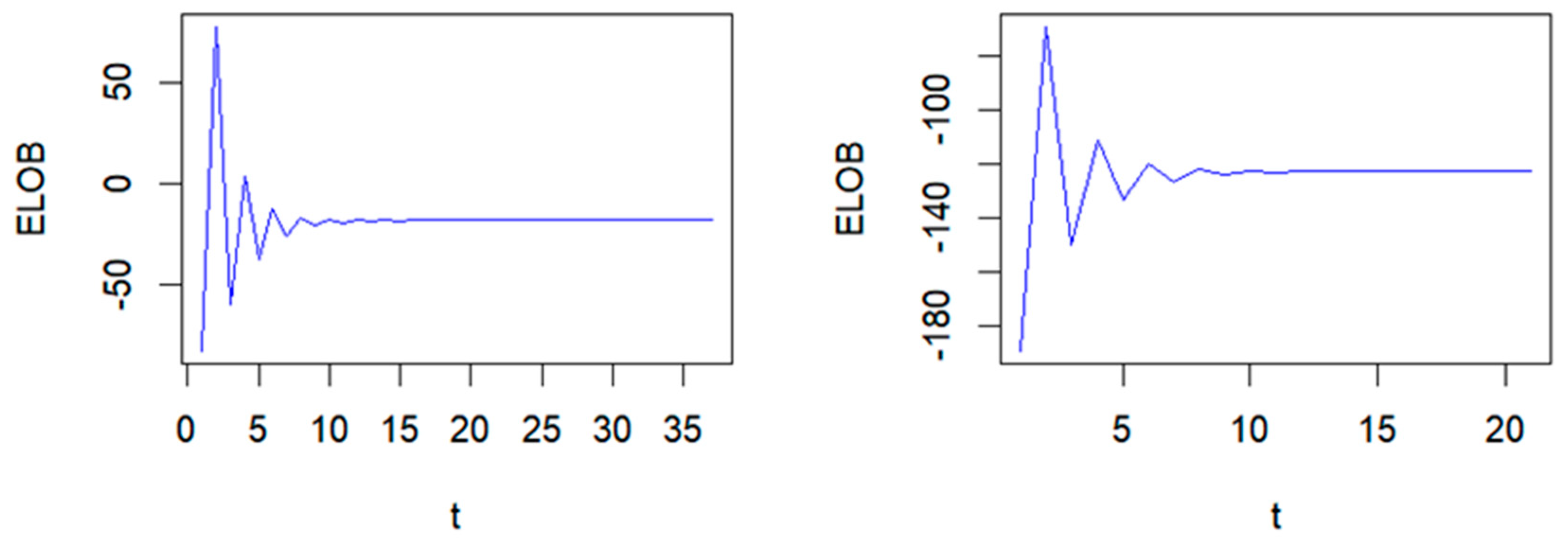
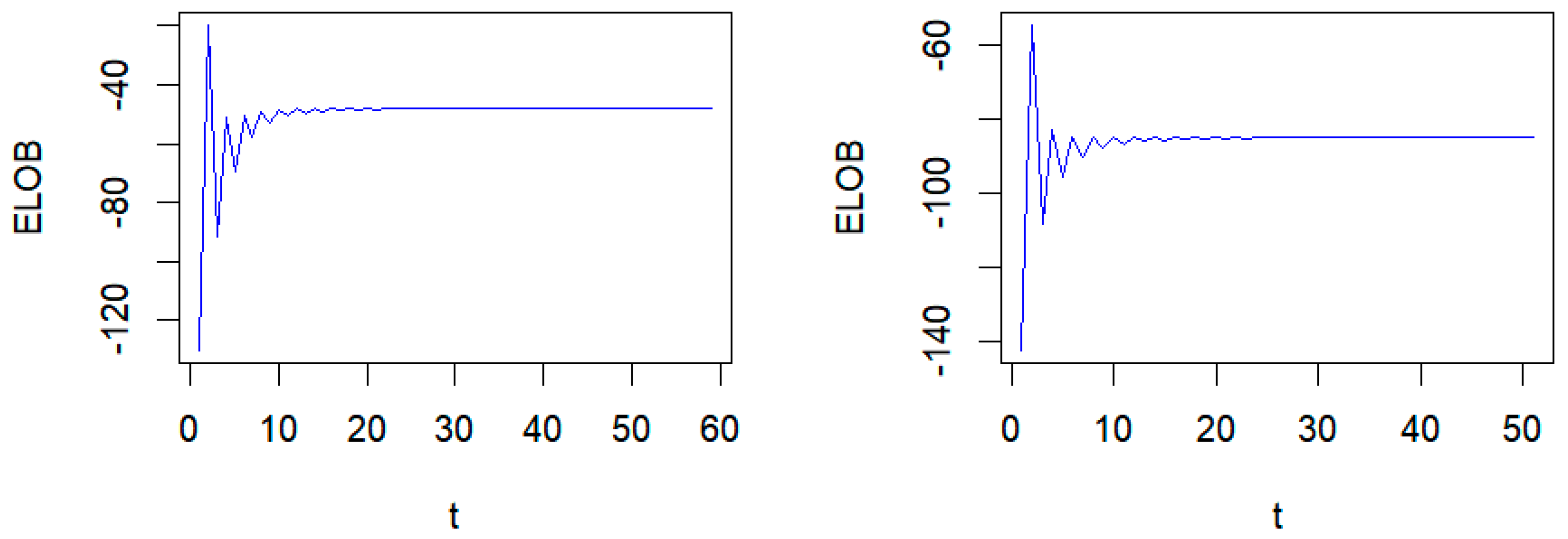
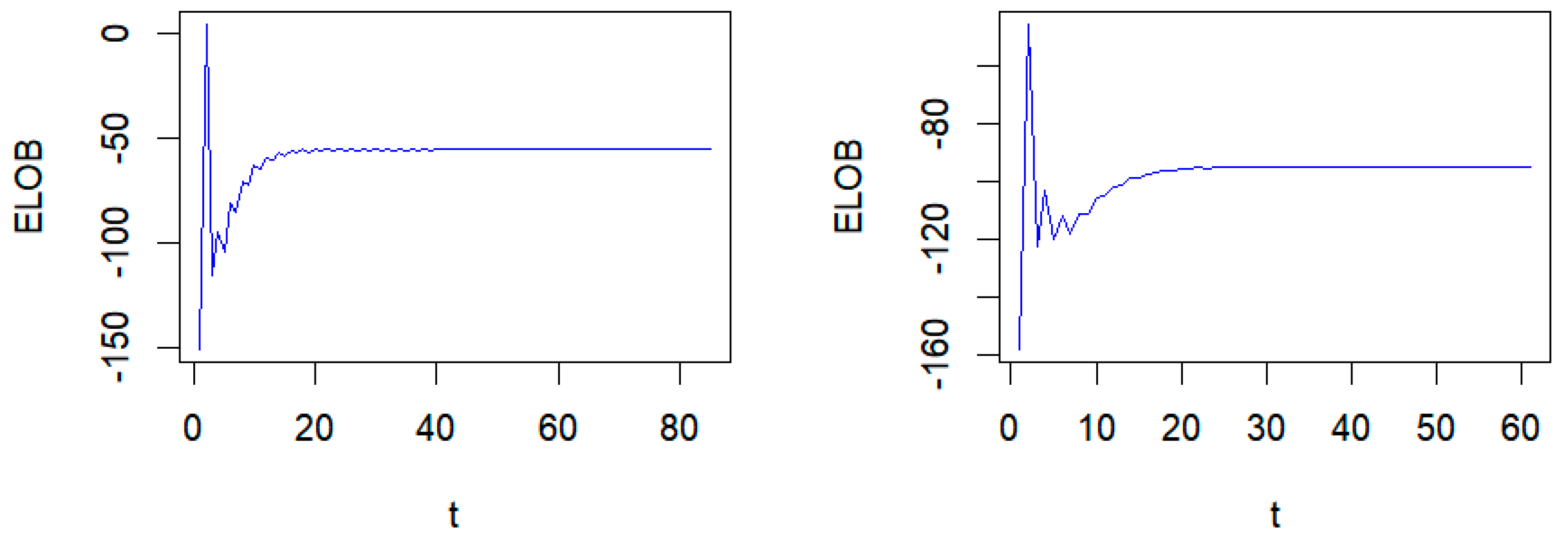
| τ | Method | MSE | MMAD | TPR | FDR | T |
|---|---|---|---|---|---|---|
| 0.25 | VBEM | 3.20 (0.19) | 1.42 (0.25) | 1.00 (0.00) | 0.00 (0.00) | 0.35 (0.06) |
| GBEM | 3.19 (0.24) | 1.44 (0.16) | 1.00 (0.00) | 0.00 (0.00) | 17.61 (1.52) | |
| BQRLM | 3.44 (0.23) | 1.52 (0.28) | 1.00 (0.00) | 0.00 (0.00) | 15.26 (1.02) | |
| QRM | 3.32 (0.33) | 2.55 (0.48) | 1.00 (0.00) | 0.95 (0.13) | 0.36 (0.12) | |
| QRML | 3.24 (0.23) | 2.35 (0.38) | 1.00 (0.00) | 0.04 (0.01) | 0.46 (0.09) | |
| 0.5 | VBEM | 3.08 (0.34) | 1.12 (0.14) | 1.00 (0.00) | 0.00 (0.00) | 0.26 (0.05) |
| GBEM | 3.15 (0.21) | 1.38 (0.17) | 1.00 (0.00) | 0.00 (0.00) | 17.45 (1.45) | |
| BQRLM | 3.35 (0.21) | 1.49 (0.32) | 1.00 (0.00) | 0.00 (0.00) | 14.26 (1.52) | |
| QRM | 3.25 (0.42) | 2.46 (0.18) | 1.00 (0.00) | 0.93 (0.10) | 0.25 (0.14) | |
| QRML | 3.20 (0.23) | 2.33 (0.29) | 1.00 (0.00) | 0.06 (0.02) | 0.45 (0.06) | |
| 0.75 | VBEM | 3.21 (0.32) | 1.44 (0.30) | 1.00 (0.00) | 0.00 (0.00) | 0.39 (0.02) |
| GBEM | 3.18 (0.19) | 1.46 (0.15) | 1.00 (0.00) | 0.00 (0.00) | 17.04 (1.02) | |
| BQRLM | 3.40 (0.23) | 1.55 (0.31) | 1.00 (0.00) | 0.00 (0.00) | 15.33 (1.05) | |
| QRM | 3.49 (0.29) | 2.48 (0.41) | 0.98 (0.03) | 0.94 (0.02) | 0.33 (0.11) | |
| QRML | 3.38 (0.23) | 2.39 (0.38) | 1.00 (0.00) | 0.08 (0.02) | 0.48 (0.10) |
| τ | Method | MSE | MMAD | TPR | FDR | T |
|---|---|---|---|---|---|---|
| 0.25 | VBEM | 5.50 (0.27) | 2.85 (0.35) | 1.00 (0.00) | 0.00 (0.00) | 0.45 (0.09) |
| GBEM | 5.32 (0.45) | 2.94 (0.16) | 1.00 (0.00) | 0.00 (0.00) | 18.73 (1.33) | |
| BQRLM | 6.47 (0.35) | 3.12 (0.18) | 1.00 (0.00) | 0.00 (0.00) | 16.39 (1.52) | |
| QRM | 5.92 (0.42) | 4.59 (0.40) | 1.00 (0.00) | 0.91 (0.12) | 0.39 (0.22) | |
| QRML | 5.84 (0.23) | 4.27 (0.29) | 1.00 (0.00) | 0.03 (0.01) | 0.52 (0.05) | |
| 0.5 | VBEM | 5.48 (0.21) | 2.62 (0.18) | 1.00 (0.00) | 0.00 (0.00) | 0.29 (0.06) |
| GBEM | 5.75 (0.21) | 2.48 (0.17) | 1.00 (0.00) | 0.00 (0.00) | 17.46 (1.63) | |
| BQRLM | 6.15 (0.20) | 2.69 (0.27) | 1.00 (0.00) | 0.00 (0.00) | 13.63 (1.01) | |
| QRM | 5.87 (0.39) | 3.16 (0.18) | 1.00 (0.00) | 0.92 (0.12) | 0.27 (0.11) | |
| QRML | 5.79 (0.23) | 3.03 (0.29) | 1.00 (0.00) | 0.07 (0.01) | 0.49 (0.07) | |
| 0.75 | VBEM | 5.53 (0.25) | 2.87 (0.39) | 1.00 (0.00) | 0.00 (0.00) | 0.46 (0.09) |
| GBEM | 5.62 (0.45) | 2.98 (0.16) | 1.00 (0.00) | 0.00 (0.00) | 19.06 (1.33) | |
| BQRLM | 6.37 (0.33) | 3.15 (0.16) | 1.00 (0.00) | 0.00 (0.00) | 18.22 (1.02) | |
| QRM | 5.98 (0.52) | 4.61 (0.37) | 1.00 (0.00) | 0.94 (0.11) | 0.38 (0.24) | |
| QRML | 5.74 (0.23) | 4.07 (0.22) | 1.00 (0.00) | 0.02 (0.01) | 0.51 (0.03) |
| τ | Method | MSE | MMAD | TPR | FDR | T |
|---|---|---|---|---|---|---|
| 0.25 | VBEM | 3.69 (0.17) | 1.46 (0.21) | 1.00 (0.00) | 0.00 (0.00) | 0.38 (0.04) |
| GBEM | 3.55 (0.16) | 1.42 (0.15) | 1.00 (0.00) | 0.00 (0.00) | 16.61 (0.14) | |
| BQRLM | 3.64 (0.25) | 1.55 (0.28) | 1.00 (0.00) | 0.00 (0.00) | 16.33 (1.05) | |
| QRM | 3.74 (0.33) | 2.45 (0.31) | 1.00 (0.00) | 0.94 (0.10) | 0.41 (0.15) | |
| QRML | 3.66 (0.23) | 2.13 (0.38) | 1.00 (0.00) | 0.04 (0.02) | 0.43 (0.06) | |
| 0.5 | VBEM | 2.88 (0.27) | 1.33 (0.29) | 1.00 (0.00) | 0.00 (0.00) | 0.37 (0.04) |
| GBEM | 2.94 (0.31) | 1.35 (0.15) | 1.00 (0.00) | 0.00 (0.00) | 17.26 (1.15) | |
| BQRLM | 3.09 (0.21) | 1.52 (0.35) | 1.00 (0.00) | 0.00 (0.00) | 16.52 (1.02) | |
| QRM | 3.33 (0.29) | 2.39 (0.15) | 1.00 (0.00) | 0.92 (0.10) | 0.29 (0.10) | |
| QRML | 3.25 (0.21) | 2.28 (0.29) | 1.00 (0.00) | 0.05 (0.02) | 0.41 (0.06) | |
| 0.75 | VBEM | 3.22 (0.39) | 1.49 (0.25) | 1.00 (0.00) | 0.00 (0.00) | 0.35 (0.03) |
| GBEM | 3.19 (0.16) | 1.45 (0.11) | 1.00 (0.00) | 0.00 (0.00) | 18.06 (1.16) | |
| BQRLM | 3.42 (0.29) | 1.57 (0.30) | 1.00 (0.00) | 0.00 (0.00) | 15.49 (1.18) | |
| QRM | 3.41 (0.29) | 2.45 (0.35) | 0.96 (0.02) | 0.92 (0.02) | 0.31 (0.21) | |
| QRML | 3.35 (0.26) | 2.37 (0.31) | 1.00 (0.00) | 0.05 (0.02) | 0.45 (0.20) |
| τ | Method | MSE | MMAD | TPR | FDR | T |
|---|---|---|---|---|---|---|
| 0.25 | VBEM | 6.61 (0.35) | 2.96 (0.22) | 1.00 (0.00) | 0.00 (0.00) | 0.47 (0.09) |
| GBEM | 6.16 (0.45) | 3.13 (0.15) | 1.00 (0.00) | 0.00 (0.00) | 17.77 (0.28) | |
| BQRLM | 6.43 (0.30) | 3.25 (0.21) | 1.00 (0.00) | 0.00 (0.00) | 15.39 (1.02) | |
| QRM | 6.95 (0.40) | 4.38 (0.45) | 1.00 (0.00) | 0.90 (0.11) | 0.35 (0.21) | |
| QRML | 6.82 (0.15) | 4.17 (0.29) | 1.00 (0.00) | 0.02 (0.01) | 0.55 (0.04) | |
| 0.5 | VBEM | 5.85 (0.25) | 2.52 (0.15) | 1.00 (0.00) | 0.00 (0.00) | 0.28 (0.07) |
| GBEM | 5.96 (0.25) | 2.33 (0.11) | 1.00 (0.00) | 0.00 (0.00) | 17.05 (0.47) | |
| BQRLM | 6.14 (0.20) | 2.61 (0.21) | 1.00 (0.00) | 0.00 (0.00) | 12.98 (1.11) | |
| QRM | 5.99 (0.34) | 3.01 (0.29) | 1.00 (0.00) | 0.90 (0.10) | 0.25 (0.10) | |
| QRML | 5.89 (0.21) | 3.12 (0.20) | 1.00 (0.00) | 0.09 (0.01) | 0.38 (0.08) | |
| 0.75 | VBEM | 6.08 (0.32) | 2.92 (0.31) | 1.00 (0.00) | 0.00 (0.00) | 0.47 (0.08) |
| GBEM | 6.21 (0.45) | 2.82 (0.14) | 1.00 (0.00) | 0.00 (0.00) | 19.33 (1.02) | |
| BQRLM | 6.39 (0.36) | 3.18 (0.11) | 1.00 (0.00) | 0.00 (0.00) | 19.20 (1.01) | |
| QRM | 6.32 (0.32) | 4.55 (0.32) | 1.00 (0.00) | 0.90 (0.15) | 0.40 (0.25) | |
| QRML | 6.36 (0.23) | 4.15 (0.25) | 1.00 (0.00) | 0.03 (0.01) | 0.55 (0.02) |
| τ | Method | MSE | MMAD | TPR | FDR | T |
|---|---|---|---|---|---|---|
| 0.25 | VBEM | 3.63 (0.15) | 1.40 (0.25) | 1.00 (0.00) | / | 0.38 (0.04) |
| GBEM | 3.42 (0.19) | 1.36 (0.14) | 1.00 (0.00) | / | 16.63 (0.22) | |
| BQRLM | 3.69 (0.28) | 1.58 (0.33) | 1.00 (0.00) | / | 17.55 (1.21) | |
| QRM | 3.70 (0.28) | 2.51 (0.35) | 1.00 (0.00) | / | 0.36 (0.22) | |
| QRML | 3.87 (0.19) | 2.59 (0.21) | 1.00 (0.00) | / | 0.41 (0.05) | |
| 0.5 | VBEM | 2.76 (0.23) | 1.35 (0.29) | 1.00 (0.00) | / | 0.35 (0.02) |
| GBEM | 2.78 (0.18) | 1.38 (0.19) | 1.00 (0.00) | / | 16.77 (0.61) | |
| BQRLM | 3.28 (0.21) | 1.49 (0.22) | 1.00 (0.00) | / | 17.02 (1.52) | |
| QRM | 3.01 (0.18) | 2.51 (0.19) | 1.00 (0.00) | / | 0.24 (0.03) | |
| QRML | 3.39 (0.19) | 2.62 (0.27) | 1.00 (0.00) | / | 0.47 (0.05) | |
| 0.75 | VBEM | 3.73 (0.23) | 1.52 (0.22) | 1.00 (0.00) | / | 0.53 (0.09) |
| GBEM | 3.56 (0.25) | 1.55 (0.19) | 1.00 (0.00) | / | 17.73 (1.28) | |
| BQRLM | 3.82 (0.20) | 1.66 (0.25) | 1.00 (0.00) | / | 15.33 (1.06) | |
| QRM | 3.61 (0.29) | 2.37 (0.35) | 1.00 (0.00) | / | 0.35 (0.02) | |
| QRML | 3.66 (0.25) | 2.52 (0.23) | 1.00 (0.00) | / | 0.41 (0.12) |
| τ | Method | MSE | MMAD | TPR | FDR | T |
|---|---|---|---|---|---|---|
| 0.25 | VBEM | 6.52 (0.26) | 2.98 (0.23) | 1.00 (0.00) | / | 0.47 (0.09) |
| GBEM | 6.04 (0.15) | 3.09 (0.17) | 1.00 (0.00) | / | 18.93 (0.21) | |
| BQRLM | 6.48 (0.22) | 3.07 (0.29) | 1.00 (0.00) | / | 16.33 (1.21) | |
| QRM | 6.56 (0.33) | 4.01 (0.36) | 1.00 (0.00) | / | 0.39 (0.15) | |
| QRML | 6.77 (0.15) | 4.59 (0.29) | 1.00 (0.00) | / | 0.50 (0.04) | |
| 0.5 | VBEM | 5.32 (0.22) | 2.69 (0.18) | 1.00 (0.00) | / | 0.35 (0.05) |
| GBEM | 5.59 (0.25) | 2.52 (0.21) | 1.00 (0.00) | / | 17.59 (1.23) | |
| BQRLM | 6.09 (0.36) | 2.77 (0.21) | 1.00 (0.00) | / | 14.15 (1.35) | |
| QRM | 5.84 (0.34) | 3.32 (0.19) | 1.00 (0.00) | / | 0.30 (0.09) | |
| QRML | 5.74 (0.21) | 3.47 (0.15) | 1.00 (0.00) | / | 0.36 (0.05) | |
| 0.75 | VBEM | 6.11 (0.52) | 2.85 (0.29) | 1.00 (0.00) | / | 0.45 (0.06) |
| GBEM | 6.39 (0.32) | 2.78 (0.11) | 1.00 (0.00) | / | 18.36 (1.05) | |
| BQRLM | 6.35 (0.31) | 3.26 (0.28) | 1.00 (0.00) | / | 19.41 (1.55) | |
| QRM | 6.18 (0.39) | 4.05 (0.25) | 1.00 (0.00) | / | 0.35 (0.21) | |
| QRML | 6.26 (0.18) | 4.01 (0.35) | 1.00 (0.00) | / | 0.53 (0.10) |
| τ | Method | MSE | MMAD | TPR | FDR | T |
|---|---|---|---|---|---|---|
| 0.25 | VBEM | 4.13 (0.18) | 1.92 (0.35) | 1.00 (0.00) | 0.00 (0.00) | 2.45 (0.12) |
| GBEM | 4.02 (0.12) | 1.88 (0.15) | 1.00 (0.00) | 0.00 (0.00) | 63.52 (2.69) | |
| BQRLM | 4.61 (0.23) | 2.18 (0.26) | 1.00 (0.00) | 0.00 (0.00) | 65.54 (1.32) | |
| QRM | 4.62 (0.35) | 2.85 (0.42) | 1.00 (0.00) | 1.00 (0.00) | 0.89 (0.25) | |
| QRML | 4.22 (0.25) | 2.48 (0.36) | 1.00 (0.00) | 0.00 (0.00) | 0.92 (0.09) | |
| 0.5 | VBEM | 2.92 (0.29) | 1.45 (0.33) | 1.00 (0.00) | 0.00 (0.00) | 1.49 (0.09) |
| GBEM | 2.72 (0.25) | 1.44 (0.14) | 1.00 (0.00) | 0.00 (0.00) | 64.41 (2.69) | |
| BQRLM | 3.05 (0.19) | 1.54 (0.22) | 1.00 (0.00) | 0.00 (0.00) | 67.33 (1.35) | |
| QRM | 3.22 (0.29) | 2.08 (0.13) | 1.00 (0.00) | 1.00 (0.00) | 0.85 (0.05) | |
| QRML | 3.84 (0.11) | 2.59 (0.17) | 1.00 (0.00) | 0.00 (0.00) | 0.88 (0.05) | |
| 0.75 | VBEM | 4.39 (0.15) | 1.73 (0.15) | 1.00 (0.00) | 0.00 (0.00) | 2.53 (0.52) |
| GBEM | 4.19 (0.21) | 1.75 (0.25) | 1.00 (0.00) | 0.00 (0.00) | 64.73 (2.35) | |
| BQRLM | 4.22 (0.17) | 1.80 (0.25) | 1.00 (0.00) | 0.00 (0.00) | 69.21 (1.89) | |
| QRM | 4.42 (0.18) | 2.08 (0.38) | 1.00 (0.00) | 1.00 (0.00) | 0.92 (0.11) | |
| QRML | 4.62 (0.22) | 2.35 (0.35) | 1.00 (0.00) | 0.00 (0.00) | 1.82 (0.25) |
| τ | Method | MSE | MMAD | TPR | FDR | T |
|---|---|---|---|---|---|---|
| 0.25 | VBEM | 5.95 (0.22) | 2.25 (0.21) | 1.00 (0.00) | 0.00 (0.00) | 3.66 (0.67) |
| GBEM | 6.21 (0.52) | 1.92 (0.18) | 1.00 (0.00) | 0.00 (0.00) | 70.47 (3.02) | |
| BQRLM | 6.23 (0.36) | 2.42 (0.36) | 1.00 (0.00) | 0.00 (0.00) | 69.33 (1.58) | |
| QRM | 6.55 (0.28) | 2.94 (0.35) | 1.00 (0.00) | 1.00 (0.00) | 0.92 (0.14) | |
| QRML | 6.50 (0.27) | 2.82 (0.39) | 1.00 (0.00) | 0.00 (0.00) | 0.95 (0.09) | |
| 0.5 | VBEM | 4.98 (0.15) | 1.62 (0.32) | 1.00 (0.00) | 0.00 (0.00) | 2.89 (0.19) |
| GBEM | 4.93 (0.32) | 1.52 (0.21) | 1.00 (0.00) | 0.00 (0.00) | 68.17 (3.19) | |
| BQRLM | 5.02 (0.33) | 1.65 (0.21) | 1.00 (0.00) | 0.00 (0.00) | 68.25 (1.98) | |
| QRM | 5.51 (0.29) | 2.74 (0.29) | 1.00 (0.00) | 1.00 (0.00) | 0.88 (0.07) | |
| QRML | 5.41 (0.32) | 2.55 (0.13) | 1.00 (0.00) | 0.00 (0.00) | 0.92 (0.12) | |
| 0.75 | VBEM | 6.89 (0.39) | 1.82 (0.19) | 1.00 (0.00) | 0.00 (0.00) | 3.92 (0.66) |
| GBEM | 7.14 (0.21) | 1.88 (0.13) | 1.00 (0.00) | 0.00 (0.00) | 71.55 (4.055) | |
| BQRLM | 7.20 (0.63) | 2.05 (0.21) | 1.00 (0.00) | 0.00 (0.00) | 72.25 (1.33) | |
| QRM | 8.05 (0.56) | 2.89 (0.42) | 1.00 (0.00) | 1.00 (0.00) | 0.95 (0.15) | |
| QRML | 7.60 (0.19) | 2.46 (0.34) | 1.00 (0.00) | 0.00 (0.00) | 1.76 (0.32) |
| Method | The Selected TFs | T |
|---|---|---|
| VBEM | “ABF1”“ARG81”“ASH1”“FKH1”“FKH2”“GAT3” “GCR1”“GCR2”“GTS1”“HMS1”“MBP1”“MET4” “MSN4”“NDD1”“ROX1”“SIP4”“STB1”“STP1” “SWI4”“SWI6”“YAP6” “ZAP1” | 156.36 |
| VBEM | “ABF1”“ARG81”“ASH1”“FKH2”“GAT3”“GCR2” “MBP1”“MET4”“MSN4”“NDD1”“ROX1”“STB1” “STP1”“SWI4”“SWI6”“YAP6” | 159.63 |
| VBEM ) | “ABF1”“ASH1”“FKH2”“GAT3”“GCR2”“MBP1” “MSN4”“NDD1”“STB1”“STP1”“SWI4”“SWI6” | 159.61 |
| PGEE | “ABF1”“FKH1”“FKH2”“GAT3”“GCR2”“MBP1” “MSN4”“NDD1”“PHD1”“RGM1”“RLM1”“SMP1” “SRD1”“STB1”“SWI4”“SWI6” | 1331.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Tian, M. Variational Bayesian EM Algorithm for Quantile Regression in Linear Mixed Effects Models. Mathematics 2024, 12, 3311. https://doi.org/10.3390/math12213311
Wang W, Tian M. Variational Bayesian EM Algorithm for Quantile Regression in Linear Mixed Effects Models. Mathematics. 2024; 12(21):3311. https://doi.org/10.3390/math12213311
Chicago/Turabian StyleWang, Weixian, and Maozai Tian. 2024. "Variational Bayesian EM Algorithm for Quantile Regression in Linear Mixed Effects Models" Mathematics 12, no. 21: 3311. https://doi.org/10.3390/math12213311
APA StyleWang, W., & Tian, M. (2024). Variational Bayesian EM Algorithm for Quantile Regression in Linear Mixed Effects Models. Mathematics, 12(21), 3311. https://doi.org/10.3390/math12213311






