A Study of Szász–Durremeyer-Type Operators Involving Adjoint Bernoulli Polynomials
Abstract
:1. Introduction and Preliminaries
2. Approximation Properties: Uniform Rate of Convergence and Order of Approximation
3. Local Approximation Results
4. Graphical and Numerical Representation of
5. Bivariate of Szász–Gamma Operators via Adjoint Bernaulli Polynomials
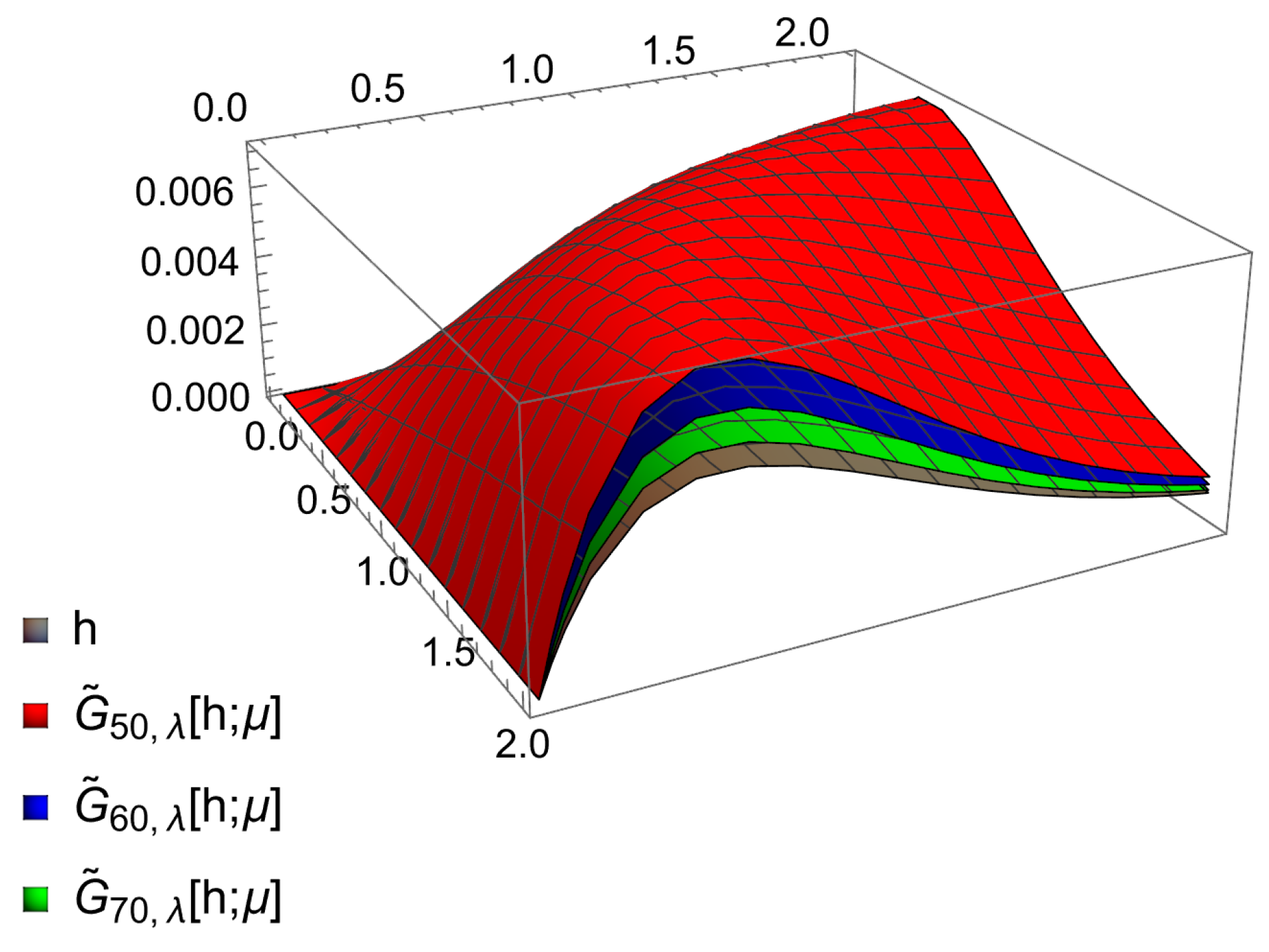
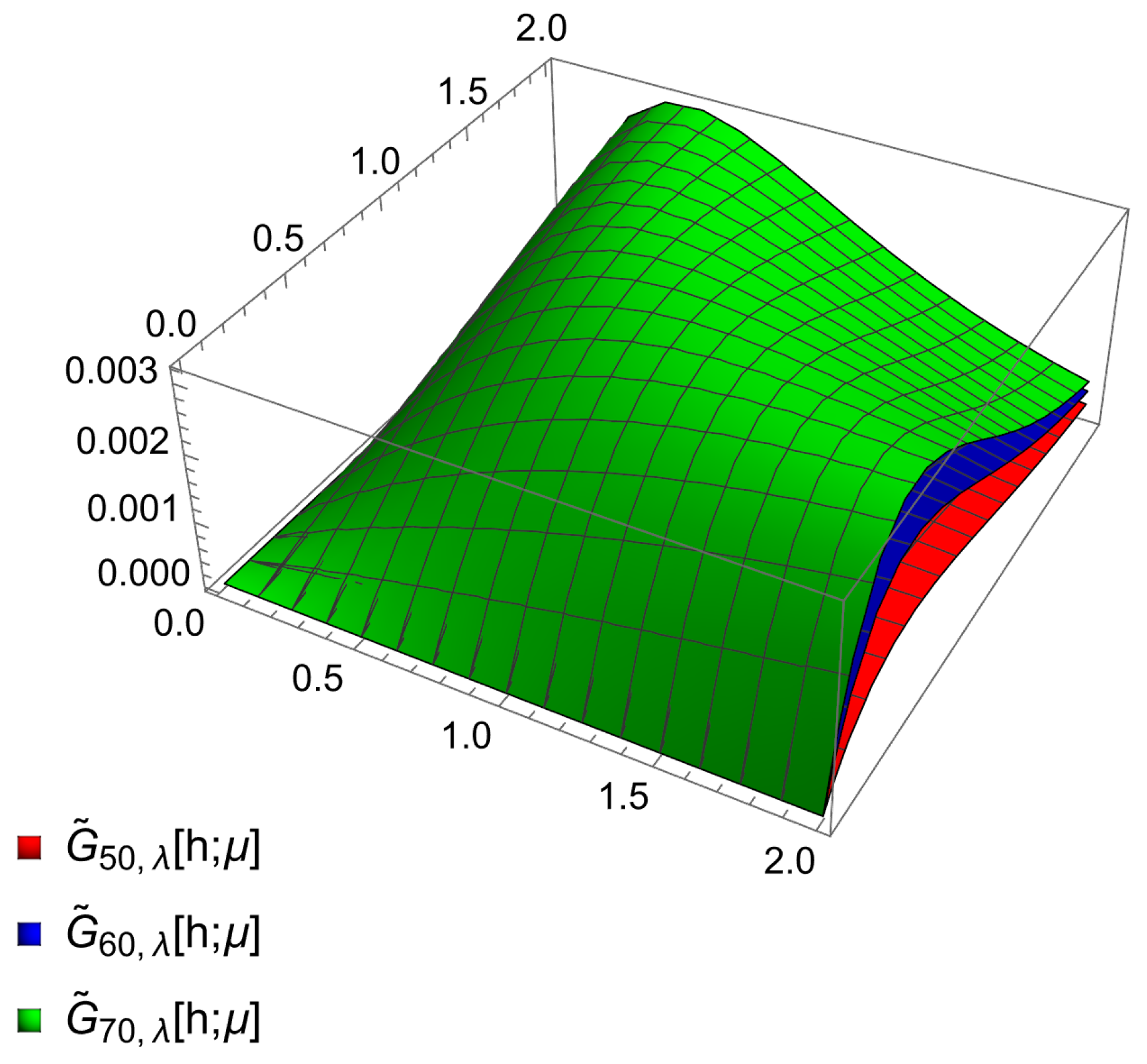
6. Bivariate Graphical Representation
7. Conclusions
- This research work connects two fields of research (special function research and operators theory).
- These sequence operators are capable of approximating in a wider class of functions, i.e., the class of Lebesgue measurable functions.
- These sequences of operators also provide better approximation results in terms of Chlodowsky.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bernstein, S.N. Démonstration du théorème de Weierstrass fondée sur le calcul de probabilités. Commun. Soc. Math. Kharkow. 1913, 13, 1–2. [Google Scholar]
- Weierstrass, K. Über die analytische Darstellbarkeit sogenannter willkürlicher Functionen einer reellen Veränderlichen. Sitzungsberichte Königlich Preußischen Akad. Wiss. Berl. 1885, 2, 633–639. [Google Scholar]
- Aslan, R. Rate of approximation of blending type modified univariate and bivariate λ-Schurer-Kantorovich operators. Kuwait J. Sci. 2024, 51, 100168. [Google Scholar] [CrossRef]
- Leinartas, E.K.; Shishkina, O.A. The discrete analogue of the Newton-Leibniz formula in the problem of summation over simple lattice points. J. Sib. Fed. Univ. Math. Phys. 2019, 12, 503–508. [Google Scholar] [CrossRef]
- Mohiuddine, S.A.; Acar, T.; Alotaibi, A. Construction of a new family of Bernstein-Kantorovich operators. Math. Methods Appl. Sci. 2017, 40, 7749–7759. [Google Scholar] [CrossRef]
- Rao, N.; Malik, P.; Rani, M. Blending type Approximations by Kantorovich variant of α-Baskakov operator. Palest. J. Math. 2022, 11, 402–413. [Google Scholar]
- Rao, N.; Gulia, K. On two dimensional Chlodowsky-Szász operators via Sheffer Polynomials. Palest. J. Math. 2023, 12, 521–531. [Google Scholar]
- Appell, P.P. Sur une class de polynômes. In Annales Scientifiques de l’É cole Normale Supérieure. Norm Supér; Société Matheématique de France: Paris, France, 1880; Volume 2, pp. 119–144. [Google Scholar]
- Natalini, P.; Ricci, E. Adjoint Appell–Euler and first kind Appell–Bernoulli’s polynomials. Appl. Appl. Math. 2019, 14, 1112–1122. [Google Scholar]
- Lyapin, A.P.; Leinartas, E.K.; Grigoriev, A.A. Summation of functions and polynomial solutions to a multidimensional difference equation. J. Sib. Fed. Univ. Math. Phys. 2023, 16, 153–161. [Google Scholar]
- Costabile, F.A.; Gualtieri, M.I.; Napoli, A. Some results on generalized Szasz operators involving Sheffer polynomials. J. Comput. Appl. Math. 2018, 337, 244–255. [Google Scholar] [CrossRef]
- Costabile, F.A. An Introduction to Modern Umbral Calculus De Gryter. In Studies in Mathematics; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019; Volume 72. [Google Scholar] [CrossRef]
- Costabile, F.A.; Gualtieri, M.I.; Capizzano, S.S. Asyptotic expansion and extrapolation for Bernstein polynomials. BIT Num. Math. 1998, 36, 676–687. [Google Scholar] [CrossRef]
- Costabile, F.A.; Gualtieri, M.I.; Capizzano, S.S. Asyptotic expansion and extrapolation for positive linear operators. Ann Univ. Ferrara ViiXiV 2000, 45, 431–442. [Google Scholar]
- Yilmaz, M.M. Rate of convergence by Kantorovich type operators involving adjoint Bernoulli’s polynomials. Publ. L’Institut Mathématique Nouv. Série Tome 2023, 114, 51–62. [Google Scholar]
- Devore, R.A.; Lorentz, G.G. Constructive Approximation; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Altomare, F.; Campiti, M. Korovkin-type approximation theory and its applications. De Gruyter Ser. Stud. Math. 1994, 17, 266–274. [Google Scholar]
- Özarslan, M.A.; Aktuğlu, H. Local approximation for certain King type operators. Filomat 2013, 27, 173–181. [Google Scholar] [CrossRef]
- Lenze, B. On Lipschitz type maximal functions and their smoothness spaces. Nederl. Akad. Indag. Math. 1988, 50, 53–63. [Google Scholar] [CrossRef]
- Volkov, V.I. On the convergence of sequences of linear positive operators in the space of continuous functions of two variables. Dokl. Akad. Nauk SSSR (NS) 1957, 115, 17–19. (In Russian) [Google Scholar]
- Stancu, F. Approximarca Funcṭiilor de Douăşi mai Multe Vsrabile Prin ṣiruri de Operatori Liniari ṣi Positivi. Ph.D. Thesis, Cluj-Napoca, Romania, 1984. [Google Scholar]
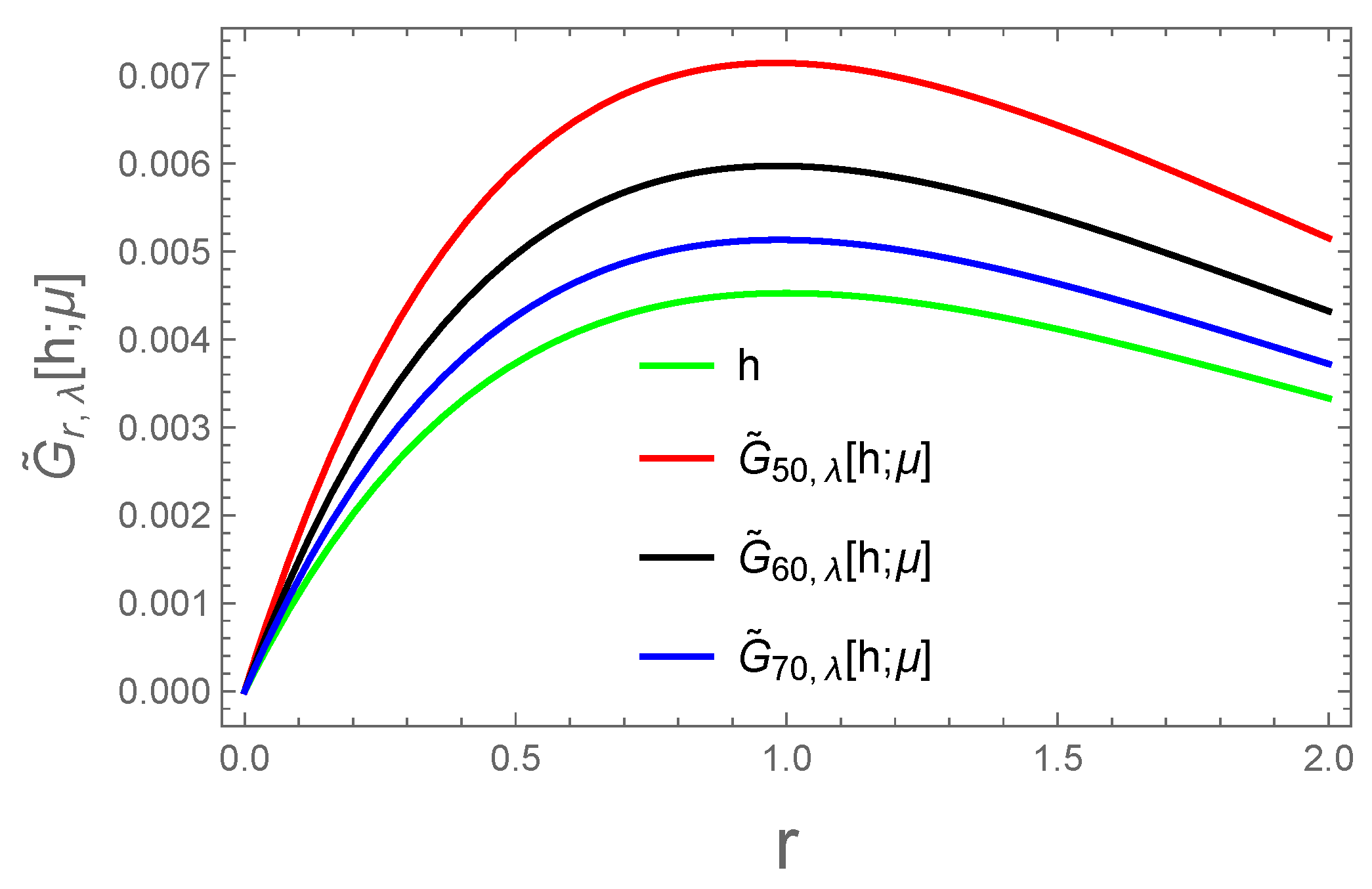
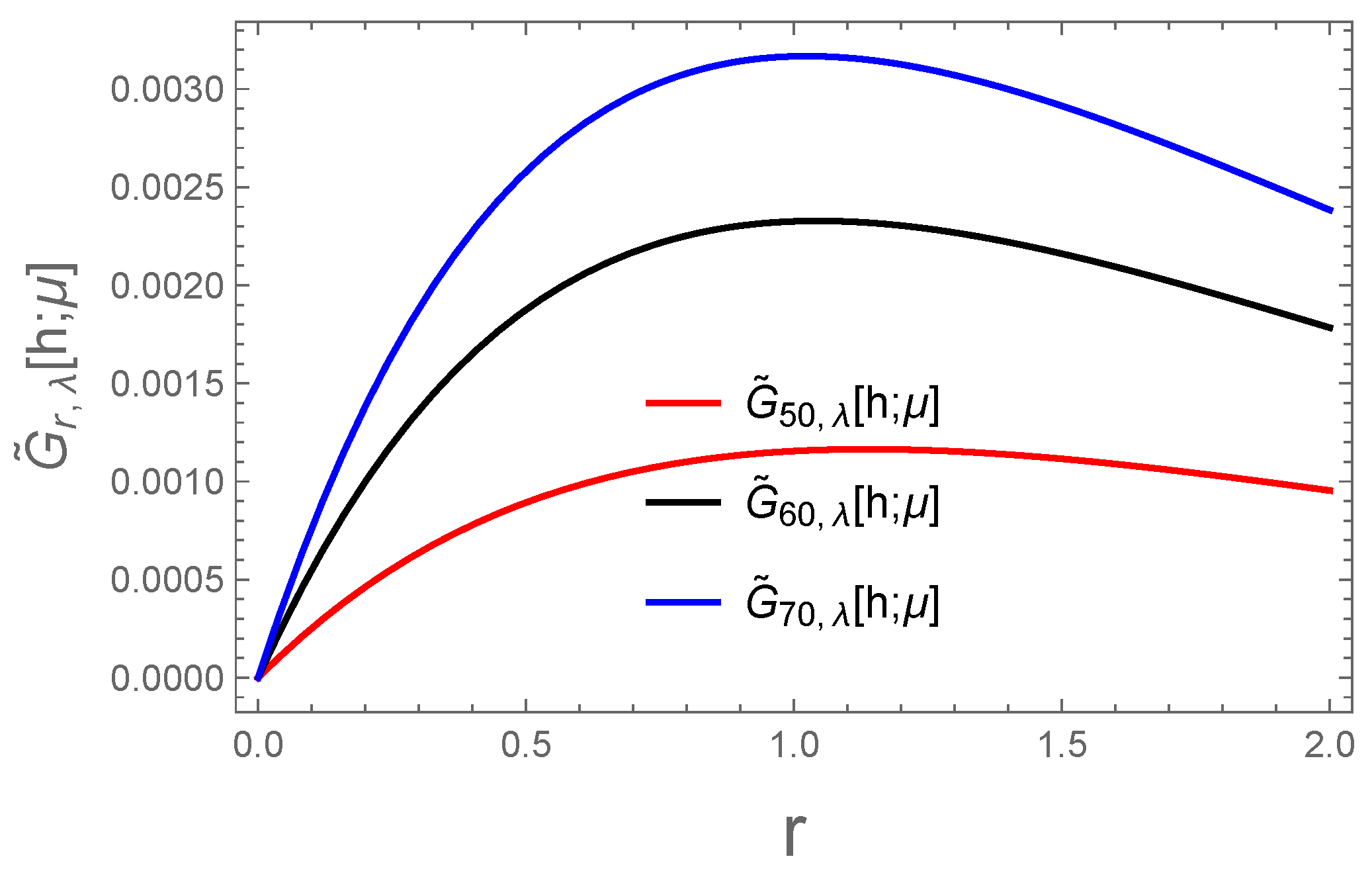
| u | |||
|---|---|---|---|
| 0.3 | 0.00437603 | 0.00365034 | 0.0031311 |
| 0.6 | 0.0064449 | 0.0053815 | 0.00461931 |
| 0.9 | 0.00711891 | 0.00595025 | 0.00511115 |
| 1.2 | 0.00698969 | 0.00584809 | 0.00502699 |
| 1.5 | 0.0064339 | 0.00538846 | 0.0046352 |
| 1.9 | 0.0056854 | 0.00476635 | 0.00410299 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, N.; Farid, M.; Ali, R. A Study of Szász–Durremeyer-Type Operators Involving Adjoint Bernoulli Polynomials. Mathematics 2024, 12, 3645. https://doi.org/10.3390/math12233645
Rao N, Farid M, Ali R. A Study of Szász–Durremeyer-Type Operators Involving Adjoint Bernoulli Polynomials. Mathematics. 2024; 12(23):3645. https://doi.org/10.3390/math12233645
Chicago/Turabian StyleRao, Nadeem, Mohammad Farid, and Rehan Ali. 2024. "A Study of Szász–Durremeyer-Type Operators Involving Adjoint Bernoulli Polynomials" Mathematics 12, no. 23: 3645. https://doi.org/10.3390/math12233645
APA StyleRao, N., Farid, M., & Ali, R. (2024). A Study of Szász–Durremeyer-Type Operators Involving Adjoint Bernoulli Polynomials. Mathematics, 12(23), 3645. https://doi.org/10.3390/math12233645






