A Collocation Procedure for Treating the Time-Fractional FitzHugh–Nagumo Differential Equation Using Shifted Lucas Polynomials
Abstract
1. Introduction
- Introducing the shifted Lucas polynomials.
- Deriving the essential formulas of these polynomials, particularly their series representation and inversion formula.
- Deriving the integer derivatives and FDs of these polynomials.
- Studying the convergence of our approximate solution using the shifted Lucas expansion.
- Designing the collocation procedure for treating the TFFNDE.
- Testing our numerical algorithm by presenting some examples.
- A new theoretical background to the shifted Lucas polynomials. More precisely, new forms of their power form representation, inversion formula, and integer- and fractional-derivative formulas will be developed.
- These new formulas provide new insights into using these polynomials in numerical analysis.
- The study of the convergence of the double-shifted Lucas expansion is new.
- In addition, we expect that the introduced polynomials will open new horizons for using other non-orthogonal polynomials in numerical analysis.
- By choosing the shifted Lucas polynomials as the basis functions, a few terms of the retained modes make it possible to produce approximations with excellent precision.
- Less calculation is required to obtain the desired approximate solution.
2. Some Fundamentals and Important Formulas
2.1. An Account on Caputo’s FD
2.2. A Brief Account of Lucas Polynomials
3. Introducing Shifted Lucas Polynomials
4. Collocation Procedure for the TFFNDE
The Algorithm of the Method
5. The Convergence and Error Analysis
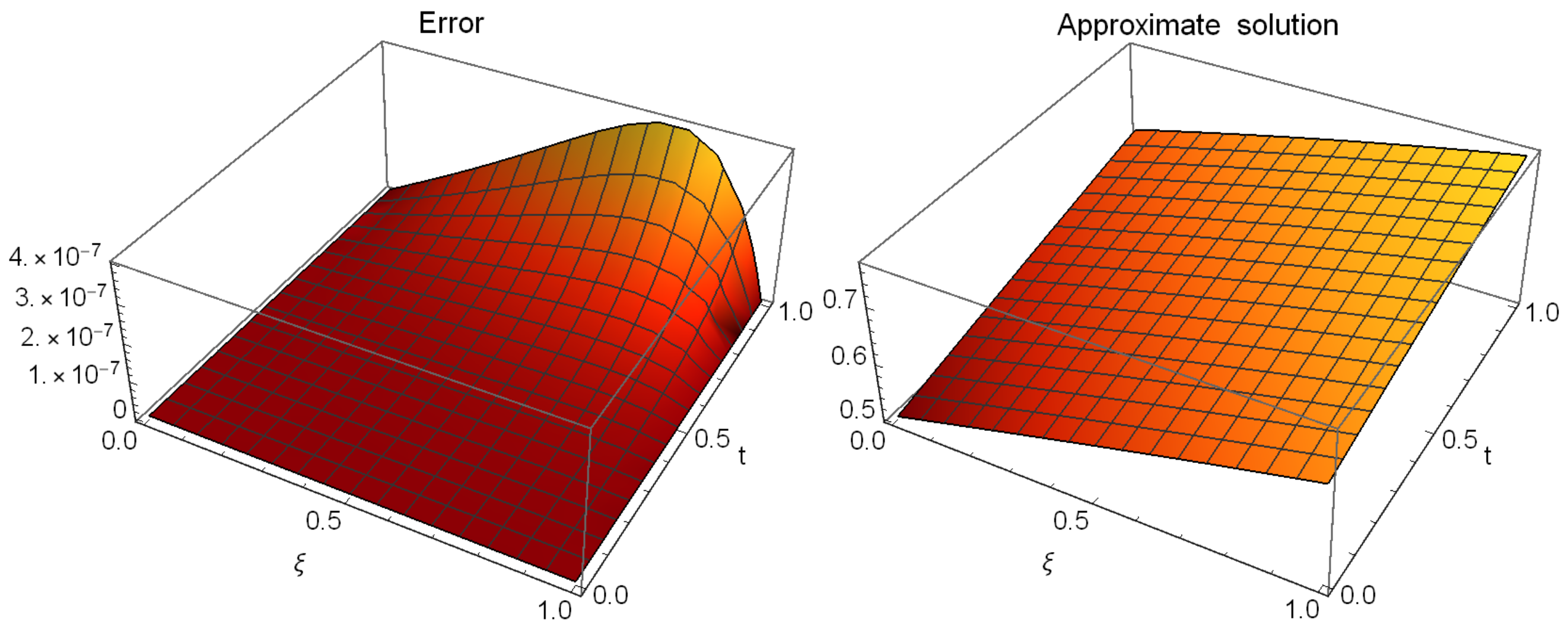
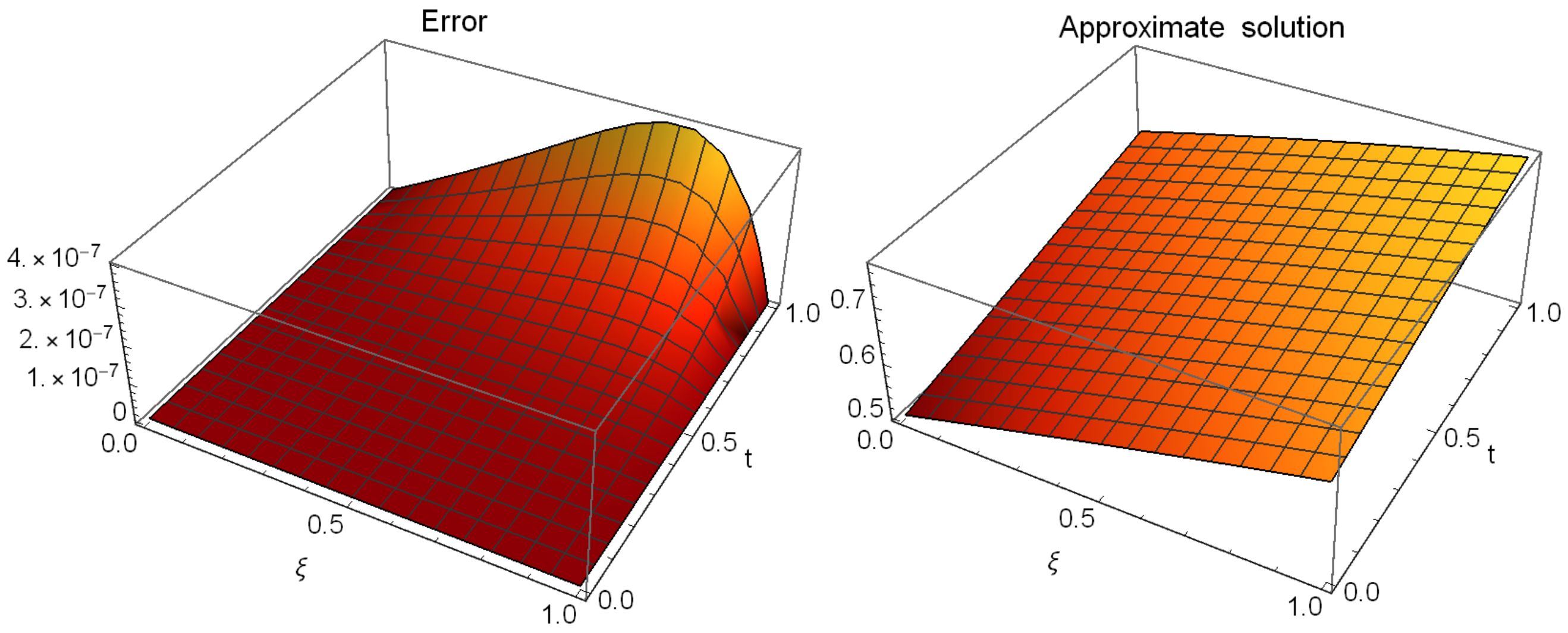
6. Illustrative Examples
| Method in [59] | Gaussians [38] | Our Method at | |||||
|---|---|---|---|---|---|---|---|
| Exact | |||||||
| (0.1,0.2) | 0.492678192949 | 0.427418 | 0.454935 | 0.492466 | 0.492564 | 0.492678192917 | 0.492678192905 |
| (0.1,0.4) | 0.467722618671 | 0.411555 | 0.429688 | 0.467632 | 0.467645 | 0.467722618641 | 0.467722618639 |
| (0.1,0.6) | 0.442927492940 | 0.401291 | 0.410894 | 0.442952 | 0.442910 | 0.442927492914 | 0.442927492915 |
| (0.1,0.6) | 0.418413552133 | 0.393583 | 0.395550 | 0.418448 | 0.418426 | 0.418413552108 | 0.418413552111 |
| (0.3,0.2) | 0.528003672504 | 0.461640 | 0.489905 | 0.527493 | 0.527735 | 0.528003672408 | 0.528003672375 |
| (0.3,0.4) | 0.503032971388 | 0.445267 | 0.464133 | 0.502797 | 0.502842 | 0.503032971299 | 0.503032971292 |
| (0.3,0.6) | 0.478047131210 | 0.434619 | 0.444777 | 0.478089 | 0.477992 | 0.478047131130 | 0.478047131136 |
| (0.3,0.8) | 0.453170661978 | 0.426595 | 0.428860 | 0.453249 | 0.453186 | 0.453170661904 | 0.453170661915 |
| (0.5,0.2) | 0.563050917309 | 0.496159 | 0.524966 | 0.562434 | 0.562736 | 0.563050917145 | 0.563050917089 |
| (0.5,0.4) | 0.538313096311 | 0.479367 | 0.498899 | 0.538014 | 0.538083 | 0.538313096160 | 0.538313096152 |
| (0.5,0.6) | 0.513385148789 | 0.468375 | 0.479131 | 0.513427 | 0.513312 | 0.513385148654 | 0.513385148666 |
| (0.5,0.8) | 0.488390434671 | 0.460051 | 0.462744 | 0.488485 | 0.488400 | 0.488390434546 | 0.488390434567 |
| (0.7,0.2) | 0.597479692513 | 0.530655 | 0.559780 | 0.596963 | 0.597225 | 0.597479692278 | 0.597479692199 |
| (0.7,0.4) | 0.573213594762 | 0.513551 | 0.533657 | 0.572956 | 0.573026 | 0.573213594547 | 0.573213594540 |
| (0.7,0.6) | 0.548589854921 | 0.502269 | 0.513645 | 0.548627 | 0.548530 | 0.548589854730 | 0.548589854751 |
| (0.7,0.8) | 0.523725855053 | 0.493674 | 0.496910 | 0.523812 | 0.523734 | 0.523725854878 | 0.523725854911 |
| (0.9,0.2) | 0.630973661925 | 0.564813 | 0.594013 | 0.630756 | 0.630870 | 0.630973661699 | 0.630973661623 |
| (0.9,0.4) | 0.607399960009 | 0.547522 | 0.568079 | 0.607291 | 0.607325 | 0.607399959803 | 0.607399959800 |
| (0.9,0.6) | 0.583314828533 | 0.536019 | 0.548003 | 0.583335 | 0.583293 | 0.583314828350 | 0.583314828375 |
| (0.9,0.8) | 0.558825335316 | 0.527198 | 0.531062 | 0.558867 | 0.558831 | 0.558825335148 | 0.558825335184 |
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Courier Corporation: Chelmsford, MA, USA, 2001. [Google Scholar]
- Hesthaven, J.; Gottlieb, S.; Gottlieb, D. Spectral Methods for Time-Dependent Problems; Cambridge University Press: Cambridge, UK, 2007; Volume 21. [Google Scholar]
- Dattoli, G.; Srivastava, H.M.; Zhukovsky, K. Theory and Applications of Special Functions: A Volume Dedicated to Mizan Rahman; Springer: New York, NY, USA, 2017. [Google Scholar]
- Gil, A.; Segura, J.; Temme, N.M. Special Functions of Mathematical Physics: A Unified Introduction with Applications; Birkhäuser: Basel, Switzerland, 2018. [Google Scholar]
- Nalli, A.; Haukkanen, P. On generalized Fibonacci and Lucas polynomials. Chaos Solitons Fractals 2009, 42, 3179–3186. [Google Scholar] [CrossRef]
- Kizilateş, C. Explicit, determinantal, recursive formulas, and generating functions of generalized Humbert–Hermite polynomials via generalized Fibonacci polynomials. Math. Meth. Appl. Sci. 2023, 46, 9205–9216. [Google Scholar] [CrossRef]
- Ali, I.; Haq, S.; Nisar, K.S.; Arifeen, S.U. Numerical study of 1D and 2D advection-diffusion-reaction equations using Lucas and Fibonacci polynomials. Arab. J. Math. 2021, 10, 513–526. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Abd-Elhameed, W.M.; Atta, A.G. Spectral Galerkin treatment of linear one-dimensional telegraph type problem via the generalized Lucas polynomials. Arab. J. Math. 2022, 11, 601–615. [Google Scholar] [CrossRef]
- Sharma, R.; Rajeev. A numerical approach to solve 2D fractional RADE of variable-order with Vieta–Lucas polynomials. Chin. J. Phys. 2023, 86, 433–446. [Google Scholar] [CrossRef]
- Sharma, R.; Rajeev. An operational matrix approach to solve a 2D variable-order reaction advection diffusion equation with Vieta–Fibonacci polynomials. Spec. Top. Rev. Porous Media Int. J. 2023, 14, 79–96. [Google Scholar] [CrossRef]
- Singh, M.; Das, S.; Rajeev. An innovative Vieta–Fibonacci wavelet collocation method for the numerical solution of three-component Brusselator reaction diffusion system of fractional order. J. Math. Chem. 2024, 62, 1558–1594. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Dabiri, A.; Lopes, A.M.; Machado, J.A.T. Numerical solution of mixed-type fractional functional differential equations using modified Lucas polynomials. Comput. Appl. Math. 2019, 38, 46. [Google Scholar] [CrossRef]
- Ali, I.; Haq, S.; Aldosary, S.F.; Nisar, K.S.; Ahmad, F. Numerical solution of one-and two-dimensional time-fractional Burgers equation via Lucas polynomials coupled with Finite difference method. Alex. Eng. J. 2022, 61, 6077–6087. [Google Scholar] [CrossRef]
- Oruç, Ö. A new algorithm based on Lucas polynomials for approximate solution of 1D and 2D nonlinear generalized Benjamin–Bona–Mahony–Burgers equation. Comput.Math. Appl. 2017, 74, 3042–3057. [Google Scholar] [CrossRef]
- Mahdy, A.M.S.; Mohamed, D.S. Approximate solution of Cauchy integral equations by using Lucas polynomials. Comput. Appl. Math. 2022, 41, 403. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers: Redding, CT, USA, 2010. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Zhang, H.; Zhang, M.; Liu, F.; Shen, M. Review of the fractional Black-Scholes equations and their solution techniques. Fractal Fract. 2024, 8, 101. [Google Scholar] [CrossRef]
- Anwar, M.S.; Alam, M.M.; Khan, M.A.; Abouzied, A.S.; Hussain, Z.; Puneeth, V. Generalized viscoelastic flow with thermal radiations and chemical reactions. Geoenergy Sci. Eng. 2024, 232, 212442. [Google Scholar] [CrossRef]
- Nadeem, M.; Alsayaad, Y. Analytical study of one dimensional time fractional Schrödinger problems arising in quantum mechanics. Sci. Rep. 2024, 14, 12503. [Google Scholar] [CrossRef] [PubMed]
- Alhejili, W.; Khader, M.M.; Lotfy, K.; El-Bary, A.A.; Adel, M. Studying of the Covid-19 model by using the finite element method: Theoretical and numerical simulation. Soft Comput. 2024, 28, 5263–5273. [Google Scholar] [CrossRef]
- Talib, I.; Jarad, F.; Mirza, M.U.; Nawaz, A.; Riaz, M.B. A generalized operational matrix of mixed partial derivative terms with applications to multi-order fractional partial differential equations. Alex. Eng. J. 2022, 61, 135–145. [Google Scholar] [CrossRef]
- Usman, M.; Hamid, M.; Zubair, T.; Haq, R.U.; Wang, W.; Liu, M.B. Novel operational matrices-based method for solving fractional-order delay differential equations via shifted Gegenbauer polynomials. Appl. Math. Comput. 2020, 372, 124985. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Lopes, A.M.; Babatin, M.M. Shifted fractional Jacobi collocation method for solving fractional functional differential equations of variable order. Chaos Solitons Fract. 2020, 134, 109721. [Google Scholar] [CrossRef]
- Shah, K.; Khan, Z.A.; Ali, A.; Amin, R.; Khan, H.; Khan, A. Haar Wavelet collocation approach for the solution of fractional order COVID-19 model using Caputo derivative. Alex. Eng. J. 2020, 59, 3221–3231. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Al-Harbi, M.S.; Atta, A.G. New convolved Fibonacci collocation procedure for the Fitzhugh-Nagumo non-linear equation. Nonlinear Eng. 2024, 13, 20220332. [Google Scholar] [CrossRef]
- Yunus, A.O.; Olayiwola, M.O.; Adedokun, K.A.; Adedeji, J.A.; Alaje, I.A. Mathematical analysis of fractional-order Caputo’s derivative of coronavirus disease model via Laplace Adomian decomposition method. Beni-Suef Univ. J. Basic Appl. Sci. 2022, 11, 144. [Google Scholar] [CrossRef] [PubMed]
- Maleknejad, K.; Rashidinia, J.; Eftekhari, T. Numerical solutions of distributed order fractional differential equations in the time domain using the Müntz–Legendre wavelets approach. Numer. Methods Partial Differ. Equ. 2021, 37, 707–731. [Google Scholar] [CrossRef]
- Kumar, Y.; Singh, S.; Srivastava, N.; Singh, A.; Singh, V.K. Wavelet approximation scheme for distributed order fractional differential equations. Comput. Math. Appl. 2020, 80, 1985–2017. [Google Scholar] [CrossRef]
- Wu, G.C.; Kong, H.; Luo, M.; Fu, H.; Huang, L.L. Unified predictor–corrector method for fractional differential equations with general kernel functions. Fract. Calc. Appl. Anal. 2022, 25, 648–667. [Google Scholar] [CrossRef]
- Saratha, S.R.; Bagyalakshmi, M.; Sai Sundara Krishnan, G. Fractional generalised homotopy analysis method for solving nonlinear fractional differential equations. Comput. Appl. Math. 2020, 39, 1–32. [Google Scholar] [CrossRef]
- Guo, T.; Nikan, O.; Avazzadeh, Z.; Qiu, W. Efficient alternating direction implicit numerical approaches for multi-dimensional distributed-order fractional integro differential problems. Comput. Appl. Math. 2022, 41, 236. [Google Scholar] [CrossRef]
- Han, X.; Guo, T.; Nikan, O.; Avazzadeh, Z. Robust implicit difference approach for the time-fractional Kuramoto–Sivashinsky equation with the non-smooth solution. Fractals 2023, 31, 2340061. [Google Scholar] [CrossRef]
- Qiu, W.; Chen, H.; Zheng, X. An implicit difference scheme and algorithm implementation for the one-dimensional time-fractional Burgers equations. Math. Comput. Simul. 2019, 166, 298–314. [Google Scholar] [CrossRef]
- Jannelli, A. Numerical solutions of fractional differential equations arising in engineering sciences. Mathematics 2020, 8, 215. [Google Scholar] [CrossRef]
- Dwivedi, K.D.; Das, S.; Rajeev; Baleanu, D. Numerical solution of highly non-linear fractional order reaction advection diffusion equation using the cubic B-spline collocation method. Int. J. Nonlinear Sci. Numer. Simul. 2022, 23, 1157–1172. [Google Scholar] [CrossRef]
- Aronson, D.G.; Weinberger, H.F. Multidimensional nonlinear diffusion arising in population genetics. Advanc. Math. 1978, 30, 33–76. [Google Scholar] [CrossRef]
- Alam, M.; Haq, S.; Ali, I.; Ebadi, M.J.; Salahshour, S. Radial basis functions approximation method for time-fractional FitzHugh–Nagumo Equation. Fractal Fract. 2023, 7, 882. [Google Scholar] [CrossRef]
- Fan, Z.Y.; Ali, K.K.; Maneea, M.; Inc, M.; Yao, S.W. Solution of time fractional Fitzhugh–Nagumo equation using semi analytical techniques. Res. Phys. 2023, 51, 106679. [Google Scholar] [CrossRef]
- Ramani, P.; Khan, A.M.; Suthar, D.L.; Kumar, D. Approximate analytical solution for non-linear Fitzhugh–Nagumo equation of time fractional order through fractional reduced differential transform method. Int. J. Appl. Comput. Math. 2022, 8, 61. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. A new numerical algorithm for fractional Fitzhugh–Nagumo equation arising in transmission of nerve impulses. Nonlinear Dyn. 2018, 91, 307–317. [Google Scholar] [CrossRef]
- Cai, L.; Cao, J.; Jing, F.; Wang, Y. A fast time integral finite difference method for a space-time fractional FitzHugh-Nagumo monodomain model in irregular domains. J. Comput. Phys. 2024, 501, 112744. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Al-Sady, A.M.; Alqubori, O.M.; Atta, A.G. Numerical treatment of the fractional Rayleigh-Stokes problem using some orthogonal combinations of Chebyshev polynomials. Aims Math. 2024, 9, 25457–25481. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Alsuyuti, M.M. Numerical treatment of multi-term fractional differential equations via new kind of generalized Chebyshev polynomials. Fractal Fract. 2023, 7, 74. [Google Scholar] [CrossRef]
- Alsuyuti, M.M.; Doha, E.H.; Ezz-Eldien, S.S. Galerkin operational approach for multi-dimensions fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 2022, 114, 106608. [Google Scholar] [CrossRef]
- Abd Elaziz, E.A.; Boulaaras, S.; Sweilam, N.H. Numerical solution of the fractional-order logistic equation via the first-kind Dickson polynomials and spectral tau method. Math. Methods Appl. Sci. 2023, 46, 8004–8017. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Alqubori, O.M.; Al-Harbi, A.K.; Alharbi, M.H.; Atta, A.G. Generalized third-kind Chebyshev tau approach for treating the time fractional cable problem. Electron. Res. Arch. 2024, 32, 6200–6224. [Google Scholar] [CrossRef]
- Mostafa, D.; Zaky, M.A.; Hafez, R.M.; Hendy, A.S.; Abdelkawy, M.A.; Aldraiweesh, A.A. Tanh Jacobi spectral collocation method for the numerical simulation of nonlinear Schrödinger equations on unbounded domain. Math. Meth. Appl. Sci. 2023, 46, 656–674. [Google Scholar] [CrossRef]
- Hafez, R.M.; Ezz-Eldien, S.S.; Bhrawy, A.H.; Ahmed, E.A.; Baleanu, D. A Jacobi Gauss–Lobatto and Gauss–Radau collocation algorithm for solving fractional Fokker–Planck equations. Nonlinear Dyn. 2015, 82, 1431–1440. [Google Scholar] [CrossRef]
- Atta, A.G. Two spectral Gegenbauer methods for solving linear and nonlinear time fractional Cable problems. Int. J. Mod. Phys. C 2024, 35, 2450070. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Ahmed, H.M.; Zaky, M.A.; Hafez, R.M. A new shifted generalized Chebyshev approach for multi-dimensional sinh-Gordon equation. Phys. Scr. 2024, 99, 095269. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Ahmed, H.M. Tau and Galerkin operational matrices of derivatives for treating singular and Emden–Fowler third-order-type equations. Int. J. Mod. Phys. C 2022, 33, 2250061. [Google Scholar] [CrossRef]
- Baishya, C.; Veeresha, P. Laguerre polynomial-based operational matrix of integration for solving fractional differential equations with non-singular kernel. Proc. R. Soc. A 2021, 477, 20210438. [Google Scholar] [CrossRef]
- Agarwal, P.; El-Sayed, A.A.; Tariboon, J. Vieta–Fibonacci operational matrices for spectral solutions of variable-order fractional integro-differential equations. J. Comput. Appl. Math. 2021, 382, 113063. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Koshy, T. Fibonacci and Lucas Numbers with Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 51. [Google Scholar]
- Abd-Elhameed, W.M.; Napoli, A. Some novel formulas of Lucas polynomials via different approaches. Symmetry 2023, 15, 185. [Google Scholar] [CrossRef]
- Jameson, G. The incomplete gamma functions. Math. Gaz. 2016, 100, 298–306. [Google Scholar] [CrossRef]
- Patel, H.S.; Patel, T. Applications of Fractional Reduced Differential Transform Method for Solving the Generalized Fractional-order Fitzhugh–Nagumo Equation. Int. J. Appl. Comput. Math. 2021, 7, 188. [Google Scholar] [CrossRef]

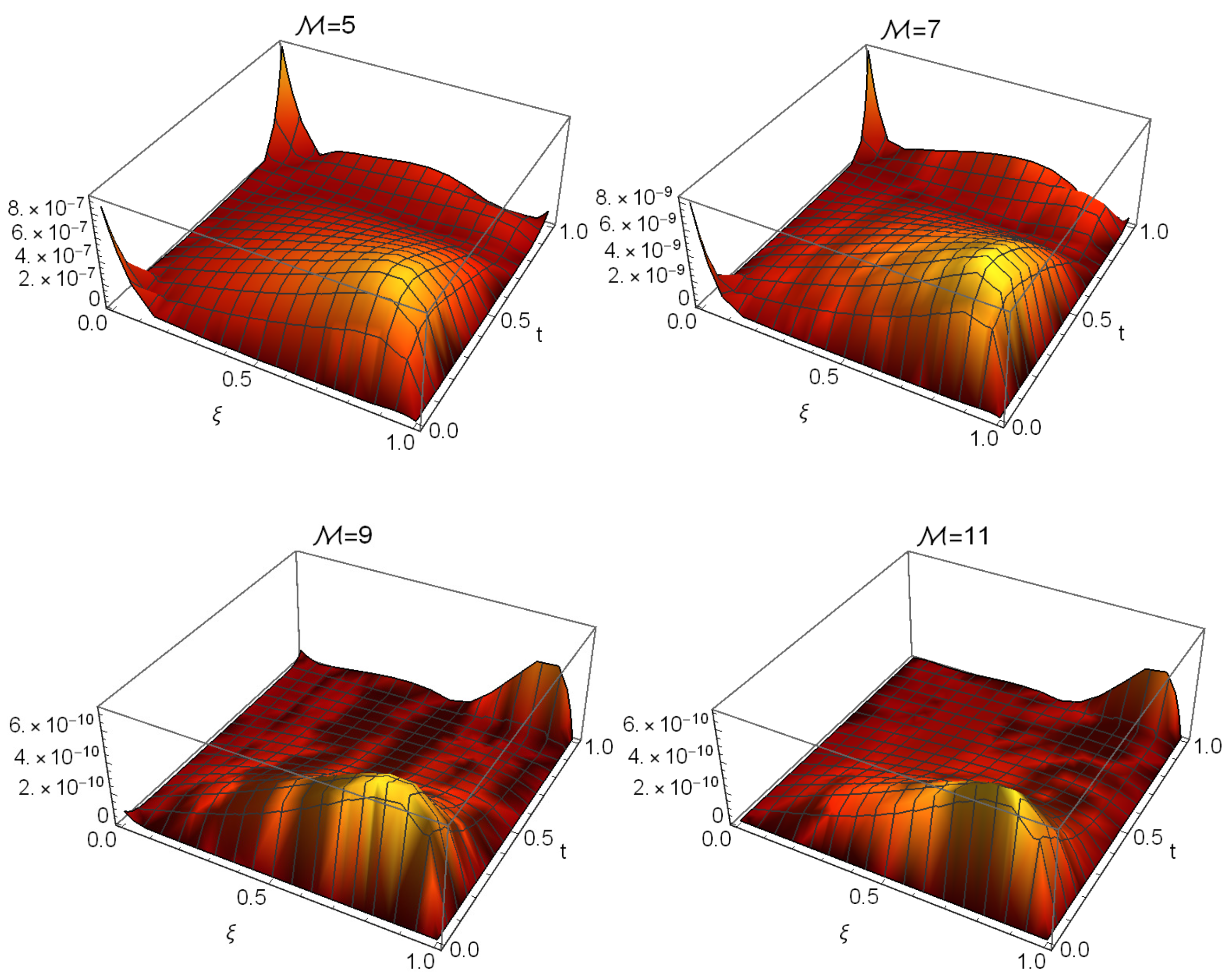
| t | Gaussians [38] | Our Method at | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||
| 3 | 5 | 7 | 9 | 11 | |
|---|---|---|---|---|---|
| MAE |
| Method in [59] | Gaussians [38] | Our Method at | ||||
|---|---|---|---|---|---|---|
| (0.001, 0.001) | ||||||
| (0.002, 0.002) | ||||||
| (0.003, 0.003) | ||||||
| (0.004, 0.004) | ||||||
| (0.005, 0.005) | ||||||
| (0.006, 0.006) | ||||||
| (0.007, 0.007) | ||||||
| (0.008, 0.008) | ||||||
| (0.009, 0.009) | ||||||
| (0.01, 0.01) | ||||||
| t | Hardy’s Multiquadric [38] | Our Method at | ||
|---|---|---|---|---|
| t | Inverse Quadric [38] | Our Method at | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | ||||||||
| t | Our Method at | ||
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd-Elhameed, W.M.; Alqubori, O.M.; Atta, A.G. A Collocation Procedure for Treating the Time-Fractional FitzHugh–Nagumo Differential Equation Using Shifted Lucas Polynomials. Mathematics 2024, 12, 3672. https://doi.org/10.3390/math12233672
Abd-Elhameed WM, Alqubori OM, Atta AG. A Collocation Procedure for Treating the Time-Fractional FitzHugh–Nagumo Differential Equation Using Shifted Lucas Polynomials. Mathematics. 2024; 12(23):3672. https://doi.org/10.3390/math12233672
Chicago/Turabian StyleAbd-Elhameed, Waleed Mohamed, Omar Mazen Alqubori, and Ahmed Gamal Atta. 2024. "A Collocation Procedure for Treating the Time-Fractional FitzHugh–Nagumo Differential Equation Using Shifted Lucas Polynomials" Mathematics 12, no. 23: 3672. https://doi.org/10.3390/math12233672
APA StyleAbd-Elhameed, W. M., Alqubori, O. M., & Atta, A. G. (2024). A Collocation Procedure for Treating the Time-Fractional FitzHugh–Nagumo Differential Equation Using Shifted Lucas Polynomials. Mathematics, 12(23), 3672. https://doi.org/10.3390/math12233672







