Analytical Models of Experimental Artefacts in an Ill-Posed Nonlinear ODE System
Abstract
1. Introduction
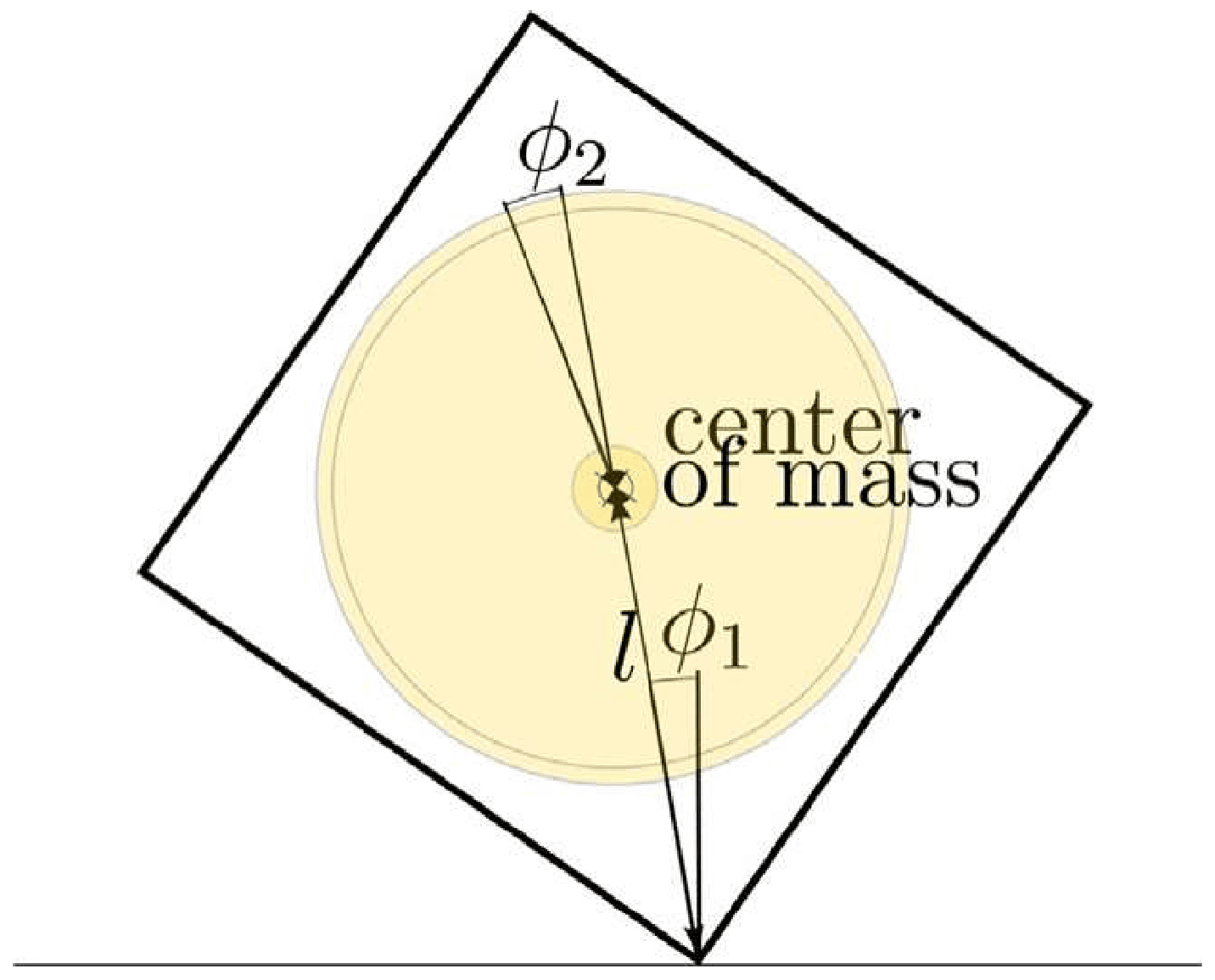
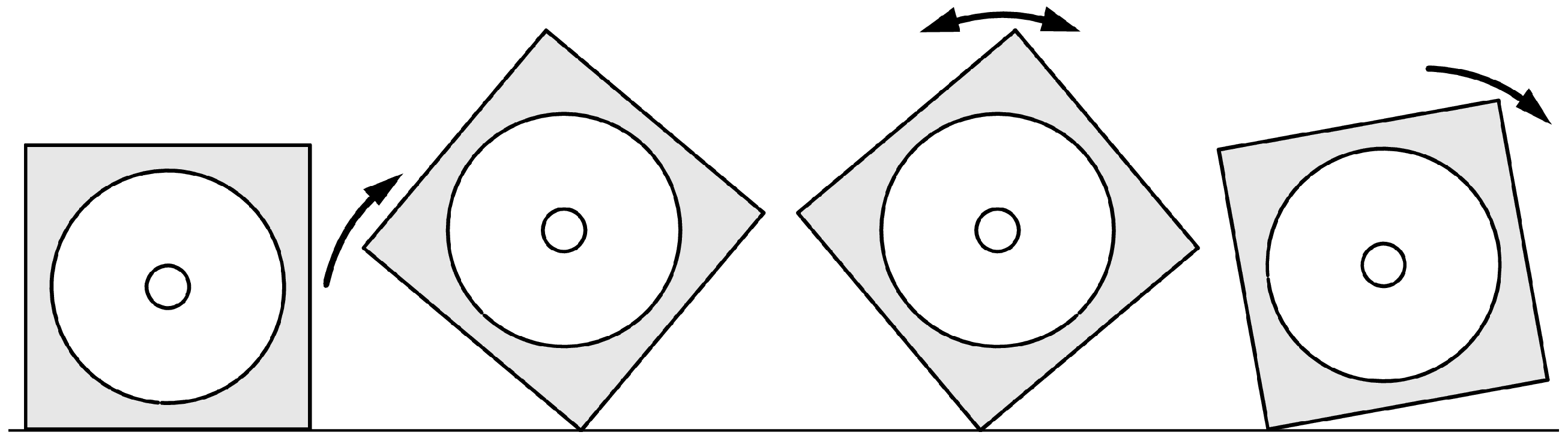
2. Mathematical Model and Experimental Reality
3. Backward Analysis: Principle
4. Backward Analysis: Examples
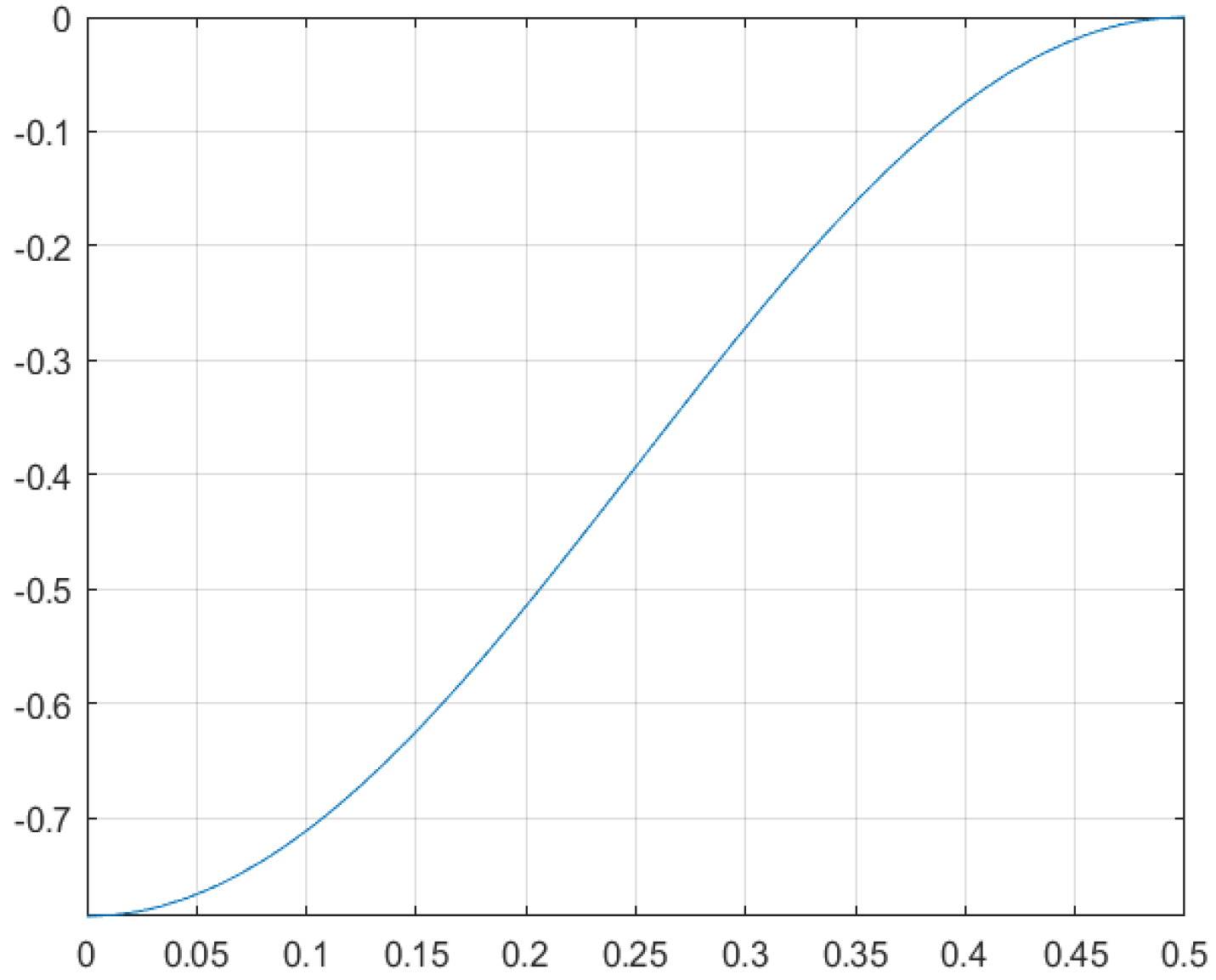
4.1. Approximating the Ideal Solution by Hermite Splines
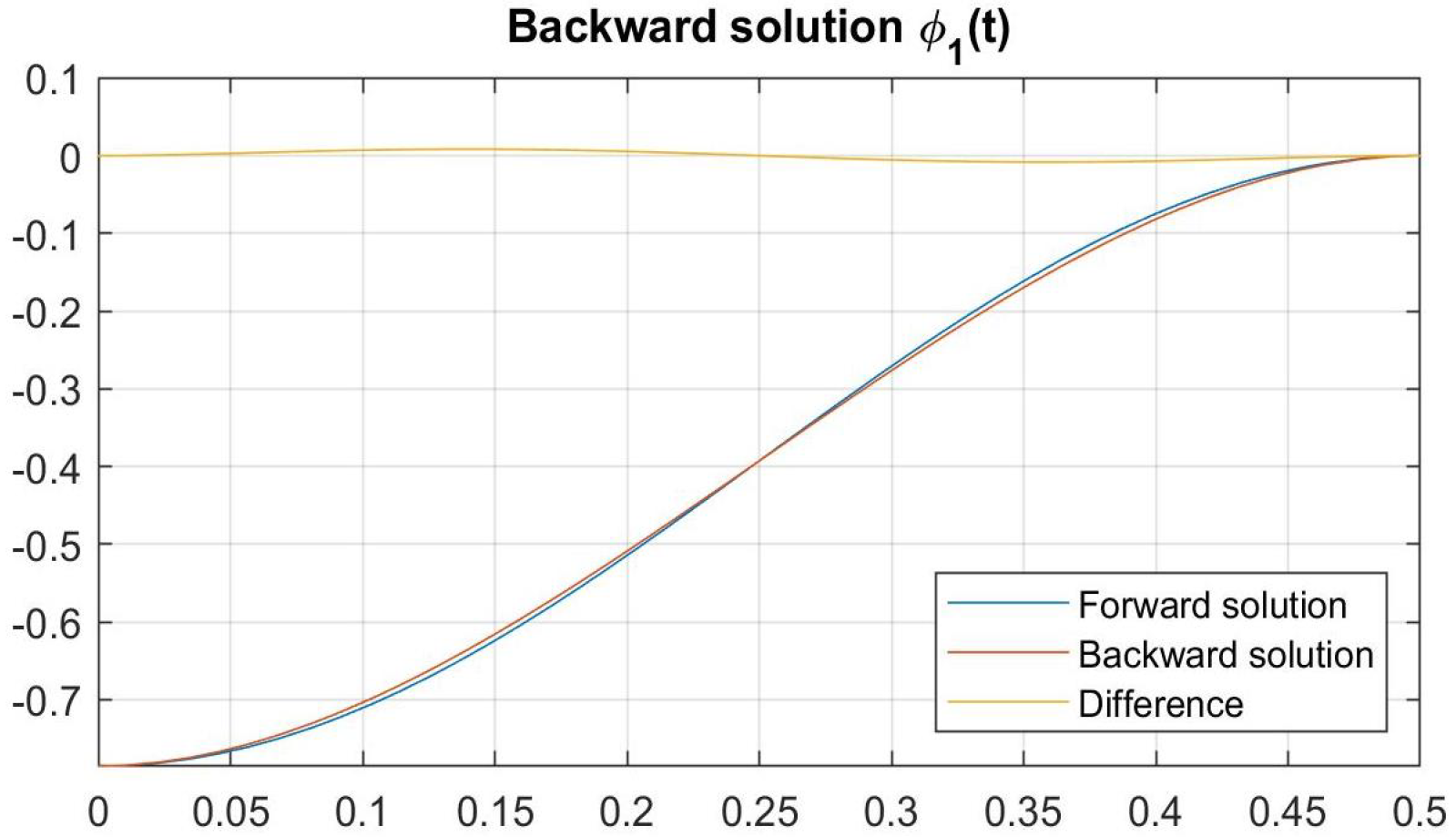
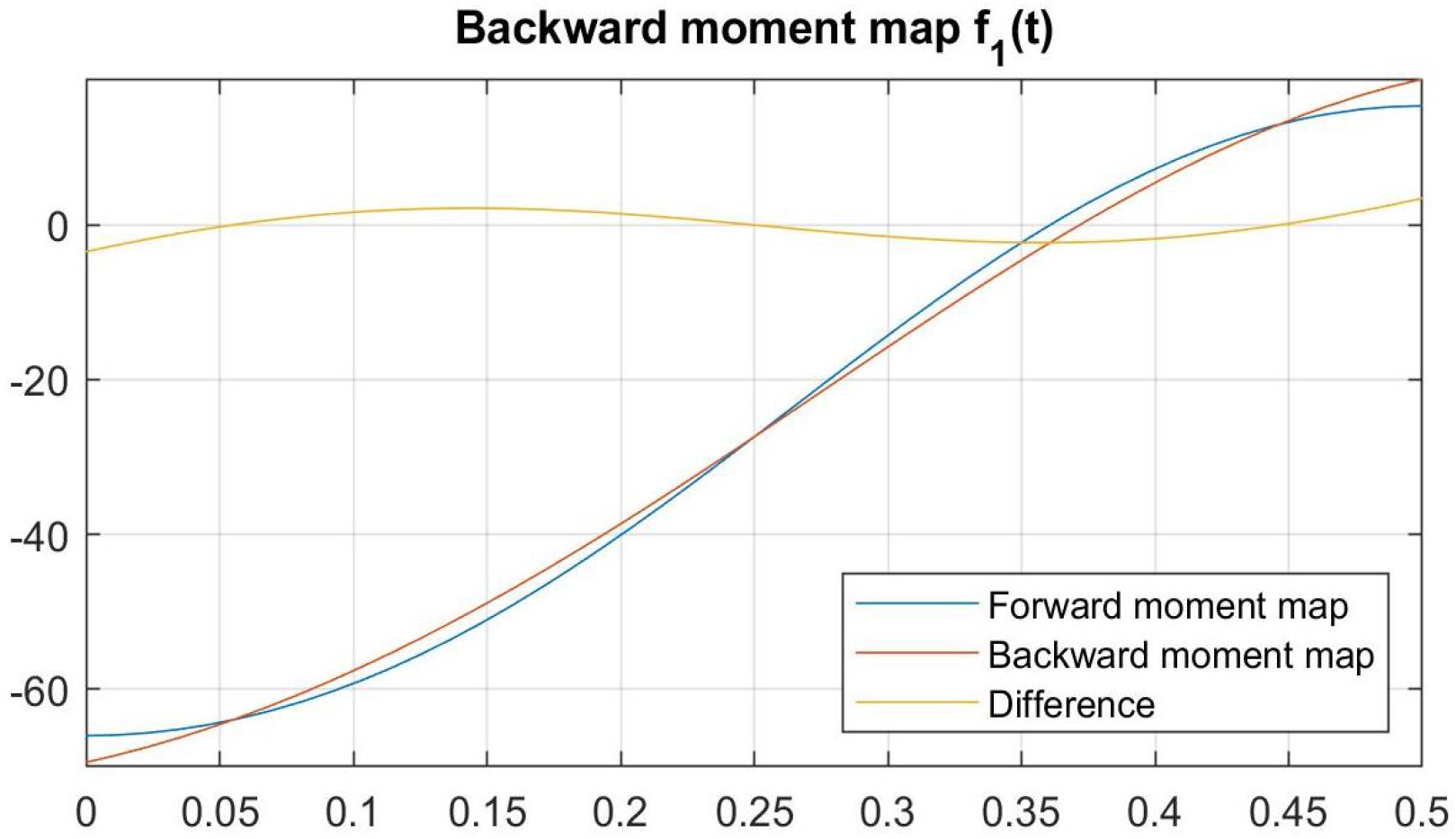
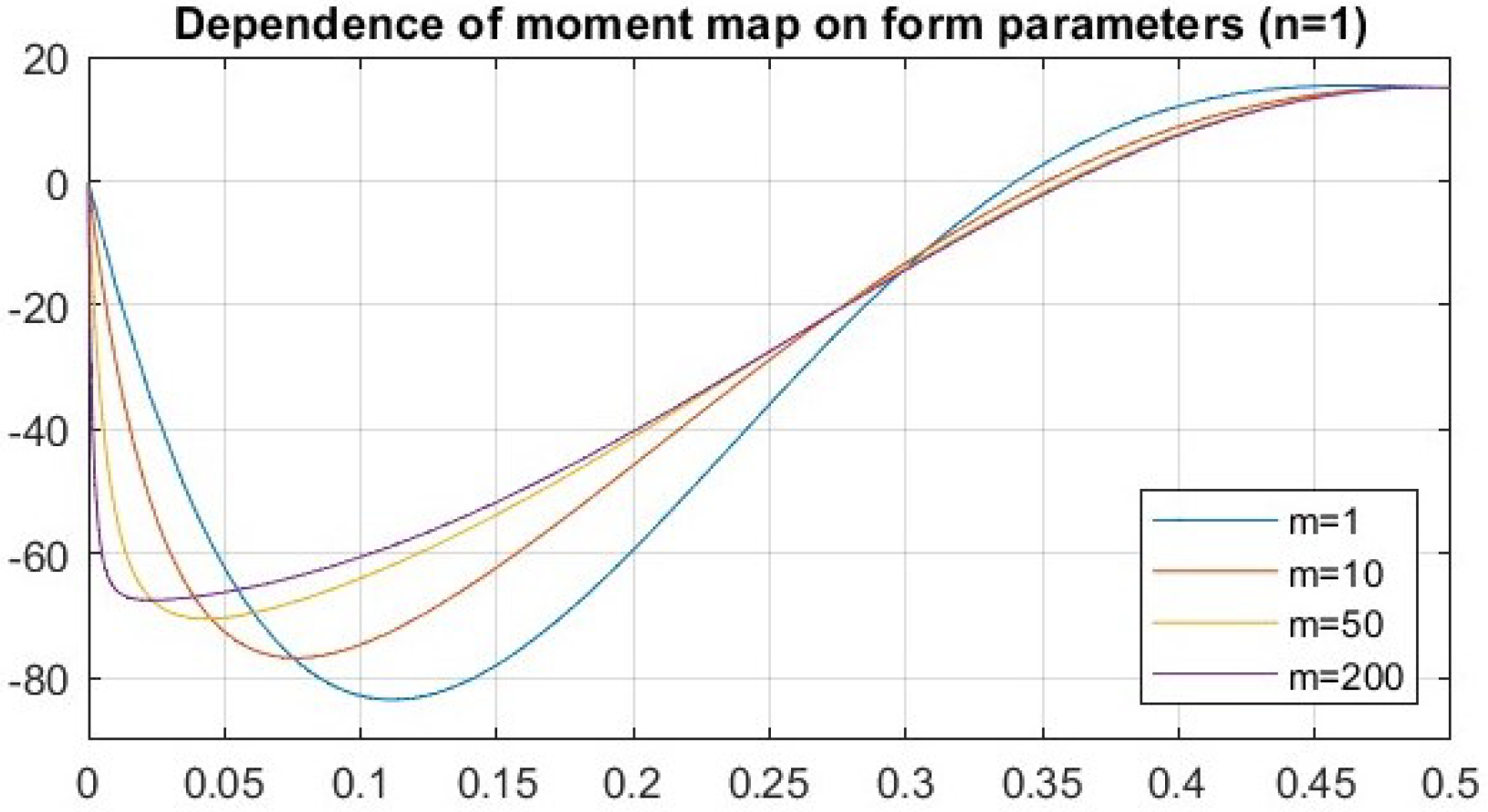
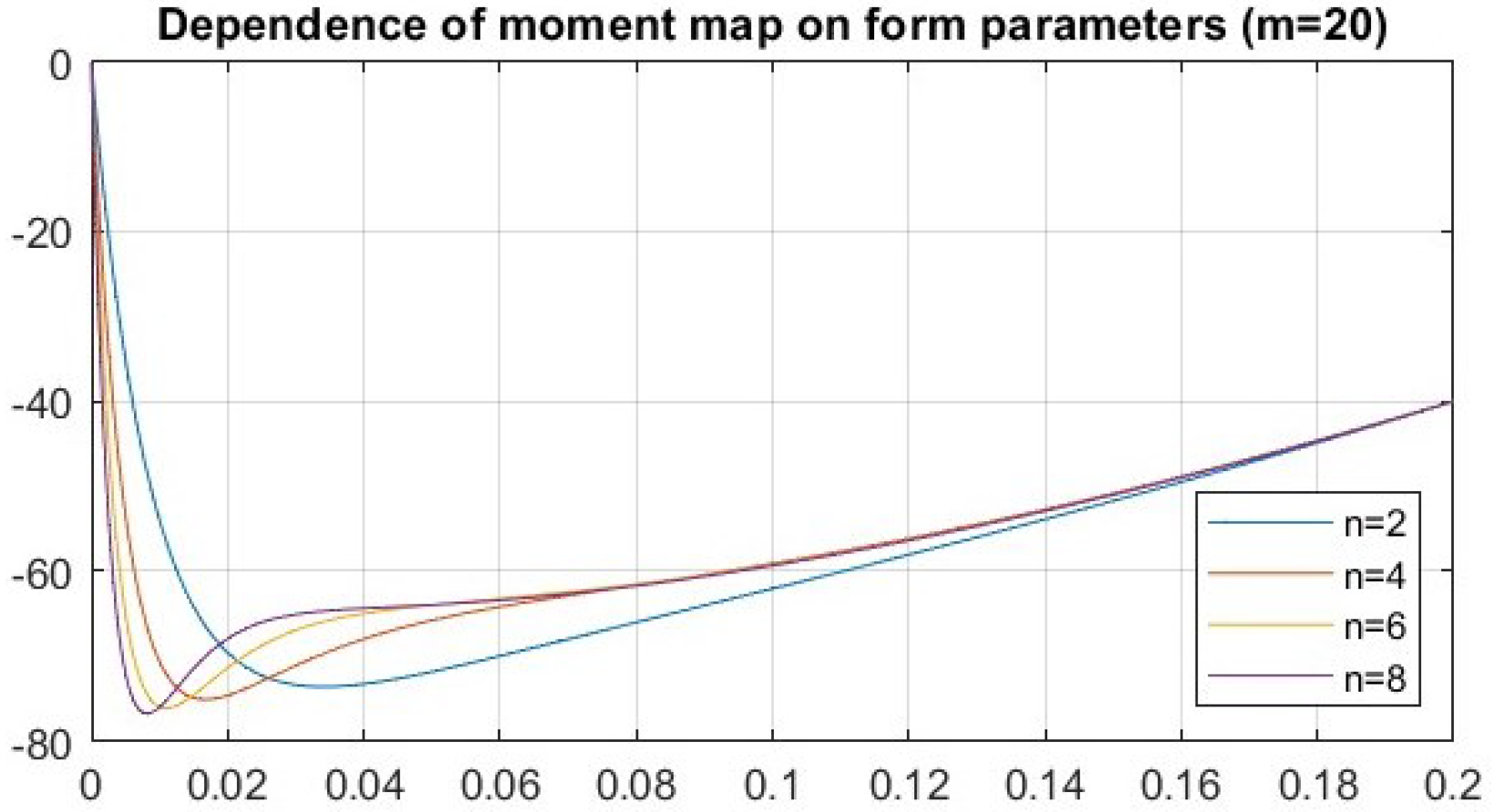
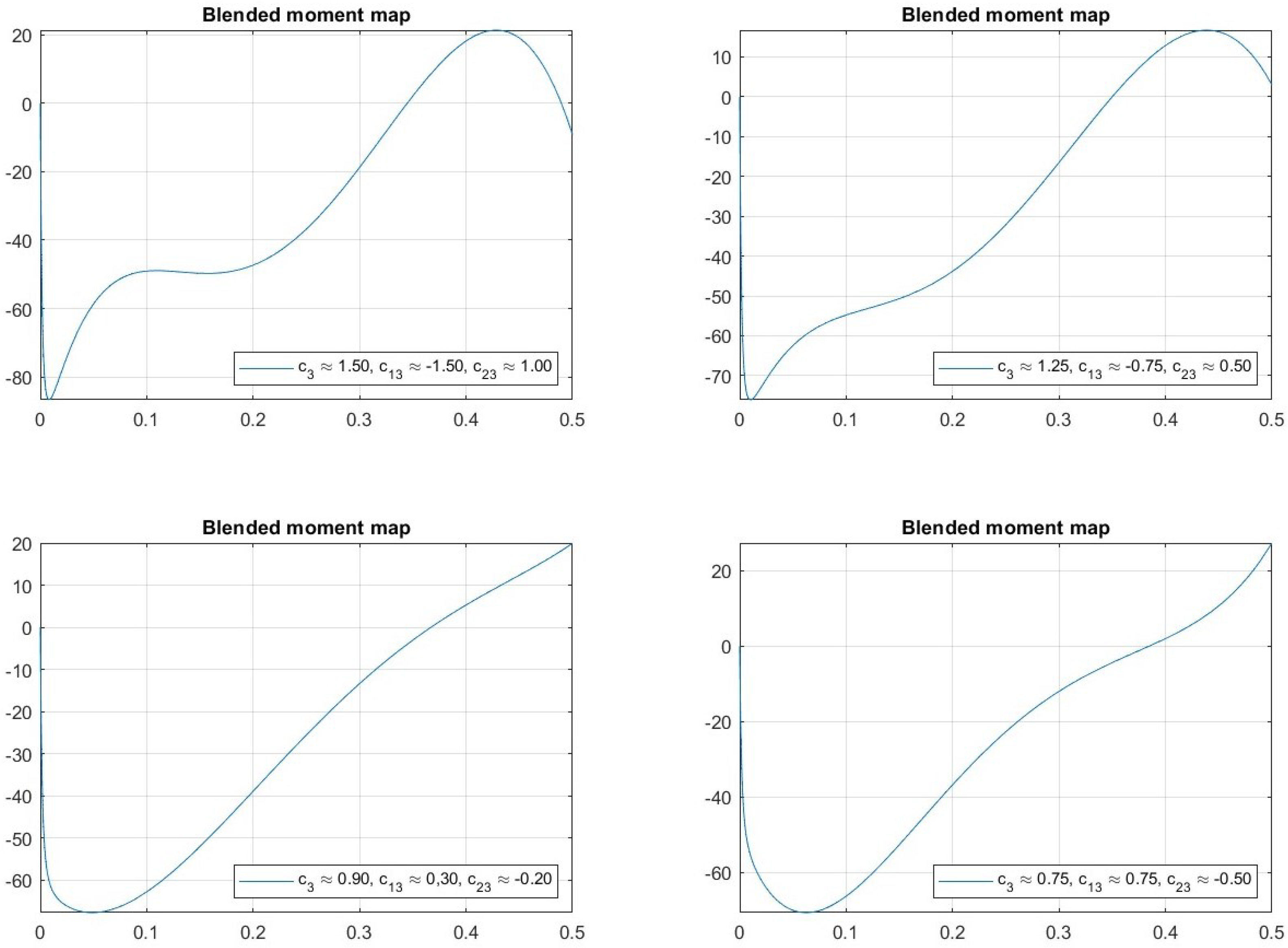
4.2. Investigating the Dependence Between Angle and Moment Trajectories
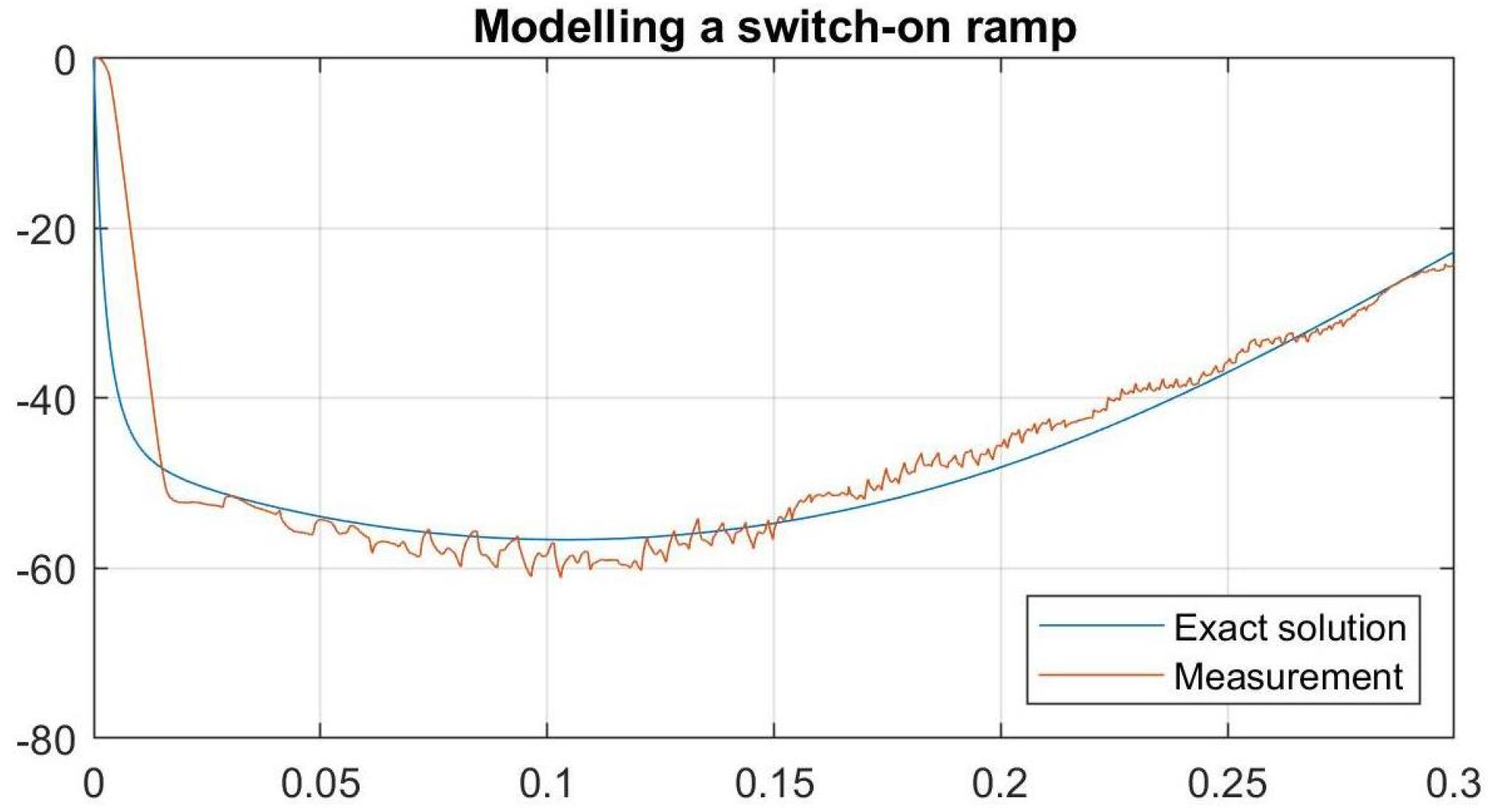
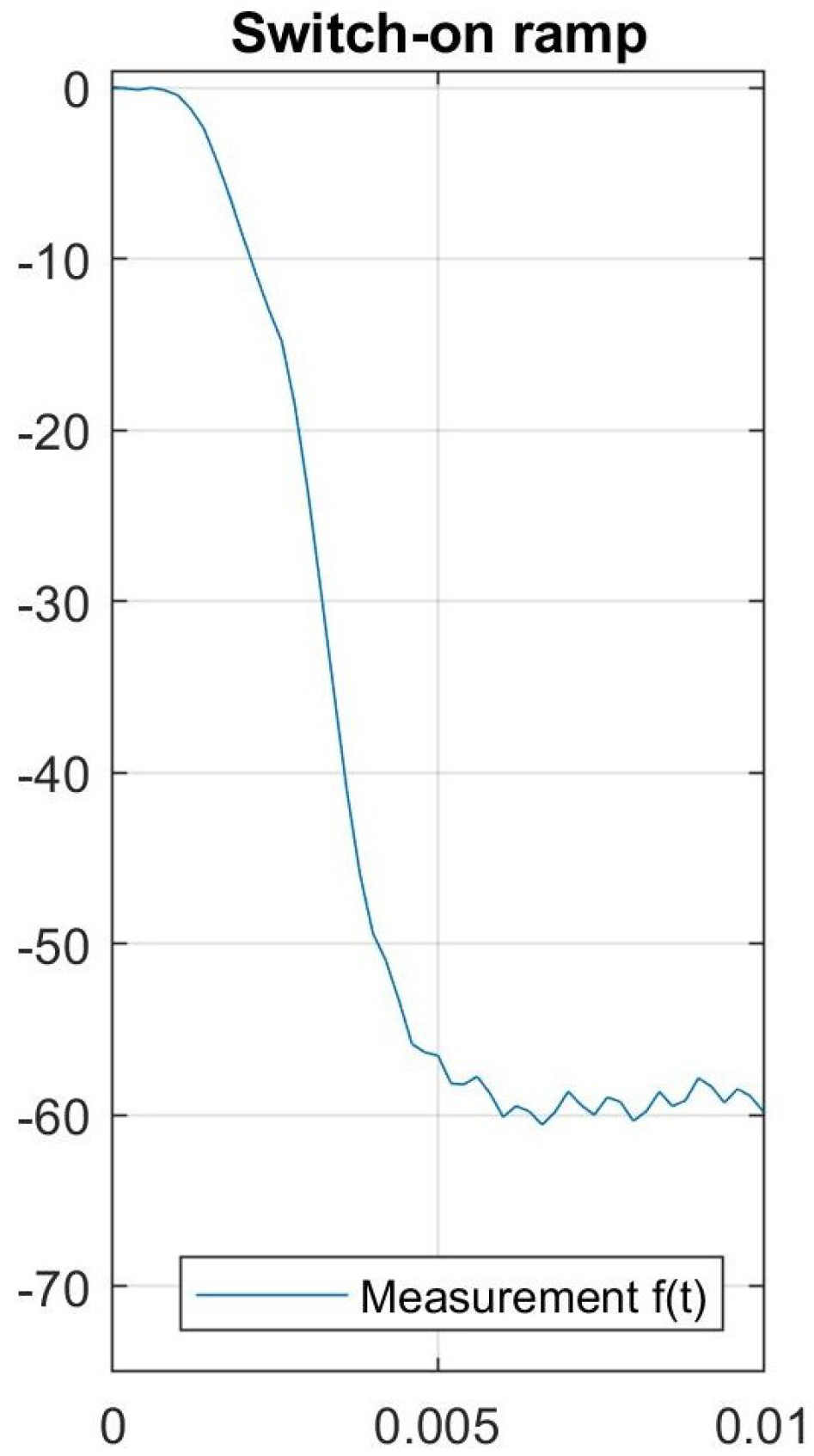
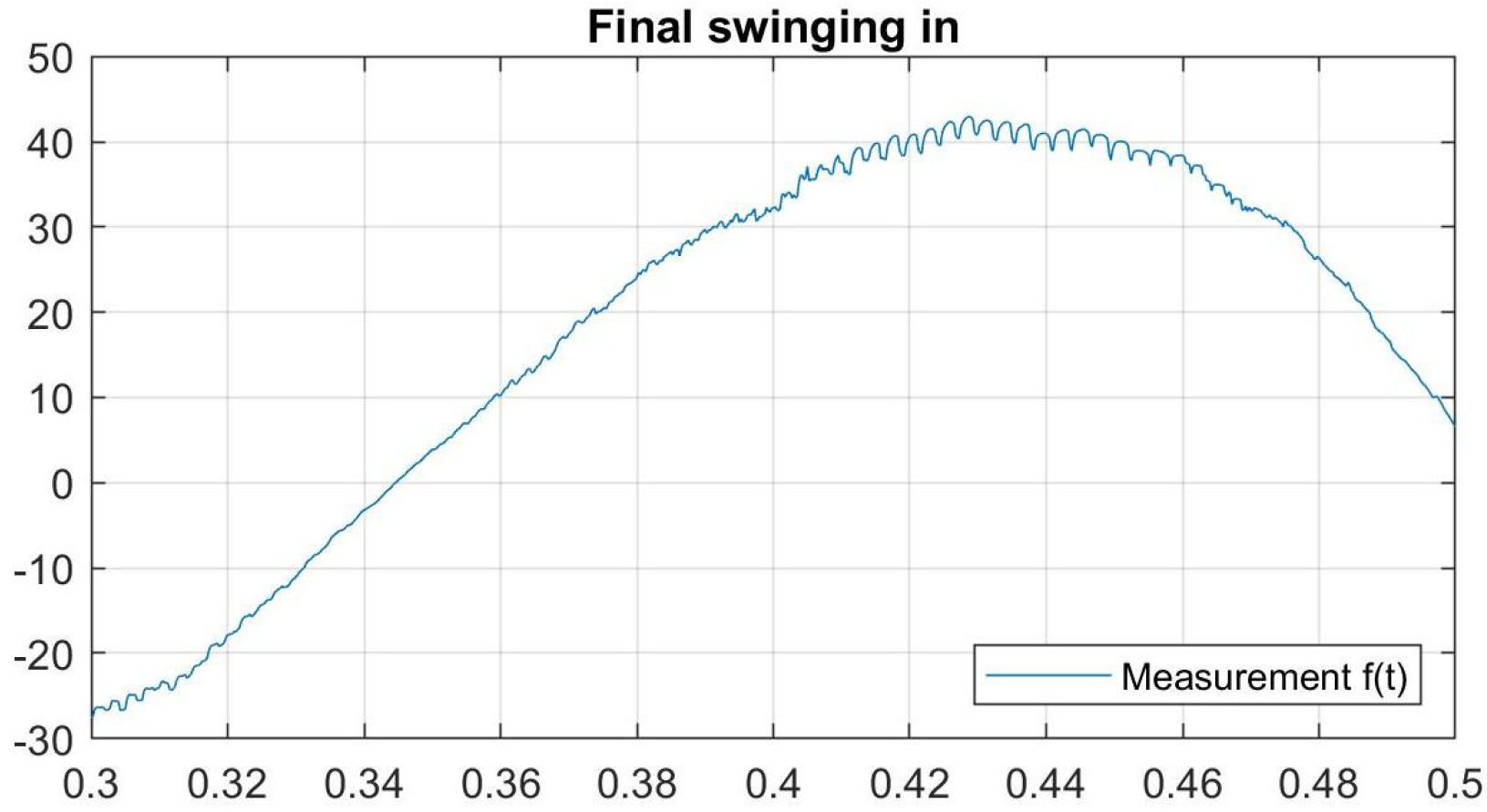
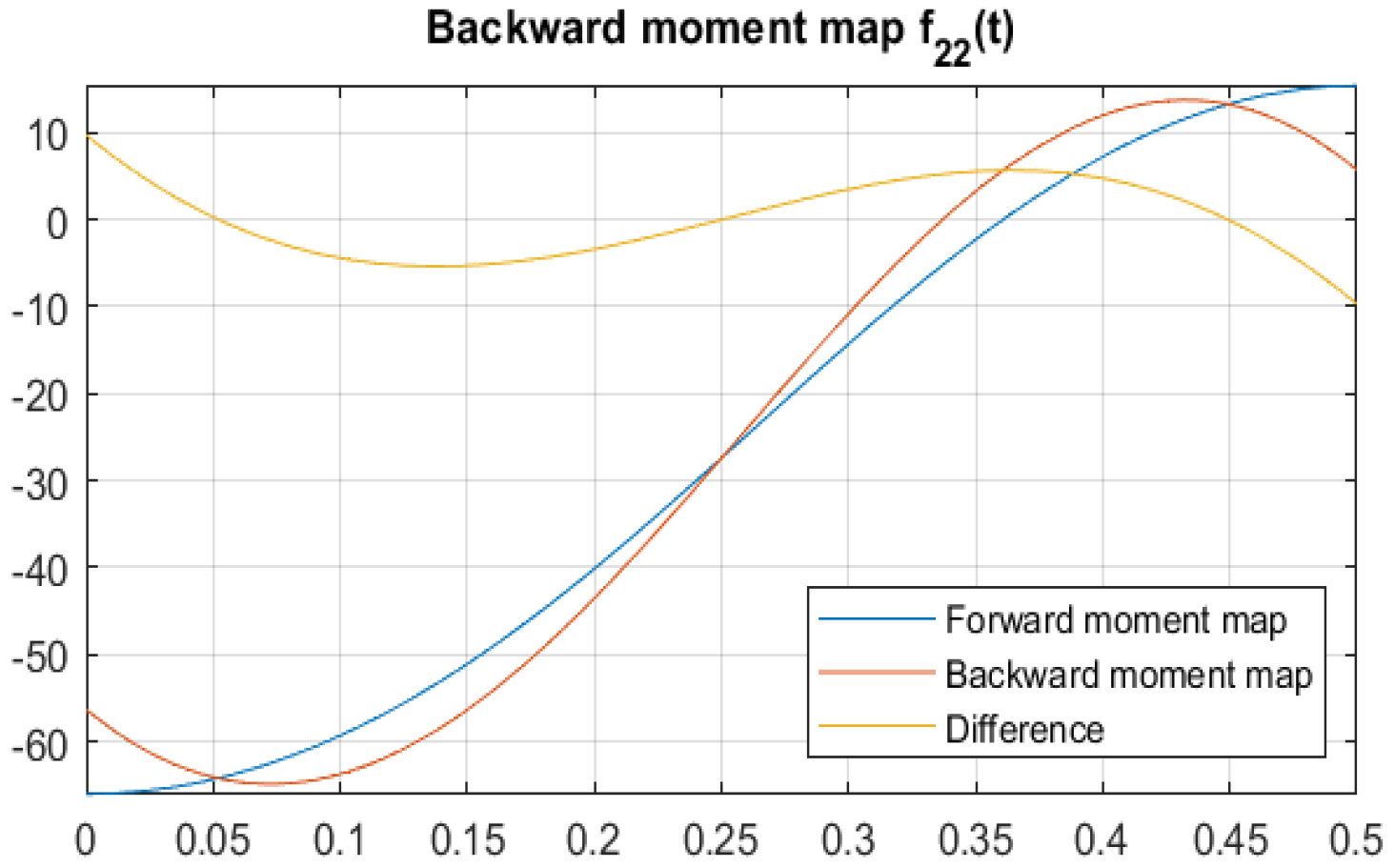
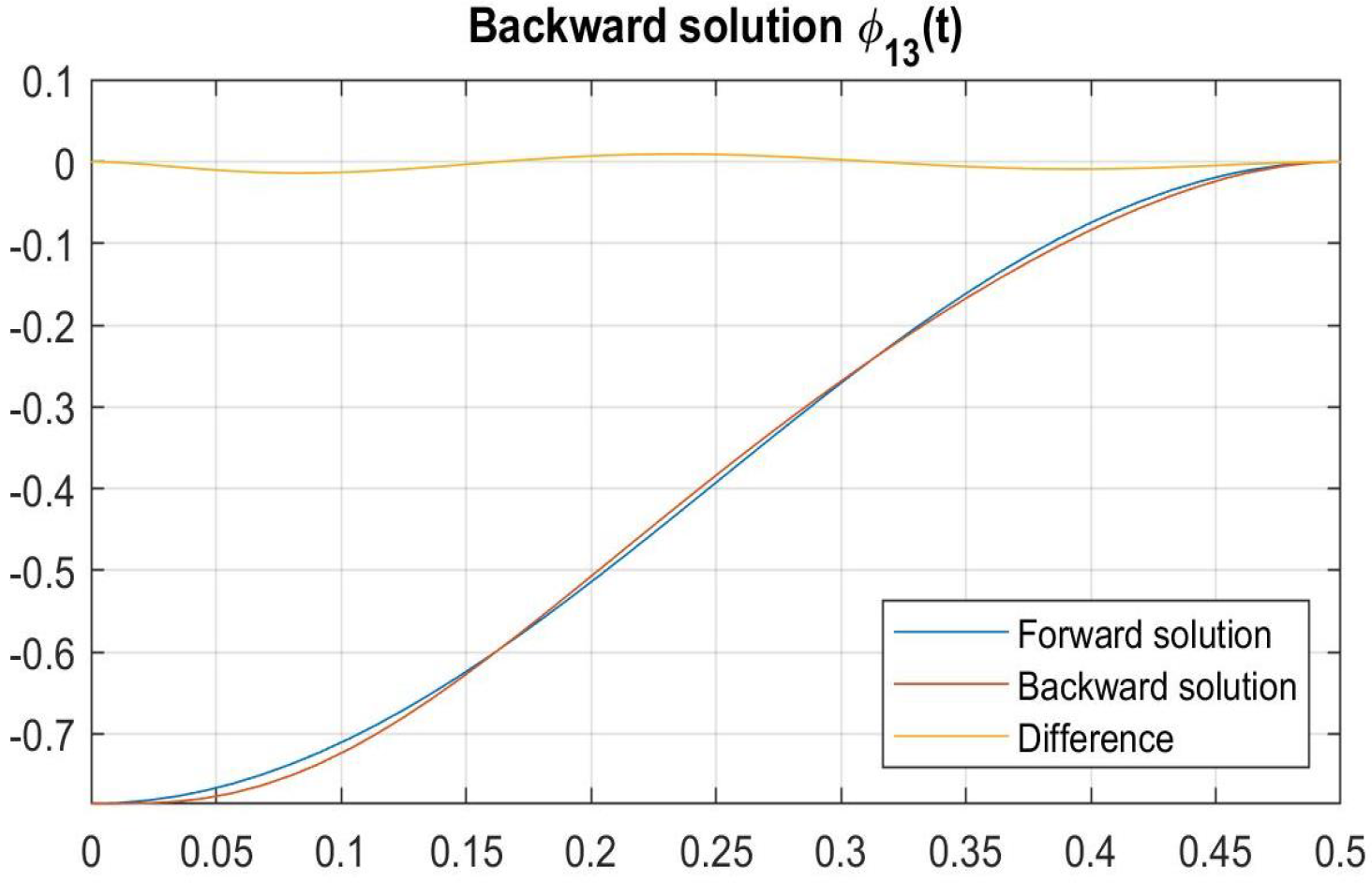
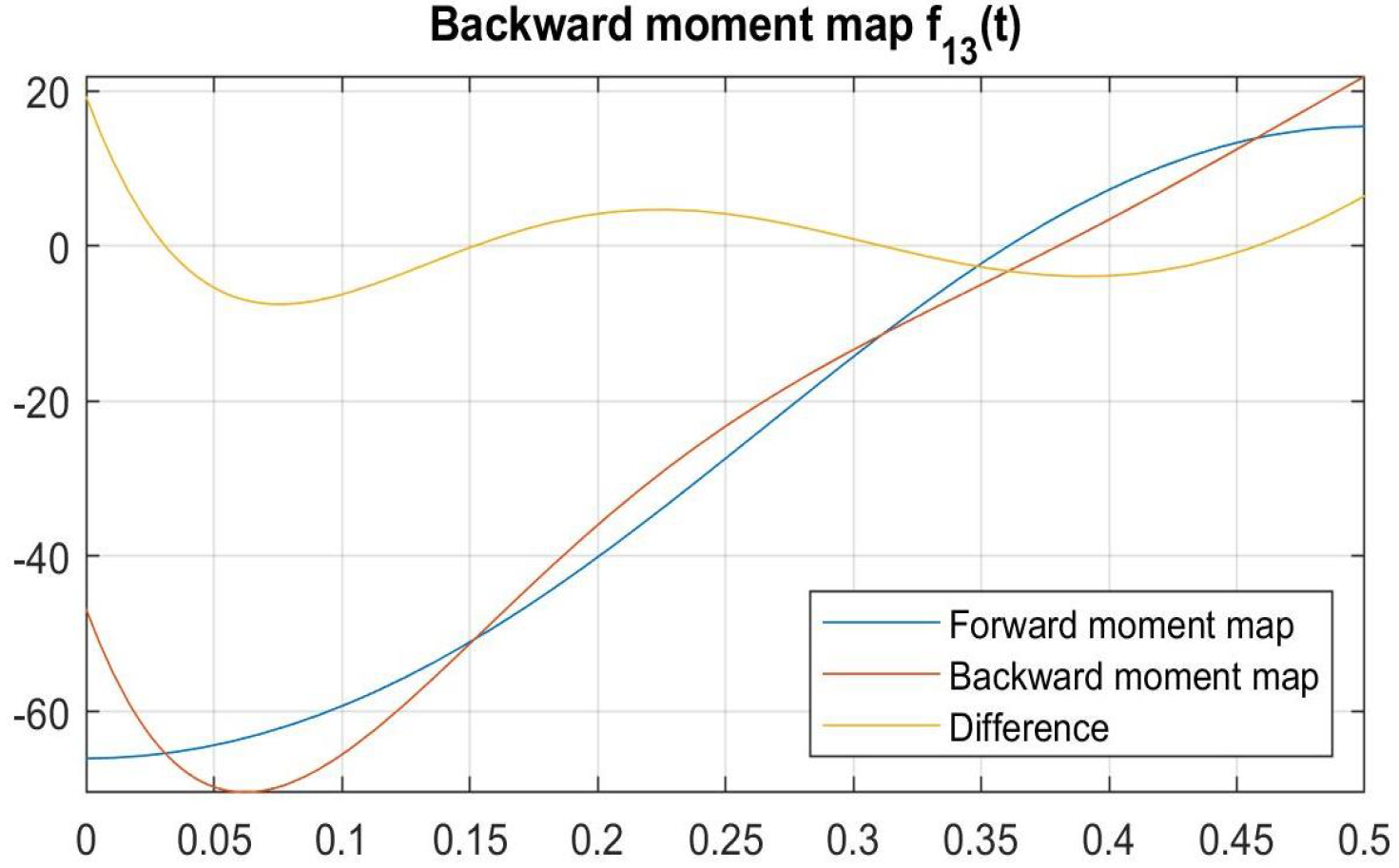
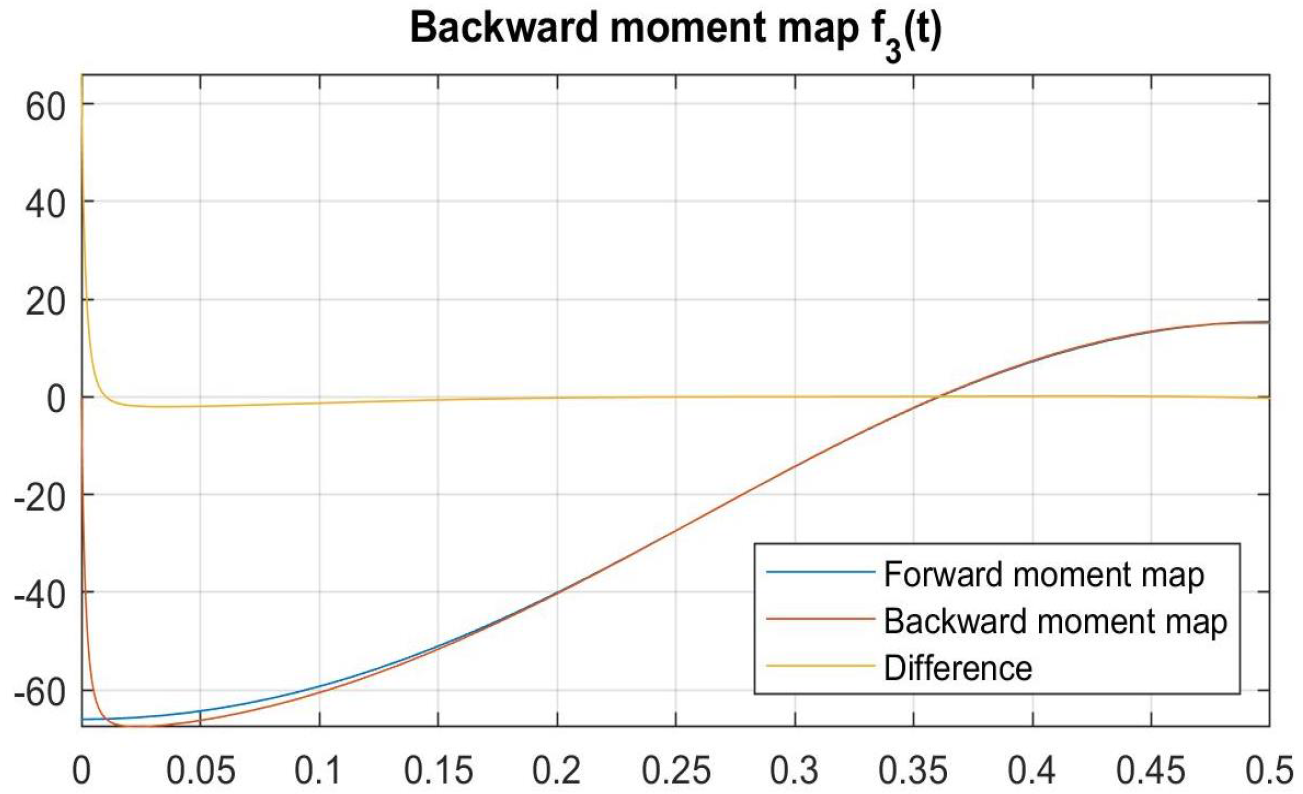
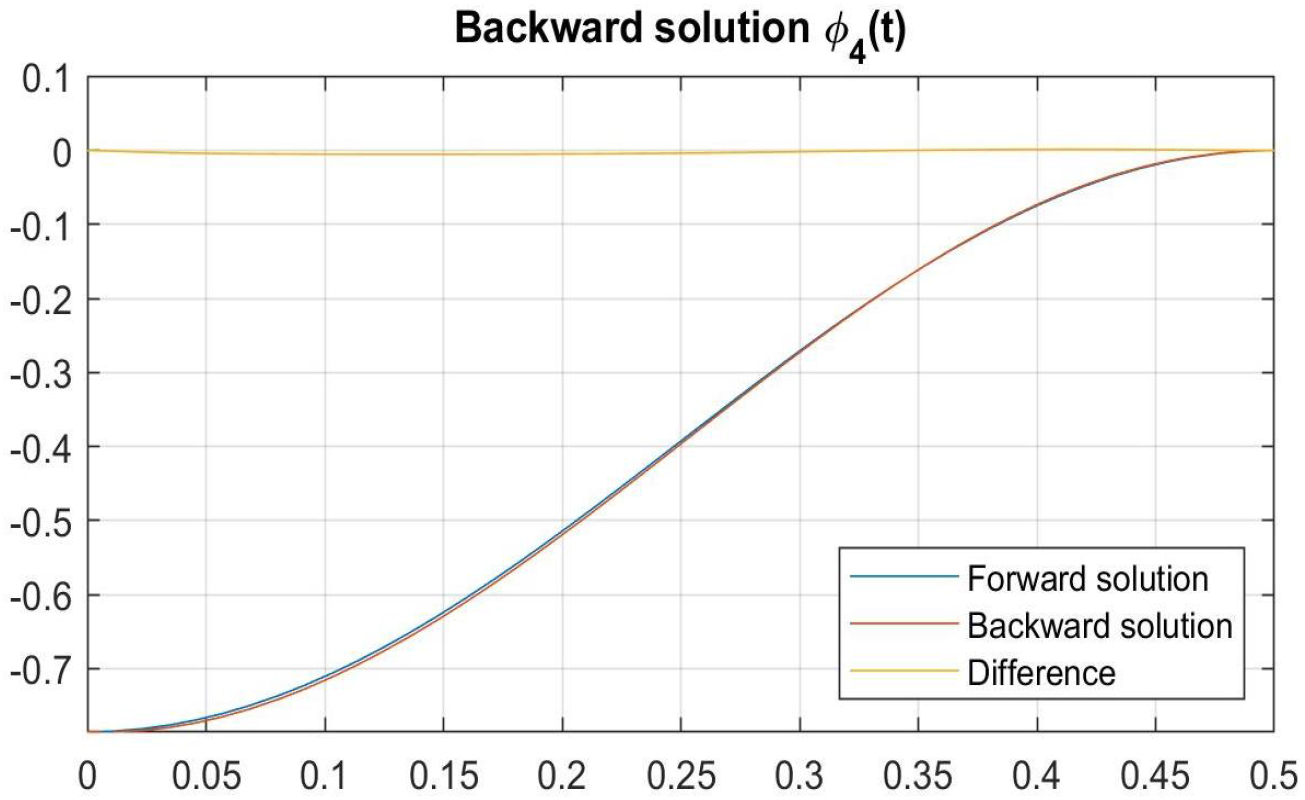
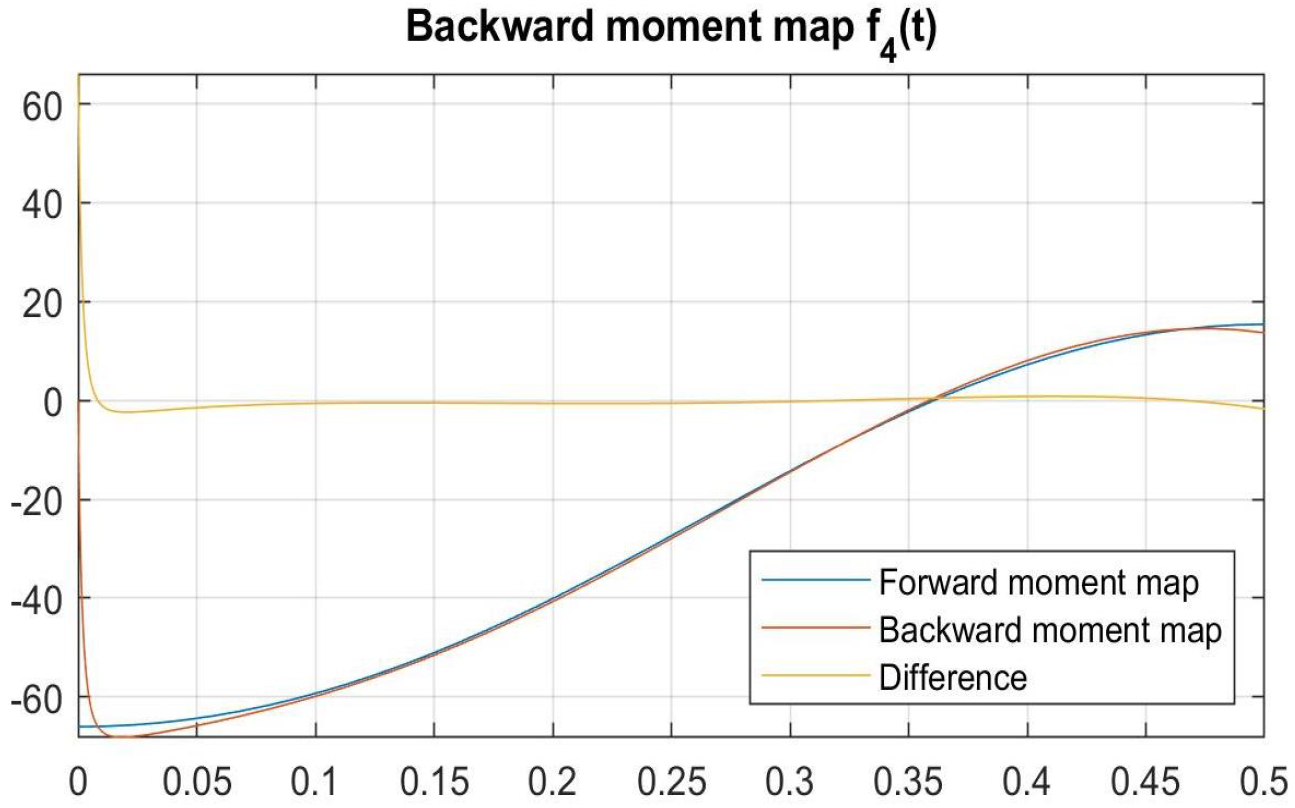
4.3. Analytical Models of Experimental Artefacts
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gajamohan, M.; Merz, M.; Thommen, I.; D’Andrea, R. The cubli: A cube that can jump up and balance. In Proceedings of the International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 3722–3727. [Google Scholar]
- Gajamohan, M.; Muehlebach, M.; Widmer, T.; D’Andrea, R. The cubli: A reaction wheel based 3d inverted pendulum. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 268–274. [Google Scholar]
- Muehlebach, M.; Mohanarajah, G.; D’Andrea, R. Nonlinear analysis and control of a reaction wheel-based 3d inverted pendulum. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 1283–1288. [Google Scholar]
- Muehlebach, M.; D’Andrea, R. Nonlinear analysis and control of a reaction- wheel-based 3-d inverted pendulum. IEEE Trans. Control Syst. Technol. 2017, 25, 235–246. [Google Scholar] [CrossRef]
- Lundberg, K.H.; Barton, T.W. History of inverted-pendulum systems. IFAC Proc. Vol. 2010, 42, 131–135. [Google Scholar] [CrossRef]
- Boubaker, O. The inverted pendulum: A fundamental benchmark in control theory and robotics. In Proceedings of the International Conference on Education and e-Learning Innovations, Sousse, Tunisia, 1–3 July 2012; pp. 1–6. [Google Scholar]
- Hofer, M.; Muehlebach, M.; D’Andrea, R. The one-wheel cubli: A 3d inverted pendulum that can balance with a single reaction wheel. Mechatronics 2023, 91, 102965. [Google Scholar] [CrossRef]
- Li, Z.; Yang, C.; Fan, L. (Eds.) Advanced Control of Wheeled Inverted Pendulum Systems, 1st ed.; Springer: London, UK, 2013. [Google Scholar]
- Boubaker, O.; Iriarte, R. (Eds.) The Inverted Pendulum in Control Theory and Robotics: From theory to new innovations. In Control, Robotics and Sensors; Institution of Engineering and Technology: Stevenage, UK, 2017. [Google Scholar]
- Altenburger, R.; Henrici, A.; Robbiani, M. Analytical solution of an ill-posed system of nonlinear ode’s. Commun. Nonlinear Sci. Numer. Simul. 2024, 130, 107762. [Google Scholar] [CrossRef]
- Smith, T. Mri artifacts and correction strategies. Imaging Med. 2010, 2, 445–457. [Google Scholar] [CrossRef]
- Xie, S.; Zheng, X.; Chen, Y.; Xie, L.; Liu, J.; Zhang, Y.; Yan, J.; Zhu, H.; Hu, Y. Artifact removal using improved googlenet for sparse-view ct reconstruction. Sci. Rep. 2018, 8, 6700. [Google Scholar] [CrossRef]
- Jiang, X.; Bian, G.-B.; Tian, Z. Removal of artifacts from eeg signals: A review. Sensors 2019, 19, 987. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.S.; Lee, K.; Kang, G. Eeg artifact removal by bayesian deep learning & ica. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 932–935. [Google Scholar]
- Nie, Y.; Guo, X.; Li, X.; Geng, X.; Quan, Z.; Zhu, G.; Yin, Z.; Zhang, J.; Wang, S. Real-time removal of stimulation artifacts in closed-loop deep brain stimulation. J. Neural Eng. 2021, 18. [Google Scholar] [CrossRef]
- Bertazzoli, G.; Esposito, R.; Mutanen, T.P.; Ferrari, C.; Ilmoniemi, R.J.; Miniussi, C.; Bortoletto, M. The impact of artifact removal approaches on tms–eeg signal. NeuroImage 2021, 239, 118272. [Google Scholar] [CrossRef]
- Ouyang, G.; Dien, J.; Lorenz, R. Handling eeg artifacts and searching individually optimal experimental parameter in real time: A system development and demonstration. J. Neural Eng. 2022, 19, 016016. [Google Scholar] [CrossRef]
- Chen, P.; Kim, T.; Rijn, E.D.; Provenza, N.R.; Sheth, S.A.; Goodman, W.K.; Borton, D.A.; Harrison, M.T.; Darbon, J. Periodic artifact removal with applications to deep brain stimulation. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 2692–2699. [Google Scholar] [CrossRef] [PubMed]
- Bahador, N.; Saha, J.; Rezaei, M.R.; Utpal, S.; Ghahremani, A.; Chen, R.; Lankarany, M. Robust removal of slow artifactual dynamics induced by deep brain stimulation in local field potential recordings using svd-based adaptive filtering. Bioengineering 2023, 10, 719. [Google Scholar] [CrossRef]
- Wang, F.; Chen, X.; Roelfsema, P.R. Comparison of electrical microstimulation artifact removal methods for high-channel-count prostheses. J. Neurosci. Methods 2024, 408, 110169. [Google Scholar] [CrossRef] [PubMed]
- Chuang, C.-H.; Chang, K.-Y.; Huang, C.-S.; Bessas, A.-M. Art: Artifact removal transformer for reconstructing noise-free multichannel electroencephalographic signals. arXiv 2024, arXiv:2409.07326. [Google Scholar]
- Gransier, R.; Carlyon, R.; Richardson, M.; Middlebrooks, J.; Wouters, J. Artifact removal by template subtraction enables recordings of the frequency following response in cochlear-implant users. Sci. Rep. 2024, 14, 6158. [Google Scholar] [CrossRef]
- Yan, P.; Abdulkadir, A.; Luley, P.-P.; Rosenthal, M.; Schatte, G.A.; Grewe, B.F.; Stadelmann, T. A comprehensive survey of deep transfer learning for anomaly detection in industrial time series: Methods, applications, and directions. IEEE Access 2024, 12, 3768–3789. [Google Scholar] [CrossRef]
- Darban, Z.Z.; Webb, G.I.; Pan, S.; Aggarwal, C.; Salehi, M. Deep learning for time series anomaly detection: A survey. ACM Comput. Surv. 2024, 57, 1–42. [Google Scholar] [CrossRef]
- Kassel, G. A formal ontology of artefacts. Appl. Ontol. 2010, 5, 223–246. [Google Scholar] [CrossRef]
- Keaveny, T.M.; Borchers, R.E.; Gibson, L.J.; Hayes, W.C. Theoretical analysis of the experimental artifact in trabecular bone compressive modulus. J. Biomech. 1993, 26, 599–607. [Google Scholar] [CrossRef]
- Nakano, T.; Nakashima, Y. Analytical expressions for the reconstructed image of a homogeneous cylindrical sample exhibiting a beam hardening artifact in x-ray computed tomography. J. X-Ray Sci. Technol. 2018, 26, 1–15. [Google Scholar] [CrossRef]
- Miller, M.S.; Straight, C.R.; Palmer, B.M. Inertial artifact in viscoelastic measurements of striated muscle: Modeling and experimental results. Biophys. J. 2022, 121, 1424–1434. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.; Kaplan, M.; Haque, M.R.; Osman, M.S.; Baleanu, D. A variety of novel exact solutions for different models with the conformable derivative in shallow water. Front. Phys. 2020, 8, 177. [Google Scholar] [CrossRef]
- Fadhal, E.; Akbulut, A.; Kaplan, M.; Awadalla, M.; Abuasbeh, K. Extraction of exact solutions of higher order sasa-satsuma equation in the sense of beta derivative. Symmetry 2022, 14, 2390. [Google Scholar] [CrossRef]
- Wang, X.; Javed, S.A.; Majeed, A.; Kamran, M.; Abbas, M. Investigation of exact solutions of nonlinear evolution equations using unified method. Mathematics 2022, 10, 2996. [Google Scholar] [CrossRef]
- Neto, J.G.M.N.; Fonseca, E.J.; Jesus-Silva, A.J. Exact solutions for non-rayleigh nondiffracting speckles. Phys. Rev. A 2022, 106, 053519. [Google Scholar] [CrossRef]


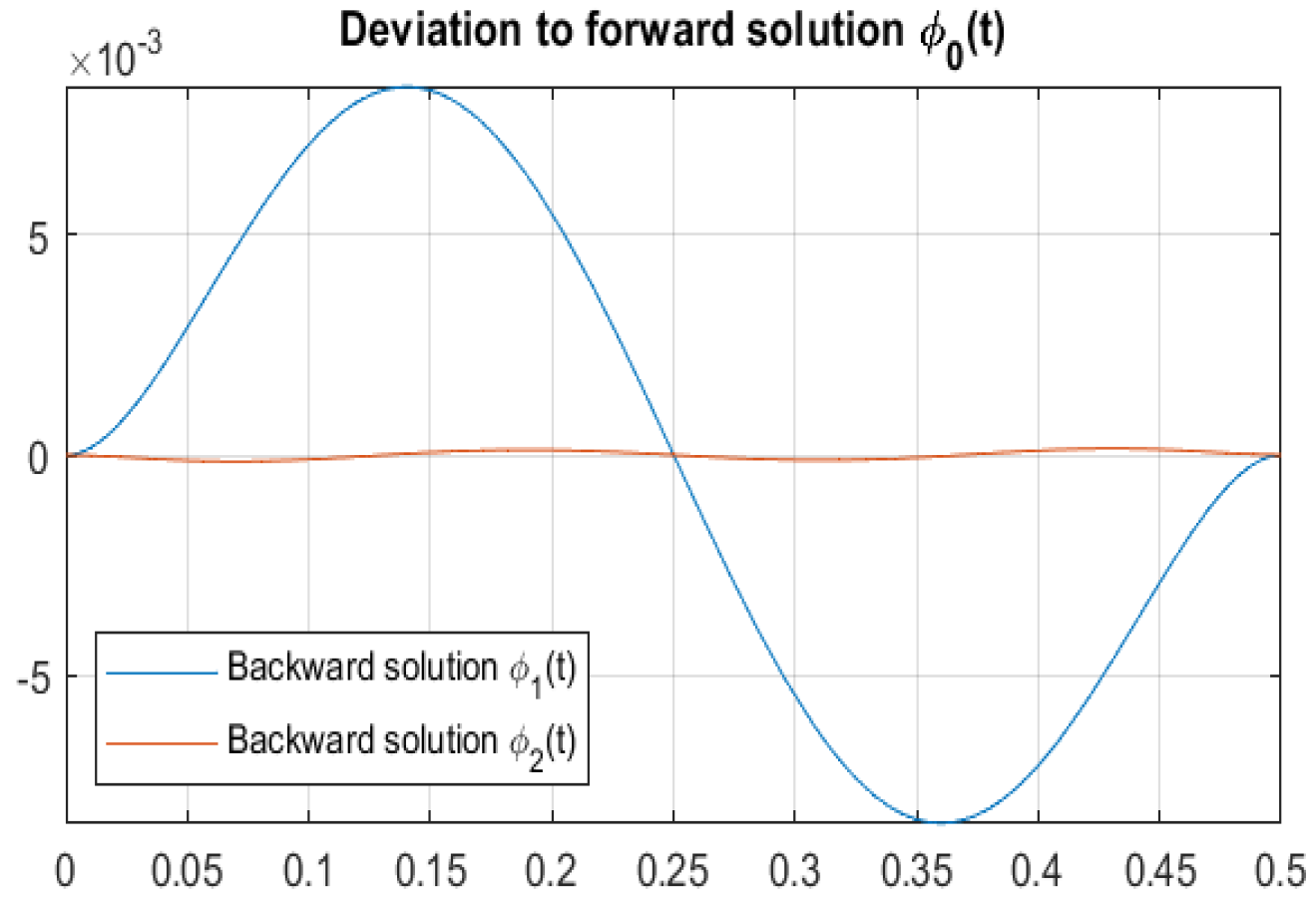

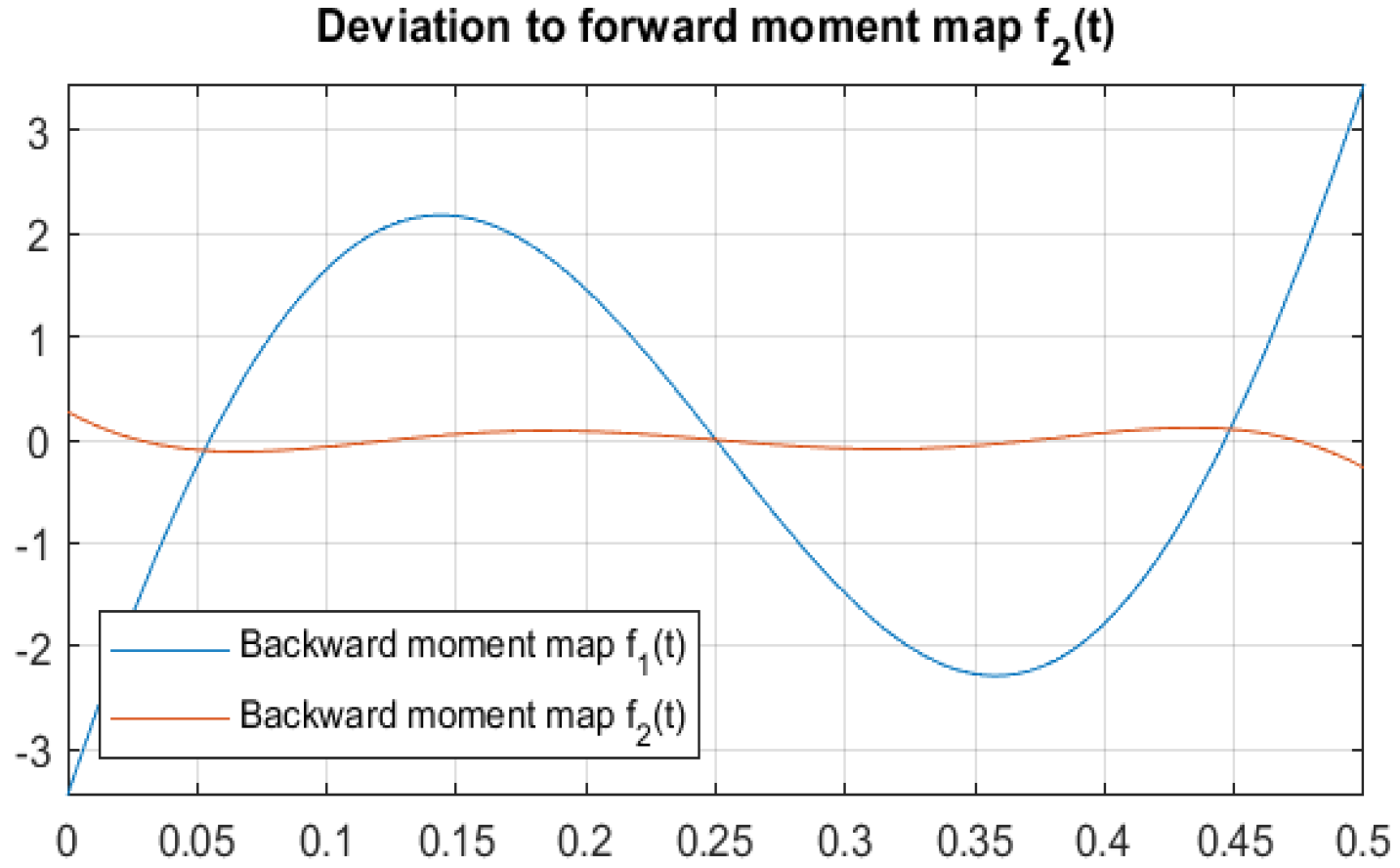

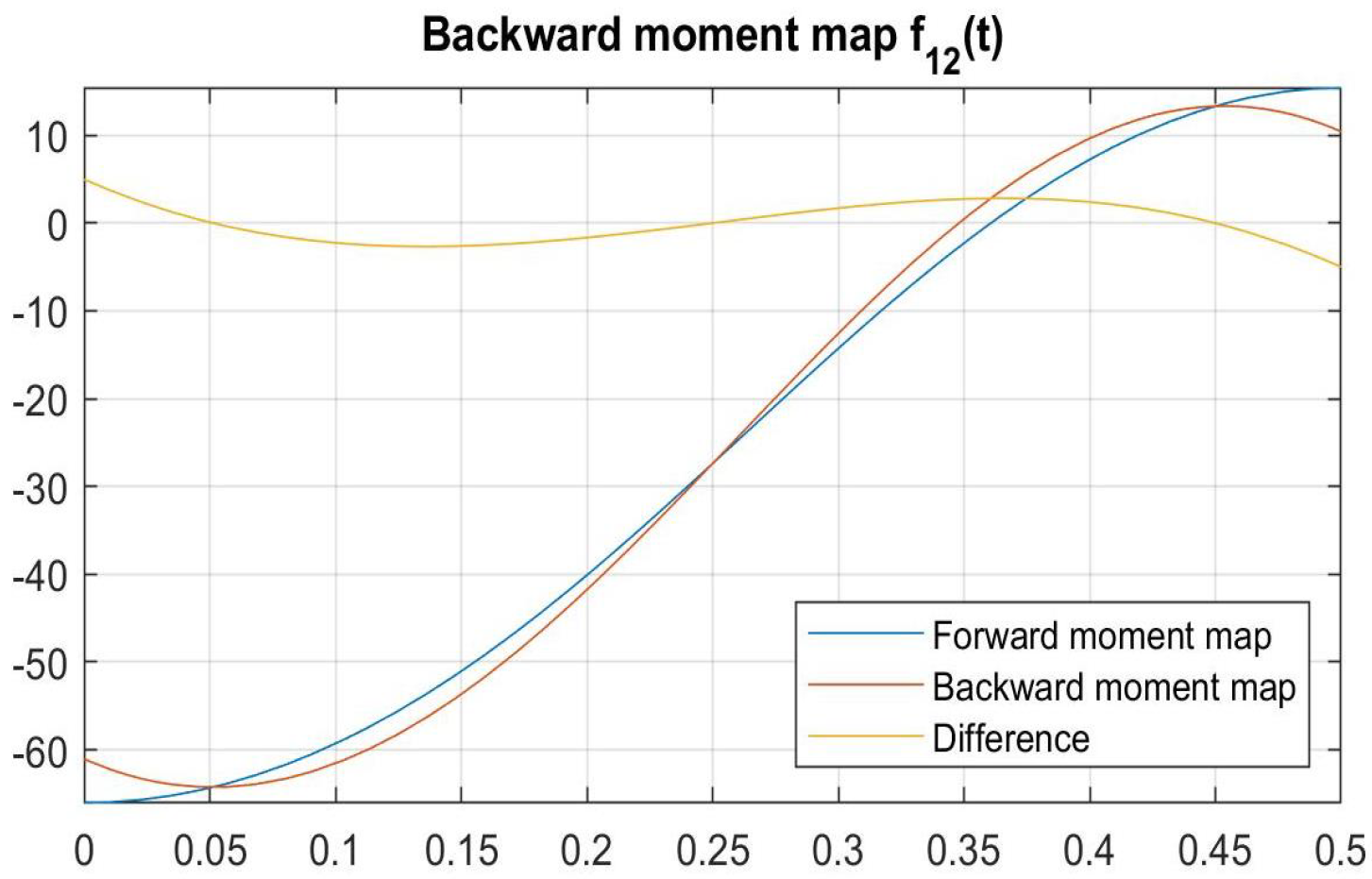
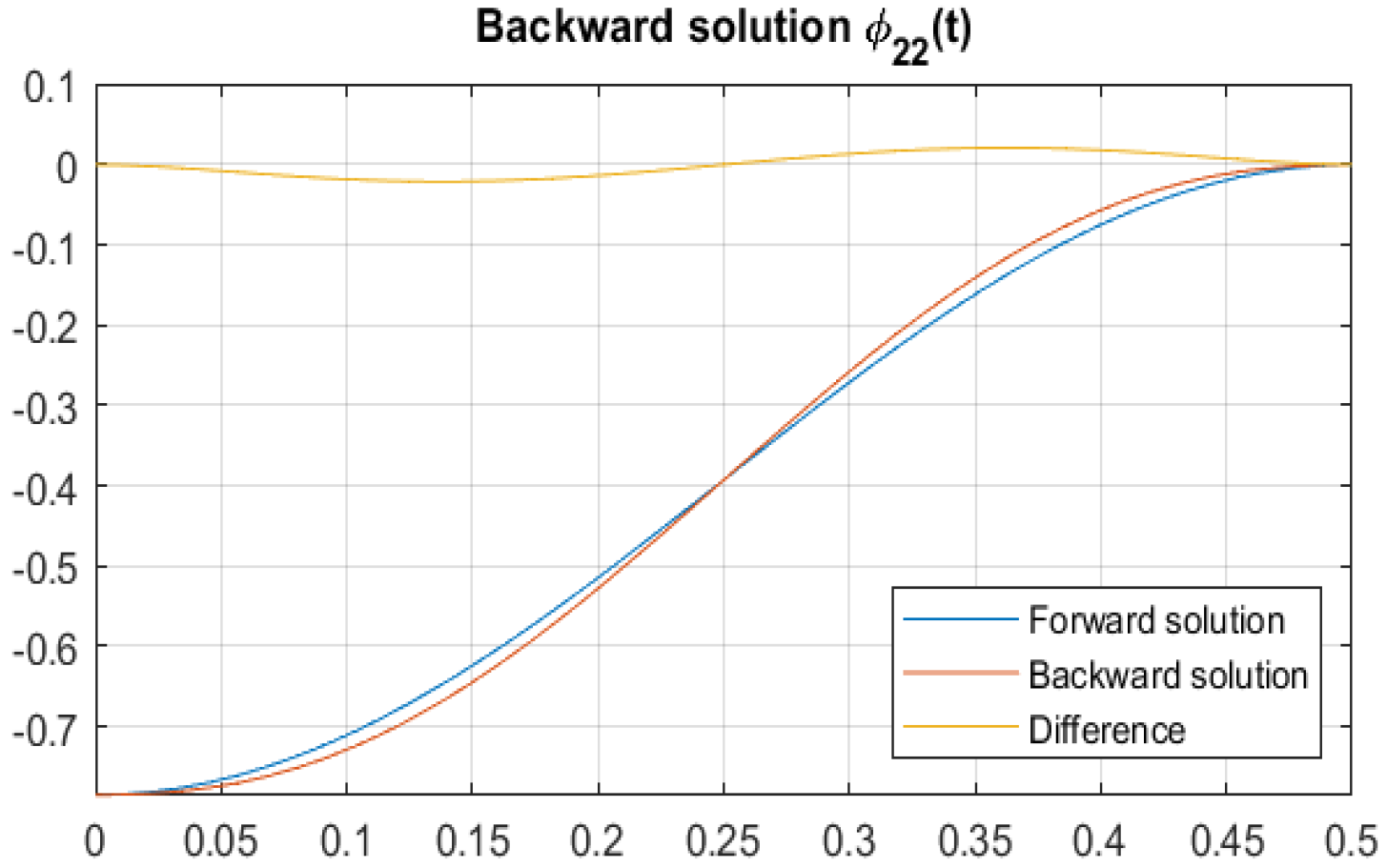



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Henrici, A.; Robbiani, M. Analytical Models of Experimental Artefacts in an Ill-Posed Nonlinear ODE System. Mathematics 2024, 12, 3675. https://doi.org/10.3390/math12233675
Henrici A, Robbiani M. Analytical Models of Experimental Artefacts in an Ill-Posed Nonlinear ODE System. Mathematics. 2024; 12(23):3675. https://doi.org/10.3390/math12233675
Chicago/Turabian StyleHenrici, Andreas, and Marcello Robbiani. 2024. "Analytical Models of Experimental Artefacts in an Ill-Posed Nonlinear ODE System" Mathematics 12, no. 23: 3675. https://doi.org/10.3390/math12233675
APA StyleHenrici, A., & Robbiani, M. (2024). Analytical Models of Experimental Artefacts in an Ill-Posed Nonlinear ODE System. Mathematics, 12(23), 3675. https://doi.org/10.3390/math12233675





