Adaptive Fault-Tolerant Tracking Control for Continuous-Time Interval Type-2 Fuzzy Systems

Abstract

This paper investigated the tracking problem of mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ adaptive fault-tolerant control (FTC) for continuous-time interval type-2 fuzzy systems (IT2FSs). For the membership function mismatch and uncertainty between the modules of the nonlinear system, the IT2 fuzzy model is applied to linearly approximate it. The observer can sensitively estimate the system state, and the adaptive fault estimation functions can estimate adaptively the fault signals, which enables the designed adaptive FTC scheme to ensure the asymptotic stability of the closed-loop control system and achieve the desired mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ tracking performance. The designed adaptive control law can achieve the purpose of dynamic compensation for faults and disturbances, and the introduced lemmas further reduce the design conservatism by adjusting the slack parameters and matrices. Finally, a mass-spring-damping system is used to illustrate the effectiveness of the designed method.

1. Introduction

As the automatic control systems tend to be large scale, randomized and complicated, the probability of faults caused by the long-term operation of system components or improper human operation is increasing greatly. Therefore, how to quickly detect a fault and repair it, or design a fault tolerance scheme to make the practical system able to tolerate a certain degree and type of fault, to achieve the purpose of fault tolerance control, has always been a hot research spot in the control field [1]. Among these, model-based fault detection makes full use of the deep knowledge inside the system and determines whether the fault occurs by residual error [2]. Then, to ensure the automatic control system is stable and reduce the impact of faults on the system performance, some targeted FTC strategies are studied [3,4,5,6,7,8,9,10]. Considering that active FTC relies too much on the fault detection module, it is easy to cause delay when reconstructing a controller according to detection results, which affects system performance [4,5,6]. Passive FTC is widely used because of its simple design, easy implementation and good real-time performance [7,8,9,10]. However, due to its conservative design and low tolerance to unknown faults, adaptive FTC can adjust its own characteristic feedback control system in real time and intelligently according to the specific fault affecting the system so that the system can work in the optimal state according to some set standards [11,12,13,14,15,16,17,18,19]. For example, ref. [13] proposed a kind of robust adaptive FTC circuit design and converted to analog control circuit implementation. The adaptive FTC strategy for an actuator fault in [12,18] has a good fault-tolerant effect. For unexpected fault situations in multi-agent systems, ref. [15] designed an compensation protocol and ${\mathcal{H}}_{\infty }$ resilient control scheme to adaptively achieve optimal control results. By designing the tracking controller, the adaptive optimal tracking problem with the FTC method of a multi-agent system and active FTC tracking problem with input constraint are embodied in [19,20], respectively. However, there are few achievements on adaptive FTC for IT2 nonlinear systems with sensor and actuator faults.

Tracking control is used to achieve the purpose of tracking the desired trajectory or path through the control system [19,20,21,22,23,24,25]. At present, attitude tracking in aerospace [22], trajectory tracking in robotics [23] and path tracking in the field of automatic driving [24,25] have a wide range of applications. Therefore, in these real-environmental applications, when the sensor or actuator failure occurs, the tracking control effect will be greatly reduced and the system may even be unstable or collapse. The adaptive fault-tolerant tracking control can realize the tracking control under the fault condition, and the control signal can be adjusted adaptively to achieve a better tracking effect. In order to achieve a better tracking effect, we generally define some quantitative indicators to describe the system performance and give their characterization and calculation methods. Examples include peak-to-peak, energy-to-energy (${\mathcal{H}}_{\infty }$), energy-to-peak ($L_2-L_{\infty }$ [26,27]), and so on. Among them, ${\mathcal{H}}_{\infty }$ can ensure the robust stability of the system, and $L_2-L_{\infty }$ is suitable for the scenario where the energy of the external interference signal is bounded and the peak value of the practical system output signal is bounded. These two kinds of performance indicators have their own application background, so if the tracking controller is designed to meet the performance requirements at the same time, it will have a wider application prospect [28,29]. For a memory neural networks system, there exist state estimation problems caused by delay and bounded perturbation. Based on the protocol, ref. [28] proposed a finite horizon mixed performance estimation method. Ref. [29] studied the hybrid control problem of measuring outliers in observer-based IT2FSs. But at present, there exist few such achievements, especially on the fuzzy system of fault-tolerant control, which is the original intention of this paper.

Note that system nonlinearity is inevitable in practical engineering in addition to other forms of nonlinear description ([30,31]). The T–S fuzzy model [32], as an effective tool, can approximate nonlinear systems through some local linear time-invariant systems, thus introducing traditional linear system theory into the study of nonlinear systems [33]. However, the type-1 T–S fuzzy model only has a good effect on dealing with system nonlinearity; if the membership function in the T–S fuzzy model contains uncertain information [9], the type-1 fuzzy model will be overwhelmed.

Based on this, the IT2 fuzzy model proposed in [34] effectively solves the above problems by defining upper and lower bound membership functions. Inspired by this, many interesting and meaningful research results have appeared successively, enriching the relevant achievements of fuzzy control and fuzzy filtering [9,25,35,36,37,38,39,40]. For example, by establishing the IT2 fuzzy model, ref. [25] effectively approximated the tire dynamic nonlinearity and speed variation in the path tracking control system and studied the path tracking control problem of autonomous ground vehicles under handover trigger and sensor attack. Ref. [36] studied the sampling exponential stability and nonlinear control of IT2 fuzzy systems. Based on event-driven faults, ref. [37] discussed the FD problem for IT2 fuzzy systems. Ref. [38] proposed an event-based control method for IT2FSs with fading channels. Ref. [39] studied a multistep model predictive control problem for IT2FSs subject to event-triggered faults. In this kind of research, FTC is indispensable in the study of fault handling, especially the membership function mismatch caused by many modules in adaptive FTC. In an IT2 fuzzy system, refs. [9,40] obtained appropriate FTC schemes for finite-time dynamic event-triggered and adaptive sliding mode control, respectively. However, the research content of other FTC problems of IT2 fuzzy systems is relatively small, which is the driving force of this paper.

Driven by the above considerations, this paper studies the tracking problem of mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ adaptive FTC for continuous-time IT2FSs. Fully considering the mismatch and uncertainty of the membership function between systems, the faults estimate functions in observer and adaptive law in the controller, ensuring stricter system stability and performance requirements. The main innovations are summarized:

• Considering the membership function mismatch and uncertainty of each part in the practical system, the proposed design scheme is aimed at the tracking problem of a mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ adaptive FTC for continuous-time IT2FSs.
• Compared with the general adaptive FTC scheme in [11,13], the adaptive control function is improved in this paper, which is simultaneously tolerant of the sensor and the actuator faults. Based on the adaptive signal, the dynamic parameters in the disturbance compensation term can be dynamically adjusted to achieve a better FTC effect.
• Mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ performance is considered in the design of the fuzzy tracking controller and observer to meet a wider range of practical requirements. Based on the matrix inequality transformation technique in the lemmas, the designed algorithm reduces conservatism by introducing suitable slack variables and matrices in the theorem.

The rest of this paper is organized as follows. The problem statement and preliminary is formulated in Section 2. The main results about adaptive FTC system performance analysis and the design control strategy are presented in Section 3 and Section 4, respectively. In Section 5, a mass-spring-damping system is used to illustrate the effectiveness of the designed method. Finally, Section 6 summarizes this paper.

2. Problem Statement and Preliminarie

In the real-environment application, due to the membership function mismatch and uncertainty between the modules of the fuzzy system, as well as the possible sensor and actuator faults in the system, this paper uses the IT2FSs to model the system, observer and controller. Moreover, in order to realize tracking control, a reference system is introduced.

2.1. Continuous-Time IT2FSs

In this section, similar to [9,37], the continuous-time IT2FSs with m fuzzy rules are expressed as

Rule i: If ${\varphi }_1\left(x\left(t\right)\right)$ is ${\mathcal{M}}_1^i$, ⋯, and ${\varphi }_{𝚤}\left(x\left(t\right)\right)$ is ${\mathcal{M}}_{𝚤}^i$, then

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)& =A_{i}x\left(t\right)+B_i{u}_f\left(t\right)+E_{i}w\left(t\right)+F_i{f}_a\left(t\right)\hfill \\ \hfill y\left(t\right)& =C_{i}x\left(t\right)+G_i{f}_s\left(t\right)\hfill \end{array}$$

(1)

where ${\mathcal{M}}_{\alpha }^i$ is an IT2 fuzzy set of the i-th fuzzy rule with the function ${\varphi }_{\alpha }\left(x\left(t\right)\right)$ where $i=1,2,\cdots ,m$ and $\alpha =1,2,\cdots$, ı. m and ı are the positive integers; $x\left(t\right)\in R^{n_x}$, $u_f\left(t\right)\in R^{n_u}$, $y\left(t\right)\in R^{n_y}$ are the state variable, the control input after the system faults, and the measurement output, respectively. $w\left(t\right)\in R^{n_w}$ is the external disturbance signal in $L_2[0,\infty )$. $f_a\left(t\right)\in R^{n_f}$ and $f_s\left(t\right)\in R^{n_f}$ are the stuck fault signals from the actuator and sensor, respectively; The matrices $A_i$, $B_i$, $E_i$, $F_i$, $C_i$, $G_i$ are known proper dimensional matrices.

The firing strength of the i-th fuzzy rule satisfies

$$\begin{array}{cc}\hfill \tilde{\alpha }& =[{\underline{\alpha }}_i,{\overline{\alpha }}_i]\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {\underline{\alpha }}_i=\prod _{\alpha =1}^{𝚤}{\underline{ϵ}}_{{\mathcal{M}}_{\alpha }^i}\left({\varphi }_{\alpha }\right),{\underline{ϵ}}_{{\mathcal{M}}_{\alpha }^i}\left({\varphi }_{\alpha }\right)\in [0,1]\\ \hfill {\overline{\alpha }}_i=\prod _{\alpha =1}^{𝚤}{\overline{ϵ}}_{{\mathcal{M}}_{\alpha }^i}\left({\varphi }_{\alpha }\right),{\overline{ϵ}}_{{\mathcal{M}}_{\alpha }^i}\left({\varphi }_{\alpha }\right)\in [0,1]\\ \hfill {\underline{ϵ}}_{{\mathcal{M}}_{\alpha }^i}\left({\varphi }_{\alpha }\right)\le {\overline{ϵ}}_{{\mathcal{M}}_{\alpha }^i}\left({\varphi }_{\alpha }\right),{\underline{\alpha }}_i\le {\overline{\alpha }}_i\end{array}$$

with ${\underline{ϵ}}_{{\mathcal{M}}_{\alpha }^i}\left({\varphi }_{\alpha }\right)$ and ${\underline{\alpha }}_i$ representing the lower grade and function of membership, ${\overline{ϵ}}_{{\mathcal{M}}_{\alpha }^i}\left({\varphi }_{\alpha }\right)$ and ${\overline{\alpha }}_i$ representing the upper grade and function of membership, respectively. The global dynamic fuzzy model can be described as

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)& =\sum _{i=1}^m{g}_i[A_{i}x\left(t\right)+B_i{u}_f\left(t\right)+E_{i}w\left(t\right)+F_i{f}_a\left(t\right)]\hfill \\ \hfill y\left(t\right)& =\sum _{i=1}^m{g}_i[C_{i}x\left(t\right)+G_i{f}_s\left(t\right)]\hfill \end{array}$$

(2)

where $g_i={\underline{p}}_i{\underline{\alpha }}_i+{\overline{p}}_i{\overline{\alpha }}_i$, $\sum _{i=1}^m{g}_i=1$, while the nonlinear functions have $0\le {\underline{p}}_i\le {\overline{p}}_i\le 1$ and satisfy ${\underline{p}}_i+{\overline{p}}_i=1$.

In addition to the additive bounded faults existing in the system, the system may also have partially degenerate multiplicative faults expressed as

$${\varsigma }_f\left(t\right)=d_{\varsigma }\varsigma \left(t\right)$$

(3)

where $d_{\varsigma }\in (0,1]$ with $\varsigma =y,u$ are the fault parameters of a partially degenerate incident.

For brevity, $\tilde{\alpha }$, ${\underline{\alpha }}_i$, ${\overline{\alpha }}_i$, ${\underline{ϵ}}_{{\mathcal{M}}_{\alpha }^i}\left({\varphi }_{\alpha }\right)$, ${\overline{ϵ}}_{{\mathcal{M}}_{\alpha }^i}\left({\varphi }_{\alpha }\right)$, ${\underline{p}}_i$, ${\overline{p}}_i$, and $g_i$ are used to stand for $\tilde{\alpha }\left(x\left(t\right)\right)$, ${\underline{\alpha }}_i\left(x\left(t\right)\right)$, ${\overline{\alpha }}_i\left(x\left(t\right)\right)$, ${\underline{ϵ}}_{{\mathcal{M}}_{\alpha }^i}\left({\varphi }_{\alpha }\left(x\left(t\right)\right)\right)$, ${\overline{ϵ}}_{{\mathcal{M}}_{\alpha }^i}\left({\varphi }_{\alpha }\left(x\left(t\right)\right)\right)$, ${\underline{p}}_i\left(x\left(t\right)\right)$, ${\overline{p}}_i\left(x\left(t\right)\right)$, and $g_i\left(x\left(t\right)\right)$ in the IT2 fuzzy system. By the same token, the following symbols $\tilde{\vartheta }$, ${\underline{\vartheta }}_l$, ${\overline{\vartheta }}_l$, ${\underline{\upsilon }}_{{\mathcal{H}}_{\vartheta }^l}\left({\psi }_{\vartheta }\right)$, ${\overline{\upsilon }}_{{\mathcal{H}}_{\vartheta }^l}\left({\psi }_{\vartheta }\right)$, $s_l$, ${\underline{r}}_l$, ${\overline{r}}_l$, $\tilde{\beta }$, ${\underline{\beta }}_j$, ${\overline{\beta }}_j$, ${\underline{\epsilon }}_{{\mathcal{N}}_{\beta }^j}\left({\phi }_{\beta }\right)$, ${\overline{\epsilon }}_{{\mathcal{N}}_{\beta }^j}\left({\phi }_{\beta }\right)$, $h_j$, ${\underline{q}}_j$, and ${\overline{q}}_j$ are also abbreviations in the IT2 fuzzy observer and controller.

2.2. Reference Model

To reflect the control effect under the fault condition and to realize the tracking control, the following reference system is adopted in this paper

$$\begin{array}{c}{\dot{x}}_r\left(t\right)=A_r{x}_r\left(t\right)+B_r{i}_r\left(t\right)\\ y_r\left(t\right)=C_r{x}_r\left(t\right)\end{array}$$

(4)

where $x_r\left(t\right)\in R^{n_r}$, $y_r\left(t\right)\in R^{n_y}$, and $i_r\left(t\right)\in R^{n_i}$ are the state, the reference output and reference input of the reference model, respectively. To verify the tracking effect of the controller, $A_r$ is designed as a Hurwitz matrix. Moreover, $B_r$ and $C_r$ are known proper dimensional matrices.

2.3. IT2 Fuzzy Observer

Considering the practical engineering, the observer is nonlinear and does not match the membership function of other parts in the system. Similar to [9], to design the appropriate adaptive controller, the sensor/actuator fault values and system state are necessary to be estimated, so an IT2 fuzzy observer in the following form is designed as

Rule l: If ${\psi }_1\left(\widehat{x}\left(t\right)\right)$ is ${\mathcal{H}}_1^l$, ⋯, and ${\psi }_{\ell }\left(\widehat{x}\left(t\right)\right)$ is ${\mathcal{H}}_{\ell }^l$, then

$$\begin{array}{cc}\hfill \dot{\widehat{x}}\left(t\right)& =\sum _{i=1}^m\sum _{l=1}^m{g}_i{s}_l[A_i\widehat{x}\left(t\right)+B_i{u}_f\left(t\right)+E_{i}w\left(t\right)\hfill \\ \hfill & +F_i{\widehat{f}}_a\left(t\right)+L_{l}r\left(t\right)]\hfill \\ \hfill \widehat{y}\left(t\right)& =\sum _{i=1}^m{g}_i[C_i\widehat{x}\left(t\right)+G_i{\widehat{f}}_s\left(t\right)]\hfill \end{array}$$

(5)

where ${\mathcal{H}}_{\vartheta }^l$ is an IT2 fuzzy set of the l-th fuzzy rule with the function ${\psi }_{\vartheta }\left(\widehat{x}\left(t\right)\right)$ where $l=1,2,\cdots ,m$ and $\vartheta =1,2,\cdots ,\ell$. m and ℓ are the positive integers; $\widehat{x}\left(t\right)\in R^{n_x}$, $\widehat{y}\left(t\right)\in R^{n_y}$, and $r\left(t\right)\in R^{n_y}$ are the state, the output, and the residual vector estimated by the IT2 fuzzy observer, respectively. $L_l$ is the designed observer gain matrix. In a similar way, the firing strength of the l-th rule satisfies

$$\begin{array}{cc}\hfill \tilde{\vartheta }& =[{\underline{\vartheta }}_l,{\overline{\vartheta }}_l]\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {\underline{\vartheta }}_l=\prod _{\vartheta =1}^{\ell }{\underline{\upsilon }}_{{\mathcal{H}}_{\vartheta }^l}\left({\psi }_{\vartheta }\right),{\underline{\upsilon }}_{{\mathcal{H}}_{\vartheta }^l}\left({\psi }_{\vartheta }\right)\in [0,1]\\ \hfill {\overline{\vartheta }}_l=\prod _{\vartheta =1}^{\ell }{\overline{\upsilon }}_{{\mathcal{H}}_{\vartheta }^l}\left({\psi }_{\vartheta }\right),{\overline{\upsilon }}_{{\mathcal{H}}_{\vartheta }^l}\left({\psi }_{\vartheta }\right)\in [0,1]\\ \hfill {\underline{\upsilon }}_{{\mathcal{H}}_{\vartheta }^l}\left({\psi }_{\vartheta }\right)\le {\overline{\upsilon }}_{{\mathcal{H}}_{\vartheta }^l}\left({\psi }_{\vartheta }\right),{\underline{\vartheta }}_l\le {\overline{\vartheta }}_l\end{array}$$

where ${\underline{\upsilon }}_{{\mathcal{H}}_{\vartheta }^l}\left({\psi }_{\vartheta }\right)$ and ${\underline{\vartheta }}_l$ are the lower grade and function of membership, and ${\overline{\upsilon }}_{{\mathcal{H}}_{\vartheta }^l}\left({\psi }_{\vartheta }\right)$ and ${\overline{\vartheta }}_l$ are the upper grade and function of membership, respectively; $s_l={\displaystyle \frac{{\underline{r}}_l{\underline{\vartheta }}_l+{\overline{r}}_l{\overline{\vartheta }}_l}{{\displaystyle \sum _{j=1}^m}({\underline{r}}_l{\underline{\vartheta }}_l+{\overline{r}}_l{\overline{\vartheta }}_l)}}$, ${\displaystyle \sum _{l=1}^m}{s}_l=1$, ${\underline{r}}_l\in [0,1]$ and ${\overline{r}}_l\in [0,1]$ are the nonlinear functions and satisfy ${\underline{r}}_l+{\overline{r}}_l=1$.

Moreover, the adaptive fault information estimation functions are

$$\begin{array}{c}{\dot{\widehat{f}}}_s\left(t\right)=s\parallel {\xi }^T\left(t\right)P\mathcal{L}\parallel \\ {\dot{\widehat{f}}}_a\left(t\right)=a\parallel \zeta \left(t\right)\parallel \end{array}$$

(6)

where $\zeta \left(t\right)={\xi }^T\left(t\right)P\mathcal{B}$ and $r\left(t\right)=y_f\left(t\right)-\widehat{y}\left(t\right)$, while the estimated values of state and fault information are represented by $\widehat{x}\left(t\right)$, ${\widehat{f}}_s\left(t\right)$, and ${\widehat{f}}_a\left(t\right)$, respectively. $s,a$ are any positive constants.

2.4. IT2 Fuzzy Adaptive Tracking Controller

Based on this, an observer-based adaptive tracking controller can be proposed.

Rule j: If ${\phi }_1\left(\widehat{x}\left(t\right)\right)$ is ${\mathcal{N}}_1^j$, ⋯, and ${\phi }_{𝚥}\left(\widehat{x}\left(t\right)\right)$ is ${\mathcal{N}}_{𝚥}^j$, then

$$\begin{array}{c}\hfill u\left(t\right)={\displaystyle \sum _{j=1}^o}{h}_j[K_j\widehat{y}\left(t\right)+K_{rj}{y}_r\left(t\right)+K_a\left(t\right)]\end{array}$$

(7)

where ${\mathcal{N}}_{\beta }^j$ is an IT2 fuzzy set of the j-th fuzzy rule with the function ${\phi }_{\beta }\left(\widehat{x}\left(t\right)\right)$ where $j=1,2,\cdots ,o$ and $\beta =1,2,\cdots$, 𝚥. m and 𝚥 are the positive integers; $K_a\left(t\right)$ is the adaptive control function. $K_j$ and $K_{rj}$ are the controller gain matrices. In a similar way, the firing strength of the j-th rule satisfies

$$\begin{array}{cc}\hfill \tilde{\beta }& =[{\underline{\beta }}_j,{\overline{\beta }}_j]\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {\underline{\beta }}_j=\prod _{\beta =1}^{𝚥}{\underline{\epsilon }}_{{\mathcal{N}}_{\beta }^j}\left({\phi }_{\beta }\right),{\underline{\epsilon }}_{{\mathcal{N}}_{\beta }^j}\left({\phi }_{\beta }\right)\in [0,1]\\ \hfill {\overline{\beta }}_j=\prod _{\beta =1}^{𝚥}{\overline{\epsilon }}_{{\mathcal{N}}_{\beta }^j}\left({\phi }_{\beta }\right),{\overline{\epsilon }}_{{\mathcal{N}}_{\beta }^j}\left({\phi }_{\beta }\right)\in [0,1]\\ \hfill {\underline{\epsilon }}_{{\mathcal{N}}_{\beta }^j}\left({\phi }_{\beta }\right)\le {\overline{\epsilon }}_{{\mathcal{N}}_{\beta }^j}\left({\phi }_{\beta }\right),{\underline{\beta }}_j\le {\overline{\beta }}_j\end{array}$$

where ${\underline{\epsilon }}_{{\mathcal{N}}_{\beta }^j}\left({\phi }_{\beta }\right)$ and ${\underline{\beta }}_j$ are the lower grade and function of membership, while ${\overline{\epsilon }}_{{\mathcal{N}}_{\beta }^j}\left({\phi }_{\beta }\right)$ and ${\overline{\beta }}_j$ are the upper grade and function of membership, respectively; $h_j={\displaystyle \frac{{\underline{q}}_j{\underline{\beta }}_j+{\overline{q}}_j{\overline{\beta }}_j}{{\displaystyle \sum _{j=1}^m}({\underline{q}}_j{\underline{\beta }}_j+{\overline{q}}_j{\overline{\beta }}_j)}}$, ${\displaystyle \sum _{j=1}^o}{h}_j=1$, ${\underline{q}}_j\in [0,1]$ and ${\overline{q}}_j\in [0,1]$ are the nonlinear functions and satisfy ${\underline{q}}_j+{\overline{q}}_j=1$.

The adaptive control function is defined as

$$\begin{array}{c}\hfill K_a\left(t\right)=-{\zeta }^T\left(t\right){\displaystyle \frac{a\left(t\right)}{{\parallel \zeta \left(t\right)\parallel }^2{d}_{min}}}\end{array}$$

where

$$\begin{array}{c}{d}_{min}=min\{min\left\{d_y\right\},min\left\{d_u\right\}\}\\ a\left(t\right)= \parallel {\xi }^T\left(t\right)P\mathcal{L}\parallel {\widehat{f}}_s\left(t\right)+\parallel \zeta \left(t\right)\parallel {\widehat{f}}_a\left(t\right)+\parallel \zeta \left(t\right)\parallel \rho \left(t\right){\int }_{t_0}^t\parallel \xi \left(\tau \right)\parallel d\tau .\end{array}$$

There has $\rho \left(t\right)\ge 0$ in the compensation term $\rho \left(t\right){\int }_{t_0}^t\parallel \xi \left(\tau \right)\parallel d\tau$ to achieve the compensation effect to the system fault and disturbance.

Assumption 1. 

Similar to [13], sensor/actuator faults and disturbances can be expressed in the relevant segmented bounded functions, and it can be assumed that there exist matrices ${\overline{E}}_i$, ${\overline{F}}_i$, ${\overline{G}}_i$ and unknown constants ${\overline{\varpi }}_1$, ${\overline{\varpi }}_2$ such that the following inequality conditions were established

$$\begin{array}{c}\parallel {\varpi }_1\left(t\right)\parallel = \parallel {\overline{E}}_{i}w\left(t\right)+{\overline{F}}_i{f}_a{\left(t\right)\parallel \le \parallel \xi \left(t\right)\parallel }^{\alpha }+{\overline{\varpi }}_1\\ \parallel {\varpi }_2\left(t\right)\parallel = \parallel {\overline{G}}_i{f}_s\left(t\right)\parallel \le {\overline{\varpi }}_2\end{array}$$

where $E_i=B_i{\overline{E}}_i$, $F_i=B_i{\overline{F}}_i$ and $G_i=C_i{\overline{G}}_i$.

Remark 1. 

Different from other papers ([11,13]), the adaptive control strategy for the faults from the sensor and actuator is considered in the adaptive function, and in the compensation part of external disturbance and faults, the parameter

$$\rho \left(t\right)=\left\{\begin{array}{cc}\hfill \rho & when\xi \left(t\right)\ne 0\\ \hfill 0& when\xi \left(t\right)=0\end{array}\right.$$

with a large enough constant ρ, which will be changed according to the compensation situation. When the influence of faults and disturbances on the IT2FSs ends, the compensation can be quickly compensated, and the compensation item is 0 after the influence ends. In this way, better control can be achieved.

2.5. Adaptive FTC System

Based on the above description and definition, the constructed augmented closed-loop adaptive FTC system (in Figure 1) gives

$$\begin{array}{cc}\hfill \dot{\xi }\left(t\right)& =\sum _{i=1}^m\sum _{l=1}^m\sum _{j=1}^o{g}_i{s}_l{h}_j[(\mathcal{A}+d_u\mathcal{B}\mathcal{K})\xi \left(t\right)+{\mathcal{E}}_s{e}_s\left(t\right)\hfill \\ \hfill & +{\mathcal{E}}_a{e}_a\left(t\right)+d_u\mathcal{B}{K}_a\left(t\right)+\mathcal{B}{\varpi }_1\left(t\right)+\mathcal{L}{\varpi }_2\left(t\right)\hfill \\ \hfill & +{\mathcal{B}}_r{i}_r\left(t\right)]\hfill \\ \hfill e_y\left(t\right)& =\sum _{i=1}^m{g}_i[\mathcal{C}\xi \left(t\right)+G_i{e}_s\left(t\right)]\hfill \end{array}$$

(8)

where

$$\begin{array}{cc}\hfill \mathcal{A}& =\left[\begin{array}{ccc}{A}_i-{\overline{d}}_y{L}_l{C}_i& -d_y{L}_l{C}_i& 0\\ -{\overline{d}}_y{L}_l{C}_i& A_i-d_y{L}_l{C}_i& 0\\ 0& 0& A_r\end{array}\right],\mathcal{B}=\left[\begin{array}{c}{B}_i\\ 0\\ 0\end{array}\right]\hfill \\ \hfill \mathcal{C}& =\left[\begin{array}{ccc}{C}_i& 0& -C_r\end{array}\right],\mathcal{K}=\left[\begin{array}{ccc}{K}_j{C}_i& 0& K_{rj}{C}_r\end{array}\right],{\overline{d}}_y=1-d_y\hfill \\ \hfill \mathcal{L}& =\left[\begin{array}{c}{d}_u{B}_i{K}_j{C}_i-{\overline{d}}_y{L}_l{C}_i\\ -{\overline{d}}_y{L}_l{C}_i\\ 0\end{array}\right],{\mathcal{E}}_s=\left[\begin{array}{c}{d}_u{B}_i{K}_j{G}_i-L_l{G}_i\\ -L_l{G}_i\\ 0\end{array}\right]\hfill \\ \hfill {\mathcal{E}}_a& =\left[\begin{array}{c}0\\ F_i\\ 0\end{array}\right],{\mathcal{B}}_r=\left[\begin{array}{c}0\\ 0\\ B_r\end{array}\right],\xi \left(t\right)=\left[\begin{array}{c}\widehat{x}\left(t\right)\\ e_x\left(t\right)\\ x_r\left(t\right)\end{array}\right]\hfill \end{array}$$

with $e_y\left(t\right)=\widehat{y}\left(t\right)-y_r\left(t\right)$, $e_x\left(t\right)=\widehat{x}\left(t\right)-x\left(t\right)$, $e_s\left(t\right)={\widehat{f}}_s\left(t\right)-f_s\left(t\right)$, and $e_a\left(t\right)={\widehat{f}}_a\left(t\right)-f_a\left(t\right)$.

Figure 1. Framework of closed-loop adaptive FTC system.

Definition 1 

([29]). The adaptive FTC system (8) is said to be asymptotically stable when $\overline{w}\left(t\right)=0$, and it has the mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ performances if under the zero initial condition, with the existed matrices ${\Xi }_1\le 0,{\Xi }_2>0,{\Xi }_3\ge 0$, the following inequality holds

$${\int }_0^{t_a}J\left(t\right)dt\ge \underset{0\le t\le t_a}{sup}\left\{e_y^T\left(t\right){\Xi }_3{e}_y\left(t\right)\right\}$$

(9)

with $J\left(t\right)=e_y^T\left(t\right){\Xi }_1{e}_y\left(t\right)+{\overline{w}}^T\left(t\right){\Xi }_2\overline{w}\left(t\right)$. With the different selection of matrices, system (8) has different performance:

(1) 

The adaptive FTC system (8) has the ${\mathcal{H}}_{\infty }$ performance if ${\Xi }_1=-I,{\Xi }_2={\gamma }^{2}I,{\Xi }_3=0$.

(2) 

The adaptive FTC system (8) has the $L_2-L_{\infty }$ performance if ${\Xi }_1=0,{\Xi }_2={\gamma }^{2}I,{\Xi }_3=I$.

Lemma 1 

([41]). For the real matrices ${\mathbb{T}}_0$, ${\mathbb{T}}_1$, ${\mathbb{T}}_2$ and ${\mathbb{T}}_3$ with the proper dimensions and scalar β, the inequality ${\mathbb{T}}_0+{\mathbb{T}}_3^T{\mathbb{T}}_1{\mathbb{T}}_3<0$ holds if there exists the following situation

$$\left[\begin{array}{cc}{\mathbb{T}}_0& *\\ {\mathbb{T}}_2{\mathbb{T}}_3& -He\left\{\beta {\mathbb{T}}_2\right\}+{\beta }^2{\mathbb{T}}_1\end{array}\right]<0.$$

Lemma 2 

([33]). For the real matrices ${\mathbb{X}}_1$, ${\mathbb{X}}_2$, and real symmetric matrix ${\mathbb{X}}_0$ with the proper dimension and scalar ℘, the inequality ${\mathbb{X}}_0+He\left\{{\mathbb{X}}_1{\mathbb{X}}_2\right\}<0$ holds if there exists matrix $\mathbb{S}$ satisfying

$$\left[\begin{array}{cc}{\mathbb{X}}_0& *\\ \wp {\mathbb{X}}_1^T+\mathbb{S}{\mathbb{X}}_2& -He\{\wp \mathbb{S}\}\end{array}\right]<0.$$

3. Adaptive FTC System Performance Analysis

In the following, the sufficient conditions of asymptotic stability with the mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ performances for the adaptive FTC system (8) are provided.

Theorem 1. 

Consider the adaptive FTC system (8). If there exist matrices $P>0$ and $\Psi ={\Psi }^T$ with the given performance index γ and parameters ${\eta }_i$ such that the inequalities hold with $i=1,2,\cdots ,m;l=1,2,\cdots ,m;j=1,2,\cdots ,o$

$${\Lambda }_{ilj}-\Psi <0$$

(10)

$${\eta }_i{\Lambda }_{ili}-{\eta }_i\Psi +\Psi <0$$

(11)

$${\eta }_j{\Lambda }_{ilj}+{\eta }_i{\Lambda }_{jli}-{\eta }_j\Psi -{\eta }_i\Psi +2\Psi <0$$

(12)

$$\sum _{i=1}^m{g}_i\Gamma \le 0$$

(13)

where

$$\begin{array}{cc}\hfill {\Lambda }_{ilj}& =\left[\begin{array}{cc}{\Lambda }_1+{\mathcal{C}}^T\mathcal{C}& *\\ {\Lambda }_2+{\mathcal{G}}_1^T\mathcal{C}& {\Lambda }_3+{\mathcal{G}}_1^T{\mathcal{G}}_1\end{array}\right]\hfill \\ \hfill \Gamma & =\left[\begin{array}{cc}{\mathcal{C}}^T\mathcal{C}-P& *\\ {\mathcal{G}}_2^T\mathcal{C}& -diag\{s^{-1}I,a^{-1}I\}+{\mathcal{G}}_2^T{\mathcal{G}}_2\end{array}\right]\hfill \\ \hfill {\Lambda }_1& ={(\mathcal{A}+d_u\mathcal{B}\mathcal{K})}^{T}P+P(\mathcal{A}+d_u\mathcal{B}\mathcal{K})\hfill \\ \hfill {\Lambda }_2^T& =\left[\begin{array}{ccc}P{\mathcal{E}}_s& P{\mathcal{E}}_a& P{\mathcal{B}}_r\end{array}\right],{\mathcal{G}}_2=\left[\begin{array}{cc}{G}_i& 0\end{array}\right]\hfill \\ \hfill {\Lambda }_3& =-diag\{{\gamma }^{2}I,{\gamma }^{2}I,{\gamma }^{2}I\},{\mathcal{G}}_1=\left[\begin{array}{ccc}{G}_i& 0& 0\end{array}\right].\hfill \end{array}$$

Then, the fuzzy observer (5) and controller (7) can ensure the adaptive FTC system (8) is asymptotically stable and meets the mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ performances.

Proof. 

Consider a Lyapunov function as

$$V\left(t\right)={\xi }^T\left(t\right)P\xi \left(t\right)+s^{-1}{e}_s^2\left(t\right)+a^{-1}{e}_a^2\left(t\right).$$

(14)

Then, since $f_s\left(t\right)$ and $f_a\left(t\right)$ are the stuck faults, i.e., there has ${\dot{f}}_s\left(t\right)={\dot{f}}_a\left(t\right)=0$. The difference equation of $V\left(t\right)$ can be obtained

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)& ={\dot{\xi }}^T\left(t\right)P\xi \left(t\right)+{\xi }^T\left(t\right)P\dot{\xi }\left(t\right)+2s^{-1}{e}_s\left(t\right){\dot{e}}_s\left(t\right)\hfill \\ \hfill & +2a^{-1}{e}_a\left(t\right){\dot{e}}_a\left(t\right)\hfill \\ \hfill & ={\xi }^T\left(t\right)[{(\mathcal{A}+d_u\mathcal{B}\mathcal{K})}^{T}P+P(\mathcal{A}+d_u\mathcal{B}\mathcal{K})]\xi \left(t\right)\hfill \\ \hfill & +2{\xi }^T\left(t\right)P{\mathcal{E}}_s{e}_s\left(t\right)+2{\xi }^T\left(t\right)P{\mathcal{E}}_a{e}_a\left(t\right)+2{\xi }^T\left(t\right)P\mathcal{B}{\varpi }_1\left(t\right)\hfill \\ \hfill & +2{\xi }^T\left(t\right)P\mathcal{L}{\varpi }_2\left(t\right)+2{\xi }^T\left(t\right)P{\mathcal{B}}_r{i}_r\left(t\right)\hfill \\ \hfill & +2d_u\zeta \left(t\right)K_a\left(t\right)+2s^{-1}{e}_s\left(t\right){\dot{e}}_s\left(t\right)+2a^{-1}{e}_a\left(t\right){\dot{e}}_a\left(t\right)\hfill \\ \hfill & ={\xi }^T\left(t\right)[{(\mathcal{A}+d_u\mathcal{B}\mathcal{K})}^{T}P+P(\mathcal{A}+d_u\mathcal{B}\mathcal{K})]\xi \left(t\right)\hfill \\ \hfill & +2{\xi }^T\left(t\right)P{\mathcal{E}}_s{e}_s\left(t\right)+2{\xi }^T\left(t\right)P{\mathcal{E}}_a{e}_a\left(t\right)+2{\xi }^T\left(t\right)P\mathcal{B}{\varpi }_1\left(t\right)\hfill \\ \hfill & +2{\xi }^T\left(t\right)P\mathcal{L}{\varpi }_2\left(t\right)+2{\xi }^T\left(t\right)P{\mathcal{B}}_r{i}_r\left(t\right)\hfill \\ \hfill & +2s^{-1}{e}_s\left(t\right){\dot{e}}_s\left(t\right)+2a^{-1}{e}_a\left(t\right){\dot{e}}_a\left(t\right)\hfill \\ \hfill & -2d_u\zeta \left(t\right){\zeta }^T\left(t\right){\displaystyle \frac{a\left(t\right)}{{\parallel \zeta \left(t\right)\parallel }^2{d}_{min}}}\hfill \\ \hfill & \le {\xi }^T\left(t\right)[{(\mathcal{A}+d_u\mathcal{B}\mathcal{K})}^{T}P+P(\mathcal{A}+d_u\mathcal{B}\mathcal{K})]\xi \left(t\right)\hfill \\ \hfill & +2{\xi }^T\left(t\right)P{\mathcal{E}}_s{e}_s\left(t\right)+2{\xi }^T\left(t\right)P{\mathcal{E}}_a{e}_a\left(t\right)+2{\xi }^T\left(t\right)P\mathcal{B}{\varpi }_1\left(t\right)\hfill \\ \hfill & +2{\xi }^T\left(t\right)P\mathcal{L}{\varpi }_2\left(t\right)+2{\xi }^T\left(t\right)P{\mathcal{B}}_r{i}_r\left(t\right)\hfill \\ \hfill & +2s^{-1}{e}_s\left(t\right){\dot{e}}_s\left(t\right)+2a^{-1}{e}_a\left(t\right){\dot{e}}_a\left(t\right)-2\parallel {\xi }^T\left(t\right)P\mathcal{L}\parallel {\widehat{f}}_s\left(t\right)\hfill \\ \hfill & -2\parallel \zeta \left(t\right)\parallel {\widehat{f}}_a\left(t\right)-2\parallel \zeta \left(t\right)\parallel \rho \left(t\right){\int }_{t_0}^t\parallel \xi \left(\tau \right)\parallel d\tau .\hfill \end{array}$$

(15)

By recalling the conditions in Assumption 1, (15) is reduced as

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)& \le {\xi }^T\left(t\right)[{(\mathcal{A}+d_u\mathcal{B}\mathcal{K})}^{T}P+P(\mathcal{A}+d_u\mathcal{B}\mathcal{K})]\xi \left(t\right)\hfill \\ \hfill & +2{\xi }^T\left(t\right)P{\mathcal{E}}_s{e}_s\left(t\right)+2{\xi }^T\left(t\right)P{\mathcal{E}}_a{e}_a\left(t\right)+2{\xi }^T\left(t\right)P{\mathcal{B}}_r{i}_r\left(t\right)\hfill \\ \hfill & +2s^{-1}{e}_s\left(t\right){\dot{e}}_s\left(t\right)+2a^{-1}{e}_a\left(t\right){\dot{e}}_a\left(t\right)-2\parallel {\xi }^T\left(t\right)P\mathcal{L}\parallel {\widehat{f}}_s\left(t\right)\hfill \\ \hfill & -2\parallel \zeta \left(t\right)\parallel {\widehat{f}}_a\left(t\right)-2\parallel \zeta \left(t\right)\parallel \rho \left(t\right){\int }_{t_0}^t\parallel \xi \left(\tau \right)\parallel d\tau \hfill \\ \hfill & +{2\parallel \zeta \left(t\right)\parallel \parallel \xi \left(t\right)\parallel }^{\alpha }+2\parallel \zeta \left(t\right)\parallel {\overline{\varpi }}_1+2\parallel {\xi }^T\left(t\right)P\mathcal{L}\parallel {\overline{\varpi }}_2.\hfill \end{array}$$

(16)

Similar to [13], the following inequality will hold

$$\begin{array}{cc}\hfill & \parallel {\zeta }^T\left(t\right)\parallel {\overline{\varpi }}_1\le \parallel {\zeta }^T\left(t\right)\parallel f_a\left(t\right)\hfill \\ \hfill & \parallel {\xi }^T\left(t\right)P\mathcal{L}\parallel {\overline{\varpi }}_2\le \parallel {\xi }^T\left(t\right)P\mathcal{L}\parallel f_s\left(t\right).\hfill \end{array}$$

(17)

The nonlinear function $\rho \left(t\right){\int }_{t_0}^t\parallel \xi \left(\tau \right)\parallel d\tau$ is obviously a monotonically increasing function of the augmented vector $\xi \left(t\right)$. Therefore, when $\xi \left(t\right)>0$ holds, if the parameter $\rho$ is large enough, and if the parameter $\alpha \le 2$ exists, one obtains

$$\begin{array}{c}\hfill {\parallel \xi \left(t\right)\parallel }^{\alpha }\le \rho \left(t\right){\int }_{t_0}^t\parallel \xi \left(\tau \right)\parallel d\tau .\end{array}$$

(18)

Then, combining (6), (17), and (18), the inequality (16) is reduced as

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)& \le {\xi }^T\left(t\right)[{(\mathcal{A}+d_u\mathcal{B}\mathcal{K})}^{T}P+P(\mathcal{A}+d_u\mathcal{B}\mathcal{K})]\xi \left(t\right)\hfill \\ \hfill & +2{\xi }^T\left(t\right)P{\mathcal{E}}_s{e}_s\left(t\right)+2{\xi }^T\left(t\right)P{\mathcal{E}}_a{e}_a\left(t\right)+2{\xi }^T\left(t\right)P{\mathcal{B}}_r{i}_r\left(t\right).\hfill \end{array}$$

(19)

Similar to [9], by introducing $\overline{\xi }\left(t\right)={\left[\begin{array}{cc}{\xi }^T\left(t\right)& {\overline{w}}^T\left(t\right)\end{array}\right]}^T$ with $\overline{w}\left(t\right)={\left[\begin{array}{ccc}{e}_s^T\left(t\right)& e_a^T\left(t\right)& i_r^T\left(t\right)\end{array}\right]}^T$ and the slack matrix $\Psi ={\Psi }^T$, based on the membership function information and its characters, there exists ${\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{l=1}^m}{\displaystyle \sum _{j=1}^o}{g}_i{s}_l\times (s_j-h_j)\Psi ={\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{l=1}^m}({\displaystyle \sum _{j=1}^o}{s}_j-{\displaystyle \sum _{j=1}^o}{h}_j)\Psi ={\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{l=1}^m}(1-1)\Psi =0$. One has

$$\begin{array}{cc}\hfill & \sum _{i=1}^m\sum _{l=1}^m\sum _{j=1}^o{g}_i{s}_l{h}_j{\overline{\xi }}^T\left(t\right){\Lambda }_{ilj}\overline{\xi }\left(t\right)\hfill \\ \hfill & +\sum _{i=1}^m\sum _{l=1}^m\sum _{j=1}^o{g}_i{s}_l\times (s_j-h_j)\Psi \hfill \\ \hfill \le & \sum _{i=1}^m\sum _{l=1}^m{g}_i{g}_i\left(\widehat{x}\left(t\right)\right)s_l{\overline{\xi }}^T\left(t\right)({\eta }_i{\Lambda }_{ili}-{\eta }_i\Psi +\Psi )\overline{\xi }\left(t\right)\hfill \\ \hfill & +\sum _{i=1}^m\sum _{l=1}^m\sum _{j=1}^o{g}_i{s}_l(h_j-{\eta }_i{g}_j)\overline{\xi }\left(t\right)({\Lambda }_{ilj}-\Psi ){\overline{\xi }}^T\left(t\right)\hfill \\ \hfill & +\sum _{i=1}^m\sum _{l=1}^m\sum _{i<j}{g}_i{s}_l{h}_j\times {\overline{\xi }}^T\left(t\right)({\eta }_j{\Lambda }_{ilj}+{\eta }_i{\Lambda }_{jli}-{\eta }_j\Psi \hfill \\ \hfill & -{\eta }_i\Psi +2\Psi )\overline{\xi }\left(t\right).\hfill \end{array}$$

(20)

Furthermore, using congruence properties in (10)–(12) yields

$$\begin{array}{c}\hfill \dot{V}\left(t\right)-J\left(t\right)<0.\end{array}$$

(21)

If the given matrices ${\Xi }_1=-I,{\Xi }_2={\gamma }^{2}I$, the above inequality is reduced to

$$\begin{array}{c}\hfill \dot{V}\left(t\right)+e_y^T\left(t\right)e_y\left(t\right)-{\gamma }^2{\overline{w}}^T\left(t\right)\overline{w}\left(t\right)<0.\end{array}$$

(22)

When external input variable $\overline{w}\left(t\right)=0$, with the situation of $e_y^T\left(t\right)e_y\left(t\right)>0$, that means $\dot{V}\left(t\right)<0$, so the adaptive FTC system (8) is asymptotically stable.

When external input variable $\overline{w}\left(t\right)\ne 0$, under zero initial conditions, integral from 0 to $t_a$ at both ends of the inequality (22), one obtains

$$\begin{array}{c}\hfill {\int }_0^{t_a}J\left(\tau \right)d\tau >V\left(t_a\right)-V\left(0\right)=V\left(t_a\right)\end{array}$$

(23)

with the condition $V\left(t_a\right)\ge 0$ and ${\Xi }_3=0$, the ${\mathcal{H}}_{\infty }$ performance condition ${\int }_0^{t_a}{e}_y^T\left(t\right)e_y\left(t\right)d\tau <{\gamma }^2{\int }_0^{t_a}{\overline{w}}^T\left(t\right)\overline{w}\left(t\right)d\tau$ is obtained.

In addition, using congruence properties with ${\Xi }_1=0$, ${\Xi }_2={\gamma }^{2}I$, ${\Xi }_4=I$, and $\widehat{\xi }\left(t\right)={\left[\begin{array}{ccc}{\xi }^T\left(t\right)& e_s^T\left(t\right)& e_a^T\left(t\right)\end{array}\right]}^T$ to inequality (13) yields

$$\begin{array}{cc}\hfill & e_y^T\left(t\right)e_y\left(t\right)-[{\xi }^T\left(t\right)P\xi \left(t\right)+s^{-1}{e}_s^T\left(t\right)e_s\left(t\right)\hfill \\ \hfill & +a^{-1}{e}_a^T\left(t\right)e_a\left(t\right)]\hfill \\ \hfill & =e_y^T\left(t\right)e_y\left(t\right)-V\left(t\right)\le 0.\hfill \end{array}$$

(24)

Furthermore, with the situation $0\le t\le t_a$, one has

$$\begin{array}{c}\hfill e_y^T\left(t_a\right)e_y\left(t_a\right)-V\left(t_a\right)\le 0.\end{array}$$

(25)

By combining inequality (23), we can obtain the result

$$\begin{array}{c}\hfill \underset{0\le t\le t_a}{sup}\left\{e_y^T\left(t\right)e_y\left(t\right)\right\}\le {\gamma }^2{\int }_0^{t_a}{\overline{w}}^T\left(t\right)\overline{w}\left(t\right)d\tau \end{array}$$

which implies that the system (8) satisfies $L_2-L_{\infty }$ performance. The proof is completed. □

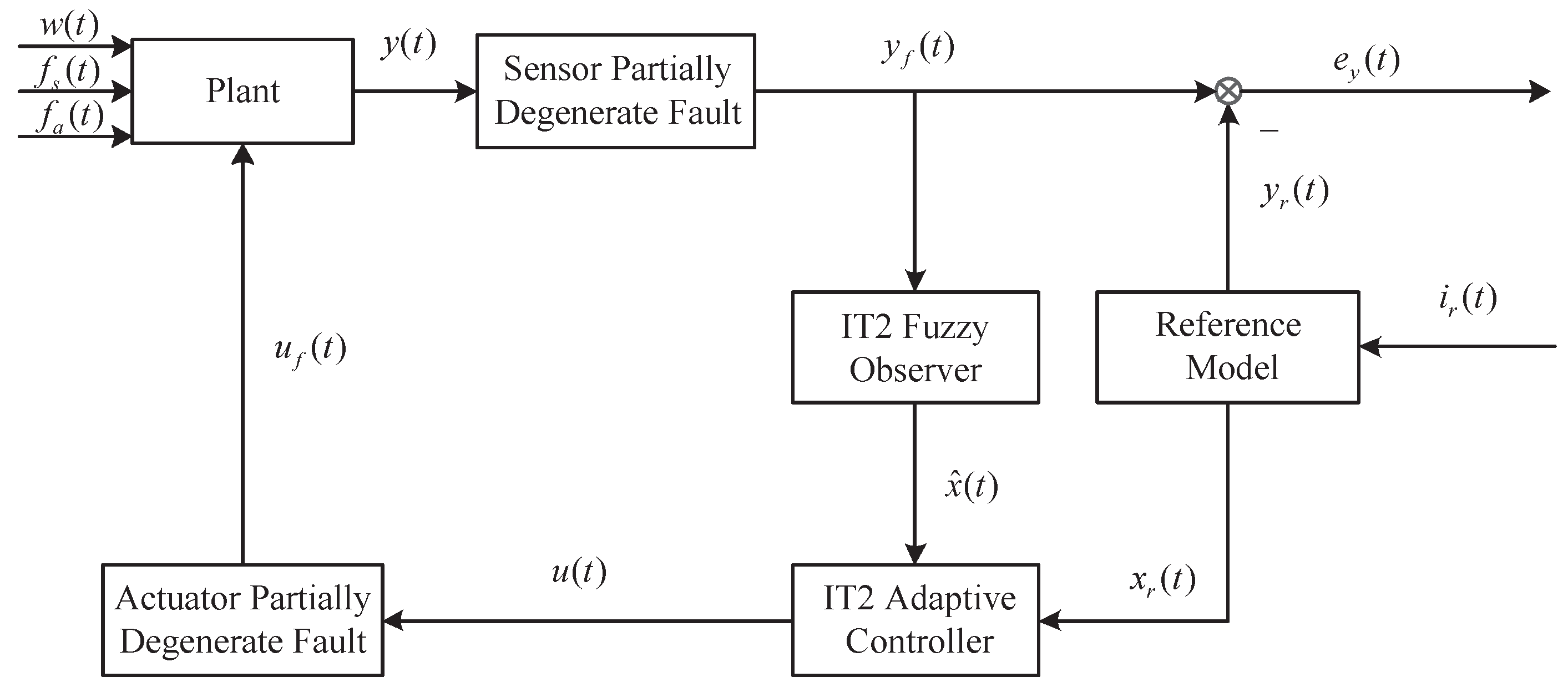
4. Fuzzy Observer and Controller Design

The nonlinear coupling terms in Theorem 1 mean that the unknown observer and controller gain matrices cannot be solved directly, so they need to be designed and obtained through the following theorem obtained by some lemmas.

Theorem 2. 

Consider the adaptive FTC system (8). For given performance index γ, positive parameters ${\beta }_1$, ${\beta }_2$, ℘, ${\eta }_i$, partial degradation failure coefficients $d_y$, $d_u$, if there exist matrices $P_1>0$, $P_2>0$, ${\overline{L}}_l$, ${\overline{K}}_j$, ${\overline{K}}_{rj}$, S, ${\mathbb{T}}_2^1$, ${\mathbb{T}}_2^2$, and $\overline{\Psi }={\overline{\Psi }}^T$ such that the inequalities hold with $i=1,2,\cdots ,m;l=1,2,\cdots ,m;j=1,2,\cdots ,o$

$${\widehat{\Lambda }}_{ilj}-\overline{\Psi }<0$$

(26)

$${\eta }_i{\widehat{\Lambda }}_{ili}-{\eta }_i\overline{\Psi }+\overline{\Psi }<0$$

(27)

$${\eta }_j{\widehat{\Lambda }}_{ilj}+{\eta }_i{\widehat{\Lambda }}_{jli}-{\eta }_j\overline{\Psi }-{\eta }_i\overline{\Psi }+2\overline{\Psi }<0$$

(28)

$$\sum _{i=1}^m{g}_i\overline{\Gamma }\le 0$$

(29)

where

$$\begin{array}{cc}\hfill {\widehat{\Lambda }}_{ilj}& =\left[\begin{array}{cc}{\overline{\mathbb{X}}}_0& *\\ \wp {\overline{\mathbb{X}}}_1^T+\mathbb{S}{\overline{\mathbb{X}}}_2& -He\{\wp \mathbb{S}\}\end{array}\right],{\widehat{\mathbb{X}}}_0=\left[\begin{array}{cc}{\overline{\mathbb{X}}}_{01}& *\\ {\overline{\mathbb{X}}}_{02}& {\Lambda }_3\end{array}\right]\hfill \\ \hfill {\overline{\mathbb{X}}}_0& =\left[\begin{array}{cc}{\widehat{\mathbb{X}}}_0& *\\ {\mathbb{T}}_2^1{\mathbb{T}}_3^1& -He\left\{{\beta }_1{\mathbb{T}}_2^1\right\}+{\beta }_1^{2}I\end{array}\right]\hfill \\ \hfill {\overline{\mathbb{X}}}_{01}& =\left[\begin{array}{ccc}{\overline{X}}_1& *& *\\ {\overline{X}}_2& {\overline{X}}_3& *\\ C_r^T{\overline{K}}_{rj}^T{B}_i^T& 0& He\left\{P_2{A}_r\right\}\end{array}\right]\hfill \\ \hfill {\overline{X}}_1& =He\{P_1{A}_i-{\overline{d}}_y{\overline{L}}_l{C}_i+B_i{\overline{K}}_j{C}_i\}\hfill \\ \hfill {\overline{X}}_2& =-{\overline{d}}_y{\overline{L}}_l{C}_i-d_y{C}_i^T{\overline{L}}_l^T,{\overline{X}}_3=He\{P_1{A}_i-d_y{\overline{L}}_l{C}_i\}\hfill \\ \hfill {\overline{\mathbb{X}}}_2& =S^{-T}\left[\begin{array}{cc}{d}_u{B}_i^T{P}_1^T-S^T{B}_i^T& {\mathbf{0}}_6\end{array}\right],\mathbb{S}=S^T\hfill \\ \hfill {\overline{\mathbb{X}}}_1& ={\left[\begin{array}{ccccc}{\overline{K}}_j{C}_i& 0& {\overline{K}}_{rj}{C}_r& {\overline{K}}_j{G}_i& {\mathbf{0}}_3\end{array}\right]}^T,{\mathbb{T}}_3^1=\left[\begin{array}{cc}\mathcal{C}& {\mathcal{G}}_1\end{array}\right]\hfill \\ \hfill {\overline{\mathbb{X}}}_{02}& =\left[\begin{array}{ccc}{G}_i^T{\overline{K}}_j^T{B}_i^T-G_i^T{\overline{L}}_l^T& -G_i^T{\overline{L}}_l^T& 0\\ 0& F_i^T{P}_1& 0\\ 0& 0& B_r^T{P}_2\end{array}\right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill \overline{\Gamma }& =\left[\begin{array}{cc}{\mathbb{T}}_0^2& *\\ {\mathbb{T}}_2^2{\mathbb{T}}_3^2& -He\left\{{\beta }_2{\mathbb{T}}_2^2\right\}+{\beta }_2^{2}I\end{array}\right]\hfill \\ \hfill {\mathbb{T}}_0^2& =-diag\{P_1,P_1,P_2,s^{-1}I,a^{-1}I\},{\mathbb{T}}_3^2=\left[\begin{array}{cc}\mathcal{C}& {\mathcal{G}}_2\end{array}\right].\hfill \end{array}$$

Then, the fuzzy observer (5) and controller (7) can ensure the adaptive FTC system (8) is asymptotically stable and has the mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ performances. Accordingly, the gains of a fuzzy tracking controller and observer are obtained as follows

$$L_l=P_1^{-1}{\overline{L}}_l,K_j=S^{-1}{\overline{K}}_j,K_{rj}=S^{-1}{\overline{K}}_{rj}.$$

(30)

Proof. 

By choosing the matrix $P=diag\{P_1,P_1,P_2\}$ to the (10)–(13) and defining the following matrices

$$\begin{array}{cc}\hfill {\mathbb{T}}_0^1& =\left[\begin{array}{cc}{\overline{\Lambda }}_1& *\\ {\overline{\Lambda }}_2& {\Lambda }_3\end{array}\right],{\mathbb{T}}_1^1={\mathbb{T}}_1^2=I\hfill \\ \hfill {\overline{\Lambda }}_1& =\left[\begin{array}{ccc}{X}_1& *& *\\ X_2& X_3& *\\ d_u{C}_r^T{K}_{rj}^T{B}_i^T{P}_1^T& 0& He\left\{P_2{A}_r\right\}\end{array}\right]\hfill \\ \hfill X_1& =He\{P_1{A}_i-{\overline{d}}_y{P}_1{L}_l{C}_i+d_u{P}_1{B}_i{K}_j{C}_i\}\hfill \\ \hfill X_2& =-{\overline{d}}_y{P}_1{L}_l{C}_i-d_y{C}_i^T{L}_l^T{P}_1^T,X_3=He\{P_1{A}_i-d_y{P}_1{L}_l{C}_i\}\hfill \\ \hfill {\overline{\Lambda }}_2& =\left[\begin{array}{ccc}{d}_u{G}_i^T{K}_j^T{B}_i^T{P}_1^T-G_i^T{L}_l^T{P}_1^T& -G_i^T{L}_l^T{P}_1^T& 0\\ 0& F_i^T{P}_1^T& 0\\ 0& 0& B_r^T{P}_2^T\end{array}\right].\hfill \end{array}$$

Recalling the matrices ${\mathbb{T}}_2^1$, ${\mathbb{T}}_3^1$, ${\mathbb{T}}_0^2$, ${\mathbb{T}}_2^2$, ${\mathbb{T}}_3^2$ and introducing the scalars ${\beta }_1$, ${\beta }_2$. By using Lemma 1 to (10)–(13), the condition (29) is obtained and there is

$$\begin{array}{c}\hfill \left[\begin{array}{cc}{\mathbb{T}}_0^1& *\\ {\mathbb{T}}_2^1{\mathbb{T}}_3^1& -He\left\{{\beta }_1{\mathbb{T}}_2^1\right\}+{\beta }_1^{2}I\end{array}\right]<0.\end{array}$$

(31)

Furthermore, recalling the matrices ${\mathbb{X}}_2$, $\mathbb{S}$ and defining the matrices

$$\begin{array}{cc}\hfill {\mathbb{X}}_0& =\left[\begin{array}{cc}\left[\begin{array}{cc}{\widehat{\Lambda }}_1& *\\ {\widehat{\Lambda }}_2& {\Lambda }_3\end{array}\right]& *\\ {\mathbb{T}}_2^1{\mathbb{T}}_3^1& -He\left\{{\beta }_1{\mathbb{T}}_2^1\right\}+{\beta }_1^{2}I\end{array}\right]\hfill \\ \hfill {\widehat{\Lambda }}_1& =\left[\begin{array}{ccc}{\widehat{X}}_1& *& *\\ X_2& X_3& *\\ C_r^T{K}_{rj}^T{S}^T{B}_i^T& 0& He\left\{P_2{A}_r\right\}\end{array}\right]\hfill \\ \hfill {\widehat{X}}_1& =He\{P_1{A}_i-{\overline{d}}_y{P}_1{L}_l{C}_i+B_{i}S{K}_j{C}_i\}\hfill \\ \hfill {\widehat{\Lambda }}_2& =\left[\begin{array}{ccc}{G}_i^T{K}_j^T{S}^T{B}_i^T-G_i^T{L}_l^T{P}_1^T& -G_i^T{L}_l^T{P}_1^T& 0\\ 0& F_i^T{P}_1^T& 0\\ 0& 0& B_r^T{P}_2^T\end{array}\right]\hfill \\ \hfill {\mathbb{X}}_1& ={\left(S\left[\begin{array}{ccccc}{K}_j{C}_i& 0& K_{rj}{C}_r& K_j{G}_i& {\mathbf{0}}_3\end{array}\right]\right)}^T.\hfill \end{array}$$

Then, by using the Lemma 2 to (31), by defining the matrices ${\overline{L}}_l=P_1{L}_l,{\overline{K}}_j=S{K}_j,$${\overline{K}}_{rj}=S{K}_{rj}$, so that the feasibility conditions (26)–(29) are obtained. The proof is completed. □

Remark 2. 

In actual engineering, due to different models, environmental changes, human factors, aging and other reasons, if the same membership function is used to model the system modules (observer and controller) and the nonlinear system, an accurate fuzzy model cannot be established. However, IT2 fuzzy modeling is designed to model each module separately with the upper and lower membership degree and membership function, and the method in [9] is adopted. The slack matrix and membership function properties are introduced to obtain (20), which further describes the mismatching and uncertainty of membership functions between system modules.

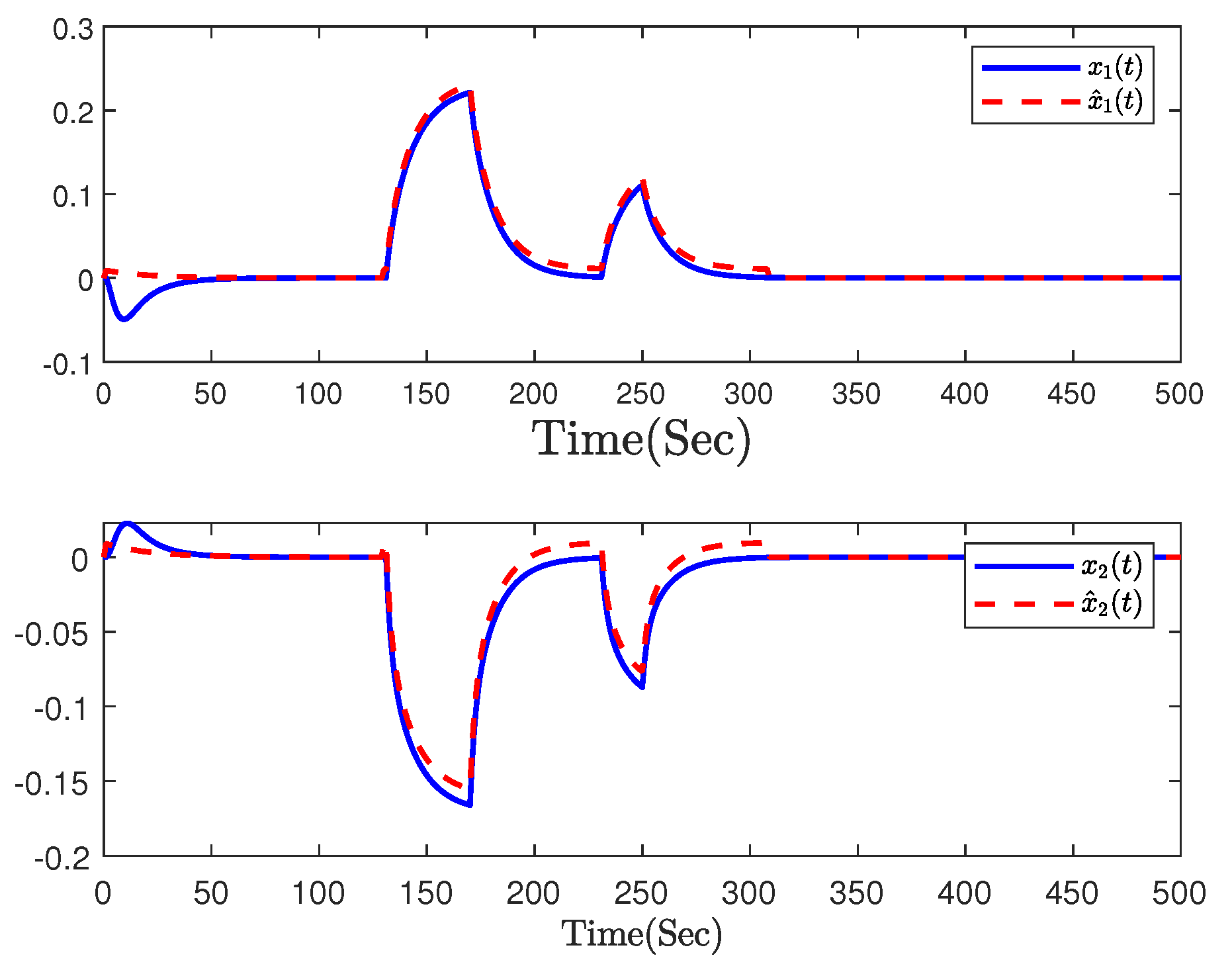
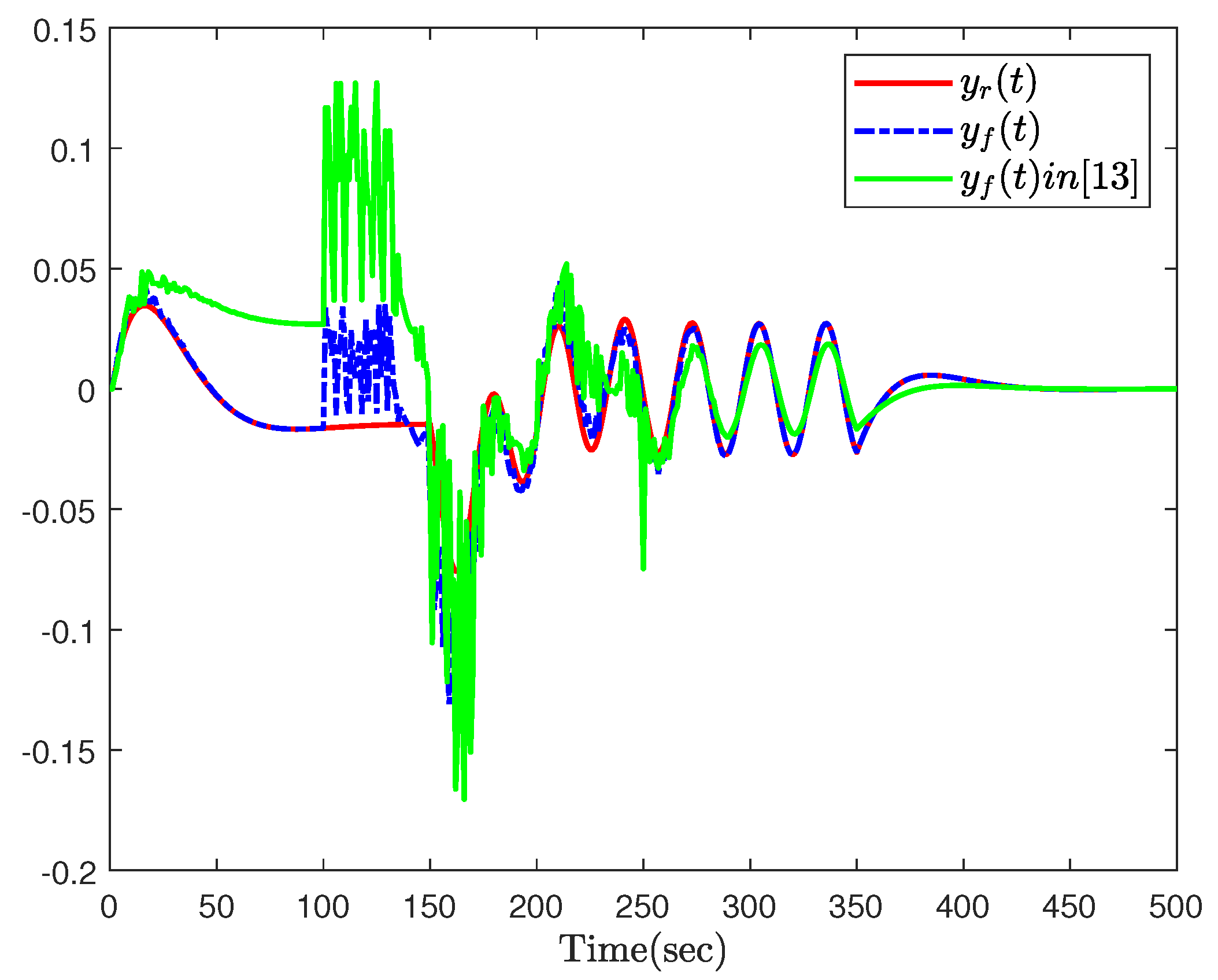
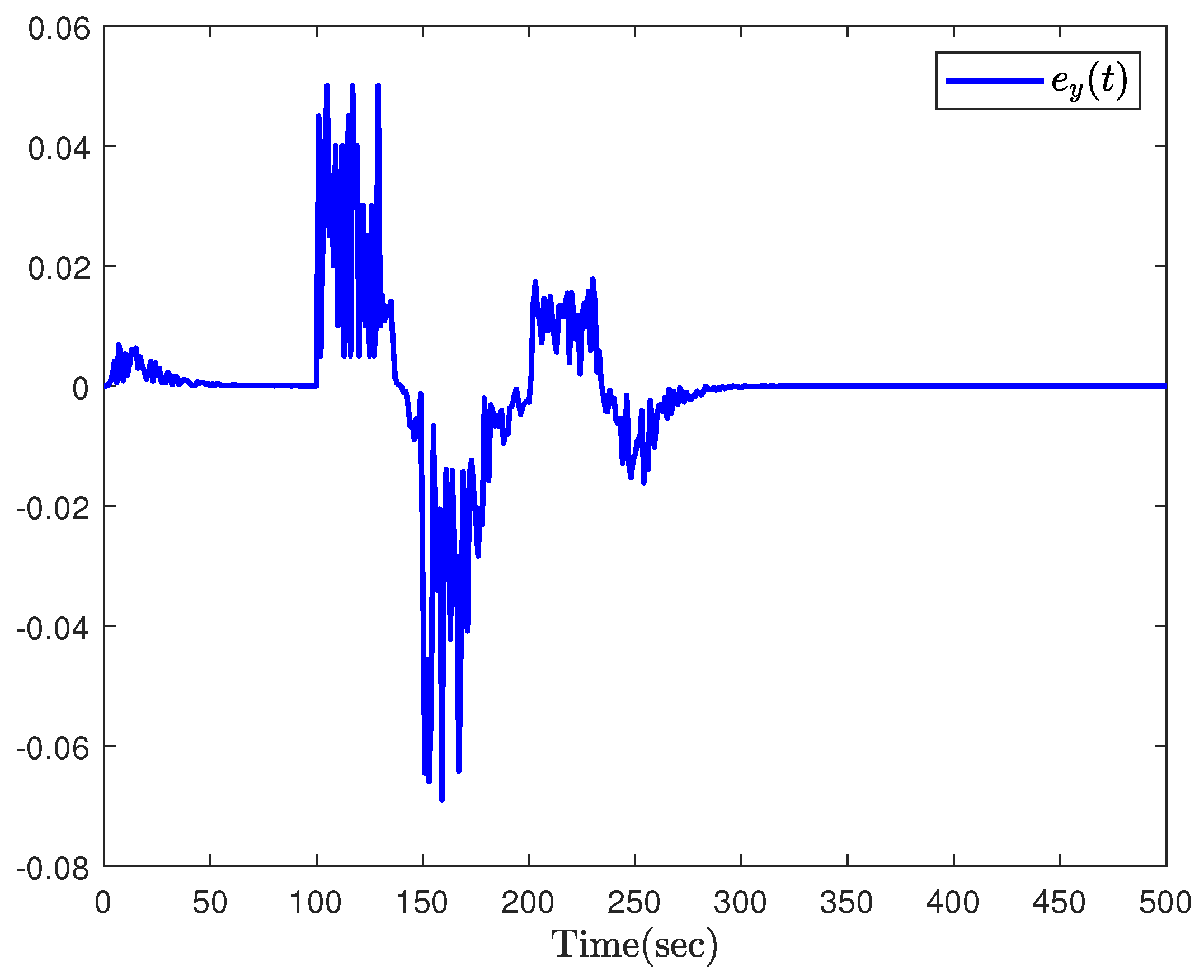
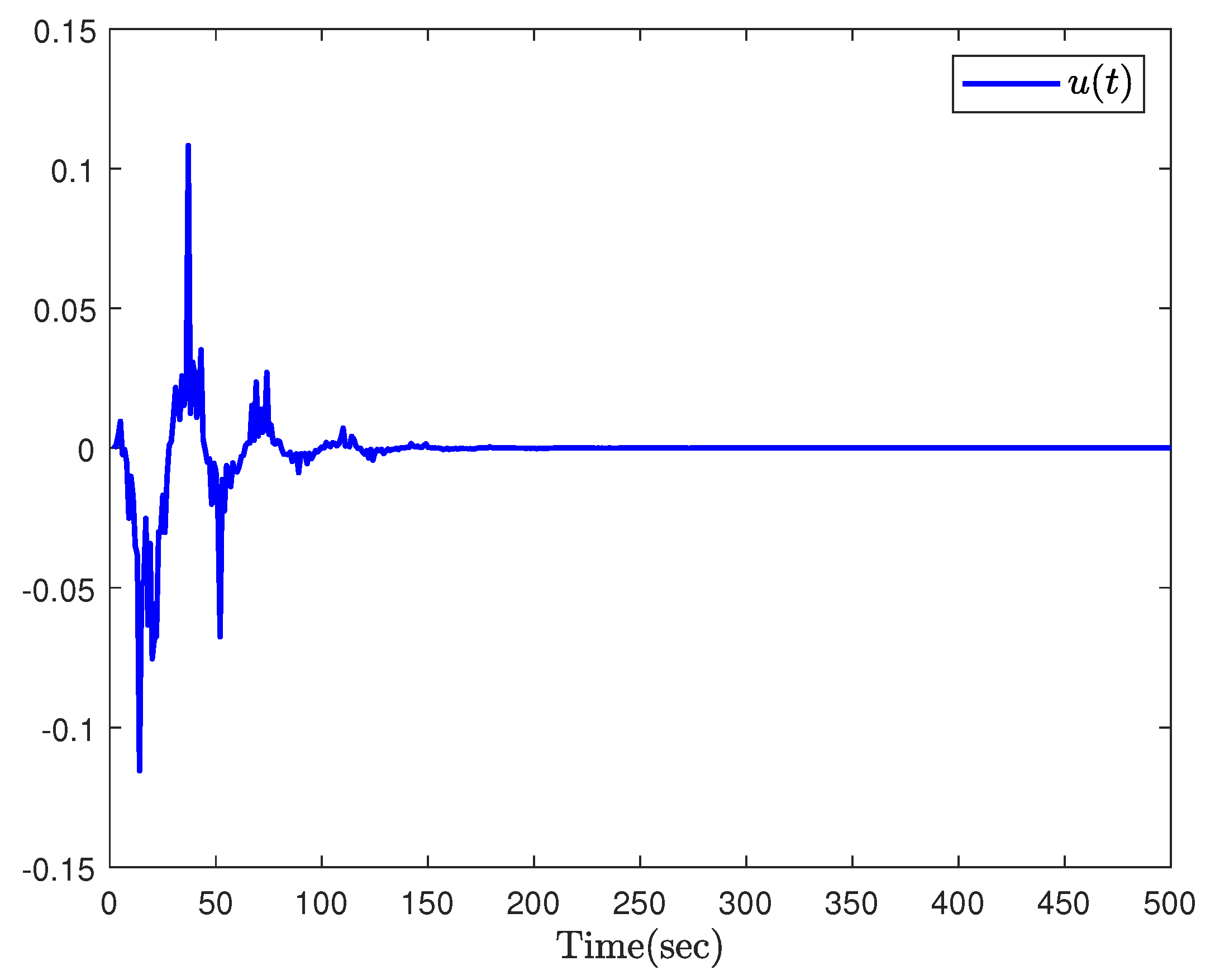
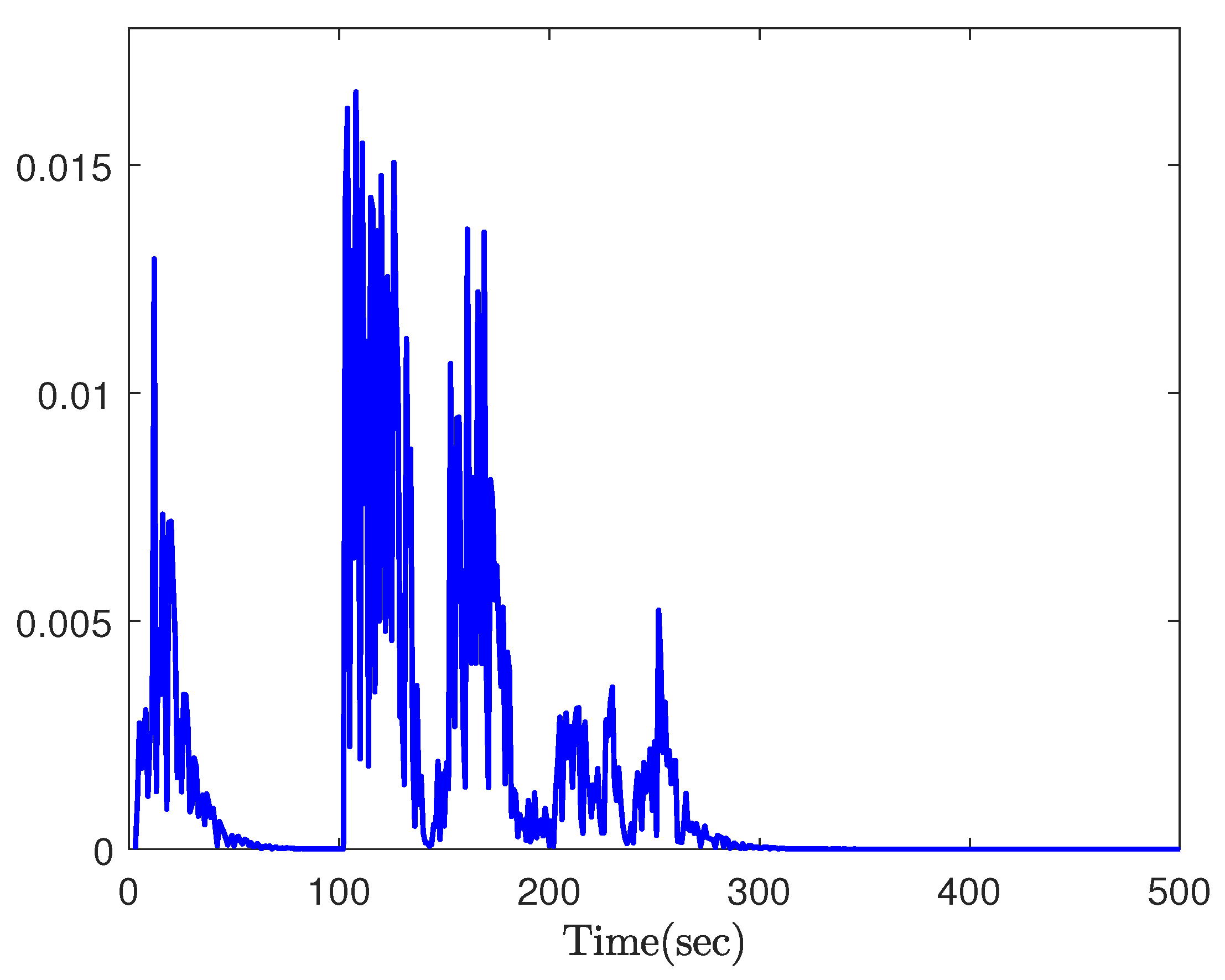
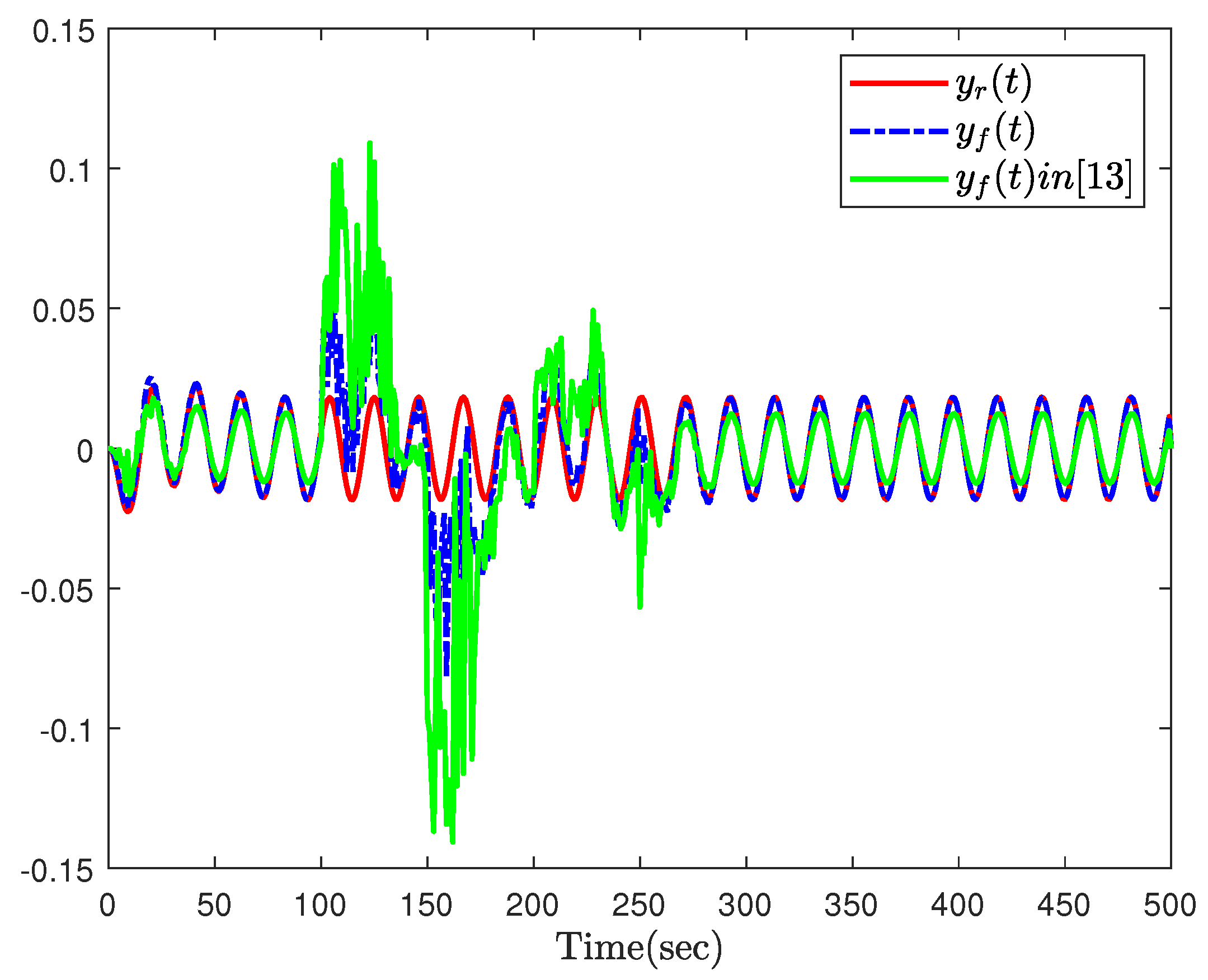
5. Simulations

A mass-spring-damping system [35,39] is selected to demonstrate the effectiveness of the designed method. According to Newton’s law,

$$\begin{array}{c}\hfill m\ddot{x}+F_f+F_s=u\end{array}$$

(32)

where $F_f=\overline{c}\dot{x}$, $F_s=\overline{k}(1+{\overline{a}}^2{x}^2)x$, m, and u are the friction force, hardening spring force, mass, and control input, respectively, and $\overline{c}>0$ and $\overline{k}$ and $\overline{a}$ are constants. Then, (32) is rewritten as

$$\begin{array}{c}\hfill m\ddot{x}+\overline{c}\dot{x}+\overline{k}x+\overline{k}{\overline{a}}^2{x}^3=u\end{array}$$

(33)

where x is the displacement of mass from the reference point. Defending $x\left(t\right)={\left[\begin{array}{cc}{x}_1^T\left(t\right)& x_2^T\left(t\right)\end{array}\right]}^T={\left[\begin{array}{cc}{x}^T& {\dot{x}}^T\end{array}\right]}^T$ and $\overline{b}\left(t\right)=(-\overline{k}-\overline{k}{\overline{a}}^2{x}_1^2\left(t\right))/m$, assume $x_1\left(t\right)\in [-1,1]$, $m=2 \mathrm{kg}$, $\overline{c}=6 \mathrm{N}·\mathrm{m}/\mathrm{s}$, $\overline{a}=0.5 {\mathrm{m}}^{-1}$, and $\overline{k}\in [5,8]$, so that $\overline{b}\left(t\right)\in [{\overline{b}}_{min},{\overline{b}}_{max}]=[-2,-1]$.

Then, the IT2 T–S fuzzy system matrices are

$$\begin{array}{cc}\hfill A_{1,2}& =\left[\begin{array}{cc}0& 1\\ \overline{b}\left(t\right)& -{\displaystyle \frac{\overline{c}}{m}}\end{array}\right],B_1=B_2=\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{m}}\end{array}\right].\hfill \end{array}$$

Based on the property of membership function ${\alpha }_1+{\alpha }_2=1$, there has $\overline{b}\left(t\right)={\alpha }_1{\overline{b}}_{min}+{\alpha }_2{\overline{b}}_{max}$ with ${\alpha }_1={\displaystyle \frac{{\overline{b}}_{max}-\overline{b}\left(t\right)}{{\overline{b}}_{max}-{\overline{b}}_{min}}}$ and ${\alpha }_2={\displaystyle \frac{\overline{b}\left(t\right)-{\overline{b}}_{min}}{{\overline{b}}_{max}-{\overline{b}}_{min}}}$. Then, with the parameter $\overline{k}$, the homologous upper and lower membership functions are

$$\begin{array}{cc}\hfill {\underline{\alpha }}_1& ={\alpha }_1,{\underline{\alpha }}_2={\alpha }_2,\overline{k}=5\hfill \\ \hfill {\overline{\alpha }}_1& ={\alpha }_1,{\overline{\alpha }}_2={\alpha }_2,\overline{k}=8.\hfill \end{array}$$

Define the nonlinear weighting functions ${\underline{p}}_1={\underline{r}}_1={\underline{q}}_1={sin}^2\left(x_1\left(t\right)\right)$, ${\overline{p}}_1={\overline{r}}_1={\overline{q}}_1=1-{sin}^2\left(x_1\left(t\right)\right)$, ${\underline{p}}_2={\underline{r}}_2={\underline{q}}_2={cos}^2\left(x_1\left(t\right)\right)$, ${\overline{p}}_2={\overline{r}}_2={\overline{q}}_2=1-{cos}^2\left(x_1\left(t\right)\right)$. The membership functions of the observer and controller are selected as ${\underline{\vartheta }}_1={\underline{\beta }}_1=e^{-{\widehat{x}}_1^2\left(t\right)/0.5}$, ${\overline{\vartheta }}_1={\overline{\beta }}_1=e^{-{\widehat{x}}_1^2\left(t\right)}$, ${\underline{\vartheta }}_2={\underline{\beta }}_2=1-e^{-{\widehat{x}}_1^2\left(t\right)}$, ${\overline{\vartheta }}_2={\overline{\beta }}_2=1-e^{-{\widehat{x}}_1^2\left(t\right)/0.5}$.

The corresponding matrices are

$$\begin{array}{cc}\hfill A_1& =\left[\begin{array}{cc}0& 1\\ -2& -3\end{array}\right],A_2=\left[\begin{array}{cc}0& 1\\ -1& -3\end{array}\right]\hfill \\ \hfill B_1& =B_2=\left[\begin{array}{c}0\\ 0.5\end{array}\right],E_1=E_2=\left[\begin{array}{c}-0.2\\ -0.1\end{array}\right],F_1=F_2=\left[\begin{array}{c}-0.5\\ -0.3\end{array}\right]\hfill \\ \hfill C_1& =C_2=\left[\begin{array}{cc}0.1& 0.2\end{array}\right],G_1=G_2=0.3.\hfill \end{array}$$

Assume that the disturbance $w\left(t\right)=0.5e^{-0.3t}sin\left(0.2t\right)$; then, the corresponding mathematical expression of sensor fault and actuator fault are

$$\begin{array}{cc}\hfill f_s\left(t\right)& =\left\{\begin{array}{ccc}\hfill 0.5,& & 100\le t\le 150,\hfill \\ \hfill 0.2,& & 200\le t\le 250,\hfill \\ \hfill 0,& & else.\hfill \end{array}\right.\hfill \\ \hfill f_a\left(t\right)& =\left\{\begin{array}{ccc}\hfill 0.5,& & 130\le t\le 170,\hfill \\ \hfill 0.3,& & 230\le t\le 250,\hfill \\ \hfill 0,& & else.\hfill \end{array}\right.\hfill \end{array}$$

Moreover, the matrices in the reference system are

$$\begin{array}{cc}\hfill A_r& =\left[\begin{array}{cc}0.1& 1.6\\ -0.3& -1\end{array}\right],B_r=\left[\begin{array}{c}0.2\\ -0.2\end{array}\right]\hfill \\ \hfill C_r& =\left[\begin{array}{cc}-0.5& 0.8\end{array}\right].\hfill \end{array}$$

with the reference input

$$i_r\left(t\right)=\left\{\begin{array}{ccc}\hfill -0.2,& & t\le 150,\hfill \\ \hfill 0.2cos\left(0.2t\right),& & 150\le t\le 350,\hfill \\ \hfill 0,& & else.\hfill \end{array}\right.$$

Set the parameters ${\eta }_1=0.4$, ${\eta }_2=0.7$; then, the observer and controller gain matrices are obtained as

$$\begin{array}{cc}\hfill L_1& ={\left[\begin{array}{cc}0.2597& -1.0683\end{array}\right]}^T\hfill \\ \hfill L_2& ={\left[\begin{array}{cc}-0.1621& 0.6746\end{array}\right]}^T\hfill \\ \hfill K_1& =-0.4141,K_2=0.5073\hfill \\ \hfill K_{r1}& =0.0104,K_{r2}=-0.0383.\hfill \end{array}$$

The system and observer initial values are selected as $x\left(0\right)=\widehat{x}\left(0\right)={\left[00\right]}^T$. Figure 2 shows the observer’s estimation of the system states, indicating that the observer has good estimation performance. In Figure 3, a comparison is added with the method proposed in reference [13]. Initially, the system output with faults $y_f\left(t\right)$ can be quickly achieved under the action of disturbance compensation. Next, when the fault occurs, the tracking effect is better than the method in [13], and the reference output $y_r\left(t\right)$ can be tracked as soon as the fault ends. Figure 3 and Figure 4 illustrate the tracking effect of the system output on the reference output. It can be seen that the system can still achieve the tracking effect even under the influence of external disturbances and faults. Figure 5 represents the control signals that vary with the faults and external inputs. The ratio history curves of $\sqrt{\underset{0\le t\le t_a}{sup}\left\{e_y^T\left(t\right)e_y\left(t\right)\right\}/{\int }_0^{t_a}{\overline{w}}^T\left(\tau \right)\overline{w}\left(\tau \right)d\tau }$ and $\sqrt{{\int }_0^{t_a}{e}_y^T\left(\tau \right)e_y\left(\tau \right)d\tau /{\int }_0^{t_a}{\overline{w}}^T\left(\tau \right)\overline{w}\left(\tau \right)d\tau }$ (i.e., the trajectories of $L_2-L_{\infty }$ and ${\mathcal{H}}_{\infty }$ performance) are shown in Figure 6 and Figure 7, which means, under the influence of disturbance $w\left(t\right)$ and faults ($f_s\left(t\right)$ and $f_a\left(t\right)$), the ratio curve can quickly tends to stabilize, and the maximum value $0.0166$ of $L_2-L_{\infty }$ performance and $0.0480$ of ${\mathcal{H}}_{\infty }$ performance are lower than the performance index $\gamma =1$. To sum up, these simulation results demonstrate that the FTC method is effective and can ensure asymptotic stability and desired mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ performances for the system (8).

Figure 2. System states $x\left(t\right)$ and observer states $\widehat{x}\left(t\right)$.

Figure 3. System output with faults $y_f\left(t\right)$ and reference output $y_r\left(t\right)$.

Figure 4. System tracking error $e_y\left(t\right)$.

Figure 5. Adaptive control signal $u\left(t\right)$.

Figure 6. The trajectory of $L_2-L_{\infty }$ performance.

Figure 7. The trajectory of ${\mathcal{H}}_{\infty }$ performance.

In order to further verify the tracking effect of the system, the reference input is changed to $i_r\left(t\right)=0.2sin\left(0.3t\right)$. Compared with the results without the adaptive sensor fault compensation term in [13], we can see from Figure 8 that the system output containing faults has a good tracking effect following the reference output, which shows the effectiveness of the consequence.

Figure 8. System output with faults $y_f\left(t\right)$ and reference output $y_r\left(t\right)$.

Comparative Explanations: Compared with the design schemes of adaptive FTC for actuator faults in [11,13] and overcompensation for external disturbances, that is, compensation item ${\int }_{t_0}^t\parallel \xi \left(\tau \right)\parallel d\tau$ will always exist after the disturbance and fault disappear. Therefore, this paper designs an adaptive compensation scalar $\rho \left(t\right)$ based on this, which avoids channel congestion caused by too much data and saves communication resources under the condition of limited bandwidth. Moreover, a more practical application scenario of FTC is considered. The fault cases under consideration include not only partial degenerate faults of multiplicative type but also stuck fault of additive type. Both the observer and controller of the joint design meet the mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ performances, and the conservative design is reduced by introducing appropriate Lemmas 1 and 2.

6. Conclusions

In this paper, the tracking problem of mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ adaptive FTC for continuous-time IT2FSs is studied. The IT2 fuzzy model was used to figure out the problem of mismatch and uncertainty of membership functions between system modules, while the fuzzy observer and adaptive fault estimation functions were used to estimate the system state and fault signals, in order for the adaptive tracking controller to realize the tracking control of the reference output under disturbance and fault conditions. Both the jointly designed observer and controller can satisfy the mixed ${\mathcal{H}}_{\infty }$ and $L_2-L_{\infty }$ performances while ensuring the asymptotic stability of the system. In addition, the designed adaptive control law can achieve the purpose of dynamic compensation for disturbances and faults, and the conservatism of the observer and controller was further reduced by the slack parameters in the lemmas. Finally, a mass-spring-damping system effectively validated the design method. Our future work will improve the adaptive control algorithm on this basis or adopt an active fault tolerance scheme to further improve the FTC capability of the system.