Fermatean Vague Soft Set and Its Application in Decision Making
Abstract
:1. Introduction
2. Preliminary
2.1. Soft Set
2.2. Vague Soft Sets
- i.
- ,
- ii.
- .
- i.
- ,
- ii.
- i.
- ,
- ii.
3. Fermatean Vague Soft Set
4. Some Properties of Union, Intersection, and Complementation
- i.
- ,
- ii.
- ,
- i.
- ii.
- i.
- ii.
- i.
- To find the union of two Fermatean vague soft sets:
- ii.
- To find the intersection of two Fermatean vague soft sets:
- i.
- ii.
- i.
- ii.
- i.
- ,
- ii.
- .
- i.
- ii.
5. An Application Based on the Fermatean Vague Soft Set
- : Membership degree
- : Non-membership degree
- : Hesitation degree ().
- , ensure valid
- It offers greater flexibility than intuitionistic and Pythagorean vague sets.
- Alternative rank: calculate the score for each using the score function:
- Select the best system: Identify the system with the highest aggregate score across all :
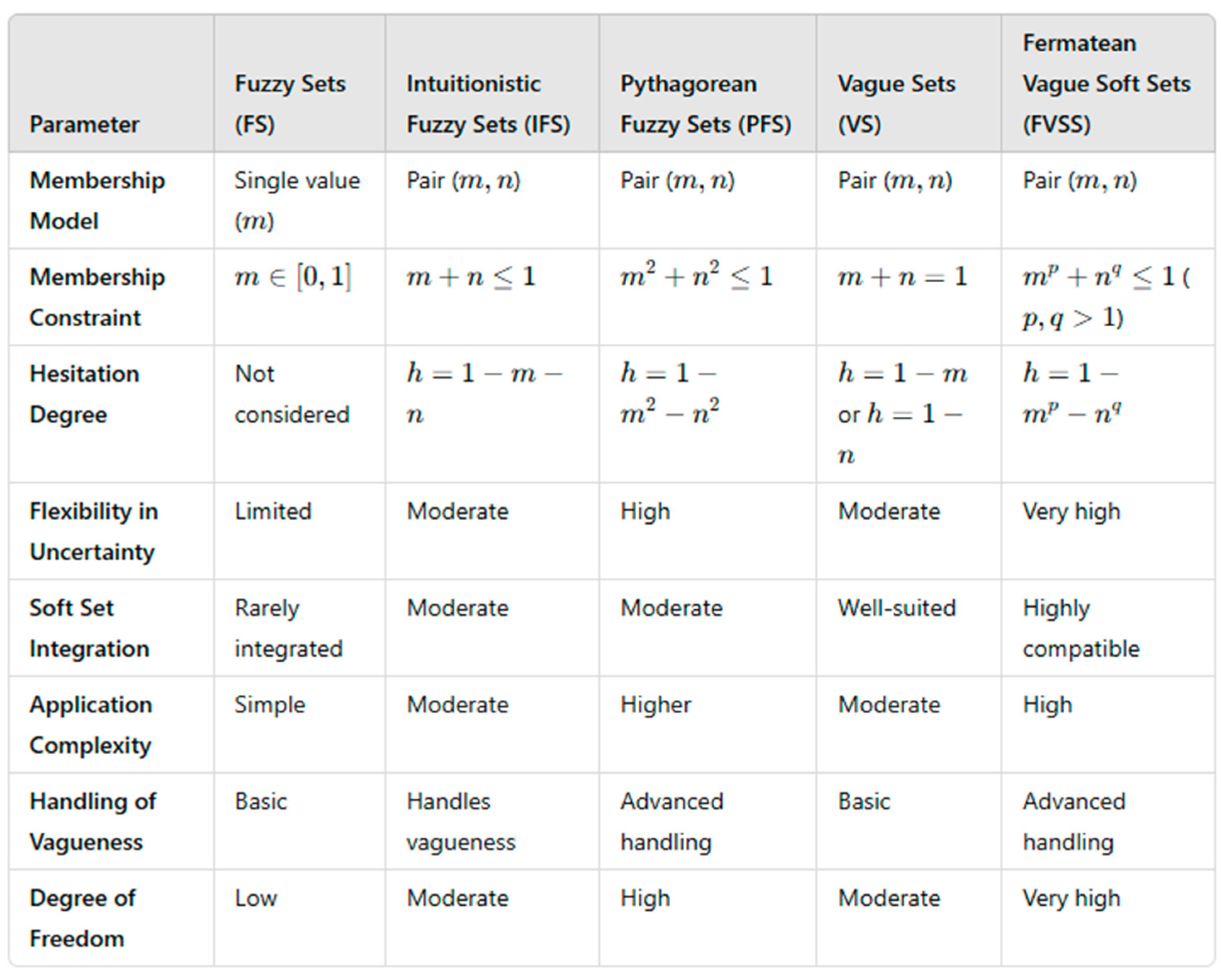
6. Results and Comparisons of Fermatean Vague Soft Sets (FVSS) with Other Conventional Models
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T. Operators over interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1994, 64, 159–174. [Google Scholar] [CrossRef]
- AL-Omeri, W.F.; Kaviyarasu, M. Study on Neutrosophic Graph with Application on Earthquake Response Center in Japan. Symmetry 2024, 16, 743. [Google Scholar] [CrossRef]
- AL-Omeri, W. Fuzzy Totally Continuous Mappings based on Fuzzy αm-Open Sets in Šostaks Sense. Int. J. Appl. Comput. Math. 2024, 10, 73. [Google Scholar] [CrossRef]
- Al-omeri, W.F. On Fuzzy Completely Irresolute on Smart Decision-Making for Electric Vehicle Systems; Elsevier Ebooks: Amsterdam, The Netherlands, 2024; pp. 397–416. [Google Scholar] [CrossRef]
- AL-Omeri, W.F.; Kaviyarasu, M.; Rajeshwari, M. Translation of Neutrosophic INK-Algebra. Neutrosophic Sets Syst. 2024, 66, 8. [Google Scholar]
- AL-Omeri, A.; Kaviyarasu, M.; Rajeshwari, M. Identifying Internet Streaming Services using Max Product of Complement in Neutrosophic Graphs. Int. J. Neutrosophic Sci. 2023, 23, 257–272. [Google Scholar] [CrossRef]
- Priyalatha, S.P.R.; Al-omeri, W.F.; Vanitha, S. On nano soft ideal topological space. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2023. [Google Scholar] [CrossRef]
- Gincy, G.; Al Omeri, W.F.; Janaki, C. Some Weaker Forms of Bipolar Neutrosophic Nano* Open Sets. Neutrosophic Sets Syst. 2023, 61, 414–425. [Google Scholar]
- Al-Omeri, W.F. The Property (P) and New Fixed Point Results on Ordered Metric Spaces in Neutrosophic Theory. Neutrosophic Sets Syst. 2023, 56, 18. [Google Scholar]
- AL-Omeri, A. Neutrosophic G* -Closed Sets in Neutrosophic Topological Spaces. Int. J. Neutrosophic Sci. 2023, 20, 210–222. [Google Scholar] [CrossRef]
- Gau, W.-L.; Buehrer, D.J. Vague sets. IEEE Trans. Syst. Man Cybern. 1993, 23, 610–614. [Google Scholar] [CrossRef]
- Bustince, H.; Burillo, P. Vague sets are intuitionistic fuzzy sets. Fuzzy Sets Syst. 1996, 79, 403–405. [Google Scholar] [CrossRef]
- Chen, S.-M. Analyzing Fuzzy System Reliability Using Vague Set Theory. Int. J. Appl. Sci. Eng. 2003, 1, 82–88. [Google Scholar] [CrossRef]
- Chen, S.-M. Similarity measures between vague sets and between elements. IEEE Trans. Syst. Man Cybern. 1997, 27, 153–158. [Google Scholar] [CrossRef]
- Molodtsov, D. Soft set theory—First results. Comput. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Maji, P.K.; Roy, A.R.; Biswas, R. An application of soft sets in a decision making problem. Comput. Math. Appl. 2002, 44, 1077–1083. [Google Scholar] [CrossRef]
- Aktaş, H.; Çağman, N. Soft sets and soft groups. Inf. Sci. 2007, 177, 2726–2735. [Google Scholar] [CrossRef]
- Majumdar, P.; Samanta, S.K. Similarity measure of soft sets. New Math. Nat. Comput. 2007, 4, 1–12. [Google Scholar] [CrossRef]
- Hong, D.H.; Choi, C.-H. Multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 2000, 114, 103–113. [Google Scholar] [CrossRef]
- Gorzałczany, M.B. A method of inference in approximate reasoning based on interval-valued fuzzy sets. Fuzzy Sets Syst. 1987, 21, 1–17. [Google Scholar] [CrossRef]
- Kumar, A.; Yadav, S.P.; Kumar, S. Fuzzy Reliability of a Marine Power Plant Using Interval Valued Vague Sets. Int. J. Appl. Sci. Eng. 2006, 4, 71–82. [Google Scholar] [CrossRef]
- Kumar, A.; Yadav, S.P.; Kumar, S. Fuzzy system reliability analysis using Tω (the weakest t-norm) based arithmetic operations on L-R type interval valued vague sets. Int. J. Qual. Reliab. Manag. 2007, 24, 846–860. [Google Scholar] [CrossRef]
- Xu, W.; Ma, J.; Wang, S.; Hao, G. Vague soft sets and their properties. Comput. Math. Appl. 2010, 59, 787–794. [Google Scholar] [CrossRef]
- Alhazaymeh, K.; Al-Qudah, Y.; Hassan, N.; Nasruddin, A.M. Cubic Vague Set and its Application in Decision Making. Entropy 2020, 22, 963. [Google Scholar] [CrossRef] [PubMed]
- Alhazaymeh, K.; Hassan, N. Possibility interval-valued vague soft set. Appl. Math. Sci. 2013, 7, 6989–6994. [Google Scholar] [CrossRef]
- Alhazaymeh, K.; Hassan, N. Generalized interval-valued vague soft set. Appl. Math. Sci. 2013, 7, 6983–6988. [Google Scholar] [CrossRef]
- Alhazaymeh, K.; Hassan, N. Vague soft set relations and functions. J. Intell. Fuzzy Syst. 2015, 28, 1205–1212. [Google Scholar] [CrossRef]
- Alhazaymeh, K.; Hassan, N. Generalized vague soft set and its applications. Int. J. Pure Appl. Math. 2012, 77, 391–401. [Google Scholar]
- Alhazaymeh, K.; Hassan, N. Possibility vague soft set and its application in decision Making. Int. J. Pure Appl. Math. 2012, 77, 549–563. [Google Scholar]
- Zhang, S.; Zhang, P.; Zhang, M. Fuzzy Emergency Model and Robust Emergency Strategy of Supply Chain System under Random Supply Disruptions. Complexity 2019, 2019, 3092514. [Google Scholar] [CrossRef]
- Zhang, S.; Hou, Y.; Zhang, S.; Zhang, M. Fuzzy Control Model and Simulation for Nonlinear Supply Chain System with Lead Times. Complexity 2017, 2017, 2017634. [Google Scholar] [CrossRef]
- Wu, J.; Cheng, J.; Yan, H.; Rutkowski, L.; Cao, J. Observer-Based Sliding Mode Control for Stochastic Sampling Fuzzy Systems with Stochastic Communication Protocol. IEEE Trans. Fuzzy Syst. 2024, 1–9. [Google Scholar] [CrossRef]
- Sun, Q.; Ren, J.; Zhao, F. Sliding mode control of discrete-time interval type-2 fuzzy Markov jump systems with the preview target signal. Appl. Math. Comput. 2022, 435, 127479. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-shboul, A.; Alhazaymeh, K.; Wang, K.L.; Wong, K.B. Fermatean Vague Soft Set and Its Application in Decision Making. Mathematics 2024, 12, 3699. https://doi.org/10.3390/math12233699
Al-shboul A, Alhazaymeh K, Wang KL, Wong KB. Fermatean Vague Soft Set and Its Application in Decision Making. Mathematics. 2024; 12(23):3699. https://doi.org/10.3390/math12233699
Chicago/Turabian StyleAl-shboul, Abedallah, Khaleed Alhazaymeh, Kah Lun Wang, and Kok Bin Wong. 2024. "Fermatean Vague Soft Set and Its Application in Decision Making" Mathematics 12, no. 23: 3699. https://doi.org/10.3390/math12233699
APA StyleAl-shboul, A., Alhazaymeh, K., Wang, K. L., & Wong, K. B. (2024). Fermatean Vague Soft Set and Its Application in Decision Making. Mathematics, 12(23), 3699. https://doi.org/10.3390/math12233699









