The Capped Separable Difference of Two Norms for Signal Recovery
Abstract
1. Introduction
1.1. Related Work
- The minimax concave penalty (MCP) method was proposed in [6]. For any and , its regularization term withTherefore, if the effect of constants is excluded, its equivalent regularization term goes toso that the MCP method corresponds to the special case of the CSDTN method with , , and . Additionally, according to [16], this CSDTN regularization method corresponds to a continuous probability distribution function on ; that is,
- The proposed regularization function exhibits a form of the separable difference of two norms when . Therefore, if the scale parameter is appropriately chosen to satisfy the constraint condition , it becomes the hybrid - regularization method proposed in [19] when . In the special case of and , it reduces to the piecewise quadratic approximation (PQA) approach studied in [20,21]. The springback model in [22] uses as the regularization function, which performs similarly to the PQA when the weight is well-selected.
1.2. Contribution
- (i)
- We propose the CSDTN model, which integrates the difference of two norms framework with a capped function to enhance sparse signal recovery. This approach effectively mitigates the bias commonly introduced by convex regularizers, such as the minimization, thereby improving the accuracy of signal reconstruction.
- (ii)
- We provide a detailed theoretical analysis of the CSDTN, establishing the condition for exact recovery under this model in terms of a generalized null space property.
- (iii)
- To solve the CSDTN-regularized problem efficiently, we develop an algorithm based on the iteratively reweighted (IRL1).
- (iv)
- We conduct comprehensive experiments on electrocardiogram (ECG) and synthetic data, illustrating the advantages of the CSDTN model in sparse recovery scenarios. Our method outperforms traditional -based approaches and other nonconvex regularizers in terms of accuracy and robustness.
1.3. Organization
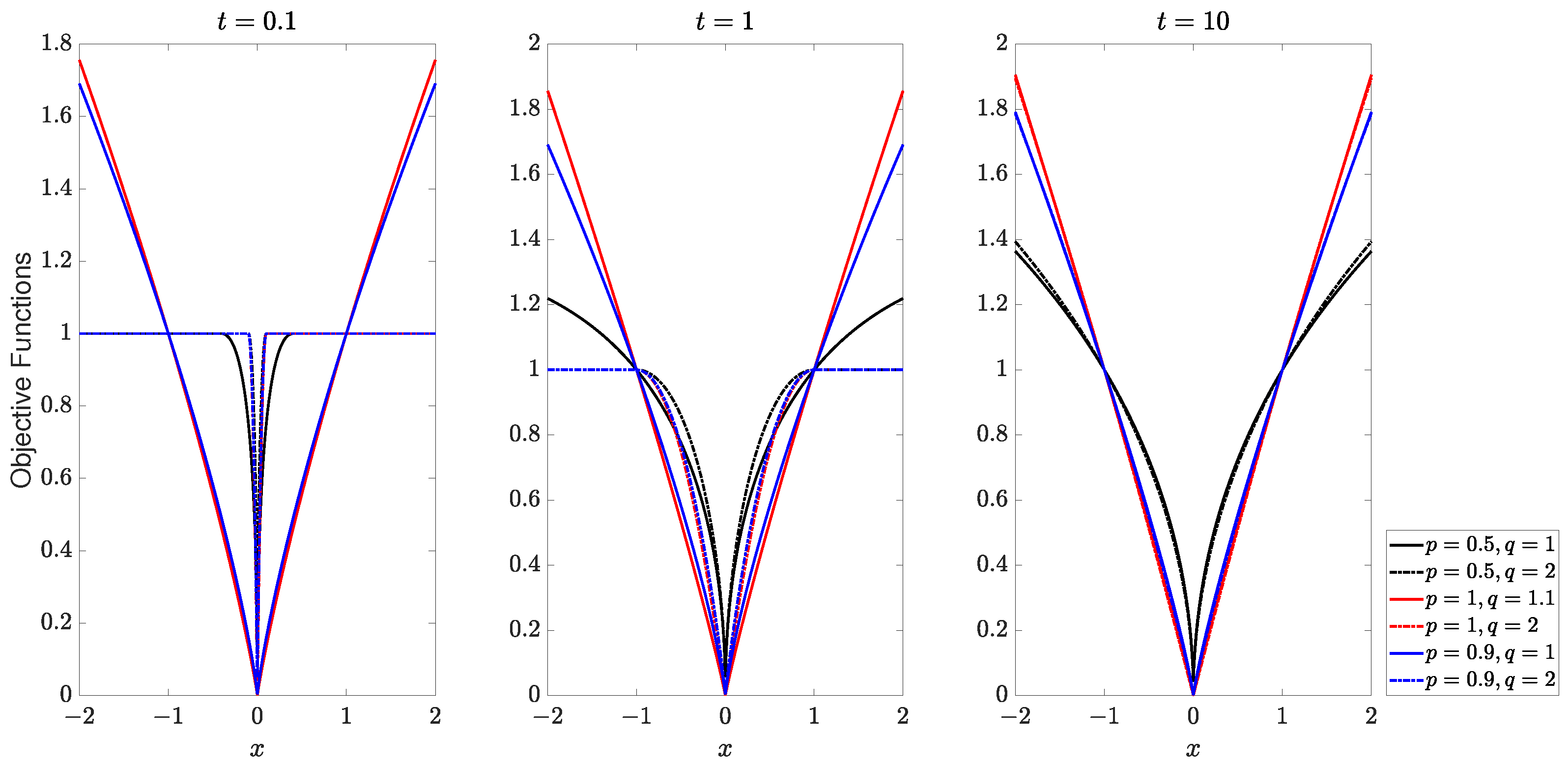
2. The CSDTN Regularization Function
- (i)
- with , as .
- (ii)
- , as .
- (iii)
- when and (or when and ).
3. Theoretical Result
- Remark: Since is both separable and symmetric on , as well as concave on , Proposition 4.6 of [24] readily establishes that the gNSP relative to is less stringent than the NSP for -minimization. Moreover, the extension of the gNSP to its stable and robust versions to address the problems of sparsity defect and measurement error could be carried out as in Chapter 4 of [2].
4. Algorithm
| Algorithm 1 IRL1 for CSDTN |
|
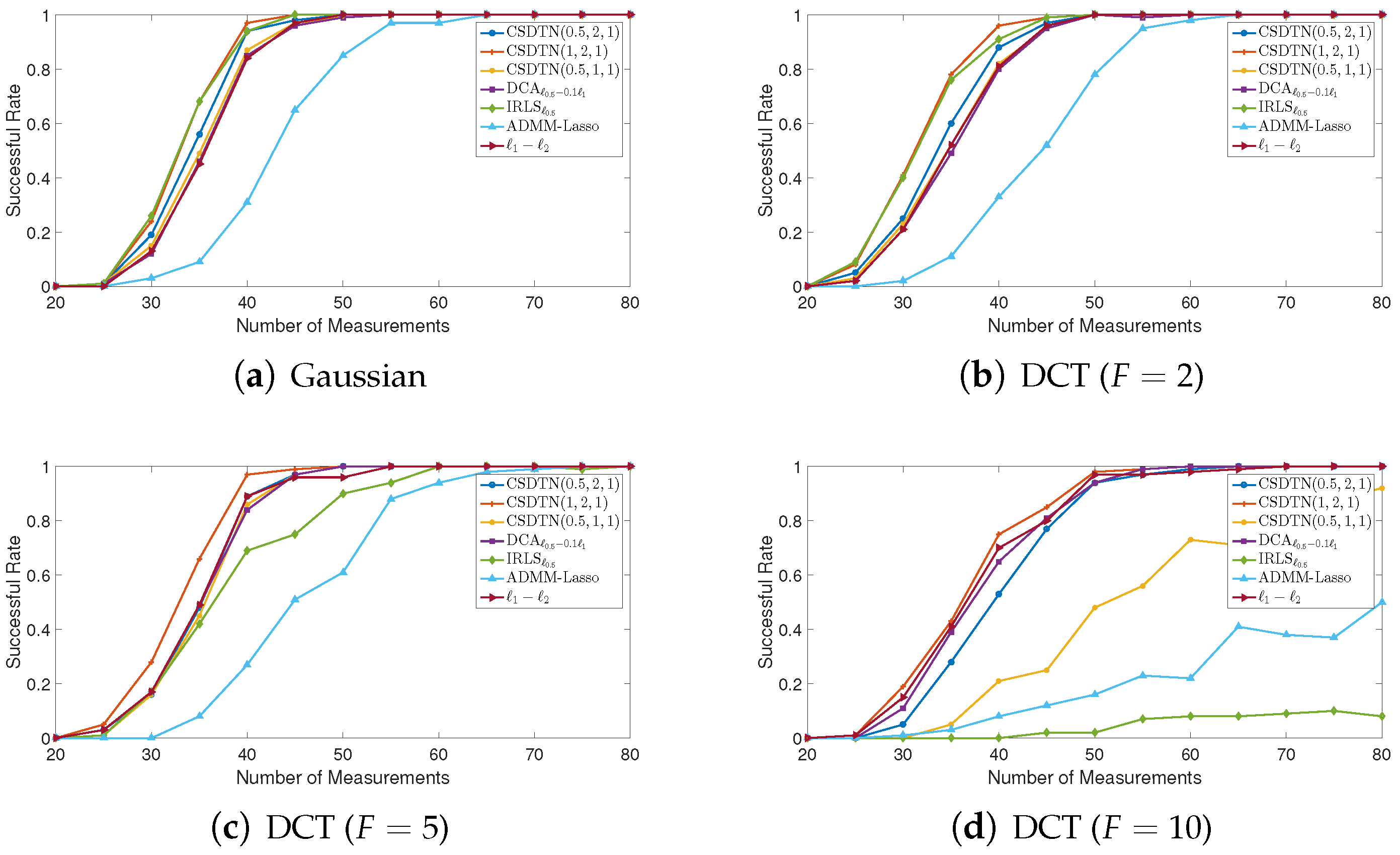
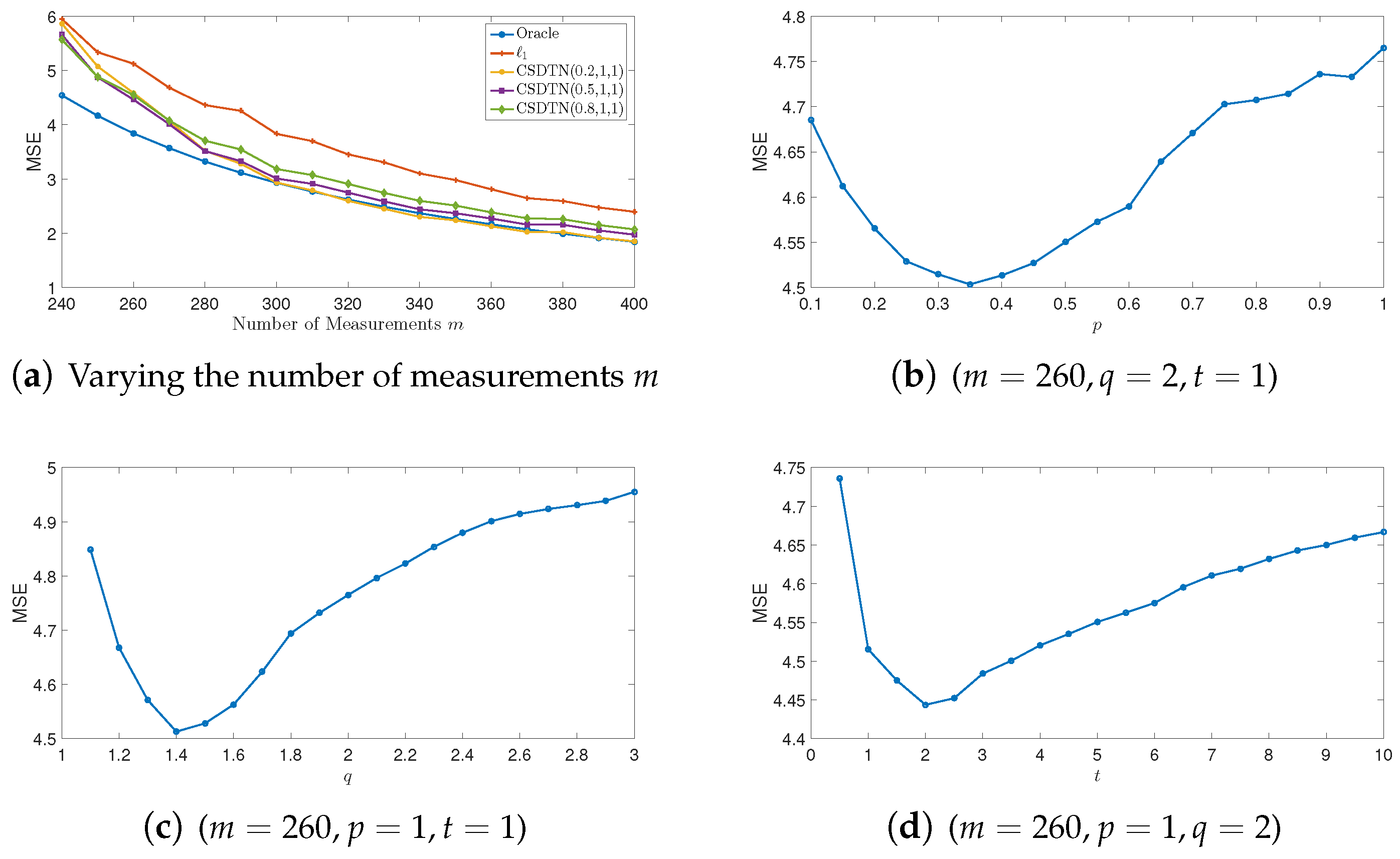
5. Numerical Experiments
5.1. ECG Signal Recovery
5.2. Synthetic Signal Recovery
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hastie, T.; Tibshirani, R.; Wainwright, M. Statistical Learning with Sparsity: The Lasso and Generalizations; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Foucart, S.; Rauhut, H. A Mathematical Introduction to Compressive Sensing; Birkhäuser: Basel, Switzerland, 2013; Volume 1. [Google Scholar]
- Wen, F.; Chu, L.; Liu, P.; Qiu, R.C. A survey on nonconvex regularization-based sparse and low-rank recovery in signal processing, statistics, and machine learning. IEEE Access 2018, 6, 69883–69906. [Google Scholar] [CrossRef]
- Chartrand, R.; Yin, W. Iteratively reweighted algorithms for compressive sensing. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 3869–3872. [Google Scholar]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zhang, C.H. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef] [PubMed]
- Yin, P.; Lou, Y.; He, Q.; Xin, J. Minimization of ℓ1–2 for compressed sensing. SIAM J. Sci. Comput. 2015, 37, A536–A563. [Google Scholar] [CrossRef]
- Zhou, Z.; Yu, J. A new nonconvex sparse recovery method for compressive sensing. Front. Appl. Math. Stat. 2019, 5, 14. [Google Scholar] [CrossRef]
- Zhou, Z. RIP analysis for the weighted ℓr−ℓ1 minimization method. Signal Process. 2023, 202, 108754. [Google Scholar] [CrossRef]
- Du, K.L.; Swamy, M.; Wang, Z.Q.; Mow, W.H. Matrix factorization techniques in machine learning, signal processing, and statistics. Mathematics 2023, 11, 2674. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Iterative hard thresholding for compressed sensing. Appl. Comput. Harmon. Anal. 2009, 27, 265–274. [Google Scholar] [CrossRef]
- Zhou, Z. A Unified Framework for Constructing Nonconvex Regularizations. IEEE Signal Process. Lett. 2022, 29, 479–483. [Google Scholar] [CrossRef]
- Zhang, C.H.; Zhang, T. A general theory of concave regularization for high-dimensional sparse estimation problems. Stat. Sci. 2012, 27, 576–593. [Google Scholar] [CrossRef]
- Liu, J.; Jin, J.; Gu, Y. Robustness of sparse recovery via F-minimization: A topological viewpoint. IEEE Trans. Inf. Theory 2015, 61, 3996–4014. [Google Scholar] [CrossRef]
- Gao, X.; Bai, Y.; Li, Q. A sparse optimization problem with hybrid L2-Lp regularization for application of magnetic resonance brain images. J. Comb. Optim. 2019, 42, 760–784. [Google Scholar] [CrossRef]
- Li, Q.; Bai, Y.; Yu, C.; Yuan, Y.x. A new piecewise quadratic approximation approach for L0 norm minimization problem. Sci. China Math. 2019, 62, 185–204. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, W.; Bai, Y.; Wang, G. A non-convex piecewise quadratic approximation of ℓ0 regularization: Theory and accelerated algorithm. J. Glob. Optim. 2022, 38, 1–23. [Google Scholar]
- An, C.; Wu, H.N.; Yuan, X. The springback penalty for robust signal recovery. Appl. Comput. Harmon. Anal. 2022, 61, 319–346. [Google Scholar] [CrossRef]
- Cohen, A.; Dahmen, W.; DeVore, R. Compressed sensing and best k-term approximation. J. Am. Math. Soc. 2009, 22, 211–231. [Google Scholar] [CrossRef]
- Tran, H.; Webster, C. A class of null space conditions for sparse recovery via nonconvex, non-separable minimizations. Results Appl. Math. 2019, 3, 100011. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted ℓ1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Ochs, P.; Dosovitskiy, A.; Brox, T.; Pock, T. On iteratively reweighted algorithms for nonsmooth nonconvex optimization in computer vision. SIAM J. Imaging Sci. 2015, 8, 331–372. [Google Scholar] [CrossRef]
- Zhao, Y.B.; Li, D. Reweighted ℓ1-minimization for sparse solutions to underdetermined linear systems. SIAM J. Optim. 2012, 22, 1065–1088. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers; Now Publishers Inc.: Hanover, MA, USA, 2011. [Google Scholar]
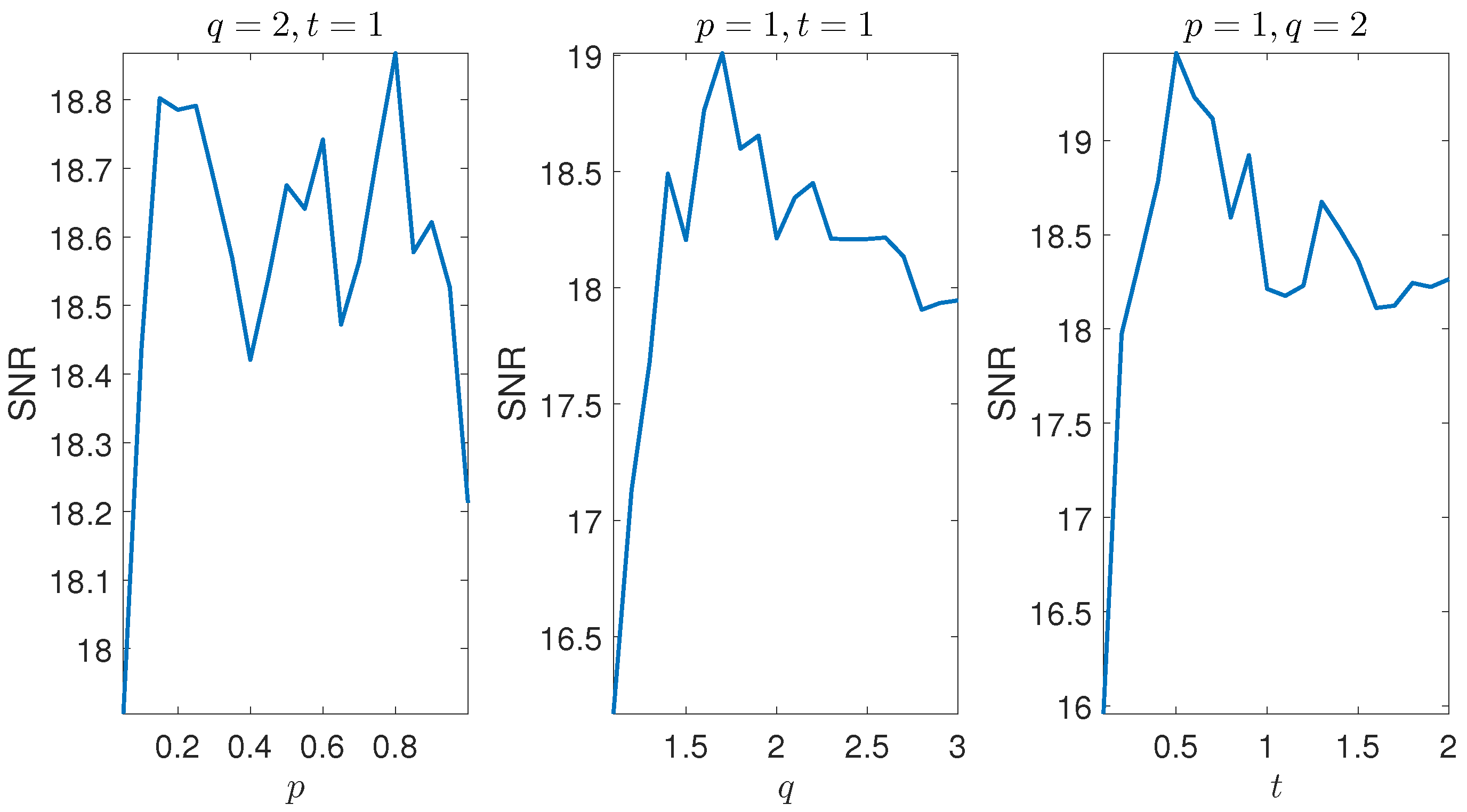
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Wang, G. The Capped Separable Difference of Two Norms for Signal Recovery. Mathematics 2024, 12, 3717. https://doi.org/10.3390/math12233717
Zhou Z, Wang G. The Capped Separable Difference of Two Norms for Signal Recovery. Mathematics. 2024; 12(23):3717. https://doi.org/10.3390/math12233717
Chicago/Turabian StyleZhou, Zhiyong, and Gui Wang. 2024. "The Capped Separable Difference of Two Norms for Signal Recovery" Mathematics 12, no. 23: 3717. https://doi.org/10.3390/math12233717
APA StyleZhou, Z., & Wang, G. (2024). The Capped Separable Difference of Two Norms for Signal Recovery. Mathematics, 12(23), 3717. https://doi.org/10.3390/math12233717





