A Generalization of Fixed-Point Theorems for Mappings with a Contractive Iterate
Abstract
:1. Introduction
2. Preliminaries
- i--regular if for any sequence , convergent to , such that for all , there holds for all
- d--regular if for any sequence , convergent to , such that for all , there holds , for all .
- for any , , such that , there holds
- for any , , such that , there holds .
3. Main Results
- (i)
- is T-closed and has the transitive property;
- (ii)
- T either has a closed graph or the triple is i--regular;
- (iii)
- there exists , such that ;
- (iv)
- there exists , so that for any there is , such that for all holds
- (a)
- and for any arbitrary chosen , such that the iterated sequence converges to an element
- (b)
- For any and , so that , satisfying or , the sequences and are Cauchy equivalent and, hence, converges to , where
- (c)
- If and either or or there is , so that either or then
- (d)
- If, additionally, we suppose that for every , such that neither nor , there is , so that either or then .
4. Illustrative Examples and Coupled Fixed Points
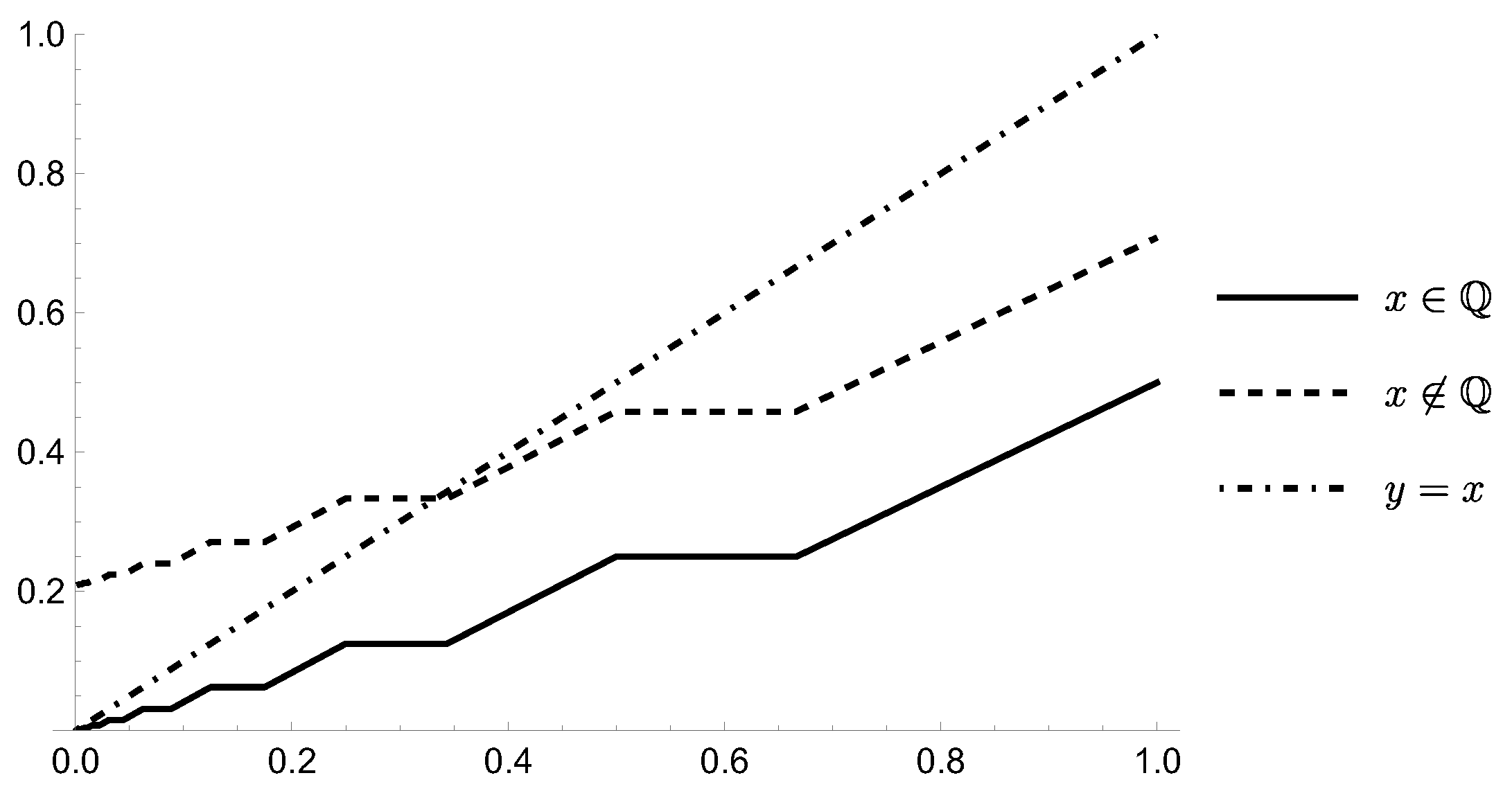
4.1. Examples
4.2. Coupled Fixed Points
- (a)
- i--regular if for any convergent to sequence , with for all , we have , for all .
- (b)
- d--regular if for any convergent to sequence , with for all , we have , for all .
- (I)
- is -closed and has the transitive property
- (II)
- F and f have a closed graph or the triple is i--regular;
- (III)
- there exists , such that ;
- (IV)
- there exists , such that for all there is a positive integer such that for all , we have
- (a)
- has at least one fixed point and the sequenceconverges to an element ;
- (b)
- For any such that or , the sequences and are Cauchy equivalent (i.e., ) and hence converges to the same point ;
- (c)
- If additionally we suppose that for every for which neither nor there exists such that , then and converges to as .
- (a)
- has a closed graph with respect to
- (b)
- there exists , such that
- (c)
- there exists , such that for all , we have
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kannan, R. Some results on fixed points. Bull. Calcutta Math. Soc. 1968, 44, 27–36. [Google Scholar]
- Chatterjea, S.K. Fixed-point theorems. Comptes Rendus L’Academie Bulg. Des Sci. 1972, 25, 727–730. [Google Scholar] [CrossRef]
- Zamfirescu, T. Fix point theorems in metric spaces. Arch. Math. 1972, 23, 292–298. [Google Scholar] [CrossRef]
- Hardy, G.; Rogers, T. A generalization of a fixed point theorem of Reich. Can. Math. Bull. 1973, 16, 201–206. [Google Scholar] [CrossRef]
- Reich, S. Kannan’s fixed point theorem. Bull. Univ. Mat. Ital. 1971, 4, 1–11. [Google Scholar]
- Meir, A.; Keeler, E. A theorem on contractive mappings. J. Math. Anal. Appl. 1969, 28, 326–329. [Google Scholar] [CrossRef]
- Khamsi, M.A.; Kozlowski, W.M.; Reich, S. Fixed point theory in modular function spaces. Nonlinear Anal. 1990, 14, 935–953. [Google Scholar] [CrossRef]
- Bakhtin, I.A. The contraction mapping principle in almost metric spaces. Funct. Anal. 1989, 30, 26–37. [Google Scholar]
- Valero, O. On Banach fixed point theorems for partial metric spaces. Appl. Gen. Topol. 2005, 6, 229–240. [Google Scholar] [CrossRef]
- Kaleva, O.; Seikkala, S. On fuzzy metric spaces. Fuzzy Sets Syst. 1984, 12, 215–229. [Google Scholar] [CrossRef]
- Karapinar, E.; Khojasteh, F. Super metric spaces. Filomat 2022, 36, 3545–3549. [Google Scholar] [CrossRef]
- Bhaskar, T.G.; Lakshmikantham, V. Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Anal. Theory Methods Appl. 2006, 65, 1379–1393. [Google Scholar] [CrossRef]
- Guo, D.; Lakshmikantham, V. Coupled fixed points of nonlinear operators with applications. Nonlinear Anal. Theory Methods Appl. 1987, 11, 623–632. [Google Scholar] [CrossRef]
- Soleimani Rad, G.; Shukla, S.; Rahimi, H. Some relations between n-tuple fixed point and fixed point results. Rev. Real Acad. Cienc. Exactas FíSicas Nat. Ser. A Matemáticas 2015, 109, 471–481. [Google Scholar] [CrossRef]
- Roldań, A.; Martínez-Moreno, J.; Roldań, C.; Karapinar, E. Some Remarks on Multidimensional Fixed Point Theorems. Fixed Point Theory 2014, 15, 545–558. [Google Scholar]
- Agarwal, R.; Karapinar, E.; Roldań-López-de-Hierro, A.-F. Some remarks on “Multidimensional fixed point theorems for isotone mappings inpartially ordered metric spaces”. Fixed Point Theory Appl. 2014, 2014, 245. [Google Scholar] [CrossRef]
- Petruşel, A. Fixed points vs. coupled fixed points. J. Fixed Point Theory Appl. 2018, 20, 150. [Google Scholar] [CrossRef]
- Petruşel, A.; Petruşel, G.; Xiao, Y.-B.; Yao, J.-C. Fixed point theorems for generalized contractions with applications to coupled fixed point theory. J. Nonlinear Convex Anal. 2018, 19, 71–81. [Google Scholar]
- Sehgal, V. A Fixed point theorem for mappings with a contractive iterate. Proc. Am. Math. Soc. 1969, 23, 631–634. [Google Scholar] [CrossRef]
- Guseman, L. Fixed point theorems for mappings with a contractive iterate at a point. Proc. Am. Math. Soc. 1970, 26, 615–618. [Google Scholar] [CrossRef]
- Karaibyamov, S.; Zlatanov, B. Fixed points for mappings with a contractive iterate at each point. Math. Slovaca 2014, 64, 455–468. [Google Scholar] [CrossRef]
- Jachymski, J. The contraction principle for mappings on a metric space with a graph. Proc. Am. Math. Soc. 2008, 136, 1359–1373. [Google Scholar] [CrossRef]
- Armaki, A.A.; Pashapournia, A.; Rad, G.S. Best proximity points of graphical (Φ-ψ)-weak contractive mappings and applications to graphical integral-type inequalities. J. Nonlinear Convex Anal. 2024, 25, 1777–1789. [Google Scholar]
- Samet, B.; Vetro, C. Coupled fixed point, f-invariant set and fixed point of n-order. Ann. Funct. Anal. 2010, 1, 46–56. [Google Scholar] [CrossRef]
- Ran, A.C.M.; Reurings, M.C.B. A fixed point theorem in partially ordered sets and some application to matrix equations. Proc. Am. Math. Soc. 2004, 132, 1435–1443. [Google Scholar] [CrossRef]
- Turinici, M. Abstract comparison principles and multivariable Gronwall-Bellman inequalities. J. Math. Anal. Appl. 1986, 117, 100–127. [Google Scholar] [CrossRef]
- Kabaivanov, S.; Zhelinski, V.; Zlatanov, B. Coupled fixed points for Hardy–Rogers type of maps and their applications in the investigations of market equilibrium in duopoly markets for non-differentiable, nonlinear response functions. Symmetry 2022, 14, 605. [Google Scholar] [CrossRef]
- Ajeti, L.; Ilchev, A.; Zlatanov, B. On coupled best proximity points in reflexive Banach spaces. Mathematics 2022, 10, 1304. [Google Scholar] [CrossRef]
- Kabaivanov, S.; Zlatanov, B. A variational principle, coupled fixed points and market equilibrium. Nonlinear Anal. Model. Control 2021, 26, 169–185. [Google Scholar] [CrossRef]
- Dzhabarova, Y.; Kabaivanov, S.; Ruseva, M.; Zlatanov, B. Existence, uniqueness and stability of market equilibrium in oligopoly markets. Adm. Sci. 2020, 10, 70. [Google Scholar] [CrossRef]
- Zlatanov, B. Coupled best proximity points for cyclic contractive maps and their applications. Fixed Point Theory 2021, 22, 431–452. [Google Scholar] [CrossRef]
- Kutbi, M.A.; Roldán, A.; Sintunavarat, W.; Martínez-Moreno, J.; Roldán, C. F-Closed sets and coupled fixed point theorems without the mixed monotone property. Fixed Point Theory Appl. 2013, 2013, 330. [Google Scholar] [CrossRef]
- Narici, L.; Beckenstein, E. Topological Vector Spaces, 2nd ed.; Chapman and Hall/CRC: New York, NY, USA, 2010; pp. 459–460. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Georgiev, V.; Zlatanov, B. A Generalization of Fixed-Point Theorems for Mappings with a Contractive Iterate. Mathematics 2024, 12, 3725. https://doi.org/10.3390/math12233725
Georgiev V, Zlatanov B. A Generalization of Fixed-Point Theorems for Mappings with a Contractive Iterate. Mathematics. 2024; 12(23):3725. https://doi.org/10.3390/math12233725
Chicago/Turabian StyleGeorgiev, Valentin, and Boyan Zlatanov. 2024. "A Generalization of Fixed-Point Theorems for Mappings with a Contractive Iterate" Mathematics 12, no. 23: 3725. https://doi.org/10.3390/math12233725
APA StyleGeorgiev, V., & Zlatanov, B. (2024). A Generalization of Fixed-Point Theorems for Mappings with a Contractive Iterate. Mathematics, 12(23), 3725. https://doi.org/10.3390/math12233725





