Anomaly Detection Based on Graph Convolutional Network–Variational Autoencoder Model Using Time-Series Vibration and Current Data
Abstract
:1. Introduction
- Lack of fault data: Collecting normal data is relatively straightforward in industrial environments, but obtaining fault data is significantly more difficult. Robots typically halt operation upon experiencing a fault, preventing data collection at the moment of failure. Furthermore, faults are infrequent and unpredictable, making it challenging to gather sufficient fault data.
- Diversity of data features: Mechanical characteristics of robots result in differences between initial-state data and data collected over time as the system’s durability decreases. Consequently, even for the same robot, data features can change over time, complicating fault detection using a classification model.
- Variability of environmental and operating conditions: Data features for robots with identical specifications can vary significantly depending on environmental factors and operating conditions. This variability leads to differences in fault timing and types, making consistent detection of pre-failure signals across diverse conditions highly challenging.
- Integration of vibration and current data: This study enhances anomaly detection performance by integrating vibration and current data, leveraging the complementary features of these two types of data. This approach effectively detects subtle anomaly signals that deviate from normal patterns, addressing the limitations of single-sensor-based methods while providing a more comprehensive understanding of anomalies.
- Validation using statistical feature-based anomaly detection: This study introduces a novel comparison framework to validate the anomaly detection performance of deep learning models against statistical feature-based methods. Statistical feature-based anomaly detection utilizes the entire dataset to detect anomalies through filtering, RMS variation rates, and reconstruction errors, whereas the deep learning models rely solely on the initial data for anomaly detection. By leveraging this statistical baseline, this study evaluates the performance of individual deep learning models and assesses the suitability of hybrid deep learning models.
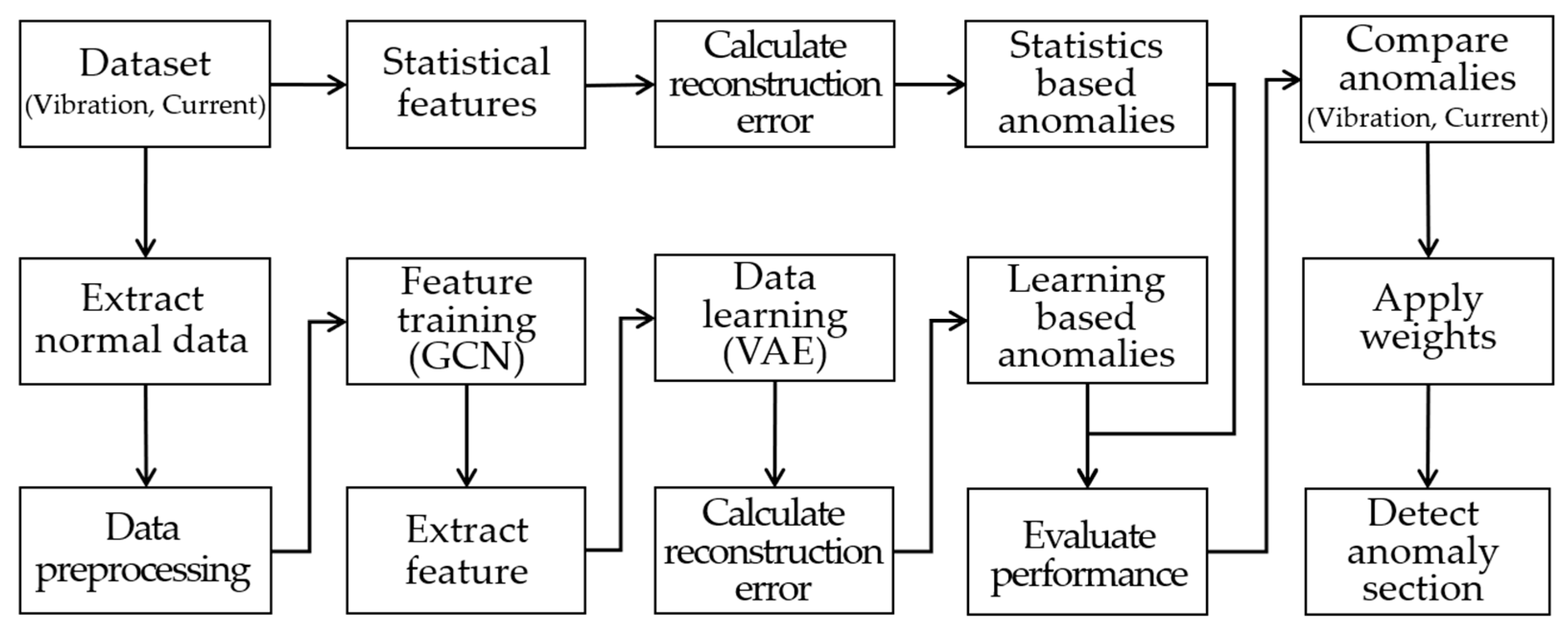
- Semi-supervised learning with GCN-VAE: To effectively detect pre-failure anomaly signals, a novel semi-supervised learning-based GCN-VAE model is proposed. The model extracts spatial features by incorporating temporal continuity and inter-data relationships, mapping these features into a latent space to identify abnormal patterns effectively through reconstruction errors.
- Weighted anomaly detection considering temporal progression and continuity: To enhance the detection performance of pre-failure anomalies, this study introduces a weighting mechanism that accounts for both temporal progression and the continuity of detected anomalies. This mechanism increases the detection probability for subtle anomaly signals that evolve over time and emphasizes the significance of consecutive anomalies, enabling more effective detection of pre-failure anomalies. By integrating this weighting mechanism, the GCN-VAE model demonstrated exceptional anomaly detection performance, even in scenarios characterized by high noise levels and complex temporal dependencies.
2. Related Works
3. Conditions and Methods of Endurance Test for the Driving Modules
4. Anomaly Detection Test Results of the Driving Modules
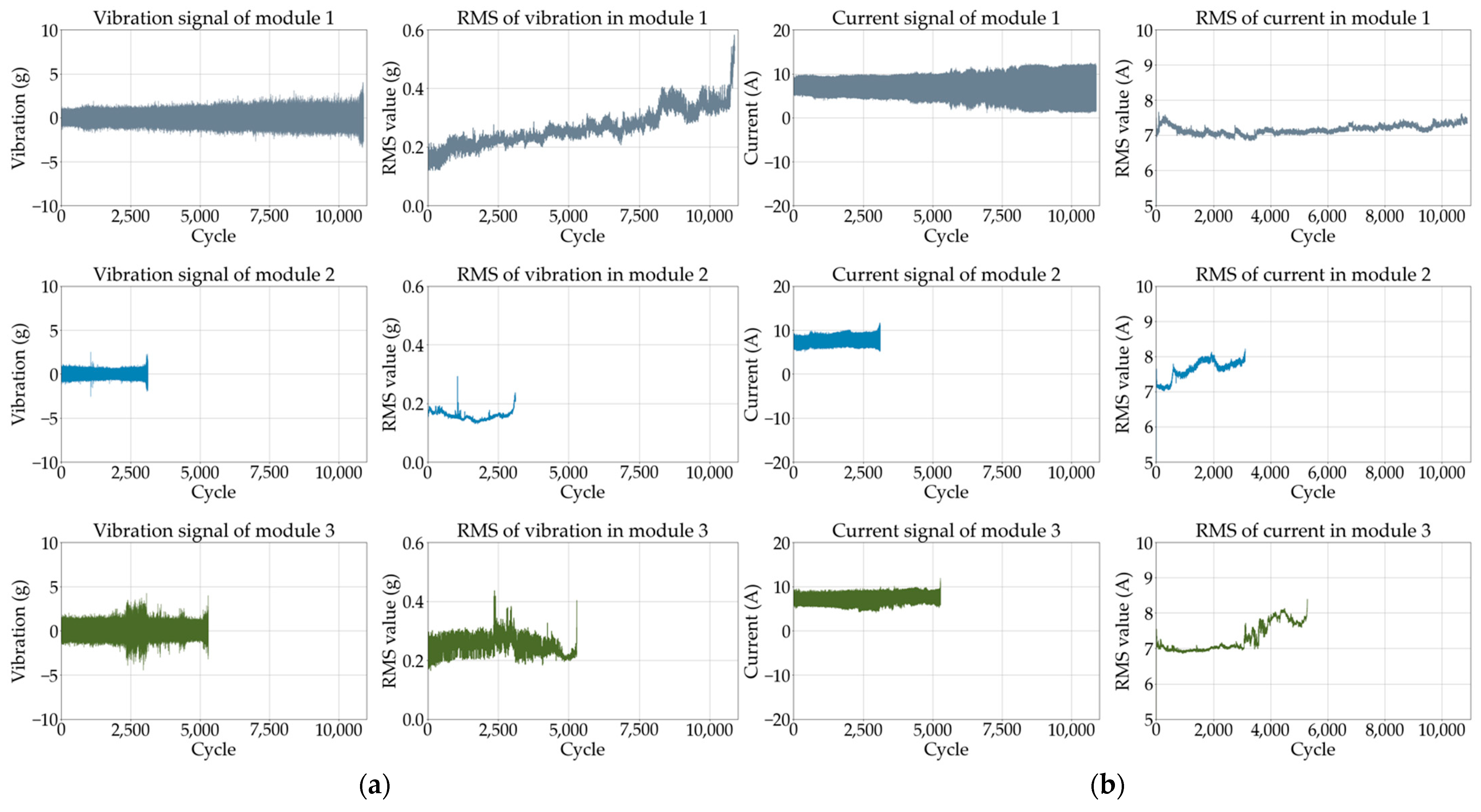
4.1. Anomaly Detection Based on Statistical Features
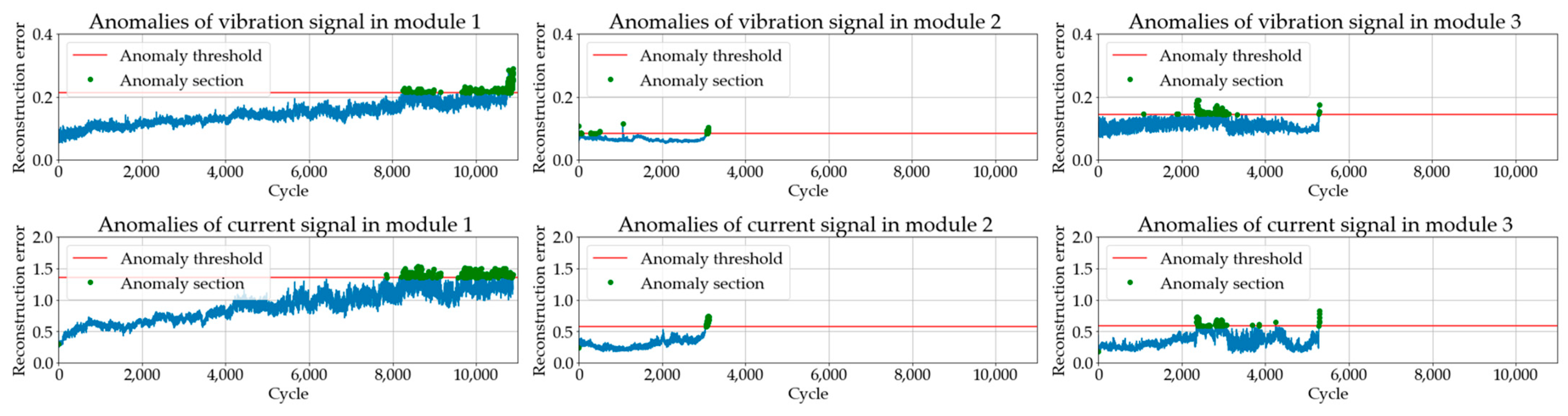
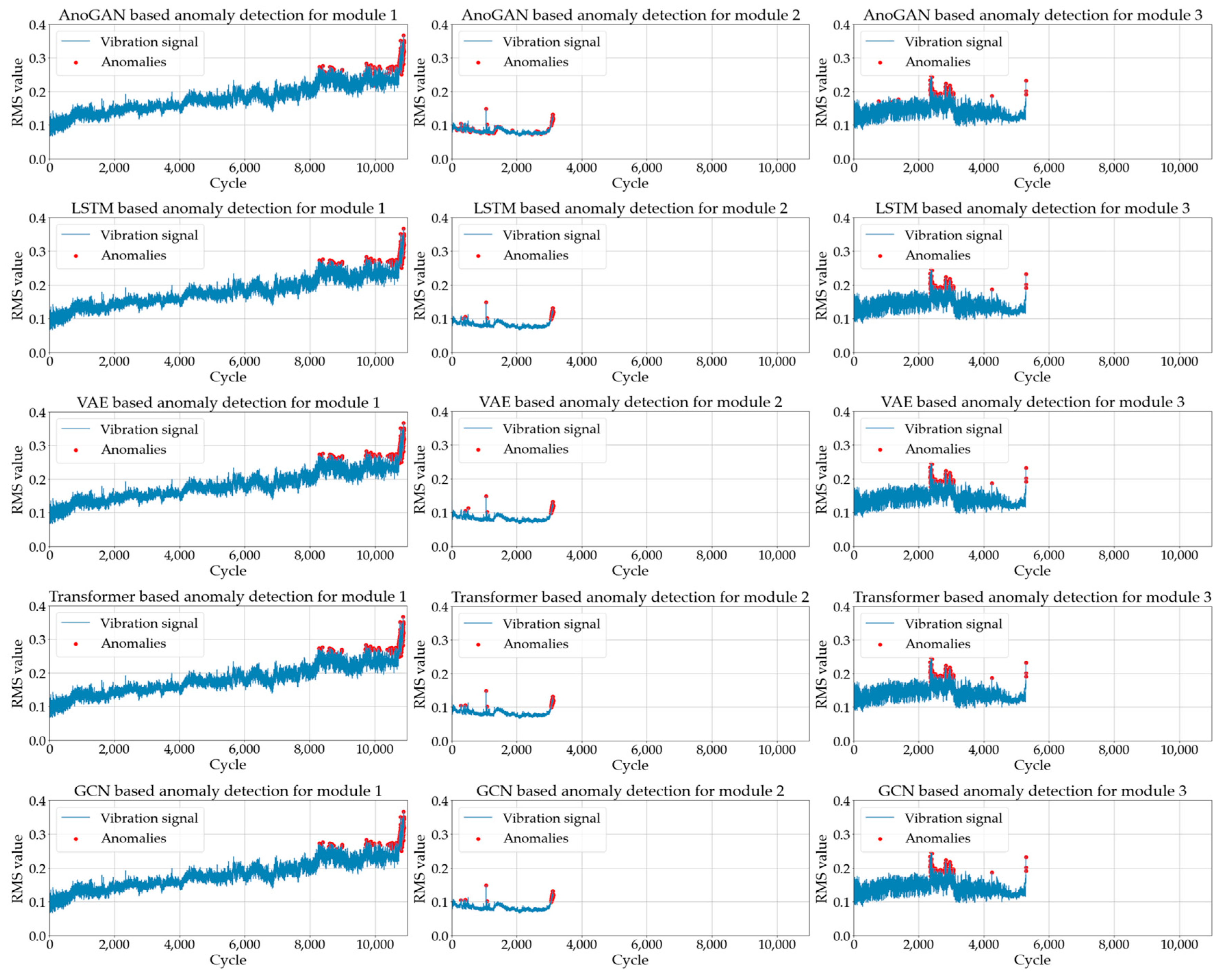
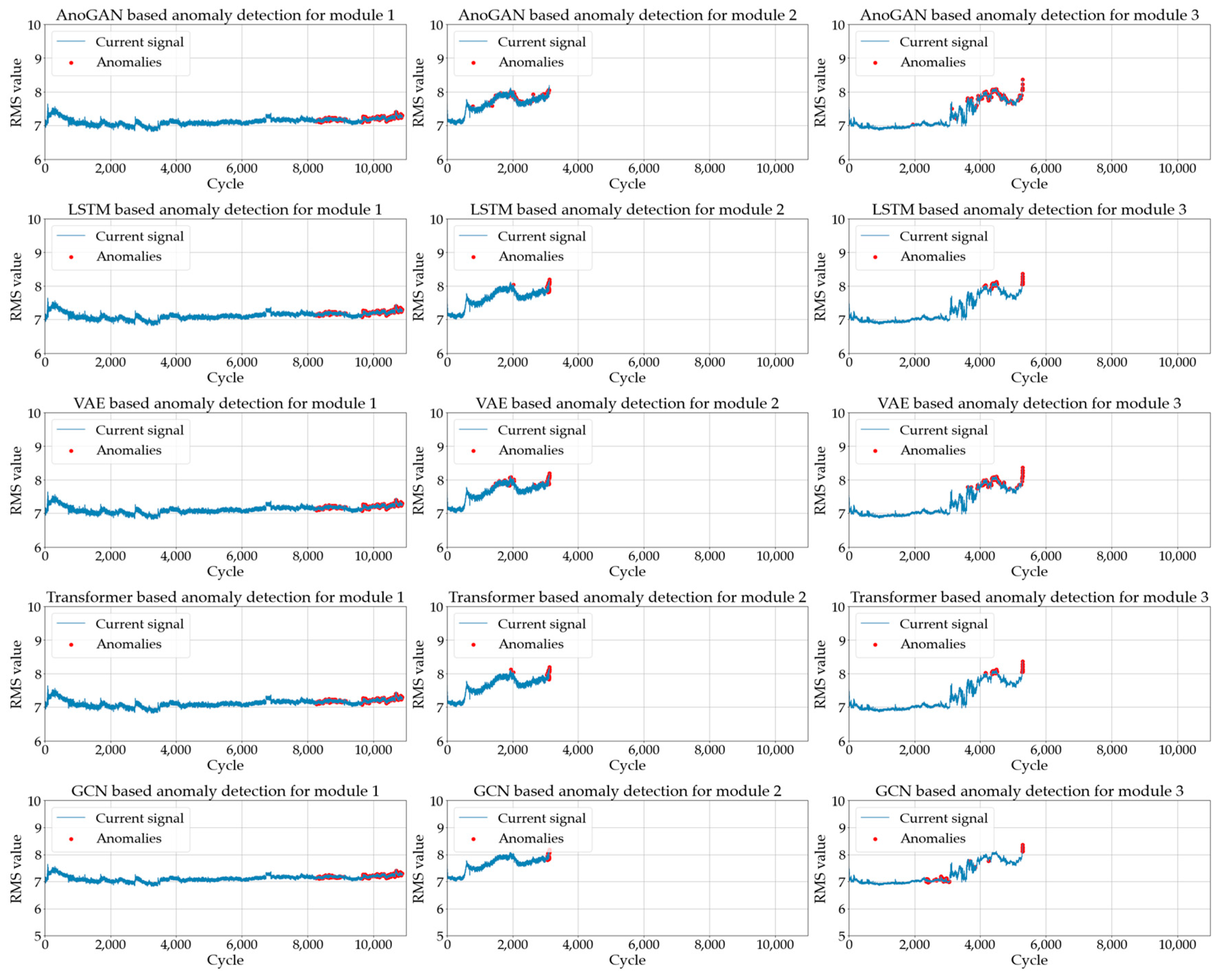
4.2. Anomaly Detection Based on a Deep Learning Model
| Algorithm 1 GCN-VAE Based Anomaly Detection |
| Require: train and test dataset , 01: Initialize: GCN model , VAE model , optimizer , 02: Define Loss function 03: Construct graph from 04: For each epoch : 05: For each mini-batch from 06: Compute GCN output 07: Compute 08: Update GCN weights using and 09: end for 10: For each mini-batch from : 11: Encode GCN output into latent space: 12: Reconstruct data from latent space: 13: Compute VAE reconstruction loss 14: Update VAE weights using and 15: end for 16: Compute overall loss 17: end for 18: Anomaly detection on : 19: For each node : 20: Compute reconstruction error 21: end for 22: Return: Anomalies detected where |
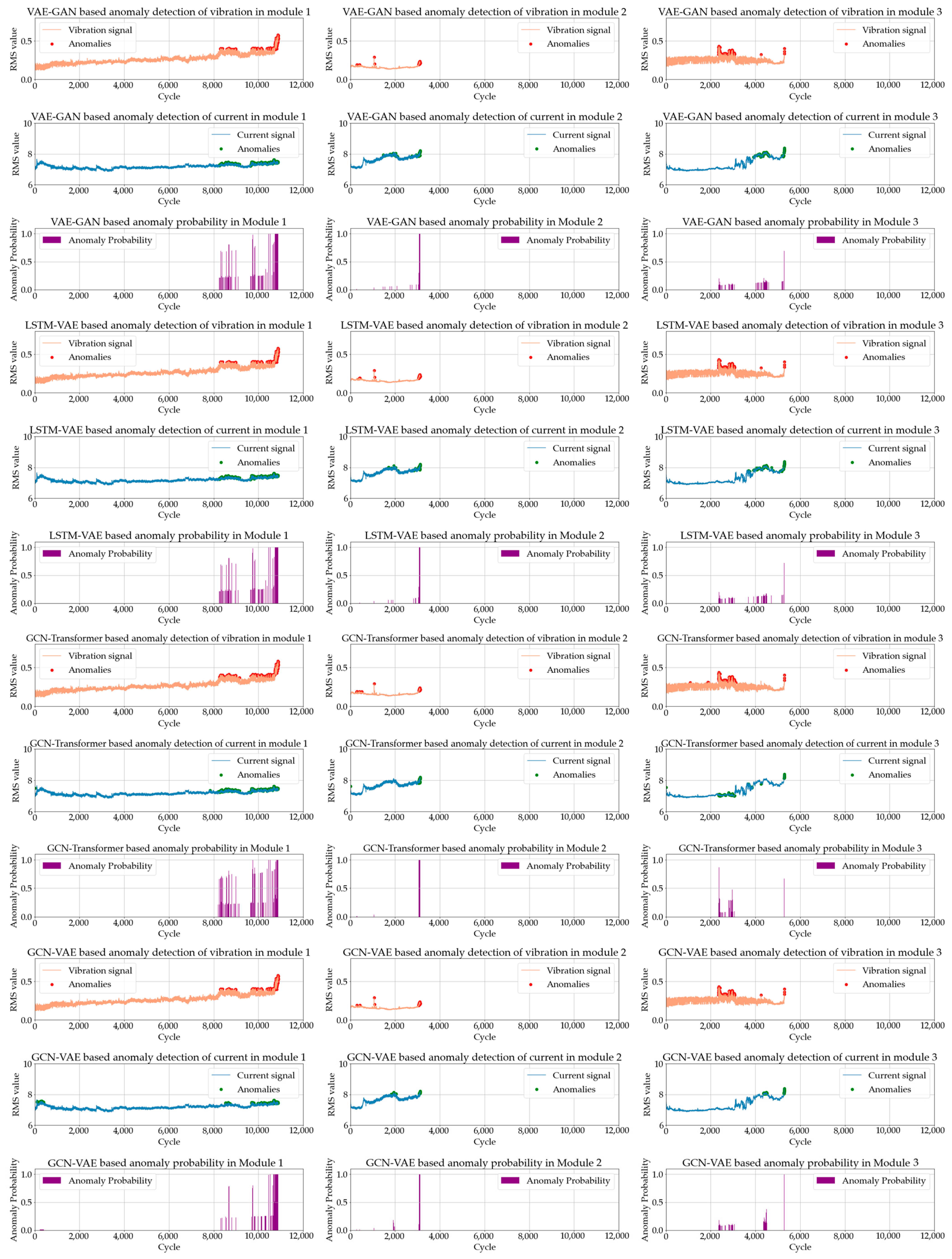
- In Module 1, all models effectively detected anomalies in the latter part of the data, with particularly strong performance observed from 50 cycles before failure, where all models achieved an anomaly score of 1. At the 200-cycle mark, the ranking of anomaly scores was as follows: GCN-VAE, GCN-Transformer, VAE-GAN, and LSTM-VAE. The superior performance of the proposed GCN-VAE model can be attributed to its ability to effectively leverage both spatial and temporal dependency features. Although the GCN-Transformer model also demonstrated strong performance, the integration of VAE’s reconstruction-based anomaly detection likely provided the GCN-VAE model with a distinct advantage in identifying subtle pre-failure anomalies.
- In Module 2, the GCN-Transformer model recorded slightly higher anomaly scores compared to the other three models up to 100 cycles before failure. However, as the data approached failure (50, 20, and 10 cycles before failure), all deep learning models achieved an anomaly score of 1, demonstrating robust detection performance. This indicates that all models effectively detect anomalies as the system nears failure. Additionally, the GCN-VAE model consistently maintained high performance throughout, confirming its capability to detect subtle warning signs even in the earlier cycles leading up to failure.
- In Module 3, all deep learning models exhibited relatively lower anomaly scores compared to Modules 1 and 2, with weaker performance observed even in the pre-failure region. This reduced performance can be attributed to the original signals in Module 3, which exhibited higher noise levels and complex distortions compared to Modules 1 and 2, making anomaly detection more challenging. At 10 cycles before failure, the anomaly scores were ranked as follows: GCN-VAE, LSTM-VAE, VAE-GAN, and GCN-Transformer. The GCN-Transformer effectively modeled spatial and temporal dependencies through its graph and attention mechanisms but lacked a reconstruction-based approach, limiting its ability to detect subtle anomalies. In contrast, the GCN-VAE model consistently achieved the highest anomaly scores across all pre-failure cycles. By leveraging its reconstruction-based capabilities, the GCN-VAE model demonstrated robust and superior anomaly detection performance, even in challenging conditions characterized by high noise levels and complex data distributions.
- Integration of Spatial and Temporal Dependencies: The GCN component effectively captures spatial and relational features by modeling interactions between data points through graph structures. By incorporating temporal dependencies, the model is able to identify subtle patterns in time-series data that are critical for early anomaly detection. This integration enables the GCN-VAE model to learn complex relationships that may be overlooked by traditional approaches.
- Reconstruction-Based Anomaly Detection: The VAE component adds a critical layer of sensitivity by learning the underlying distribution of normal data and identifying deviations through reconstruction errors. This mechanism is particularly advantageous in pre-failure scenarios, where subtle anomalies may remain undetected by other models. The combination of VAE’s reconstruction-based approach with GCN’s feature extraction provides the GCN-VAE model with an edge in accurately detecting early fault indicators.
- Adaptability to Challenging Data Distributions: The experimental results, especially in Module 3, demonstrate the GCN-VAE model’s robustness in handling complex and noisy datasets. While other models showed reduced performance under such conditions, the GCN-VAE model consistently achieved high anomaly scores, reflecting its adaptability and effectiveness in varying data environments.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rousopoulou, V.; Vafeiadis, T.; Nizamis, A.; Iakovidis, I.; Samaras, L.; Kirtsoglou, A.; Georgiadis, K.; Ioannidis, D.; Tzovaras, D. Cognitive analytics platform with AI solutions for anomaly detection. Comput. Ind. 2022, 134, 103555. [Google Scholar] [CrossRef]
- Vincent, M.; Thomas, S.; Suresh, S.; Prathap, B.R. Enhancing Industrial Equipment Reliability: Advanced Predictive Maintenance Strategies Using Data Analytics and Machine. In Proceedings of the IEEE International Conference on Contemporary Computing and Communications, Bangalore, India, 15–16 March 2024. [Google Scholar]
- Serradilla, O.; Zugasti, E.; Okariz, J.R.; Rodriguez, J.; Zurutuza, U. Adaptable and Explainable Predictive Maintenance: Semi-Supervised Deep Learning for Anomaly Detection and Diagnosis in Press Machine Data. App. Sci. 2021, 11, 7376. [Google Scholar] [CrossRef]
- Kumar, P.; Khalid, S.; Kim, H.S. Prognostics and Health Management of Rotating Machinery of Industrial Robot with Deep Learning Applications-A Review. Mathematics 2023, 11, 3008. [Google Scholar] [CrossRef]
- Deng, C.; Deng, Z.; Lu, S.; He, M.; Miao, J.; Peng, Y. Fault Diagnosis Method for Imbalanced Data Based on Multi-Signal Fusion and Improved Deep Convolution Generative Adversarial Network. Sensors 2023, 23, 2542. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Lin, T.; Feng, K.; Zhu, Y.; Liu, Z.; Yan, K. A Systematic Review on Imbalanced Learning Methods in Intelligent Fault Diagnosis. IEEE Trans. Instrum. Meas. 2023, 72, 3508535. [Google Scholar] [CrossRef]
- Soori, M.; Dastres, R.; Arezoo, B.; Jough, F.K.G. Intelligent robotic systems in Industry 4.0: A review. J. Adv. Manuf. Sci. Technol. 2024, 4, 2024007. [Google Scholar]
- Monteiro, R.P.; Lozada, M.C.; Mendieta, D.R.C.; Loja, R.V.S.; Filho, C.J.A.B. A hybrid prototype selection-based deep learning approach for anomaly detection in industrial machines. Expert Syst. Appl. 2022, 204, 117528. [Google Scholar] [CrossRef]
- Ahmed, I.; Ahmed, M.; Chehri, A.; Jeon, G. A Smart-Anomaly-Detection System for Industrial Machines Based on Feature Autoencoder and Deep Learning. Micromachines 2023, 14, 154. [Google Scholar] [CrossRef] [PubMed]
- Webert, H.; Döß, T.; Kaupp, L.; Simons, S. Fault Handling in Industry 4.0: Definition, Process and Applications. Sensors 2022, 22, 2205. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Raouf, I.; Kim, H.S. Transfer learning for servomotor bearing fault detection in the industrial robot. Adv. Eng. Softw. 2024, 194, 103672. [Google Scholar] [CrossRef]
- Sabry, A.H.; Amirulddin, U.A.B.U. A review on fault detection and diagnosis of industrial robots and multi-axis machines. Results Eng. 2024, 23, 102397. [Google Scholar] [CrossRef]
- Graabæk, S.G.; Ancker, E.V.; Fugl, A.R.; Christensen, A.L. An Experimental Comparison of Anomaly Detection Methods for Collaborative Robot Manipulators. IEEE Access 2023, 11, 65834–65848. [Google Scholar] [CrossRef]
- Deng, C.; Song, J.; Chen, C.; Wang, T.; Cheng, L. Semi-Supervised Informer for the Compound Fault Diagnosis of Industrial Robots. Sensors 2024, 24, 3732. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Liu, Y.; Jin, Y.; Chen, J.; Wu, H. A Novel Semi-Supervised Learning Approach for Network Intrusion Detection on Cloud-Based Robotic System. IEEE Access 2018, 6, 50927–50938. [Google Scholar] [CrossRef]
- Cohen, J.; Ni, J. Semi-Supervised Learning for Anomaly Classification Using Partially Labeled Subsets. J. Manuf. Sci. Eng. 2022, 144, 061008. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, M.; Yin, X.; Zhang, J.; Meijering, E.; Hu, J. Deep Learning in Diverse Intelligent Sensor Based Systems. Sensors 2023, 23, 62. [Google Scholar] [CrossRef]
- Choi, K.; Yi, J.; Park, C.; Yoon, S. Deep Learning for Anomaly Detection in Time-Series Data: Review, Analysis, and Guidelines. IEEE Access 2021, 9, 120043–120065. [Google Scholar] [CrossRef]
- He, Q.; Wang, G.; Wang, H.; Chen, L. Multivariate time-series anomaly detection via temporal convolutional and graph attention networks. J. Intell. Fuzzy Syst. 2023, 44, 5953–5962. [Google Scholar] [CrossRef]
- Fan, Z.; Wang, Y.; Meng, L.; Zhang, G.; Qin, Y.; Tang, B. Unsupervised Anomaly Detection Method for Bearing Based on VAE-GAN and Time-Series Data Correlation Enhancement. IEEE Sens. J. 2023, 23, 29345–29356. [Google Scholar] [CrossRef]
- Ou, X.; Wen, G.; Huang, X.; Su, Y.; Chen, X.; Lin, H. A deep sequence multi-distribution adversarial model for bearing abnormal condition detection. Measurement 2021, 182, 109529. [Google Scholar] [CrossRef]
- Yang, G.; Tao, H.; Du, R.; Zhong, Y. Compound Fault Diagnosis of Harmonic Drives Using Deep Capsule Graph Convolutional Network. IEEE Trans. Ind. Electron. 2023, 70, 4189–4195. [Google Scholar] [CrossRef]
- Yan, J.; Cheng, Y.; Wang, Q.; Liu, L.; Zhang, W.; Jin, B. Transformer and Graph Convolution-Based Unsupervised Detection of Machine Anomalous Sound Under Domain Shifts. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 8, 2827–2842. [Google Scholar] [CrossRef]
- Jin, M.; Koh, H.Y.; Wen, Q.; Zambon, D.; Alippi, C.; Webb, G.I.; King, I.; Pan, S. A Survey on Graph Neural Networks for Time Series: Forecasting, Classification, Imputation, and Anomaly Detection. arXiv 2024, arXiv:2307.03759v3. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.H.; Nguyen, C.N.; Dao, X.T.; Duong, Q.T.; Kim, D.P.T.; Pham, M.T. Variational Autoencoder for Anomaly Detection: A Comparative Study. arXiv 2024, arXiv:2408.13561v1. [Google Scholar]
- Collin, T.; Kindlmann, G.; Scott, L.R. An Adaptive Savitsky-Golay Filter for Smoothing Finite Element Computation. arXiv 2019, arXiv:1911.00790v2. [Google Scholar]
- Ochieng, P.J.; Maróti, Z.; Dombi, J.; Krész, M.; Békési, J.; Kalmár, T. Adaptive Savitzky–Golay Filters for Analysis of Copy Number Variation Peaks from Whole-Exome Sequencing Data. Information 2023, 14, 128. [Google Scholar] [CrossRef]
- Yun, H.; Kim, H.; Jeong, Y.H.; Martin, J.B.G. Autoencoder-based anomaly detection of industrial robot arm using stethoscope-based internal sound sensor. J. Intell. Manuf. 2023, 34, 1427–1444. [Google Scholar] [CrossRef]
- Jung, Y.; Park, E.G.; Jeong, S.H.; Kim, J.H. AI-Based Anomaly Detection Techniques for Structural Fault Diagnosis Using Low-Sampling-Rate Vibration Data. Aerospace 2024, 11, 509. [Google Scholar] [CrossRef]
- Wang, F.; Wang, K.; Yao, B. Time series anomaly detection with reconstruction-based state-space models. arXiv 2023, arXiv:2303.03324v3. [Google Scholar]
- Sun, S.; Ding, H. Fault Feature Extraction Based on Unsupervised Graph Embedding for Harmonic Reducers Diagnosis. In The 2nd International Conference on Mechanical System Dynamics; Springer: Singapore, 2023; pp. 3375–3389. [Google Scholar]
- Chen, Z.; Xu, J.; Alippi, C.; Ding, S.X.; Shardt, Y.; Peng, T.; Yang, C. Graph neural network-based fault diagnosis: A review. arXiv 2021, arXiv:2111.08185. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2017, arXiv:1609.02907v4. [Google Scholar]
- Zhang, S.; Ye, F.; Wang, B.; Habetler, T.G. Semi-Supervised Learning of Bearing Anomaly Detection via Deep Variational Autoencoders. arXiv 2019, arXiv:1912.01096v2. [Google Scholar]
- Ghanim, J.; Issa, M.; Awad, M. An Asymmetric Loss with Anomaly Detection LSTM Framework for Power Consumption Prediction. arXiv 2023, arXiv:2302.10889. [Google Scholar]
- Baidya, R.; Jeong, H. Anomaly Detection in Time Series Data Using Reversible Instance Normalized Anomaly Transformer. Sensors 2023, 23, 9272. [Google Scholar] [CrossRef]
- Li, J.; Izakian, H.; Pedrycz, W.; Jamal, I. Clustering-based anomaly detection in multivariate time series data. Appl. Soft Comput. J. 2021, 100, 106919. [Google Scholar] [CrossRef]
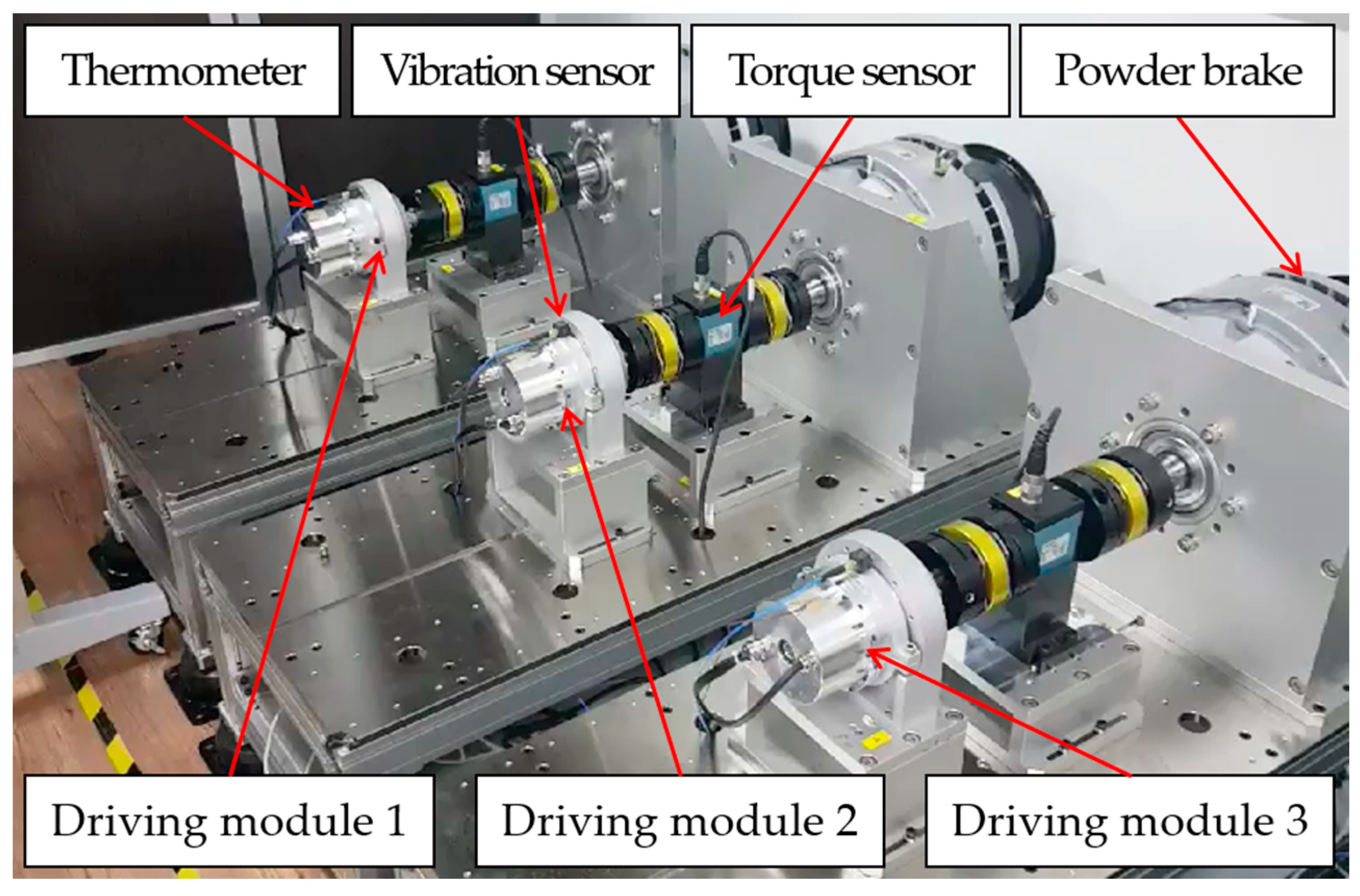
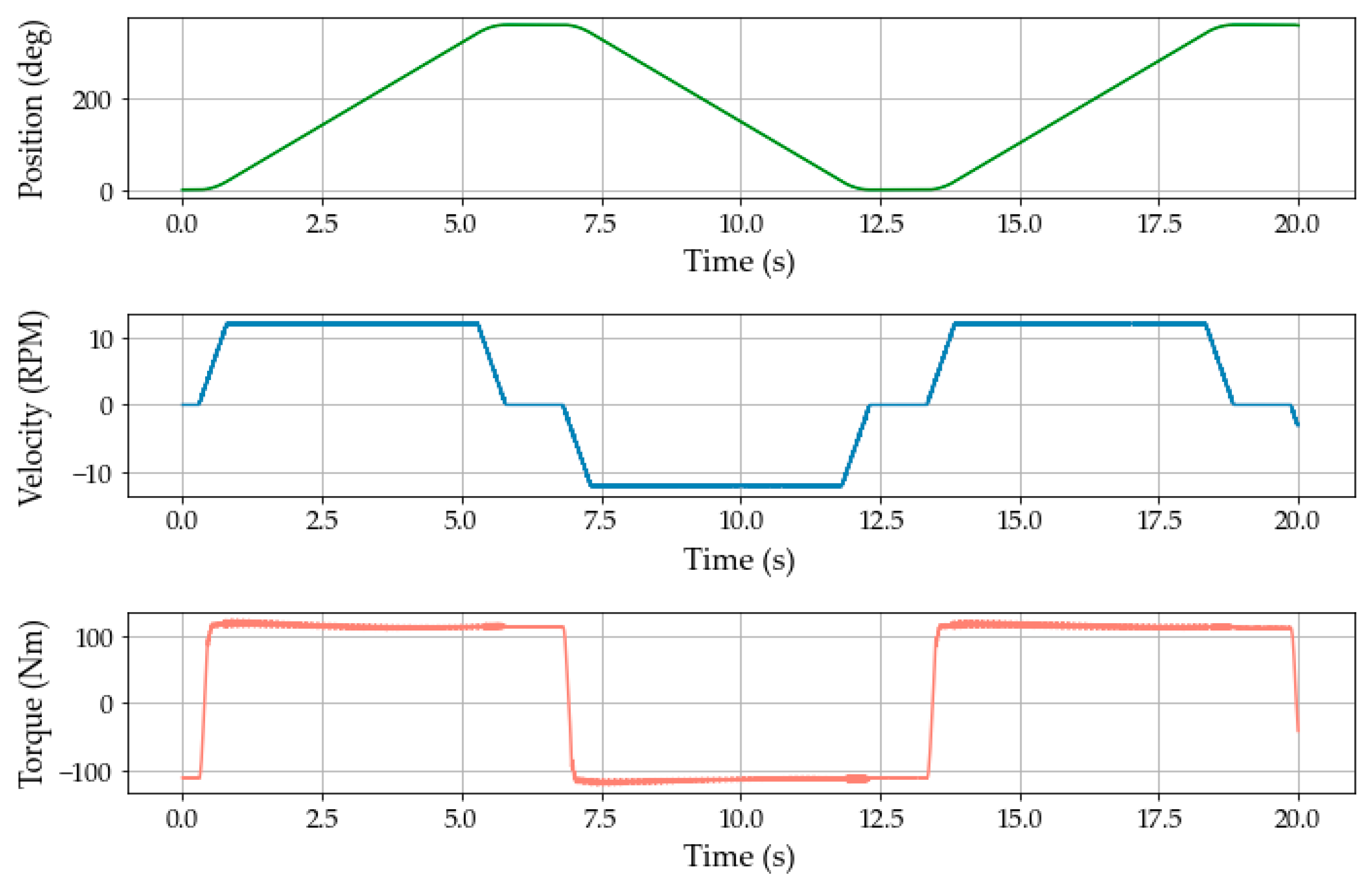
| Torque | Const. Velocity | Acc/Dec Velocity | Const. Velocity Time | Acc/Dec Time | Stop Time | Cycle |
|---|---|---|---|---|---|---|
| 113 Nm | 12 RPM | 24 RPM/s2 | 4.5 s | 0.5 s | 1 s | 13 s |
| Train Module | Test Module | Data | Matching Accuracy of Statistical Features and Learning Models (%) | ||||
|---|---|---|---|---|---|---|---|
| AnoGAN | LSTM | VAE | Transformer | GCN | |||
| 1, 2 | 3 | Vibration | 98.9418 | 98.7150 | 99.3197 | 99.3953 | 99.3197 |
| Current | 96.1640 | 96.3152 | 96.3152 | 96.3152 | 99.6788 | ||
| 1, 3 | 2 | Vibration | 96.3426 | 99.2942 | 99.4225 | 99.4225 | 99.4225 |
| Current | 96.3747 | 98.4921 | 98.6846 | 99.3904 | 99.9038 | ||
| 2, 3 | 1 | Vibration | 99.0702 | 99.0702 | 99.2311 | 99.3018 | 99.3018 |
| Current | 98.9361 | 98.9003 | 99.2758 | 99.2926 | 99.0170 | ||
| Average | Vibration | 98.1182 | 99.0265 | 99.3245 | 99.3732 | 99.3480 | |
| Current | 97.1583 | 97.9025 | 98.0859 | 98.3327 | 99.5332 | ||
| Test Module | Model | Anomaly Scores for Pre-Failure Cycles | ||||||
|---|---|---|---|---|---|---|---|---|
| Total Cycle | 500 Cycle | 200 Cycle | 100 Cycle | 50 Cycle | 20 Cycle | 10 Cycle | ||
| 1 | VAE-GAN | 0.0221 | 0.3534 | 0.7664 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| LSTM-VAE | 0.0219 | 0.3461 | 0.7509 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| GCN-Trans | 0.0186 | 0.5018 | 0.8217 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| GCN-VAE | 0.0222 | 0.4231 | 0.8776 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| 2 | VAE-GAN | 0.0175 | 0.1063 | 0.2648 | 0.5268 | 1.0000 | 1.0000 | 1.0000 |
| LSTM-VAE | 0.0169 | 0.1035 | 0.2575 | 0.5140 | 1.0000 | 1.0000 | 1.0000 | |
| GCN-Trans | 0.0185 | 0.1150 | 0.2875 | 0.5751 | 1.0000 | 1.0000 | 1.0000 | |
| GCN-VAE | 0.0180 | 0.1032 | 0.2581 | 0.5161 | 1.0000 | 1.0000 | 1.0000 | |
| 3 | VAE-GAN | 0.0054 | 0.0093 | 0.0233 | 0.0451 | 0.0781 | 0.1726 | 0.3149 |
| LSTM-VAE | 0.0054 | 0.0115 | 0.0288 | 0.0520 | 0.0945 | 0.2210 | 0.3799 | |
| GCN-Trans | 0.0070 | 0.0058 | 0.0144 | 0.0289 | 0.0577 | 0.1443 | 0.2885 | |
| GCN-VAE | 0.0077 | 0.0201 | 0.0503 | 0.1006 | 0.2012 | 0.5029 | 0.7029 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, S.-H.; An, D.; Lee, I.; Lee, S. Anomaly Detection Based on Graph Convolutional Network–Variational Autoencoder Model Using Time-Series Vibration and Current Data. Mathematics 2024, 12, 3750. https://doi.org/10.3390/math12233750
Choi S-H, An D, Lee I, Lee S. Anomaly Detection Based on Graph Convolutional Network–Variational Autoencoder Model Using Time-Series Vibration and Current Data. Mathematics. 2024; 12(23):3750. https://doi.org/10.3390/math12233750
Chicago/Turabian StyleChoi, Seung-Hwan, Dawn An, Inho Lee, and Suwoong Lee. 2024. "Anomaly Detection Based on Graph Convolutional Network–Variational Autoencoder Model Using Time-Series Vibration and Current Data" Mathematics 12, no. 23: 3750. https://doi.org/10.3390/math12233750
APA StyleChoi, S.-H., An, D., Lee, I., & Lee, S. (2024). Anomaly Detection Based on Graph Convolutional Network–Variational Autoencoder Model Using Time-Series Vibration and Current Data. Mathematics, 12(23), 3750. https://doi.org/10.3390/math12233750






