Abstract
Recently, lossy source coding based on linear block code has been designed using the duality principle, i.e., the channel decoding algorithm is employed to realize the lossy source coding. However, the quantization structure has not been analyzed in this compression technique, and the codebook design does not match the source characteristics well. Hence, the compression performance is not so good. To overcome this problem, the codebook design is correlated with the quantization structure in this work. It is found that the lossy source coding based on the linear block code can be defined as lattice vector quantization (VQ), which provides a new analytical perspective for the coding methodology. Then, the VQ scheme is generalized with the noisy channel to evaluate the transmission robustness of the continuous source compression. Finally, the codebook of the VQ scheme is optimally designed by uniforming the radiuses of the quantization subspace to reduce the quantization distortion. The proposed codebook outperforms existing codes in terms of its proximity to the rate–distortion limit, while also exhibiting enhanced robustness against channel noise.
MSC:
68P30
1. Introduction
Lossy source coding provides a high-efficiency method for data compression, which is useful for saving communication bandwidth and reducing hardware complexity in the physical layer [1,2,3]. Conventionally, linear block codes, such as low-density parity-check (LDPC) codes, are employed for source and channel coding due to their good hardware realizability [4,5,6]. The code matrices of linear block codes are different since the source coding aims to realize data compression and the channel coding is for error correction. However, this is not a hardware-friendly design in chip manufacturing. Recent works have embraced the principle of “duality”, which suggests repurposing the channel code as a source code and implements channel-decoding techniques for the lossy source coding [7,8]. Based on the principle of duality, the cost of chip manufacturing can be reduced by reusing the source and the channel coding modules in circuit implementation.
It has been demonstrated that LDPC code has a capacity-approaching property, and can be applied for channel coding with good error correction performance. The duality principle indicates that lossy compression based on LDPC code can also approach the rate–distortion limit of the binary source [9,10]. To simplify the parity-check matrix of the LDPC code, the protograph LDPC (P-LDPC) code is introduced to compress the binary sources with equal probability [11]. Compared with the parity-check matrix of the LDPC code, the protomatrix of the P-LDPC code has lower encoding and decoding complexities [12,13,14]. Referring to the duality principle, the belief propagation (BP) algorithm, which achieves good decoding performance, is used to implement the lossy source coding. For instance, the reinforced BP (RBP) algorithm accomplishes the lossy source coding in [15]. Then, the shuffled RBP algorithm was proposed to improve the encoding efficiency for compressing the binary source [11]. Subsequently, the lossy compression of the Gaussian source was considered. Ref. [16] proposes a multi-level coding (MLC) structure to preprocess the floating sequence by mapping one float into a bit string. To further increase the compression efficiency, the BP algorithm is modified to transform one float into one bit in [17]. In addition, the source model is extended to the general source by applying neural networks (NNs) in [18], including the Gaussian and Laplacian source models.
The aforementioned works focus on improving the compression efficiency using different methods which can be classified into two categories; one optimally searches the better codebooks, the other designs the BP-like algorithms. The optimization principle of these works is to improve the code matrices and BP-like algorithms based on the mutual information transfer (MIT) strategy [17]. The MIT strategy assumes the minimum distortion to be the maximum mutual information, and it is an optimization criterion for searching the objective codebook.
However, the rate–distortion performances of these works still need to be improved. The main reasons are the following: First, more coding gains are obtained in channel coding than lossy source coding since the data compression generates more distortion and its structure is more complicated. Second, the MIT strategy is only appropriate for optimizing lossy compression based on the determined source, i.e., it lacks universality for variable sources. Since the codebook and the coding algorithm should be designed based on the source characteristic, it is difficult to achieve compatible performance for different source distributions. Third, it is unreasonable to evaluate data compression systems using only the MIT strategy since the shape of the quantization space should also be another optimization criterion. In consequence, a new strategy should be explored as a supplement to the MIT strategy.
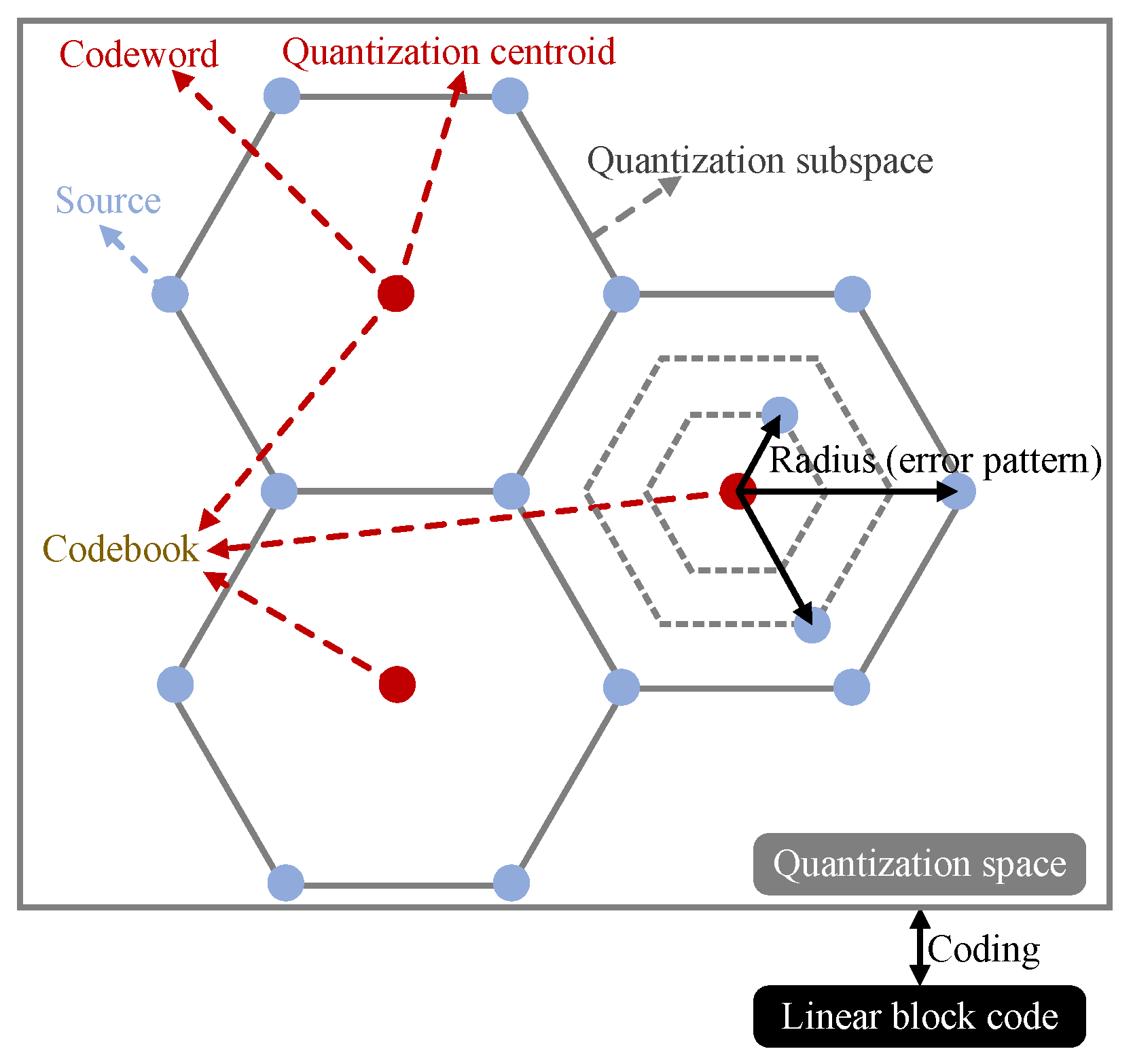
Lossy source coding based on linear block code can be regarded as a VQ scheme since the codeword is N-dimensional. The VQ is a classical quantization technique in signal processing that allows the modeling of probability density functions by the distribution of prototype vectors [19,20,21,22,23,24,25]. Refs. [26,27] indicate that the compression performance mainly depends on the spatial structure of the quantizer. In this case, the rate–distortion performance can be optimized by improving the quantization space. The coding relation between the quantization space and the linear block code is shown in Figure 1. The codebook optimization of the linear block code aims to allocate the quantization space according to the source distribution appropriately since the codebook contains all the central codewords of the quantization subspaces. Hence, the radius of the quantization subspace can be determined by the coding property of the linear block code.
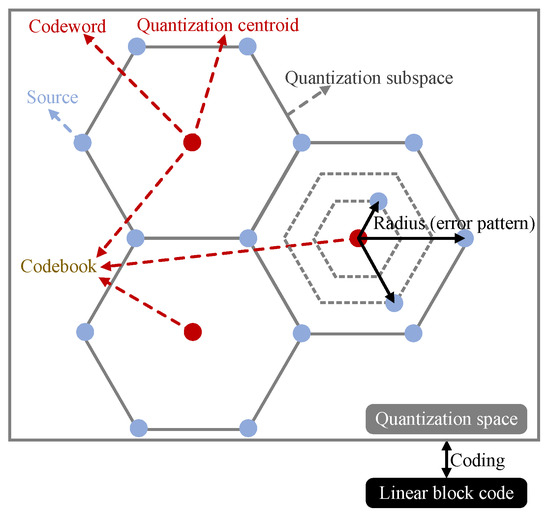
Figure 1.
The coding relation between the quantization space and the linear block code.
Referring to Figure 1, the lossy source coding based on block code can be defined as a lattice VQ scheme since the shapes of the quantization subspaces are regular. As the lattice VQ scheme has some advantages [28], namely, intuitive architecture and simple realization, the coding methodology will be simplified. The error pattern of the block code is expressed as the radius of a quantization subspace. Usually, all the error patterns are similar in one codeword, so all the quantization subspaces have the same shape. However, the quantization subspaces are inhomogeneous in N-dimensional spaces. In this case, each source codeword has an unequal distance from the center codeword at any dimension, which will increase the quantization distortion.
There is a technical challenge in the existing VQ scheme in terms of compressing the source with variable statistical properties. This source compression needs a more complicated quantization structure, which will exponentially increase the design complexity. To overcome this challenge, ref. [29] designed a VQ scheme based on block code, and showed that the codebook based on the short block code will generate less quantization distortion. However, split and multistage structures are considered in the VQ scheme with higher complexities. In addition, its codebook is not designed using the duality principle. Hence, the structural complexity and performance improvement needed to be solved in [29].
To overcome the above issues, a VQ scheme based on linear block code is proposed and the P-LDPC code is designed based on the quantization structure in this work. The motivations can summarized as follows: First, the preprocessing module is modified with a scalar quantizer and linear decoding is used in the proposed VQ scheme, which will significantly reduce the structural complexity. The VQ structure is employed for the codeword matching module for quantization, which is implemented by the BP algorithm with lower complexity. Second, the codebook is optimized based on the quantization structure, where the error correction property is used to improve the compression performance. With the codebook optimization, all the quantization subspaces become homogeneous to improve the quantization performance. In this case, the proposed VQ scheme is hardware friendly with lower complexity and better compression performance for practical implementation.
In practice, transmission distortion deriving from the noisy channel also needs to be considered in the VQ scheme, while the compression distortion of quantization is influenced by the transmission distortion. If the VQ scheme is robust over the noisy channel, the transmission power will be reduced. Ref. [30] concludes that the quantization performance based on LDPC code is increased by channel noise. To solve the problem, ref. [30] introduces index allocation to ameliorate the channel robustness. The existing works demonstrate that index allocation is effective for resisting channel noise and for obtaining a better compression performance in the VQ scheme [26,28,31,32]. For instance, ref. [29] designed a block coding method based on linear mapping to implement index allocation by employing linear prediction, and [33] modifies the simulated annealing algorithm to appropriately allocate the indices. Hence, the index allocation is also supplemented to optimally design the P-LDPC code to reduce the noisy influence in this work. It should be noted that reference [30] only considers the lossy compression of the binary source over nosiy channels, while the continuous source is generalized in this work.
Reference [30] finds that the distortion caused by channel noise is reduced when the weight of the check-parity matrix is decreased. Based on this discovery, a search global degree allocation (S-GDA) algorithm is proposed to optimally design the protomatrix of the P-LDPC code with lower weight. The theoretical derivation of the S-GDA algorithm is demonstrated in this work. Furthermore, the P-LDPC codes are optimally searched with the properties of the channel noise resistance and variable source adaption. The validity of the code design based on the quantization structure is evaluated by the relation between the compression distortion and the code rate, and the code robustness is presented by the performance of the compression distortion and the signal-to-noise ratio (SNR). The availability of the proposed scheme is verified by the coding gains of the objective codes. In this work, it is illustrated that the channel distortion tends towards zero in the higher SNR since better compression performance can be obtained in the higher SNR and good robustness performance is present in the lower SNR.
Overall, the three main contributions can be summarized as follows:
(1) The lossy source coding based on linear block code is analyzed by the lattice VQ scheme, which is a new analytical perspective for the coding methodology.
(2) A general VQ scheme over the noisy channel is proposed with lower structural complexity, and it has universality for variable source distributions.
(3) A valid improvement of the coding performance is designed by the quantization structure, and its principle is equalizing the radiuses of the quantization subspace to reduce the quantization distortion.
The rest of this paper is organized as follows: The proposed VQ scheme and its methodology are introduced in Section 2. In Section 3, the P-LDPC codes are designed for different source distributions over the noisy channels. The simulation results and analyses are presented in Section 4. The conclusion is summarized in Section 5.
2. VQ Scheme over Noisy Channel
2.1. Generalized VQ Scheme
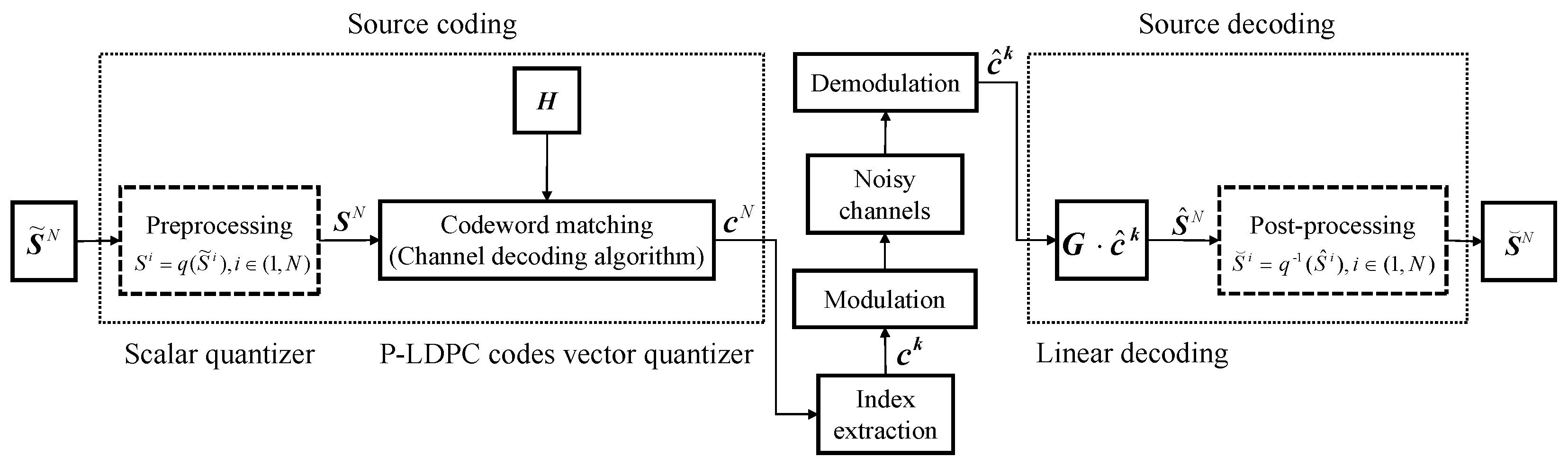
The proposed VQ scheme based on P-LDPC code over the noisy channel is shown in Figure 2, and it contains source coding, source decoding, and coding channel modules. The source is a joint independent and identically distributed sequence of length N, and presents the reconstructed source.
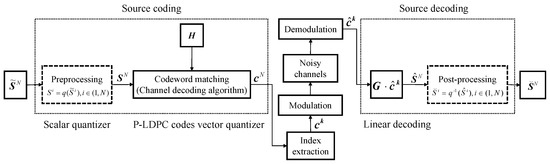
Figure 2.
The proposed VQ scheme based on linear block codes over noisy channels.
In the source coding module, the source sequence is preprocessed by a scalar quantizer, and each variable is quantified as a binary of length L as follows:
where q represents the preprocessor of scalar quantization, represents a binary sequence or one bit since its length L can be taken any positive integer, the parameters satisfy and , and is the set of positive integers.
Each local sampling point is quantified to achieve the highest bit rate. Since all the scalar quantizers are the same at each sampling point, this provides a feasible condition for constructing a regular VQ scheme based on P-LDPC code. It should be noted that the preprocessor performance will not influence the final design of the P-LDPC codes. The reason is that each sampling point needs to be compressed with the same expected distortion to change the VQ scheme from irregular to regular. In this case, the quantization complexity is simplified and the P-LDPC codes can be compatibly designed.
After that, the binary sequence will pass through the source coding module based on the P-LDPC codes. The quantization codebook is determined by the check-parity matrix of the P-LDPC code, and the codeword should be closest to the center of quantization subspace to obtain the better compression performance. The source is quantified as the legal codeword . The quantization subspace is determined by the codeword space, which is formed by the weight distribution of the P-LDPC codes.
In the transmission module, the index sequence of the codeword is extracted, and it is transmitted through the noisy channels as the receiving . is obtained by the information bits of length k. Hence, the compression rate is defined as
where R is the compression rate, N is signified as the length of , there are codewords encoded by bits, and .
In the source decoding module, the generator matrix corresponding to the check-parity matrix is multiplied with the demodulated to accomplish the linear decoding as follows:
After that, the source is reconstructed as
where is the post-processer which is a reverse of q, , and .
Overall, the distortion is mainly generated from two modules, the source coding and the channel noise modules. Hence, the total distortion of the VQ scheme is defined as
2.2. Coding Methodology of VQ Scheme
Different from the design of conventional quantization, the VQ scheme based on linear block code needs to be appropriately designed with the codebook and the source space. Generally, the compression performance is determined by the codebook and the source subspace. In [20], the locally optimal quantizer is obtained by a training process, which is iteratively updated by the generalized Lloyd algorithm (GLA) based on the initial codebook and subspace.
On the contrary, the proposed VQ scheme does not need the training process. The corresponding codebook is determined by the given parity-check matrix of the linear block code, and the subspace is related to the coding property of this linear block code. Hence, the compression performance of the proposed VQ scheme mainly depends on the employed linear block code. Replacing the training process by designing the linear block code, the structure of the proposed VQ scheme has lower complexity. In addition, source decoding is implemented by the linear decoding method, which reduces the decoding complexity compared with the look-up table operation in the existing methods.
In the proposed VQ scheme, the preprocessing module is necessary since the source statistic distributions are diversiform. The preprocessing will average the source probability distribution and allocates the compression rate to the corresponding probability density. For example, the quantization performance is locally optimized with subspace partitioning to reasonably allocate the compression rate in [34]. In this way, there will be multi-levels in quantization to refine the signal region while the code rate is increased with the constriction of the signal region. Hence, the preprocessing module is useful for improving the compression efficiency.
In the codeword matching module, the subspace is partitioned according to the block code. The source is replaced by the closest codeword, and these source subsets are centered on the codeword form of the quantization subspace. Then, the distance between the subspace with the codeword is calculated as
where “+” represents the modulo 2 addition, , is defined as the radius vector of the quantization subspace, and the codeword matching relation satisfies
This codeword matching relation indicates the proposed coding methodology as follows:
Then, the i-th quantization subspace can be expressed as
Assume that there are quantization subspaces in total, and each subspace contains source vectors. In this case, the number of radiuses is . For each codeword, the set of radiuses is the same, which is determined by the weight distribution of the parity-check matrix. Specifically, a set of radiuses is signified as .
The quantization subspace of lattice VQ is regular. Referring to the aforementioned methodology, it can be seen that the quantization based on the linear block code is lattice VQ. This structure is suitable for realizing high-dimensional quantization, and its regular subspace structure is appropriate for uniform quantization. Most of the lattice VQ can be obtained by linear calculations with lower coding complexity. For the lattice VQ, the generation matrix of the linear block code needs to be used as the system matrix, and the source decoding is implemented as
where and represent the reconstructed source and the demodulated codeword, respectively, and the check-parity matrix can be partitioned as follows:
where is an identity matrix of the dimension , represents a partition matrix of dimension , and . If the generation and the check-parity matrices are determined, the degrees of information bits can be allocated correspondingly.
In addition, the N-dimensional source is considered in the proposed VQ scheme. For example, the N-dimensional source follows the independent and identically distributed Gaussian distribution, and its rate–distortion function is
where presents the variance of the ith Gaussian source, , and the function log is replaced by ln to express the as
The partial derivative of is calculated as
This equation indicates that the minimum is a constant. That is, each dimension should be assigned with the same quantization accuracy. Specifically, if each dimension of the linear block code has the same coding ability, the VQ scheme will obtain the overall minimum average distortion. For example, ref. [30] proposes the GDA codes to balance the coding ability by averaging the degree distribution to reduce the distortion.
In summary, the minimum number of codewords is determined by the codeword length and the rate distortion function as follows:
2.3. Robust Code Design
In the proposed VQ scheme, the overall distortion is composed of quantization distortion () and channel distortion () [35] as follows:
where D is calculated by the mean-squared error (MSE) distortion.
In the VQ scheme, the channel distortion is generated from the noise influence. Reference [30] finds that the channel distortion will be increased when the generation matrix of the P-LDPC code has a larger weight. The reason is as follows:
where represents the average distortion generated by the e-bits error of the binary indices, is the degree of the j-th variable node, and is the total weight of the generation matrix.
Hence, the P-LDPC codes with the lower weights should be considered. For the code design, the weight constraint is supplemented to search the objective code, and the S-GDA algorithm is proposed, shown in Algorithm 1. The parameters can be explained as follows:
: the threshold of quantization distortion reduction;
: the degree of the j-th variable node ();
: the degree of the i-th check node ();
d: the total degree of the variable nodes associated with the information bits in the protomatrix;
: the number of edges connecting the i-th check node and the y-th variable node ();
: the number of edges connecting the j-th variable node and the x-th check node ().
To suppress the channel noise, the quantization distortion reduction is given as a small value in the S-GDA algorithm so that the distortion is decreased. Then, the S-GDA codes with the minimum weight will be obtained with the minimum . The optimal S-GDA code has good robustness to the channel noise. Furthermore, the tradeoff between the quantization distortion () and the channel distortion () should be balanced.
| Algorithm 1 S-GDA |
|
Mathematically, the principle of Algorithm 1 is as follows:
where is the floor function, the code rate is defined as , implies , and indicates . The objective code will be obtained when the quantization distortion reduction is less than the threshold ; otherwise, the total degree d will be decreased to search the objective code.
3. Two System Cases: Code Design of VQ Scheme
3.1. Codes Design for Lossy Gaussian Source Compression System
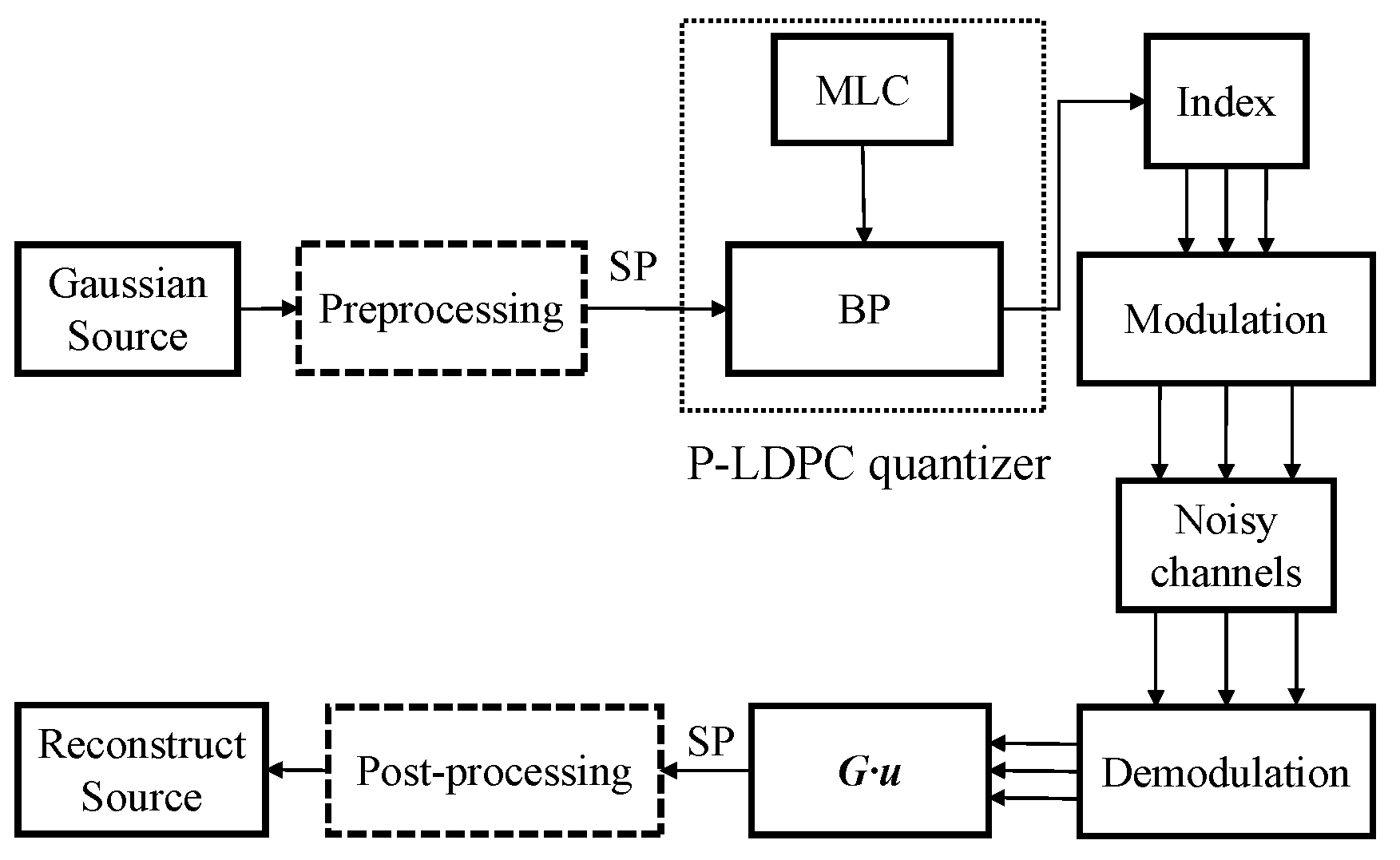
In this paper, the MLC structure proposed in [16] is modified with the noisy channel as shown in Figure 3. First, the source is quantified based on the probability distribution intervals using non-uniform quantization. Then, a set of floating codebooks is transformed as the binary with the corresponding centroid. After that, the obtained binary indices are encoded by the set partition (SP) mapping method, which divides one-dimensional source space into quantization subspaces. Finally, the mapped indices are vectorized by the P-LDPC codes.
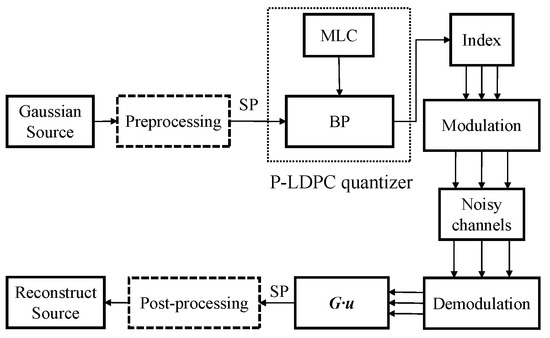
Figure 3.
The VQ scheme for the Gaussian source over the noisy channels.
The S-GDA algorithm can be utilized in the MLC structure-based VQ scheme to search the objective P-LDPC codes assuming there are L levels in the MLC, and the corresponding P-LDPC codes can be generated with the minimum quantization distortion () at each level. For example, when the compression rate is 1.5, the MLC structure has three levels, and the code rates of each level are 0.15, 0.4, and 0.95, respectively. In this case, the objective codes of three levels will be constructed by the S-GDA algorithm, namely, the S-GDA17×20, S-GDA3×5, and S-GDA2×40.
Considering the bits at the first level is not important for improving the system distortion; therefore, it is possible to discard the bits at the first level. In this case, the code rate is increased to a higher level and it will generate less compression distortion than using the code given in [16].
For example, the code rates are divided into 0.1 and 0.4 at two levels when the total code rate is 0.5. It should be noted that the overall distortion mainly depends on the higher code rate. Hence, the bits are discarded and replaced with random bits at the first level, and the code rate is updated as 0.5 at the second level. The objective code is obtained by the S-GDA algorithm to be
where the dimension of the protomatrix is , and the total degree is 7, indicating that there are seven linking edges between the variable nodes and the information bits expect the identity matrix.
Assuming there are three levels in the MLC structure, since the dimensions are the same at all levels, the ratio of the code rate is equal to the ratio of the index length at each level as follows:
Referring to Equation (17), the ratio of distortion bits caused by each level is calculated as
where the bit error ratio (BER) is signified as , the subscripts 1, 2, and 3 indicate three levels, respectively, is defined as the average row density of the generator matrix, and the channel distortion is expressed as the average Hamming distortion of a single dimension, i.e., .
In this MLC structure-based VQ scheme, the coding performance cannot achieve the optimum for all levels. However, it is found that the distortion is mainly generated from the higher levels. Hence, the S-GDA algorithm is only implemented to search the objective codes at the higher levels, and the structural complexity of the system is greatly reduced.
3.2. Codes Design for Lossy General Source Compression System
The continuous source has uneven distribution, which is more difficult to compress than the binary source. The Gaussian and Laplacian sources are considered as the general source in this section, and their compression performance can be improved by increasing the dimension. When the dimension is large enough, the statistical properties of the general source will be uniformly distributed in the N dimensions.
The joint probability density of the independent and identically distributed general source is defined as
where the length of source is N. Then, the log product is calculated as
where is the differential entropy of the independent variables, and the joint probability density distribution can be expressed as
It can be seen that the independent (memoryless) source obeys an approximately uniform distribution in a high dimension, and the lattice VQ will be suitable when N is taken to be a large value. For example, the Gaussian source follows the distribution of , and the shape of the quantization subspace of the equivalently uniform distribution is regarded as an N-dimensional hypersphere as follows:
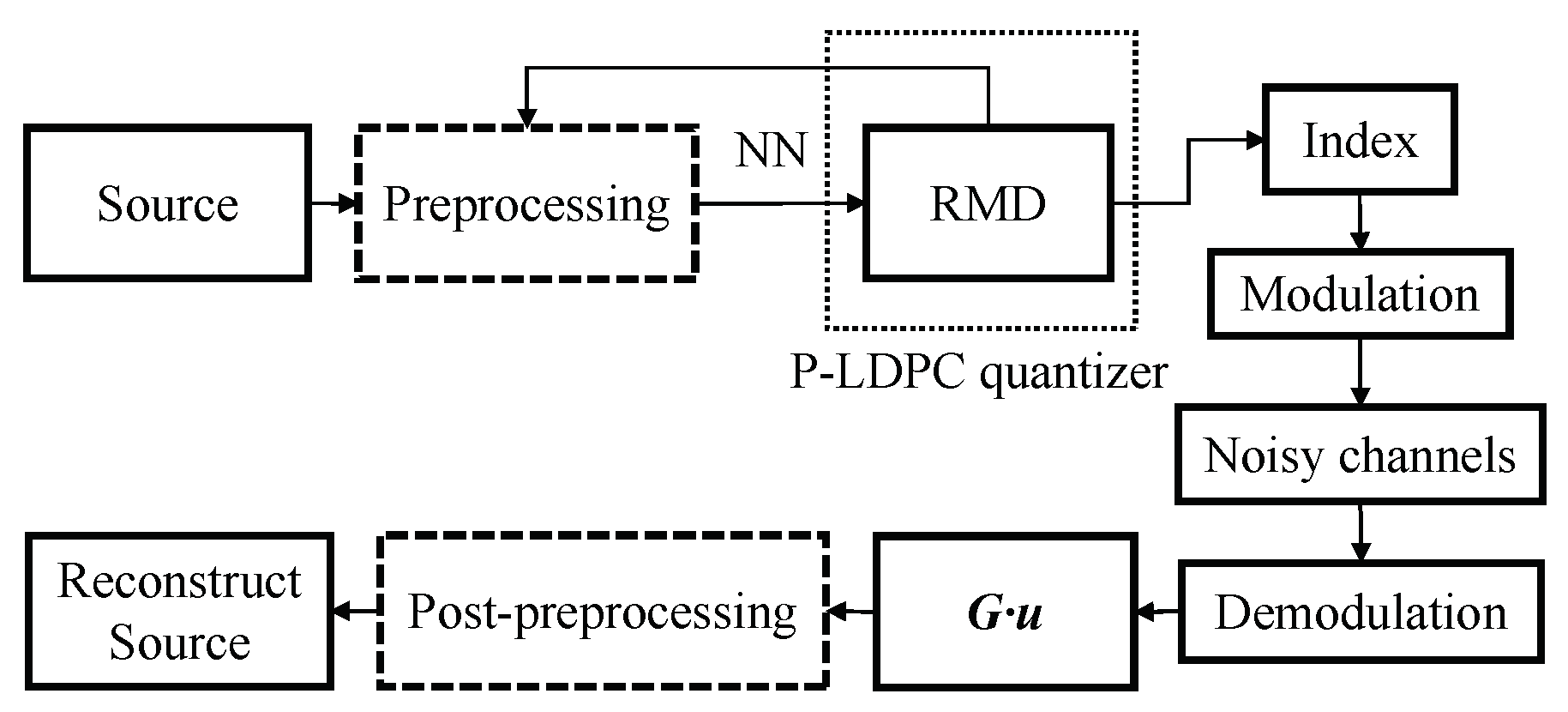
Referring to [18], a lossy source coding system is proposed to compress the general source, as shown in Figure 4. In [18], the scalar quantization of the preprocessing is accomplished through the utilization of neural networks (NNs), and the restrict minimum distortion (RMD) is an error correction algorithm based on the BP algorithm. In this work, the proposed system is modified with the noisy channel and supplements the modulation modules. Then, the objective code is designed by the S-GDA algorithm as follows:
where the code dimension is and .
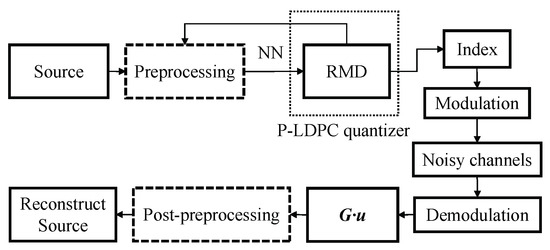
Figure 4.
The VQ scheme for the general source over the noisy channels.
Compared with the existing codes, the AR3A code needs to be punctured to enlarge the code rate to 0.5, while the S-GDA code can achieve the 0.5 rate without puncturing. Furthermore, according to quantization theory, it is found that the compression performance of the AR3A and the AR4JA codes [36,37,38] cannot be improved with the larger dimensions. However, the S-GDA codes are designed based on the quantization theory and their dimensions can be expanded arbitrarily. Hence, the S-GDA codes will have less compression distortion than the punctured codes with lower design complexity.
4. Simulation Results and Analyses
4.1. Performance Analyses of Code Design for Gaussian Source
In this section, the Gaussian source compression is analyzed based on the MLC structure-based VQ scheme. The protomatrix of the P-LDPC code is lifted to 600. The iteration number is 1500. The channel is the additive white Gaussian noise (AWGN) with binary phase-shift keying (BPSK) modulation. The system distortion D is composed by the quantization distortion and the channel distortion . The channel environment is defined so that the system distortion approximates the quantization distortion, i.e., , when the BER is less than in the AWGN channel. In this case, the compression distortion will be stabilized without the channel noise impact.
Next, the S-GDA algorithm is used to optimally designed three objective codes at rates of 0.5, 1, and 1.5, respectively, as shown in Figure 5, Figure 6 and Figure 7. The searching process of the S-GDA algorithm is detailed in three steps. First, the number of layers is allocated the given code rate. Second, the GDA code family is obtained according to the rate allocation number. Third, the objective S-GDA codes are determined by selecting the appropriate GDA codes in different layers. Specifically, the selection criterion satisfies the threshold of quantization distortion reduction as
where is set as a small value according to the code rate and the range of distortion reduction. To balance the channel and the quantization distortions, is usually taken as suboptimal at the lower layer to achieve the robustness with a lower SNR.
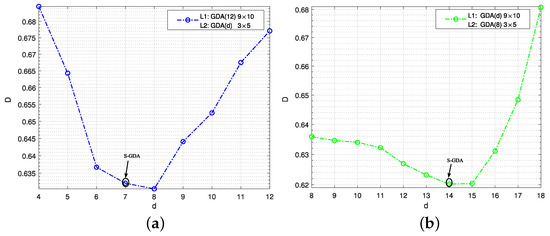
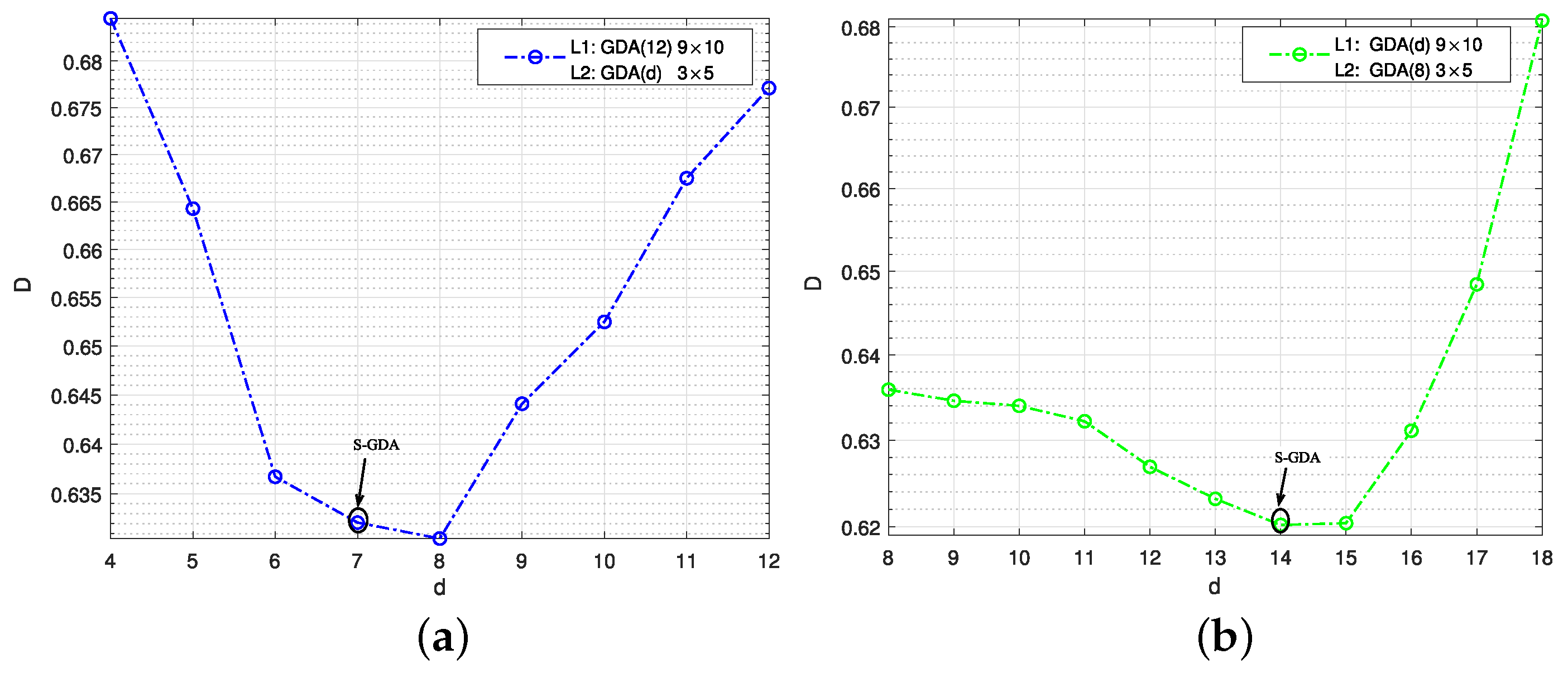
Figure 5.
The distortion and total degree performance for code searching. The objective code is searched by the S-GDA algorithm at when SNR = 7 dB and BER = , and the initial degrees are given as (a) : GDA9×10; (b) : GDA3×5.
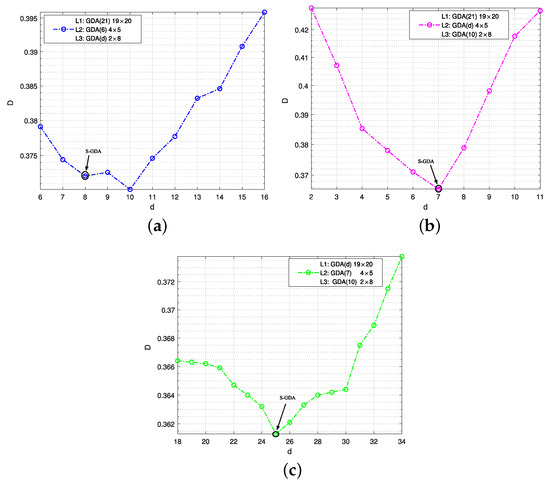
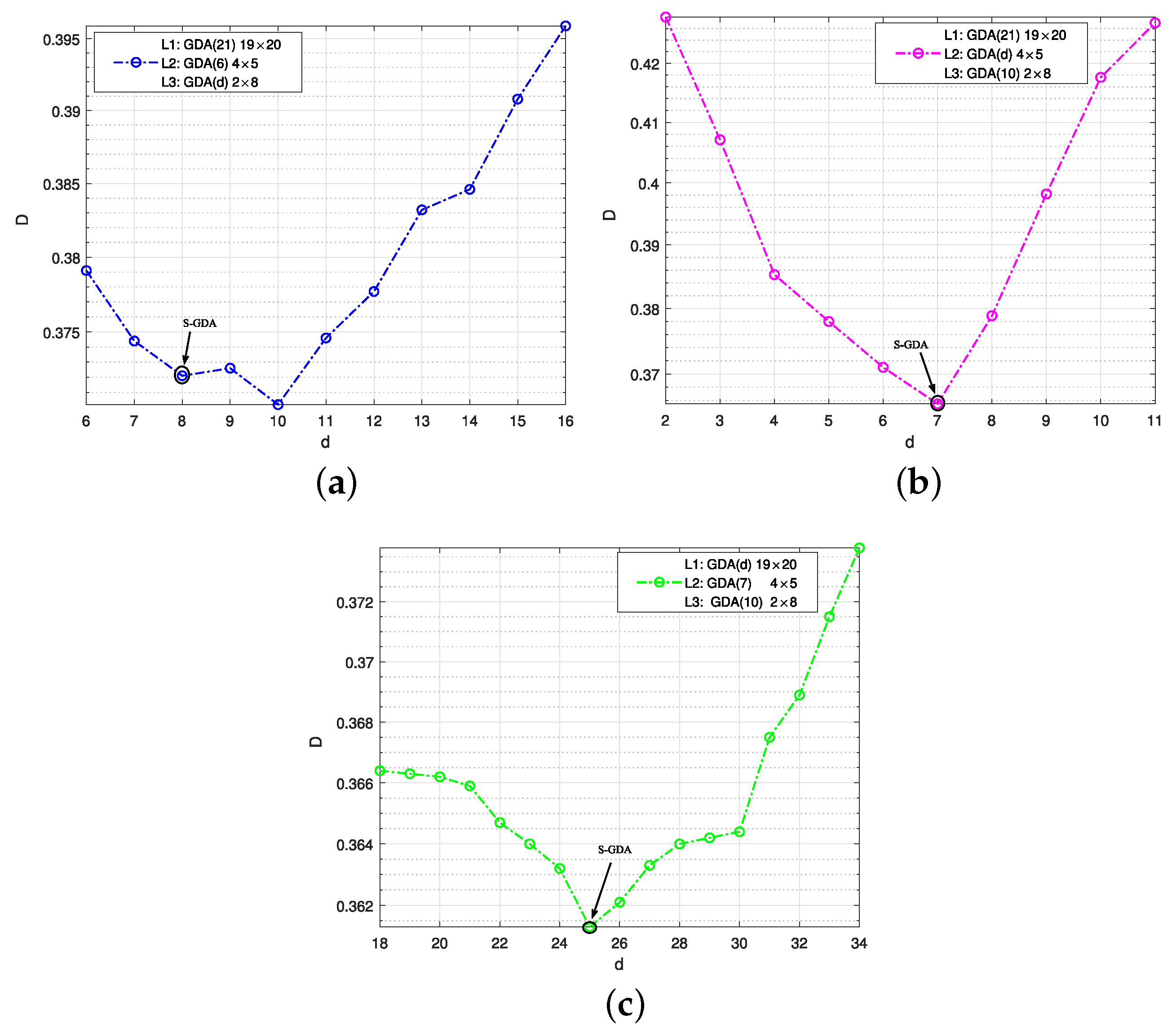
Figure 6.
The distortion and total degree performance for code searching. The objective code is searched by the S-GDA algorithm at when SNR = 7 dB and BER = , and the initial degrees are given as (a) : GDA19×20, : GDA4×5; (b) : GDA19×20, : GDA2×8; (c) : GDA4×5, : GDA2×8.
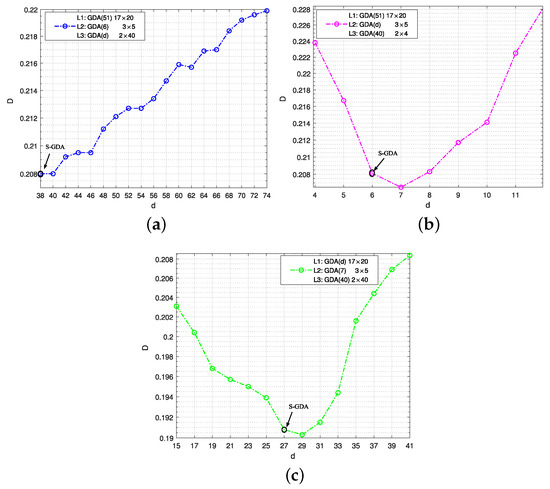
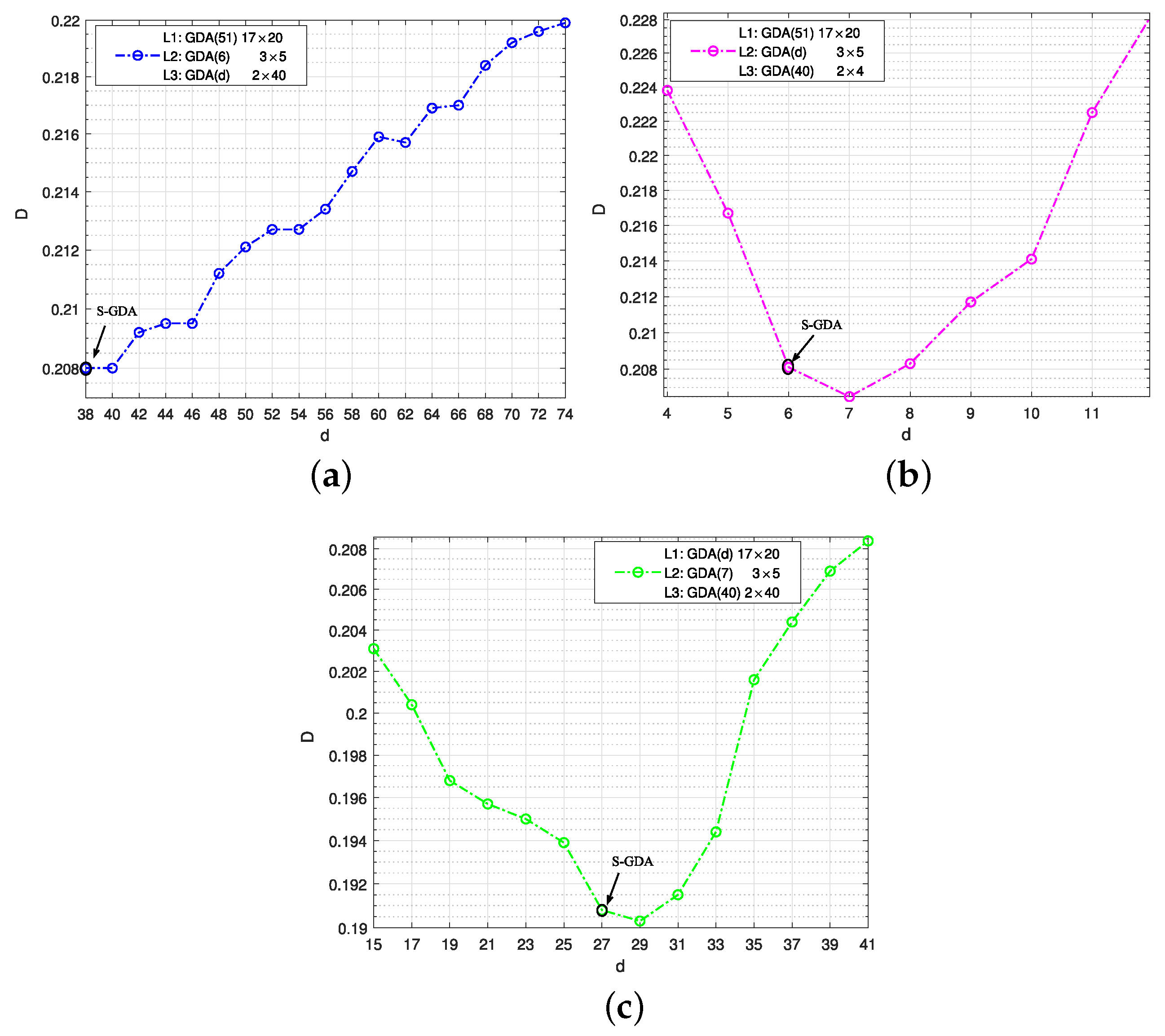
Figure 7.
The distortion and total degree performance for code searching. The objective code is searched by the S-GDA algorithm at when SNR = 7 dB and BER = , and the initial degrees are given as (a) : GDA17×20, : GDA3×5; (b) : GDA17×20, : GDA2×40; (c) : GDA3×5, : GDA2×40.
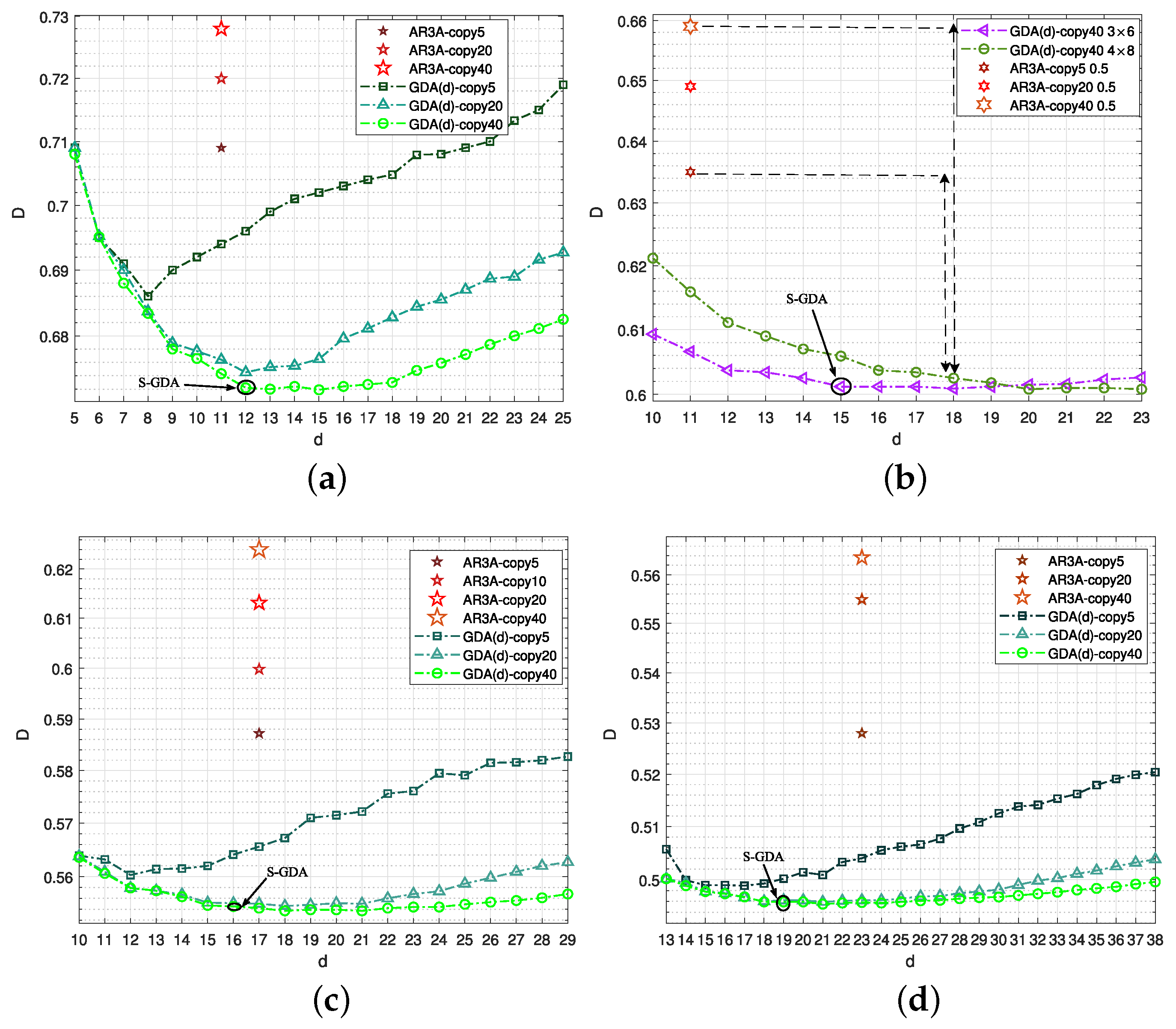
In Figure 5, the compression rate is 0.5, which is divided into 0.1 and 0.4, and the two objective codes are obtained by the S-GDA algorithm as S-GDA9×10 and S-GDA3×5 at the and layers, respectively. The initial degrees are taken as at the layer and at the layer. The distortion is decreased when the degree is given as at , as shown in Figure 5a. In this way, the code GDA9×10 with the suboptimal value is selected as the objective code S-GDA9×10 at the layer. At the layer, the optimal GDA3×5 with the minimum distortion is obtained as the objective code S-GDA3×5, as shown in Figure 5b. Overall, the objective S-GDA codes consist of S-GDA9×10 and S-GDA3×5.
In Figure 6, the compression rate is 1, which is divided into 0.05, 0.2, and 0.75, and three codes need to be obtained using the S-GDA algorithm, S-GDA19×20, S-GDA4×5, and S-GDA2×8 at , , and , respectively. The initial degrees are taken as at the layer, at the layer, and at the layer. Finally, the objective codes are obtained as S-GDA19×20, S-GDA4×5, and S-GDA2×8 at the three layers, respectively.
In Figure 7, the compression rate is 1.5, which is divided into 0.15, 0.4, and 0.95, and the three objective codes are S-GDA17×20, S-GDA3×5, and S-GDA2×40 at , , and , respectively. The initial degrees are taken as at the layer, at the layer, and at the layer. Finally, the objective codes are obtained as S-GDA17×20, S-GDA3×5, and S-GDA2×40 at the three layers, respectively.
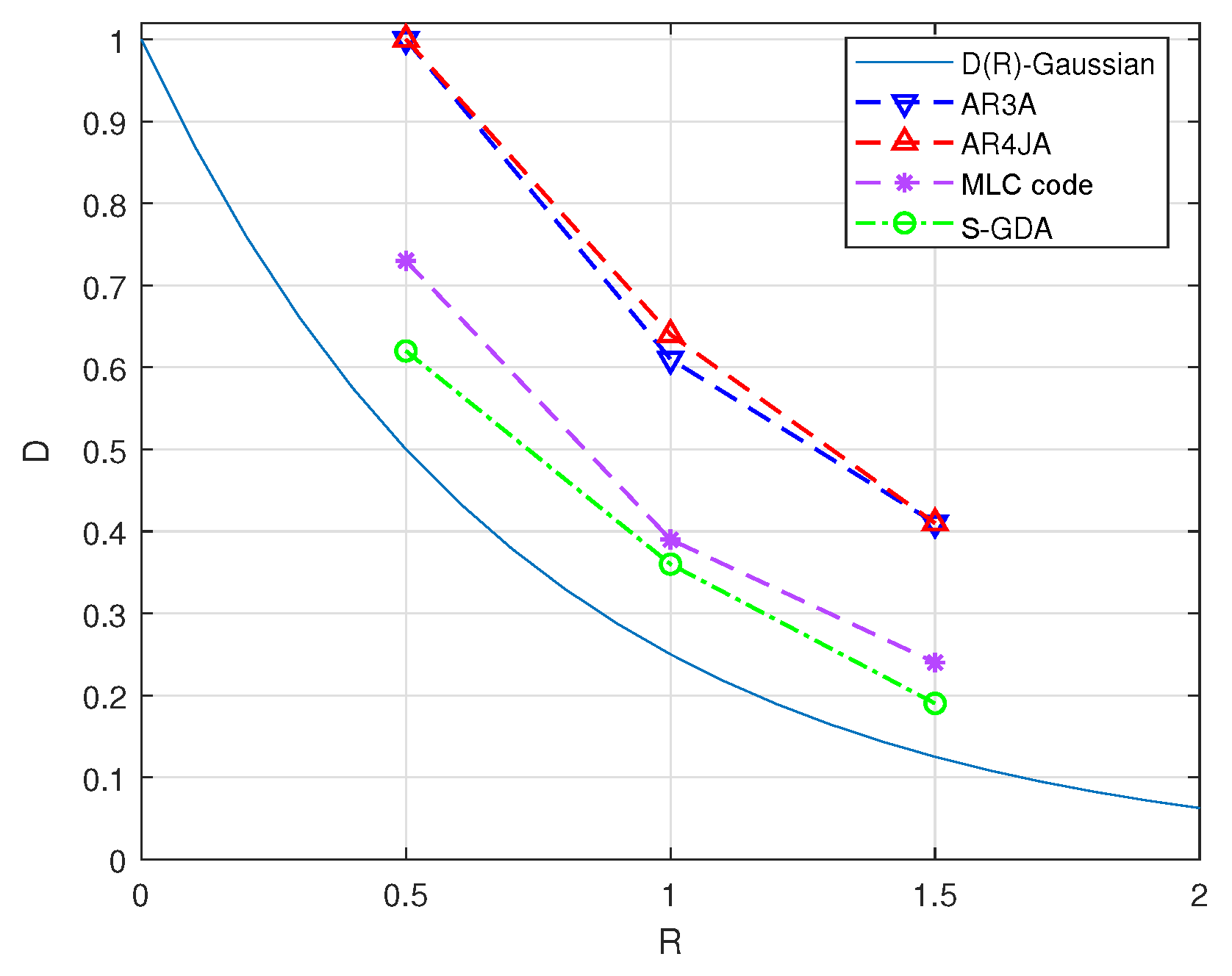
Furthermore, the distortion–rate performance based on different P-LDPC codes is shown in Figure 8. The AR3A and AR4JA codes are benchmark codes [37], and the MLC code is proposed in [16] for Gaussian source compression. It is clear that the S-GDA codes present obvious coding gains and they approach the distortion–rate limit compared to other codes.
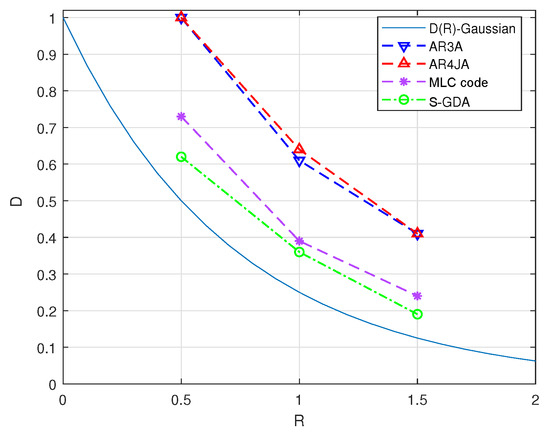
Figure 8.
The distortion–rate performance is tested based on the Gaussian source compression using the MLC structure with the SP mapping over the AWGN channel with BPSK modulation when SNR = 7 dB and BER = .
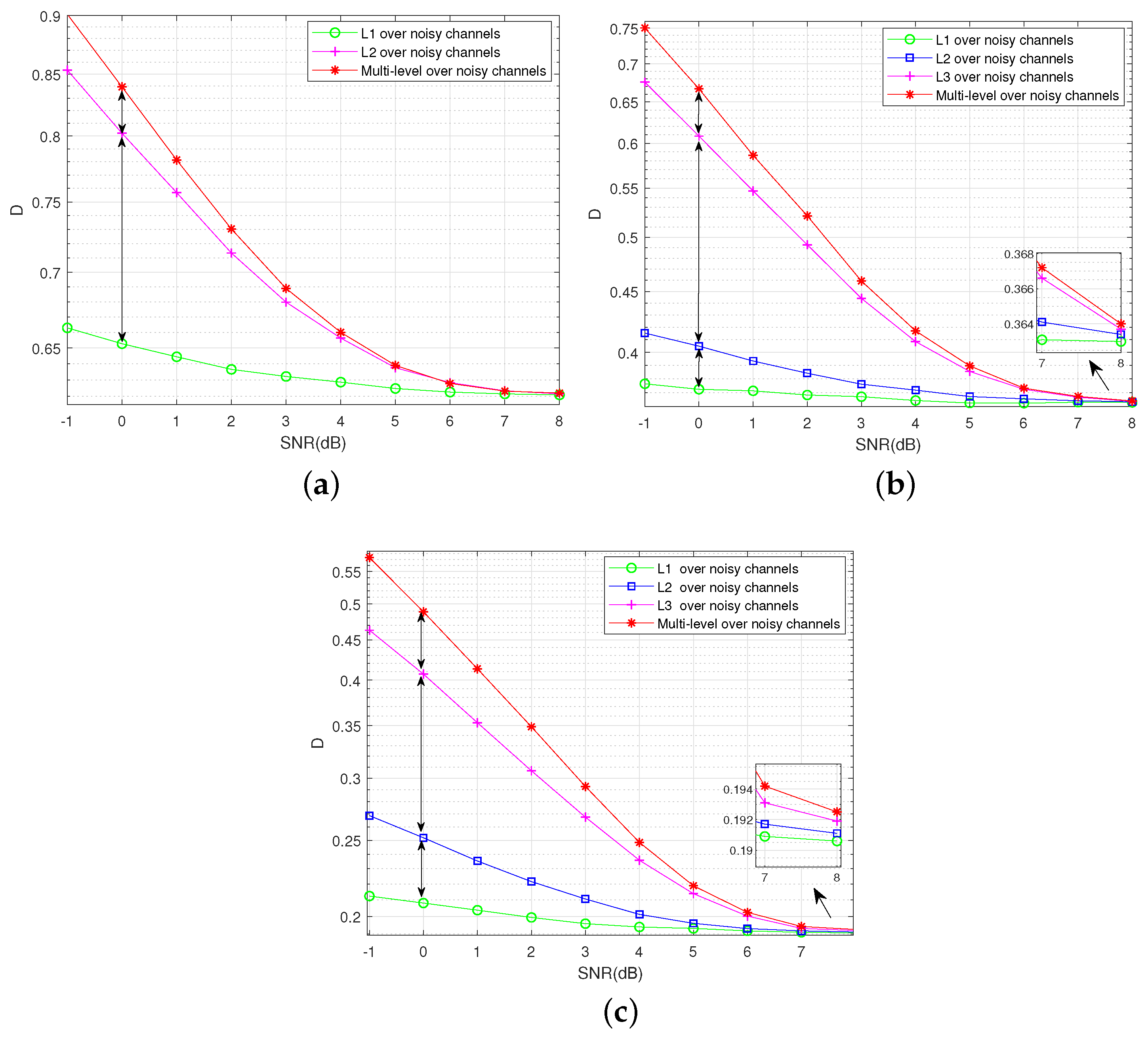
In Figure 9, the distortion sensitivity of each layer under the channel noise is shown by the distortion–SNR performance at three compression rates, 0.5, 1, and 1.5. The variance of the Gaussian source is given as . The simulation shows that the distortion is increased at the higher layer in the lower SNR region, which indicates that the higher layer is more sensitive to the channel noise and the lower layer is more robust. Compared with the multi-level scheme [16], the distortion can be reduced by the proposed VQ scheme.
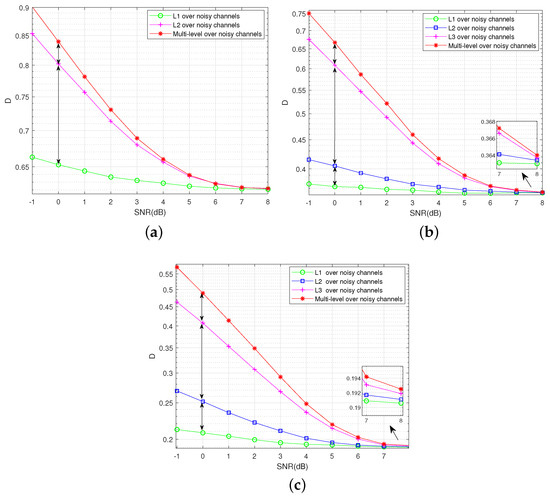
Figure 9.
The distortion sensitivity is compared with each layer under the channel noise, and the codes are (a) GDA9×10, GDA3×5 at ; (b) GDA19×20, GDA4×5, GDA2×8 at ; (c) GDA17×20, GDA3×5, GDA2×40 at .
4.2. Performance Analyses of Code Design for General Source
In this section, the general source compression is analyzed based on the NN structure-based VQ scheme, mainly including the Gaussian () and Laplacian () sources. The P-LDPC codes are lifted to 5, 20, and 40 times for the analyses, respectively. The simulation scale is set to . The channel environment is the AWGN with BPSK modulation. The distortion D is composed by the quantization distortion and the channel distortion .
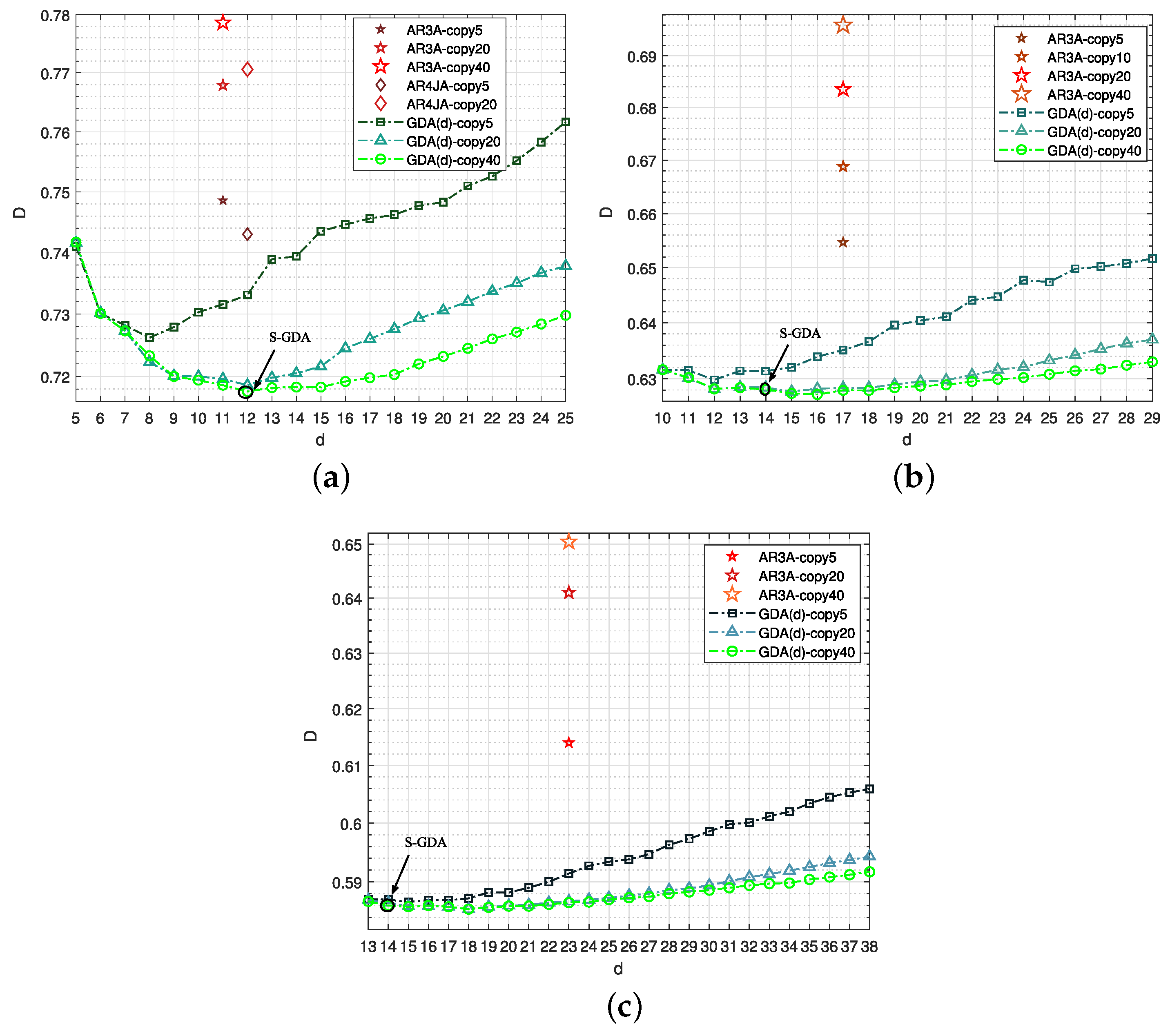
First, the Gaussian source is compressed as shown in Figure 10. The AR3A codes with the determined code rates are introduced to be the benchmarks of distortion comparison. The distortion will be increased with the decreased lifting numbers (signified as copy times) of the P-LDPC codes. This satisfies the VQ principle and the characteristics of the lattice VQ for high-dimensional compression. The codes with the lifting number of 40 have fewer distortions. Furthermore, the objective S-GDA codes are obtained at different code rates, namely, S-GDA3×5, S-GDA3×6, S-GDA3×7, and S-GDA3×9, as shown in Figure 10a, b, c and d, respectively.
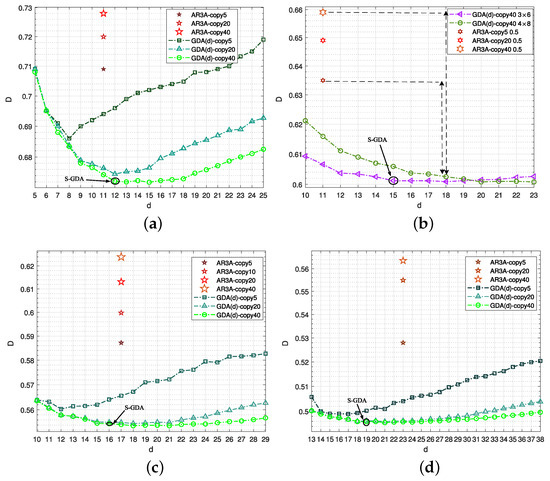
Figure 10.
The distortion and total degree performance are tested for different code comparisons based on the Gaussian source compression over the AWGN channel with BPSK modulation when SNR = 7 dB and BER = , and the codes are given as (a) GDA3×5 at ; (b) GDA3×6 at ; (c) GDA3×7 at ; (d) GDA3×9, at .
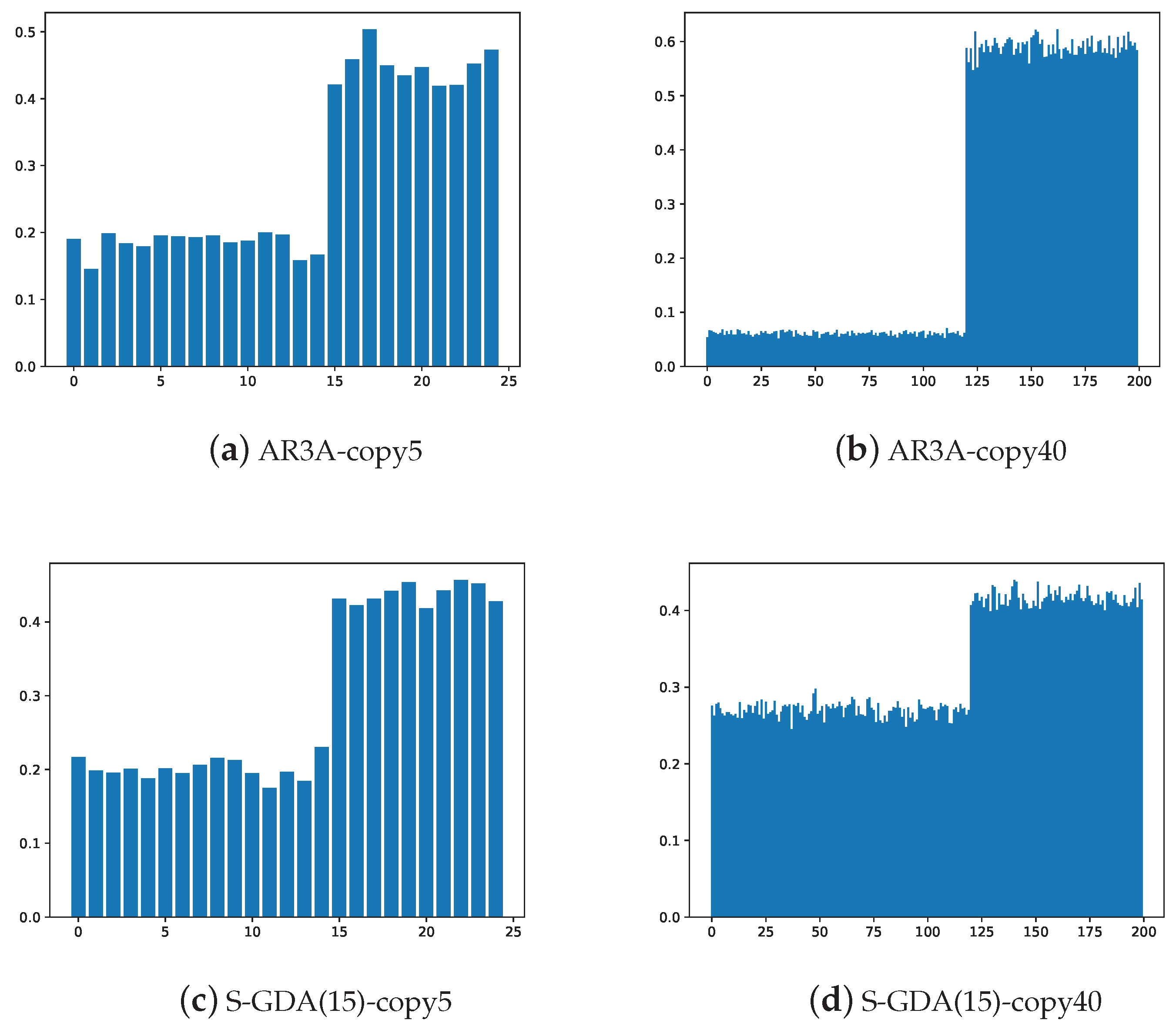
In Figure 11, the energy distribution of nodes is compared with the AR3A and the S-GDA3×5 codes at different lifting numbers, respectively. When the lifting number is 5, the energy distributions of two codes are similar. On the contrary, the code S-GDA3×5 has more uniform energy distribution than the AR3A when the lifting number is enlarged to 40. This indicates that the code S-GDA3×5 can uniformly smooth the distortion distributions and reduces the overall distortion in the VQ scheme.
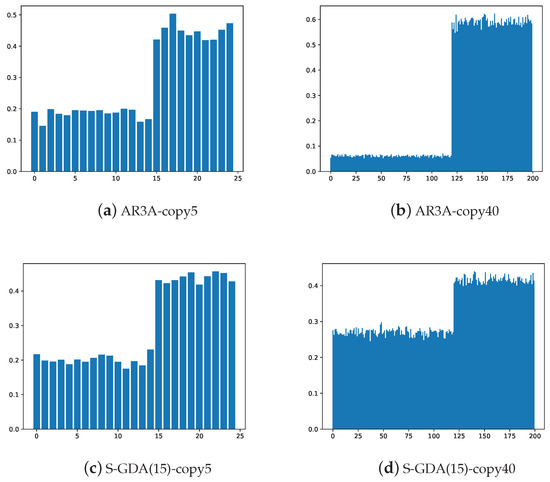
Figure 11.
The energy distribution of nodes is compared with the AR3A and S-GDA3×5 codes at different lifting numbers.
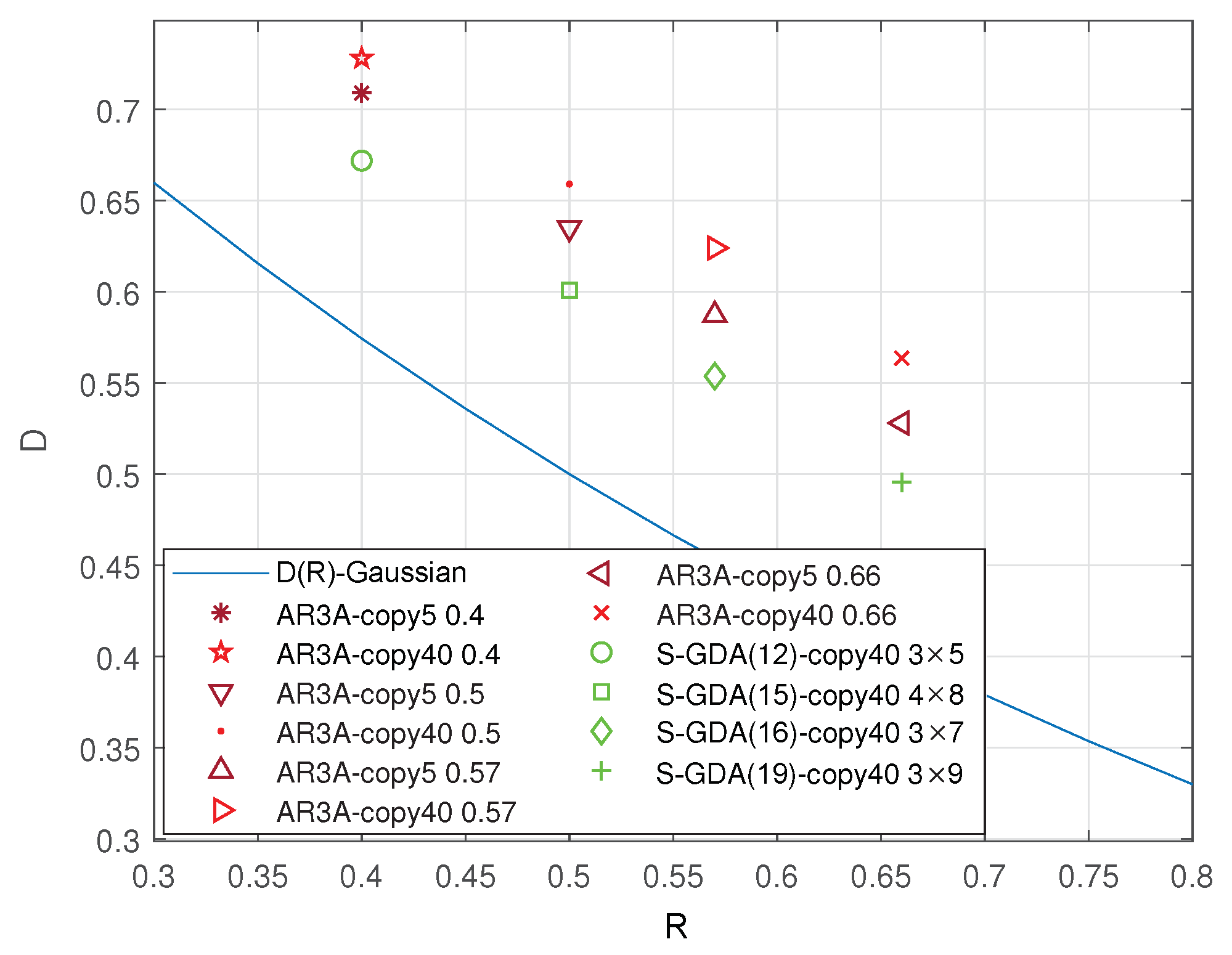
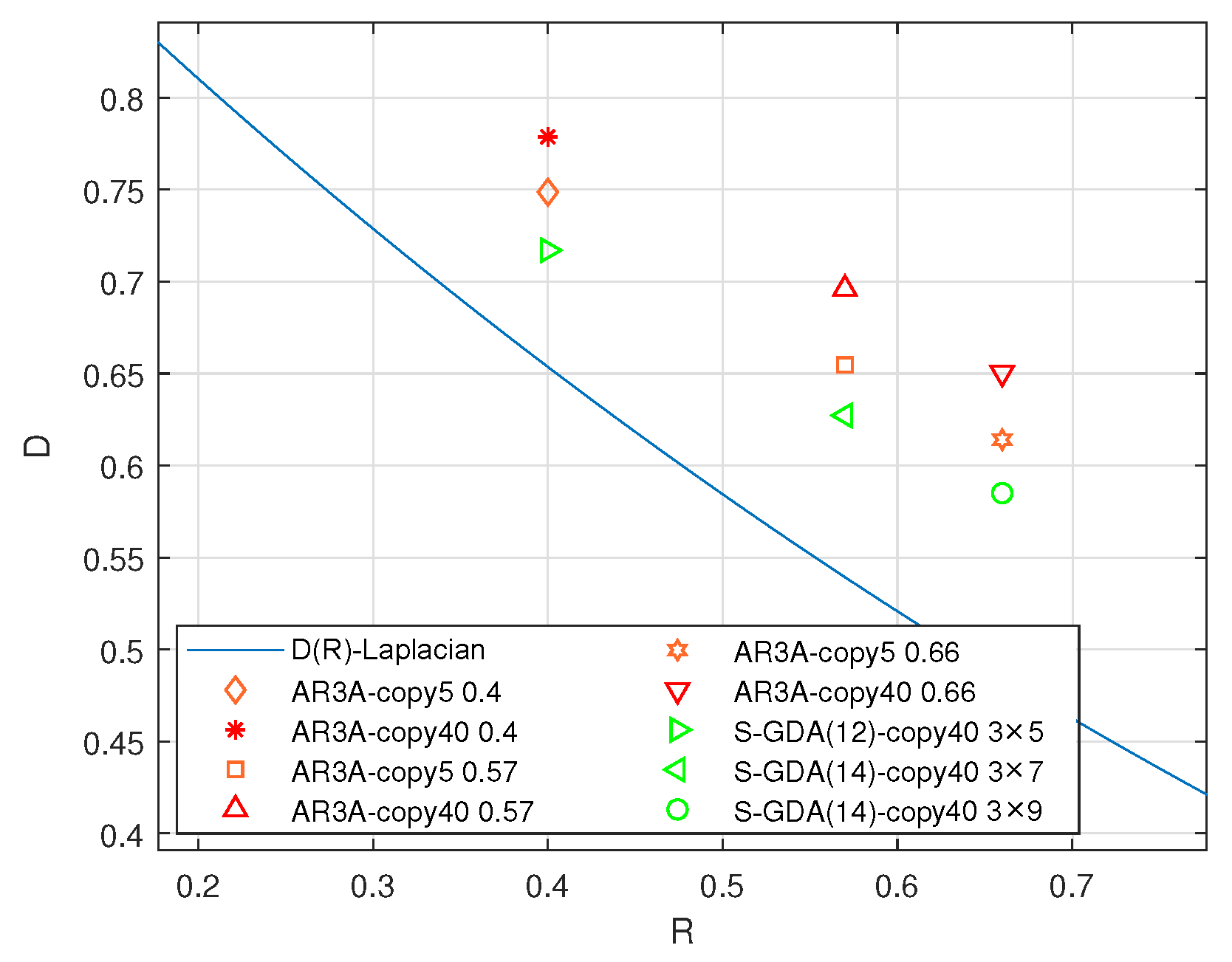
Furthermore, the distortion–rate performance is compared with the AR3A and the S-GDA codes for the Gaussian source compression, as shown in Figure 12. It is obvious that the S-GDA codes present coding gains in any conditions, including the different lifting numbers and code rates.
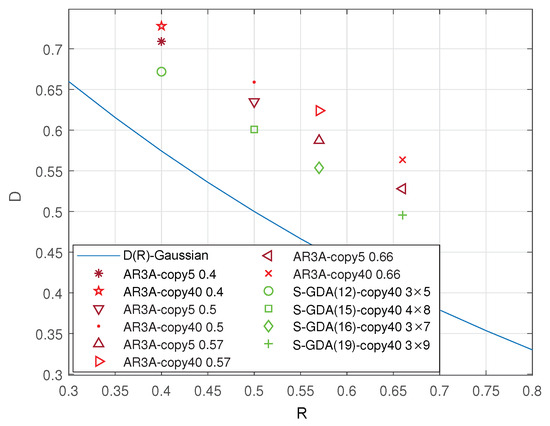
Figure 12.
The distortion–rate performance is tested based on Gaussian source compression by using the NN structure over the AWGN channel with BPSK modulation when SNR = 7 dB and BER = .
Table 1 compares the lattice topological splicing (LTS) codes [17] and the S-GDA codes. It should be noted that the LTS codes are designed for Gaussian source compression, and the S-GDA codes are designed for general source compression. The LTS codes are obtained by the differential evolution (DE) algorithm based on the MIT strategy, which is locally optimal and has a higher coding complexity. Compared with the DE algorithm, the S-GDA algorithm has lower complexity. In addition, since the LTS code is proposed for a Gaussian source over the noise-free environment, the S-GDA codes present the better compression performance and system compatibility.

Table 1.
Distortion comparisons between the LTS and S-GDA codes for Gaussian source compression over the AWGN channel with BPSK modulation when SNR = 7 dB and BER = .
Second, the Laplacian source is compressed as shown in Figure 13. As in Figure 10, the AR3A code family is introduced as the benchmark. The objective S-GDA codes are obtained at different code rates, namely, S-GDA3×5, S-GDA3×7, and S-GDA3×9, as shown in Figure 13a, b and c, respectively. Figure 14 shows the distortion–rate performance based on the Laplacian source compression. It can be seen that the S-GDA codes have better performance.
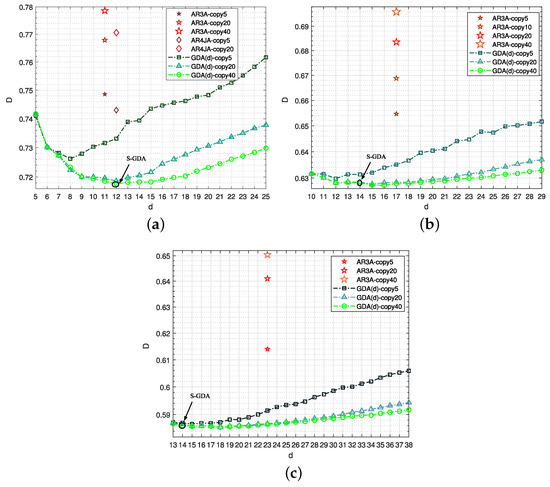
Figure 13.
The distortion and total degree performance are tested for different code comparisons based on Laplacian source compression over the AWGN channel with BPSK modulation when SNR = 7 dB and BER = , and the codes are given as (a) GDA3×5 at ; (b) GDA3×7 at ; (c) GDA3×9, at .
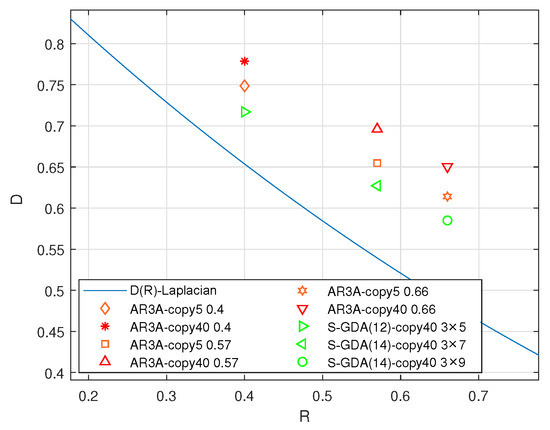
Figure 14.
The distortion–rate performance is tested based on Laplacian source compression using the NN structure over the AWGN channel with BPSK modulation when SNR = 7 dB and BER = .
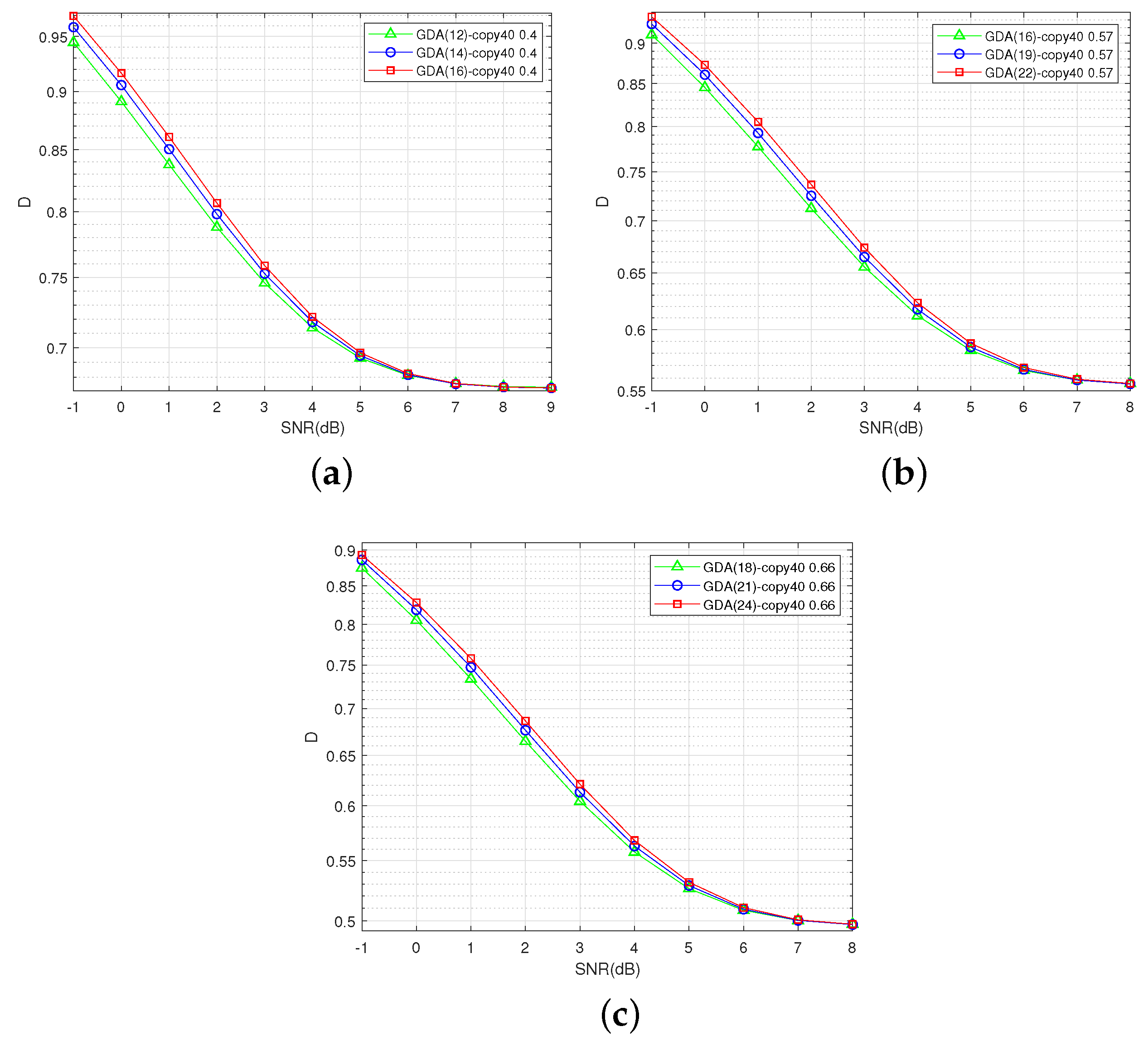
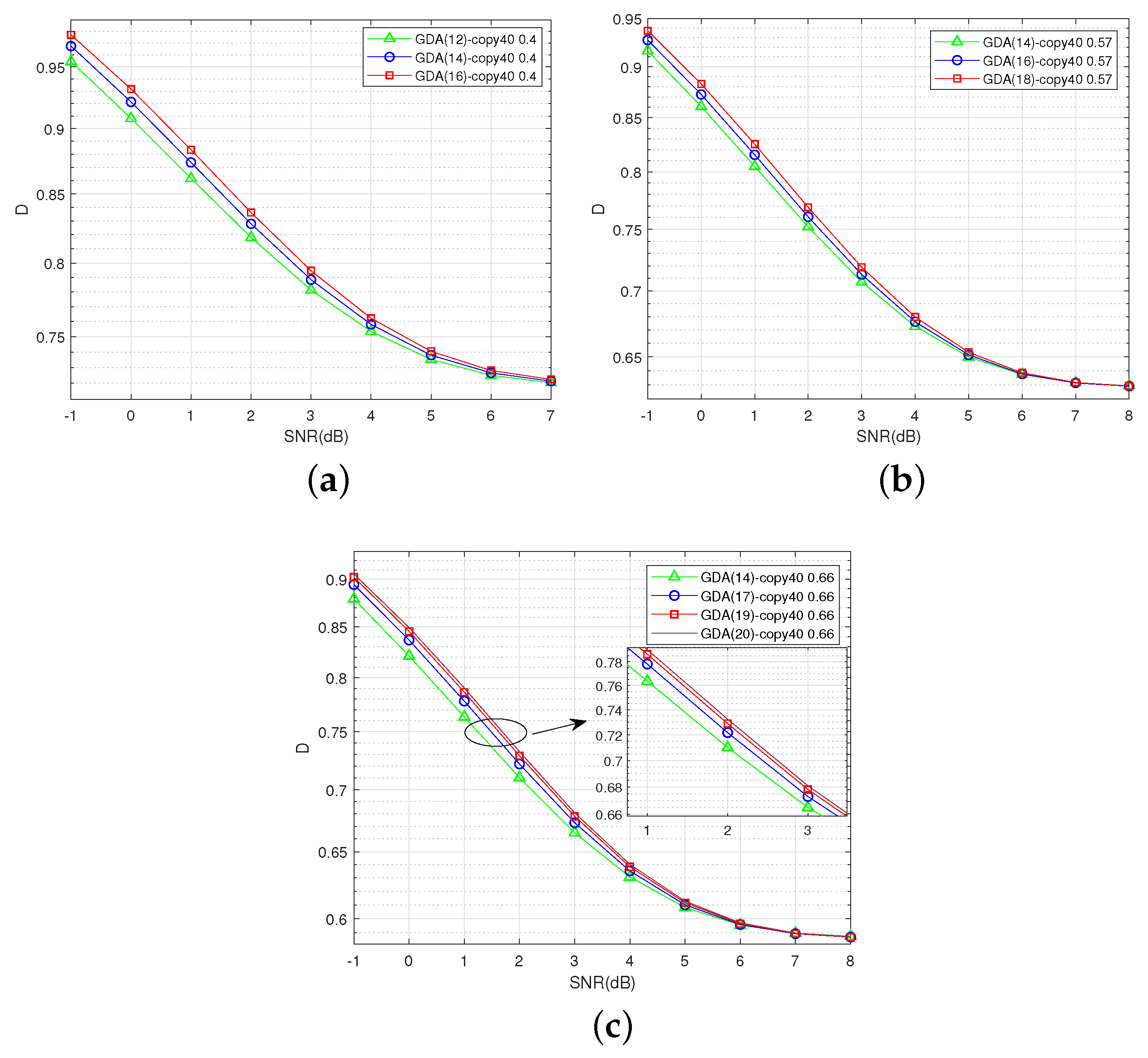
The distortion–SNR performances based on the Gaussian and Laplacian source compressions are shown in Figure 15 and Figure 16, respectively. The S-GDA codes are tested at three code rates, namely, 0.4, 0.57, and 0.66. The S-GDA codes have less distortion in the lower-SNR region. Hence, the S-GDA codes have excellent source compression performance and channel noise robustness.
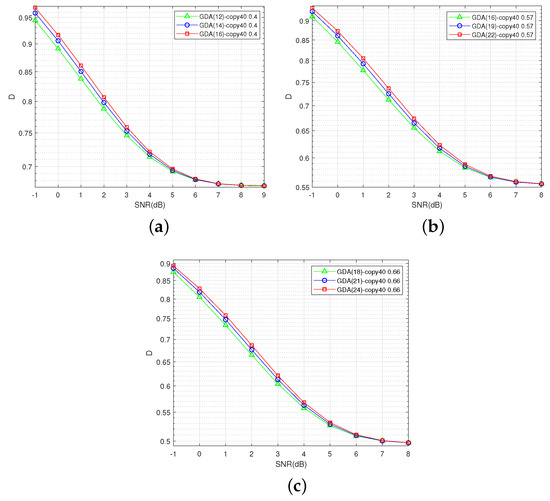
Figure 15.
The distortion–SNR performance is tested for different degree comparisons based on the Gaussian source with . (a) S-GDA code: GDA3×5, . (b) S-GDA code: GDA3×7, . (c) S-GDA code: GDA3×9, .
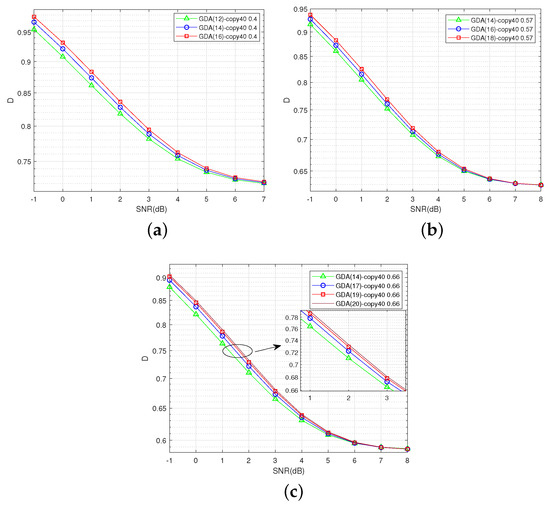
Figure 16.
The distortion–SNR performance is tested for different degree comparisons based on the Laplacian source with . (a) S-GDA code: GDA3×5, . (b) S-GDA code: GDA3×7, . (c) S-GDA code: GDA3×9, .
Overall, the limitation of the proposed study is that the source and channel are only formulated as some statistical models, since the compression bound should be presented based on the statistical characteristics. Some complicated signals (including the image, video, or radio) and practical environments (including non-stationary and fading environments) will be tested by this VQ scheme in the future.
5. Conclusions
In this paper, a general VQ scheme over the noisy channel is proposed based on block code for lossy source compression. The compression performance is improved by matching the codebook and quantization structure well. This is a new optimization perspective for codebook design. It is proved that the coding methodology of the duality principle can be validated with lower source distortion and channel noise. The optimal codebook outperforms the existing codes to approach the rate–distortion limit, and it enhances robustness against channel noise. The existing MIT method only focuses on formulating mutual information propagation to improve the compression performance, without considering the quantization structure. In contrast, the proposed scheme constructs a well-matching relation between the codebook and the quantization structure, and it integrates the MIT method to optimize the source code. Next, the proposed VQ scheme will be applied with complicated source models and a non-stationary channel environment.
Author Contributions
Conceptualization, R.W., D.S. and L.W.; methodology, R.W.; software, R.W. and J.R.; validation, D.S.; formal analysis, R.W.; investigation, R.W.; resources, R.W.; data curation, R.W. and J.R.; writing—original draft preparation, R.W.; writing—review and editing, D.S.; visualization, R.W. and D.S.; supervision, L.W.; project administration, D.S., Z.X. and L.W.; funding acquisition, D.S., Z.X. and L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Fujian Provincial Natural Science Foundation of China (nos. 2024J01101, 2024J01120), Open Project of the Key Laboratory of Underwater Acoustic Communication and Marine Information Technology (Xiamen University) of the Ministry of Education, China (no. UAC202304), Fujian Province Young and Middle-Aged Teacher Education Research Project (no. JAT231044), National Science Foundation of Xiamen, China (no. 3502Z202372013), and Jimei University Startup Research Project (nos. ZQ2024058, ZQ2022015).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Berger, T.; Gibson, J. Lossy source coding. IEEE Trans. Inform. Theory 1998, 44, 2693–2723. [Google Scholar] [CrossRef]
- Xu, L.D.; He, W.; Li, S. Internet of things in industries: A survey. IEEE Trans. Ind. Inform. 2014, 10, 2233–2243. [Google Scholar] [CrossRef]
- Chowdhury, M.R.; Tripathi, S.; De, S. Adaptive multivariate data compression in smart metering internet of things. IEEE Trans. Ind. Inform. 2021, 17, 1287–1297. [Google Scholar] [CrossRef]
- Davey, M.; MacKay, D. Low density parity check codes over gf(q). IEEE Commun. Lett. 1998, 2, 165–167. [Google Scholar] [CrossRef]
- Gallager, R. Low-density parity-check codes. IRE Trans. Inform. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef]
- Song, D.; Wang, L.; Chen, P. Mesh model-based merging method for DP-LDPC code pair. IEEE Trans. Commun. 2023, 71, 1296–1308. [Google Scholar] [CrossRef]
- Gupta, A.; Verdu, S. Operational duality between lossy compression and channel coding. IEEE Trans. Inform. Theory 2011, 57, 3171–3179. [Google Scholar] [CrossRef]
- Martinian, E.; Wainwright, M. Low density codes achieve the rate-distortion bound. In Proceedings of the Data Compression Conference (DCC’06), Snowbird, UT, USA, 28–30 March 2006; pp. 153–162. [Google Scholar]
- Matsunaga, Y.; Yamamoto, H. A coding theorem for lossy data compression by LDPC codes. IEEE Trans. Inform. Theory 2003, 49, 2225–2229. [Google Scholar] [CrossRef]
- Honda, J.; Yamamoto, H. Variable length lossy coding using an LDPC code. IEEE Trans. Inform. Theory 2014, 60, 762–775. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Wu, H.; Liu, S. Performance of lossy P-LDPC codes over GF(2). In Proceedings of the 2020 14th International Conference on Signal Processing and Communication Systems (ICSPCS), Adelaide, Australia, 14–16 December 2020; pp. 1–5. [Google Scholar]
- Nguyen, T.V.; Nosratinia, A.; Divsalar, D. The design of rate-compatible protograph LDPC codes. IEEE Trans. Commun. 2012, 60, 2841–2850. [Google Scholar] [CrossRef]
- Mitchell, D.G.M.; Lentmaier, M.; Costello, D.J. Spatially coupled LDPC codes constructed from protographs. IEEE Trans. Inform. Theory 2015, 61, 4866–4889. [Google Scholar] [CrossRef]
- Hu, X.Y.; Eleftheriou, E.; Arnold, D. Regular and irregular progressive edge-growth tanner graphs. IEEE Trans. Inform. Theory 2005, 51, 386–398. [Google Scholar] [CrossRef]
- Braunstein, A.; Kayhan, F.; Montorsi, G.; Zecchina, R. Encoding for the blackwell channel with reinforced belief propagation. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 1891–1895. [Google Scholar]
- Deng, H.; Song, D.; Miao, M.; Wang, L. Design of lossy compression of the gaussian source with protograph LDPC codes. In Proceedings of the 2021 15th International Conference on Signal Processing and Communication Systems (ICSPCS), Sydney, Australia, 13–15 December 2021; pp. 1–6. [Google Scholar]
- Song, D.; Ren, J.; Wang, L.; Chen, G. Gaussian source coding based on P-LDPC code. IEEE Trans. Commun. 2023, 71, 1970–1981. [Google Scholar] [CrossRef]
- Ren, J.; Song, D.; Wu, H.; Wang, L. Lossy P-LDPC codes for compressing general sources using neural networks. Entropy 2023, 25, 252–261. [Google Scholar] [CrossRef]
- Fu, Q.; Xie, H.; Qin, Z.; Slabaugh, G.; Tao, X. Vector quantized semantic communication system. IEEE Wirel. Commun. Lett. 2023, 12, 982–986. [Google Scholar] [CrossRef]
- Linde, Y.; Buzo, A.; Gray, R. An algorithm for vector quantizer design. IEEE Trans. Commun. 1980, 28, 84–95. [Google Scholar] [CrossRef]
- Fischer, T.; Dicharry, R. Vector quantizer design for memoryless Gaussian, Gamma, and Laplacian sources. IEEE Trans. Commun. 1984, 32, 1065–1069. [Google Scholar] [CrossRef]
- Equitz, W. A new vector quantization clustering algorithm. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1568–1575. [Google Scholar] [CrossRef]
- Hang, H.M.; Woods, J. Predictive vector quantization of images. IEEE Trans. Commun. 1985, 33, 1208–1219. [Google Scholar] [CrossRef]
- Makhoul, J.; Roucos, S.; Gish, H. Vector quantization in speech coding. Proc. IEEE 1985, 73, 1551–1588. [Google Scholar] [CrossRef]
- Charusaie, M.A.; Amini, A.; Rini, S. Compressibility measures for affinely singular random vectors. IEEE Trans. Inform. Theory 2022, 68, 6245–6275. [Google Scholar] [CrossRef]
- Gersho, A. Asymptotically optimal block quantization. IEEE Trans. Inform. Theory 1979, 25, 373–380. [Google Scholar] [CrossRef]
- Jegou, H.; Douze, M.; Schmid, C. Product quantization for nearest neighbor search. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 117–128. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zhao, S.; Ma, X.; Bai, B. A new joint source-channel coding scheme based on nested lattice codes. IEEE Commun. Lett. 2012, 16, 730–733. [Google Scholar] [CrossRef]
- Hagen, R. Robust LPC spectrum quantization-vector quantization by a linear mapping of a block code. IEEE Trans. Speech Audio Process. 1996, 4, 266–280. [Google Scholar] [CrossRef]
- Wang, R.; Liu, S.; Wu, H.; Wang, L. The efficient design of lossy P-LDPC codes over AWGN channels. Electronics 2022, 11, 3337. [Google Scholar] [CrossRef]
- Farvardin, N.; Vaishampayan, V. Optimal quantizer design for noisy channels: An approach to combined source-channel coding. IEEE Trans. Inform. Theory 1987, 33, 827–838. [Google Scholar] [CrossRef]
- Qi, Y.; Hoshyar, R.; Tafazolli, R. The error-resilient compression of correlated binary sources and exit chart based performance evaluation. In Proceedings of the 2010 7th International Symposium on Wireless Communication Systems, York, UK, 19–22 September 2010; pp. 741–745. [Google Scholar]
- Huang, H.C.; Pan, J.S.; Lu, Z.M.; Sun, S.H.; Hang, H.M. Vector quantization based on genetic simulated annealing. Signal Process. 2001, 81, 1513–1523. [Google Scholar] [CrossRef]
- Gersho, A.; Gray, R.M. Vector Quantization and Signal Compression; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 159. [Google Scholar]
- Farvardin, N. A study of vector quantization for noisy channels. IEEE Trans. Inform. Theory 1990, 36, 799–809. [Google Scholar] [CrossRef]
- Abbasfar, A.; Divsalar, D.; Yao, K. Accumulate-repeat-accumulate codes. IEEE Trans. Commun. 2007, 55, 692–702. [Google Scholar] [CrossRef]
- Divsalar, D.; Jones, C.; Dolinar, S.; Thorpe, J. Protograph based LDPC codes with minimum distance linearly growing with block size. In Proceedings of the GLOBECOM’05, IEEE Global Telecommunications Conference, St. Louis, MO, USA, 28 November–2 December 2005; p. 5. [Google Scholar]
- Divsalar, D.; Dolinar, S.; Jones, C.R.; Andrews, K. Capacity-approaching protograph codes. IEEE J. Select. Areas Commun. 2009, 27, 876–888. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).