Study on Selection Diversity for MIMO 3-User Interference Channel with Interference Alignment

Abstract

This paper explores selection diversity in the context of MIMO 3-user interference channels with interference alignment (IA), focusing on enhancing reliability through diversity order (DO) analysis. While degrees of freedom (DoF) have traditionally been emphasized for throughput optimization in IA, limited research has addressed diversity order to improve error performance. In this work, we define a conditional DO and propose a beamforming vector selection method that achieves a conditional DO of $M^2/2$, where M is the number of antennas per transceiver. The proposed scheme employs a two-stage decoding approach, combining zero-forcing for interference cancellation with maximum likelihood (ML) decoding for desired signal recovery, which is augmented by orthogonalization techniques. Simulations demonstrate the superiority of the proposed scheme in both error probability and conditional DO values compared to conventional IA methods, particularly in scenarios with higher antenna counts. These results provide insights into optimizing IA for enhanced reliability and form the foundation for future exploration of advanced decoding and beamforming strategies.

1. Introduction

Interference alignment (IA) remains a crucial technique in modern wireless communications, particularly as the demand for high data rates and spectrum efficiency grows. IA has emerged as a vital strategy in 5G-and-beyond networks, enabling more efficient interference management and allowing for higher throughput in interference-limited environments. IA optimizes the degrees of freedom (DoF) by aligning interference within lower-dimensional subspaces, particularly in dense multi-user networks like small cell deployments, where interference poses significant challenges [1].

IA has also demonstrated its effectiveness in cognitive radio networks (CRNs), where it is used to improve spectrum efficiency and manage the interference between primary and secondary users. Secondary users can align their interference in such a way that it minimizes the impact on primary users while maximizing their own throughput, significantly enhancing spectral efficiency in dynamic spectrum-sharing environments [2]. Furthermore, with the integration of massive multiple-input multiple-output (Massive MIMO) systems, IA can leverage spatial diversity to align interference across multiple users, further boosting spectral efficiency in dense networks [1].

The development of IA has focused heavily on optimizing the DoF, especially in scenarios like the K-user interference channel and the $M\times N$ X channel, where IA schemes can asymptotically achieve the maximum DoF [3,4]. While DoF are a crucial measure for spectral efficiency, the reliability of the communication system, often quantified by the diversity order (DO) introduced in [5], is also important. Research on the DO of IA has been limited, with most efforts focusing on maximizing throughput rather than improving error performance. An algorithm that applies the K-user interference alignment technique using time division has also been introduced as part of this effort, allowing the desired degrees of freedom (DoF) to be achieved with fewer antennas and low computation complexity [6].

Additionally, there have been studies exploring the use of relays to assist in IA. Relays can help to more flexibly adjust interference and enhance IA performance, particularly in scenarios with limited channel state information. For example, research on quasi-static X channels has shown that relays can significantly improve the IA’s effectiveness in such environments [7], and in the opposite directional interference alignment scenario, it was proven that interference signals are aligned using relays to enhance system performance [8].

Moreover, opportunistic interference alignment (OIA) has emerged as a promising approach in scenarios where perfect channel state information (CSI) is not available at all nodes. OIA leverages multi-user diversity by opportunistically selecting users who can align interference effectively, thus further improving spectral efficiency without the need for full CSI at all transmitters [9,10,11].

Although beamforming selection schemes based on maximizing the sum rate have been proposed [12], they may not be optimal for minimizing the error rate. In peer-to-peer (P2P) multi-input and multi-output (MIMO) communication systems, various selection schemes, such as transmit antenna selection or equivalent path selection, are based on the signal-to-noise ratio (SNR) at the receiver. These selection methods, however, often assume a zero-forcing linear receiver, which can degrade error performance. In contrast, maximum likelihood (ML) decoding offers better error performance, although at the cost of increased computational complexity [13].

Recent advancements in interference alignment (IA) techniques have increasingly leveraged machine learning, particularly reinforcement learning and deep learning. These approaches have demonstrated significant potential in improving IA performance, especially in dynamic and complex wireless environments. Reinforcement learning (RL) has been employed to optimize IA in various scenarios by adapting to dynamic channel conditions and resource management challenges.

A deep Q-network (DQN)-based approach was proposed to optimize user selection policies in cache-enabled IA networks, where the wireless environment was modeled as a finite-state Markov channel, achieving an improved sum rate and energy efficiency [14]. A deep deterministic policy gradient (DDPG) algorithm was developed for jointly optimizing IA and power control in dense networks. This method effectively managed computational complexity and enhanced spectral efficiency [15]. Additionally, a deep RL framework for edge caching and user selection in heterogeneous networks was introduced, where edge caches were dynamically updated to optimize spectral and energy efficiency in opportunistic IA scenarios [16].

Pure deep learning (DL) techniques have been focused on simplifying IA by using neural networks to model and predict IA strategies. An autoencoder-based transmission strategy was utilized for distributed IA, enabling effective alignment with only local channel state information [17]. Deep learning was applied to enhance IA for discrete constellations, where encoder and decoder functions were designed to maximize the sum rate in interference channels [18]. A neural network framework was developed to predict optimal precoding matrices for IA in MIMO systems, demonstrating improved IA performance [19]. Finally, a hybrid approach was proposed, combining traditional signal processing with deep learning for IA and channel estimation in 6G heterogeneous network environments [20].

Machine learning-based algorithms can address problems that are difficult to model mathematically; however, they require learning the optimal weights under varying channel conditions and often involve high relative complexity, making their practical application in real communication environments challenging. Therefore, this paper aims to explore scenarios where both the transmitter and receiver use M identical antennas, focusing on mathematical beamforming and interference alignment.

Previous works without using machine learning technology have attempted to address this gap by incorporating space–time block codes (STBCs) into IA schemes to enhance the error performance, particularly for systems like the $2\times 2$ X channel. In such systems, each transmitter uses only the CSI of its connected links, allowing for improved error performance through the use of STBCs [21,22]. Under this assumption, global CSI is assumed to be available at both the transmitter and receiver, making beamforming-based approaches for selecting matrices a more effective method from the perspective of throughput [23].

The key contributions of this paper can be summarized as follows:

• Analysis of Diversity Order and Error Performance with and without Selection:
  This study compares scenarios with and without selection, clearly analyzing the performance improvement achievable through selection from the viewpoints of diversity order. Research on systematically deriving the diversity order for interference alignment (IA) with multiple antennas has been limited. This paper quantitatively analyzes and verifies that selection diversity, when using M antennas, can enhance the performance of IA from the perspective of error probability. Without selection, the conditional DO is limited to $M/2$, while selection improves it to $M^2/2$, resulting in significant error probability reduction at high SNR levels.
• Improvement of Conditional Diversity Order (DO) through Beamforming Selection:
  This paper proposes a novel beamforming vector selection method in the interference alignment (IA) environment, achieving a conditional DO of $M^2/2$. This ensures higher reliability and improved error performance compared to existing methods [23].
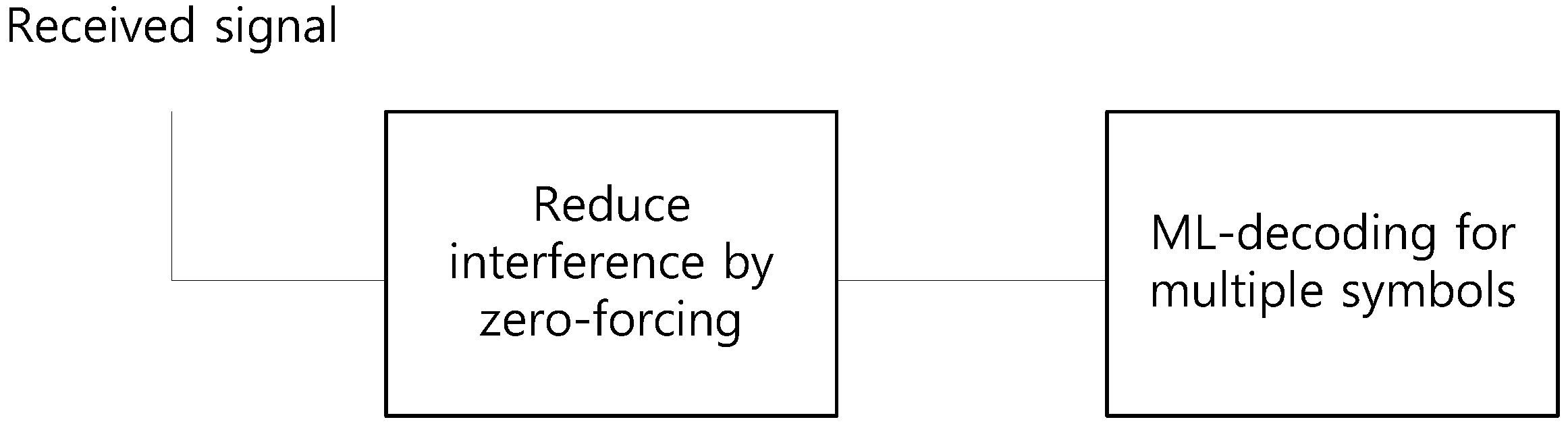
• Proposed Two-Stage Decoding Approach:
  The proposed decoding procedure removes interference signals using zero-forcing and then recovers the desired signal with maximum likelihood (ML) decoding. This significantly reduces error probability compared to conventional zero-forcing-based decoding methods.
• Utilization of Orthogonalization Techniques:
  The paper optimizes the design of beamforming matrices using QR factorization and singular-value decomposition (SVD)-based orthogonalization techniques. In particular, the SVD-based approach demonstrates better Symbol Error Rate (SER) performance compared to QR factorization, improving signal quality in multi-antenna environments.

2. Characteristic Function of Multivariate Rayleigh Random Variables

Usually, the characteristic function of multivariate Rayleigh random variables is used for analysis of the error probability. Therefore, in this section, we introduce the results from [24].

Consider $L\times 1$ complex Gaussian random vector x given by

$$\begin{array}{cc}\hfill \mathbf{x}& ={\mathbf{x}}_c+j{\mathbf{x}}_s\hfill \\ \hfill & =\left[\begin{array}{c}{x}_{c_1}\\ ⋮\\ x_{c_L}\end{array}\right]+j\left[\begin{array}{c}{x}_{s_1}\\ ⋮\\ X_{s_L}\end{array}\right]\hfill \end{array}$$

(1)

with covariance matrix ${\mathbf{K}}_{cc}$ and ${\mathbf{K}}_{ss}$ and cross-covariance matrix ${\mathbf{K}}_{cs}$ such that $E\left[x_{c_i}{x}_{s_i}\right]={\left({\mathbf{K}}_{cs}\right)}_{ii}=0$.

Let ${\gamma }_i={|x_{c_i}+j{x}_{s_i}|}^2$ and $\gamma ={({\gamma }_i,\cdots ,{\gamma }_L)}^T$. Then, the characteristic function ${\Psi }_{\gamma }\left(j\omega \right)$ of $\gamma$ is given as [24]

$$\begin{array}{cc}\hfill {\Psi }_{\gamma }\left(j\omega \right)& =E[exp(j\omega \gamma \left)\right]\hfill \\ \hfill & ={\left(det({\mathbf{I}}_L-2j\mathrm{diag}\left(\omega \right){\mathbf{K}}_{ss})\right)}^{-{\displaystyle \frac{1}{2}}}\hfill \\ \hfill & \times (det({\mathbf{I}}_L-2j\mathrm{diag}\left(\omega \right){\mathbf{K}}_{cc}\hfill \\ \hfill & +4\mathrm{diag}\left(\omega \right){\mathbf{K}}_{cs}{[I_L-2j\mathrm{diag}\left(\omega \right){\mathbf{K}}_{ss}]}^{-1}\hfill \\ \hfill & \times \mathrm{diag}\left(\omega \right){\mathbf{K}}_{cs}^T){)}^{-{\displaystyle \frac{1}{2}}}.\hfill \end{array}$$

(2)

If X is a circularly symmetric complex Gaussian random vector, that is

$${\mathbf{K}}_{cc}={\mathbf{K}}_{ss},{\mathbf{K}}_{cs}^T=-{\mathbf{K}}_{cs},$$

(2) is simplified as

$$\begin{array}{cc}\hfill {\Psi }_{\gamma }\left(j\omega \right)& =det({\mathbf{I}}_L-2j\mathrm{diag}\left(\omega \right)[{\mathbf{K}}_{cc}+j{\mathbf{K}}_{cs}])\hfill \\ \hfill & \times det({\mathbf{I}}_L-2j\mathrm{diag}\left(\omega \right)[{\mathbf{K}}_{cc}-j{\mathbf{K}}_{cs}])\hfill \\ \hfill & \times det{({\mathbf{I}}_L-j\mathrm{diag}\left(\omega \right)\mathbf{K})}^{-{\displaystyle \frac{1}{2}}}\hfill \\ \hfill & \times det{({\mathbf{I}}_L-j\mathrm{diag}\left(\omega \right){\mathbf{K}}^{†})}^{-{\displaystyle \frac{1}{2}}}.\hfill \end{array}$$

(3)

where K is the covariance matrix of x.

In general, for analysis on the error performance, (2) and (3) are important formulas, because the error probability is given as a Q function, which is upper-bounded by the exponential function. Let $\omega =j{(\rho ,\rho ,\cdots ,\rho )}^T$, and then (2) is given as

$$\begin{array}{cc}\hfill {\Psi }_{\gamma }(-\rho )& ={\left(det({\mathbf{I}}_L+2\rho {\mathbf{K}}_{ss})\right)}^{-{\displaystyle \frac{1}{2}}}\hfill \\ \hfill & \times {\left(det([{\mathbf{I}}_L+2\rho {\mathbf{K}}_{cc}]+4{\rho }^2{\mathbf{K}}_{cs}{[{\mathbf{I}}_L+2\rho {\mathbf{K}}_{ss}]}^{-1}{\mathbf{K}}_{cs}^T)\right)}^{-{\displaystyle \frac{1}{2}}}\hfill \end{array}$$

and (3) is also given as

$$\begin{array}{cc}\hfill {\Psi }_{\gamma }(-\rho )& =det{({\mathbf{I}}_L+\rho \mathbf{K})}^{-{\displaystyle \frac{1}{2}}}\times det{({\mathbf{I}}_L+\rho {\mathbf{K}}^{†})}^{-{\displaystyle \frac{1}{2}}}\hfill \end{array}$$

In a high SNR region, where $\rho \to \infty$, we have

$$\begin{array}{cc}\hfill {\Psi }_{\gamma }(-\rho )& \approx {\left(2\rho \right)}^{-{\displaystyle \frac{\mathrm{rank}\left({\mathbf{K}}_{ss}\right)+\mathrm{rank}({\mathbf{K}}_{cc}+{\mathbf{K}}_{cs}{\mathbf{K}}_{ss}^{-1}{\mathbf{K}}_{cs}^T)}{2}}}\hfill \\ \hfill & \times \prod {\lambda }_{K_{ss}}\prod {\lambda }_{{\mathbf{K}}_{cc}+{\mathbf{K}}_{cs}{\mathbf{K}}_{ss}^{-1}{\mathbf{K}}_{cs}^T}.\hfill \end{array}$$

where ${\lambda }_{*}$ denotes the eigenvalues of the matrix. If there is no deterministic relation among the element of X, K is a full-rank matrix.

For (3), we have

$$\begin{array}{cc}\hfill {\Psi }_{\gamma }(-\rho )& ={\rho }^{-\mathrm{rank}\left(\mathbf{K}\right)}{|\prod {\lambda }_{\mathbf{K}}|}^2.\hfill \end{array}$$

(4)

From this result, the following lemma can be obtained.

Lemma 1.

Consider that the received SNR is expressed as $\gamma ={\rho \left|\mathbf{x}\right|}^2$, where  x is a circularly symmetric Gaussian random vector. The DO of the decoder is the number of the random variables with non-deterministic relation in x.

3. Selection of Beamforming Matrices for 3-User MIMO Interference Channel

3.1. System Model and Interference Alignment for 3-User MIMO Interference Channel

In this subsection, the system model for 3-user MIMO interference channel and IA is explained [3]. And then, the proposed scheme, the selection scheme of beamforming matrices for IA, is introduced. Here is a system model for the 3-user interference channel with M antennas.

• For even M, we have

  $${\mathbf{Y}}_{e,k}=\sqrt{\rho }\sum _{i=1}^3{\mathbf{H}}_{ki}{\mathbf{V}}_i{\mathbf{d}}_k+{\mathbf{n}}_k$$

  where ${\mathbf{H}}_{ki}$ and ${\mathbf{V}}_i$ denote an $M\times M$ channel matrix between transmitter i and receiver k and $M\times {\displaystyle \frac{M}{2}}$ beamforming matrix of transmitter i, respectively. ${\mathbf{d}}_k$ is an ${\displaystyle \frac{M}{2}}\times 1$ data stream vector, and $\rho$ is the parameter linearly proportional to the average transmit SNR. It is assumed that all channel coefficients are independent and identically distributed with the Rayleigh distribution.
• For odd M, we have

  $${\mathbf{Y}}_{o,k}=\sqrt{\rho }\sum _{i=1}^3{\mathbf{H}}_{o,ki}{\mathbf{V}}_i{\mathbf{d}}_k+{\mathbf{n}}_k$$

  where ${\mathbf{H}}_{o,ki}$ is given as

  $${\mathbf{H}}_{o,ki}=\left[\begin{array}{cc}{\mathbf{H}}_{ki}& \mathbf{0}\\ \mathbf{0}& {\mathbf{H}}_{ki}\end{array}\right]$$

  and ${\mathbf{V}}_i$ denotes a $2M\times M$ beamforming matrix, respectively. ${\mathbf{d}}_k$ is an $M\times 1$ data stream vector.

We can generate the beamforming matrices for IA as follows. From the result in [3], the beamforming matrices for IA are obtained by the following relation:

$$\begin{array}{cc}\hfill \mathrm{span}\left({\mathbf{H}}_{12}{\mathbf{V}}_2\right)& =\mathrm{span}\left({\mathbf{H}}_{13}{\mathbf{V}}_3\right)\hfill \\ \hfill {\mathbf{H}}_{21}{\mathbf{V}}_1& ={\mathbf{H}}_{23}{\mathbf{V}}_3\hfill \\ \hfill {\mathbf{H}}_{31}{\mathbf{V}}_1& ={\mathbf{H}}_{32}{\mathbf{V}}_2.\hfill \end{array}$$

(5)

It is rewritten as

$$\begin{array}{cc}\hfill \mathrm{span}\left({\mathbf{V}}_1\right)& =\mathrm{span}\left({\mathbf{H}}_{31}^{-1}{\mathbf{H}}_{32}{\mathbf{H}}_{12}^{-1}{\mathbf{H}}_{13}{\mathbf{H}}_{23}^{-1}{\mathbf{H}}_{21}{\mathbf{V}}_1\right)\hfill \\ \hfill {\mathbf{V}}_2& ={\mathbf{H}}_{32}^{-1}{\mathbf{H}}_{31}{\mathbf{V}}_1\hfill \\ \hfill {\mathbf{V}}_3& ={\mathbf{H}}_{23}^{-1}{\mathbf{H}}_{21}{\mathbf{V}}_1.\hfill \end{array}$$

(6)

Therefore, ${\mathbf{V}}_1$ consists of the eigenvectors of

$$\begin{array}{c}\hfill {\mathbf{H}}_{31}^{-1}{\mathbf{H}}_{32}{\mathbf{H}}_{12}^{-1}{\mathbf{H}}_{13}{\mathbf{H}}_{23}^{-1}{\mathbf{H}}_{21}(=\mathbf{A})\end{array}$$

(7)

and ${\mathbf{V}}_2$ and ${\mathbf{V}}_3$ can be obtained from (6).

• For even M, we have

  $${\mathbf{V}}_1=\left[{\mathbf{b}}_1{\mathbf{b}}_2\cdots {\mathbf{b}}_{{\displaystyle \frac{M}{2}}}\right]$$

  (8)

  where ${\mathbf{b}}_i$ is an eigenvector of A.
• For odd M, we have

  $${\mathbf{V}}_1=\left[\begin{array}{cccccc}{\mathbf{b}}_1& 0& {\mathbf{b}}_3& 0\cdots & 0& {\mathbf{b}}_M\\ 0& {\mathbf{b}}_2& 0& {\mathbf{b}}_4\cdots & {\mathbf{b}}_{M-1}& 0\end{array}\right].$$

  (9)

In this way, at each receiver, interference signal vectors are aligned as described in Figure 1. In Figure 1, the desired signal of transmitter 1 is represented in red, the desired signal of transmitter 2 is in green, and the desired signal of transmitter 3 is in black. Each receiver 1, 2, and 3 must receive the corresponding transmitter’s signal without interference. On the right side of Figure 1, it can be observed that the desired and undesired signals at each receiver are linearly independent and aligned. This represents the core result of interference alignment (IA).

In fact, for odd M, all eigenvectors of A should be used as in (9), and thus, the selection of beamforming matrices is complicated, and the IA should be modified for selection. Therefore, for simplicity, we consider the case that M is even in this paper.

3.2. Orthogonalization of Beamforming Matrices

In general, the orthogonalization of transmit signals can achieve the improvement in performance. Equation (6) guarantees the perfect IA but does not guarantee the orthogonalization between beamforming vectors at each transmitter. Therefore, we should modify the design of the beamforming matrices.

In [12], the QR factorization is used for the orthogonalization of beamforming matrices, which is identical to the Gram–Schmidt orthogonalization. In the Gram–Schmidt orthogonalization, there exists a critical drawback. Let us orthogonalize two beamforming matrices by using the Gram–Schmidt orthogonalization as follows:

$$\begin{array}{cc}\hfill & \mathrm{Beamforming}\mathrm{matrix}1:\left({\mathbf{b}}_{\mathbf{1}}{\mathbf{b}}_{\mathbf{2}}\right)=\left({\mathbf{b}}_{\mathbf{1}}{{\mathbf{b}}_{\mathbf{2}}}^{\mathbf{\prime }}\right)\hfill \\ \hfill & \mathrm{Beamforming}\mathrm{matrix}2:\left({\mathbf{b}}_{\mathbf{1}}{\mathbf{b}}_{\mathbf{3}}\right)=\left({\mathbf{b}}_{\mathbf{1}}{{\mathbf{b}}_{\mathbf{3}}}^{\mathbf{\prime }}\right)\hfill \end{array}$$

(10)

In (10), it can be seen that ${\mathbf{b}}_1$ is the beamforming vector for the beamforming matrix 1 and 2. If the data symbol is (x,0), $\left({\mathbf{b}}_{\mathbf{1}}{\mathbf{b}}_{\mathbf{2}}\right){(x,0)}^T=\left({\mathbf{b}}_{\mathbf{1}}{\mathbf{b}}_{\mathbf{3}}\right){(x,0)}^T=x{\mathbf{b}}_{\mathbf{1}}$. If the error rate becomes high for beamforming matrix 1 for $(x,0)$, the error rate also becomes high for beamforming matrix 2. In this case, we cannot use the advantage of the selection of beamforming vectors. In [12], this case does not occur almost surely, because it is focused on the sum rate where the Gaussian source is assumed. However, the practical communication system uses the quadrature amplitude modulation (QAM) or phase shift keying modulation (PSK). Therefore, the weakness of this scheme can be exposed in the practical communication system.

In this paper, instead of Gram–Schmidt orthogonalization, we use SVD for the orthogonalization of beamforming matrices as follows:

$$\begin{array}{cc}\hfill \mathrm{span}\left({\mathbf{V}}_i\right)& =\mathrm{span}({\mathbf{U}}_i\Sigma {\mathcal{V}}^{†})=\mathrm{span}\left({\mathbf{U}}_i\left({\displaystyle \frac{M}{2}}\right)\right)\hfill \end{array}$$

where ${\mathbf{U}}_i$, $\Sigma$, and ${\mathcal{V}}^{†}$ can be obtained by SVD, and ${\mathbf{U}}_i\left({\displaystyle \frac{M}{2}}\right)$ is the submatrix consisting of the first $M/2$ columns of ${\mathbf{U}}_i$. In this way, the problem of Gram–Schmidt orthogonalization is overcome, and therefore, we can use ${\mathbf{U}}_i\left({\displaystyle \frac{M}{2}}\right)$ as a beamforming matrix for the transmitter i in order to improve the performance.

3.3. Two-Stage Decoding and Selection of Beamforming Matrices

In [3], each transmitter can send $M/2$ data streams, and each receiver can detect them without interference. In general, each receiver decodes the desired signal by only zero-forcing because of its complexity. However, zero-forcing can make error performance worse. Therefore, in this paper, we consider two cascaded decoding procedures which consist of zero-forcing for the interference signal and ML decoding for the desired signal. However, in the case of ML decoding, the decoding complexity increases with $M_{\mathrm{QAM}}^d$ as the degrees of freedom and the number of QAM symbols ($M_{\mathrm{QAM}}$) increase. In contrast, zero-forcing has a complexity proportional to $M_{\mathrm{QAM}}$, resulting in higher complexity for ML decoding. This decoding procedure is described in Figure 2. In an MIMO communication system, given a channel matrix H, the pairwise error probability (PEP) is given as

$${\mathrm{P}}_{\mathrm{PEP}}=\mathrm{Pr}(\mathbf{x}\to \widehat{\mathbf{x}}|\mathbf{H})=\mathrm{Q}\left(\right|\mathbf{H}\left(\mathbf{x}-\widehat{\mathbf{x}}\right)\left|\right).$$

(11)

Considering M-QAM, the symbol error probability (SER) can be obtained approximately by the union bound of the PEP, thus lowering the PEP is related to lowering the SER directly. If the error probability of all pair-wise error patterns can be reduced, for M-QAM, the SER can be reduced. Therefore, we can select the eigenvectors for ${\mathbf{V}}_1$ as follows:

$$\begin{array}{cc}\hfill {\mathbf{V}}_{1,\mathrm{sel}}=& arg\underset{{\mathbf{V}}_1\in \mathrm{eig}\left(\mathbf{A}\right)}{max}min(|{\mathbf{R}}_1^{†}{\mathbf{H}}_{11}{\mathbf{V}}_1{\tilde{\mathbf{d}}}_1|,\hfill \\ \hfill & |{\mathbf{R}}_2^{†}{\mathbf{H}}_{22}{\mathbf{V}}_2{\tilde{\mathbf{d}}}_2|,|{\mathbf{R}}_3^{†}{\mathbf{H}}_{33}{\mathbf{V}}_3{\tilde{\mathbf{d}}}_3\left|\right).\hfill \end{array}$$

(12)

where ${\tilde{\mathbf{d}}}_i={\mathbf{x}}_i-{\widehat{\mathbf{x}}}_i$, which can be various vectors, because there are various pair-wise error pattens for M-QAM.

Definition 1.

In general, the DO is defined as $DO={lim}_{SNR\to \infty }{\displaystyle \frac{log{P}_{P}EP\left(\mathrm{SNR}\right)}{log\mathrm{SNR}}}$. In this paper, we define the contional DO for simplicity as follows:

$$DO|\mathbf{A}=\underset{SNR\to \infty }{lim}{\displaystyle \frac{log{P}_{PEP|\mathbf{A}}\left(\mathrm{SNR}\right)}{log\mathrm{SNR}}}.$$

(13)

where A is defined in (6). The contional DO does not describe the error performance in the fading environment directly like the DO. However, it can make the analysis for the selection of beamforming vectors for the interference channel as that of that for the P2P MIMO channel, and we can expect that as the contitional DO become higher, the error performance become better.

4. Diversity Analysis

In this section, the conditional DO of the proposed scheme is derived. In fact, it is too complicated to derive the exact DO, and thus, we analyze the contional DO of the proposed scheme. First, we derive the DO of the case without the selection of beamforming matrices and then analyze the conditional DO of the two-stage decoding with the selection of beamforming matrices.

4.1. Diversity Analysis for the Case Without Selection

In this subsection, we analyze the DO of IA without selection.

$$\begin{array}{cc}\hfill E_{{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33}}& \mathrm{Pr}(\mathbf{x}\to \widehat{\mathbf{x}}|\mathbf{A},{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33})\hfill \\ \hfill & ={\displaystyle \frac{1}{3}}{E}_{{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33}|\mathbf{A}}\left(\mathrm{Pr}(\mathbf{x}\to \widehat{\mathbf{x}}|\mathbf{A},{\mathbf{H}}_{11})+\mathrm{Pr}(\mathbf{x}\to \widehat{\mathbf{x}}|\mathbf{A},{\mathbf{H}}_{22})+\mathrm{Pr}(\mathbf{x}\to \widehat{\mathbf{x}}|\mathbf{A},{\mathbf{H}}_{33})\right)\hfill \\ \hfill & =\sum _{i=1}^3{E}_{{\mathbf{H}}_{ii}}Q\left(\sqrt{\rho }{\left|{\mathbf{R}}_i^{†}{\mathbf{H}}_{ii}{\mathbf{V}}_i{\tilde{\mathbf{d}}}_i\right|}^2\right)\hfill \\ \hfill & \le \sum _{i=1}^3{E}_{{\mathbf{H}}_{ii}}exp\left(-{\displaystyle \frac{\rho }{2}}{\left|{\mathbf{R}}_i^{†}{\mathbf{H}}_{ii}{\mathbf{V}}_i{\tilde{\mathbf{d}}}_i\right|}^2\right).\hfill \end{array}$$

(14)

We have

$$|{\mathbf{R}}_i^{†}{\mathbf{H}}_{ii}{\mathbf{V}}_i\widetilde{{\mathbf{d}}_i}{|}^2=\sum _{k=1}^{{\displaystyle \frac{M}{2}}}{|{\mathbf{r}}_k^{†}{\mathbf{H}}_{ii}\sum _{l=1}^{{\displaystyle \frac{M}{2}}}{\mathbf{v}}_{i,l}{\tilde{d}}_l|}^2$$

(15)

where ${\tilde{d}}_l$ is the lth element of ${\tilde{\mathbf{d}}}_i$.

${\mathbf{R}}_i$ and ${\mathbf{V}}_i$ consist of orthonormal columns, and thus, each ${\mathbf{r}}_k^{†}{\mathbf{H}}_{ii}{\sum }_{l=1}{\mathbf{u}}_k{\tilde{d}}_l$ is a complex Gaussian random variable and independent from the others. $E\left\{|{\mathbf{r}}_k^{†}{\mathbf{H}}_{ii}{\sum }_{l=1}{\mathbf{v}}_{i,k}{\tilde{d}}_l{|}^2\right\}\ge E\left\{|{\mathbf{r}}_k^{†}{\mathbf{H}}_{ii}{\mathbf{v}}_{l^{\prime }}{\tilde{d}}_{l^{\prime }}{|}^2\right\}={\left|{\tilde{d}}_{l^{\prime }}\right|}^2\ne 0$. Therefore,

$$\begin{array}{cc}\hfill & \sum _{i=1,2,3}{E}_{{\mathbf{H}}_{ii}}exp(-{\displaystyle \frac{\rho }{2}}|{\mathbf{R}}_i^{†}{\mathbf{H}}_{ii}{\mathbf{V}}_i\tilde{\mathbf{d}}{|}^2)\hfill \\ \hfill & =3E_{{\mathbf{H}}_{ii}}\prod _{k=1}^{{\displaystyle \frac{M}{2}}}exp(-{\displaystyle \frac{\rho }{2}}|{\mathbf{r}}_k^{†}{\mathbf{H}}_{ii}\sum _{l=1}{\mathbf{v}}_{i,l}{\tilde{d}}_l{|}^2)\hfill \\ \hfill & \le 3\prod _{k=1}^{{\displaystyle \frac{M}{2}}}{\left(1+{\displaystyle \frac{\rho |{\tilde{d}}_l^{\prime }{|}^2}{2}}\right)}^{-1}\hfill \end{array}$$

(16)

each $E_{{\mathbf{H}}_{ii}}Q(\sqrt{\rho }|{\mathbf{R}}_i^{†}{\mathbf{H}}_{ii}{\mathbf{V}}_i\tilde{\mathbf{d}}{|}^2)$ has a DO of $M/2$ regardless of A, which means that the conditional DO is also $M/2$. Finally, without selection, IA and two-stage decoding can achieve a DO of $M/2$.

4.2. Diversity Analysis for the Case with Selection

The DO depends on the beamforming vector corresponding to the worst SNR; therefore, the analysis for the worst case is enough for diversity analysis. In fact, there are $\left({\displaystyle \genfrac{}{}{0pt}{}{M}{M/2}}\right)$ choices for the selection of beamforming matrices. Let each set containing $M/2$ beamforming vectors be $S_k$ and S be a set consisting of $S_k$. Thus, $\left|S\right|=\left({\displaystyle \genfrac{}{}{0pt}{}{M}{M/2}}\right)$, and we let L be $\left|S\right|$. From the selection criterion, the following PEP analysis is possible for a given A.

$$\begin{array}{cc}\hfill & E_{{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33}|\mathbf{A}}\mathrm{Pr}(\mathbf{x}\to \widehat{\mathbf{x}}|\mathbf{A},{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33})\hfill \\ \hfill & ={\displaystyle \frac{1}{3}}{E}_{{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33}|\mathbf{A}}\left(\mathrm{Pr}(\mathbf{x}\to \widehat{\mathbf{x}}|\mathbf{A},{\mathbf{H}}_{11})+\mathrm{Pr}(\mathbf{x}\to \widehat{\mathbf{x}}|\mathbf{A},{\mathbf{H}}_{22})+\mathrm{Pr}(\mathbf{x}\to \widehat{\mathbf{x}}|\mathbf{A},{\mathbf{H}}_{33})\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{3}}\sum _{i=1}^3{E}_{{\mathbf{H}}_{ii}|\mathbf{A}}Q\left(\sqrt{\rho }{\left|{\mathbf{R}}_{i,\mathrm{sel}}^{†}{\mathbf{H}}_{ii}{\mathbf{V}}_{i,\mathrm{sel}}\tilde{\mathbf{d}}\right|}^2\right)\hfill \\ \hfill & \le E_{{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33}|\mathbf{A}}Q\left(\sqrt{\rho }\underset{k\in \{1,\dots ,L\}}{max}\underset{i_k\in \{1,2,3\}}{min}{\left|{\mathbf{R}}_{i_k,k}^{†}{\mathbf{H}}_{i_k{i}_k}{\mathbf{V}}_{i_k,k}\tilde{\mathbf{d}}\right|}^2\right)\hfill \\ \hfill & \le E_{{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33}|\mathbf{A}}exp\left(-{\displaystyle \frac{\rho }{2}}\underset{k\in \{1,\dots ,L\}}{max}\underset{i_k\in \{1,2,3\}}{min}{\left|{\mathbf{R}}_{i_k,k}^{†}{\mathbf{H}}_{i_k{i}_k}{\mathbf{V}}_{i_k,k}\tilde{\mathbf{d}}\right|}^2\right)\hfill \\ \hfill & \le E_{{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33}|\mathbf{A}}exp\left(-{\displaystyle \frac{\rho }{2L}}\sum _{k=1}^L\underset{i_k\in \{1,2,3\}}{min}{\left|{\mathbf{R}}_{i_k,k}^{†}{\mathbf{H}}_{i_k{i}_k}{\mathbf{V}}_{i_k,k}\tilde{\mathbf{d}}\right|}^2\right)\hfill \\ \hfill & \le E_{{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33}|\mathbf{A}}\underset{\{i_1,\dots ,i_L\}\in {\{1,2,3\}}^L}{max}exp\left(-{\displaystyle \frac{\rho }{2L}}\sum _{k=1}^L{\left|{\mathbf{R}}_{i_k,k}^{†}{\mathbf{H}}_{i_k{i}_k}{\mathbf{V}}_{i_k,k}\tilde{\mathbf{d}}\right|}^2\right)\hfill \\ \hfill & \le E_{{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33}|\mathbf{A}}\sum _{\{i_1,\dots ,i_L\}\in {\{1,2,3\}}^L}exp\left(-{\displaystyle \frac{\rho }{2L}}\sum _{k=1}^L{\left|{\mathbf{R}}_{i_k,k}^{†}{\mathbf{H}}_{i_k{i}_k}{\mathbf{V}}_{i_k,k}\tilde{\mathbf{d}}\right|}^2\right)\hfill \end{array}$$

(17)

When $M=4$, we have six choices for beamforming matrices. From (17),

$$\begin{array}{cc}\hfill & E_{{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33}|\mathbf{A}}Pr\left(\mathbf{x}\to \widehat{\mathbf{x}}\right|\mathbf{A},{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33})\hfill \\ \hfill & \le E_{{\mathbf{H}}_{11},{\mathbf{H}}_{22},{\mathbf{H}}_{33}|\mathbf{A}}\sum _{\{i_1,...,i_6\}\in {\{1,2,3\}}^6,\tilde{\mathbf{d}}}exp\left(-{\displaystyle \frac{\rho }{6}}\sum _{k=1}^6{\left|{\mathbf{R}}_{i_k,k}^{†}{\mathbf{H}}_{i_k{i}_k}{\mathbf{V}}_{i_k,k}\tilde{\mathbf{d}}\right|}^2\right)\hfill \end{array}$$

(18)

From Equation (18), we are able to independently analyze the diversity order for each transmitter–receiver pair. In other words, if we analyze the diversity order for one transmitter–receiver pair, the result will be the same for all pairs. Therefore, we will analyze the diversity order for the first pair $i_k=1$.

Let $\tilde{\mathbf{d}}=(d_1,d_2)$, ${\mathbf{V}}_{1,1}=\left[{\mathbf{u}}_{1,1}{\mathbf{u}}_{1,2}\right]$ and ${\mathbf{R}}_{1,1}=[{\mathbf{r}}_{1,11},{\mathbf{r}}_{1,12}]$ be the zero-forcing matrix for ${\mathbf{V}}_{1,1}$. Then,

$$\begin{array}{cc}\hfill |{\mathbf{R}}_{1,1}^{†}{\mathbf{H}}_{11}{\mathbf{V}}_{1,1}\tilde{\mathbf{d}}{|}^2& =|\underset{{\tilde{h}}_1}{\underbrace{{\mathbf{r}}_{1,11}^{†}{\mathbf{H}}_{11}\sum _{i=1}^2{\mathbf{u}}_{1,i}{d}_i}}{|}^2+{|\underset{{\tilde{h}}_2}{\underbrace{{\mathbf{r}}_{1,12}^{†}{\mathbf{H}}_{11}\sum _{i=1}^2{\mathbf{u}}_{1,i}{d}_i}}|}^2\hfill \end{array}$$

(19)

Similarly, define the other ${\mathbf{V}}_{1,k}$s and ${\mathbf{R}}_{1,k}$; then,

$$\begin{array}{cc}\hfill |{\mathbf{R}}_{1,k}^{†}{\mathbf{H}}_{11}{\mathbf{V}}_{1,k}\tilde{\mathbf{d}}{|}^2& =|\underset{{\tilde{h}}_{2k+1}}{\underbrace{{\mathbf{r}}_{1,k1}^{†}{\mathbf{H}}_{11}\sum _{i=1}^2{\mathbf{u}}_{k,i}{d}_i}}{|}^2+{|\underset{{\tilde{h}}_{2k+2}}{\underbrace{{\mathbf{r}}_{1,k2}^{†}{\mathbf{H}}_{11}\sum _{i=1}^2{\mathbf{u}}_{k,i}{d}_i}}|}^2\hfill \end{array}$$

(20)

From (5), it can be seen that ${\sum }_{i=1}^2{\mathbf{u}}_{1,i}{d}_i$, ${\sum }_{i=1}^2{\mathbf{u}}_{2,i}{d}_i$, ${\sum }_{i=1}^2{\mathbf{u}}_{3,i}{d}_i$, and ${\sum }_{i=1}^2{\mathbf{u}}_{4,i}{d}_i$ are randomly generated from $\mathrm{span}\left({\mathbf{b}}_1{\mathbf{b}}_2\right),\mathrm{span}\left({\mathbf{b}}_1{\mathbf{b}}_3\right),\mathrm{span}\left({\mathbf{b}}_1{\mathbf{b}}_4\right),$ and $\mathrm{span}\left({\mathbf{b}}_2{\mathbf{b}}_3\right)$, respectively. Since the ${\sum }_{i=1}^2{\mathbf{u}}_{k,i}{d}_i$s are $4\times 1$ vectors, we can obtain only four linearly independent vectors among the ${\sum }_{i=1}^2{\mathbf{u}}_{k,i}{d}_i$s. Similar to this, we can also obtain the linearly independent vector among ${\mathbf{r}}_{1,lm}$

For non-zero vectors ${\mathbf{r}}_{1,lm}$ and ${\mathbf{r}}_{1,l^{\prime }{m}^{\prime }}$, even though ${\mathbf{r}}_{1,lm}={\mathbf{r}}_{1,l^{\prime }{m}^{\prime }}$, if ${\sum }_{i=1}^2{\mathbf{u}}_{1,i}{d}_i$ and ${\sum }_{i^{\prime }=1}^2{\mathbf{u}}_{1,i^{\prime }}{d}_i^{\prime }$ are linearly independent, ${\mathbf{r}}_{1,lm}{\mathbf{H}}_{11}{\sum }_{i^{\prime }=1}^2{\mathbf{u}}_{1,i^{\prime }}{d}_{i^{\prime }}$ and ${\mathbf{r}}_{1,l^{\prime }{m}^{\prime }}{\mathbf{H}}_{11}{\sum }_{i=1}^2{\mathbf{u}}_{1,i}{d}_i$ cannot have a deterministic relation. Therefore, at least eight ${\tilde{h}}_i^{\prime }s$ does not have non-deterministic relations. From Lemma 1, the eighth conditional DO is guaranteed by the proposed scheme.

Theorem 1.

When M is an even number, IA with the selection criterion in (12) and the decoding scheme with zero-forcing and multi-symbol decoding can achieve the $M^2/2$ conditional DO at least.

Proof. 

When each node has M antennas, the $M/2$ DoFs are achieved and thus in (17). Therefore, we can obtain the following relation like (19) and (20):

$$\begin{array}{cc}\hfill |{\mathbf{R}}_{1,1}^{*}{\mathbf{H}}_{11}{\mathbf{V}}_{1,1}{\mathbf{d}|}^2& =|{\mathbf{r}}_{11}^{*}{\mathbf{H}}_{11}\sum _{i=1}^{M/2}{\mathbf{u}}_{1,i}{d}_i{|}^2+|{\mathbf{r}}_{12}^{*}{\mathbf{H}}_{11}\sum _{i=1}^{M/2}{\mathbf{u}}_{1,i}{d}_i{|}^2+\cdots +{|{\mathbf{r}}_{1{\displaystyle \frac{M}{2}}}^{*}{\mathbf{H}}_{11}\sum _{i=1}^{M/2}{\mathbf{u}}_{1,i}{d}_i|}^2\hfill \\ \hfill |{\mathbf{R}}_{1,L}^{*}{\mathbf{H}}_{11}{\mathbf{V}}_{1,L}{\mathbf{d}|}^2& =|{\mathbf{r}}_{L1}^{*}{\mathbf{H}}_{11}\sum _{i=1}^{M/2}{\mathbf{u}}_{L,i}{d}_i{|}^2+|{\mathbf{r}}_{L2}^{*}{\mathbf{H}}_{11}\sum _{i=1}^{M/2}{\mathbf{u}}_{L,i}{d}_i{|}^2+\cdots +{|{\mathbf{r}}_{L{\displaystyle \frac{M}{2}}}^{*}{\mathbf{H}}_{11}\sum _{i=1}^{M/2}{\mathbf{u}}_{L,i}{d}_i|}^2\hfill \end{array}$$

(21)

where $L=\left({\displaystyle \genfrac{}{}{0pt}{}{M}{\frac{M}{2}}}\right)$. Similar to the four-antenna case, we can obtain M linearly independent vectors among the ${\sum }_{i=1}^{M/2}{\mathbf{u}}_{k,i}{d}_i$s and M linearly independent zero-forcing vectors. In (21), since each equation has $M/2$ terms, we have $M^2/2$ terms, which do not have the deterministic relation. Therefore, from lemma 1, the proposed scheme can achieve the $M^2/2$ conditional DO. □

4.3. Expected Diversity Order

In the previous subsection, we only achieved the conditional DO $M^2/2$, which is not the DO. From (18) and Theorem 1, it can be seen that the average PEP is bounded as

$$\begin{array}{c}\hfill \mathrm{PEP}\le E_{\mathit{A}}c·{\rho }^{-{\displaystyle \frac{M^2}{2}}}=E_{c}c·{\rho }^{-{\displaystyle \frac{M^2}{2}}}\end{array}$$

(22)

In fact, c is a variable related to the A, and it belongs to $(0,\infty )$. In order to achieve the DO $M^2/2$, a requirement should be added to the selection criterion, which is the minimum value of $|R_{i,\mathrm{sel}}^{†}{H}_{ii}{V}_{i,\mathrm{sel}}\tilde{\mathbf{d}}|$. If the selected beamforming vector and the corresponding zeroforcing vector cannot satisfy this value, the data are not transferred through them. In [25], this requirement can be satisfied numerically. Therefore, we can achieve the $M^2/2$ DO.

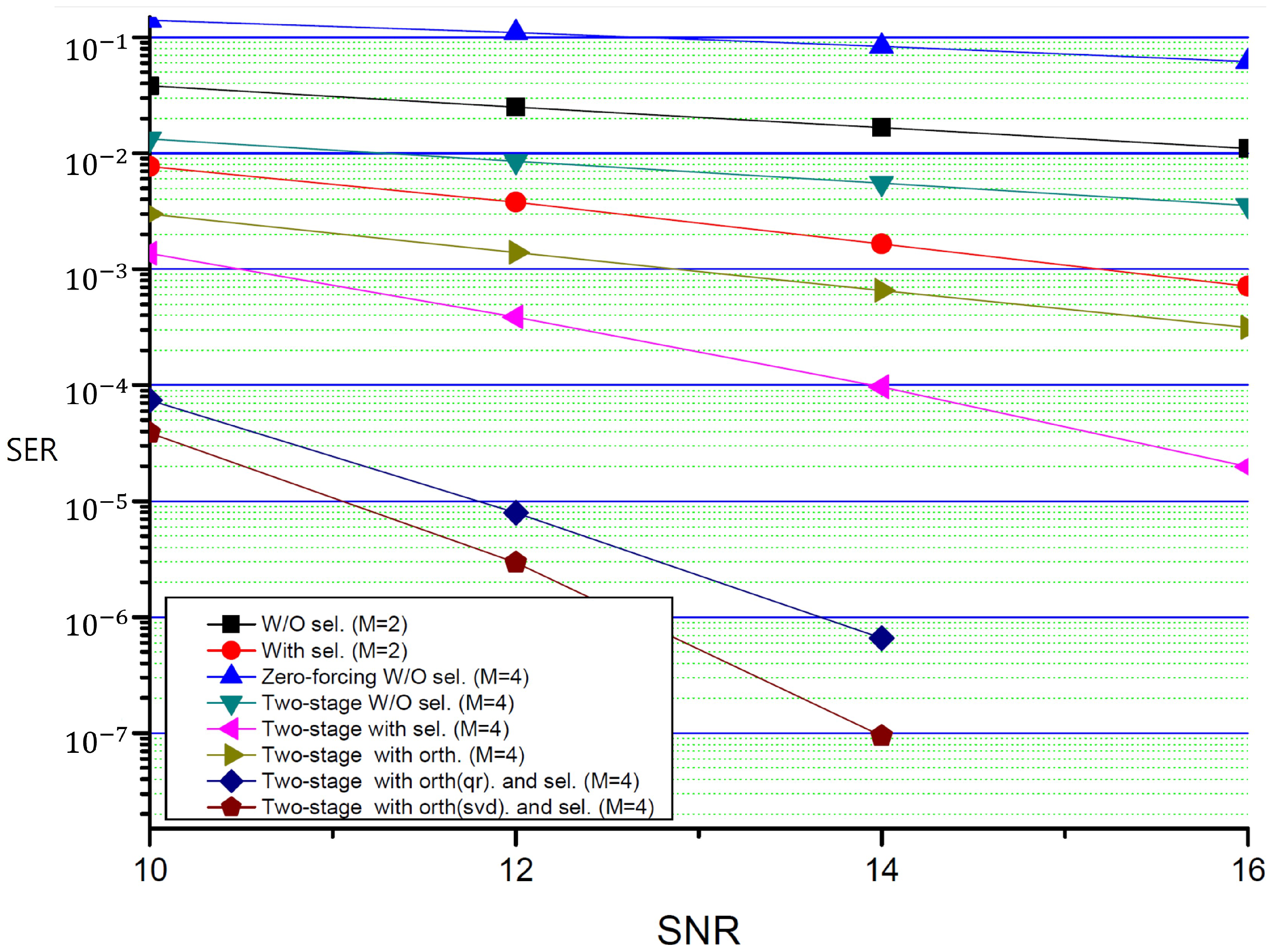
5. Simulation Results

In this section, the simulation results for the proposed scheme are presented and analyzed in detail. Each transmitter used BPSK modulation, and it was assumed that all channel coefficients followed identical distributions. Each channel coefficient was generated from a complex Gaussian distribution, with the mean and variance of the real and imaginary parts set to 0 and ${\displaystyle \frac{1}{2}}$, respectively. The error probabilities ranged from ${10}^{-1}$ to ${10}^{-7}$, covering both low and high signal-to-noise ratio (SNR) regimes.

Figure 3 compares the symbol error probability (SER) performance of various schemes for $M=2$ and $M=4$. For $M=2$, the two-stage decoding scheme behaved identically to zero-forcing decoding, as orthogonalization of beamforming matrices is not required when transmitting a single desired symbol. However, for $M=4$, the two schemes diverged significantly. The consequently arrived at the following observations:

• Observation 1: Impact of diversity order
  It can be observed that there was a significant difference in SER performance between cases with and without selection. In particular, when selection was not applied, the beamforming vector was not chosen as an optimal vector from the perspective of error probability. Interestingly, for $M=4$, the SER was observed to increase compared to $M=2$. As the DoF increased in the MIMO interference channel, the number of transmission streams grew. This deteriorated the condition number of the system’s transmit–receive matrix, since the power needed to be divided among each stream. A poor condition number amplified small noise significantly during the zero-forcing process, leading to a higher probability of errors.
  It can be observed that a significant reduction in error probability was achieved in the case of $M=4$ compared to $M=2$. This is because the diversity order is 2 for $M=2$, whereas it is 8 for $M=4$, indicating that the difference in diversity order leads to a larger decrease in error probability. As the number of antennas increased, the number of eigenvector options for selection also grew, which aligns with the analysis presented in the previous section.
• Observation 2: Impact of orthogonalization
  Even in scenarios where selection was not applied and only two-stage decoding was used, the effect of orthogonalizing the beamforming matrix was clearly evident. Without orthogonalization, the SER for $M=4$ in the absence of selection was approximately $3.0\times {10}^{-3}$ for an SNR of 12 db, whereas with orthogonalization, it improved to around $1.2\times {10}^{-3}$. For $M=4$, the benefits of using QR factorization versus SVD for selection could also be observed from the perspective of the SER. Ultimately, it can be concluded that optimizing the beamforming matrix using an appropriate orthogonalization technique is essential.
• Observation 3: Two-stage decoding performance
  In this paper, it was shown that through two-stage decoding, interference was first eliminated, allowing each transmitter–receiver pair to form an independent MIMO channel. While using zero-forcing in an independent MIMO channel did not provide any diversity order, performing ML decoding, as proven in Section 4, offered an additional diversity order, leading to further performance gains from an error probability perspective. Simulations also confirmed that when $M=4$, the performance gap between zero-forcing decoding without selection and two-stage ML decoding became increasingly pronounced as the SNR increased.

In conclusion, the simulation results presented in this section clearly demonstrate the advantages of selection and the two-stage decoding scheme in various scenarios. By leveraging diversity order and optimizing beamforming through orthogonalization, significant improvements in error probability were achieved compared to conventional zero-forcing approaches. These results emphasize the importance of proper selection and orthogonalization techniques, particularly as the number of antennas increases. These findings validate the theoretical analyses presented earlier in this paper and lay the groundwork for further exploration of advanced decoding schemes.

6. Conclusions

In this paper, a selection method of beamforming matrices for IA was proposed and its DO was analyzed for a three-user interference channel, where each node had even M antennas. For the error performance enhancement, two-stage decoding was considered, which consisted of the zero-forcing for mitigation of interference signals and the ML decoding for the desired signals, and the orthogonalization of beamforming matrices was also used.

First, by using the two-stage decoding without selection of beamforming matrices, it was confirmed that a DO of $M/2$ could be achieved, and then by using the selection scheme of beamforming matrices and two-stage decoding, it was proved that an $M^2/2$ conditional DO could be guaranteed. Also, the $M^2/2$ DO could be achieved by using an additional requirement. Through the simulation, it was also shown that the performance of the proposed scheme was superior to that of the conventional IA and the $M^2/2$ is achieved.

As a further work, we analyzed the DO for odd M values. In addition, the proposed scheme can be easily extended to the other wireless communication environment where IA can be used. Therefore, the analysis on the selection diversity for the other channel models is considered to be a good further work.