Integral Reinforcement Learning-Based Online Adaptive Dynamic Event-Triggered Control Design in Mixed Zero-Sum Games for Unknown Nonlinear Systems
Abstract
:1. Introduction
- 1.
- 2.
- By establishing the actor NNs to approximate the optimal control strategies and auxiliary control inputs of each player, a novel event-triggered IRL algorithm is proposed to solve the mixed zero-sum games problem without using the information of system functions.
- 3.
- In the developed off-policy DETC method, by introducing the dynamic adaptive parameters to the triggering conditions, compared with the static event-triggered mechanism, the triggering frequency is further reduced, thereby achieving greater utilization of communication resources.
2. Problem Formulation
3. ADP-Based Near-Optimal Control for MZSGs Under DETC Mechanism
4. Dynamic Event-Triggered IRL Algorithm for MZSG Problem
| Algorithm 1 On-Policy ADP Algorithm |
Step 1: The initial admissible control inputs are expressed as also let . Step 2: Solve the following Bellman Equation (27) for . Step 4: If max ( is a set positive number), stop at step 3; otherwise, return to step 2. |
| Algorithm 2 Model-Free IRL Algorithm for MZSGs |
Step 1: Set initial policies . Step 2: Solve the Bellman Equation (31) to acquire Step 3: If max ( is a set positive number), stop it; otherwise, return to step 2. |
5. Stability Analysis
6. Simulation
6.1. A Nonlinear Example
6.2. A Comparison Simulation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, L.; Yu, Z.Y. Maximum principle for nonzero-sum stochastic differential game with delays. IEEE Trans. Automa. Control 2014, 60, 1422–1426. [Google Scholar] [CrossRef]
- Yasini, S.; Sitani, M.B.N.; Kirampor, A. Reinforcement learning and neural networks for multi-agent nonzero-sum games of nonlinear constrained-input systems. Int. J. Mach. Learn. Cybern. 2016, 7, 967–980. [Google Scholar] [CrossRef]
- Rupnik Poklukar, D.; Žerovnik, J. Double Roman Domination: A Survey. Mathematics 2023, 11, 351. [Google Scholar] [CrossRef]
- Leon, J.F.; Li, Y.; Peyman, M.; Calvet, L.; Juan, A.A. A Discrete-Event Simheuristic for Solving a Realistic Storage Location Assignment Problem. Mathematics 2023, 11, 1577. [Google Scholar] [CrossRef]
- Tanwani, A.; Zhu, Q.Y.Z. Feedback nash equilibrium for randomly switching differential-algebraic games. IEEE Trans. Automa. Control 2020, 65, 3286–3301. [Google Scholar] [CrossRef]
- Peng, B.W.; Stancu, A.; Dang, S.P. Differential graphical games for constrained autonomous vehicles based on viability theory. IEEE Trans. Cybern. 2022, 52, 8897–8910. [Google Scholar] [CrossRef]
- Wu, S. Linear-quadratic non-zero sum backward stochastic differential game with overlapping information. IEEE Trans. Autom. Control 2023, 60, 1800–1806. [Google Scholar] [CrossRef]
- Dong, B.; Feng, Z.; Cui, Y.M. Event-triggered adaptive fuzzy optimal control of modular robot manipulators using zero-sum differential game through value iteration. Int. J. Adapt. Control Signal Process. 2023, 37, 2364–2379. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, M.M.; Ha, M.M. Stability and admissibility analysis for zero-sum games under general value iteration formulation. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 8707–8718. [Google Scholar] [CrossRef]
- Du, W.; Ding, S.F.; Zhang, C.L. Modified action decoder using Bayesian reasoning for multi-agent deep reinforcement learning. Int. J. Mach. Learn. Cybern. 2021, 12, 2947–2961. [Google Scholar] [CrossRef]
- Lv, Y.F.; Ren, X.M. Approximate nash solutions for multiplayer mixed-zero-sum game with reinforcement learning. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2739–2750. [Google Scholar] [CrossRef]
- Qin, C.B.; Zhang, Z.W.; Shang, Z.Y. Adaptive optimal safety tracking control for multiplayer mixed zero-sum games of continuous-time systems. Appl. Intell. 2023, 53, 17460–17475. [Google Scholar] [CrossRef]
- Ming, Z.Y.; Zhang, H.G.; Zhang, J.; Xie, X.P. A novel actor-critic-identifier architecture for nonlinear multiagent systems with gradient descent method. Automatica 2023, 155, 645–657. [Google Scholar] [CrossRef]
- Ming, Z.Y.; Zhang, H.G.; Wang, Y.C.; Dai, J. Policy iteration Q-learning for linear ito stochastic systems with markovian jumps and its application to power systems. IEEE Trans. Cybern. 2024, 54, 7804–7813. [Google Scholar] [CrossRef] [PubMed]
- Song, R.Z.; Liu, L.; Xia, L.; Frank, L. Online optimal event-triggered H∞ control for nonlinear systems with constrained state and input. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 1–11. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.G.; Yu, R. H∞ tracking control of discrete-time system with delays via data-based adaptive dynamic programming. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4078–4085. [Google Scholar] [CrossRef]
- Zhang, H.G.; Liu, Y.; Xiao, G.Y. Data-based adaptive dynamic programming for a class of discrete-time systems with multiple delays. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 432–441. [Google Scholar] [CrossRef]
- Wang, R.G.; Wang, Z.; Liu, S.X. Optimal spin polarization control for the spin-exchange relaxation-free system using adaptive dynamic programming. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 5835–5847. [Google Scholar] [CrossRef]
- Wen, Y.; Si, J.; Brandt, A. Online reinforcement learning control for the personalization of a robotic knee prosthesis. IEEE Trans. Cybern. 2020, 50, 2346–2356. [Google Scholar] [CrossRef]
- Yu, S.H.; Zhang, H.G.; Ming, Z.Y. Adaptive optimal control via continuous-time Q-learning for Stackelberg-Nash games of uncertain nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 2023, 54, 2346–2356. [Google Scholar] [CrossRef]
- Rizvi, S.A.A.; Lin, Z.L. Adaptive dynamic programming for model-free global stabilization of control constrained continuous-time systems. IEEE Trans. Cybern. 2022, 52, 1048–1060. [Google Scholar] [CrossRef] [PubMed]
- Vrabie, D.; Pastravanu, O.; Abu-Khalaf, M. Adaptive optimal control for continuous-time linear systems based on policy iteration. Automatica 2009, 45, 477–484. [Google Scholar] [CrossRef]
- Cui, X.H.; Zhang, H.G.; Luo, Y.H. Adaptive dynamic programming for tracking design of uncertain nonlinear systems with disturbances and input constraints. Int. J. Adapt. Control Signal. Process. 2017, 31, 1567–1583. [Google Scholar] [CrossRef]
- Zhang, Q.C.; Zhao, D.B. Data-based reinforcement learning for nonzero-sum games with unknown drift dynamics. IEEE Trans. Cybern. 2019, 48, 2874–2885. [Google Scholar] [CrossRef] [PubMed]
- Song, R.Z.; Lewis, F.L.; Wei, Q.L. Off-policy integral reinforcement learning method to solve nonlinear continuous-time multiplayer nonzero-sum games. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 704–713. [Google Scholar] [CrossRef]
- Liang, T.L.; Zhang, H.G.; Zhang, J. Event-triggered guarantee cost control for partially unknown stochastic systems via explorized integral reinforcement learning strategy. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 7830–7844. [Google Scholar] [CrossRef]
- Ren, H.; Dai, J.; Zhang, H.G. Off-policy integral reinforcement learning algorithm in dealing with nonzero sum game for nonlinear distributed parameter systems. Trans. Inst. Meas. Control 2024, 42, 2919–2928. [Google Scholar] [CrossRef]
- Yoo, J.; Johansson, K.H. Event-triggered model predictive control with a statistical learning. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2571–2581. [Google Scholar] [CrossRef]
- Huang, Y.L.; Xiao, X.; Wang, Y.H. Event-triggered pinning synchronization and robust pinning synchronization of coupled neural networks with multiple weights. Int. J. Adapt. Control Signal. Process. 2022, 37, 584–602. [Google Scholar] [CrossRef]
- Sun, L.B.; Huang, X.C.; Song, Y.D. A novel dual-phase based approach for distributed event-triggered control of multiagent systems with guaranteed performance. IEEE Trans. Cybern. 2024, 54, 4229–4240. [Google Scholar] [CrossRef]
- Li, Z.X.; Yan, J.; Yu, W.W. Adaptive event-triggered control for unknown second-order nonlinear multiagent systems. IEEE Trans. Cybern. 2021, 51, 6131–6140. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Yang, Y.; Zhang, Y. Sampling-based event-triggered consensus for multi-agent systems. Neurocomputing 2016, 191, 141–147. [Google Scholar] [CrossRef]
- Girard, A. Dynamic triggering mechanisms for event-triggered control. IEEE Trans. Autom. Control 2015, 60, 1992–1997. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, D.; Wang, Y.; Zhou, B. Dynamic event-based tracking control of boiler turbine systems with guaranteed performance. IEEE Trans. Autom. Sci. Eng. 2023, 21, 4272–4282. [Google Scholar] [CrossRef]
- Xu, H.C.; Zhu, F.L.; Ling, X.F. Observer-based semi-global bipartite average tracking of saturated discrete-time multi-agent systems via dynamic event-triggered control. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 3156–3160. [Google Scholar] [CrossRef]
- Chen, J.J.; Chen, B.S.; Zeng, Z.G. Adaptive dynamic event-triggered fault-tolerant consensus for nonlinear multiagent systems with directed/undirected networks. IEEE Trans. Cybern. 2023, 53, 3901–3912. [Google Scholar] [CrossRef]
- Hou, Q.H.; Dong, J.X. Cooperative fault-tolerant output regulation of linear heterogeneous multiagent systems via an adaptive dynamic event-triggered mechanism. IEEE Trans. Cybern. 2023, 53, 5299–5310. [Google Scholar] [CrossRef]
- Song, R.Z.; Yang, G.F.; Lewis, F.L. Nearly optimal control for mixed zero-sum game based on off-policy integral reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 2793–2804. [Google Scholar] [CrossRef]
- Han, L.H.; Wang, Y.C.; Ma, Y.C. Dynamic event-triggered non-fragile dissipative filtering for interval type-2 fuzzy Markov jump systems. Int. J. Mach. Learn. Cybern. 2024, 15, 4999–5013. [Google Scholar] [CrossRef]

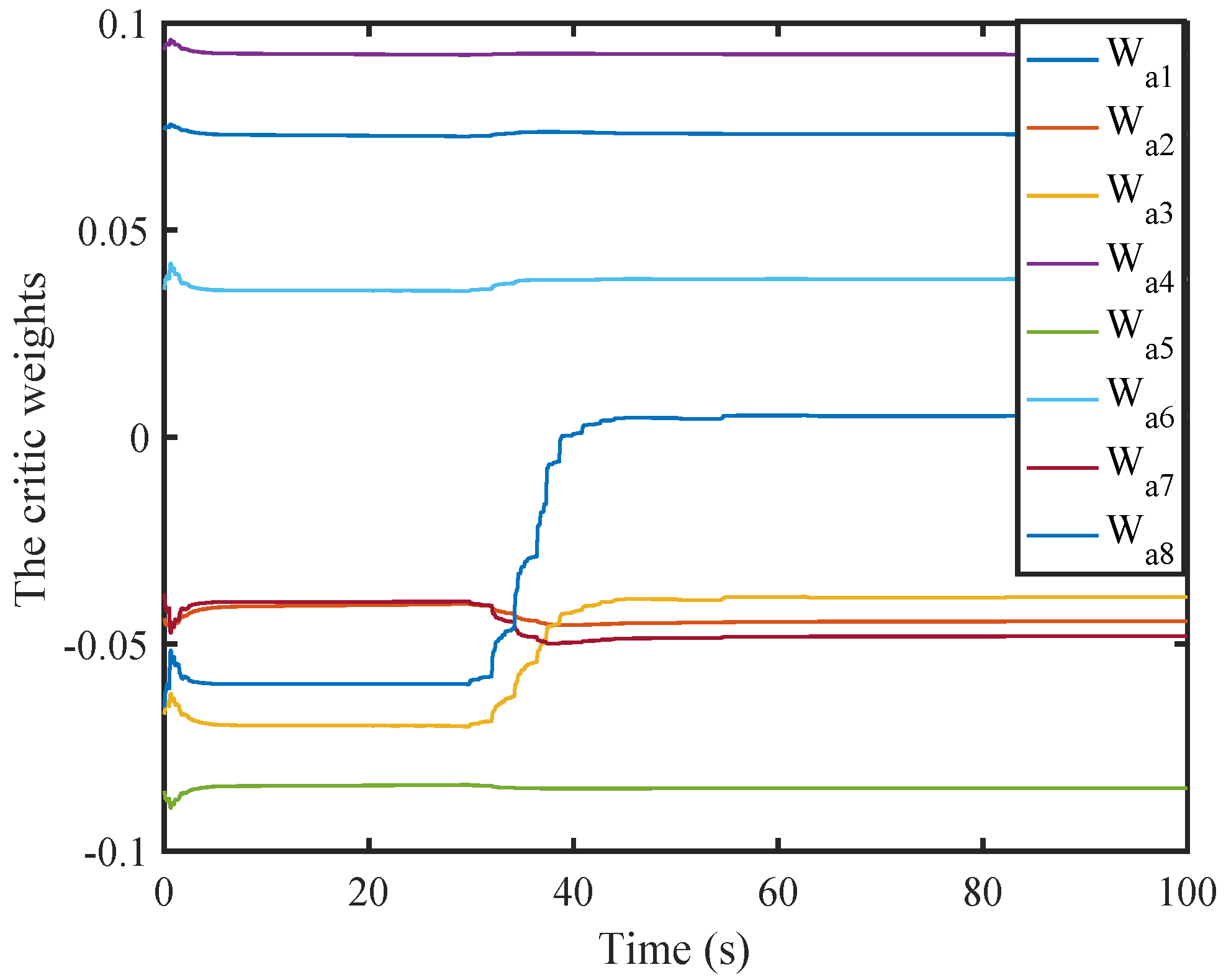


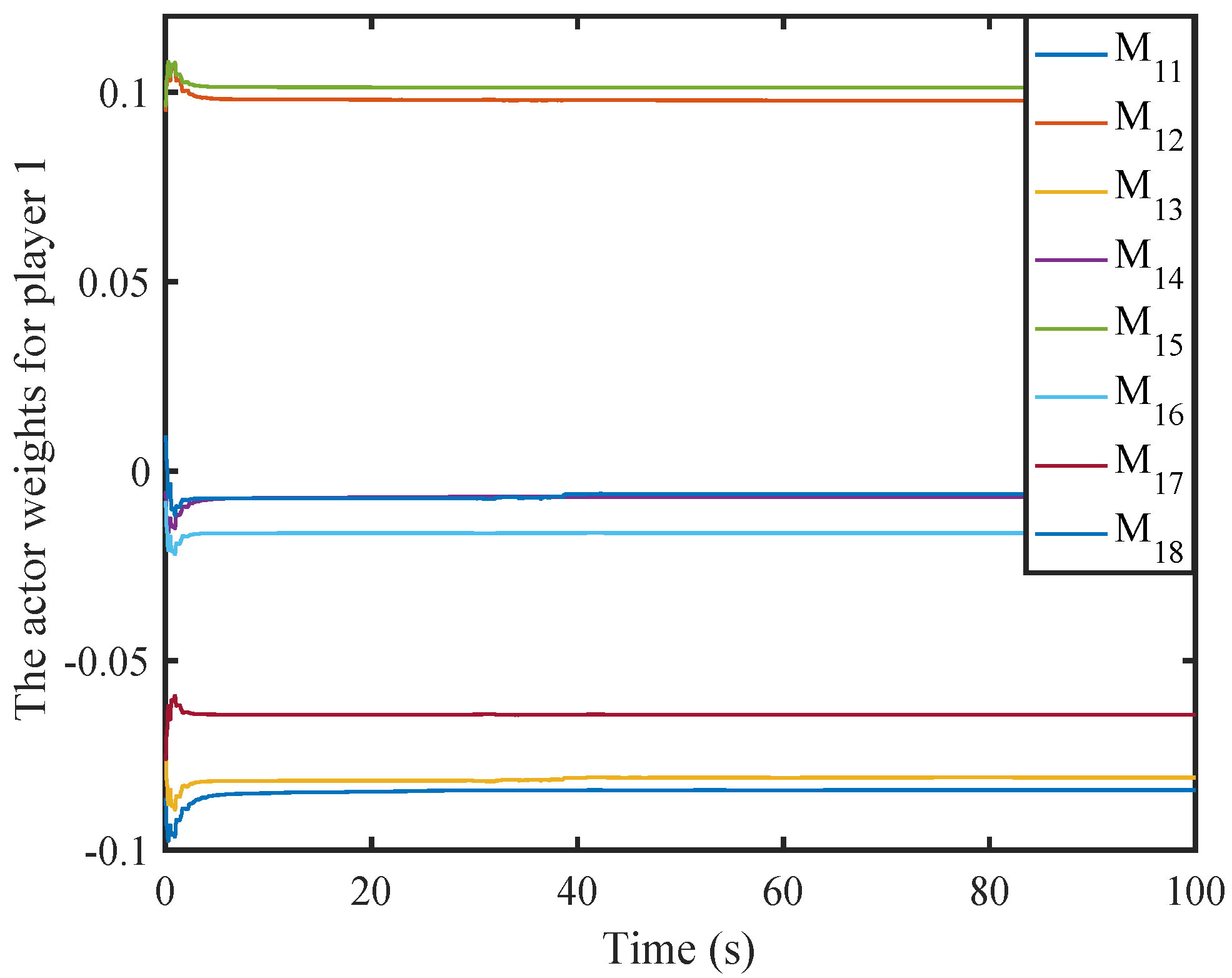
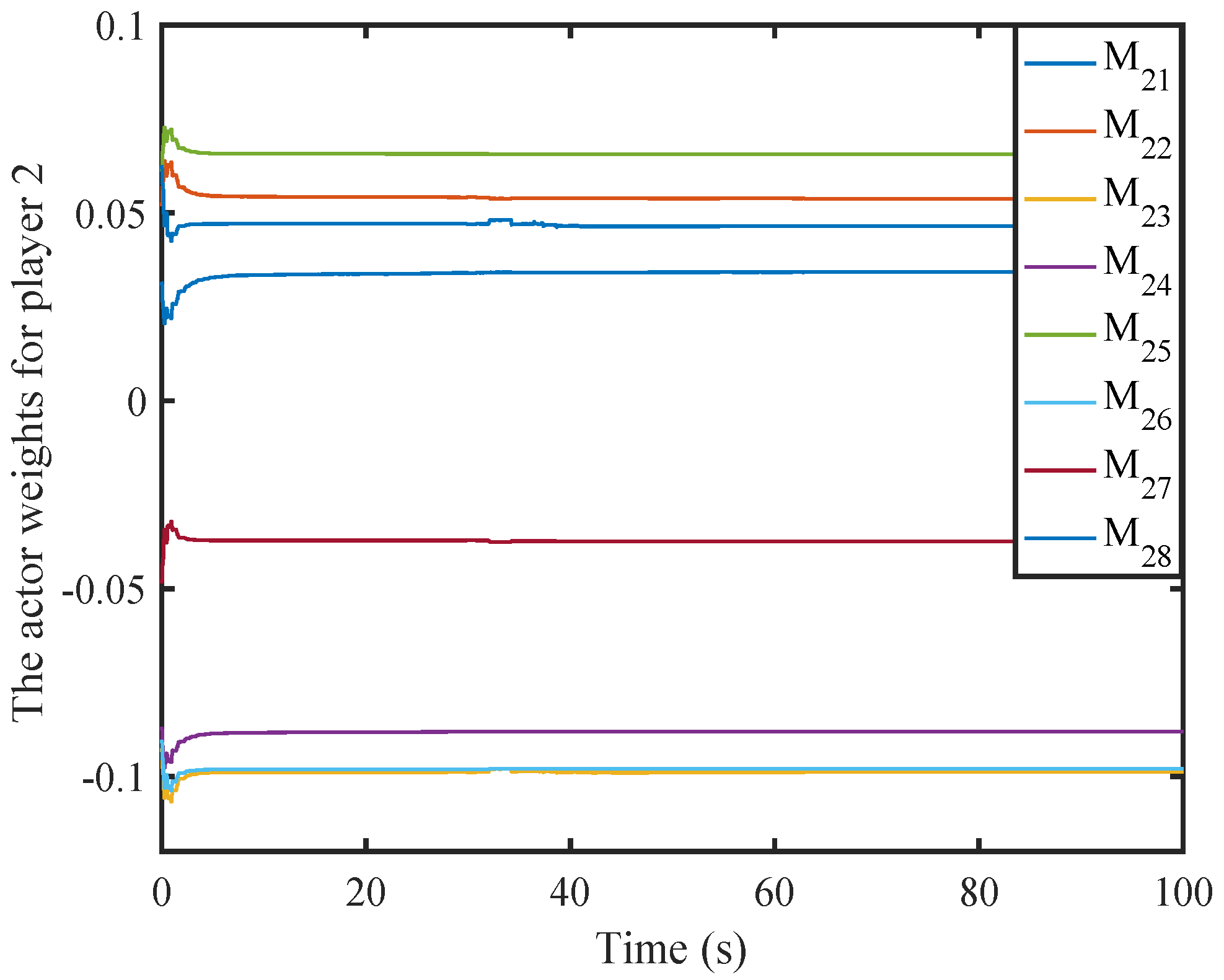
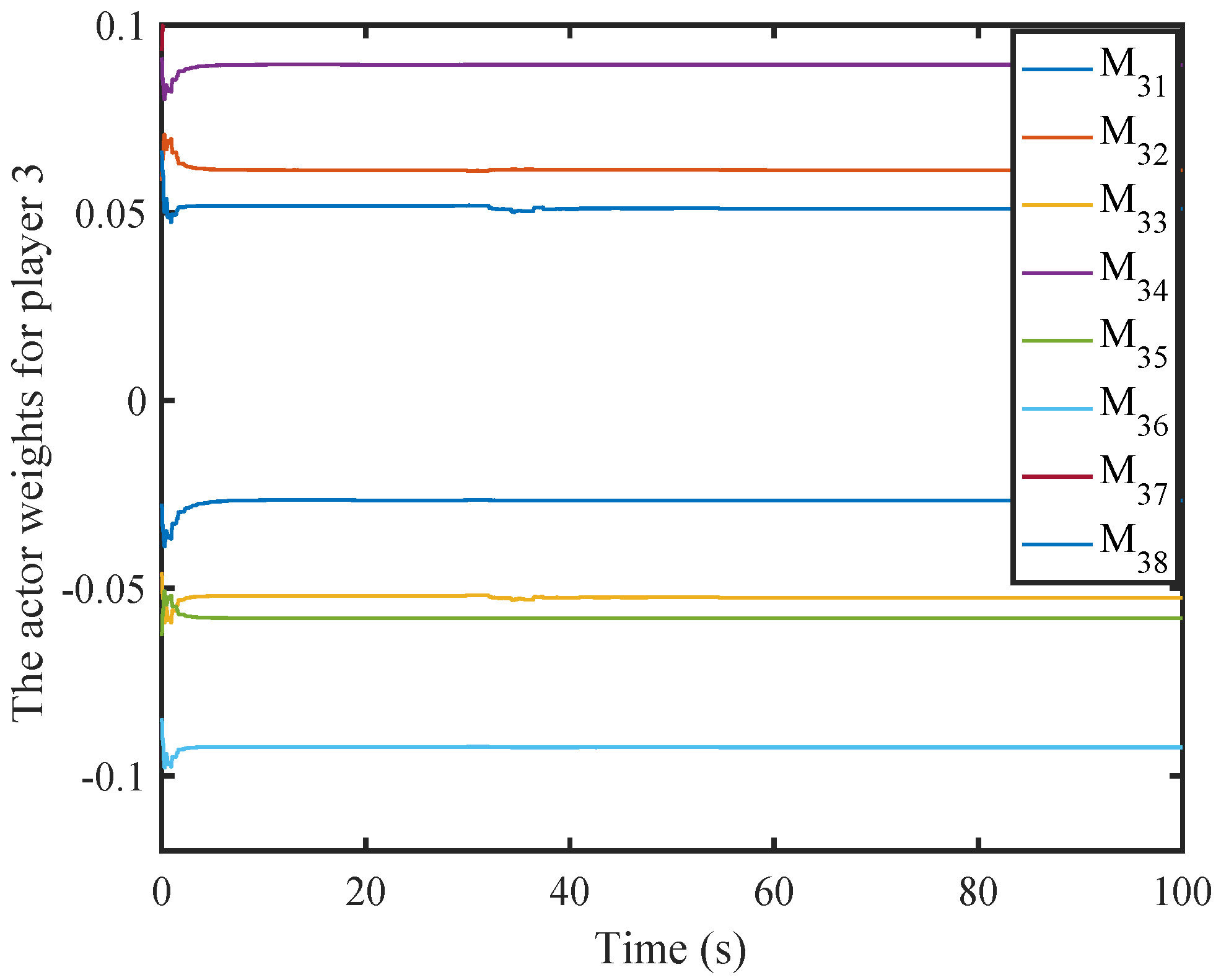
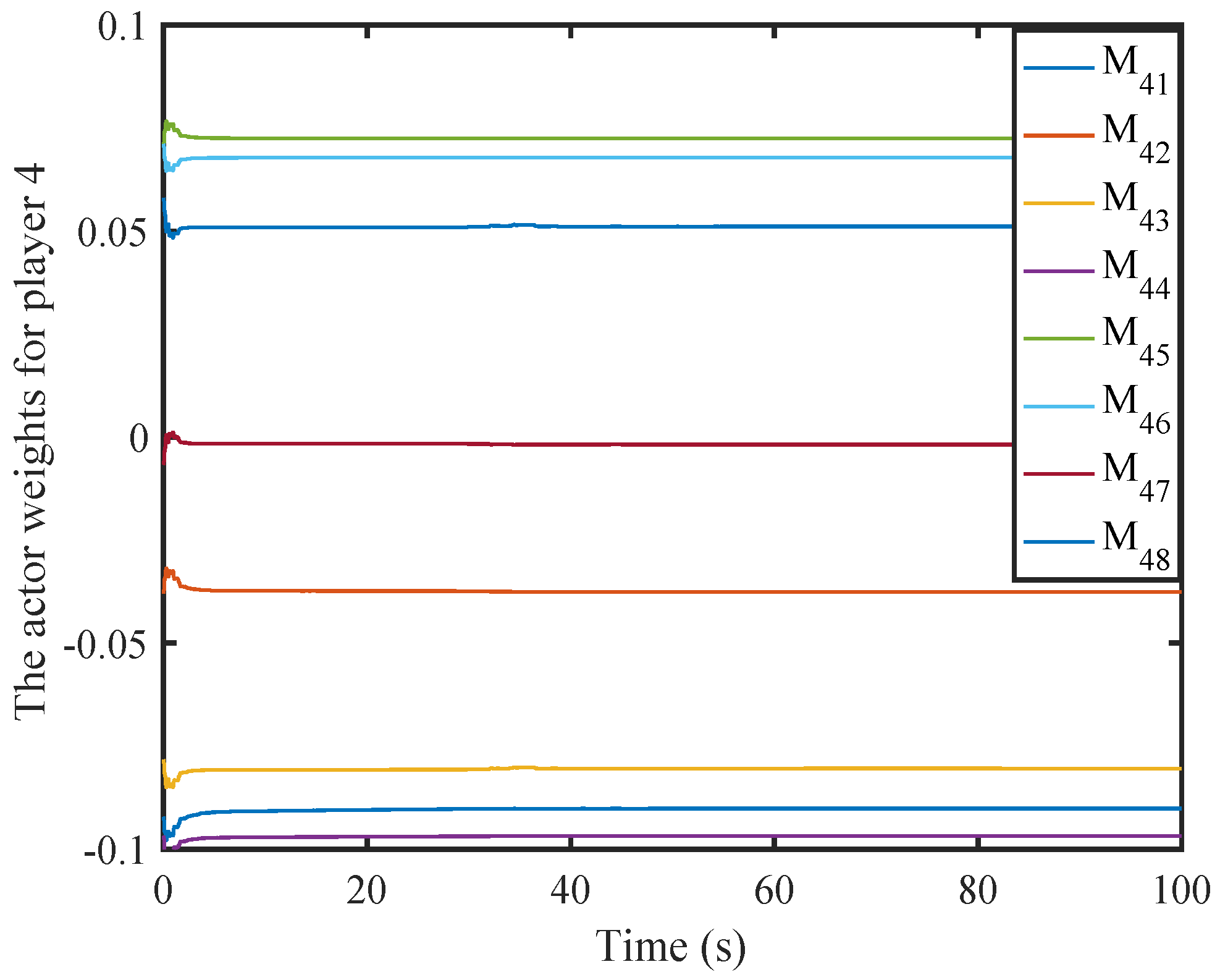
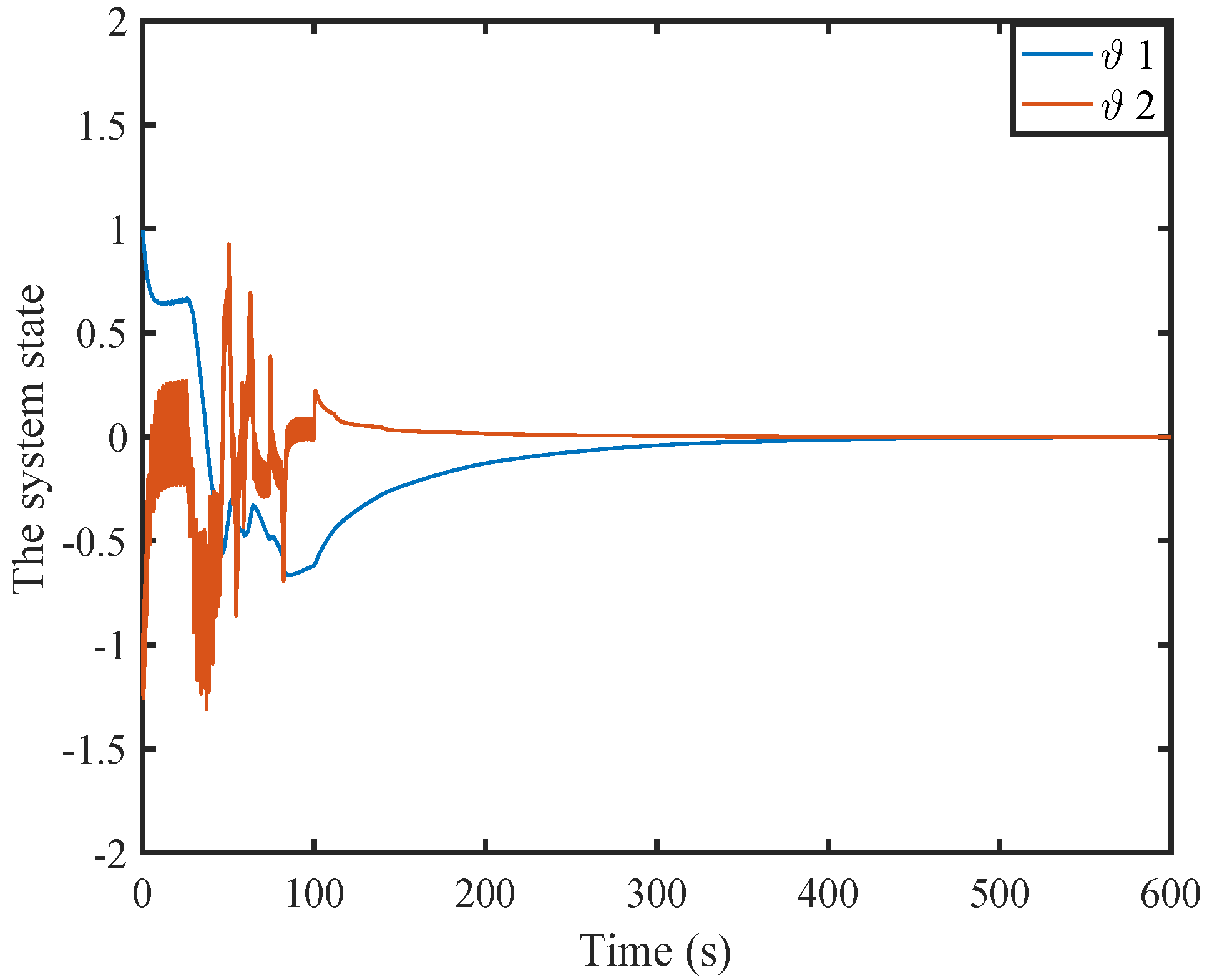
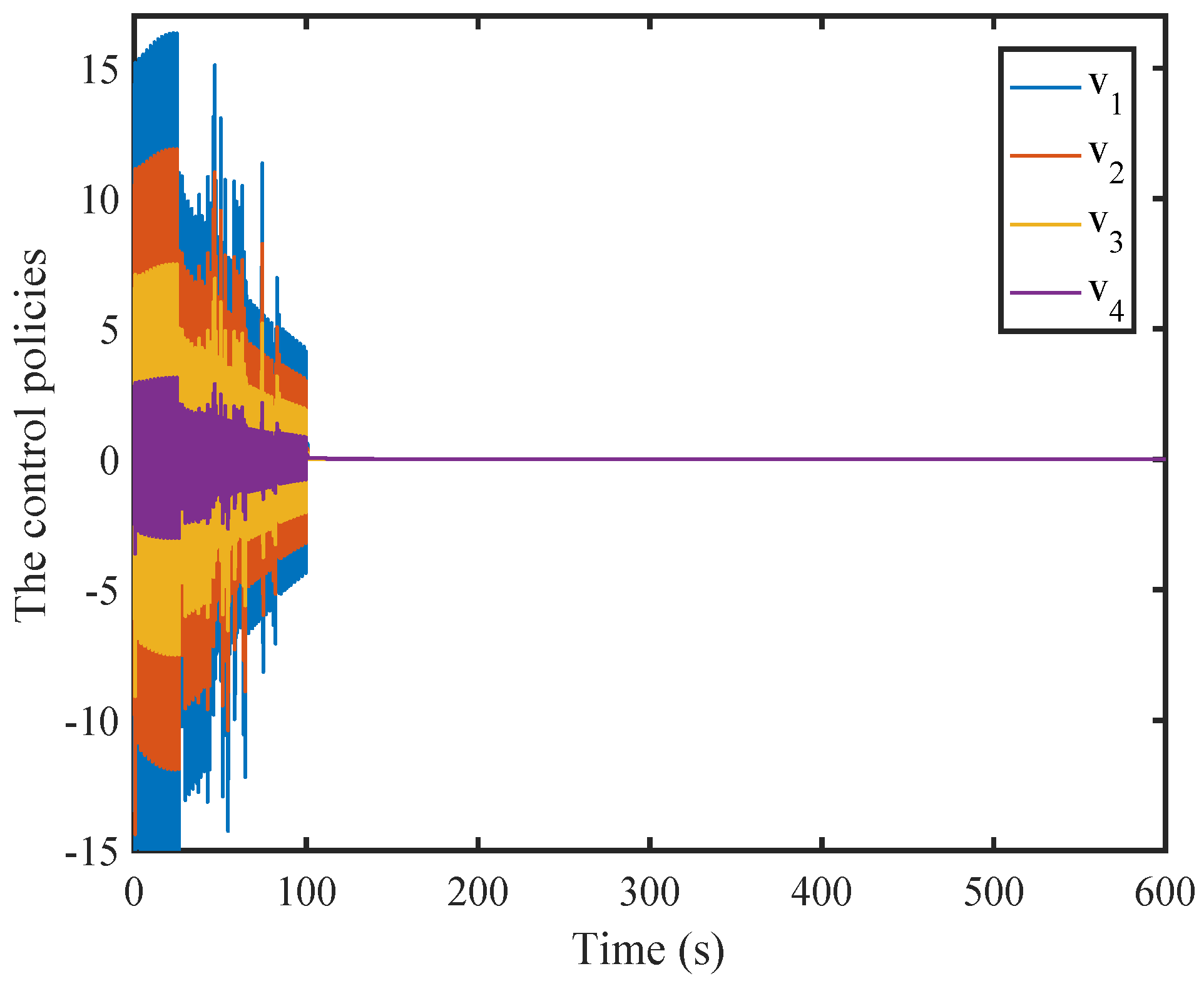
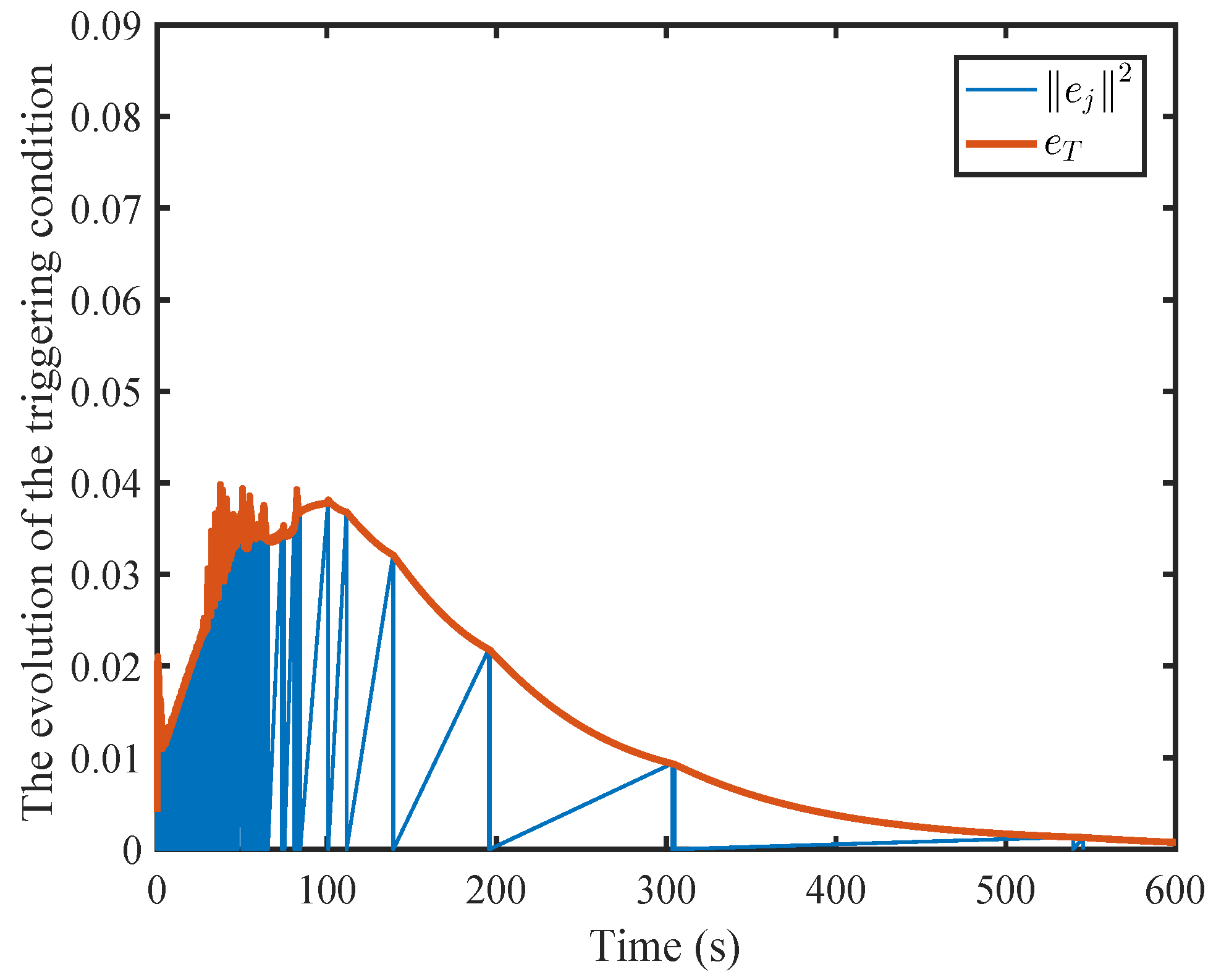

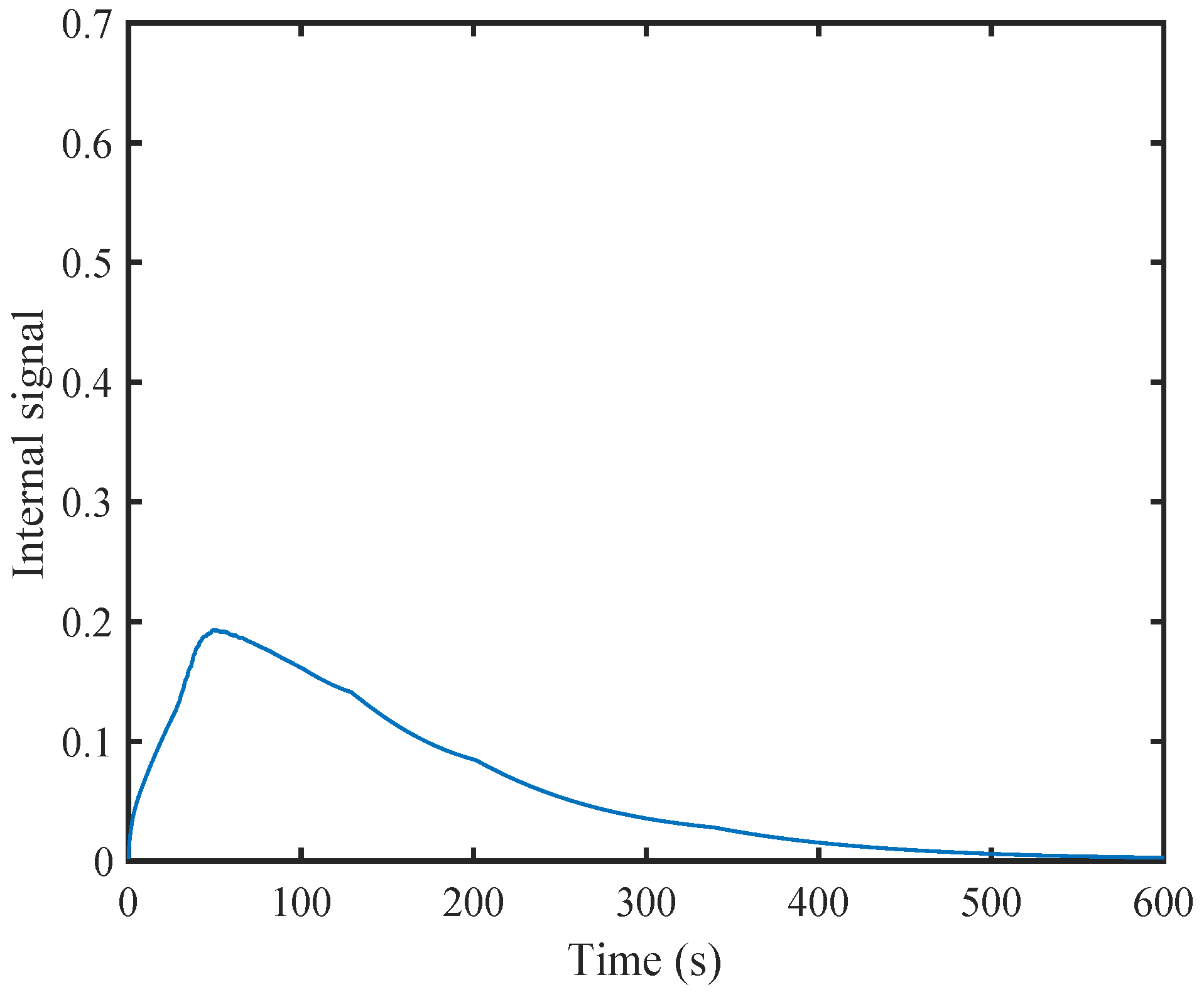


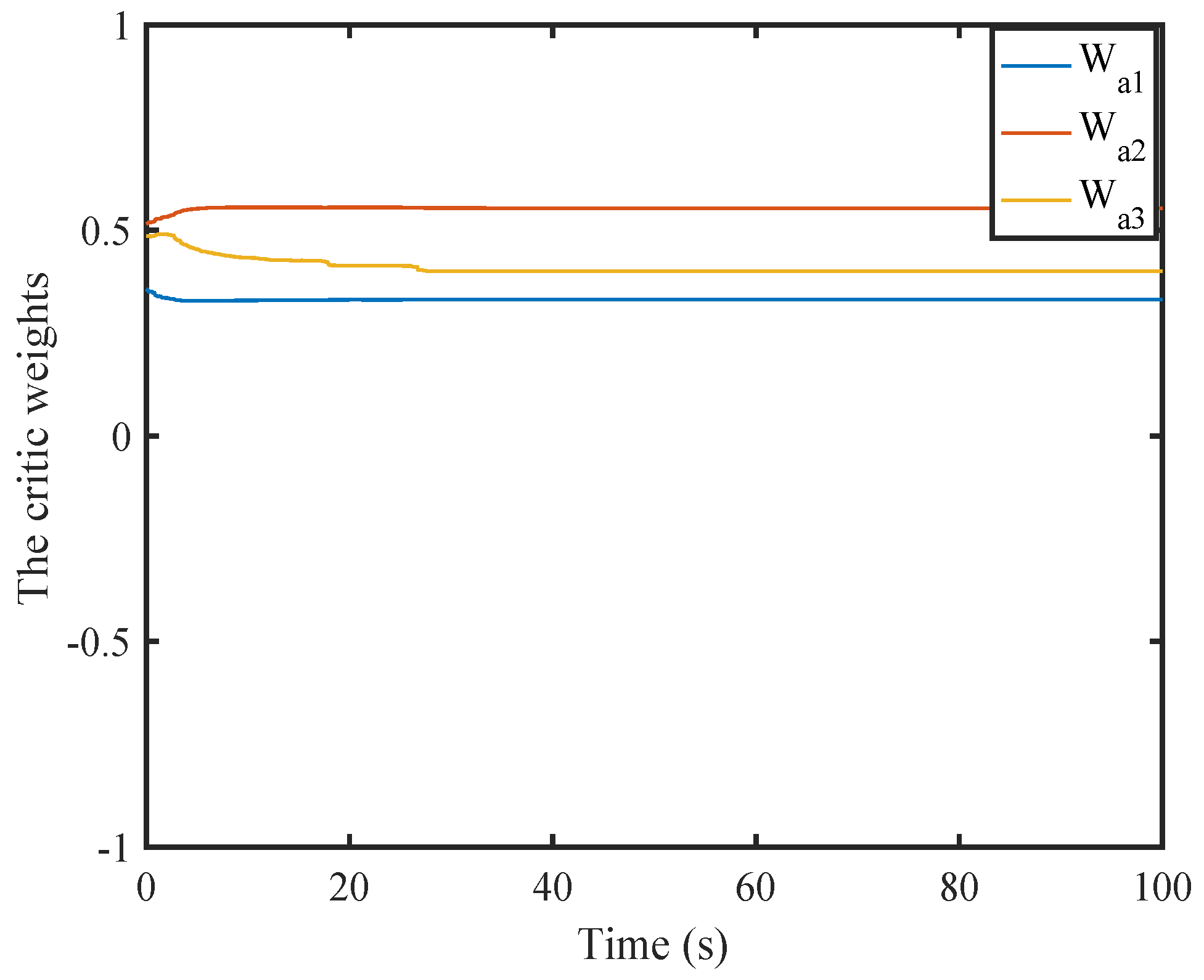





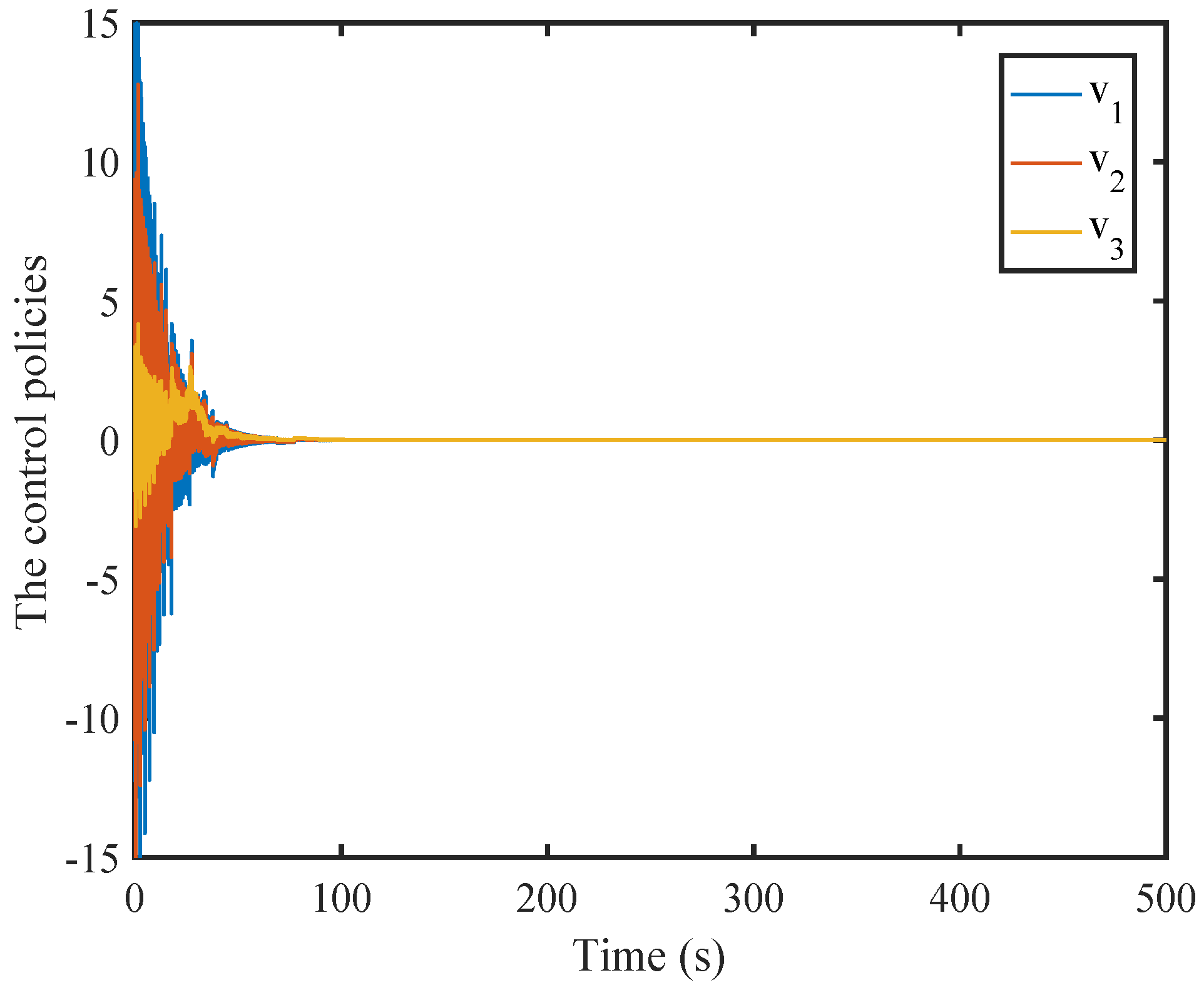
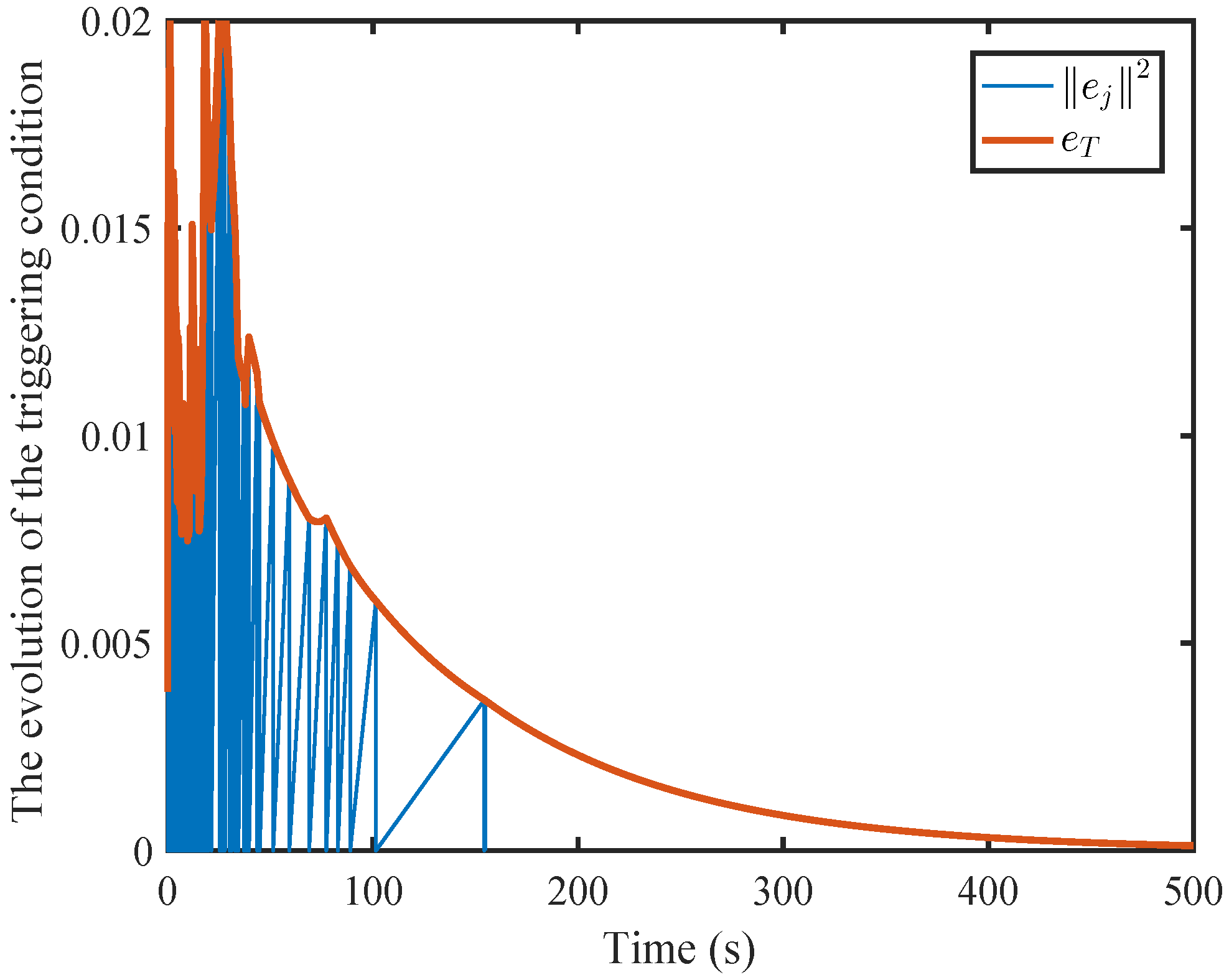
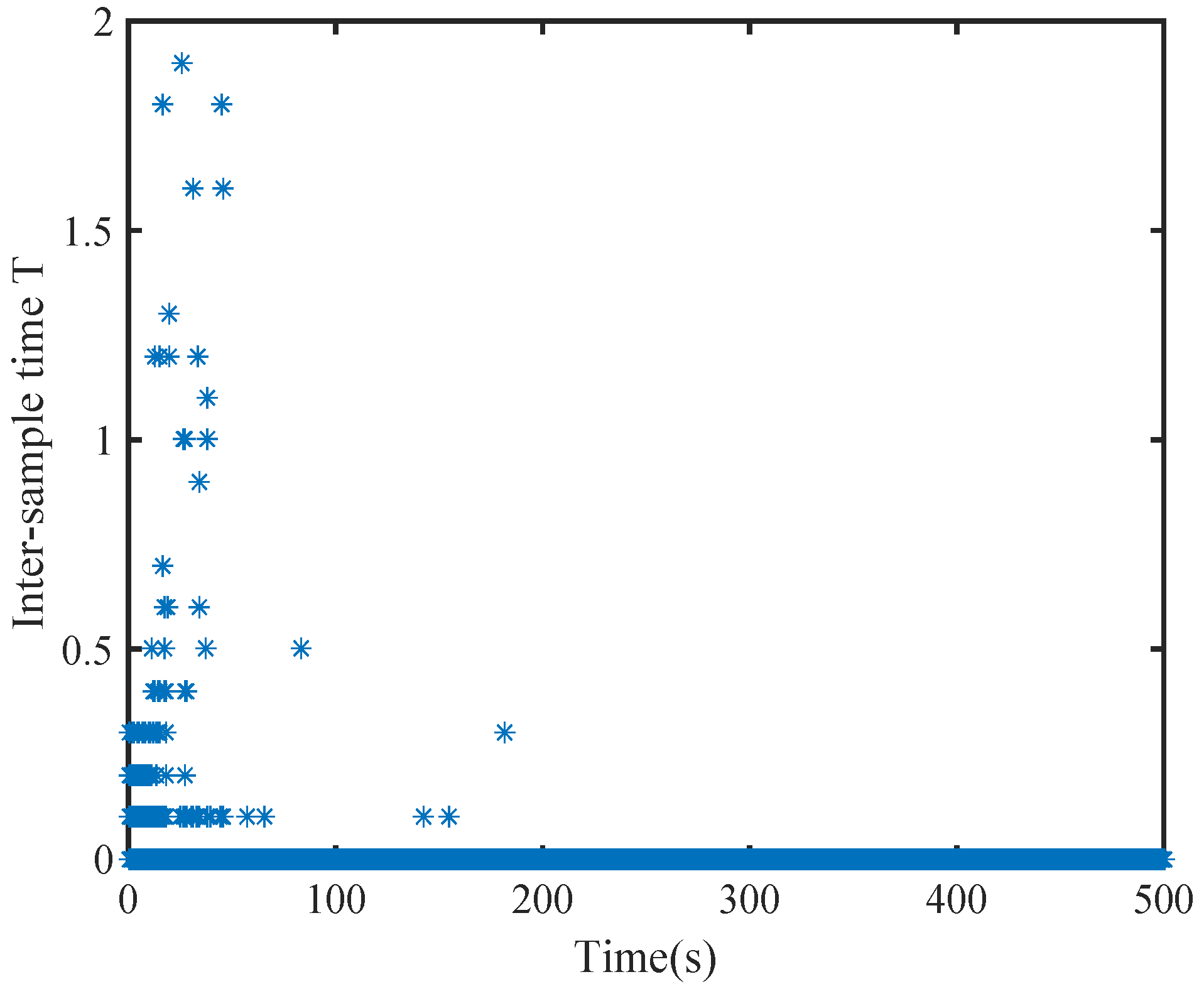
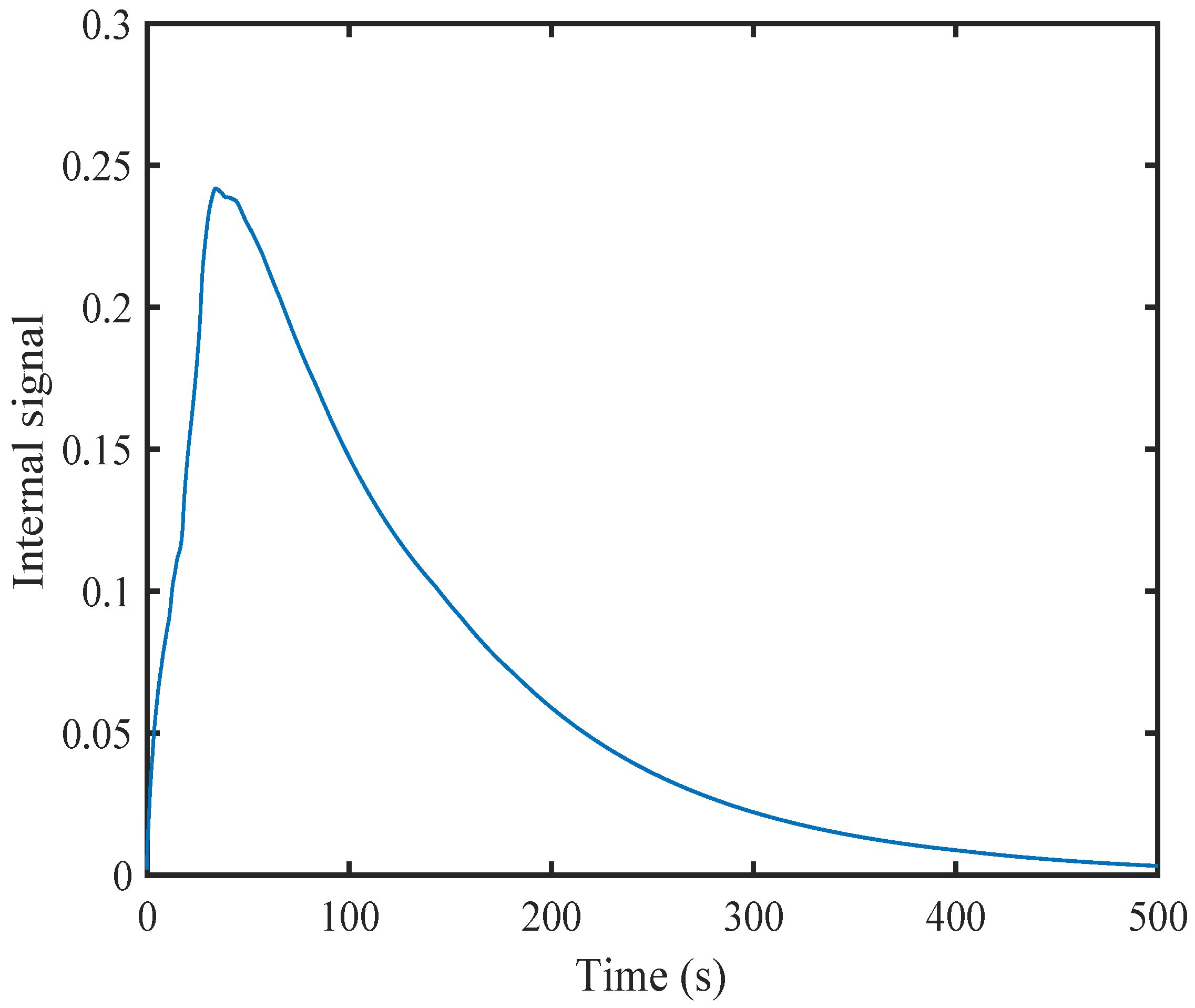
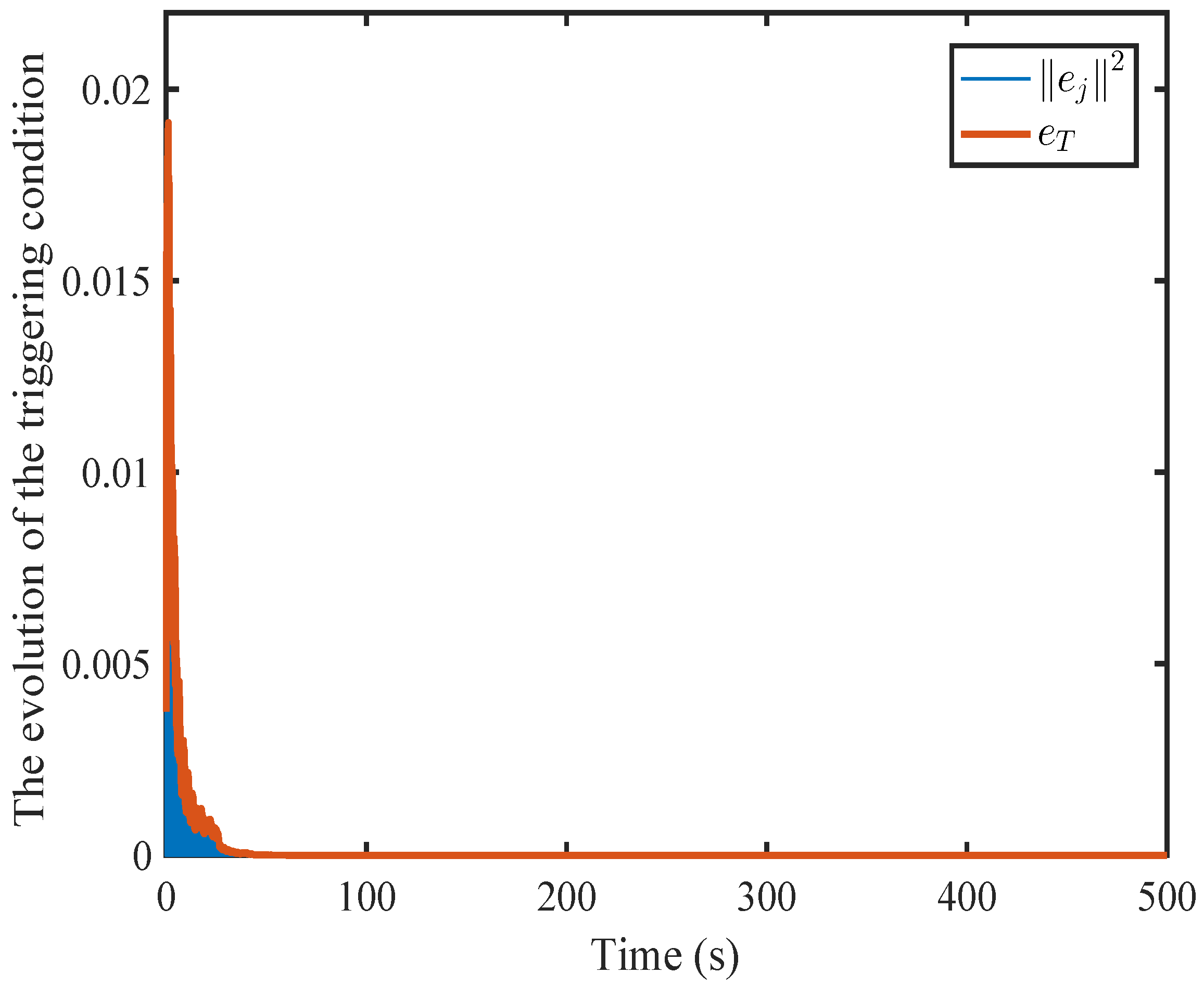
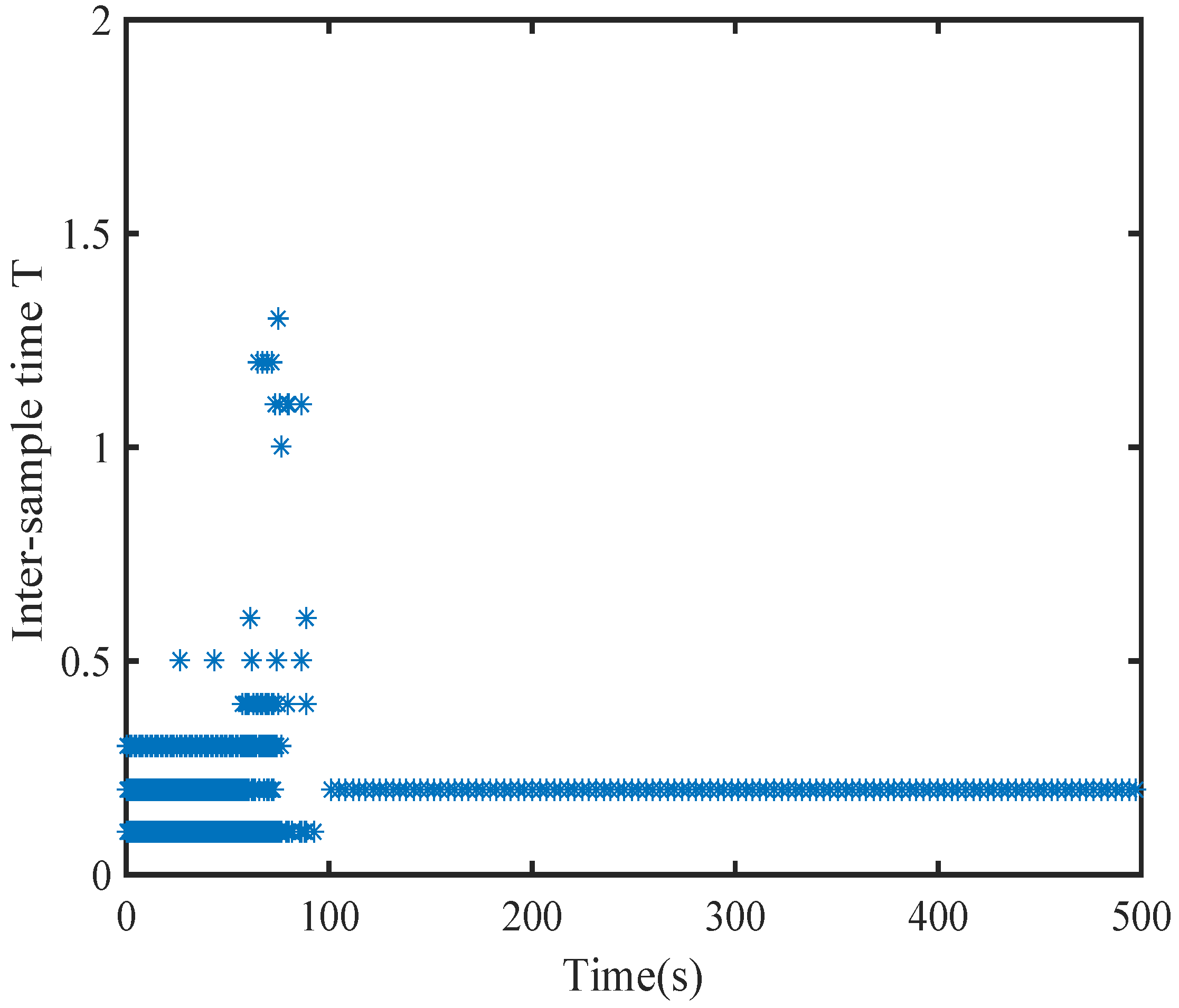
| simulation 1 | |||||||
| 8 | 0.75 | 0.1 | 0.1 | 0.1 | 1.2 | 0.5 | |
| simulation 2 | |||||||
| 5 | 0.7 | 0.1 | 0.1 | 0.1 | 1.2 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Shao, Z.; Su, H.; Liu, L.; Mao, X. Integral Reinforcement Learning-Based Online Adaptive Dynamic Event-Triggered Control Design in Mixed Zero-Sum Games for Unknown Nonlinear Systems. Mathematics 2024, 12, 3916. https://doi.org/10.3390/math12243916
Liang Y, Shao Z, Su H, Liu L, Mao X. Integral Reinforcement Learning-Based Online Adaptive Dynamic Event-Triggered Control Design in Mixed Zero-Sum Games for Unknown Nonlinear Systems. Mathematics. 2024; 12(24):3916. https://doi.org/10.3390/math12243916
Chicago/Turabian StyleLiang, Yuling, Zhi Shao, Hanguang Su, Lei Liu, and Xiao Mao. 2024. "Integral Reinforcement Learning-Based Online Adaptive Dynamic Event-Triggered Control Design in Mixed Zero-Sum Games for Unknown Nonlinear Systems" Mathematics 12, no. 24: 3916. https://doi.org/10.3390/math12243916
APA StyleLiang, Y., Shao, Z., Su, H., Liu, L., & Mao, X. (2024). Integral Reinforcement Learning-Based Online Adaptive Dynamic Event-Triggered Control Design in Mixed Zero-Sum Games for Unknown Nonlinear Systems. Mathematics, 12(24), 3916. https://doi.org/10.3390/math12243916





