Nonlinear Adaptive Optimal Control Design and Implementation for Trajectory Tracking of Four-Wheeled Mecanum Mobile Robots
Abstract
:1. Introduction
2. Mathematical Model of the WMR
2.1. The Dynamic Equations of WMR
2.2. Dynamic Equations of Trajectory Tracking Error for WMR
3. Nonlinear Adaptive Optimal Control Design
3.1. Adaptive H2 Trajectory Tracking Control Design
3.2. Analytical Solution for Adaptive H2 Control Design
4. Simulation Verification
4.1. Simulation Configurations
4.2. Simulation Results
4.2.1. Scenario 1 (Rectangular Trajectory)
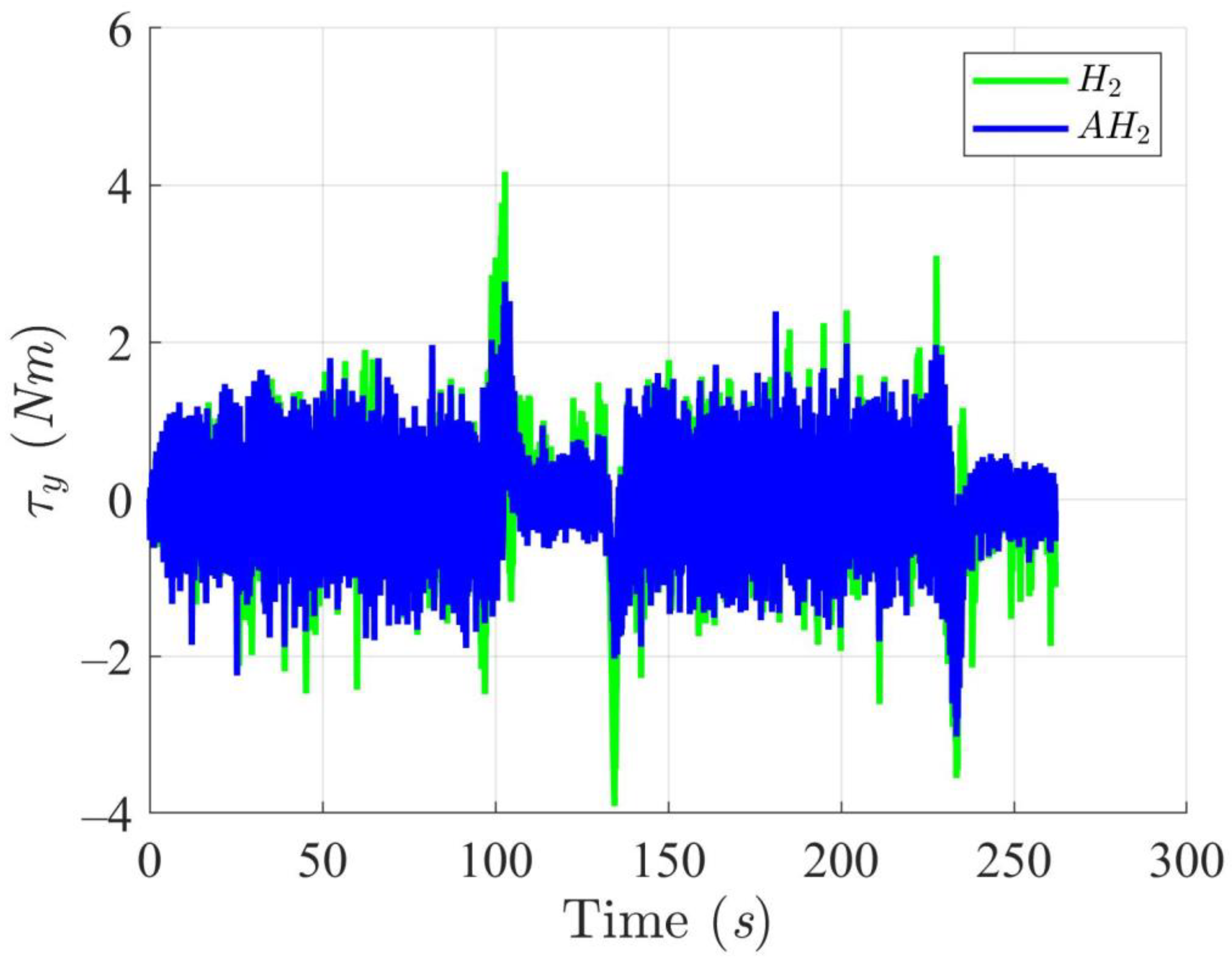
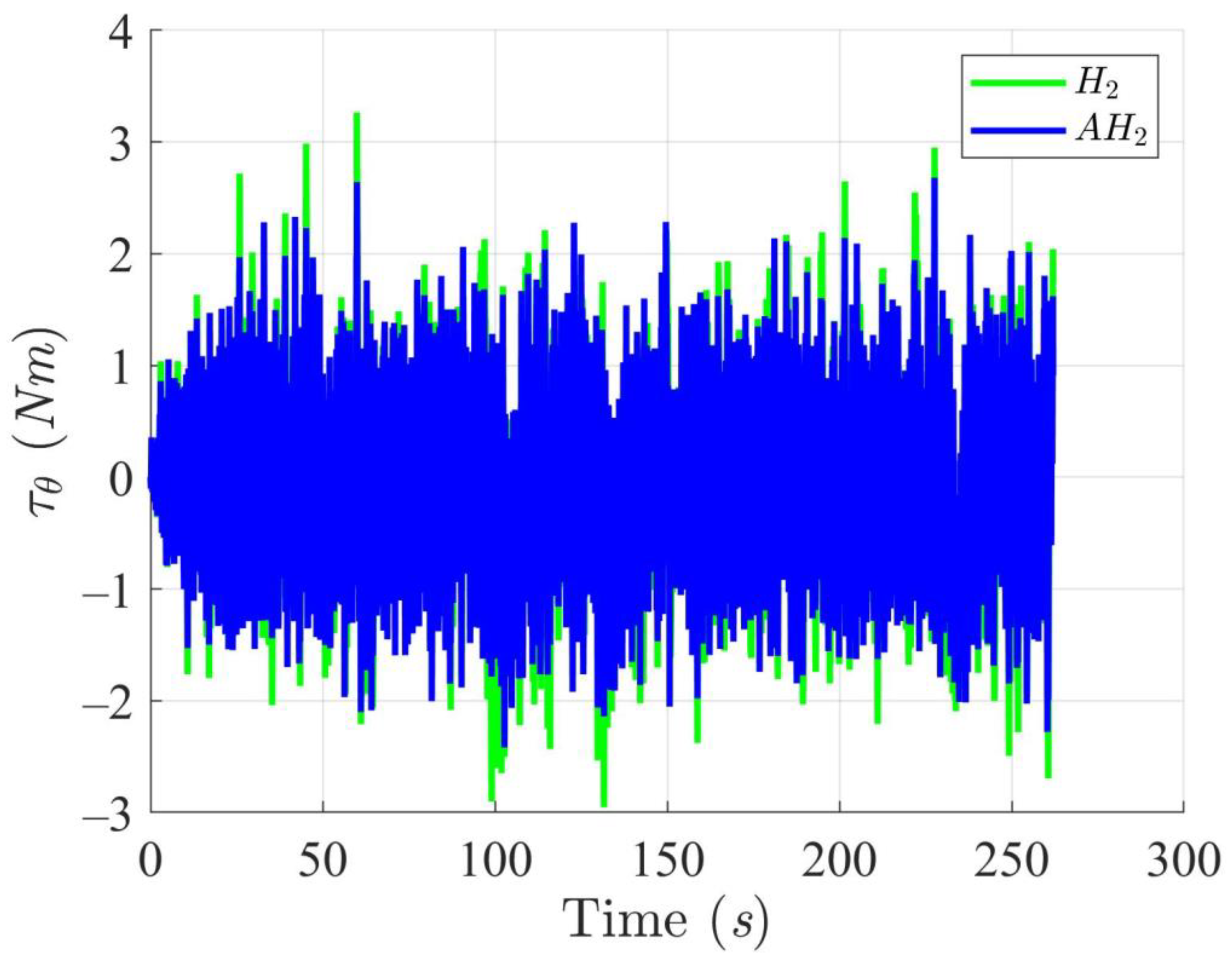
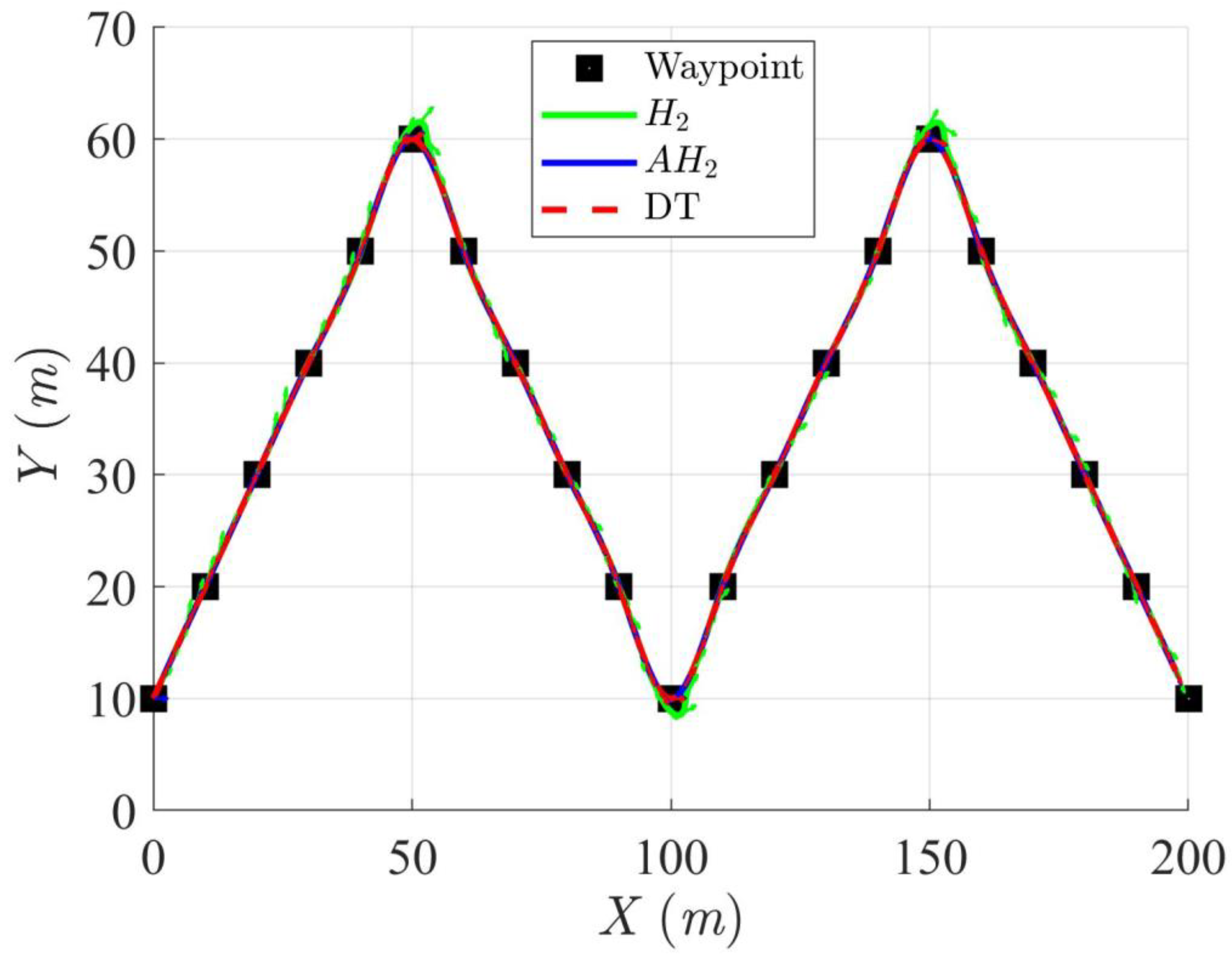
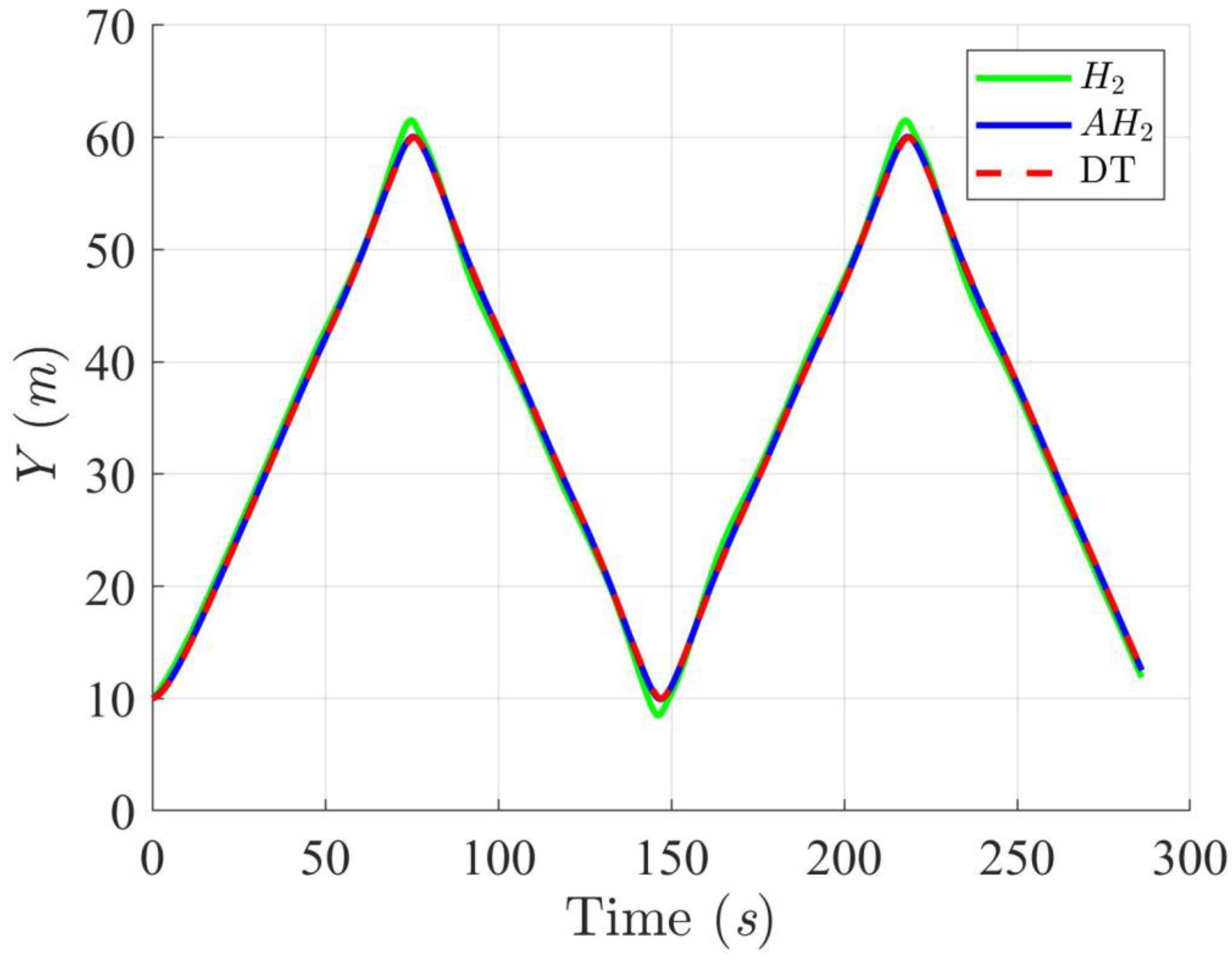
4.2.2. Scenario 2 (Double Triangle Trajectory)
5. Experiments
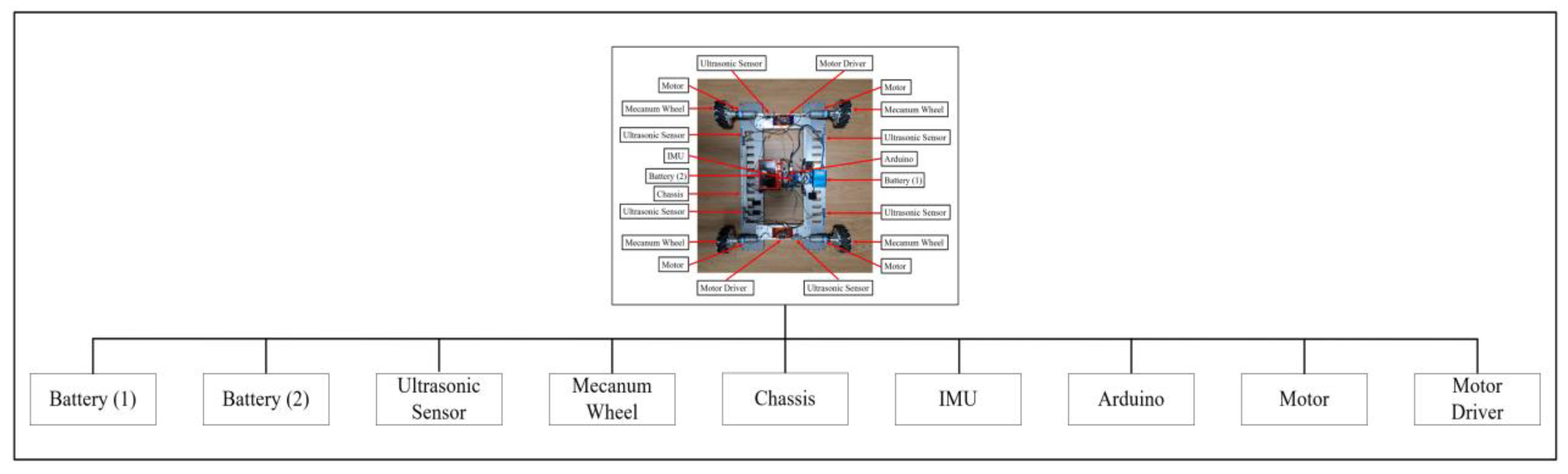
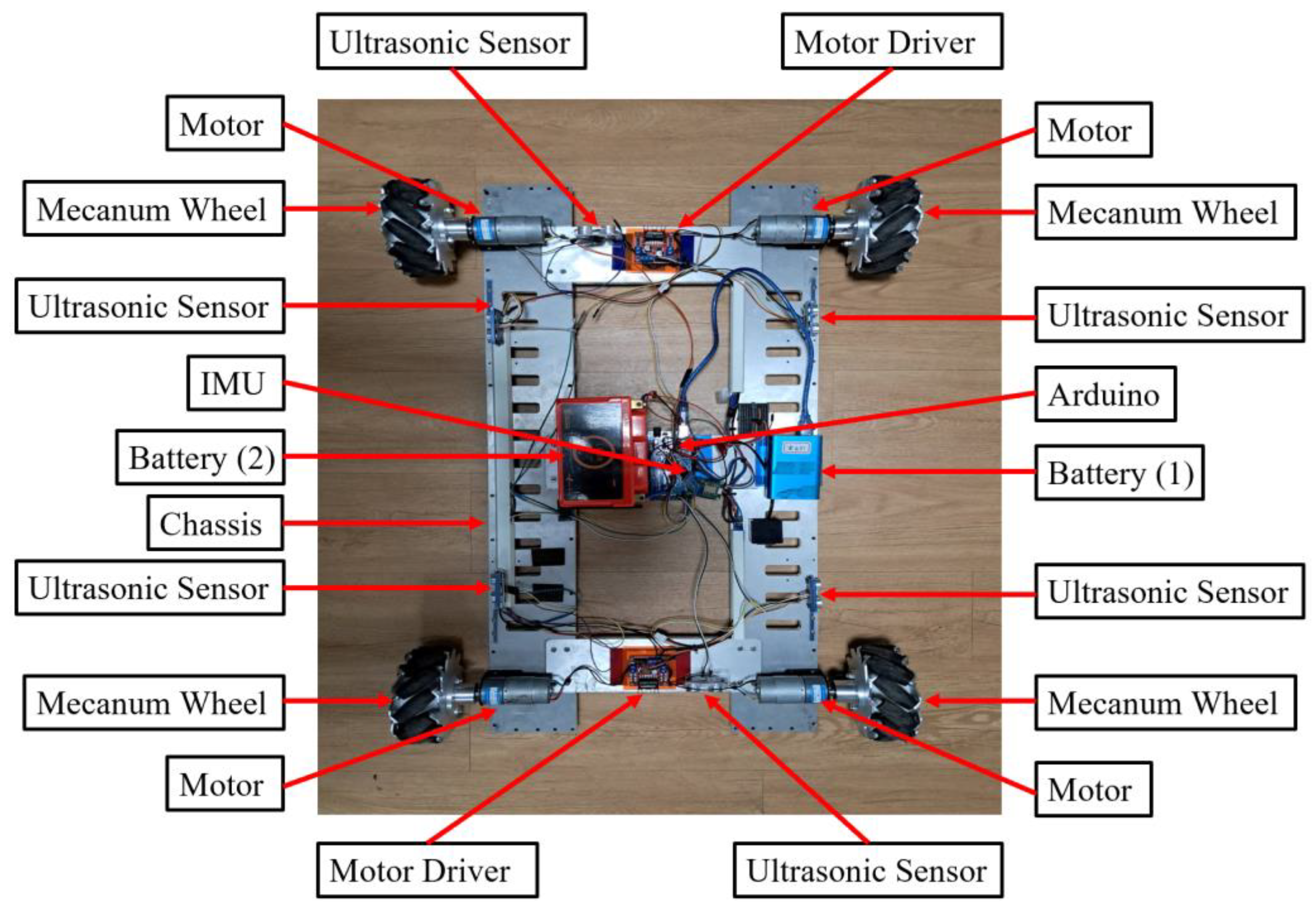
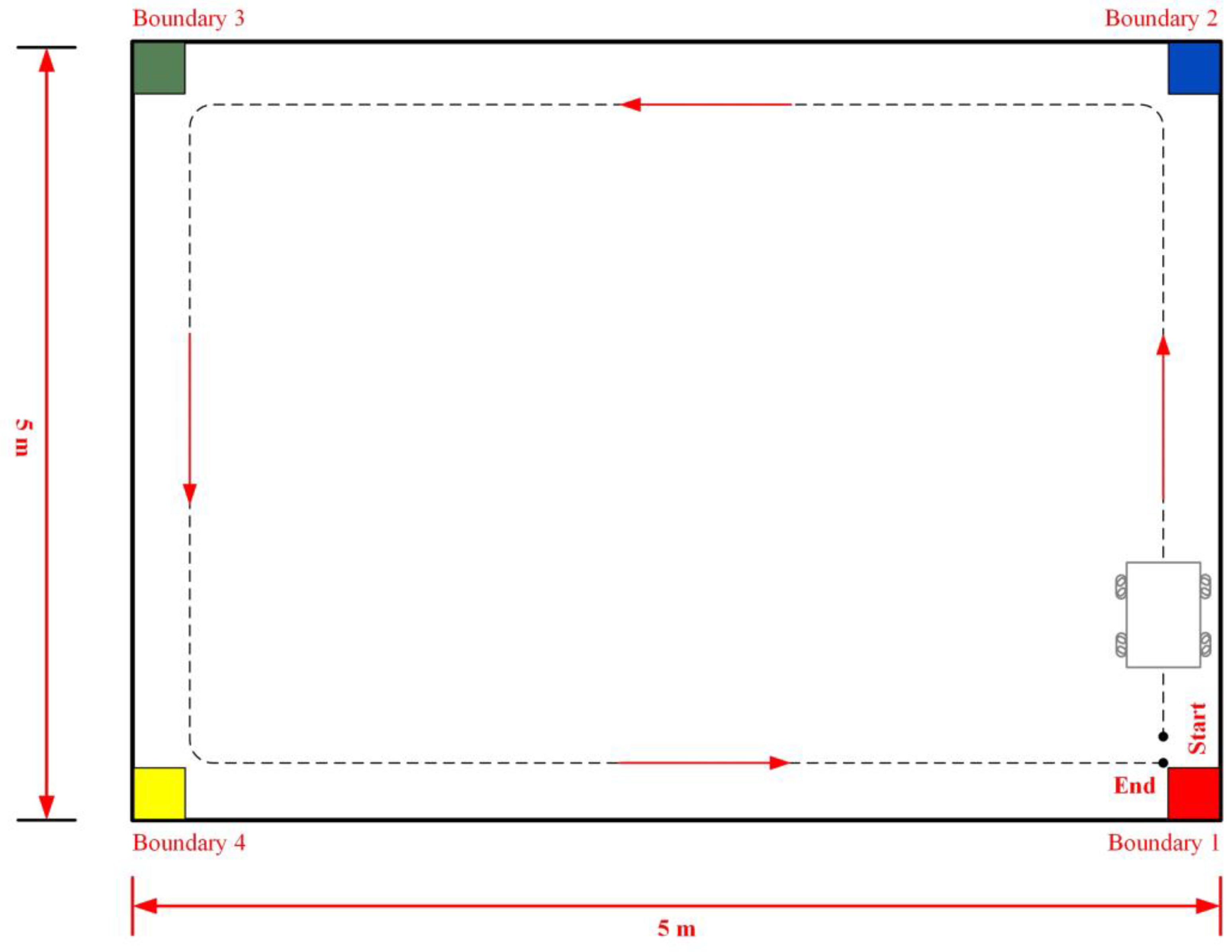
5.1. WMR Hardware Configurations
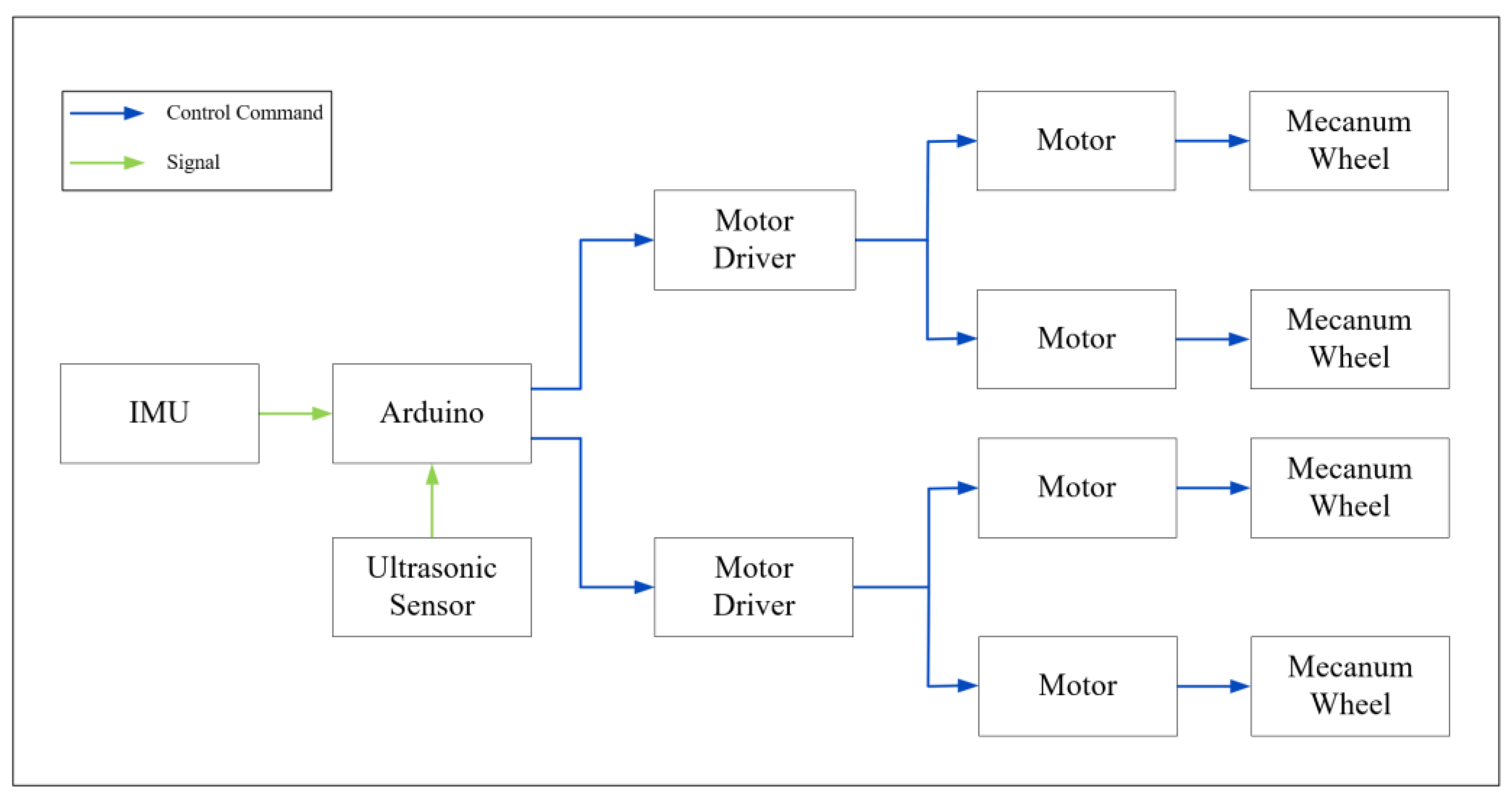
5.2. WMR Integration Operations
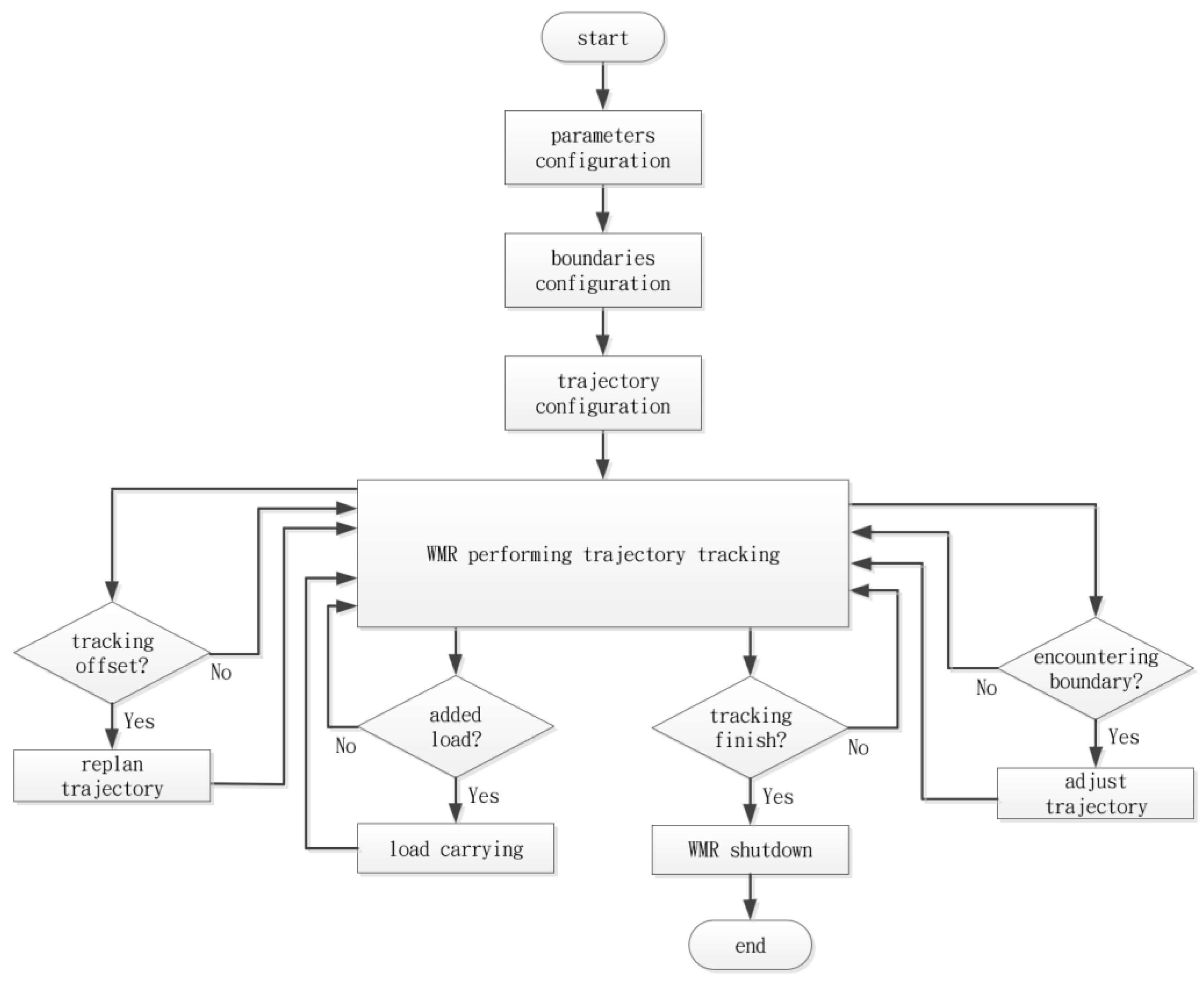
5.3. WMR Verification Process
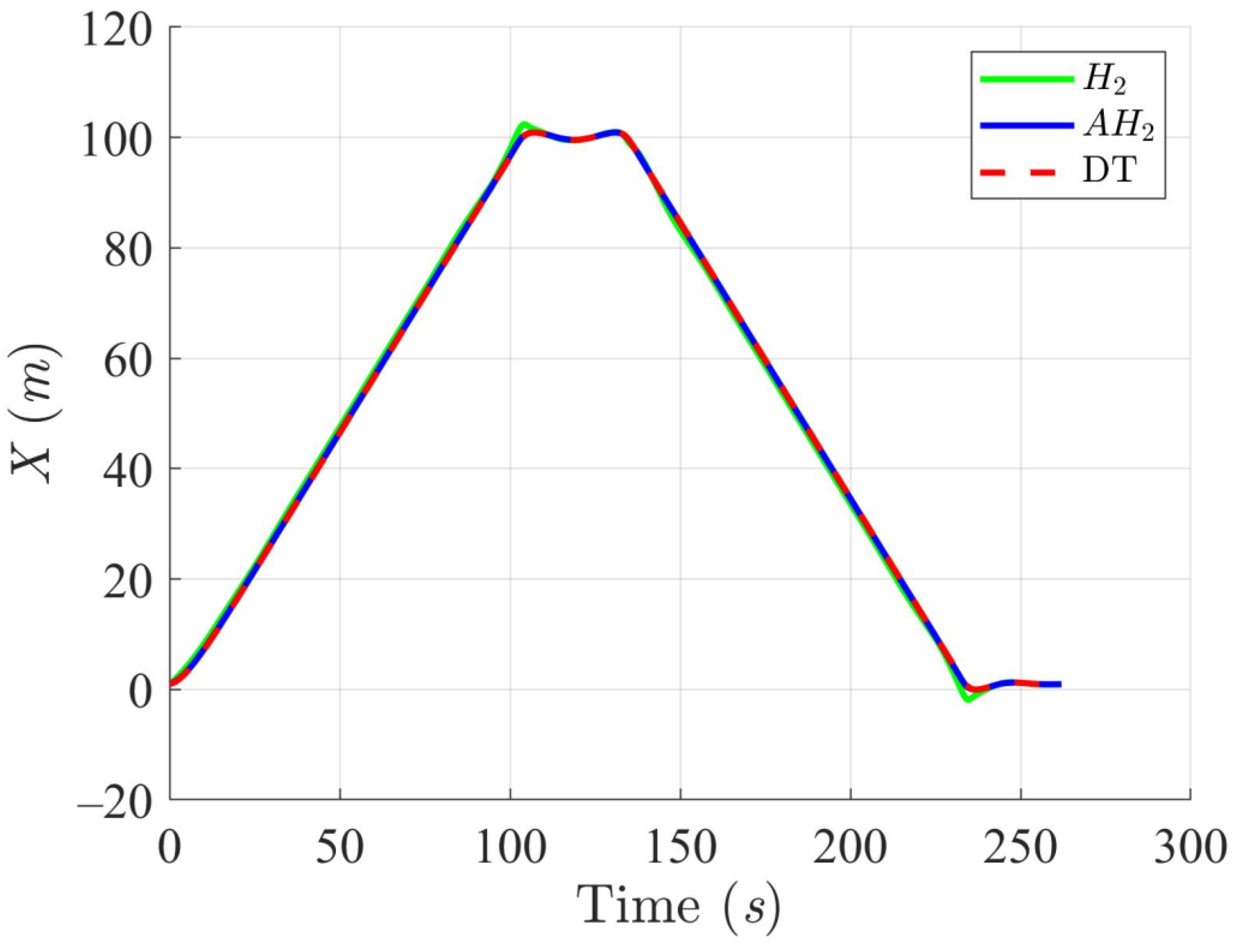
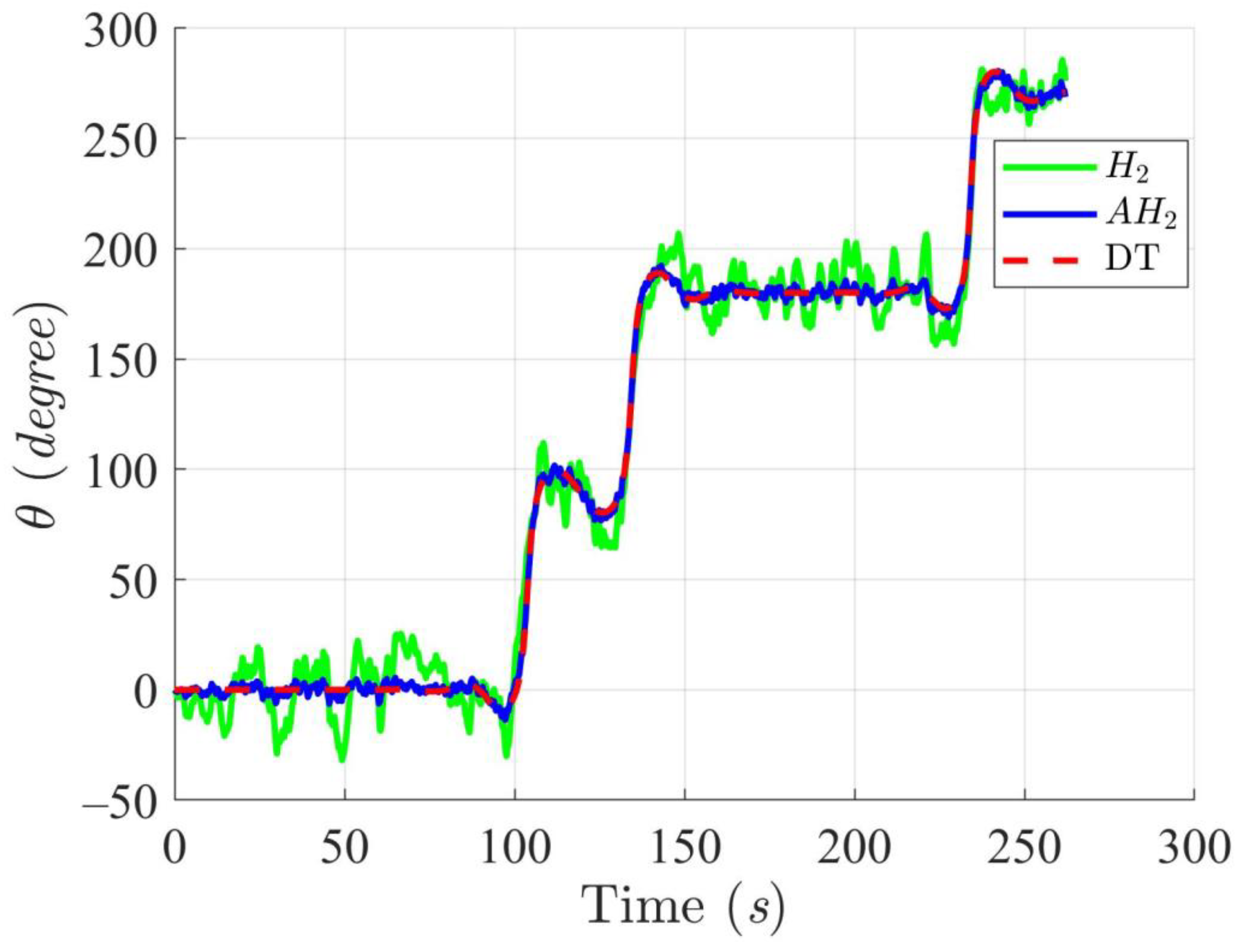
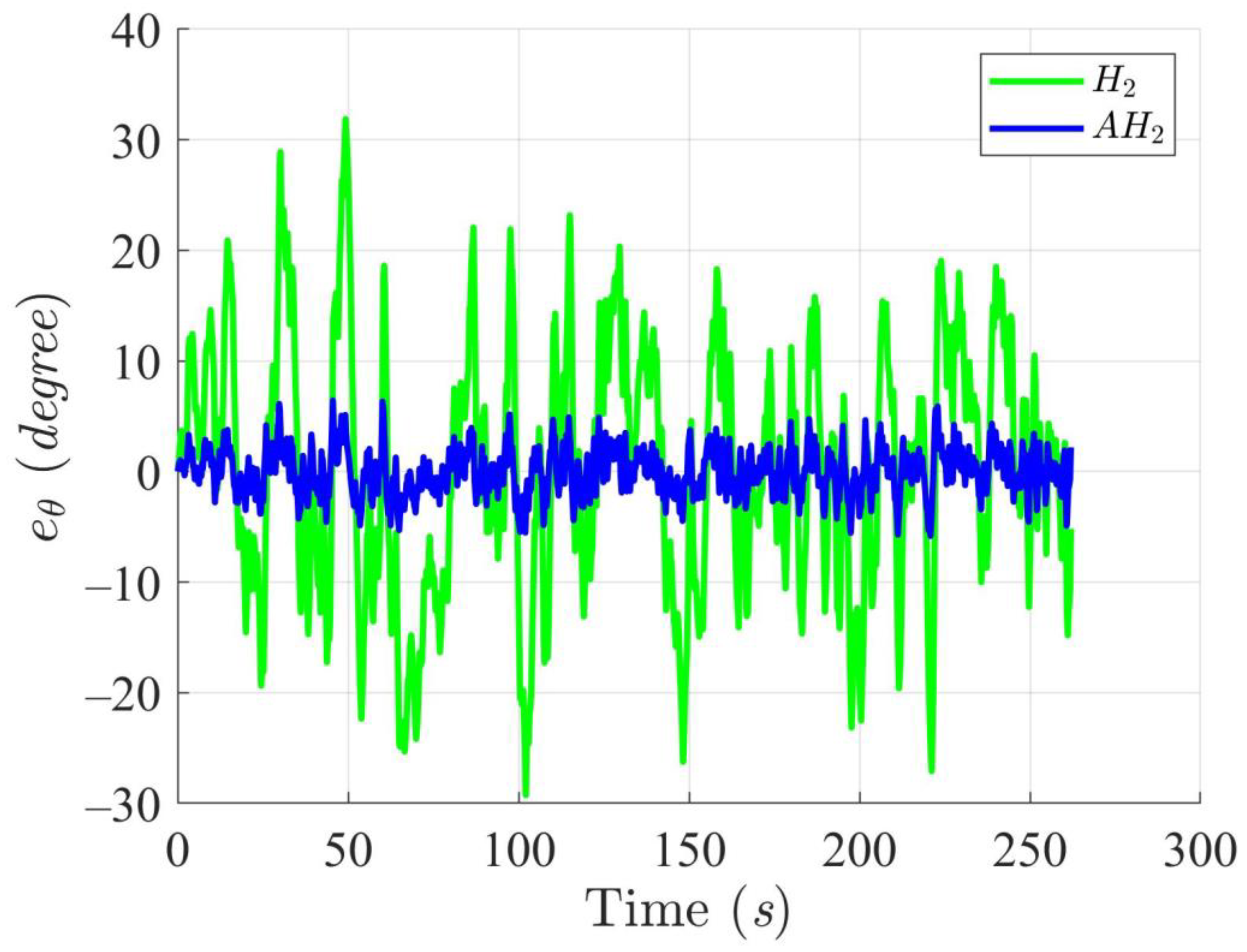
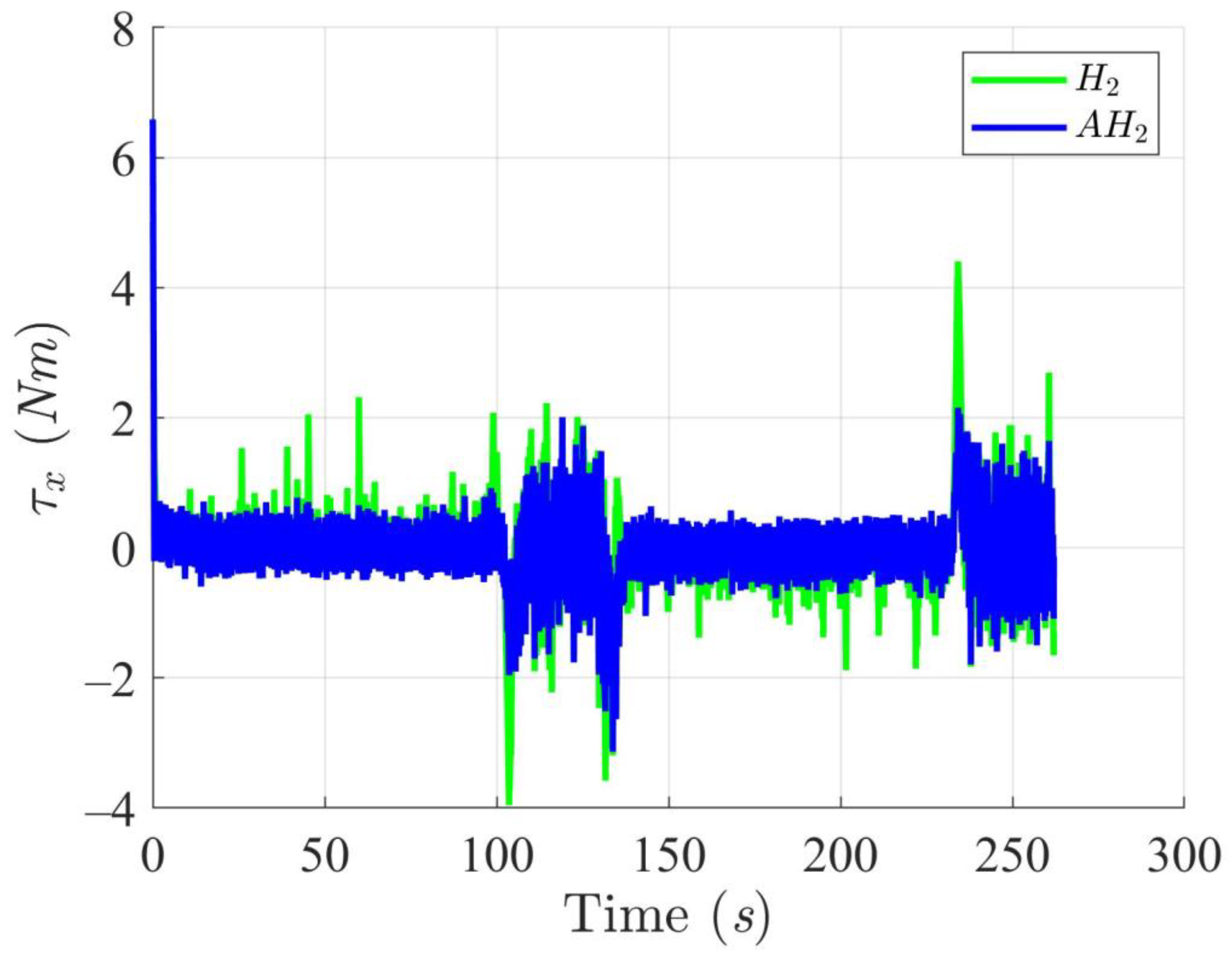
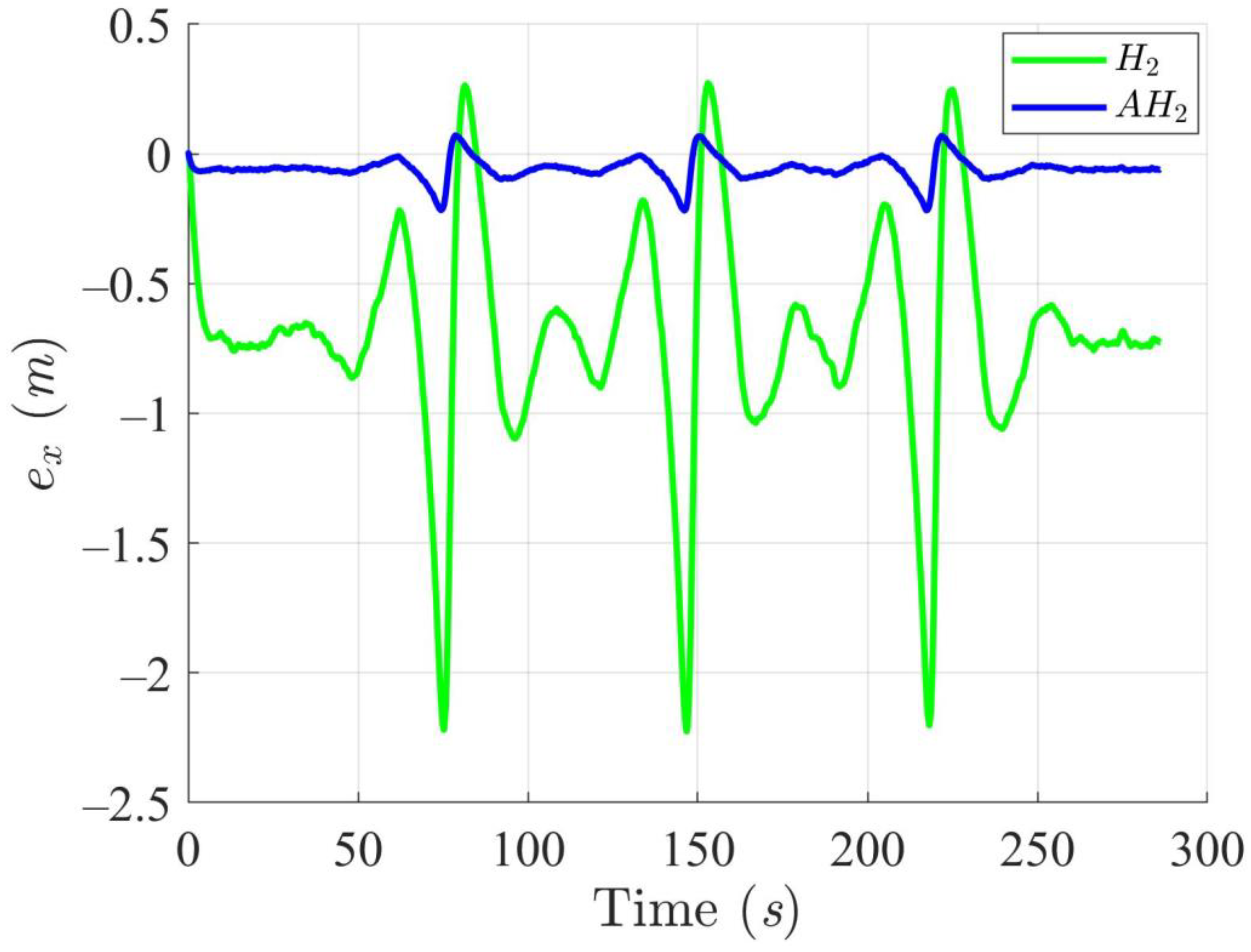
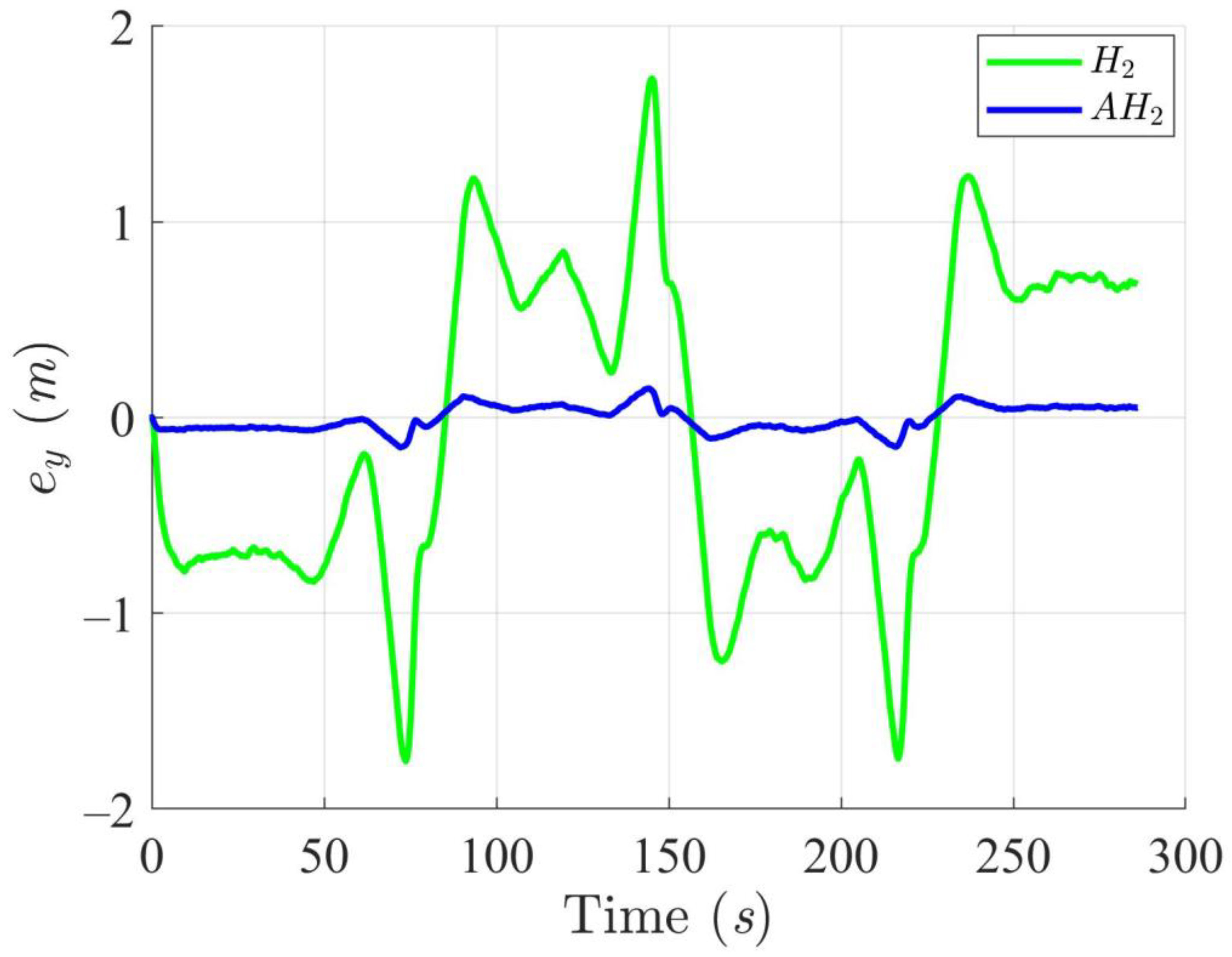
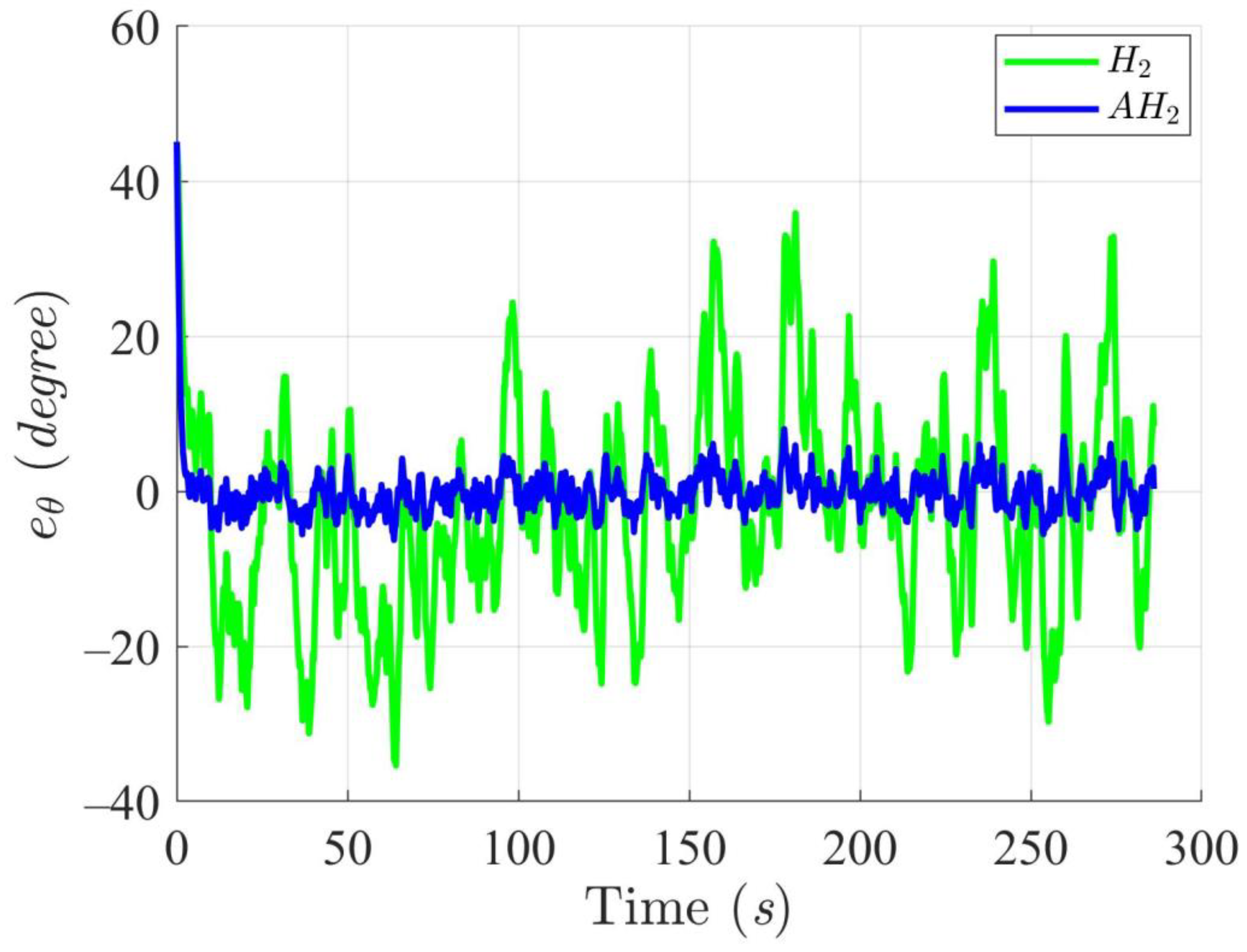
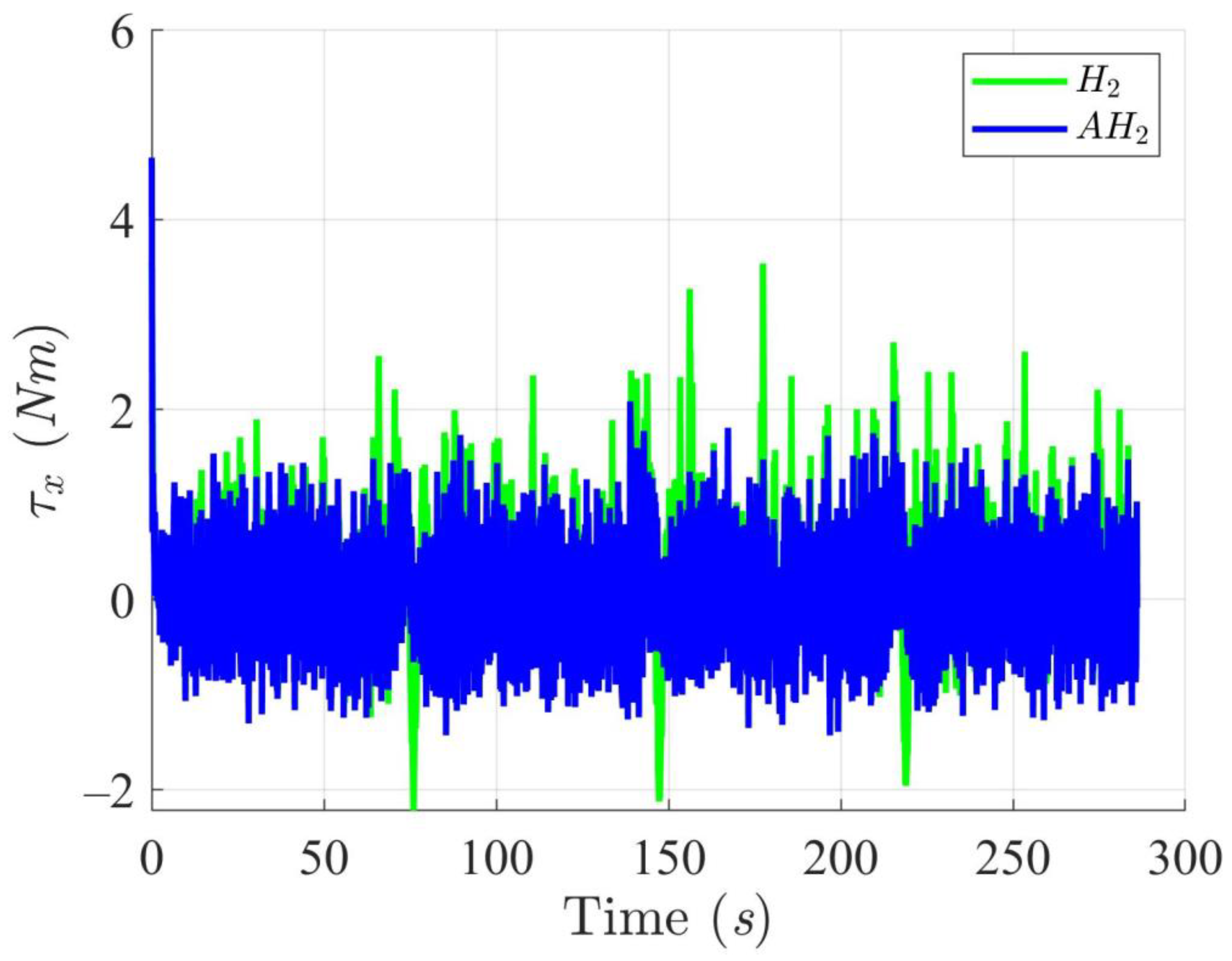
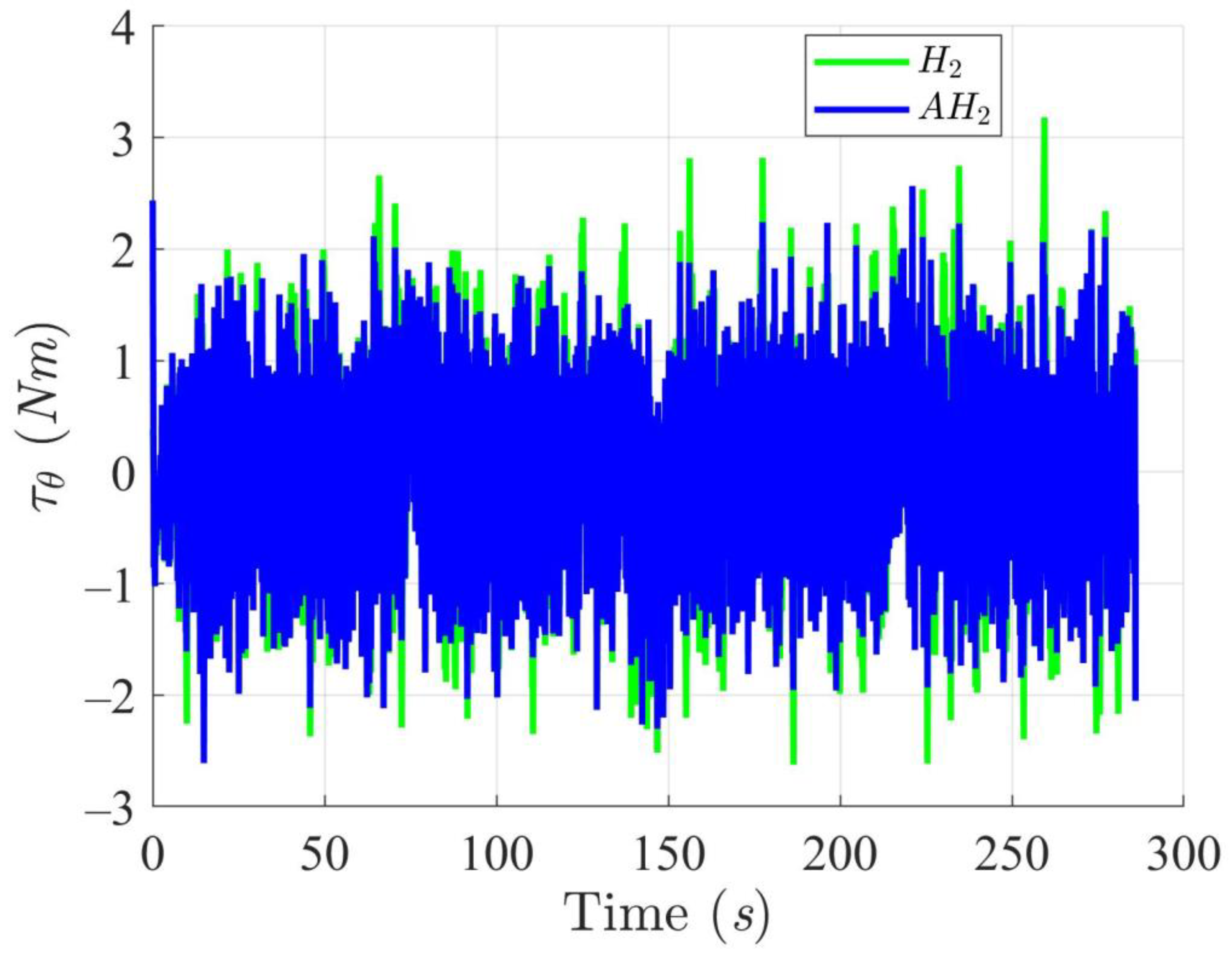
5.4. WMR Tracking Results
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Maddahi, Y.; Maddahi, A.; Monsef, S. Design Improvement of Wheeled Mobile Robots: Theory and Experiment. World Appl. Sci. J. 2012, 16, 263–274. [Google Scholar]
- Demetris, S.; Demetrios, G.E.; Christos, G.P.; Marios, M.P. Fault Detection for Service Mobile Robots Using Model-Based Method. Auton. Robot. 2016, 40, 383–394. [Google Scholar]
- Gao, X.; Li, J.; Fan, L.; Zhou, Q.; Yin, K.; Wang, J.; Song, C.; Huang, L.; Wang, Z. Review of Wheeled Mobile Robots’ Navigation Problems and Application Prospects in Agriculture. IEEE Access 2018, 6, 49248–49268. [Google Scholar] [CrossRef]
- Mishra, S.; Sharma, M.; Mohan, S.B. Fault Tolerant Control of an Omni Directional Mobile Robot with Four Mecanum Wheels. Def. Sci. J. 2019, 69, 353–360. [Google Scholar] [CrossRef]
- Rubio, F.; Valero, F.; Llopis-Albert, C. A Review of Mobile Robots: Concepts, Methods, Theoretical Framework, and Applications. Int. J. Adv. Robot. Syst. 2019, 16, 172988141983959. [Google Scholar] [CrossRef]
- Luigi, T.; Giovanni, C.; Andrea, B.; Paride, C.; Lorenzo, B.; Giuseppe, Q. Wheeled Mobile Robots: State of the Art Overview and Kinematic Comparison Among Three Omnidirectional Locomotion Strategies. J. Intell. Robot. Syst. 2022, 106, 57. [Google Scholar]
- Luis, M.C.; Andrés, S.M.R.; Francisco, R.; Vicente, F.B. Advanced Motor Control for Improving the Trajectory Tracking Accuracy of a Low-Cost Mobile Robot. Machines 2023, 11, 14. [Google Scholar]
- Nitin, S.; Jitendra, K.P.; Surajit, M. A Review of Mobile Robots: Applications and Future Prospect. Int. J. Precis. Eng. Manuf. 2023, 24, 1695–1706. [Google Scholar]
- Zhang, C.; Cen, C.; Huang, J. An Overview of Model-Free Adaptive Control for the Wheeled Mobile Robot. World Electr. Veh. J. 2024, 15, 396. [Google Scholar] [CrossRef]
- Linjie, X.; Qinglin, W.; Jinhua, S.; Yuan, L. Robust Adaptive Tracking Control of Wheeled Mobile Robot. Robot. Auton. Syst. 2016, 78, 36–48. [Google Scholar]
- Xie, H.; Zheng, J.; Sun, Z.; Wang, H.; Chai, R. Finite-time Tracking Control for Nonholonomic Wheeled Mobile Robot Using Adaptive Fast Nonsingular Terminal Sliding Mode. Nonlinear Dyn. 2022, 110, 1437–1453. [Google Scholar] [CrossRef]
- Bong, S.P.; Sung, J.Y.; Jin, B.P.; Yoon, H.C. A Simple Adaptive Control Approach for Trajectory Tracking of Electrically Driven Nonholonomic Mobile Robots. IEEE Trans. Control Syst. Technol. 2010, 18, 1199–1206. [Google Scholar]
- Sameh, F.H.; Hassan, M.A. Modeling and Control of Wheeled Mobile Robot with Four Mecanum Wheels. Eng. Technol. J. 2021, 39, 779–789. [Google Scholar]
- Swati, M.; Santhakumar, M.; Santosh, K.V. Performance Investigations of an Improved Backstepping Operational-space Position Tracking Control of a Mobile Manipulator. Def. Sci. J. 2021, 71, 436–447. [Google Scholar]
- Jiang, M.; Chen, L.; Wang, Y.; Wu, H. Adaptive Backstepping Control for Mecanum-Wheeled Omnidirectional Vehicle Using Neural Networks. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 378–386. [Google Scholar] [CrossRef]
- Umar, Z.; Salinda, B.; Mohamad, S.Z.A.; Mohd, S.A.M.; Hameedah, S.H. Nonlinear PID Controller for Trajectory Tracking of a Differential Drive Mobile Robot. J. Mech. Eng. Res. Dev. 2020, 43, 255–270. [Google Scholar]
- Nguyen, H.T.; Trinh, T.K.L.; Hoang, T.; Le, Q.D. Trajectory Tracking Control for Differential-Drive Mobile Robot by a Variable Parameter PID Controller. Int. J. Mech. Eng. Robot. Res. 2022, 11, 614–621. [Google Scholar]
- Nguyen, H.T.; Trinh, T.K.L.; Le, Q.D. Trajectory Tracking Control for Mecanum Wheel Mobile Robot by Time-Varying Parameter PID Controller. Bull. Electr. Eng. Inform. 2022, 11, 1902–1910. [Google Scholar]
- Rasha, M.H. Design a New Hybrid Controller Based on an Improvement Version of Grey Wolf Optimization for Trajectory Tracking of Wheeled Mobile Robot. FME Trans. 2023, 51, 140–148. [Google Scholar]
- Muhamad, A.; Riky, D.P. Mecanum 4 Omni Wheel Directional Robot Design System Using PID Method. J. Fuzzy Syst. Control. 2023, 1, 6–13. [Google Scholar]
- Veer, A.; Shital, S.C. Adaptive Robust Control of Mecanum-wheeled Mobile Robot with Uncertainties. Nonlinear Dyn. 2017, 87, 2147–2169. [Google Scholar]
- Wang, G.; Zhou, C.; Yu, Y.; Liu, X. Adaptive Sliding Mode Trajectory Tracking Control for WMR Considering Skidding and Slipping via Extended State Observer. Energies 2019, 12, 3305. [Google Scholar] [CrossRef]
- Yuan, Z.; Tian, Y.; Yin, Y.; Wang, S.; Liu, J.; Wu, L. Trajectory Tracking Control of a Four Mecanum Wheeled Mobile Platform: An Extended State Observer-Based Sliding Mode Approach. IET Control. Theory Appl. 2020, 14, 415–426. [Google Scholar] [CrossRef]
- Rishabh, D.Y.; Viswa, N.S. Adaptive Sliding Mode Control for Autonomous Vehicle Platoon under Unknown Friction Forces. In Proceedings of the Conference: 2021 20th International Conference on Advanced Robotics (ICAR), Ljubljana, Slovenia, 6–10 December 2021. [Google Scholar]
- Pankaj, S.Y.; Vandana, A.; Mohanta, J.; Ahmed, M.D.F. A Robust Sliding Mode Control of Mecanum Wheel-Chair for Trajectory Tracking. Mater. Today Proc. 2022, 56, 623–630. [Google Scholar]
- Javad, M.; Akbar, S.; Reza, A.T. Design of Fixed-Time Terminal Sliding Mode Control for Robot with Mecanum Wheels. J. Nonlinear Syst. Electr. Eng. 2022, 8, 19–37. [Google Scholar]
- Pham, A.T.; Nguyen, M.L. Trajectory Tracking Control of Omnidirectional Mobile Robots: A Model-Free Control-Based Approach. J. Appl. Sci. Eng. 2023, 27, 3687–3696. [Google Scholar]
- Mohanty, P.K.; Parhi, D.R. A New Hybrid Intelligent Path Planner for Mobile Robot Navigation Based on Adaptive Neuro-Fuzzy Inference System. Aust. J. Mech. Eng. 2015, 13, 195–207. [Google Scholar] [CrossRef]
- Dong, N.M.; Hiep, D.Q.; Nam, D.P.; Tien, N.M.; Duy, N.B. An Adaptive Fuzzy Dynamic Surface Control Tracking Algorithm for Mecanum Wheeled Mobile Robot. Int. J. Mech. Eng. Robot. Res. 2023, 12, 354–361. [Google Scholar]
- Chen, Y.-H.; Chen, Y.-Y. Nonlinear Adaptive Fuzzy Control Design for Wheeled Mobile Robots with Using the Skew Symmetrical Property. Symmetry 2023, 15, 221. [Google Scholar] [CrossRef]
- Zenon, H. Robust Neural Networks Control of Omni-Mecanum Wheeled Robot with Hamilton-Jacobi Inequality. J. Theor. Appl. Mech. 2018, 56, 1193–1204. [Google Scholar]
- Mateusz, S.; Marcin, S. Neural Tracking Control of a Four-Wheeled Mobile Robot with Mecanum Wheels. Appl. Sci. 2022, 12, 5322. [Google Scholar] [CrossRef]
- Ma, C.; Li, X.; Xing, G.; Dian, S. A T-S Fuzzy Quaternion-Value Neural Network-Based Data-Driven Generalized Predictive Control Scheme for Mecanum Mobile Robot. Processes 2022, 10, 1964. [Google Scholar] [CrossRef]
- Trinh, T.K.L.; Nguyen, T.T.; Hoang, T.; Thai, N. A Neural Network Controller Design for the Mecanum Wheel Mobile Robot. Eng. Technol. Appl. Sci. Res. 2023, 13, 10541–10547. [Google Scholar]
- Chen, Y.-H.; Li, T.H.S.; Chen, Y.-Y. A Novel Nonlinear Control Law with Trajectory Tracking Capability for Mobile Robots: Closed-Form Solution Design. Appl. Math. Inf. Sci. 2013, 7, 749–754. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Lou, S.-J. Control Design of a Swarm of Intelligent Robots: A Closed-Form H2 Nonlinear Control Approach. Appl. Sci. 2020, 10, 1055. [Google Scholar] [CrossRef]
- Samia, M.; Guillaume, G.; El-Mostafa, E.; Mustapha, O.; Alain, P. Trajectory Tracking and Time Delay Management of Four-Mecanum Wheeled Mobile Robots (4-MWMR). In Proceedings of the 15th European Workshop on Advanced Control and Diagnosis (ACD 2019), Bologna, Italy, 21–22 November 2019. [Google Scholar]
- Matthew, T.W.; Daniel, T.G.; Tony, J.P. Collinear Mecanum Drive: Modeling, Analysis, Partial Feedback Linearization, and Nonlinear Control. IEEE Trans. Robot. 2021, 37, 642–658. [Google Scholar]
- Chen, Y.-H. Control Design and Implementation of Autonomous Robotic Lawnmower. Mathematics 2024, 12, 3324. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Chen, Y.-Y. Trajectory Tracking Design for A Swarm of Autonomous Mobile Robots: A Nonlinear Adaptive Optimal Approach. Mathematics 2022, 10, 3901. [Google Scholar] [CrossRef]
- Sameh, F.H.; Hassan, M.A. Design of Hybrid Controller for the Trajectory Tracking of Wheeled Mobile Robot with Mecanum Wheels. J. Mech. Eng. Res. Dev. 2020, 43, 400–414. [Google Scholar]















| Description | Parameter | Value |
|---|---|---|
| Wheel radius | 0.05 (m) | |
| Distance from Q to Q1 | 0.02 (m) | |
| Distance from Q to each wheel | 0.25 (m) | |
| WMR platform mass | 3.1 (kg) | |
| Wheel mass | 0.35 (kg) | |
| WMR platform inertia | 0.032 (kg m2) | |
| Wheel inertia | 6.25 × 10−4 (kg m2) |
| No. | Waypoints (x, y) (m) | No. | Waypoints (x, y) (m) |
|---|---|---|---|
| 1 | (1, 5) | 15 | (90, 35) |
| 2 | (10, 5) | 16 | (80, 35) |
| 3 | (20, 5) | 17 | (70, 35) |
| 4 | (30, 5) | 18 | (60, 35) |
| 5 | (40, 5) | 19 | (50, 35) |
| 6 | (50, 5) | 20 | (40, 35) |
| 7 | (60, 5) | 21 | (30, 35) |
| 8 | (70, 5) | 22 | (20, 35) |
| 9 | (80, 5) | 23 | (10, 35) |
| 10 | (90, 5) | 24 | (1, 35) |
| 11 | (100, 5) | 25 | (1, 25) |
| 12 | (100, 15) | 26 | (1, 15) |
| 13 | (100, 25) | 27 | (1, 5) |
| 14 | (100, 35) |
| X (m) | Y (m) | (Degree) |
|---|---|---|
| 1 | 5 | 0 |
| No. | Waypoints (x, y) (m) | No. | Waypoints (x, y) (m) |
|---|---|---|---|
| 1 | (0, 10) | 12 | (110, 20) |
| 2 | (10, 20) | 13 | (120, 30) |
| 3 | (20, 30) | 14 | (130, 40) |
| 4 | (30, 40) | 15 | (140, 50) |
| 5 | (40, 50) | 16 | (150, 60) |
| 6 | (50, 60) | 17 | (160, 50) |
| 7 | (60, 50) | 18 | (170, 40) |
| 8 | (70, 40) | 19 | (180, 30) |
| 9 | (80, 30) | 20 | (190, 20) |
| 10 | (90, 20) | 21 | (200, 10) |
| 11 | (100, 10) |
| X (m) | Y (m) | (Degree) |
|---|---|---|
| 0 | 10 | 0 |
| Unit | Volume | Attribute |
|---|---|---|
| Battery (1) | 1 | minimum discharge cutoff voltage: 5 V rated capacity: 6400 mAh |
| Battery (2) | 1 | minimum discharge cutoff voltage: 12 V rated capacity: 5500 mAh |
| Ultrasonic Sensor | 6 | measure distance: 2 cm~400 cm accuracy: 0.3 cm sensing angle: 15 degree |
| Mecanum Wheel | 4 | diameter: 13 cm weight: 400 g maximum load: 15 kg (single) |
| Chassis | 1 | length: 80 cm width: 38.8 cm height: 1 cm weight: 8.4 kg |
| Inertial Measurement Unit (IMU) | 1 | sensor axis: X, Y, Z input voltage: 3~5.5 V input current: 20 mA bandwidth: 5 Hz~50 Hz acceleration: −8 g~+8 g measurement: −125~+125 degree |
| Arduino | 1 | model: MEGA 2560 clock speed: 16 MHz flash memory: 256 KB I/O Pins: 54 pins |
| Motor | 4 | input voltage: 12 V revolutions per minute: 100 rpm |
| Motor Driver | 2 | input voltage: 5~35 V input current: 0~36 mA maximum power consumption: 20 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-H. Nonlinear Adaptive Optimal Control Design and Implementation for Trajectory Tracking of Four-Wheeled Mecanum Mobile Robots. Mathematics 2024, 12, 4013. https://doi.org/10.3390/math12244013
Chen Y-H. Nonlinear Adaptive Optimal Control Design and Implementation for Trajectory Tracking of Four-Wheeled Mecanum Mobile Robots. Mathematics. 2024; 12(24):4013. https://doi.org/10.3390/math12244013
Chicago/Turabian StyleChen, Yung-Hsiang. 2024. "Nonlinear Adaptive Optimal Control Design and Implementation for Trajectory Tracking of Four-Wheeled Mecanum Mobile Robots" Mathematics 12, no. 24: 4013. https://doi.org/10.3390/math12244013
APA StyleChen, Y.-H. (2024). Nonlinear Adaptive Optimal Control Design and Implementation for Trajectory Tracking of Four-Wheeled Mecanum Mobile Robots. Mathematics, 12(24), 4013. https://doi.org/10.3390/math12244013






