Analytical Solutions and Computer Modeling of a Boundary Value Problem for a Nonstationary System of Nernst–Planck–Poisson Equations in a Diffusion Layer
Abstract
:1. Introduction
2. Mathematical Model of Non-Stationary Transport of 1:1 Salt Ions in the Diffusion Layer of the Ion Exchange Membrane
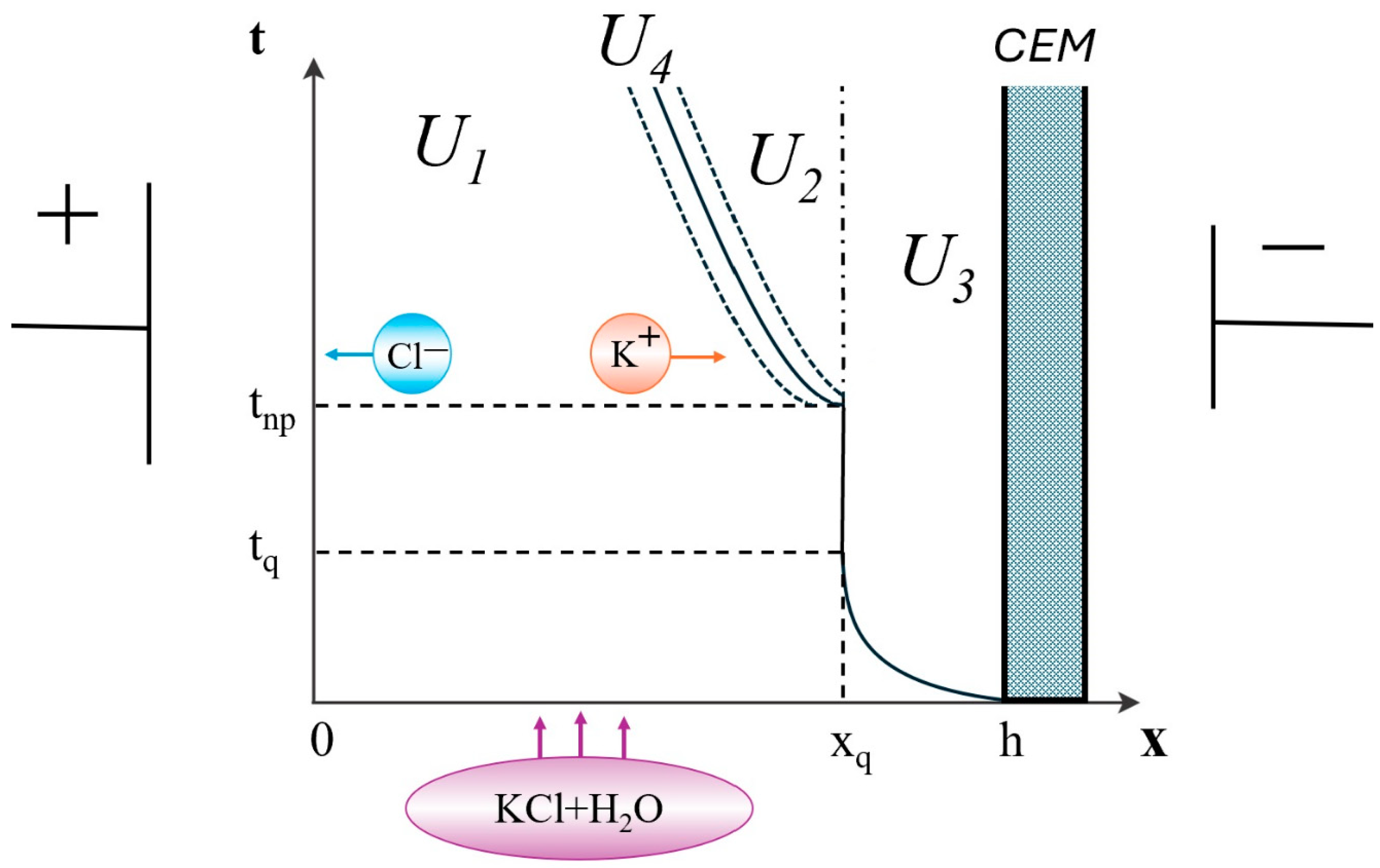
2.1. Diffusion Layer at the Cation-Exchange Membrane (CEM)
- (1)
- In potentiodynamic (potentiostatic) mode, a potential drop is set, and the corresponding current density flowing through the electromembrane system (for example, a diffusion layer) is determined (in mathematical models, it is calculated from the found solution). Since it is the potential difference (drop) that matters, rather than specific values, an arbitrary constant can be set for the potential at one of the boundaries of the region under consideration, for example, zero at , i.e., . Then, at , we assume , where the function is specified. For example, when calculating the current–voltage characteristic (CVC), we assume , where is the initial value (usually ) and the potential sweep rate, with the sweep rate being chosen small enough to ensure a quasi-stationary mode and coincidence with the CVC calculated for the potentiostatic mode with the required accuracy [29].
- (2)
- For the galvanodynamic (galvanostatic) mode, an external current (current in the circuit including the EMS) is set, and the corresponding potential drop is determined. Below, we consider the galvanodynamic mode, which is determined by the galvanodynamic boundary condition, for example, at , which was first proposed in [30].
2.2. Mathematical Model
2.3. Boundary Conditions
2.4. Initial Conditions ()
3. Characteristic Quantities and Transition to Dimensionless Form
4. Boundary Value Problem for a One-Dimensional Non-Stationary System of Equations of the NPP in Dimensionless Form
5. The Relationship Between the Currents in the Circuit and in the Diffusion Layer
6. Stationary Boundary Value Problem
7. Algorithm for Solving a Non-Stationary Boundary Value Problem
- (1)
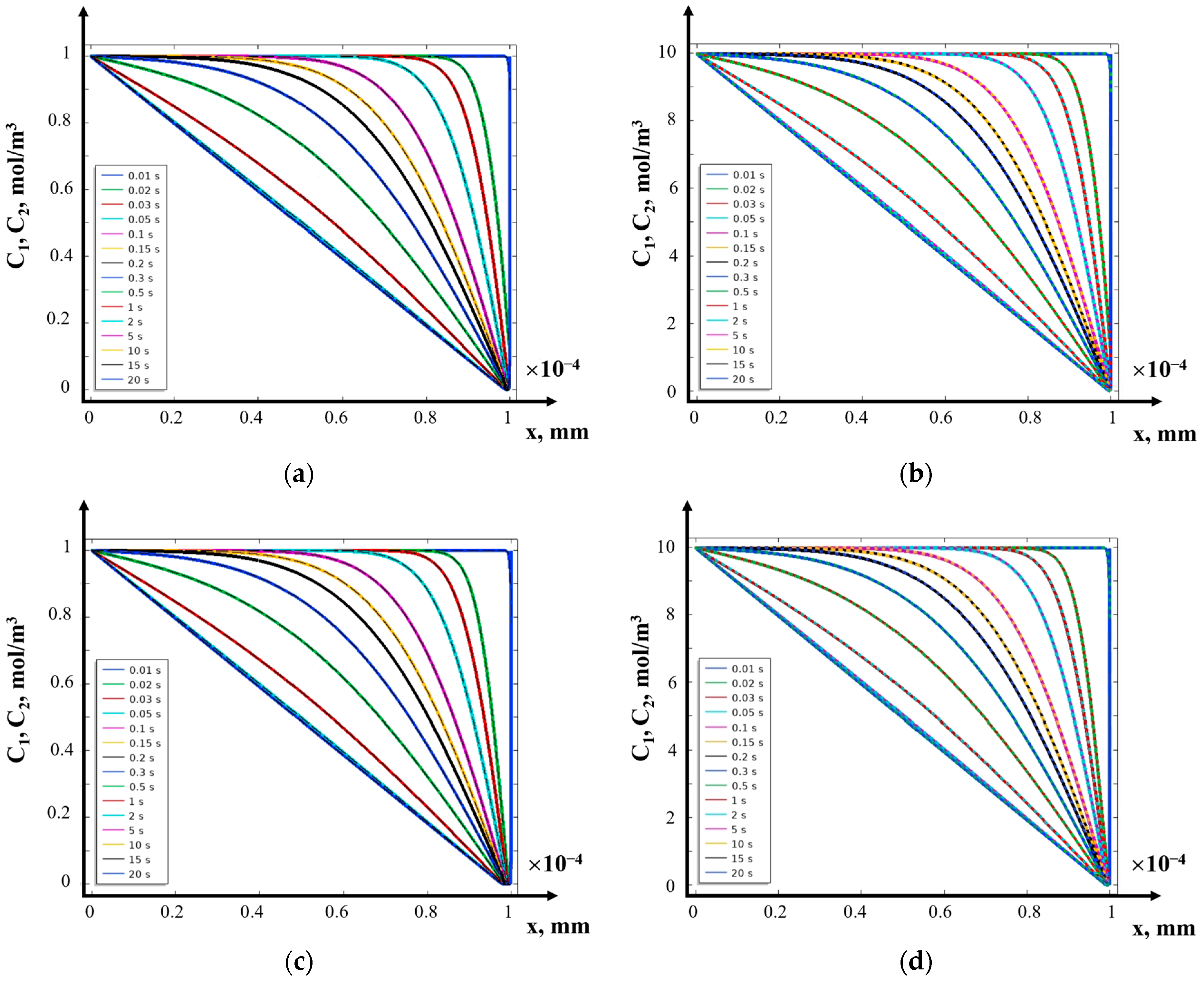
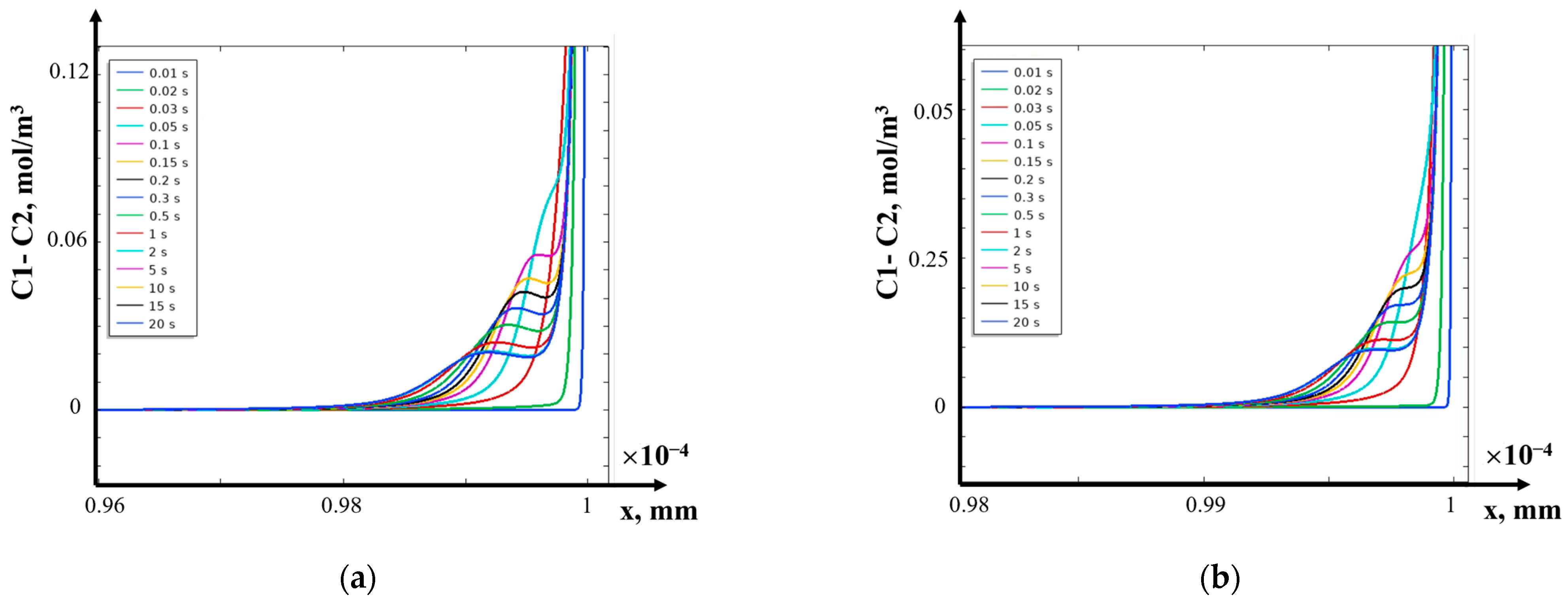
- Analysis of the numerical solution
- (a)
- Galvanostatic mode

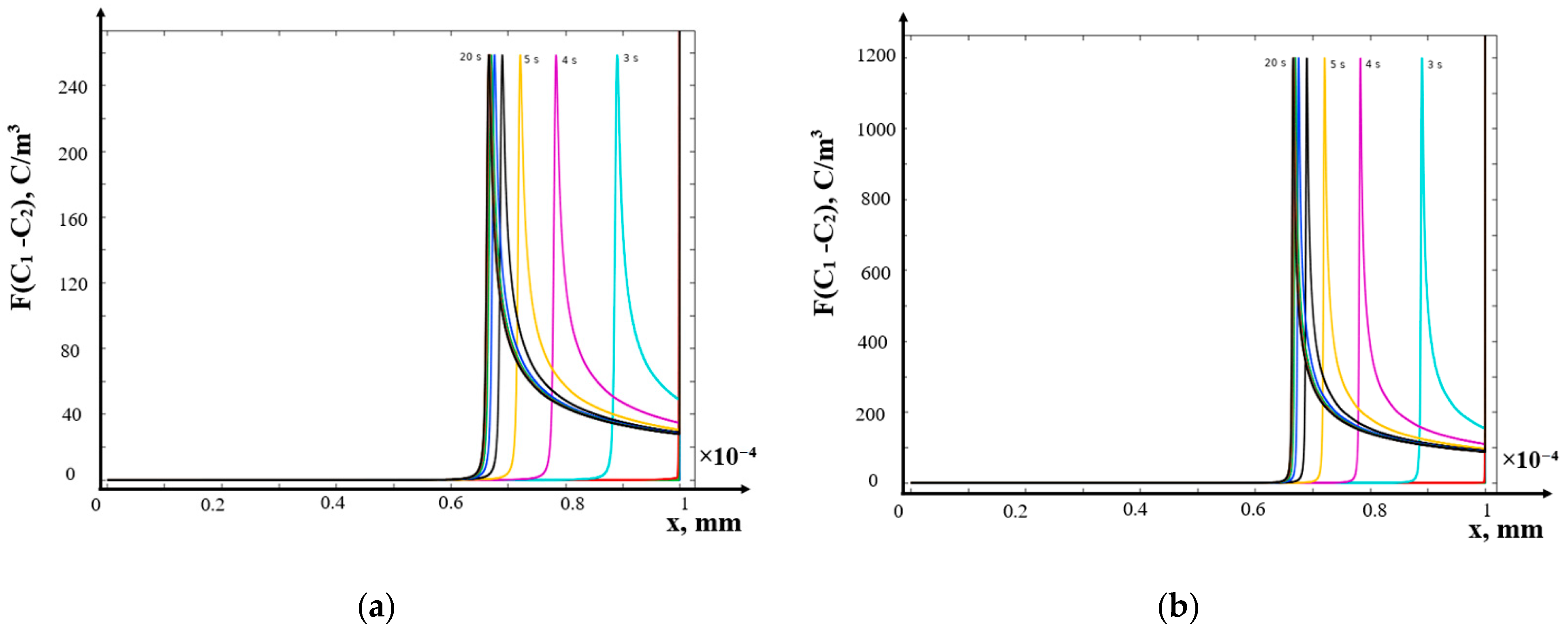
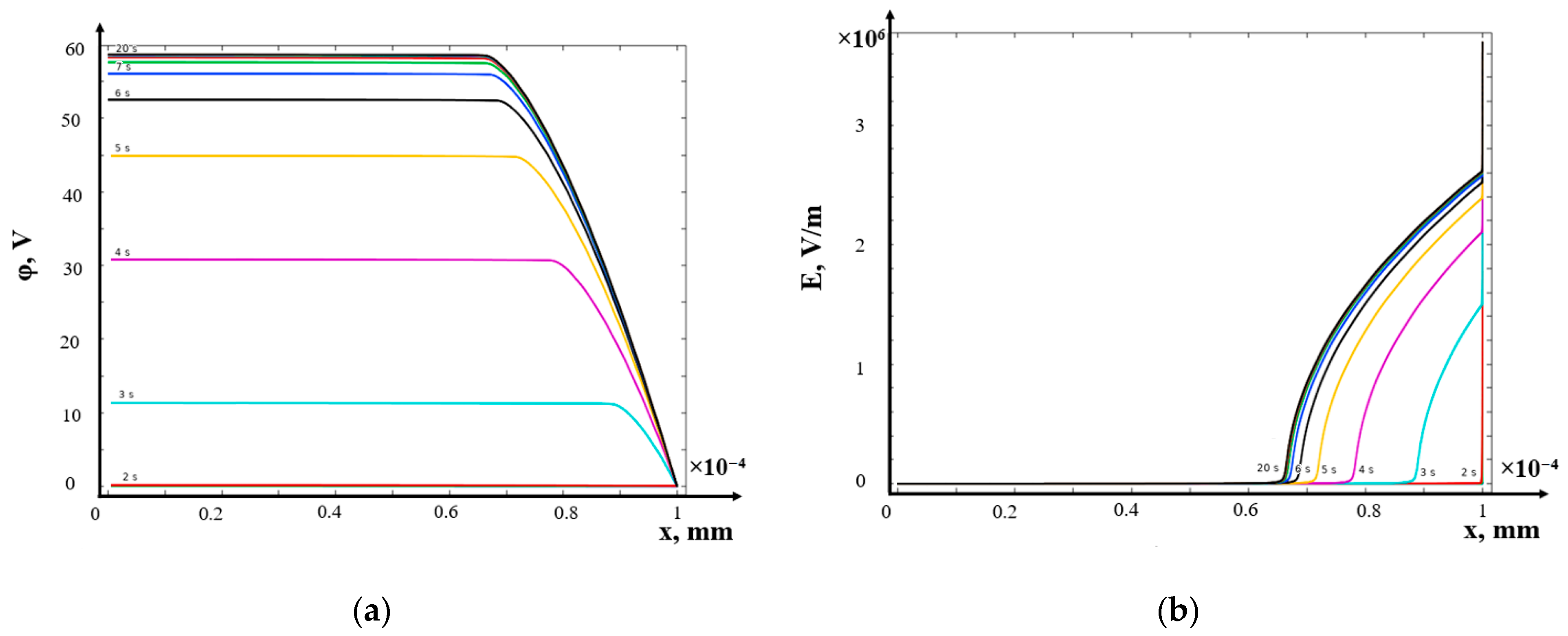
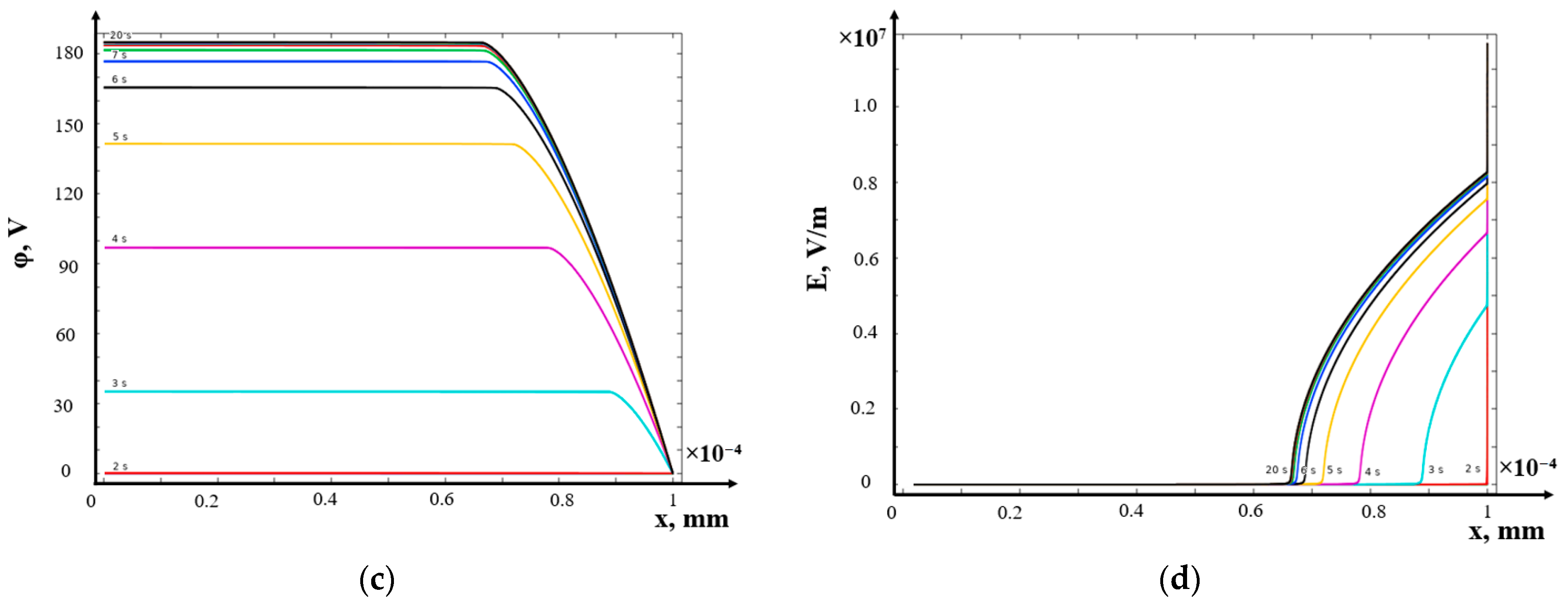
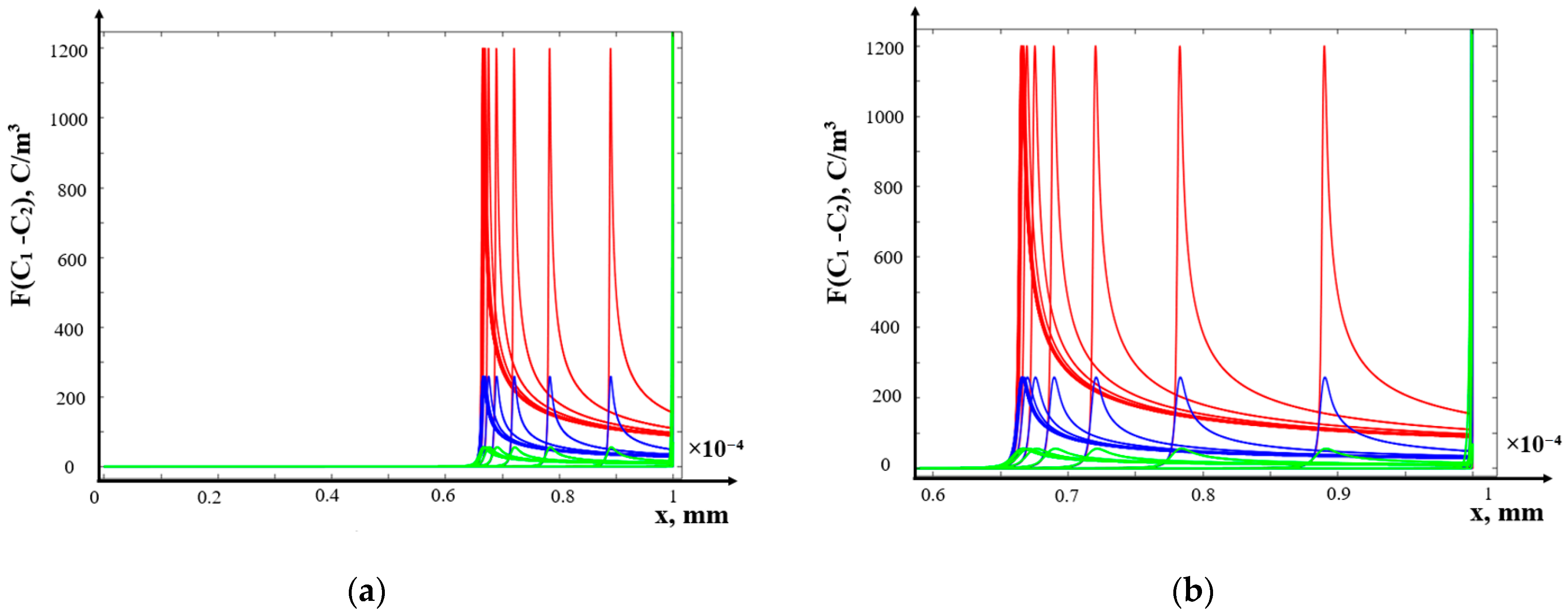
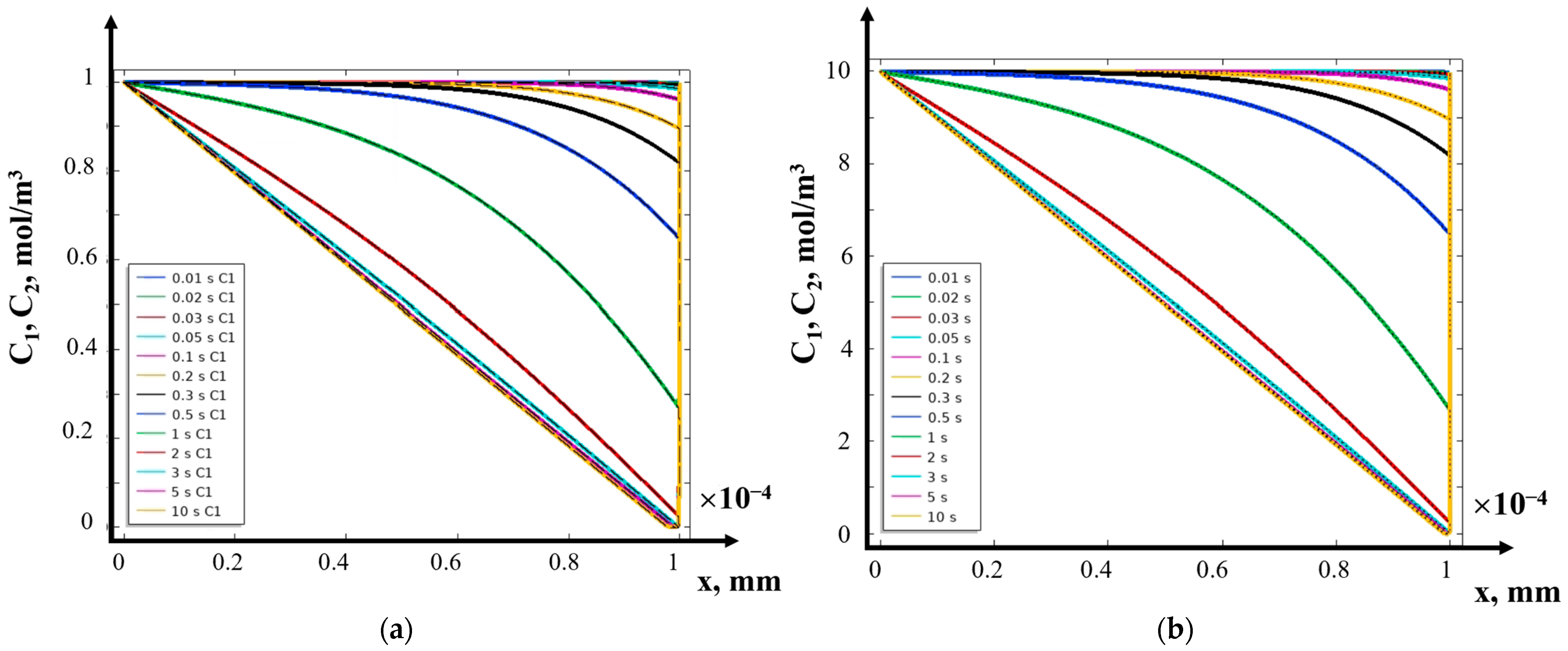
- (b)
- Galvanodynamic mode
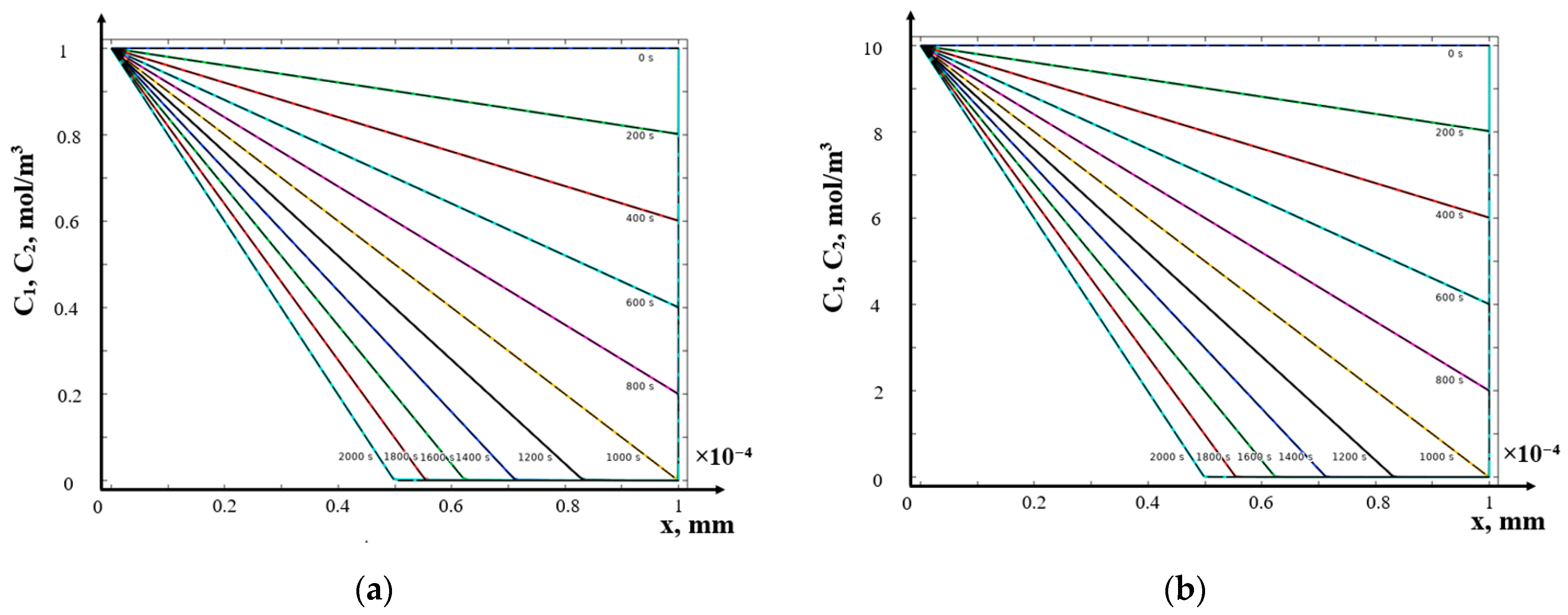
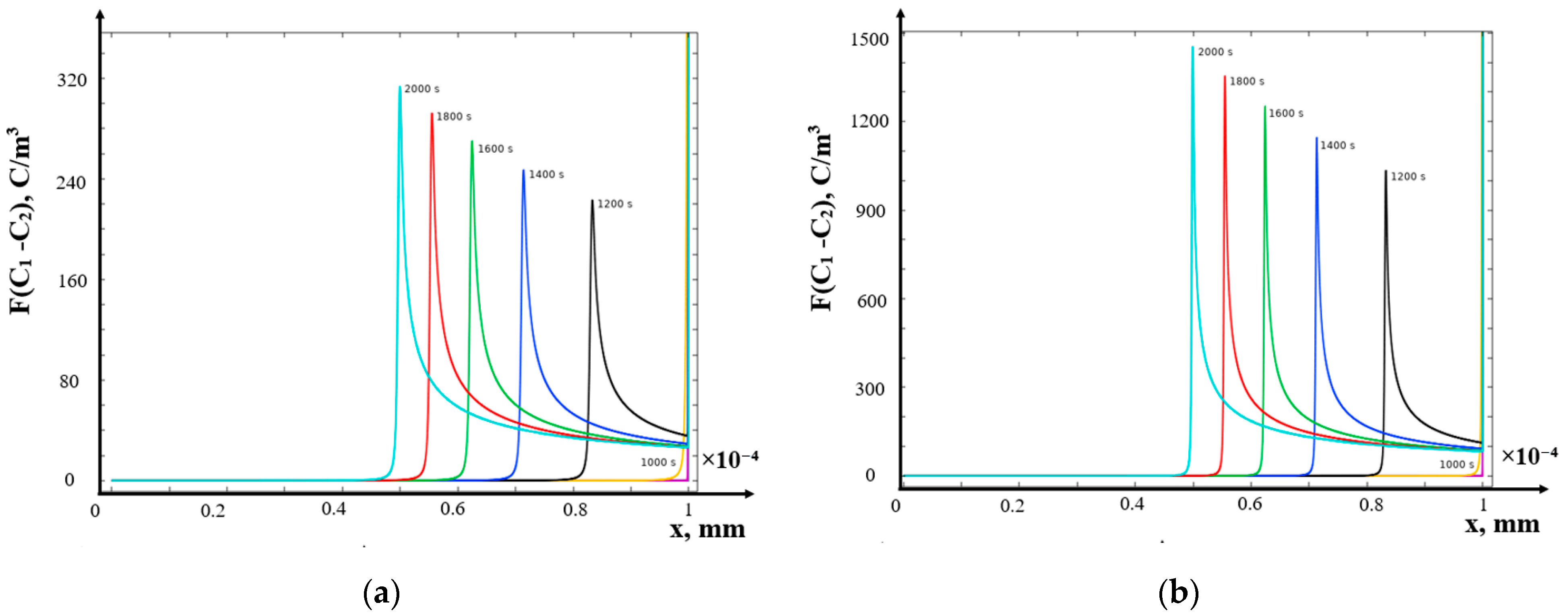
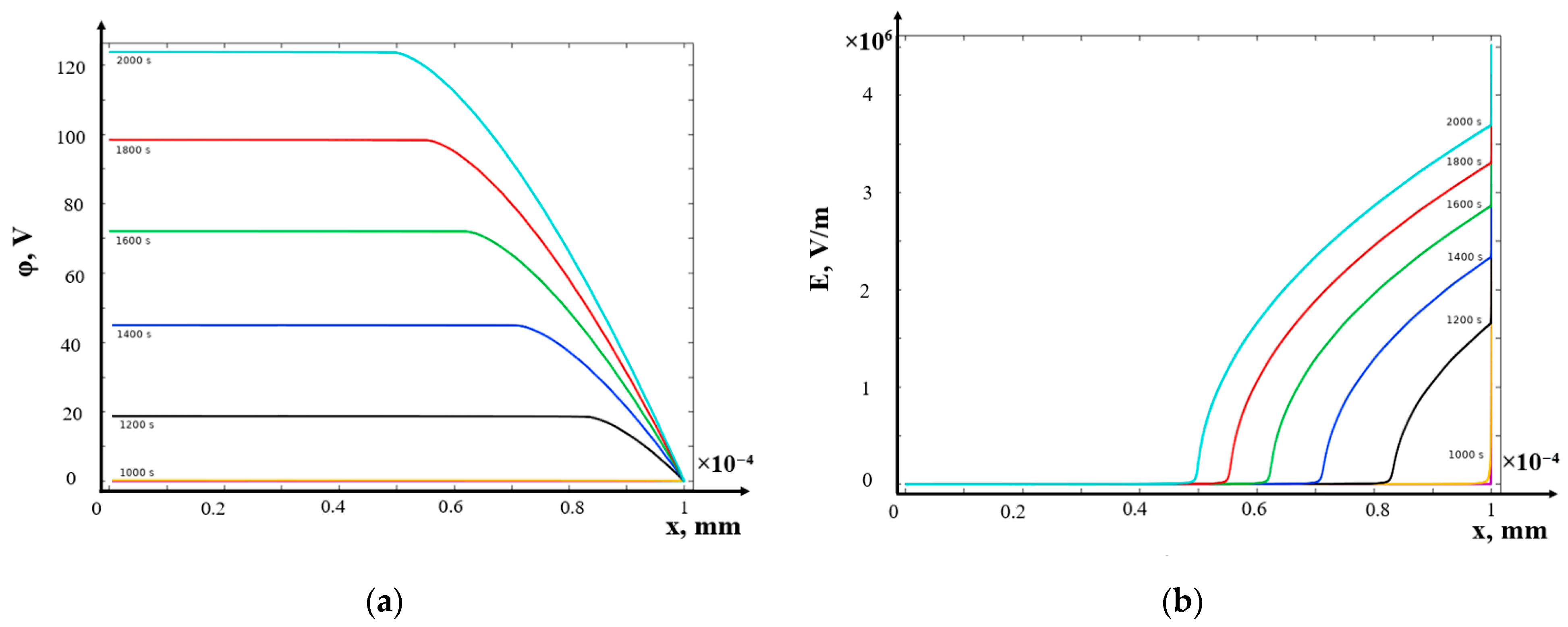
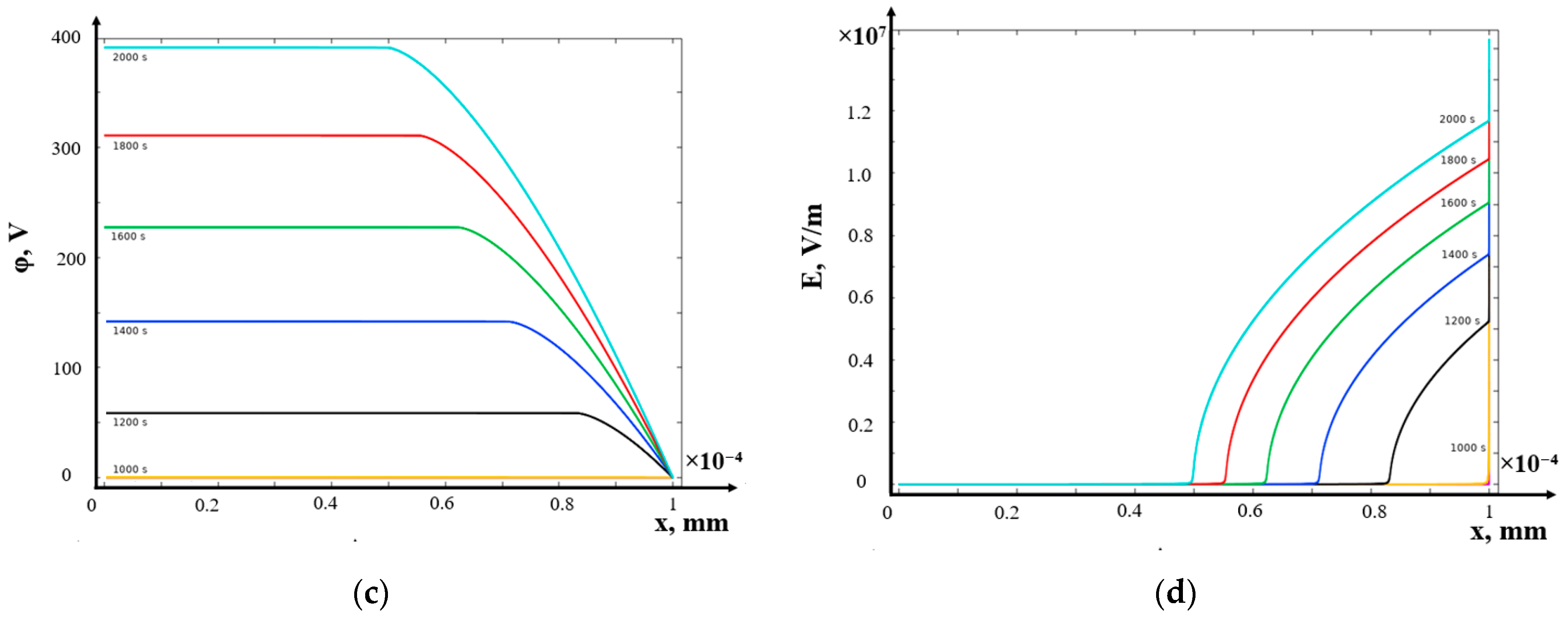
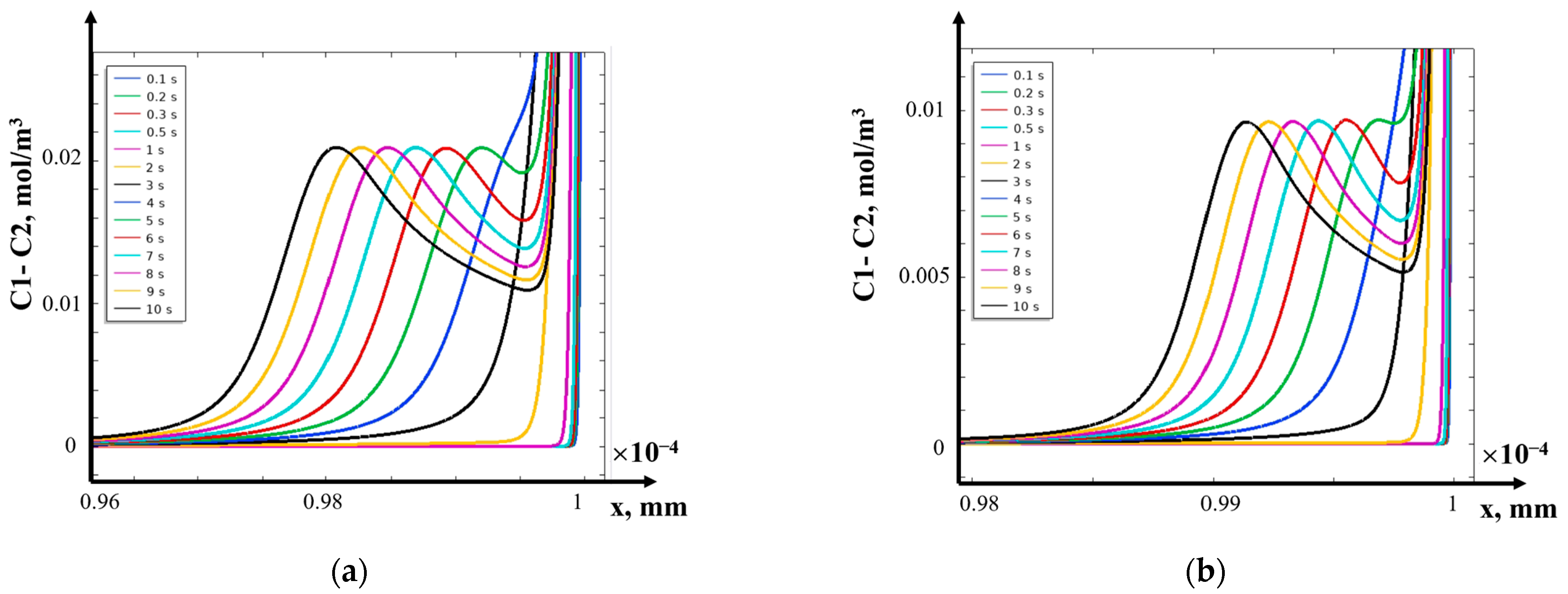
- (c)
- Potentiostatic mode

- (d)
- Potentiodynamic mode
- (2)
- The structure of the diffusion layer in the CEM
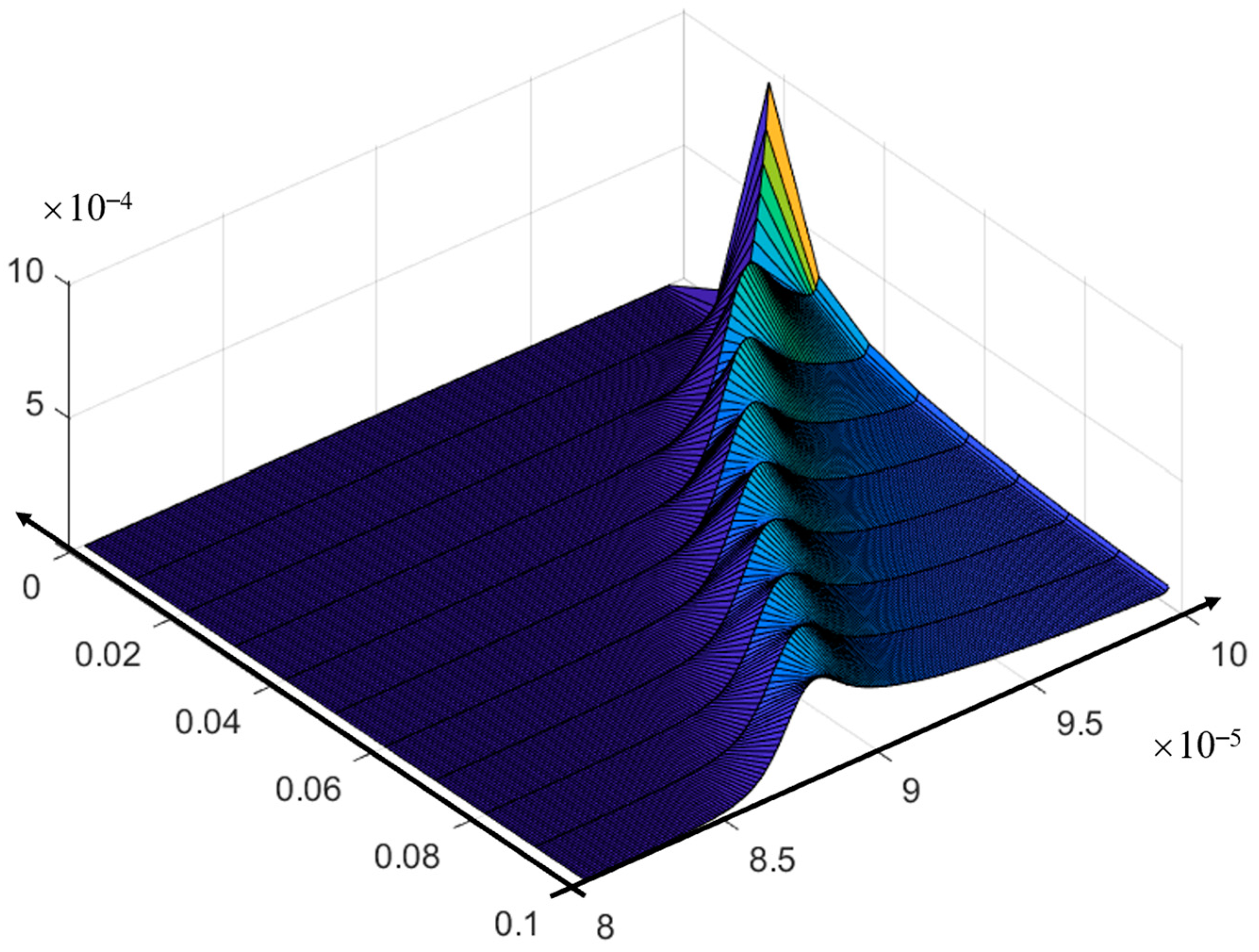
- (3)
- Asymptotic solution algorithm
8. Solution in the Field of Electroneutrality
- (1)
- Boundary value problem for the equilibrium concentration.
- (2)
- Calculation of potential in ENR
9. Derivation of Equation for the Potential in the SCR of the CEM
10. Analytical Solution of the Equation for Inside the Region
- (1)
- Simplified analytical solution of the equation for inside the region
- (2)
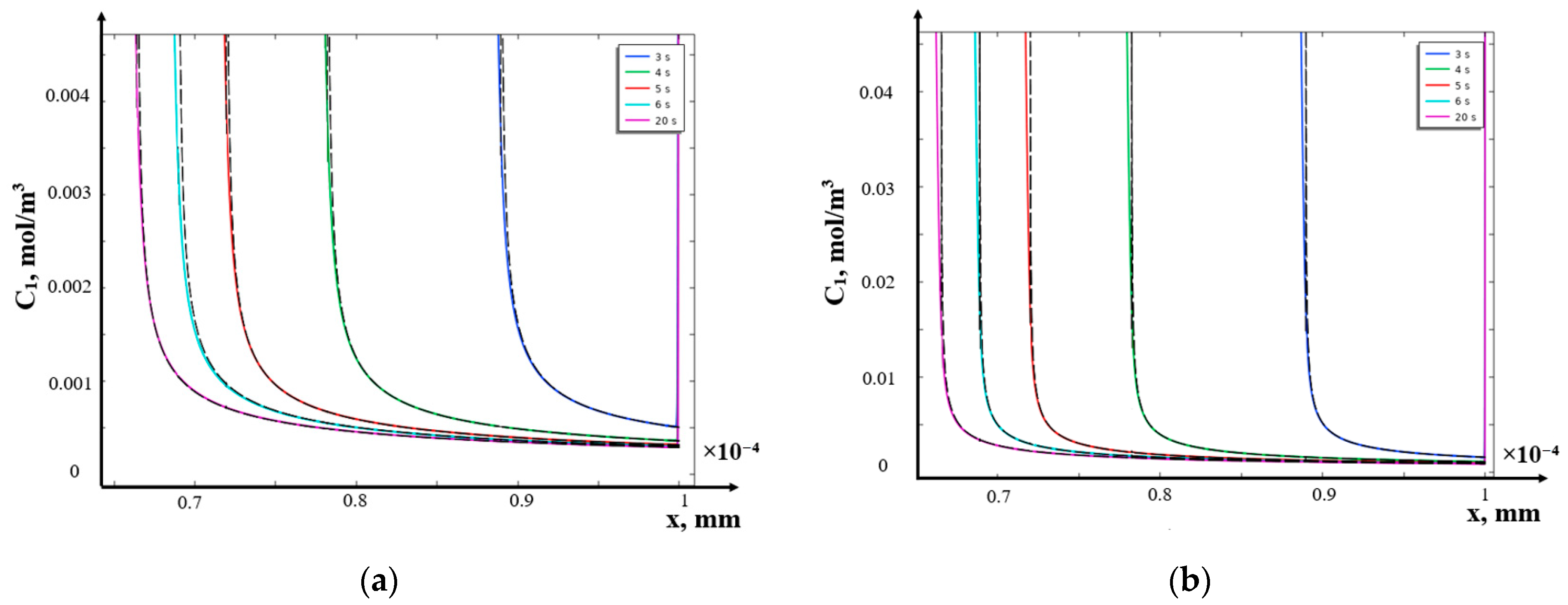
- Comparison of the obtained analytical solution with the numerical solution inside the domain
11. Reduction of Equation for in the SCR to an Auxiliary Linear Differential Equation of Parabolic Type
12. Diffusion Layer of an Anion Exchange Membrane (AEM)—Derivation of Equation for the Potential in the SCR at the AEM
13. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jasielec, J.J. Electrodiffusion Phenomena in Neuroscience and the Nernst–Planck–Poisson Equations. Electrochem 2021, 2, 197–215. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, L.; Zhang, M. Studies on Ionic Flows via Poisson–Nernst–Planck Systems with Bikerman’s Local Hard-Sphere Potentials under Relaxed Neutral Boundary Conditions. Mathematics 2024, 12, 1182. [Google Scholar] [CrossRef]
- Cartailler, J. Asymptotic of Poisson-Nernst-Planck Equations and Application to the Voltage Distribution in Cellular Micro-Domains. Analysis of PDEs [Math.AP]. Ph.D. Thesis, Université Pierre et Marie Curie—Paris VI, Paris, France, 2017. (In English). [Google Scholar]
- Sun, L.; Liu, W. Non-localness of Excess Potentials and Boundary Value Problems of Poisson–Nernst–Planck Systems for Ionic Flow: A Case Study. J. Dyn. Differ. Equ. 2018, 30, 779–797. [Google Scholar] [CrossRef]
- Chao, Z.; Xie, D. An improved Poisson-Nernst-Planck ion channel model and numerical studies on effects of boundary conditions, membrane charges, and bulk concentrations. J. Comput. Chem. 2021, 42, 1929. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Wang, Z. A free energy satisfying discontinuous Galerkin method for one-dimensional Poisson–Nernst–Planck systems. J. Comput. Phys. 2017, 328, 413–437. [Google Scholar] [CrossRef]
- Gwecho, A.; Shu, W.; Mboya, O.; Khan, S. Solutions of Poisson-Nernst Planck Equations with Ion Interaction. Appl. Math. 2022, 13, 263–281. [Google Scholar] [CrossRef]
- Grafov, B.M.; Chernenko, A.A. Theory of direct current flow through a binary electrolyte solution. Dokl. Akad. Nauk. SSSR 1962, 146, 135–138. [Google Scholar]
- Urtenov, M.K.; Nikonenko, V.V. Analysis of the boundary-value problem solution of the Nernst-Planck-Poisson equations 1/1 electrolytes. Russ. Electrochem. 1993, 29, 314–324. [Google Scholar]
- Uzdenova, A.; Kovalenko, A.; Urtenov, M.K.; Nikonenko, V. 1D mathematical modelling of non-stationary ion transfer in the diffusion layer adjacent to an ion-exchange membrane in galvanostatic mode. Membranes 2018, 8, 84. [Google Scholar] [CrossRef]
- Kumar, P.; Rubinstein, S.M.; Rubinstein, I.; Zaltzman, B. Mechanisms of hydrodynamic instability in concentration polarization. Phys. Rev. Res. 2020, 2, 033365. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electroconvection in electrodeposition: Electrokinetic regularization mechanisms of shortwave instabilities. Phys. Rev. Fluids 2024, 9, 053701. [Google Scholar] [CrossRef]
- Lebedev, K.A.; Zabolotsky, V.I.; Vasil’eva, V.I.; Akberova, E.M. Mathematical modelling of vortex structures in the channel of an electrodialysis cell with ion-exchange membranes of different surface morphology. Condens. Matter Interphases 2022, 24, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Nikonenko, V.V.; Kovalenko, A.V.; Urtenov, M.K.; Pismenskaya, N.D.; Han, J.; Sistat, P.; Pourcelly, G. Desalination at overlimiting currents: State-of-the-art and perspectives. Desalination 2014, 342, 85–106. [Google Scholar] [CrossRef]
- Kovalenko, A.V.; Nikonenko, V.V.; Chubyr, N.O.; Urtenov, M.K. Mathematical modeling of electrodialysis of a dilute solution with accounting for water dissociation-recombination reactions. Desalination 2023, 24, 483–495. [Google Scholar] [CrossRef]
- Deng, D.; Aouad, W.; Braff, W.A.; Schlumpberger, S.; Suss, M.E.; Bazant, M.Z. Water purification by shock electrodialysis: Deionization, filtration, separation, and disinfection. Desalination 2015, 357, 77–83. [Google Scholar] [CrossRef]
- Tian, H.; Alkhadra, M.A.; Bazant, M.Z. Theory of shock electrodialysis I: Water dissociation and electrosmotic vortices. J. Colloid Interface Sci. 2021, 589, 606–615. [Google Scholar] [CrossRef]
- Rybalkina, O.; Solonchenko, K.; Chuprynina, D.; Pismenskaya, N.; Nikonenko, V. Effect of Pulsed Electric Field on the Electrodialysis Performance of Phosphate-Containing Solutions. Membranes 2022, 12, 1107. [Google Scholar] [CrossRef] [PubMed]
- Gorobchenko, A.; Mareev, S.; Nikonenko, V. Mathematical Modeling of the Effect of Pulsed Electric Field on the Specific Permselectivity of Ion-Exchange Membranes. Membranes 2021, 11, 115. [Google Scholar] [CrossRef] [PubMed]
- Nichka, V.; Mareev, S.; Pismenskaya, N.; Nikonenko, V.; Bazinet, L. Mathematical Modeling of the Effect of Pulsed Electric Field Mode and Solution Flow Rate on Protein Fouling during Bipolar Membrane Electroacidificaiton of Caseinate Solution. Membranes 2022, 12, 193. [Google Scholar] [CrossRef]
- Lemay, N.; Mikhaylin, S.; Mareev, S.; Pismenskaya, N.; Nikonenko, V.; Bazinet, L. How demineralization duration by electrodialysis under high frequency pulsed electric field can be the same as in continuous current condition and that for better performances? J. Membr. Sci. 2020, 603, 117878. [Google Scholar] [CrossRef]
- Mikhaylin, S.; Nikonenko, V.; Pourcelly, G.; Bazinet, L. Intensification of demineralization process and decrease in scaling by application of pulsed electric field with short pulse/pause conditions. J. Membr. Sci. 2014, 468, 389–399. [Google Scholar] [CrossRef]
- Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Nikonenko, V.V. Effect of electroconvection during pulsed electric field electrodialysis. Numerical experiments. Electrochem. Commun. 2015, 51, 1–5. [Google Scholar] [CrossRef]
- Sistat, P.; Huguet, P.; Ruiz, B.; Pourcelly, G.; Mareev, S.A.; Nikonenko, V.V. Effect of pulsed electric field on electrodialysis of a NaCl solution in sub-limiting current regime. Electrochim. Acta 2015, 164, 267–280. [Google Scholar] [CrossRef]
- Karlin, Y.V.; Kropotov, V.N. Electrodialysis separation of Na+ and Ca2+ in a pulsed current mode. Russ. J. Electrochem. 1995, 31, 472–476. [Google Scholar]
- Mishchuk, N.A.; Koopal, L.K.; Gonzalez-Caballero, F. Intensification of electrodialysis by applying a non-stationary electric field. Colloids Surf. A Physicochem. Eng. Asp. 2001, 176, 195–212. [Google Scholar] [CrossRef]
- Dufton, G.; Mikhaylin, S.; Gaaloul, S.; Bazinet, L. Positive impact of pulsed electric field on lactic acid removal, demineralization and membrane scaling during acid whey electrodialysis. Int. J. Mol. Sci. 2019, 20, 797. [Google Scholar] [CrossRef]
- Newman, J. The polarized diffuse double layer. Trans. Faraday Soc. 1966, 61, 2229–2237. [Google Scholar] [CrossRef]
- Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Nikonenko, V.V. Theoretical Analysis of the Effect of Ion Concentration in Solution Bulk and at Membrane Surface on the Mass Transfer at Overlimiting Currents. Russ. J. Electrochem. 2017, 53, 1254–1265. [Google Scholar] [CrossRef]
- Uzdenova, A.; Urtenov, M. Mathematical Modeling of the Phenomenon of Space-Charge Breakdown in the Galvanostatic Mode in the Section of the Electromembrane Desalination Channel. Membranes 2021, 11, 873. [Google Scholar] [CrossRef]
- Uskov, V.I. Asymptotic solution of first-order equation with small parameter under the derivative with perturbed operator. Russ. Univ. Rep. Math. 2018, 23, 784–796, (In Russian, Abstract in English). [Google Scholar] [CrossRef]
- Vasil’eva, A.B.; Butuzov, V.F. Singularly Perturbed Equations in Critical Cases; Moscow University: Moscow, Russia, 1978; p. 106. [Google Scholar]
- Doolan, E.R.; Miller, J.J.H.; Schilders, W.H.A. Uniform Numerical Methods for Problems with Initial and Boundary Layers; Boole Press: Dublin, Ireland, 1980; 324p. [Google Scholar]
- Listovnichy, A.V. Concentration polarization of the ionite membrane-electrolyte solution system in the overlimiting mode. Electrochemistry 1991, 27, 316–323. [Google Scholar]
- Grafov, B.M.; Chernenko, A.A. The theory of the passage of a direct current through a solution of binary electrolyte. Dokl. Akad. Nauk. SSSR 1962, 153, 1110–1113. [Google Scholar]
- Nikonenko, V.V.; Urtenov, M.K. On a generalization of the electroneutrality condition. Russ. J. Electrochem. 1996, 32, 195–198. [Google Scholar]
- Kovalenko, S.A.; Urtenov, M.K. Asymptotic solution of the boundary value problem in the diffusion layer for the stationary system of Nernst—Planck—Poisson equations. Prospect. Sci. 2024, 6, 105–113. [Google Scholar]
- Urtenov, M.; Chubyr, N.; Gudza, V. Reasons for the Formation and Properties of Soliton-Like Charge Waves in Membrane Systems When Using Overlimiting Current Modes. Membranes 2020, 10, 189. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, C.A.J. Computational Techniques for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1991; 401p. [Google Scholar]
- Ilʹin, A.M. Matching of Asymptotic Expansions of Solutions of Boundary Value Problems; American Mathematical Society: Providence, RI, USA, 1992; 281p. [Google Scholar]
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Kudryavtsev, A.G.; Sapozhnikov, O.A. Determination of the exact solutions to the inhomogeneous Burgers equation with the use of the darboux transformation. Acoust. Phys. 2011, 57, 311–319. [Google Scholar] [CrossRef]
- Kushner, A.G.; Matviichuk, R.I. Exact solutions of the Burgers–Huxley equation via dynamics. J. Geom. Phys. 2020, 151, 103615. [Google Scholar] [CrossRef]
- Ryskin, N.M.; Trubetskov, D. Nonlinear Waves; Fizmatlit: Moscow, Russia, 2000; 296p. [Google Scholar]
- Trubetskov, D.I.; McHedlova, E.S.; Anfinogentov, V.G.; Ponomarenko, V.I.; Ryskin, N.M. Nonlinear waves, chaos and patterns in microwave electronic devices. Chaos 1996, 6, 358–367. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovalenko, S.; Kirillova, E.; Chekanov, V.; Uzdenova, A.; Urtenov, M. Analytical Solutions and Computer Modeling of a Boundary Value Problem for a Nonstationary System of Nernst–Planck–Poisson Equations in a Diffusion Layer. Mathematics 2024, 12, 4040. https://doi.org/10.3390/math12244040
Kovalenko S, Kirillova E, Chekanov V, Uzdenova A, Urtenov M. Analytical Solutions and Computer Modeling of a Boundary Value Problem for a Nonstationary System of Nernst–Planck–Poisson Equations in a Diffusion Layer. Mathematics. 2024; 12(24):4040. https://doi.org/10.3390/math12244040
Chicago/Turabian StyleKovalenko, Savva, Evgenia Kirillova, Vladimir Chekanov, Aminat Uzdenova, and Mahamet Urtenov. 2024. "Analytical Solutions and Computer Modeling of a Boundary Value Problem for a Nonstationary System of Nernst–Planck–Poisson Equations in a Diffusion Layer" Mathematics 12, no. 24: 4040. https://doi.org/10.3390/math12244040
APA StyleKovalenko, S., Kirillova, E., Chekanov, V., Uzdenova, A., & Urtenov, M. (2024). Analytical Solutions and Computer Modeling of a Boundary Value Problem for a Nonstationary System of Nernst–Planck–Poisson Equations in a Diffusion Layer. Mathematics, 12(24), 4040. https://doi.org/10.3390/math12244040







