A Frequency/Phase/Amplitude Estimator for Three-Phase Applications Operating at a Low Sampling Rate
Abstract
:1. Introduction
- Open-Loop Nature of the Algorithm: The proposed algorithm operates in an open-loop manner, ensuring unconditional stability due to the absence of feedback in its control loop. This characteristic is significantly beneficial for synchronizing power converters under weak grid conditions. Moreover, the algorithm does not require tuning control parameters, which is advantageous from an application standpoint. It also provides a rapid dynamic response, crucial for quick post-fault re-tracking capabilities, as demanded by modern grid codes;
- High Disturbance Rejection Capability: The algorithm demonstrates an exceptional ability to reject disturbances. In the context of the ever-increasing power quality issues in power systems, this feature is particularly advantageous for synchronization in three-phase applications;
- Robustness at Low Sampling Rates: The algorithm exhibits remarkable robustness even at low sampling rates. The analysis and design of synchronization systems at such rates have been largely overlooked in the existing literature, making this aspect of the algorithm particularly noteworthy.
2. Traditional Frequency Estimation Method
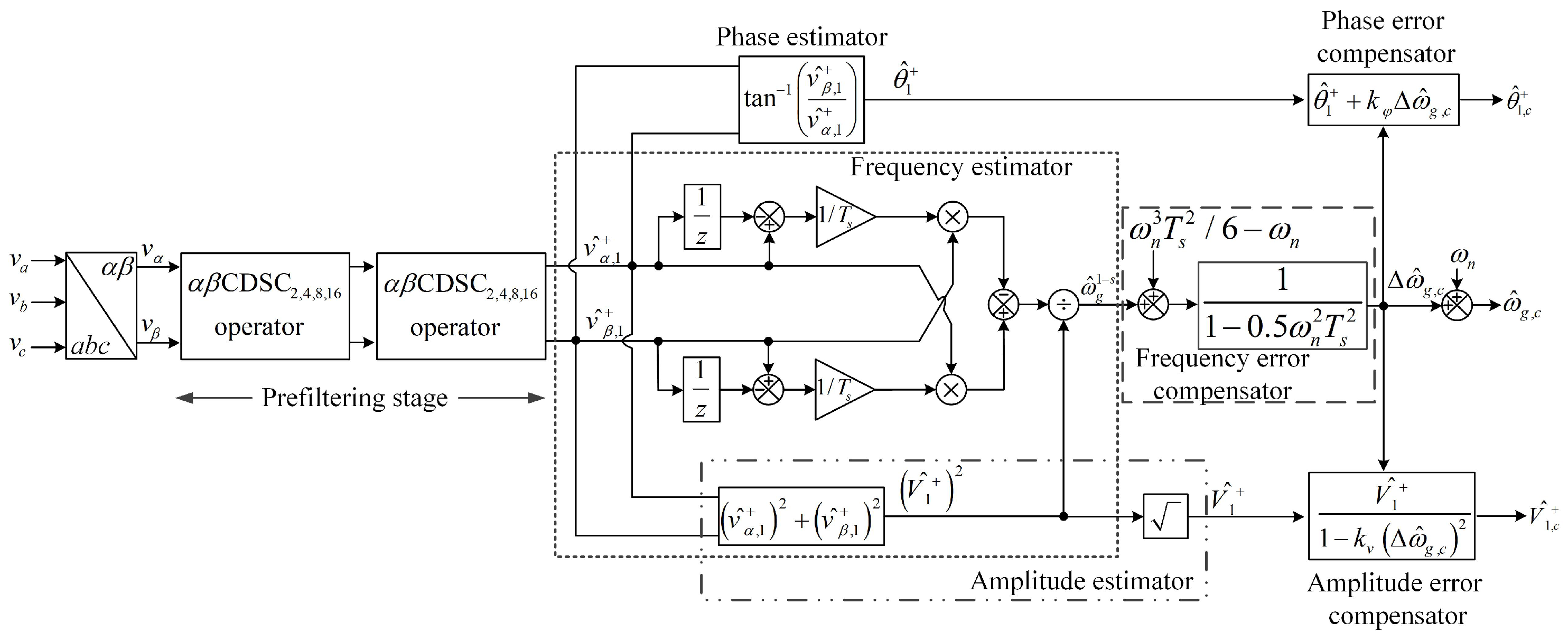
3. Frequency Error Correction
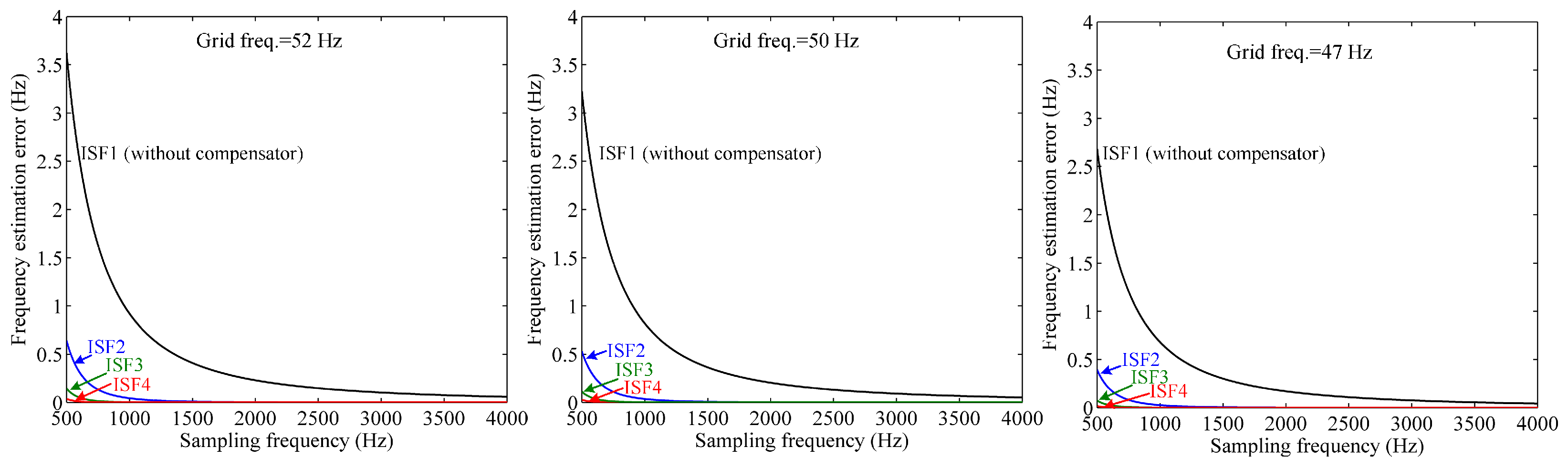
3.1. Frequency Error Correction Using Inverse Sine Function
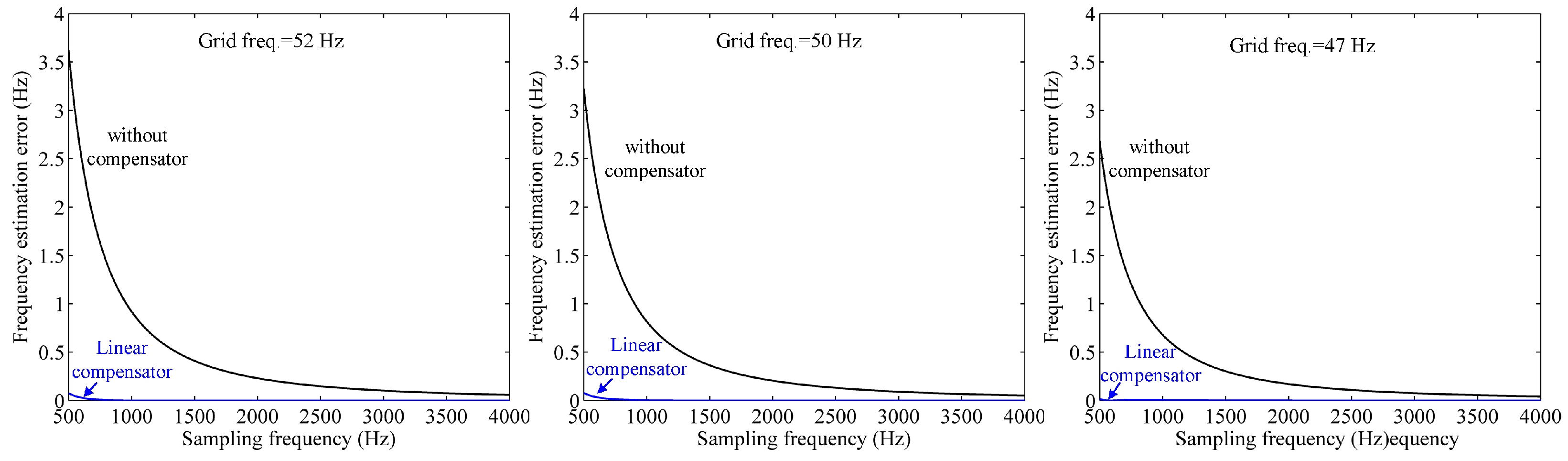
3.2. Frequency Error Correction Using a Linear Compensator
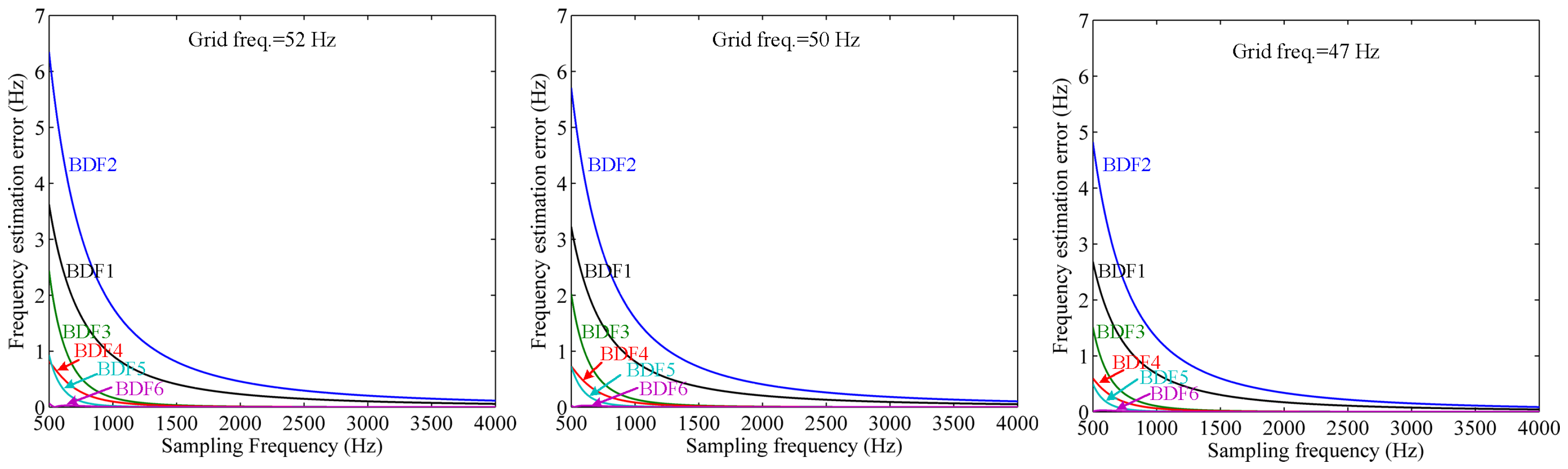
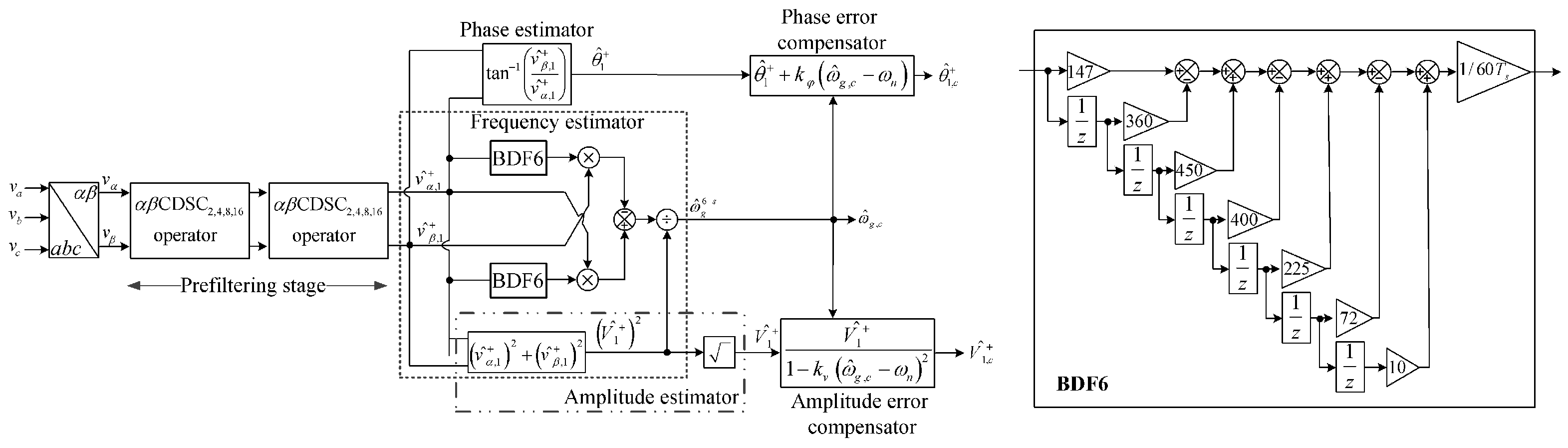
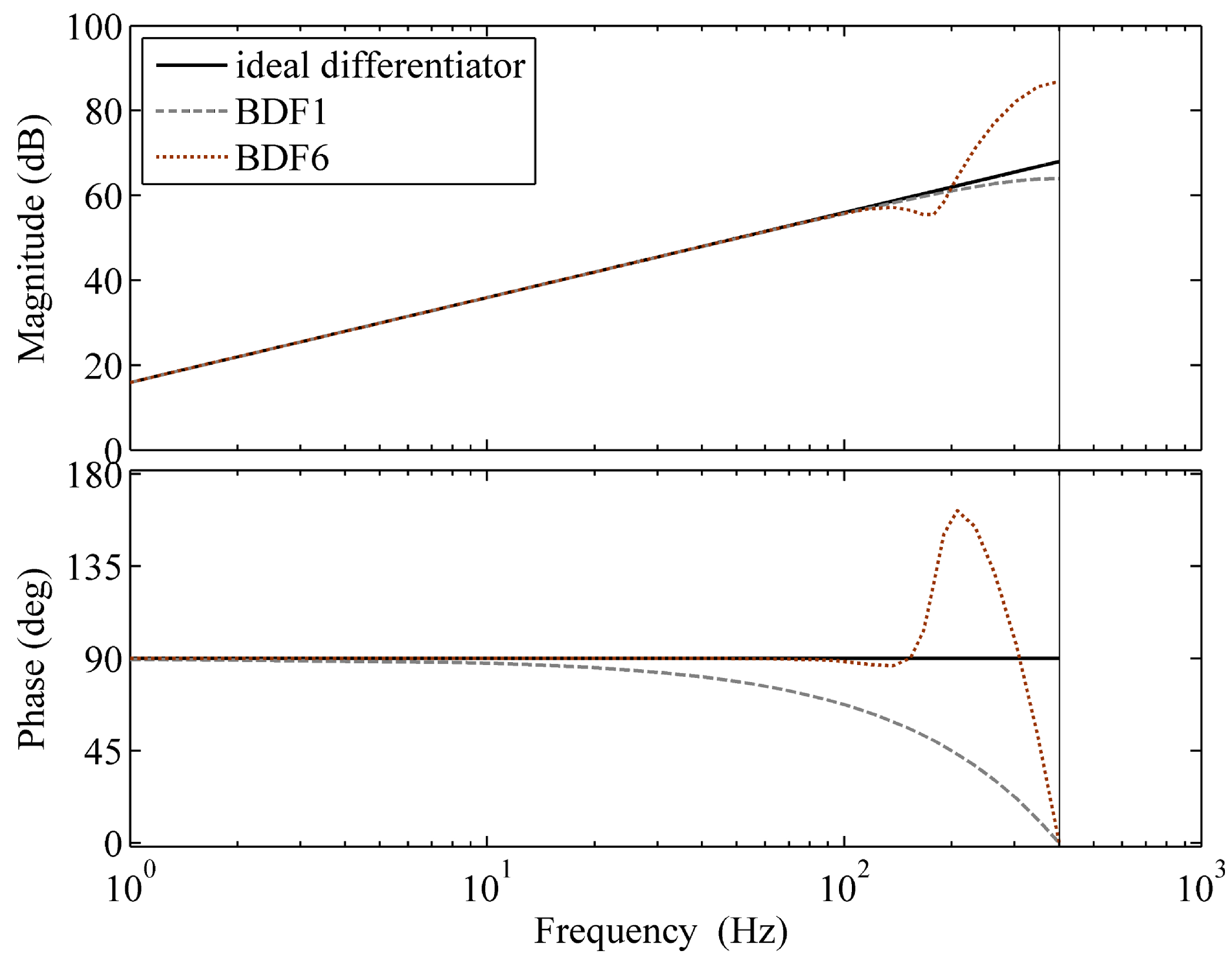
3.3. Frequency Error Correction Using s-Step () BDF
4. Filtering of the Grid Voltage Disturbance Components
5. Phase and Amplitude Estimation
6. Real-Time Simulation Results
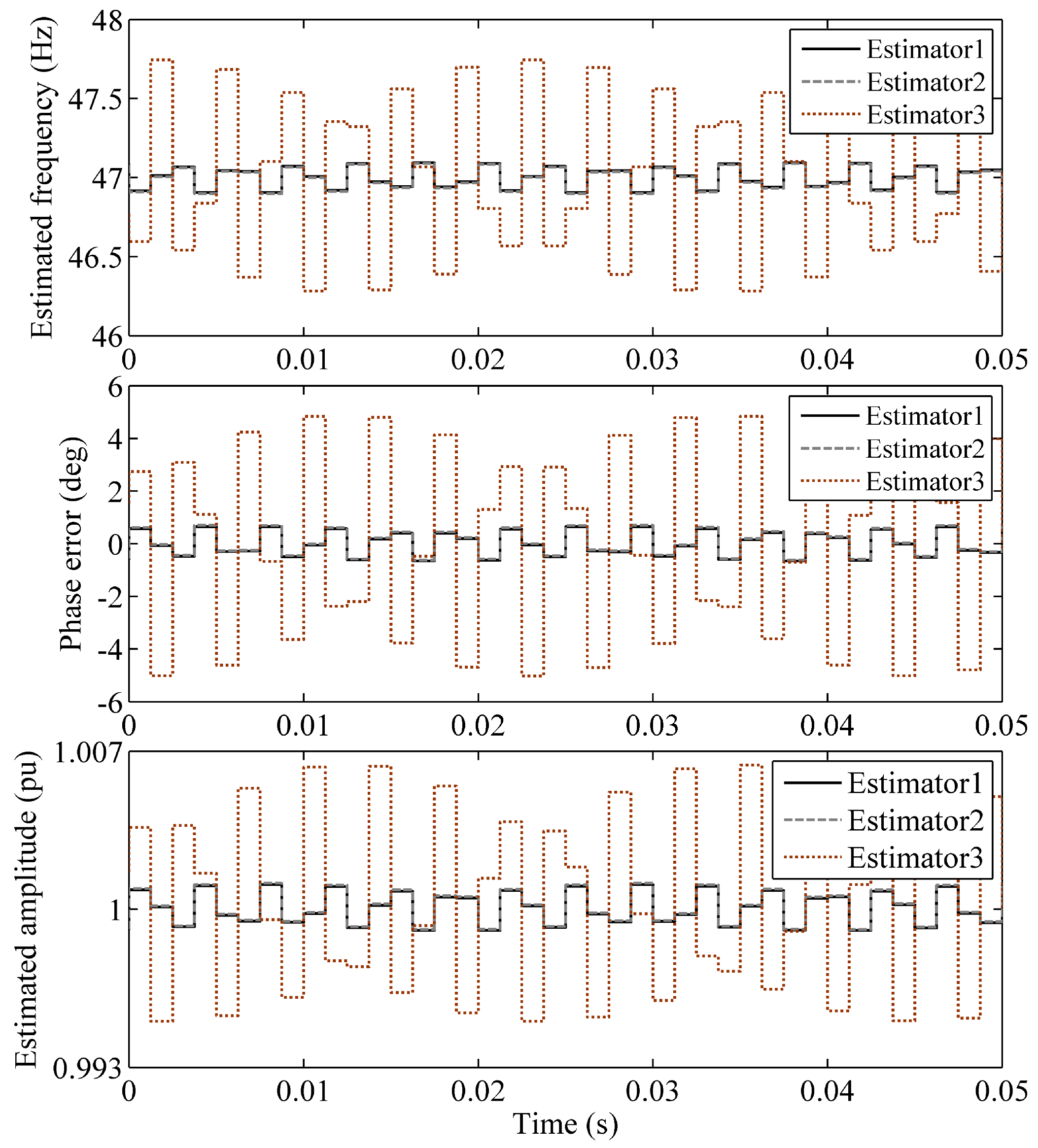
6.1. Comparison between Different Versions of the Proposed Estimator
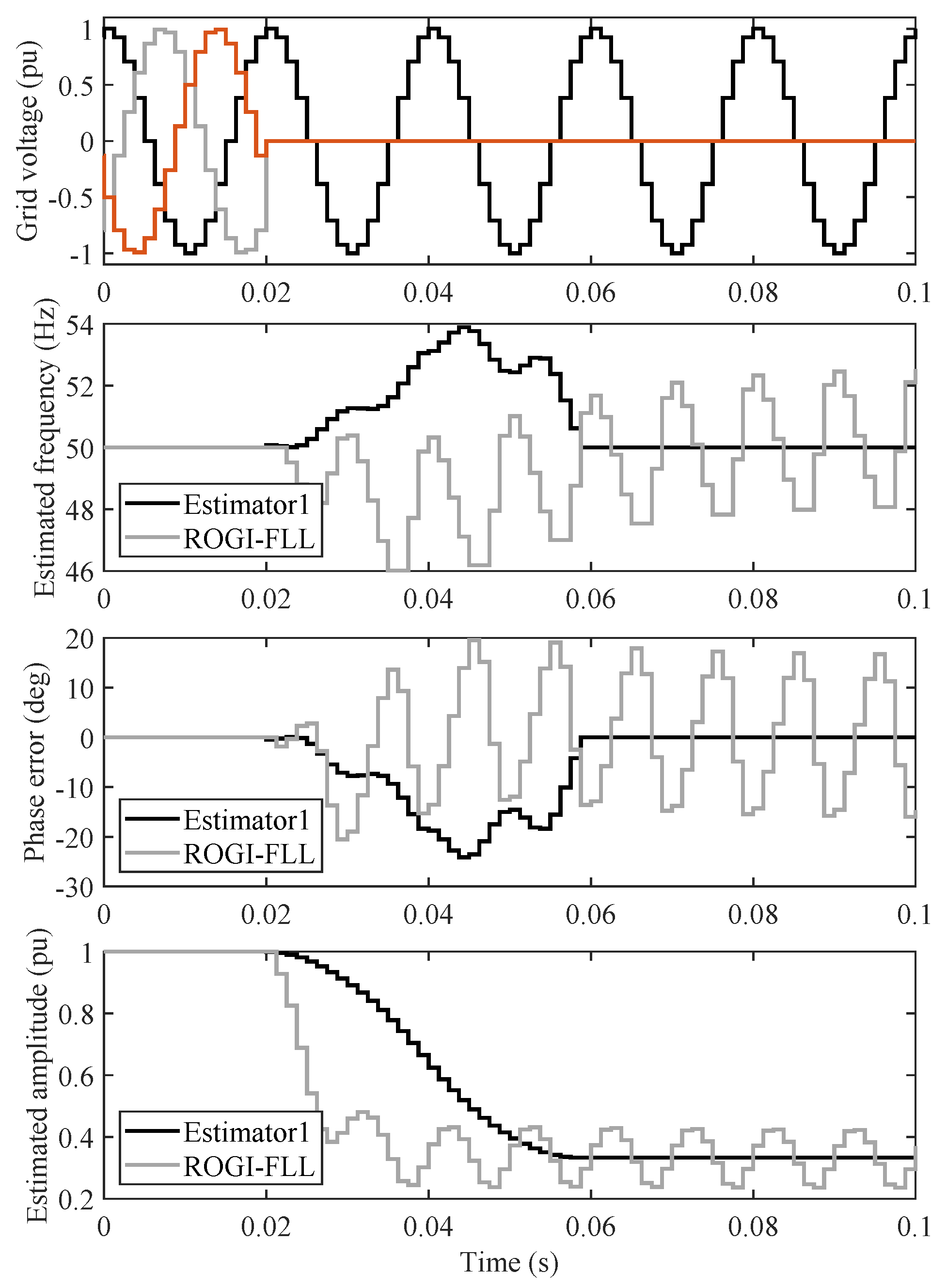
- Test Case 1: A step change of occurs in the grid voltage phase angle;
- Test Case 2: A step change of Hz occurs in the grid voltage frequency;
- Test Case 3: The grid voltage is harmonically distorted. In this test, the grid voltage components are pu, pu, and pu, resulting in a total harmonic distortion of approximately . The grid frequency is fixed at +47 Hz during this test. This test is conducted under off-nominal grid frequency because the prefiltering stage completely blocks harmonics when the grid frequency is at its nominal value;
- Test Case 4: An exaggeratedly large (0.5 pu) DC component is added to the “A” phase of the grid voltage. As in the previous test, the grid frequency is +47 Hz during this test.
6.2. Comparison with a Standard FLL
- Test Case A: The grid voltage is initially clean and free of noise or disturbances. Then, a 5% DC component is suddenly introduced to Phase A of the grid voltage;
- Test Case B: The grid voltage is in a balanced condition. Suddenly, a double-line-to-ground fault occurs;
- Test Case C: The grid voltage is distorted with harmonics of orders −5 and +7;
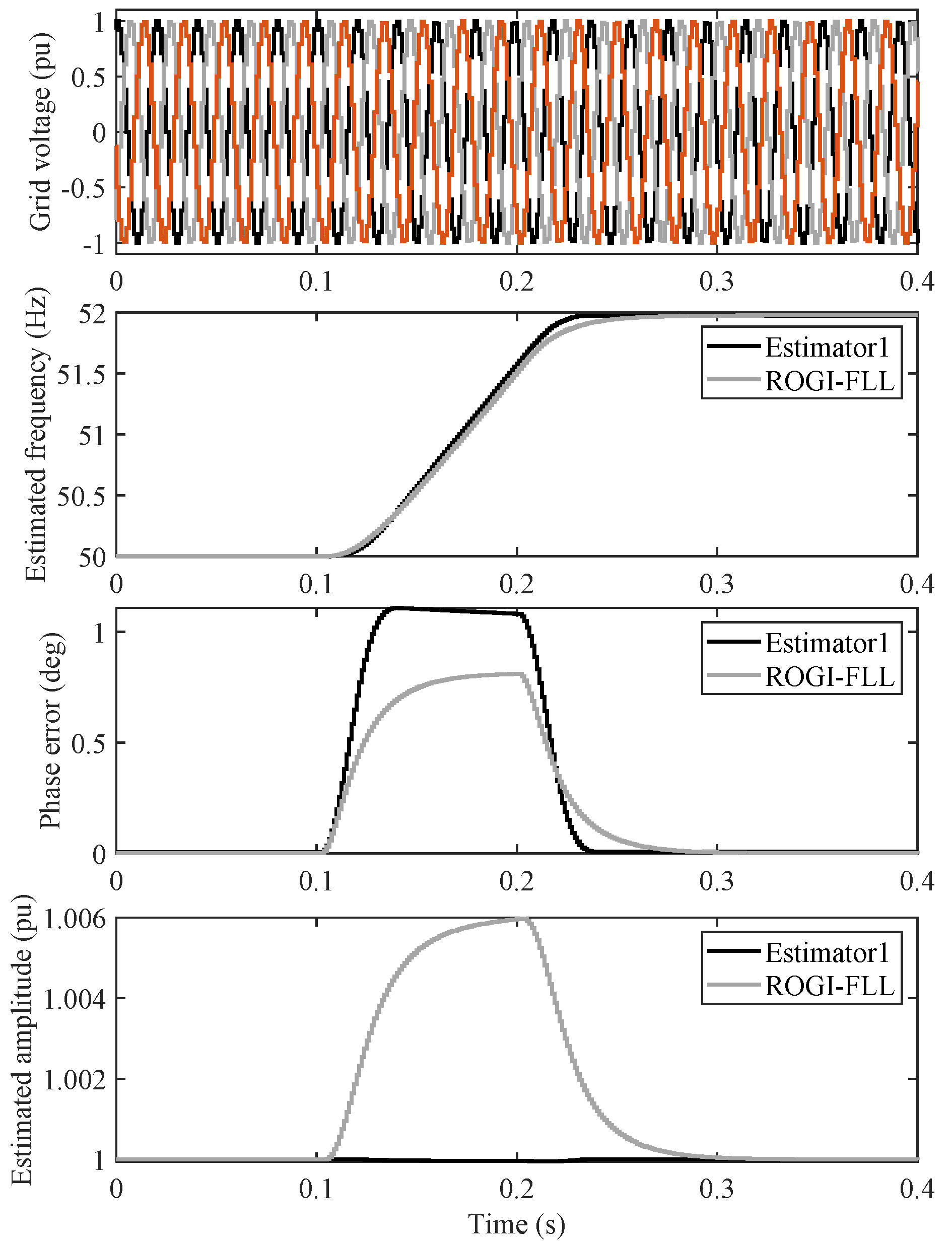
- Test Case D: The grid voltage undergoes a ramping change in the grid frequency at 20 Hz/s for a duration of 0.1 s.
- Estimator1 effectively filters the DC component. However, ROGI-FLL suffers from large fundamental-frequency oscillatory ripples in the presence of a DC component (see Figure 16);
- Estimator1 effectively handles unbalanced grid scenarios with a fast dynamic response. However, ROGI-FLL suffers from large double-frequency oscillatory errors under this condition (see Figure 17);
- Estimator1 effectively filters dominant harmonics of orders −5 and +7. In contrast, ROGI-FLL suffers from large harmonics at six times the fundamental frequency in this condition (see Figure 18);
- Both Estimator1 and ROGI-FLL have a phase offset error during the frequency ramping interval. This error is slightly larger for Estimator1 compared to ROGI-FLL. In contrast, the estimated amplitude of Estimator1, unlike ROGI-FLL, has no offset error during the frequency ramping interval, and the estimated frequency of Estimator1 converges to the final value faster (see Figure 19).
7. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smadi, I.A.; Atawi, I.E.; Ibrahim, A.A. An Improved Delayed Signal Cancelation for Three-Phase Grid Synchronization with DC Offset Immunity. Energies 2023, 16, 2873. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, F.; Li, S.; Zhao, W.; Chen, L.; Huang, S.; Wang, S.; Li, H. An Optimization of Least-Square Harmonic Phasor Estimators in Presence of Multi-Interference and Harmonic Frequency Variance. Energies 2023, 16, 3397. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, Y.; Wang, X.; Yu, Z.; Deng, T. Real-Time Wind Field Estimation and Pitot Tube Calibration Using an Extended Kalman Filter. Mathematics 2021, 9, 646. [Google Scholar] [CrossRef]
- Ullah, F.U.M.; Khan, N.; Hussain, T.; Lee, M.Y.; Baik, S.W. Diving Deep into Short-Term Electricity Load Forecasting: Comparative Analysis and a Novel Framework. Mathematics 2021, 9, 611. [Google Scholar] [CrossRef]
- Bizon, N.; Thounthong, P. A Simple and Safe Strategy for Improving the Fuel Economy of a Fuel Cell Vehicle. Mathematics 2021, 9, 604. [Google Scholar] [CrossRef]
- Hmad, J.; Houari, A.; Bouzid, A.E.M.; Saim, A.; Trabelsi, H. A Review on Mode Transition Strategies between Grid-Connected and Standalone Operation of Voltage Source Inverters-Based Microgrids. Energies 2023, 16, 5062. [Google Scholar] [CrossRef]
- Bindi, M.; Piccirilli, M.C.; Luchetta, A.; Grasso, F. A Comprehensive Review of Fault Diagnosis and Prognosis Techniques in High Voltage and Medium Voltage Electrical Power Lines. Energies 2023, 16, 7317. [Google Scholar] [CrossRef]
- Friedman, V. A zero crossing algorithm for the estimation of the frequency of a single sinuosoid in white noise. IEEE Trans. Signal Process. 1994, 42, 1565–1569. [Google Scholar] [CrossRef]
- Pauluk, M.; Piątek, P.; Baranowski, J. Efficient Zero-Value-Cross Detection for Single-Phase Mains-Powered Motors: A Comparative Study. Energies 2023, 16, 6298. [Google Scholar] [CrossRef]
- Wang, Y.F.; Li, Y.W. An overview of grid fundamental and harmonic components detection techniques. In Proceedings of the IEEE ECCE 2013, Denver, CO, USA, 15–19 September 2013; p. 51855192. [Google Scholar]
- Ciobotaru, M. Reliable Grid Condition Detection and Control of Single Phase Distributed Power Generation Systems. Ph.D. Thesis, Aalborg University, Aalborg, Denmark, 2009. [Google Scholar]
- Duric, M.B.; Durisic, Z.R. Frequency measurement in power networks in the presence of harmonics using Fourier and zero crossing technique. In Proceedings of the Power Tech 2005, St. Petersburg, Russia, 27–30 June 2005; pp. 1–6. [Google Scholar]
- Vainio, O.; Ovaska, S.J.; Polla, M. Adaptive filtering using multiplicative general parameters for zero-crossing detection. IEEE Trans. Ind. Electron. 2003, 50, 1340–1342. [Google Scholar] [CrossRef]
- Sozanski, K.; Szczesniak, P. Advanced Control Algorithm for Three-Phase Shunt Active Power Filter Using Sliding DFT. Energies 2023, 16, 1453. [Google Scholar] [CrossRef]
- Darwish, H.A.; Fikri, M. Practical considerations for recursive DFT implementation in numerical relays. IEEE Trans. Power Deliv. 2007, 22, 42–49. [Google Scholar] [CrossRef]
- Sadinezhad, I.; Agelidis, V.G. Slow sampling online optimization approach to estimate power system frequency. IEEE Trans. Smart Grid 2011, 2, 265–277. [Google Scholar] [CrossRef]
- Martin-Martinez, S.; Gomez-Lazaro, E.; Molina-Garcia, A.; Fuentes, J.A.; Vigueras-Rodrguez, A.; Plata, S.A. A new three-phase DPLL frequency estimator based on nonlinear weighted mean for power system disturbances. IEEE Trans. Power Deliv. 2013, 28, 179–187. [Google Scholar] [CrossRef]
- Dong, D.; Wen, B.; Boroyevich, D.; Mattavelli, P.; Xue, Y. Analysis of phase-locked loop low-frequency stability in three-phase grid-connected power converters considering impedance interactions. IEEE Trans. Ind. Electron. 2015, 62, 310–321. [Google Scholar] [CrossRef]
- Rodriguez, P.; Luna, A.; Etxeberria, I.; Teodorescu, R.; Blaabjerg, F. A stationary reference frame grid synchronization system for three-phase grid-connected power converters under adverse grid conditions. IEEE Trans. Power Electron. 2012, 27, 99–112. [Google Scholar] [CrossRef]
- Ghartemani, M.K.; Khajehoddin, S.A.; Jain, P.K.; Bakhshai, A. Problems of startup and phase jumps in PLL systems. IEEE Trans. Power Electron. 2012, 27, 1830–1838. [Google Scholar] [CrossRef]
- Yim, J.-S.; Sul, S.-K.; Bae, B.-H.; Patel, N.R.; Hiti, S. Modified current control schemes for high-performance permanent-magnet AC drives with low sampling to operating frequency ratio. IEEE Trans. Ind. Appl. 2009, 45, 763–771. [Google Scholar] [CrossRef]
- Freijedo, F.D.; Vidal, A.; Yepes, A.; Guerrero, J.; Lopez, O.; Malvar, J.; Doval-Gandoy, J. Tuning of synchronous-frame PI current controllers in grid-connected converters operating at a low sampling rate by MIMO root locus. IEEE Trans. Ind. Electron. 2015, 62, 5006–5017. [Google Scholar] [CrossRef]
- Suli, E.; Mayers, D.F. An Introduction to Numerical Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Wang, Y.F.; Li, Y.W. Grid synchronization PLL based on cascaded delayed signal cancellation. IEEE Trans. Power Electron. 2011, 26, 1987–1997. [Google Scholar] [CrossRef]
- Wang, Y.F.; Li, Y.W. Analysis and digital implementation of cascaded delayed-signal-cancellation PLL. IEEE Trans. Power Electron. 2011, 26, 1067–1080. [Google Scholar] [CrossRef]
- Laakso, T.I.; Valimaki, V.; Karjalainen, M.; Laine, U.K. Splitting the unit delay. IEEE Signal Process. Mag. 1996, 13, 30–60. [Google Scholar] [CrossRef]
- Golestan, S.; Freijedo, F.D.; Vidal, A.; Yepes, A.G.; Guerrero, J.M.; Doval-Gandoy, J. An efficient implementation of generalized delayed signal cancellation PLL. IEEE Trans. Power Electron. 2015, 31, 1085–1094. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C.; Abusorrah, A.M.; Al-Turki, Y. Linear Time-Periodic Modeling, Examination, and Performance Enhancement of Grid Synchronization Systems With DC Component Rejection/Estimation Capability. IEEE Trans. Power Electron. 2021, 36, 4237–4253. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C.; Abusorrah, A.M.; Al-Turki, Y. A Study on Three-Phase FLLs. IEEE Trans. Power Electron. 2019, 34, 213–224. [Google Scholar] [CrossRef]
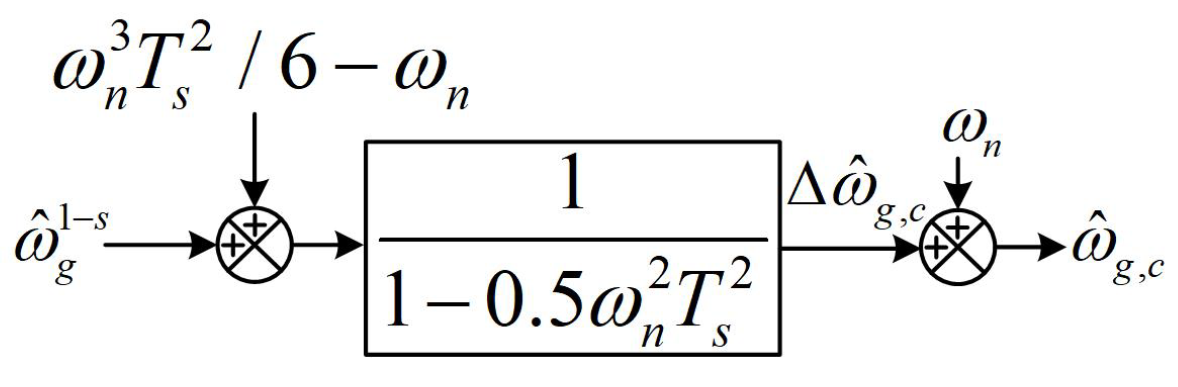
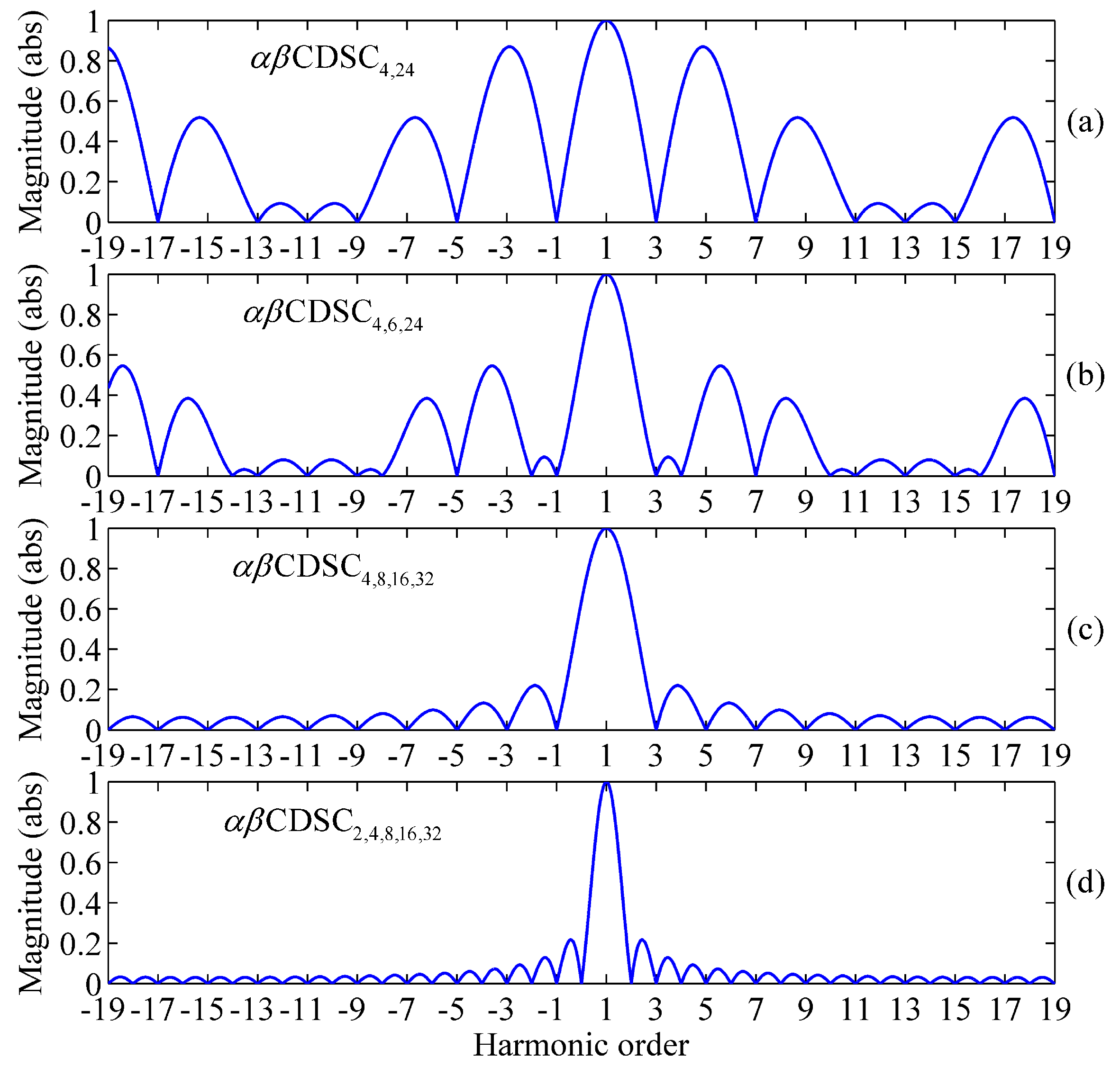








| Grid Harmonic Pattern | Proper CDSC | |
|---|---|---|
| Known | non-triplen odd harmonics of order , , , , , | |
| symmetrical | ||
| odd harmonic components | ||
| asymmetrical | ||
| Unknown | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abusorrah, A.M.; Sepahvand, H. A Frequency/Phase/Amplitude Estimator for Three-Phase Applications Operating at a Low Sampling Rate. Mathematics 2024, 12, 363. https://doi.org/10.3390/math12030363
Abusorrah AM, Sepahvand H. A Frequency/Phase/Amplitude Estimator for Three-Phase Applications Operating at a Low Sampling Rate. Mathematics. 2024; 12(3):363. https://doi.org/10.3390/math12030363
Chicago/Turabian StyleAbusorrah, Abdullah M., and Hamed Sepahvand. 2024. "A Frequency/Phase/Amplitude Estimator for Three-Phase Applications Operating at a Low Sampling Rate" Mathematics 12, no. 3: 363. https://doi.org/10.3390/math12030363
APA StyleAbusorrah, A. M., & Sepahvand, H. (2024). A Frequency/Phase/Amplitude Estimator for Three-Phase Applications Operating at a Low Sampling Rate. Mathematics, 12(3), 363. https://doi.org/10.3390/math12030363






