The Integrability and Modification to an Auxiliary Function Method for Solving the Strain Wave Equation of a Flexible Rod with a Finite Deformation
Abstract
1. Introduction
2. Painlevé Analysis
3. Proposed Method
3.1. Method Description
- (a)
- (b)
Algorithm
- Step 2: Assuming the reduced Equation (9) has a solutionwhere is a solution of the auxiliary equation
- Step 3: Determining the positive integer N by balancing the highest power of the non-linear term with the highest order derivative terms in the auxiliary Equation (9). After some calculations, the highest order derivative term and highest power of the non-linear term with positive integer , in the reduced equation are given by
- Case I: If , then we have , respectively, and go directly to the next step.
- Case II: If , we perform the transformation to the reduced equation and assume its solution admits the form (21), i.e.,Then, go to the next step.
- (a)
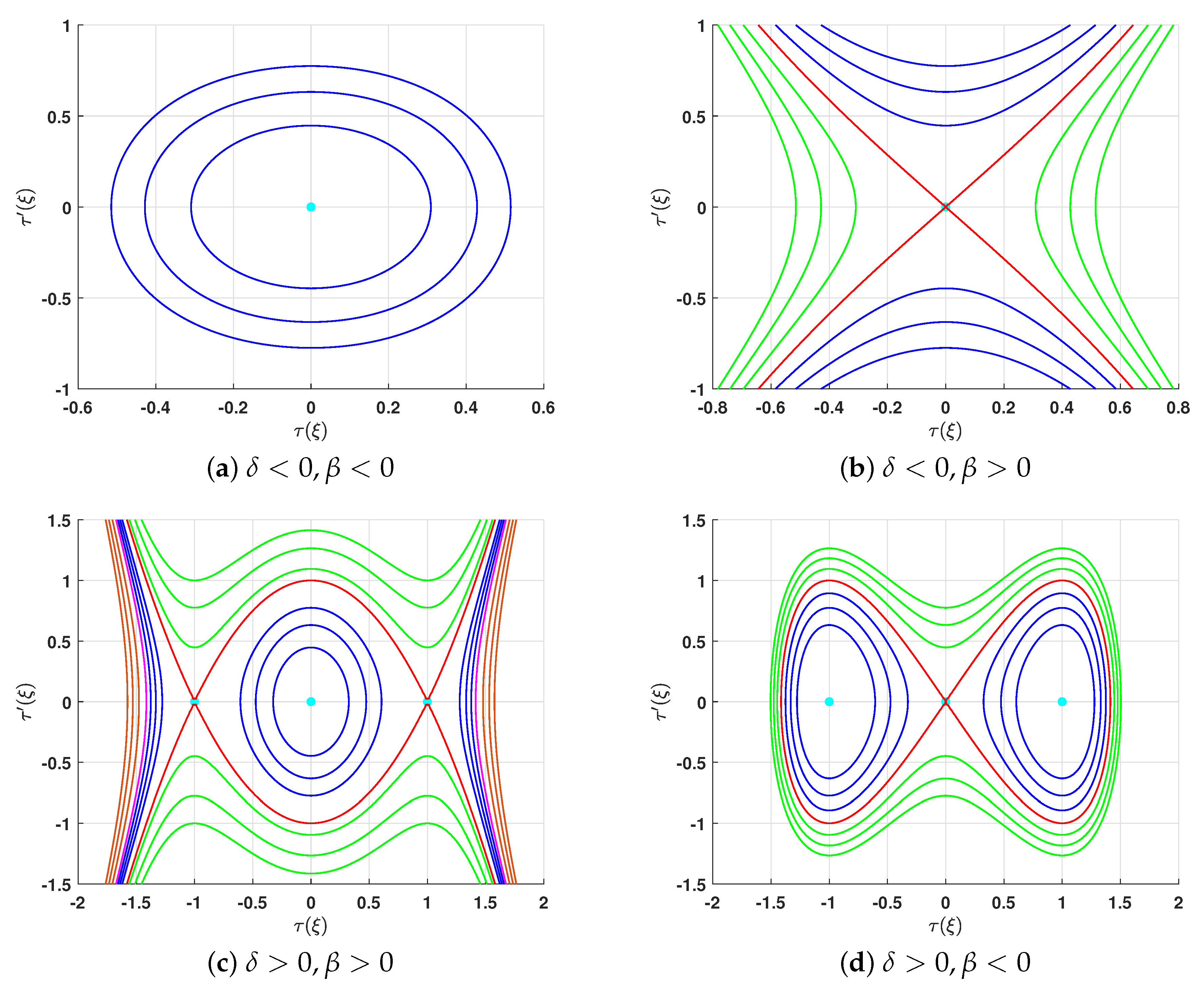
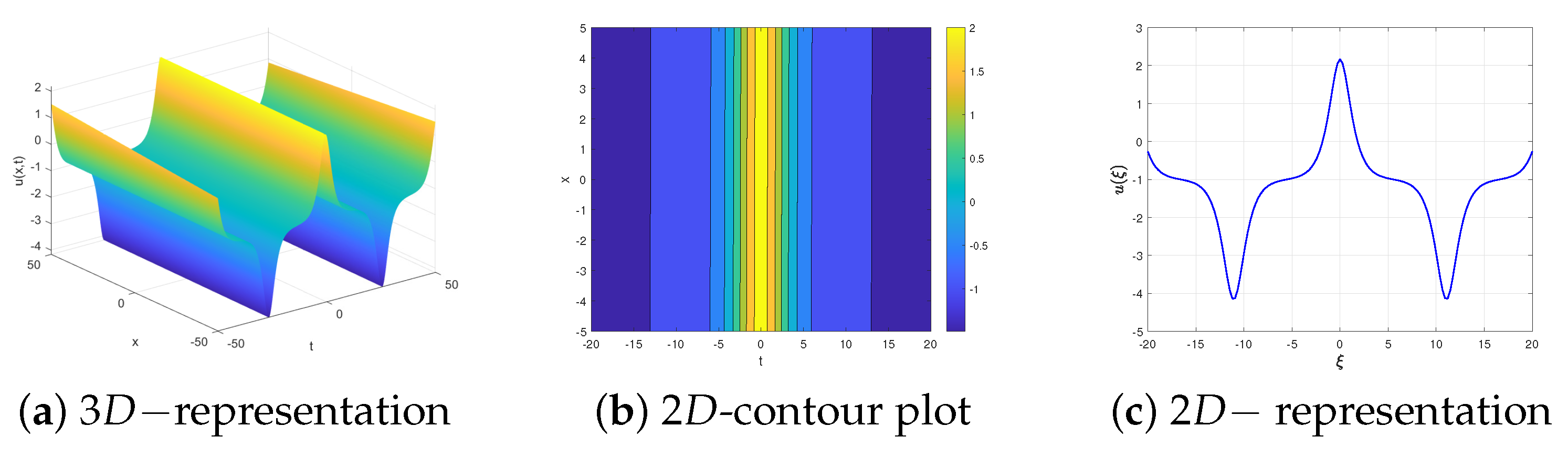
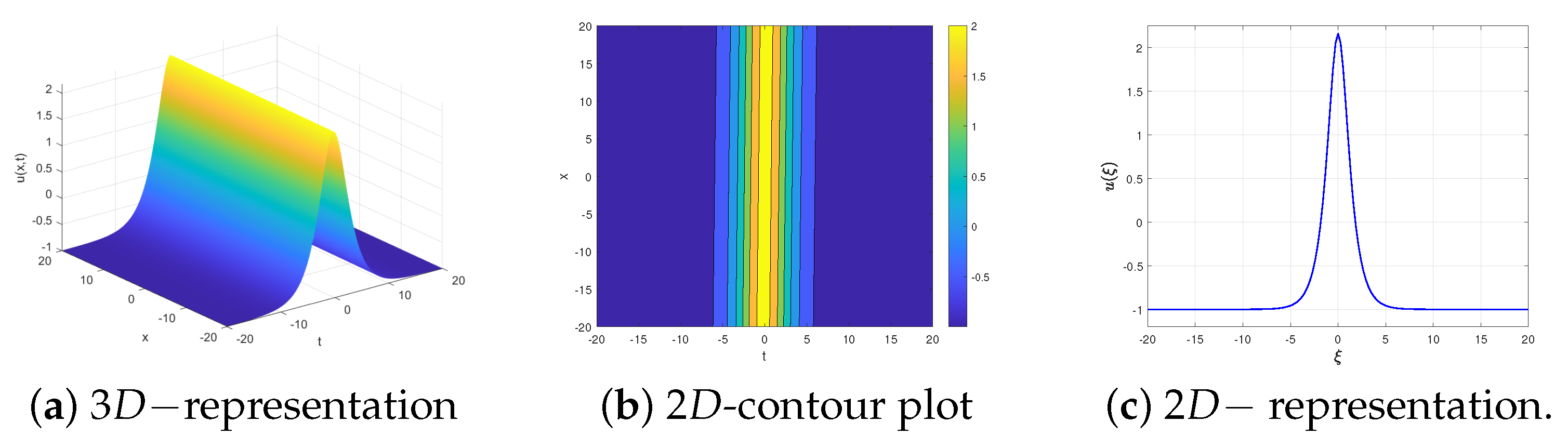
- It is utilized only to construct real (not complex) wave solutions for the given NPDE, because these solutions are constructed by integrating the conserved quantities along all possible intervals of real wave propagation. Moreover, the entering of the concept of the interval of real wave propagation intervals enables us to construct all possible wave solutions that are completely different from mathematical and physical points of view. Let us clarify this point. For the choice and , there are two solutions. One of them is periodic as illustrated by row 2 in Table 1 while the other is unbounded as outlined by row 6 in Table 3 row. Thus, we have two completely different solutions from mathematical and physics points of view for the same conditions of the parameters.
- (b)
- It enables us to know in advance the types of solutions. For example in Table 1, the first three cases are periodic solutions because they are related to periodic orbits in phase portrait while the fourth case is a super periodic solution since it corresponds to the super periodic orbit, see Figure 1. Therefore, the assumed solution can be viewed as a combination of periodic solutions or super periodic solutions, respectively. For this reason, we know the obtained solution will be periodic or supper periodic.
- (c)
- Thanks to employing bifurcation analysis, we were able to isolate all possible bounded solutions that are required and significant in real-world problems.
4. Application
- 1.
- If , Equation (1) owns the following new solution
- 2.
- If , we introduce a novel solution for Equation (1) in the form
- 3.
- If , the governing Equation (1) has a new solution
- 4.
- If , thenis a new solution for Equation (1).
- Case B: For the choice , must be negative, i.e., and hence . Therefore, the only working cases in Table 1 are Case 3 and Case 4. Let us consider them individually.
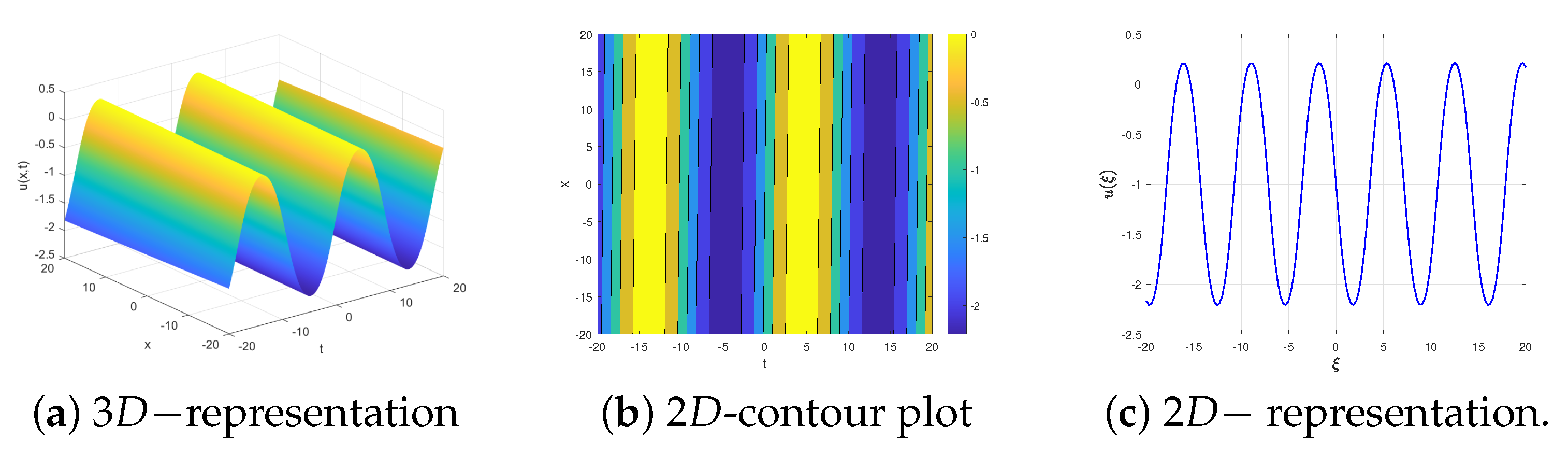
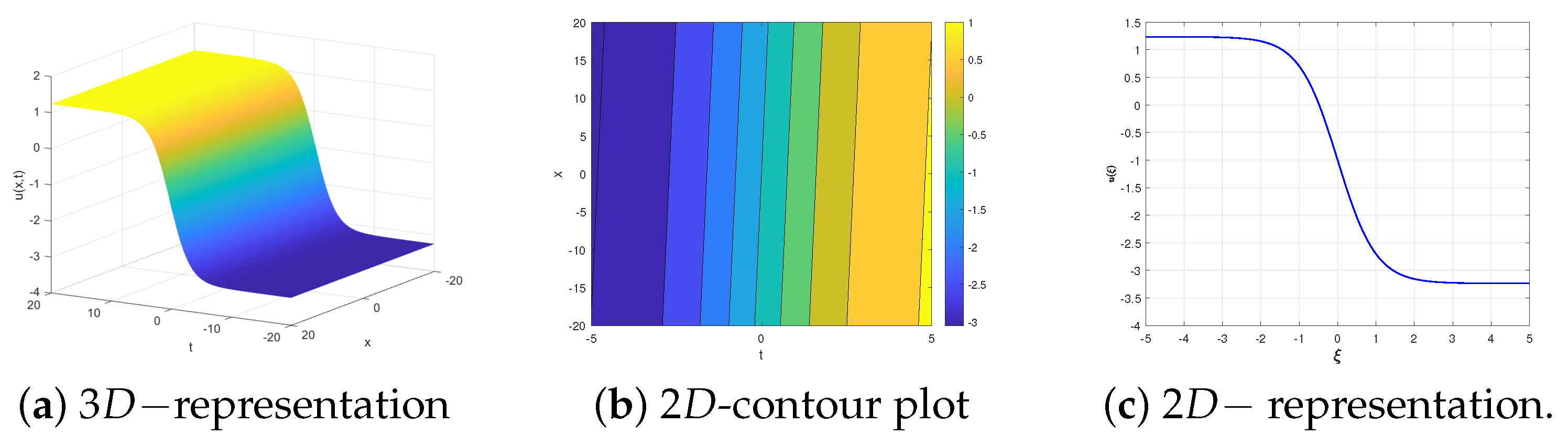
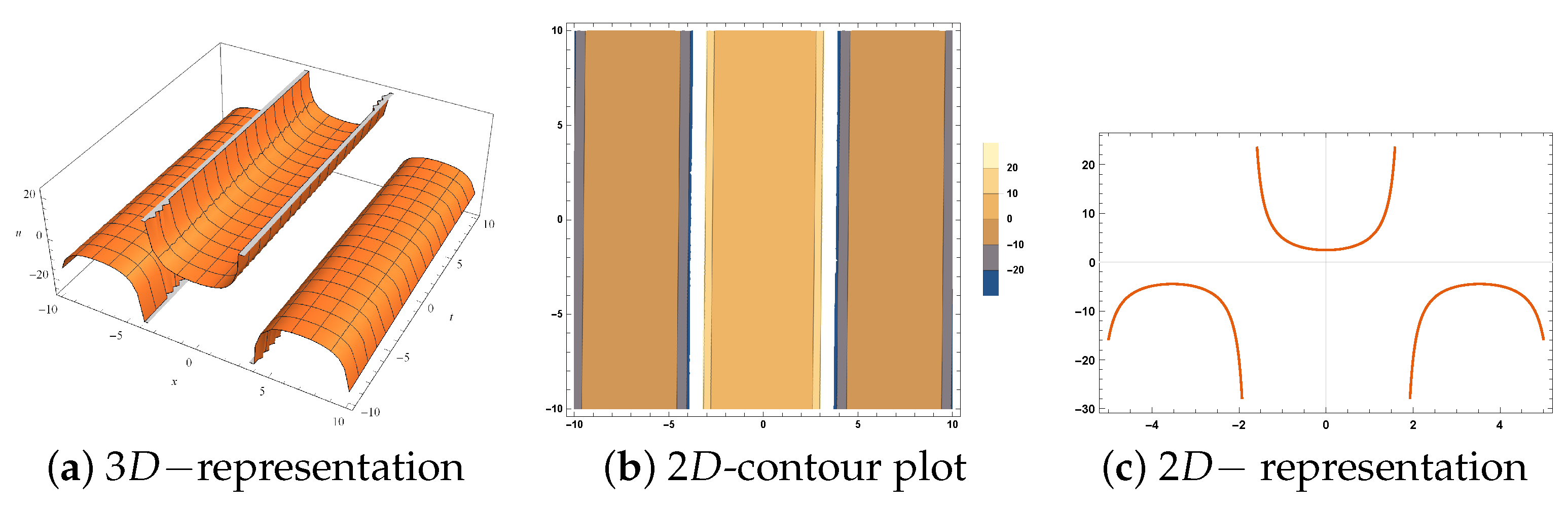
5. Physical Interpretations
- 1.
- 2.
- 1.
- 2.
6. Conclusions
- (a)
- It is only applied to construct real (not complex) wave solutions for a large class of partial differential equations by integrating the conserved quantities along the intervals of real wave propagation. Moreover, with the same conditions on the parameters and different intervals of real wave propagation, distinct solutions from mathematical and physical points of view are constructed. For instance, for the choice and , there are two solutions. One of them is periodic as illustrated by row 2 in Table 1, while the other is unbounded as outlined by row 6 in Table 3 row.
- (b)
- It enables us to know the kinds of solutions before establishing them.
- (c)
- We can isolate all bounded wave solutions, which is useful in real applications.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Step 1 (Dominate behavior): The leading order term in Laurent series (A2) is assumed to be
- Step 2 (Resonances): The resonances are defined as the powers at which the arbitrary functions appear in the Laurent series. The resonance can be determined by insertinginto Equation (A1) and comparing different powers of . Notice that all the resonances are non-negative integers except the resonance which refers to the arbitrariness of . Additionally, the resonance indicates the coefficient of the leading term is arbitrary. If all the values of resonances are non-negative except , we are going to the next step.
- Step 3 (Compatibility conditions): This step aims to check the existence of a sufficient number of arbitrary functions in the Laurent series (A2). This can be performed by inserting the expressioninto Equation (A1) and testing the existence of arbitrary functions corresponding to the obtained resonances in Step 2, where is the largest value of the resonances. If the compatibility conditions are satisfied then, the given partial differential equation has Painlevé property. Consequently, it is integrable in Painlevé sense, or sometimes it is named Painlevé integrable.
References
- Wang, M.; Zhou, Y.; Li, Z. Application of a homogeneous balance method to exact solutions of non-linear equations in mathematical physics. Phys. Lett. A 1996, 216, 67–75. [Google Scholar] [CrossRef]
- Elsherbeny, A.M.; Mirzazadeh, M.; Akbulut, A.; Arnous, A.H. Optical solitons of the perturbation Fokas–Lenells equation by two different integration procedures. Optik 2023, 273, 170382. [Google Scholar] [CrossRef]
- Yin, T.; Xing, Z.; Pang, J. Modified Hirota bilinear method to (3+1)-D variable coefficients generalized shallow water wave equation. Nonlinear Dyn. 2023, 87, 2529–2540. [Google Scholar] [CrossRef]
- Biswas, S.; Ghosh, U.; Raut, S. Construction of fractional granular model and bright, dark, lump, breather types soliton solutions using Hirota bilinear method. Chaos Solitons Fractals 2023, 172, 113520. [Google Scholar] [CrossRef]
- Vakhnenko, V.; Parkes, E.; Morrison, A. A Bäcklund transformation and the inverse scattering transform method for the generalised Vakhnenko equation. Chaos Solitons Fractals 2003, 17, 683–692. [Google Scholar] [CrossRef]
- Fan, F.C.; Xu, Z.G.; Shi, S.Y. Soliton, breather, rogue wave and continuum limit for the spatial discrete Hirota equation by Darboux–Bäcklund transformation. Nonlinear Dyn. 2023, 111, 10393–10405. [Google Scholar] [CrossRef]
- Ali, M.R.; Khattab, M.A.; Mabrouk, S. Optical soliton solutions for the integrable Lakshmanan-Porsezian-Daniel equation via the inverse scattering transformation method with applications. Optik 2023, 272, 170256. [Google Scholar] [CrossRef]
- Ali, M.R.; Khattab, M.A.; Mabrouk, S. Travelling wave solution for the Landau-Ginburg-Higgs model via the inverse scattering transformation method. Nonlinear Dyn. 2023, 111, 7687–7697. [Google Scholar] [CrossRef]
- He, C.H.; Liu, C. Variational principle for singular waves. Chaos Solitons and Fractals 2023, 172, 113566. [Google Scholar]
- Wang, Y.; Gepreel, K.A.; Yang, Y.J. Variational principles for fractal Boussinesq-like B (m, n) equation. Fractals 2023, 31, 1–8. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D. Elliptic function and solitary wave solutions of the higher-order non-linear Schrödinger dynamical equation with fourth-order dispersion and cubic-quintic non-linearity and its stability. Eur. Phys. J. Plus 2017, 132, 371. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.; Lu, D.; Wang, J. Travelling wave solutions of Drinfel’d–Sokolov–Wilson, Whitham–Broer–Kaup and (2+1)-dimensional Broer–Kaup–Kupershmit equations and their applications. Chin. J. Phys. 2017, 55, 780–797. [Google Scholar] [CrossRef]
- Rehman, H.U.; Awan, A.U.; Allahyani, S.A.; Tag-ElDin, E.M.; Binyamin, M.A.; Yasin, S. Exact solution of paraxial wave dynamical model with Kerr Media by using ϕ6 model expansion technique. Results Phys. 2022, 42, 105975. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Arshad, M.; Lu, D. Dispersive optical solitary wave solutions of strain wave equation in micro-structured solids and its applications. Phys. Stat. Mech. Its Appl. 2020, 540, 123122. [Google Scholar] [CrossRef]
- El-Ganaini, S. Solitons and other solutions to a new coupled non-linear Schrodinger type equation. J. Egypt. Math. Soc. 2017, 25, 19–27. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Wazwaz, A.M. New exact solitary wave solutions of the strain wave equation in microstructured solids via the generalized exponential rational function method. Eur. Phys. J. Plus 2020, 135, 870. [Google Scholar] [CrossRef]
- Jadaun, V.; Kumar, S. Lie symmetry analysis and invariant solutions of (3+1)-dimensional Calogero–Bogoyavlenskii–Schiff equation. Nonlinear Dyn. 2018, 93, 349–360. [Google Scholar] [CrossRef]
- Tu, J.M.; Tian, S.F.; Xu, M.J.; Zhang, T.T. On Lie symmetries, optimal systems and explicit solutions to the Kudryashov–Sinelshchikov equation. Appl. Math. Comput. 2016, 275, 345–352. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Ali, A.; Baleanu, D.; Althobaiti, S.; Alkafafy, M. Dispersive analytical wave solutions of the strain waves equation in microstructured solids and Lax’fifth-order dynamical systems. Phys. Scr. 2021, 96, 105203. [Google Scholar] [CrossRef]
- Ali, K.K.; Tarla, S.; Ali, M.R.; Yusuf, A.; Yilmazer, R. Physical wave propagation and dynamics of the Ivancevic option pricing model. Results Phys. 2023, 52, 106751. [Google Scholar] [CrossRef]
- Siddique, I.; Mehdi, K.B.; Jaradat, M.M.; Zafar, A.; Elbrolosy, M.E.; Elmandouh, A.A.; Sallah, M. Bifurcation of some new traveling wave solutions for the time–space M-fractional NEW equation via three altered methods. Results Phys. 2022, 41, 105896. [Google Scholar] [CrossRef]
- Rahman, T.; Tarofder, S.; Orani, M.; Akter, J.; Mamun, A. (3+1)-dimensional cylindrical dust ion-acoustic solitary waves in dusty plasma. Results Phys. 2023, 53, 106907. [Google Scholar] [CrossRef]
- Elbrolosy, M.; Elmandouh, A. Bifurcation and new traveling wave solutions for (2+1)-dimensional non-linear Nizhnik–Novikov–Veselov dynamical equation. Eur. Phys. J. Plus 2020, 135, 533. [Google Scholar] [CrossRef]
- Elbrolosy, M.; Elmandouh, A. Construction of new traveling wave solutions for the (2+1) dimensional extended Kadomtsev-Petviashvili equation. J. Appl. Anal. Comput. 2022, 12, 533–550. [Google Scholar] [CrossRef]
- Elbrolosy, M.; Elmandouh, A. Dynamical behaviour of nondissipative double dispersive microstrain wave in the microstructured solids. Eur. Phys. J. Plus 2021, 136, 955. [Google Scholar] [CrossRef]
- Elmandouh, A. Integrability, qualitative analysis and the dynamics of wave solutions for Biswas–Milovic equation. Eur. Phys. J. Plus 2021, 136, 638. [Google Scholar] [CrossRef]
- Elbrolosy, M. Qualitative analysis and new soliton solutions for the coupled non-linear Schrödinger type equations. Phys. Scr. 2021, 96, 125275. [Google Scholar] [CrossRef]
- Elmandouh, A.; Elbrolosy, M. Integrability, variational principal, bifurcation and new wave solutions for Ivancevic option pricing model. J. Math. 2022, 2, 3. [Google Scholar]
- El-Dessoky, M.; Elmandouh, A. Qualitative analysis and wave propagation for Konopelchenko-Dubrovsky equation. Alex. Eng. J. 2023, 67, 525–535. [Google Scholar] [CrossRef]
- Adeyemo, O.D.; Khalique, C.M.; Gasimov, Y.S.; Villecco, F. Variational and non-variational approaches with Lie algebra of a generalized (3+1)-dimensional non-linear potential Yu-Toda-Sasa-Fukuyama equation in Engineering and Physics. Alex. Eng. J. 2023, 63, 17–43. [Google Scholar] [CrossRef]
- Wang, K. Exact travelling wave solution for the local fractional Camassa-Holm-Kadomtsev-Petviashvili equation. Alex. Eng. J. 2023, 63, 371–376. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Zaghrout, A.A.; Ahmed, H.M. Travelling wave solutions for the doubly dispersive equation using improved modified extended tanh-function method. Alex. Eng. J. 2022, 61, 7987–7994. [Google Scholar] [CrossRef]
- Ali, K.K.; Osman, M.; Abdel-Aty, M. New optical solitary wave solutions of Fokas-Lenells equation in optical fiber via Sine-Gordon expansion method. Alex. Eng. J. 2020, 59, 1191–1196. [Google Scholar] [CrossRef]
- Rehman, H.U.; Awan, A.U.; Tag-ElDin, E.M.; Alhazmi, S.E.; Yassen, M.F.; Haider, R. Extended hyperbolic function method for the (2+1)-dimensional non-linear soliton equation. Results Phys. 2022, 40, 105802. [Google Scholar] [CrossRef]
- Rehman, H.; Seadawy, A.R.; Younis, M.; Rizvi, S.; Anwar, I.; Baber, M.; Althobaiti, A. Weakly non-linear electron-acoustic waves in the fluid ions propagated via a (3+1)-dimensional generalized Korteweg–de-Vries–Zakharov–Kuznetsov equation in plasma physics. Results Phys. 2022, 33, 105069. [Google Scholar] [CrossRef]
- Liu, Z.F.; Zhang, S.Y. Solitary waves in finite deformation elastic circular rod. Appl. Math. Mech. 2006, 27, 1255–1260. [Google Scholar] [CrossRef]
- Porubov, A.V.; Velarde, M.G. On non-linear waves in an elastic solid. Comptes Rendus L’AcadÉMie Des-Sci.-Ser.-Iib-Mech.-Phys.-Astron. 2000, 328, 165–170. [Google Scholar]
- Liu, Z.; Zhang, S. Nonlinear waves and periodic solution in finite deformation elastic rod. Acta Mech. Solida Sin. 2006, 19, 1–8. [Google Scholar] [CrossRef]
- Zhang, S.y.; Liu, Z.f. Three kinds of non-linear dispersive waves in elastic rods with finite deformation. Appl. Math. Mech. 2008, 29, 909–917. [Google Scholar] [CrossRef]
- Fu, Z.; Liu, S.; Liu, S. New transformations and new approach to find exact solutions to non-linear equations. Phys. Lett. A 2002, 299, 507–512. [Google Scholar] [CrossRef]
- Aljuaidan, A.; Elbrolosy, M.; Elmandouh, A. Nonlinear Wave Propagation for a Strain Wave Equation of a Flexible Rod with Finite Deformation. Symmetry 2023, 15, 650. [Google Scholar] [CrossRef]
- Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction; Wiley Interscience: Hoboken, NJ, USA, 1989. [Google Scholar]
- Zhou, T.Y.; Tian, B.; Chen, Y.Q.; Shen, Y. Painlevé analysis, auto-Bäcklund transformation and analytic solutions of a (2+1)-dimensional generalized Burgers system with the variable coefficients in a fluid. Nonlinear Dyn. 2022, 108, 2417–2428. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Two new Painlevé integrable KdV–Calogero–Bogoyavlenskii–Schiff (KdV-CBS) equation and new negative-order KdV-CBS equation. Nonlinear Dyn. 2021, 104, 4311–4315. [Google Scholar] [CrossRef]
- Singh, S.; Ray, S.S. Integrability and new periodic, kink-antikink and complex optical soliton solutions of (3+1)-dimensional variable coefficient DJKM equation for the propagation of non-linear dispersive waves in inhomogeneous media. Chaos Solitons Fractals 2023, 168, 113184. [Google Scholar] [CrossRef]
- Akbar, Y.; Afsar, H.; Al-Mubaddel, F.S.; Abu-Hamdeh, N.H.; Abusorrah, A.M. On the solitary wave solution of the viscosity capillarity van der Waals p-system along with Painlevé analysis. Chaos Solitons Fractals 2021, 153, 111495. [Google Scholar] [CrossRef]
- Nemytskii, V.V. Qualitative Theory of Differential Equations; Princeton University Press: Princeton, NJ, USA, 2015; Volume 2083. [Google Scholar]
- Sirendaoreji. A new auxiliary equation and exact travelling wave solutions of non-linear equations. Phys. Lett. A 2006, 356, 124–130. [Google Scholar] [CrossRef]
- Li, Z. Bifurcation, phase portrait, chaotic pattern and traveling wave solution of the fractional perturbed Chen-Lee-Liu model with beta time-space derivative in fiber optics. Fractals 2023, 31, 2340192. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C. Bifurcation, phase portrait and traveling wave solution of time-fractional thin-film ferroelectric material equation with beta fractional derivative. Phys. Lett. A 2023, 484, 129080. [Google Scholar] [CrossRef]
- Li, Z.; Huang, C.; Wang, B. Phase portrait, bifurcation, chaotic pattern and optical soliton solutions of the Fokas-Lenells equation with cubic-quartic dispersion in optical fibers. Phys. Lett. A 2023, 465, 128714. [Google Scholar] [CrossRef]
- Liu, C.; Li, Z. Multiplicative brownian motion stabilizes traveling wave solutions and dynamical behavior analysis of the stochastic Davey–Stewartson equations. Results Phys. 2023, 53, 106941. [Google Scholar] [CrossRef]
- Peng, C.; Li, Z. Soliton solutions and dynamics analysis of fractional Radhakrishnan–Kundu–Lakshmanan equation with multiplicative noise in the Stratonovich sense. Results Phys. 2023, 53, 106985. [Google Scholar] [CrossRef]
- Li, Z.; Hu, H. Chaotic pattern, bifurcation, sensitivity and traveling wave solution of the coupled Kundu–Mukherjee–Naskar equation. Results Phys. 2023, 48, 106441. [Google Scholar] [CrossRef]
- Goldstein, H. Classical Mechanics Addison-Wesley Series in Physics; Addison-Wesley: Reading, MA, USA, 1980. [Google Scholar]
- Saha, A.; Banerjee, S. Dynamical Systems and Nonlinear Waves in Plasmas; CRC Press: Boca Raton, FL, USA, 2021; p. x+207. [Google Scholar]
- Byrd, P.F.; Friedman, M.D. Handbook of Elliptic Integrals for Engineers and Scientists, 2nd ed.; revised; Die Grundlehren der mathematischen Wissenschaften, Band 67; Springer: New York, NY, USA; Heidelberg/Berlin, Germany, 1971; p. xvi+358. [Google Scholar]
- Ablowitz, M.J.; Ramani, A.; Segur, H. A connection between nonlinear evolution equations and ordinary differential equations of P-type. II. J. Math. Phys. 1980, 21, 1006–1015. [Google Scholar] [CrossRef]
| Case | Interval of | Range of e | Solution | ||
|---|---|---|---|---|---|
| Real Propagation | |||||
| 1. | − | − | |||
| 2. | + | + | |||
| 3. | + | − | |||
| 4. | + | − |
| Case | Interval of | Range of e | Solution | ||
|---|---|---|---|---|---|
| Real Propagation | |||||
| 1. | + | + | |||
| 2. | + | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elmandouh, A.; Aljuaidan, A.; Elbrolosy, M. The Integrability and Modification to an Auxiliary Function Method for Solving the Strain Wave Equation of a Flexible Rod with a Finite Deformation. Mathematics 2024, 12, 383. https://doi.org/10.3390/math12030383
Elmandouh A, Aljuaidan A, Elbrolosy M. The Integrability and Modification to an Auxiliary Function Method for Solving the Strain Wave Equation of a Flexible Rod with a Finite Deformation. Mathematics. 2024; 12(3):383. https://doi.org/10.3390/math12030383
Chicago/Turabian StyleElmandouh, Adel, Aqilah Aljuaidan, and Mamdouh Elbrolosy. 2024. "The Integrability and Modification to an Auxiliary Function Method for Solving the Strain Wave Equation of a Flexible Rod with a Finite Deformation" Mathematics 12, no. 3: 383. https://doi.org/10.3390/math12030383
APA StyleElmandouh, A., Aljuaidan, A., & Elbrolosy, M. (2024). The Integrability and Modification to an Auxiliary Function Method for Solving the Strain Wave Equation of a Flexible Rod with a Finite Deformation. Mathematics, 12(3), 383. https://doi.org/10.3390/math12030383






