Certain Novel Dynamic Inequalities Applicable in the Theory of Retarded Dynamic Equations and Their Applications
Abstract
:1. Introduction
2. An Overview of Time Scales and Some Fundamental Theorems
- , where is the left scattered maximum of
- , where is the right scattered minimum of
- (i)
- is continuous at if it is differentiable at .
- (ii)
- The delta derivative of a continuous function at right-scattered point is and the delta derivative of a differentiable function at right-dense point is
- (iii)
- If both are delta-differentiable, then for any where and
- (i)
- The value of and is 1;
- (ii)
- ;
- (iii)
- ;
- (iv)
- ;
- (v)
- ;
- (vi)
- for .
3. Main Results
- (1)
- For and the inequality in Theorem 6 reduces to the inequality by Pachpatte [3] (p. 40, Theorem 1.5.1).
- (2)
- If we substitute , then the inequality by G. Wang ([12], Theorem 3.2) turns out as a particular case of the above inequality.
- (3)
- For and the inequality proved above can be shrinked to the inequality due to Kendre et al. ([4], Theorem 2.1).
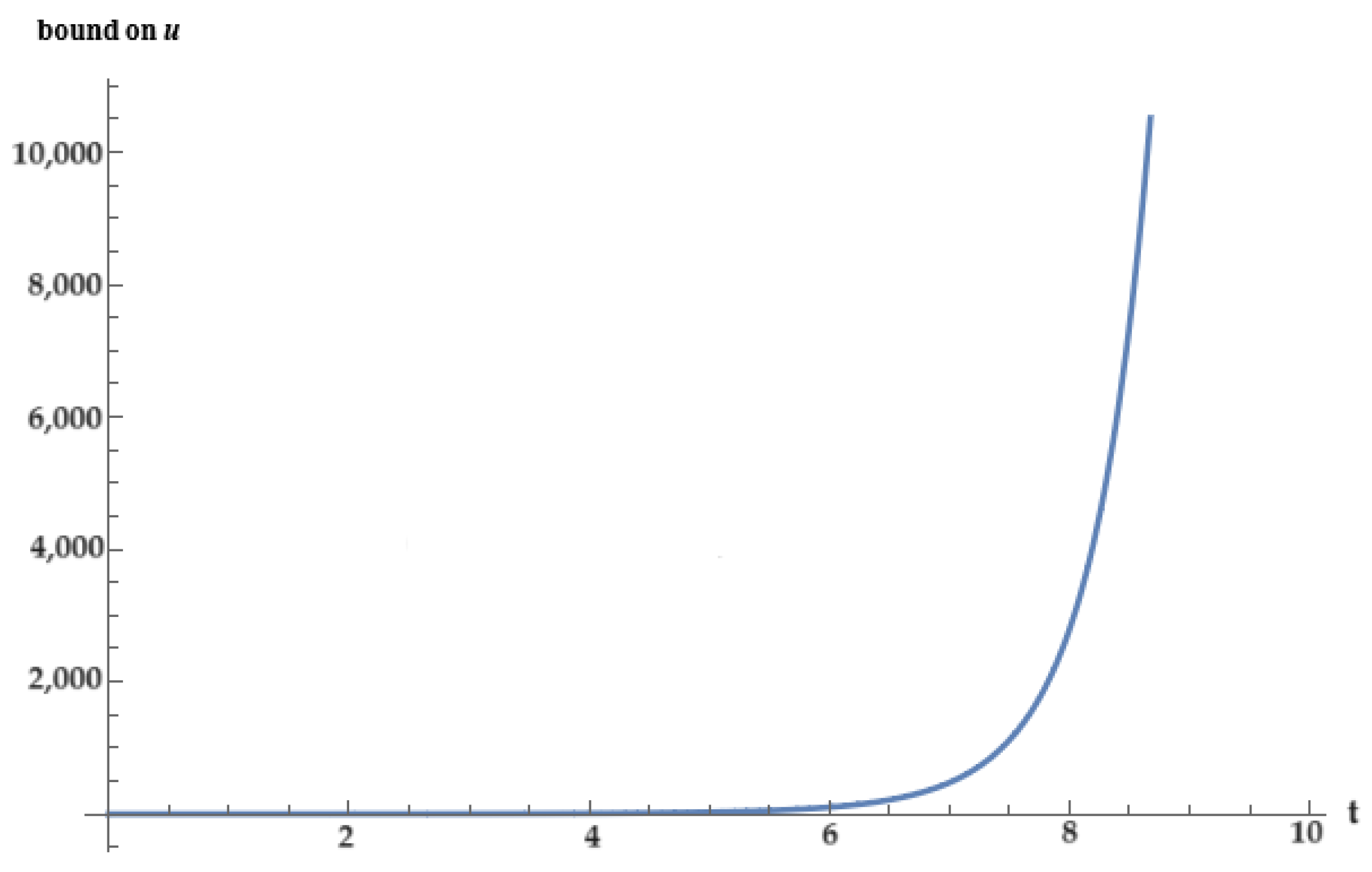
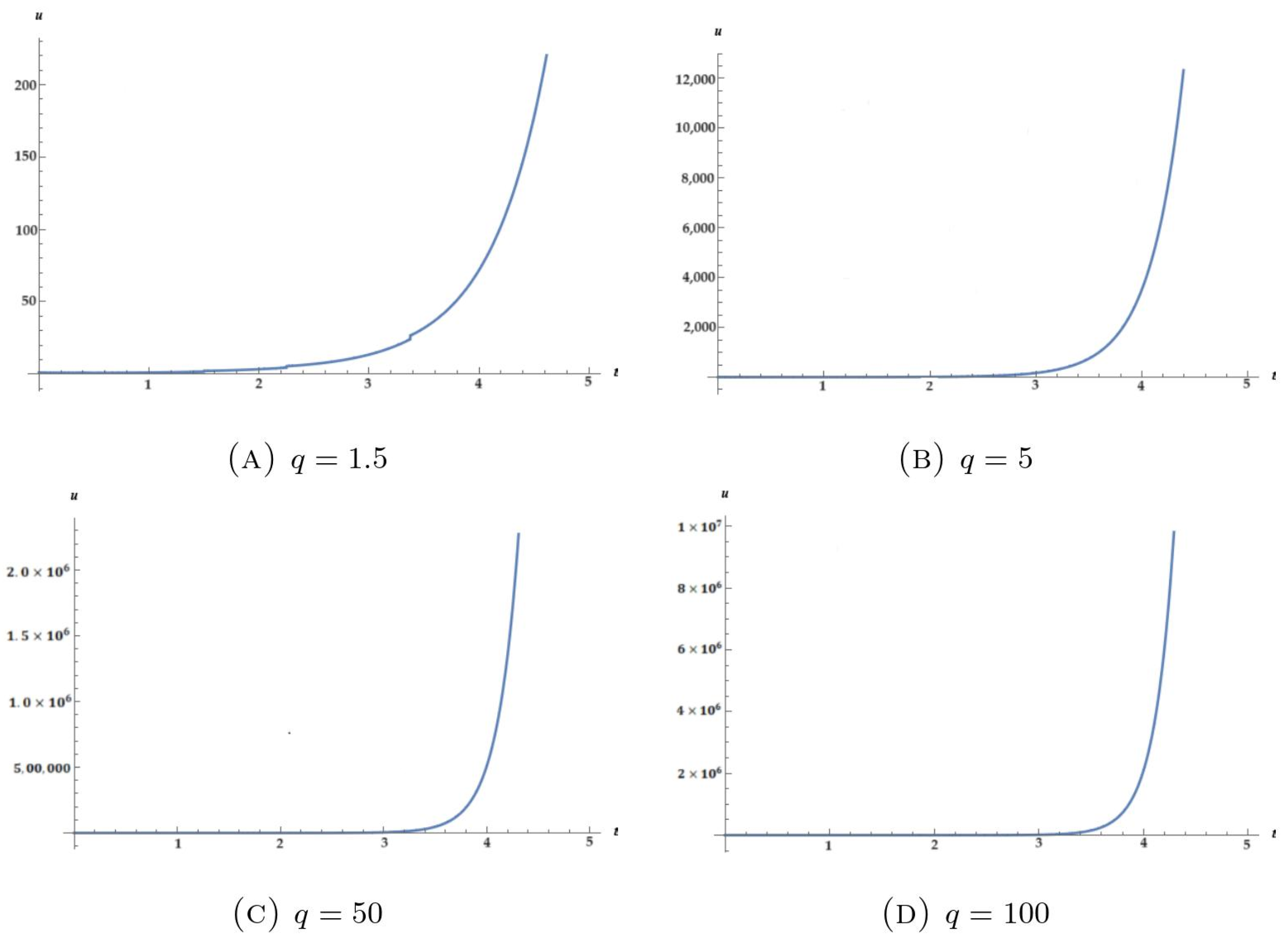
4. Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gronwall, T.H. Note on the Derivatives with Respect to a Parameter of the Solutions of a System of Differential Equations. Ann. Math. 1919, 20, 292–296. [Google Scholar] [CrossRef]
- Lipovan, O. A Retarded Gronwall-Like Inequality and Its Applications. J. Math. Anal. Appl. 2000, 252, 389–401. [Google Scholar] [CrossRef]
- Pachpatte, B.G. Integral and Finite Difference Inequalities and Applications; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Kendre, S.D.; Latpate, S.G.; Ranmal, S.S. Some Nonlinear Integral Inequalities For Volterra–Fredholm integral equations. Adv. Inequal. Appl. 2014, 2014, 21. [Google Scholar]
- El-Deeb, A.A.; Ahmed, R.G. On some generalizations of certain nonlinear retarded integral inequalities for Volterra–Fredholm integral equations and their applications in delay differential equations. J. Egypt. Math. Soc. 2017, 25, 279–285. [Google Scholar] [CrossRef]
- Hilger, S. Analysis on measure chains—A unified approach to continuous and discrete calculus. Results Math. 1990, 18, 18–56. [Google Scholar] [CrossRef]
- Hilger, S. Special functions, Laplace and Fourier transform on measure chains. Dyn. Syst. Appl. 1999, 8, 471–488. [Google Scholar]
- Bohner, M.; Peterson, A. First and second order linear dynamic equations on time scales. J. Differ. Equ. Appl. 2001, 7, 767–792. [Google Scholar] [CrossRef]
- Bohner, M.; Peterson, A. Dynamic Equations on Time Scales; Birkhouser: Boston, MA, USA, 2001. [Google Scholar]
- Agarwal, R.; Bohner, M. Basic calculus on time scales and some of its applications. Results Math. 1999, 35, 3–22. [Google Scholar] [CrossRef]
- Agarwal, R.; Bohner, M.; O’Regan, D.; Peterson, A. Dynamic equations on time scales: A survey. J. Comput. Appl. Math. 2002, 141, 1–26. [Google Scholar] [CrossRef]
- Wang, G.; El-Deeb, A.A.; Sennary, H.A. New Retarded Dynamic inequalities on time scales with applications. J. Math. Inequal. 2022, 16, 561–574. [Google Scholar] [CrossRef]
- Ozgun, S.A.; Zafer, A.; Kaymakcalan, B. Gronwall-Bihari type inequalities on time scales. In Proceedings of the Second International Conference on Difference Equations, Veszprém, Hungary, 7–11 August 1995; pp. 481–490. [Google Scholar]
- Agarwal, R.; Bohner, M.; Peterson, A. Inequalities on time scales: A survey. Math. Inequal. Appl. 2001, 4, 535–557. [Google Scholar] [CrossRef]
- Akin-Bohner, E.; Bohner, M.; Akin, F. Pachpatte Inequalities on Time Scales. J. Inequal. Pure Appl. Math. 2005, 6, 6. [Google Scholar]
- Thabet, H.; Kendre, S.; Peters, J.F. Advances in solving conformable nonlinear partial differential equations and new exact wave solutions for Oskolkov-type equations. Math. Methods Appl. Sci. 2022, 45, 2658–2673. [Google Scholar] [CrossRef]
- Li, W.N. Some Pachpatte type inequalities on time-scales. Comput. Math. Appl. 2009, 57, 275–282. [Google Scholar] [CrossRef]
- Zhao, C.J. Some integral inequalities for differential equations. J. Binzhou Teach. Coll. 2001, 17, 41–46. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhamre, S.; Kale, N.; Kendre, S.; Peters, J. Certain Novel Dynamic Inequalities Applicable in the Theory of Retarded Dynamic Equations and Their Applications. Mathematics 2024, 12, 406. https://doi.org/10.3390/math12030406
Bhamre S, Kale N, Kendre S, Peters J. Certain Novel Dynamic Inequalities Applicable in the Theory of Retarded Dynamic Equations and Their Applications. Mathematics. 2024; 12(3):406. https://doi.org/10.3390/math12030406
Chicago/Turabian StyleBhamre, Sujata, Nagesh Kale, Subhash Kendre, and James Peters. 2024. "Certain Novel Dynamic Inequalities Applicable in the Theory of Retarded Dynamic Equations and Their Applications" Mathematics 12, no. 3: 406. https://doi.org/10.3390/math12030406
APA StyleBhamre, S., Kale, N., Kendre, S., & Peters, J. (2024). Certain Novel Dynamic Inequalities Applicable in the Theory of Retarded Dynamic Equations and Their Applications. Mathematics, 12(3), 406. https://doi.org/10.3390/math12030406





