A Steady-State-Preserving Numerical Scheme for One-Dimensional Blood Flow Model
Abstract
:1. Introduction
2. Mathematical Model
3. Numerical Method
- (i)
- is the second-order and entropy-conservative flux for the homogeneous case of (3) given bywith the corresponding numerical entropy flux
- (ii)
- is the matrix of right eigenvectors of the Jacobian matrix being evaluated at the average state ; is a Roe-type matrix; and denote, respectively, the left and right limiting values of the scaled entropy variables at interface , obtained by the ENO reconstruction. The choice of this ENO method was due to the fact that it satisfies the so-called sign property [20]:which will be useful in proving the entropy stability of the flux (16).
4. Theoretical Results and Numerical Experiments
- (i)
- (ii)
4.1. Time Discretisation
4.2. Numerical Tests
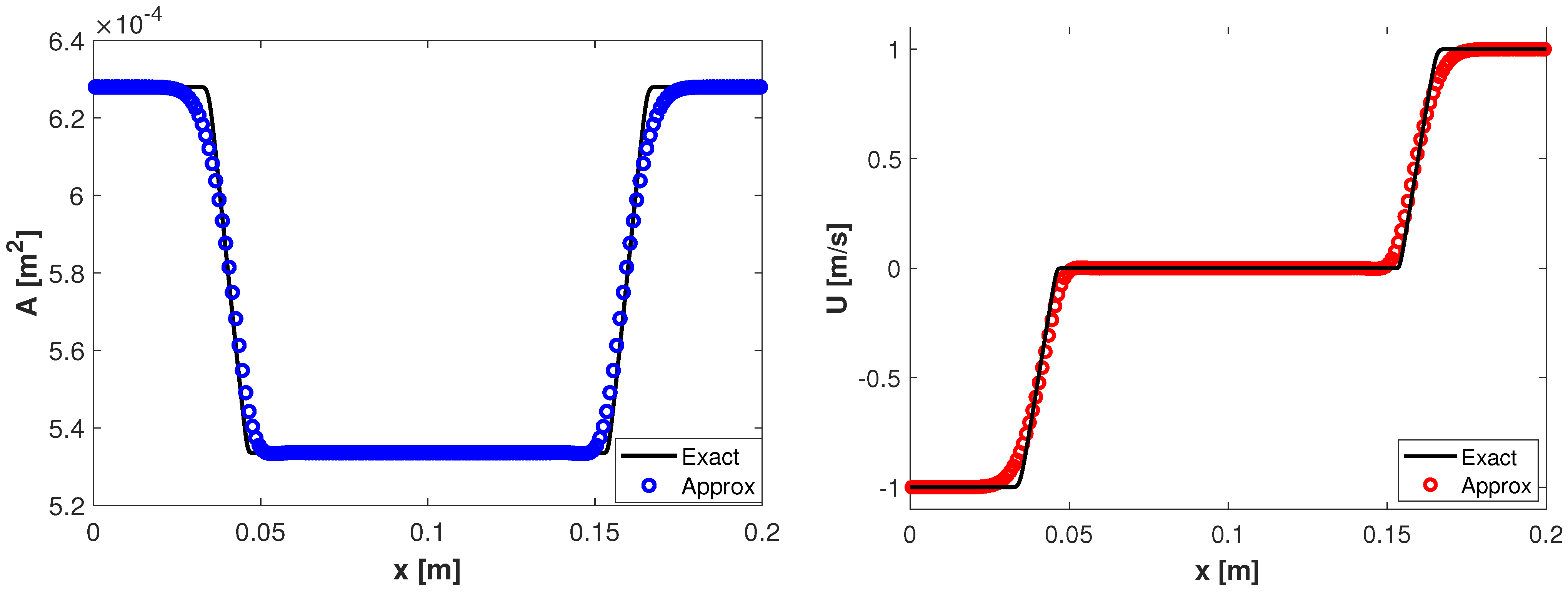
4.2.1. Example 1
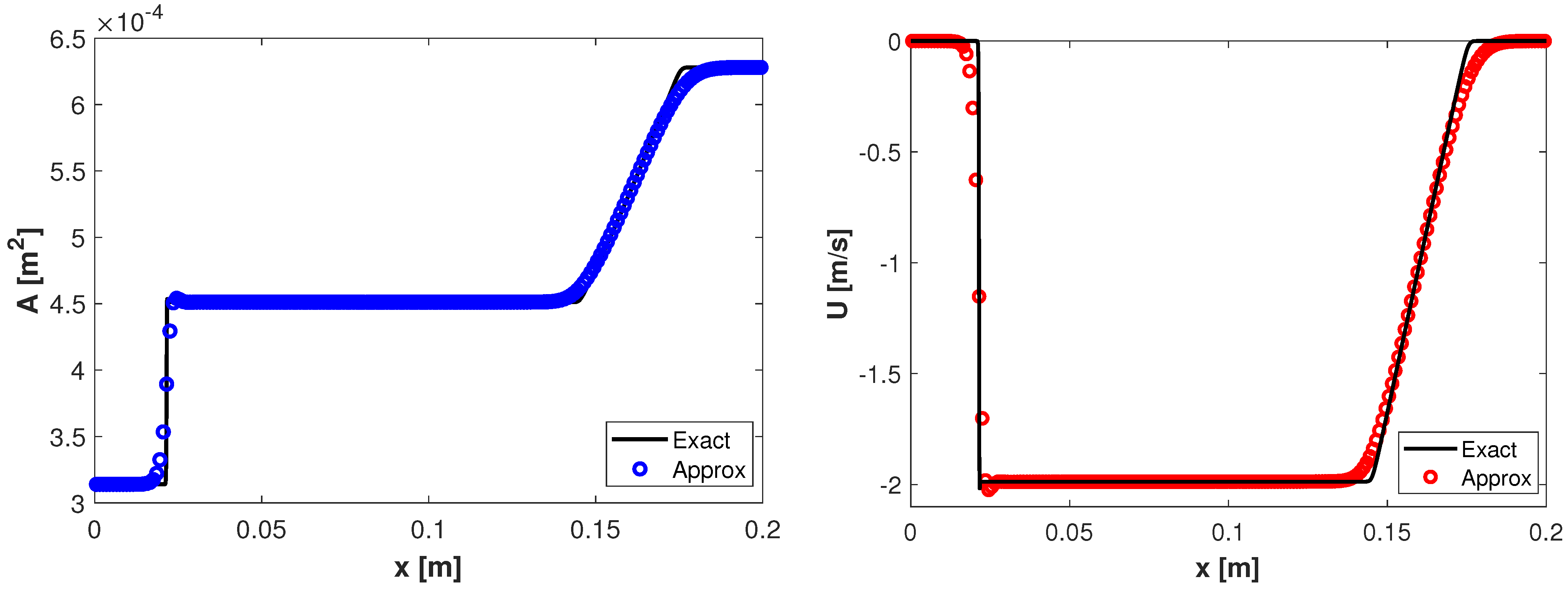
4.2.2. Example 2
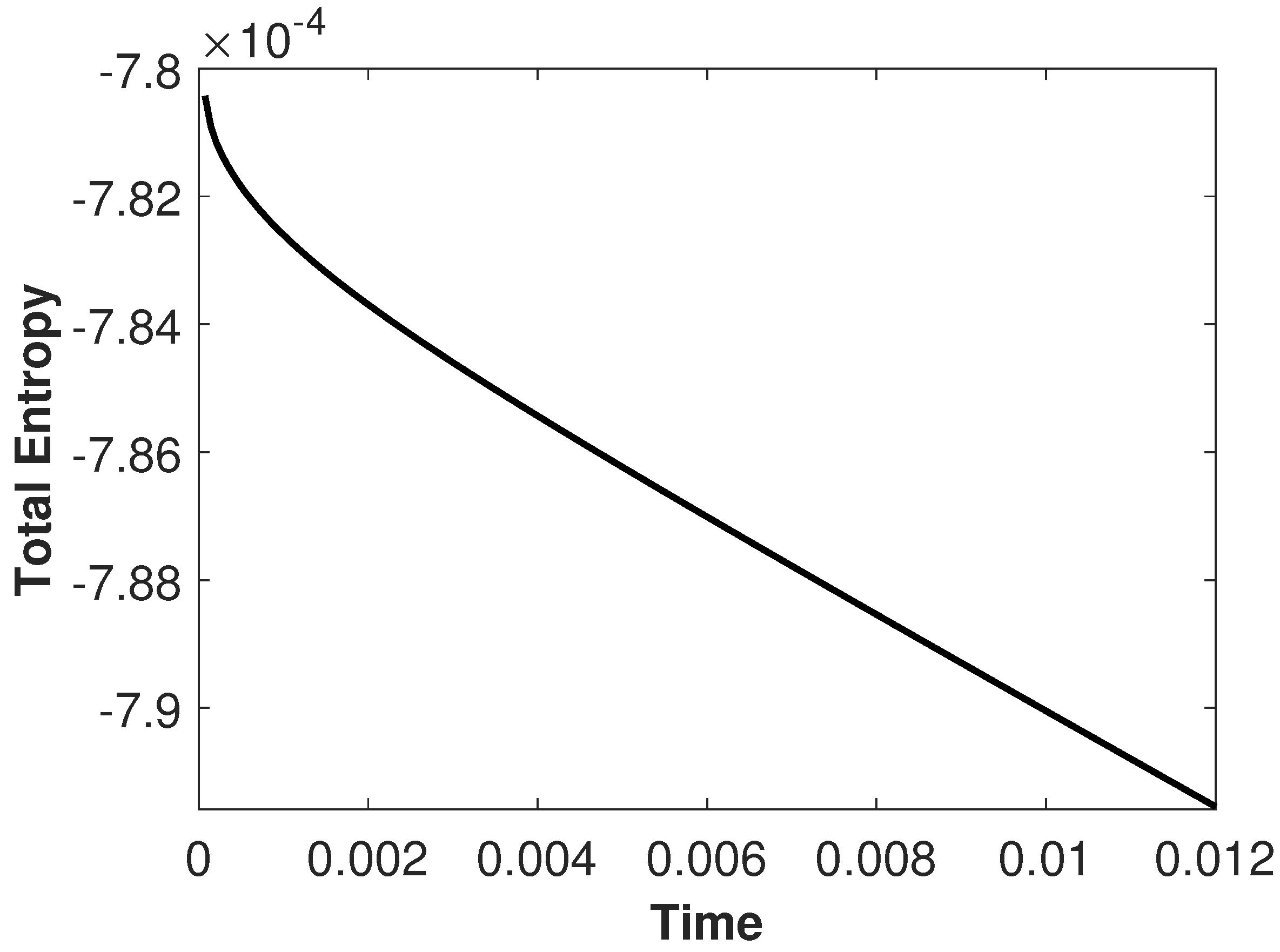
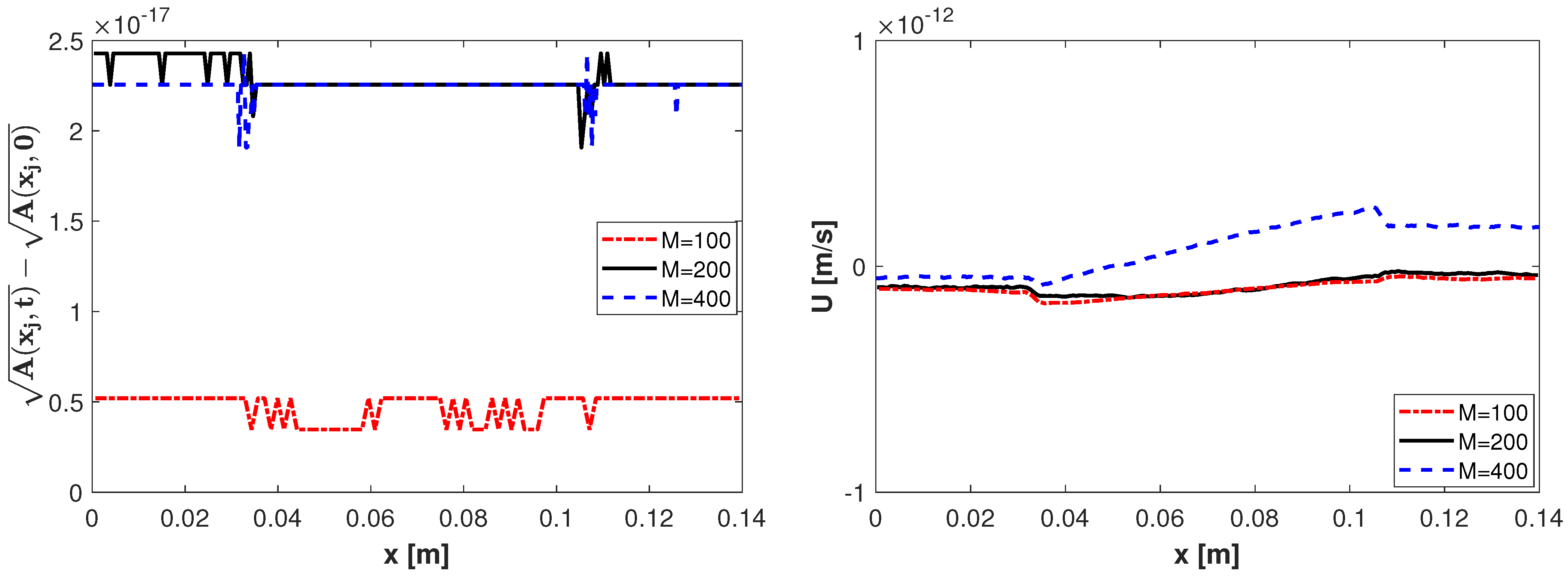
4.2.3. Example 3
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Euler, L. Principia pro motu sanguinis per arterias determinando. Opera Posthuma 1862, 2, 814–823. [Google Scholar]
- Blanco, P.J.; Bulant, C.A.; Müller, L.O.; Maso Talou, G.D.; Guedes Bezerra, C.; Lemoas, P.A.; Feijóo, R.A. Comparison of 1D and 3D Models for the Estimation of Fractional Flow Reserve. Sci. Rep. 2018, 8, 17275. [Google Scholar] [CrossRef]
- Formaggia, L.; Gerbeau, J.F.; Nobile, F.; Quarteroni, A. On the coupling of 3D and 1D Navier-Stokes equations for flow problems in compliant vessels. Comput. Methods Appl. Mech. Engrg. 2001, 191, 561–582. [Google Scholar] [CrossRef]
- Sherwin, S.J.; Franke, V.; Peiró, J.; Parker, K. One-dimensional modelling of a vascular network in space–time variables. J. Eng. Math. 2003, 47, 217–250. [Google Scholar] [CrossRef]
- Britton, J.; Xing, Y. Well-balanced discontinuous Galerkin methods for the one-dimensional blood flow through arteries model with man-at-eternal-rest and living-man equilibria. Comput. Fluids 2020, 203, 104493. [Google Scholar] [CrossRef]
- Li, G.; Delestre, O.; Yuan, Y. Well-balanced discontinuous Galerkin method and finite volume WENO scheme based on hydrostatic reconstruction for blood flow model in arteries. Int. J. Numer. Methods Fluids 2020, 86, 491–508. [Google Scholar] [CrossRef]
- Puelz, C.; Canic, S.; Rivière, B.; Rusin, C.G. Comparison of reduced models for blood flow using Runge-Kutta discontinuous Galerkin methods. Appl. Numer. Math. 2017, 115, 114–141. [Google Scholar] [CrossRef]
- Valbuena, S.; Vega, C.A. Numerical approximation of living-man steady-state solutions for blood flow in arteries using a well-balanced discontinuous Galerkin scheme. Results Appl. Math. 2023, 18, 100375. [Google Scholar] [CrossRef]
- Wang, Z.; Li, G.; Delestre, O. Well-balanced finite difference weighted essentially non-oscillatory schemes for the blood flow model. Int. J. Numer. Methods Fluids 2016, 82, 607–622. [Google Scholar] [CrossRef]
- Guitti, B.; Berton, C.; Hoang, M.; Toro, E. A fully well-balanced scheme for the 1D blood flow equations with friction source term. J. Comput. Phys. 2020, 421, 109750. [Google Scholar] [CrossRef]
- Müller, L.O.; Parés, C.; Toro, E. Well-balanced high-order numerical schemes for one-dimensional blood flow in vessels with varying mechanical properties. J. Comput. Phys. 2013, 242, 53–85. [Google Scholar] [CrossRef]
- Chu, S.; Kurganov, A. Flux globalization based well-balanced central-upwind scheme for one-dimensional blood flow models. Calcolo 2023, 60, 2. [Google Scholar] [CrossRef]
- Formaggia, L.; Nobile, F.; Quarteroni, A.; Veneziani, A. Multiscale modelling of the circulatory system: A preliminar analysis. Comput. Vis. Sci. 1999, 2, 75–83. [Google Scholar] [CrossRef]
- Dafermos, C. Hyperbolic Conservation Laws in Continuum Physics; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Guigo, A.R.; Delestre, O.; Fullana, J.M.; Lagrée, P.Y. Low-Shapiro hydrostatic reconstruction tecnique for blood flow simulation in large arteries with varying geometrical and mechanical properties. J. Comput. Phys. 2017, 331, 108–136. [Google Scholar] [CrossRef]
- Delestre, O.; Lagrée, P.Y. A ’well-balanced’ finite-volume scheme for blood flow simulation. Int. J. Numer. Methods Fluids. 2013, 72, 177–205. [Google Scholar] [CrossRef]
- Fjordholm, U.S.; Mishra, S.; Tadmor, E. Arbitrary high-order essentially non-oscillatory entropy-stable schemes for systems of conservation laws. SIAM J. Numer. Anal. 2012, 50, 544–573. [Google Scholar] [CrossRef]
- Bürger, R.; Valbuena, S.; Vega, C. A well-balanced and entropy-stable scheme for a reduced blood flow model. Numer. Meth. Part Differ. Equ. 2023, 39, 2491–2509. [Google Scholar] [CrossRef]
- Tadmor, E. The numerical viscosity of entropy-stable schemes for systems of conservation laws, I. Math. Comput. 1987, 49, 91–103. [Google Scholar] [CrossRef]
- Fjordholm, U.S.; Mishra, S.; Tadmor, E. ENO reconstruction and ENO interpolation are stable. Found. Comput. Math. 2013, 13, 139–159. [Google Scholar] [CrossRef]
- Fjordholm, U.S.; Mishra, S.; Tadmor, E. Well-balanced and energy stable schemes for the shallow water equations with discontinuous topography. J. Comput. Phys. 2011, 230, 5587–5609. [Google Scholar] [CrossRef]
- Wu, K.; Shu, C.W. Entropy Symmetrization and High-Order Accurate Entropy Stable Numerical Schemes for Relativistic MHD Equations. SIAM J. Sci. Comput. 2020, 42, A2230–A2261. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vega, C.A.; Valbuena, S.; Bojato, J.B. A Steady-State-Preserving Numerical Scheme for One-Dimensional Blood Flow Model. Mathematics 2024, 12, 407. https://doi.org/10.3390/math12030407
Vega CA, Valbuena S, Bojato JB. A Steady-State-Preserving Numerical Scheme for One-Dimensional Blood Flow Model. Mathematics. 2024; 12(3):407. https://doi.org/10.3390/math12030407
Chicago/Turabian StyleVega, Carlos A., Sonia Valbuena, and Jesús Blanco Bojato. 2024. "A Steady-State-Preserving Numerical Scheme for One-Dimensional Blood Flow Model" Mathematics 12, no. 3: 407. https://doi.org/10.3390/math12030407
APA StyleVega, C. A., Valbuena, S., & Bojato, J. B. (2024). A Steady-State-Preserving Numerical Scheme for One-Dimensional Blood Flow Model. Mathematics, 12(3), 407. https://doi.org/10.3390/math12030407






