Abstract
Reproducibility refers to getting bitwise identical floating point results from multiple runs of the same program, is an important basis for debugging or correctness checking in many codes. However the round-off error and non-associativity of floating point makes attaining reproducibility a challenge in large-scale, long-term parallel computing or solving ill conditioned problems. The performs general banded matrix-vector multiplication for double precision, is the most basic Level-2 operation in BLAS. First, we designed a reproducible algorithm for banded matrix-vector multiplication based on the technique of error-free transformation. Then the error of the algorithm is analyzed. Second, the algorithm is parallelized into on ARM and x86 platforms. The numerical test results verify that is reproducible and has higher accuracy than ordinary . In numerical experiments on ARM platform, as the number of threads increases from 1 to 8, the run time of this algorithm is reduced by 5.2–7 times, while the run time of multithreaded is only reduced by 2.2–3.8 times. In numerical experiments on x86 platform, as the number of threads increases from 1 to 15, the run time of this algorithm is reduced by 7.7–10.6 times, while the run time of multithreaded is only reduced by 4.2–6.8 times.
MSC:
65-02
1. Introduction
The development in the field of high-performance computing (HPC) have been remarkable, with the computational scale of scientific and engineering calculations continuously increasing. The limited word length of computers leads to unavoidable rounding errors in floating-point operations [1]. The combination of dynamic scheduling of parallel computing resources, and floating point nonassociativity results in irreproducibility of floating-point calculation results. For instance, the continued summation or product of multiple floating-point numbers depends on the order of calculations.
Reproducibility is the ability to obtain a bit-wise identical and accurate result for multiple executions on the same data in various parallel environments [2]. We use a floating-point arithmetic that consists in approximating real numbers by a finite, fixed-precision representation number adhering to the IEEE 754 standard, which requires correctly rounded results for the basic arithmetic operations. The correct rounding criterion guarantees a unique, well-defined answer. The main idea is to keep track of both the result and the error during the course of computations.
In the 1960s and 1970s, Knuth, Kahan, and Dekker [3] proposed the idea of error-free transformations. In 2005, Japanese scholar Ogita, Oishi, and German scholar Rump [4,5,6] systematically summarized compensation algorithms and formally introduced the concept of error-free transformations(EFTs). One approach uses EFTs to compute both the result and the rounding error and stores them in a floating-point expansion (FPE), whose components are ordered in magnitude with minimal overlap to cover the whole range of exponents [7]. Typically, FPE relies upon the use of the traditional EFT for addition. Another approach projects the finite range of exponents of floating-point numbers into a long (fixed-point) accumulator and stores every bit there. For instance, Kulisch proposed to use a 4288-bit long accumulator for the exact dot product of two vectors composed of binary64 numbers with hardware supports [8].
Emerging attention to reproducibility strives to draw more careful attention to the problem by the computer arithmetic community. Static data scheduling and deterministic reduction ensure the numerical reproducibility of the Intel Math Kernel Library [9]. Nevertheless the number of threads has to be set for all runs. Starting from version 11.0, Intel’s MKL library introduced the Conditioned Numerical Reproducibility (CNR) mode [10]. This mode provides the capability to obtain reproducible floating-point results when calling library functions from the application, under the condition of a limited number of threads. Unfortunately this decreases significantly the performance especially on recent architectures, and requires the number of threads to remain the same from run to run to ensure reproducible results. Reproblas [11,12], developed by the University of California, Berkeley, utilizes pre-rounding and 1-Reduction techniques, and is designed for CPU and distributed parallel environments. However, the current version of this library only has the most basic functions and does not support thread-level parallelism. Exblas [13,14], developed by the University of Paris-Sud, combines together long accumulator and floating-point expansion into algorithmic solutions as well as efficiently tunes and implements them on various architectures, including conventional CPUs, Nvidia and AMD GPUs, and Intel Xeon Phi co-processors. Ozblas [15,16], developed by Tokyo Woman’s University in Japan, achieves reproducibility using the Ozaki scheme. This software supports adjustable precision on both CPUs and GPUs. However, these libraries are mainly developed to demonstrate the methods proposed in their respective research papers and are not yet widely used in practical applications [17].
The latest research is a general framework for deriving reproducible and accurate variants of a Krylov subspace algorithm, which proposed by Iakymchuk [18]. The framework is illustrated on the preconditioned BiCGStab method for the solution of non-symmetric linear systems with message-passing. The algorithmic solutions are build around the ExBLAS project.
Modern supercomputer architectures consist of multiple levels of parallelism. As the level of parallelism increases, the uncertainty of computations also increases [19,20,21]. The purpose of this paper is to analyze the blocking implementation approaches of the function in the BLAS library, We designed and optimized a multi-threaded reproducible algorithm for banded matrix-vector multiplication.
The paper is organized as follows. Section 2 introduces the relevant knowledge of reproducible techniques. Section 3 describes how to achieve reproducibility in the banded matrix-vector multiplication algorithm and analyses the error bound. Then, the multi-level parallel optimization design we have performed on this algorithm is explained. Section 4 presents numerical experiments on the reproducibility, accuracy, and performance of the algorithm. The experimental results demonstrate that the algorithm is reproducible, efficient, and reliable.
2. Background
In scientific computing, the most basic operation is the addition of two floating-point numbers. The use of error-free transformations can greatly control the accumulation of rounding errors.
The algorithm [3] is used to add two floating-point numbers a and b. The core idea is to transform the floating-point pair into the floating-point pair and use compensation to improve the calculation results. The calculation result is corrected by combining a high-order term x with a low-order term y.
The algorithm is mainly used for operations on a vector of floating-point numbers, where it transforms the elements of the vector v into the sum of a high-order part and a trailing part [22]. T is the exact sum of , and r is a vector composed of . Our paper uses the reproducible k-fold accurate summation algorithm in to-nearest rounding mode (Algorithm 7, [22]). This algorithm requires FLOPs, where k is the number of fold, n is the length of vector v.
3. Parallel Reproducible Banded Matrix-Vector Multiplication
In this chapter, we will explain how we implemented the reproducible banded matrix-vector multiplication algorithm for double-precision in to-nearest rounding mode.
3.1. Basic Architecture
is a special matrix function in BLAS Level 2. Both the memory access and computational complexity reach . After special memory access processing, converts to or operations. Therefore, the performance heavily relies on the implementation of the level 1 algorithms.
The function is defined as: , where A is an n-row by m-column banded matrix, with being the element at the i-th row and j-th column of A. and are scalars, x is a vector of size m, with being the i-th element in x. y is a vector of size n, with being the i-th element in y. Let and be the number of superdiagonals and subdiagonals, respectively.
Taking , as an example, A can be represented as follows:
Compressed banded matrix exhibits special matrix properties. During storage, compressed banded matrices only store the effective computational elements (referring to the elements on the subdiagonal, main diagonal, and superdiagonal). During computation, dgbmv requires a one-to-one correspondence between matrix elements and vector elements in terms of computation order. The actual memory required for storage is smaller than the size of the uncompressed original matrix.
This paper mainly considers the row-major storage format. In memory, the banded matrix ignores the ineffective computational elements (referring to the subdiagonal and superdiagonal elements that do not participate in the computation) and rearranges them according to certain rules.
Each row has an offset added to the starting address. The offset for the first row is , and for each subsequent row, the offset is reduced by 1 until the offset becomes 0, after which each row is not offset.
Additionally, the effective computational elements of each row need to be recorded to ensure accurate and complete storage. From this, we can conclude that the memory access requires knowledge of the offset and the number of effective elements in each row. Therefore, the storage of matrix A is as follows:
In actual calculation, the compressed banded matrix takes out each row based on the offset and the number of effective elements, and also takes out the corresponding vector portion that participates in the computation. It then uses to perform the entire matrix-vector multiplication. The pseudo-code of the specific algorithm implementation is shown in Algorithm 1.
| Algorithm 1 Reproducible Compressed Banded Matrix-Vector Multiplication: |
|
Since the multiplication of two floating-point numbers is reproducible, we calculate the product at each corresponding position and store it in an array . We also store the initial value of y multiplied by in . Then, we use the algorithm to perform the reproducible summation for the array , with the number of folds k set to 2.
3.2. Error Analysis
Let be the machine precision, which is the distance between 1 and the closest floating-point number. , where p is the number of significant digits of a floating-point number. In double precision, .
Theorem 1.
In to-nearest rounding mode, for a vector v of length h and using the k-fold reproducible summation algorithm , when , the absolute error bound between the numerical result and the exact result is:
where .
Proof of Theorem 1.
Let be the j-th element of v, and be the exact sum of all elements in v. In the i-th step of the error-free vector transformation, where , we introduce the following notations: is the corresponding boundary; is the high-order part extracted in the i-th error-free vector transformation for each element; is the numerical result of the summation of , which can be computed exactly; is the low-order part remaining after the i-th extraction; is the exact sum of , which is used for proof purposes. On one hand, for EFTs,
where . Combining the above two cases, we can get:
On the other hand,
Therefore,
By applying Lemma 5 from reference [22],
we can deduce that
where will be used in proof of Theorem 2. Therefore,
Furthermore, since
we can get (1) through simple derivation. □
Based on Theorem 1, we can derive Theorem 2. For convenience, we set is the number of elements in a row. In the banded matrix A, the ith row is denoted as .
Theorem 2.
In simplified algorithm to compute , , , . and are the number of superdiagonals and subdiagonals, respectively. The error bound for each element in the numerical solution y is:
where
and M is the vector of , , and is the maximum value of
Proof of Theorem 2.
To perform a dot product operation between each row of A and x, it is necessary to first calculate the product result of each and , store it in a vector, and then perform a reproducible sum. We call this process as . By using in (2) and the same method in (3), the detailed calculation process for and x is as follows:
where . From , We can derive that
Then the error bound is
where
which is easy to deduce the result. □
Note that the error bound of [1] is
Therefore if
has a smaller error bound than . As for , it’s easy to derive in a similar way.
3.3. Blocking and Parallel Optimization
We separated the compressed banded matrix A into blocks, and used multi-level parallel reproducible summation algorithms. The number of blocks is determined by the number of threads, . We used to allocate tasks to each block. The segmentation process is as follows: first, we calculated the number of rows that each block needs to allocate based on the number of threads and the number of matrix rows. Then, we used to transfer the calculated control information to each thread. For example, when the number of threads is 4, the blocking is as shown below:
Finally, according to the received control information in different threads, we accessd A, x, and y, and used the algorithm to calculate. The calculated results are assigned to the corresponding positions of y.
We refered to this optimized multi-threaded compressed banded matrix-vector multiplication as .
4. Numerical Experiments
In this chapter, we conducted numerical experiments to verify the reproducibility, accuracy, and performance of the algorithm. In the reproducible summation used, we set the number of folds k to 2.
In experiments to verify reproducibility and accuracy, we generated a set of data using sine function to make the data more ill-conditioned, and store data in a banded matrix A of size . The number of subdiagonals and superdiagonals is set to 500. We also generate floating-point vectors x and y of size 5000 using the sine function.
The experiments were conducted on two different testing platforms: an ARM processor (National University of Defense Technology, Changsha, Hunan) and a x86 processor Intel(R) Xeon(R) Platinum 8180M (Xeon Platinum CPU), with the parameters shown in the Table 1.

Table 1.
Hardware parameters of two platforms.
4.1. Reproducibility Verification
We performed the ordinary banded matrix-vector multiplication algorithm and the algorithm on two different platforms with a single thread to verify the reproducibility.
We defined the irreproducibility rate as: the proportion of elements in the numerical results that have the same index but values differ between two results, when using the same program and the same set of input data.
To compare the numerical results, we calculated the absolute errors between different numerical results, as shown in Figure 1. In the figure, the result calculated on the ARM platform is denoted as , and the result calculated on the x86 platform is denoted as . The absolute error is calculated as:
Figure 1.
The absolute error between the two results executed on ARM and x86 of and .
To verify the reproducibility of the algorithm, we also calculated the maximum absolute error between the two results and ,
as well as the irreproducibility rate, which is the ratio of the number of irreproducible elements to the total number of elements
We showed the rate in Table 2.

Table 2.
Comparison of results executed by same algorithm on ARM and x86.
From Figure 1 and Table 2, we can see that the algorithm produces different results on the two platforms, with a maximum absolute error greater than 0. In the entire result vector, 83.38% of the elements are different. In contrast, the algorithm produces results with a maximum absolute error of 0 on both platforms, and the irreproducibility rate is 0, which means all corresponding elements of the result vectors are exactly the same. This indicates that is irreproducible, while is reproducible.
4.2. Accuracy Verification
On the ARM platform, we denoted these two results of and as y and , and then calculate the accurate result using MPFR [23]. We compare y and with , and the error results are shown in Figure 2. The maximum absolute error between exact solution and numerical results is computed by , .
Figure 2.
The absolute error between exact solution and numerical results of and .
It can be seen that the has higher accuracy than the .
4.3. Performance Verification
We tested multiple sets of subdiagonals and superdiagonals for the matrix A of size .
First, on the ARM platform, we used and to perform different sizes of matrices with single thread and 8 threads. We recorded the running time, as shown in Figure 3, and calculated speedup, as shown in Figure 4.
Figure 3.
The running time of and of single thread and 8 thread on ARM platform respectively.
Figure 4.
The speedup of and between single thread and 8 thread on ARM platform.
Furthermore, it could be calculated that with single thread, the running time of is 4 to 4.2 times that of the . With 8 threads, the running time of is 1.7 to 2.8 times that of the . Compared to , has higher parallel efficiency.
Second, on the x86 platform, we used single thread, 15 threads, and 30 threads to execute . The running time are shown in Figure 5, and the speedup between single thread and 15 threads is shown in Figure 6.
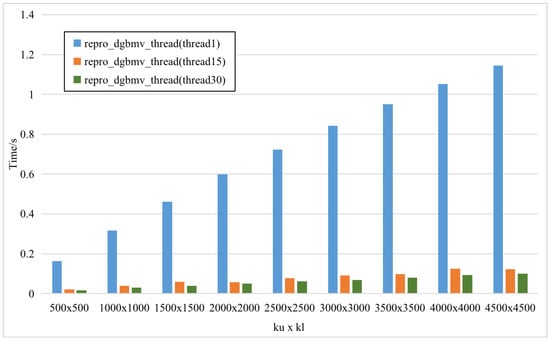
Figure 5.
The rum times of with single-thread and multithread respectively on x86 platform.
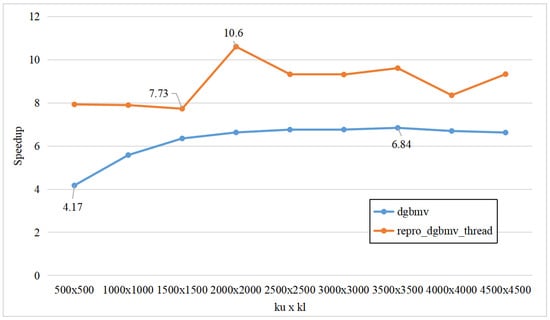
Figure 6.
The rum times of with single-thread and multithread respectively on x86 platform.
It could be calculated that the running time of with single thread is 7.7 to 10.6 times that of 15 threads, and the running time with 15 threads is 1.1 to 1.5 times that of 30 threads. However, the running time of with single thread is 4.2 to 6.8 times that of 15 threads, and the running time with 15 threads is 0.8 to 1.2 times that of 30 threads.
Increasing the number of threads further does not improve the parallel efficiency or reduce the running time, because the data size processed by each individual thread is not large enough, leading to increased the proportion of communication time and decreased parallel efficiency.
5. Conclusions
In this paper, we optimized the banded matrix-vector multiplication algorithm based on the error-free vector transformation. We implemented the reproducible extension and high-precision improvement of the algorithm. In addition, We conducted error analysis for the algorithm. The program implementation of multi-threaded parallel reproducible banded matrix-vector multiplication algorithm was on the ARM and x86 platforms. The numerical experimental results verified the reproducibility and accuracy improvement of the , as well as the performance improvement and better parallel efficiency compared to .
Author Contributions
Conceptualization, T.T.; Methodology, H.J.; Validation, H.Q.; Writing—original draft, Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key Research and Development Program of China under Grant No. 2020YFA0709803.
Data Availability Statement
Available online: https://github.com/taotang84/repro_dgemv_thread (accessed on 10 January 2024).
Conflicts of Interest
The authors declare no conflict of interest. The funders had decisive role in the decision to publish the results.
References
- Higham, N.J. Accuracy and Stability of Numerical Algorithms, 2nd ed.; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Benmouhoub, F.; Garoche, P.L.; Martel, M. An Efficient Summation Algorithm for the Accuracy, Convergence and Reproducibility of Parallel Numerical Methods. In Software Verification; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2022; Volume 13124, pp. 165–181. [Google Scholar] [CrossRef]
- Ogita, T.; Rump, S.; Oishi, S. Accurate sum and dot product. SIAM J. Sci. Comput. 2005, 26, 1955–1988. [Google Scholar]
- Ozaki, K.; Ogita, T.; Oishi, S.I.; Rump, S.M. Error-free transformations of matrix multiplication by using fast routines of matrix multiplication and its applications. Numer. Algorithms 2012, 59, 95–118. [Google Scholar] [CrossRef]
- Rump, S.M.; Ogita, T.; Oishi, S. Accurate floating-point summation part I: Faithful rounding. SIAM J. Sci. Comput. 2008, 31, 189–224. [Google Scholar]
- Rump, S.; Ogita, T.; Oishi, S. Accurate Floating-Point Summation Part II: Sign, K-Fold Faithful and Rounding to Nearest. SIAM J. Sci. Comput. 2008, 31, 1269–1302. [Google Scholar]
- Mukunoki, D.; Ogita, T.; Ozaki, K. Reproducible BLAS Routines with Tunable Accuracy Using Ozaki Scheme for Many-Core Architectures. In Parallel Processing and Applied Mathematics, Proceedings of the 13th International Conference on Parallel Processing and Applied Mathematics (PPAM 2019), Bialystok, Poland, 8–11 September 2019; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12043, pp. 516–527. [Google Scholar] [CrossRef]
- Kulisch, U.; Snyder, V. The exact dot product as basic tool for long interval arithmetic. Computing 2011, 91, 307–313. [Google Scholar]
- Todd, R. Run-to-Run Numerical Reproducibility with the Intel Math Kernel Library and Intel Composer XE 2013; Technical Report; Intel Corporation: Santa Clara, CA, USA, 2013. [Google Scholar]
- Rosenquist, T.; Fedorov, G. Introduction to Conditional Numerical Reproducibility (CNR). Available online: https://software.intel.com/content/www/us/en/develop/articles/introduction-to-the-conditional-numerical-reproducibility-cnr.html (accessed on 30 November 2023).
- Demmel, J.; Nguyen, H.D. Parallel Reproducible Summation. IEEE Trans. Comput. 2015, 64, 2060–2070. [Google Scholar]
- ReproBLAS: Reproducible BLAS. 2018. Available online: http://bebop.cs.berkeley.edu/reproblas/ (accessed on 30 November 2023).
- Iakymchuk, R.; Collange, S.; Defour, D.; Graillat, S. ExBLAS: Reproducible and Accurate BLAS Library. In Proceedings of the NRE2015 at SC15, Austin, TX, USA, 20 November 2015. [Google Scholar]
- Iakymchuk, R.; Defour, D.; Collange, C.; Graillat, S. Reproducible triangular solvers for high-performance computing. In Proceedings of the International Conference on Information Technology—New Generations (ITNG), Las Vegas, NV, USA, 13–15 April 2015; pp. 353–358. [Google Scholar]
- Mukunoki, D.; Ogita, T.; Ozaki, K. Accurate and Reproducible BLAS Routines with Ozaki Scheme for Many-core Architectures. In Proceedings of the Russian Supercomputing Days 2019, Moscow, Russia, 23–24 September 2019; pp. 202–203. [Google Scholar]
- ANSI/IEEE Standard 754-1985; IEEE Standard for Binary Floating-Point Arithmetic. Institute of Electrical and Electronics Engineers: New York, NY, USA, 1985.
- Knuth, D.E. The Art of Computer Programming Seminumerical Algorithms, 3rd ed.; Addison-Wesly: Reading, MA, USA, 1998; Volume 2. [Google Scholar]
- Iakymchuk, R.; Graillat, S.; Aliaga, J.I. General framework for re-assuring numerical reliability in parallel Krylov solvers: A case of bi-conjugate gradient stabilized methods. Int. J. High Perform. Comput. Appl. 2023, 16–29. [Google Scholar] [CrossRef]
- Collange, C.; Defour, D.; Graillat, S.; Iakymchuk, R. Numerical Reproducibility for the Parallel Reduction on Multi-and Many-Core Architectures. Parallel Comput. 2015, 49, 83–97. [Google Scholar]
- Li, K.; He, K.; Graillat, S.; Jiang, H.; Gu, T.; Liu, J. Multi-level parallel multi-layer block reproducible summation algorithm. Parallel Comput. 2023, 115, 102996. [Google Scholar]
- Chen, L.; Tang, T.; Qi, H.; Jiang, H.; He, K. Design and Implementation of Multithreaded Reproducible DGEMV on Phytium Processor. Comput. Sci. 2022, 49, 27–35. (In Chinese) [Google Scholar]
- Demmel, J.; Nguyen, H.D. Fast reproducible floating-point summation. In Proceedings of the 21st IEEE Symposium on Computer Arithmetic, Austin, TX, USA, 7–10 April 2013; pp. 163–172. [Google Scholar]
- Zimmermann, P. Reliable Computing with GNU MPFR. In Mathematical Software—ICMS 2010; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6327, pp. 42–45. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).