Fuzzy Fractional Caputo Derivative of Susceptible-Infectious- Removed Epidemic Model for Childhood Diseases

Abstract

In this work, the susceptible-infectious-removed (SIR) dynamics are considered in relation to the effects on the health system. With the help of the Caputo derivative fractional-order method, the SIR epidemic model for childhood diseases is designed. Subsequenly, a set of sufficient conditions ensuring the existence and uniqueness of the addressed model by choosing proper fuzzy approximation methods. In particular, the fuzzy Laplace method along with the Adomian decomposition transform were employed to better understand the dynamical structures of childhood diseases. This leads to the development of an efficient methodology for solving fuzzy fractional differential equations using Laplace transforms and their inverses, specifically with the Caputo sense derivative. This innovative approach facilitates the numerical resolution of the problem and numerical simulations are executed for considering parameter values.

1. Introduction

One of the most well-known fields of study in the biological sciences that looks into how disease, health, and other related factors are designed at the population level is called epidemiology. The term epidemiology is derived from the greek word ‘epi’, meaning upon, ‘demo’, meaning people, and ‘logos’, meaning study. This etymology indicates that only human populations are included in discussions of epidemiology (see [1]). One of the rich areas of applications and research for mathematics in biological sciences today is the widely studied field of infectious illnesses. Evidently, contagious diseases significantly increase both the morbidity and mortality rates of both the human race and our target populations of non-human animals.

The most severe infectious infections are those that affect children. Famous among these are rubella, poliomyelitis, and measles. A respiratory infection by a Morbillivirus causes the highly contagious disease known as measles. Children are typically affected by these diseases because they are more likely to spread among them than among adults. Thus, two broad categories, namely the premature populations and mature populations, can be made to describe the population. Maturation delay occurs when the infant population takes a consistent amount of time to mature. A disease-latent phase is determined by the dynamics of the disease in question, which means the amount of time required for the disease to become fully active in the body. Immunization is an essential approach to the global management of pediatric illnesses.

Since children’s immune systems are so fragile, they are all exposed to a wide range of infectious and noninfectious disorders while they are still young. The most prevalent pediatric illnesses are either bacterial or viral infections, as well as allergy and immunologic conditions. Children who contract the “rotavirus” infection experience diarrhea, high fever, and vomiting, which frequently worsens dehydration issues. The “chickenpox” virus is called “varicella”. Measles, commonly known as “German measles”, is brought on by the “rubeola virus”, which can have fatal consequences. Many juvenile diseases cannot spread quickly through the body of a human being; instead, they require a period called the “latent period” to manifest. To prevent all of the aforementioned pediatric illnesses, appropriate vaccination is advised on a global scale. In 1974, the WHO began a global immunization program with this goal in mind. A mathematical model can help understand how a disease spreads and offers various methods for controlling its spread. Numerous writers, scientists, and biologists, including Haq et al. [2], Ahmed et al. [3], and Kumar [4], have used a variety of analytical and numerical techniques to solve different types of bio-mathematical epidemic models. Many scientists have demonstrated over the last few decades that fractional models can more precisely explain natural occurrences than integer order differential equations. Because of this benefit, the fractional calculus has gained prominence in modeling realistic problems, particularly those with memory effects [5,6]. Furthermore, fractional calculus and mathematical modeling are used in various domains such as social sciences, engineering, and mathematical biology [7]. In 2017, the SIR model was used to discuss a fractional model of infection and recovery [8]. In [9], the SIR epidemic system, which explains a non-linear recurrence % with arbitrary order, was investigated. In [10], the authors discuss arbitrary-order SIR epidemic system solutions. In the same year, Srivastava et al. discussed the SIR epidemic system of children diseases in their article [11]. There are currently several studies active to examine the COVID-19 virus models in various ways (see [12]).

The future transmission of the disease will be caused by past events and their cumulative impact on earlier volumes. The inheritance trait and history effect reveal the spread of already infected patients. Therefore, the effects of these features on the transmission of a disease can be studied using fractional derivatives. The latest additions to present calculus and differential equations (DE) are fuzzy calculus and fractional order differential equations (FODE), respectively. In recent years, FO modeling has developed into a fruitful and stimulating area of study from a variety of angles. It is possible to illustrate arbitrary-order derivatives and integrals with singular and non-singular kernels in a variety of ways. The definition of many types of fractional derivatives, which in turn led to intriguing theories of fractional calculus, was greatly aided by the Mittag–Leffler (ML) function. Indeed, because of the frequent use of ML in engineering and real-world issues during the past five years, scientists and engineers’ vital interests in the field have significantly expanded (see [13,14]). To support the existence and uniqueness theory of solutions, several academics have studied FODEs and fuzzy integral equations [15,16,17]. It takes a long time to come up with more precise solutions for each fuzzy FODE when using them. Mathematicians have examined fuzzy FODEs in depth using a wide range of techniques, including perturbation methods, integral transform methods, and spectral techniques. Uncertainty, which expresses the unpredictability and computational difficulty of a system, is an essential concept in mathematical modeling.

According to the above facts, we consider a fuzzy fractional-order childhood disease model under the Caputo derivative. The main contributions of this paper are as follows:

• As a first attempt, in this paper, a fuzzy fractional Caputo derivatives approach subject to a SIR dynamic is developed for childhood dieases.
• The fixed point theorem of Schauder and Banach is used to demonstrate the existence and uniqueness of the solution to the addressed model.
• Perform the numerical simulations by using fuzzy Laplace and inverse Laplace transform based on the Adomian decomposition method.
• Numerical results shows the validity and effectiveness of the tracking performance of the proposed fuzzy fractional SIR dynamic.

The structure of the article is as follows. The fundamental idea of fuzzy and fuzzy fractional Caputo derivative is described in Section 2. In Section 3, the fuzzy fractional Caputo derivative model formulation has been briefly explained. The existence and uniqueness of the thallae solution of the model is established in Section 4. The scheme of the solution is described in Section 5. The numerical approximations are also provided in Section 6 for theoretical support and, finally, the conclusion is given in Section 7.

2. Preliminaries

Firstly, the following definitions will be required for the convenience of analysis.

Definition 1

([18]). Let $\nu :\mathbb{R}\to [0,1]$ be an ambiguous collection of the real line meeting the requirements as follows: ν should be normal (for any $a_0\in \mathbb{R};\nu \left(a_0\right)=1$), the upper semicontinuous on $\mathbb{R}\left(\forall \epsilon >0.\exists \delta >0\ni \left|\nu \left(a\right)-\nu \left(a_0\right)\right|<\epsilon \right.$, $\left.\left|a-a_0\right|<\delta \right)$ should be convex, and $cl\{a\in \mathbb{R},\nu (a)>0\}$ should be compact.

Definition 2

([19]). For the fuzzy number ν, the definition of the β-level set is given by

$${\left[\nu \right]}^{\beta }=\{x\in \mathbb{R}:\nu \left(x\right)\ge \beta \},$$

where $\beta \in (0,1]$ and $x\in \mathbb{R}$.

Definition 3

([20]). The following describes the fuzzy number’s parametric form: $[\underline{\nu }\left(\omega \right),\overline{\nu }\left(\omega \right)]$, where $0\le \omega \le 1$, meeting the requirements below:

• $\underline{\nu }\left(\omega \right)$ should be bounded, increasing function, right continuous at 0 and left continuous over $(0,1]$.
• $\overline{\nu }\left(\omega \right)$ should be bounded, decreasing over $[0,1]$, right continuous at 0.
• $\underline{\nu }\left(\omega \right)$ should be less than or equal to $\overline{\nu }\left(\omega \right)$.

Also, if $\underline{\nu }\left(\omega \right)=\overline{\nu }\left(\omega \right)=0$, then ω is called a crisp number.

Definition 4

([20]). $\alpha :E\times E\to \mathbb{R}$ is taken to be a mapping. Let $p=(\underline{p}\left(\omega \right),\overline{p}\left(\omega \right))$ and $q=(\underline{q}\left(\omega \right),\overline{q}\left(\omega \right))$ be the two fuzzily represented integers in parametric form. The Hausdorff distance, which is a measure of the separation between p and q, is defined as

$$\alpha (p,q)=\underset{\omega \in [0,1]}{sup}[max\{|\underline{p}\left(\omega \right)-\underline{q}\left(\omega \right)|,|\overline{p}\left(\omega \right)-\overline{q}\left(\omega \right)\left|\right\}].$$

In E, the metric α shall have the following properties:

 1. 

$\alpha (p+q,q+p)=\alpha (p,q)$ for all $p,q\in E$;

 2. 

$\alpha (p\varrho ,q\varrho )=\left|\varrho \right|\alpha (p,q)$ for all $p,q\in E,\varrho \in \mathbb{R}$;

 3. 

$\alpha (p+\xi ,q+\varsigma )\le \alpha (p,q)+\alpha (\xi ,\varsigma )$ for all $p,q,\xi ,\varsigma \in E$;

 4. 

$(E,\alpha )$ is a complete metric space.

Definition 5

([19]). Let $i_1,i_2\in E$. If there exist $i_3\in E$ such that $i_1=i_2+i_3$ then $i_3$ is said to be the H-difference of $i_1$ and $i_2$, represented by $i_1\ominus i_2$.

Definition 6

([21]). Let $\mathsf{\Theta }:\mathbb{R}\to E$ be a fuzzy mapping. Then, Θ is called continuous if for any $ϵ>0\exists ,\kappa >0$ and a fixed value of ${\mathsf{\Lambda }}_0\in \left[{\zeta }_1,{\zeta }_2\right]$, we have

$$\alpha \left(\mathsf{\Theta }\left(\mathsf{\Lambda }\right),\mathsf{\Theta }\left({\mathsf{\Lambda }}_0\right)\right)<ϵ\mathit{whenever}\left|\mathsf{\Lambda }-{\mathsf{\Lambda }}_0\right|<\kappa .$$

Definition 7

([22]). By allowing ω to be a continuous fuzzy function on $[0,b]\subseteq \mathbb{R}$, we may define a fuzzy fractional integral in the Riemann–Liouville sense that corresponds to t.

$$J^{\beta }\omega \left(x\right)=\frac{1}{\mathsf{\Gamma }\left(\beta \right)}{\int }_0^x{(x-\zeta )}^{\beta -1}\omega \left(\zeta \right)d\zeta ,\mathit{where}\beta ,\zeta \in (0,\infty ).$$

Consider $\omega \in C^F[0,b]\cap L^F[0,b]$, where $C^F[0,b]$ and $L^F[0,b]$ are the spaces of fuzzy continuous functions and fuzzy Lebesgue integrable functions, respectively. The fuzzy fractional integral is defined as follows.

$${\left[J^{\beta }\omega \left(x\right)\right]}_p=\left[J^{\beta }{\omega }_p\left(x\right),J^{\beta }{\overline{\omega }}_p\left(x\right)\right],0\le p\le 1,$$

where

$$\begin{array}{cc}& J^{\beta }{\underline{\omega }}_p\left(x\right)=\frac{1}{\mathsf{\Gamma }\left(\beta \right)}{\int }_0^x{(x-\zeta )}^{\beta -1}{\underline{\omega }}_p\left(x\right)d\zeta ,\beta ,\zeta \in (0,\infty ).\hfill \\ & J^{\beta }{\overline{\omega }}_p\left(x\right)=\frac{1}{\mathsf{\Gamma }\left(\beta \right)}{\int }_0^x{(x-\zeta )}^{\beta -1}{\overline{\omega }}_p\left(x\right)d\zeta ,\beta ,\zeta \in (0,\infty ).\hfill \end{array}$$

Definition 8

([16]). If a fuzzy function $\omega \in C^F[0,b]\cap L^F[0,b]$ is such that $\omega =\left[{\omega }_p\left(x\right)\right.$, $\left.{\overline{\omega }}_p\left(x\right)\right],0\le p\le 1$ and $x_1\in (0,b)$, then the fuzzy fractional Caputo’s derivative is defined as

$${\left[D^{\beta }\omega \left(x_0\right)\right]}_p=\left[D^{\beta }{\underline{\omega }}_p\left(x_0\right),D^{\beta }{\overline{\omega }}_p\left(t_0\right)\right],0\le \beta \le 1,$$

where

$$\begin{array}{cc}\hfill D^{\beta }{\underline{\omega }}_p\left(x_0\right)& =\frac{1}{\mathsf{\Gamma }(n-\beta )}{\left[{\int }_0^x{(x-\zeta )}^{n-\beta -1}\frac{d^n}{d{\zeta }^n}{\omega }_p\left(\zeta \right)d\zeta \right]}_{x=x_0}\hfill \\ \hfill D^{\beta }{\overline{\omega }}_p\left(x_0\right)& =\frac{1}{\mathsf{\Gamma }(n-\beta )}{\left[{\int }_0^x{(x-\zeta )}^{n-\beta -1}\frac{d^n}{d{\zeta }^n}{\overline{\omega }}_p\left(\zeta \right)d\zeta \right]}_{x=x_0}\hfill \end{array}$$

whenever $n=\lceil \beta \rceil$ and the integrals on the right sides converge.

3. Formulation of Fuzzy Fractional SIR Model

Fuzzy calculus and fractional order differential equations (FODEs) have lately been added to the realm of differential equations and modern calculus. Then, the definition of FODEs was enlarged to cover fuzzy FODEs [20,21,23]. To prove the existence and uniqueness theory of solutions, many researchers have researched FODEs and fuzzy integral equations, for example, [17,24,25,26,27,28]. When working with fuzzy FODEs, it takes a long time to compute more accurate solutions to each fuzzy FODEs. Numerous methods have been developed by mathematicians to solve fuzzy FODEs, including perturbation methods, integral transform methods, and spectral techniques [5,18,19,22,29,30]. Figure 1 shows the flow chart of the SIR model.

In this study, pay close attention to the following Caputo fractional-order model in [2] with the susceptible population $S\left(t\right)$, the infected population $I\left(t\right)$, and the removed population $R\left(t\right)$ being the three groups that make up the entire population $N\left(t\right)$ and fractional-order $\alpha$:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{D}^{\alpha }S\left(t\right)=\hfill & (1-p)\pi -\beta SI-\mu S\hfill \\ D^{\alpha }I\left(t\right)=\hfill & \beta SI-(\gamma +\mu )I\hfill \\ D^{\alpha }R\left(t\right)=\hfill & p\pi +\gamma I-\mu R,\hfill \end{array}\right.\end{array}$$

(1)

where the initial states are defined as $S\left(0\right)\ge 0, I\left(0\right)\ge 0$ and $R\left(0\right)\ge 0$.

4. Existence and Uniqueness Results

This section describes the existence and distinctiveness of the solution to the following fuzzy fractional model. The description of the prescribed model is given in

Table 1. The description of the prescribed model.

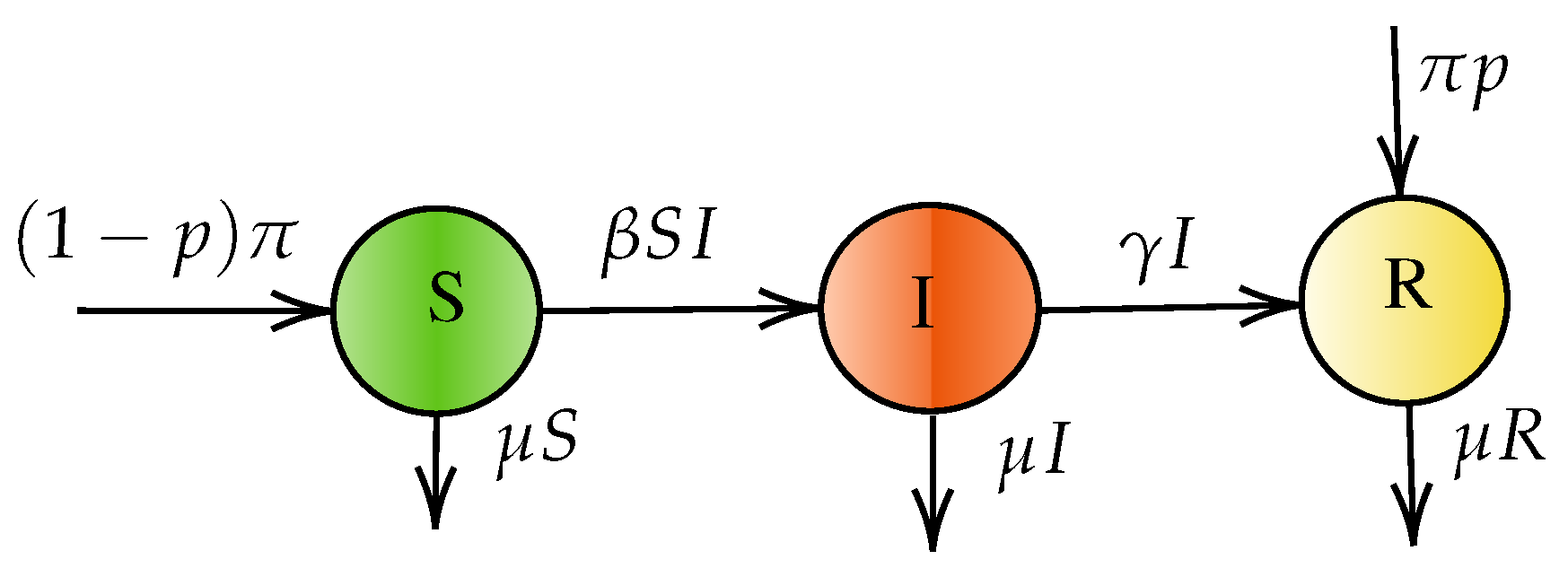
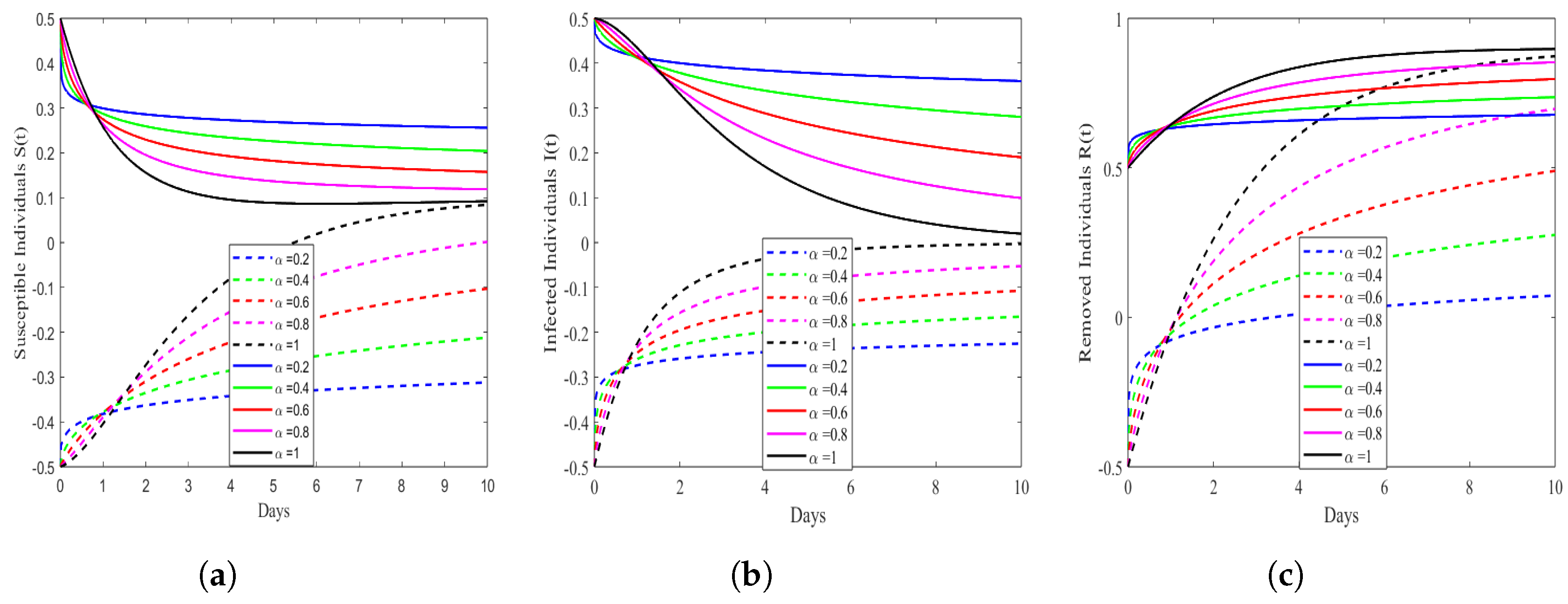
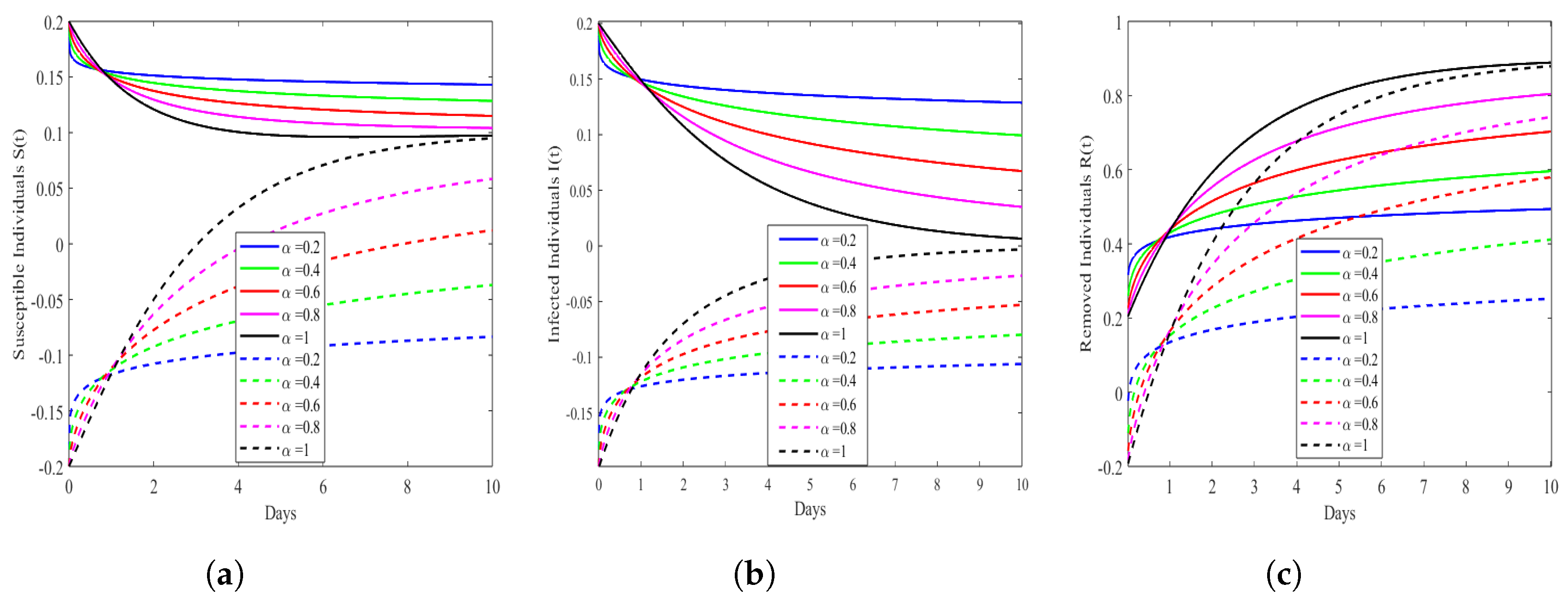
Parameters	Representation	Values
$\mu$	Natural death rate	0.4
$\pi$	Birth rate	0.4
p	Fraction of the vaccinated population at birth	0.9
$\beta$	Contact rate of susceptible individual	0.8
$\gamma$	Infected individuals recover at a rate	0.03

. Here, we looked into a set of fuzzy fractional-order differential equations in the sense of Caputo, which depicts an epidemic model of childhood sickness with initial data uncertainty. For $0<\alpha \le 1$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{D}^{\alpha }S\left(t\right)=\hfill & (1-\tilde{p})\tilde{\pi }-\tilde{\beta }SI-\tilde{\mu }S\hfill \\ D^{\alpha }I\left(t\right)=\hfill & \tilde{\beta }SI-(\tilde{\gamma }+\tilde{\mu })I\hfill \\ D^{\alpha }R\left(t\right)=\hfill & \tilde{p}\tilde{\pi }+\tilde{\gamma }I-\tilde{\mu }R.\hfill \end{array}\right.\end{array}$$

(2)

Now, the right hand side of (2) becomes

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\psi (t,S(t\left)\right)=\hfill & (1-\tilde{p})\tilde{\pi }-\tilde{\beta }SI-\tilde{\mu }S\hfill \\ \rho (t,I(t\left)\right)=\hfill & \tilde{\beta }SI-(\tilde{\gamma }+\tilde{\mu })I\hfill \\ \mathsf{{\rm Y}}(t,R(t\left)\right)=\hfill & \tilde{p}\tilde{\pi }+\tilde{\gamma }I-\tilde{\mu }R,\hfill \end{array}\right.\end{array}$$

(3)

where the fuzzy functions are $\psi ,\rho ,\mathsf{{\rm Y}}$. Then, for $r\in [0,1],$ model (2) gets the form

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{D}^{\alpha }S\left(t\right)=\hfill & \psi (t,S(t\left)\right)\hfill \\ D^{\alpha }I\left(t\right)=\hfill & \rho (t,I(t\left)\right)\hfill \\ D^{\alpha }R\left(t\right)=\hfill & \mathsf{{\rm Y}}(t,R(t\left)\right),\hfill \end{array}\right.\end{array}$$

(4)

with fuzzy initial conditions

$$\begin{array}{cc}\hfill \tilde{S}(0,r)=& [\underline{S}(0,r),\overline{S}(0,r)]\hfill \\ \hfill \tilde{I}(0,r)=& [\underline{I}(0,r),\overline{I}(0,r)]\hfill \\ \hfill \tilde{R}(0,r)=& [\underline{R}(0,r),\overline{R}(0,r)].\hfill \end{array}$$

Now, using fuzzy fractional integral $I^{\alpha }$ and using initial conditions, one can get

$$\begin{array}{c}\hfill \left\{\begin{array}{c}S\left(t\right)=\tilde{S}(0,r)+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}\psi (s,S\left(s\right))ds\hfill \\ I\left(t\right)=\tilde{I}(0,r)+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}\rho (s,I\left(s\right))ds\hfill \\ R\left(t\right)=\tilde{R}(0,r)+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}\mathsf{{\rm Y}}(s,R\left(s\right))ds.\hfill \end{array}\right.\end{array}$$

(5)

Banach Space is defined as follows based on the fuzzy norm $\mathbb{B}={\mathbb{B}}_1\times {\mathbb{B}}_2\times {\mathbb{B}}_3$ $∥S\left(t\right),I\left(t\right),R\left(t\right)∥$=${max}_{t\in [0,T]}[S\left(t\right)+I\left(t\right)+R\left(t\right)]$.

Thus, the Equation (5) is rewritten as

$$\tilde{g}\left(t\right)=\tilde{g}(0,r)+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\varsigma )}^{\alpha -1}\mathsf{\Theta }(\varsigma ,\tilde{g}\left(\varsigma \right))d\varsigma ,$$

(6)

where

$$\tilde{g}\left(t\right)=\left\{\begin{array}{cc}\hfill & S\left(t\right)\hfill \\ \hfill & I\left(t\right)\hfill \\ \hfill & R\left(t\right),\hfill \end{array}\right.$$

$$\tilde{g}(0,r)=\left\{\begin{array}{cc}\hfill & \tilde{S}(0,r)\hfill \\ \hfill & \tilde{I}(0,r)\hfill \\ \hfill & \tilde{R}(0,r),\hfill \end{array}\right.$$

$$\mathsf{\Theta }(t,\tilde{g}\left(t\right))=\left\{\begin{array}{cc}\hfill & \psi (t,S(t\left)\right)\hfill \\ \hfill & \rho (t,I(t\left)\right)\hfill \\ \hfill & \mathsf{{\rm Y}}(t,R(t\left)\right).\hfill \end{array}\right.$$

In order to obtain the required results, we consider the following assumptions

• $\left(\mathbb{A}1\right)$ There exists a constant $P_g>0$ and $Q_g>0\ni$

  $$\begin{array}{c}\hfill \left|\mathsf{\Theta }(t,\tilde{g}\left(t\right))\right|\le P_g\left|\tilde{g}\left(t\right)\right|+Q_g.\end{array}$$

  (7)
• $\left(\mathbb{A}2\right)$ There exists constant $K_g>0$ such that for each ${\tilde{g}}_1\left(t\right),{\tilde{g}}_2\left(t\right)\in \mathbb{B}$ we have

  $$\begin{array}{c}\hfill |\mathsf{\Theta }(t,{\tilde{g}}_1\left(t\right))-\mathsf{\Theta }(t,{\tilde{g}}_2\left(t\right))|\le K_g|{\tilde{g}}_1\left(t\right)-{\tilde{g}}_2\left(t\right)|.\end{array}$$

  (8)

Theorem 1.

By using the assumption $\left(\mathbb{A}1\right)$ the prescribed system has atleast one solution.

Proof. 

$\mathcal{O}=\{\tilde{g}\left(t\right)\in \mathbb{B}:|\left|\tilde{g}\left(t\right)\right||\le r\}\subset \mathbb{B}$ be a convex and closed fuzzy set is considered. Taking the mapping $\nu :\mathcal{O}\to \mathcal{O}$ such that

$$\nu \left(\tilde{g}\left(t\right)\right)=\tilde{g}(0,r)+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\varsigma )}^{\alpha -1}\mathsf{\Theta }(\varsigma ,\tilde{g}\left(\varsigma \right))d\varsigma .$$

For any $\tilde{g}\left(t\right)\in \mathcal{O}$, one can obtain

$$\begin{array}{cc}\hfill \parallel \nu \left(\tilde{g}\left(t\right)\right)\parallel =& \underset{t\in [0,T]}{max}|\tilde{g}(0,r)+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\varsigma )}^{\alpha -1}\mathsf{\Theta }(\varsigma ,\tilde{g}\left(\varsigma \right))d\varsigma |\hfill \\ \hfill & \le |\tilde{g}(0,r)|+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\varsigma )}^{\alpha -1}\left|\mathsf{\Theta }(\varsigma ,\tilde{g}\left(\varsigma \right))\right|d\varsigma \hfill \\ \hfill & \le |\tilde{g}(0,r)|+\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\varsigma )}^{\alpha -1}[P_g\left|\tilde{g}\left(t\right)\right|+Q_g]d\varsigma \hfill \\ \hfill & \le |\tilde{g}(0,r)|+\frac{t^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}[P_g\left|\tilde{g}\left(t\right)\right|+Q_g].\hfill \end{array}$$

Here, $\nu \left(\mathcal{O}\right)\subset \mathcal{O}$ and hence we conclude that $\nu$ is bounded.

Next, completely continuous property of the operator $\nu$ is proved.

For any ${\nu }_1,{\nu }_2\in [0,T]$ such that ${\nu }_2>{\nu }_1$ gives

$$\begin{array}{cc}\hfill \parallel (\nu \left(\tilde{g}\left(t\right)\right)\left({\nu }_2\right)-(\nu \left(\tilde{g}\left(t\right)\right)\left({\nu }_1\right)\parallel =& |\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{{\nu }_2}{({\nu }_2-\varsigma )}^{\alpha -1}\mathsf{\Theta }(\varsigma ,\tilde{g}\left(\varsigma \right))d\varsigma \hfill \\ \hfill & -\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^{{\nu }_1}{({\nu }_1-\varsigma )}^{\alpha -1}\mathsf{\Theta }(\varsigma ,\tilde{g}\left(\varsigma \right))d\varsigma |\hfill \\ \hfill \le & [{\nu }_2^{\alpha }-{\nu }_1^{\alpha }]\frac{[P_g\left|\tilde{g}\left(t\right)\right|+Q_g]}{\mathsf{\Gamma }(\alpha +1)}\to 0,as{\nu }_2\to {\nu }_1,\hfill \end{array}$$

which implies that $\parallel (\nu \left(\tilde{g}\left(t\right)\right)\left({\nu }_2\right)-(\nu \left(\tilde{g}\left(t\right)\right)\left({\nu }_1\right)\parallel \to 0$ as ${\nu }_2\to {\nu }_1.$ As a result, the operator $\nu$ is equi-continuous. The completely continuous nature of the operator $\nu$ is shown by the Arzela–Ascoli theorem. According to Schauder’s fixed point theorem, there is at least one solution to the aforementioned fuzzy fractional model. □

Theorem 2.

The considered system (2) has a single solution under the assumption $\left(\mathbb{A}2\right)$ provided that ${\varphi }^{\alpha }{\mathcal{L}}_{\mathcal{F}}<\mathsf{\Gamma }(\alpha +1)$

Proof. 

Let ${\tilde{g}}_1\left(t\right),{\tilde{g}}_2\left(t\right)\in \mathbb{B}$ then,

$$\begin{array}{cc}\hfill \parallel (\nu \left({\tilde{g}}_{n_1}\left(t\right)\right)-(\nu \left({\tilde{g}}_{n_2}\left(t\right)\right)\parallel =& \underset{t\in [0,T]}{max}|\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\varsigma )}^{\alpha -1}\mathsf{\Theta }(\varsigma ,{\tilde{g}}_{n_1}\left(\varsigma \right))d\varsigma \hfill \\ \hfill & -\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-\varsigma )}^{\alpha -1}\mathsf{\Theta }(\varsigma ,{\tilde{g}}_{n_2}\left(\varsigma \right))d\varsigma |\hfill \\ \hfill \le & \frac{{\varphi }^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{\mathcal{L}}_{\mathcal{F}}|{\tilde{g}}_{n_1}\left(t\right)-{\tilde{g}}_{n_2}\left(t\right)|.\hfill \end{array}$$

Hence, $\nu$ is a contraction. The Banach contraction principle guarantees that the suggested model (2) has just one solution. □

5. Method Description

The primary goal of this section is to use the Laplace transform (LT) [19,22] to determine how to solve the fuzzy fractional model under consideration. In order to obtain the fuzzy LT model, we have

$$\begin{array}{cc}\hfill \mathcal{L}\left[D^{\alpha }S\left(t\right)\right]& =\mathcal{L}\left[\psi \right(t,S\left(t\right)\left)\right]\hfill \\ \hfill \mathcal{L}\left[D^{\alpha }I\left(t\right)\right]& =\mathcal{L}\left[\rho \right(t,I\left(t\right)\left)\right]\hfill \\ \hfill \mathcal{L}\left[D^{\alpha }R\left(t\right)\right]& =\mathcal{L}\left[\mathsf{{\rm Y}}\right(t,R\left(t\right)\left)\right].\hfill \end{array}$$

Under the zero initial condition, one can obtain

$$\begin{array}{cc}\hfill s^{\alpha }\mathcal{L}\left[D^{\alpha }S\left(t\right)\right]& =s^{\alpha -1}\tilde{S}(0,r)+\mathcal{L}\left[\psi (t,S\left(t\right))\right]\hfill \\ \hfill s^{\alpha }\mathcal{L}\left[D^{\alpha }I\left(t\right)\right]& =s^{\alpha -1}\tilde{I}(0,r)+\mathcal{L}\left[\rho (t,I\left(t\right))\right]\hfill \\ \hfill s^{\alpha }\mathcal{L}\left[D_t^{y}R\left(t\right)\right]& =s^{\alpha -1}\tilde{R}(0,r)+\mathcal{L}\left[\mathsf{{\rm Y}}(t,R\left(t\right))\right],\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill \mathcal{L}\left[D^{\alpha }S\left(t\right)\right]& =\frac{1}{s}\tilde{S}(0,r)+\frac{1}{s^{\alpha }}\mathcal{L}\left[\psi (t,S\left(t\right))\right]\hfill \\ \hfill \mathcal{L}\left[D^{\alpha }I\left(t\right)\right]& =\frac{1}{s}\tilde{I}(0,r)+\frac{1}{s^{\alpha }}\mathcal{L}\left[\rho (t,I\left(t\right))\right]\hfill \\ \hfill \mathcal{L}\left[D^{\alpha }R\left(t\right)\right]& =\frac{1}{s}\tilde{R}(0,r)+\frac{1}{s^{\alpha }}\mathcal{L}\left[\mathsf{{\rm Y}}(t,R\left(t\right))\right].\hfill \end{array}$$

Based on the infinite series solution, one can obtain

$$\begin{array}{cc}\hfill S\left(t\right)=& \sum _{n=0}^{\infty }{S}_n\left(t\right)\hfill \\ \hfill I\left(t\right)=& \sum _{n=0}^{\infty }{I}_n\left(t\right)\hfill \\ \hfill R\left(t\right)=& \sum _{n=0}^{\infty }{S}_n\left(t\right).\hfill \end{array}$$

From (2), the nonlinear term can be rewritten as follows:

$$\begin{array}{cc}\hfill S\left(t\right)I\left(t\right)=& \sum _{n=0}^{\infty }{B}_{1,n}.\hfill \end{array}$$

Here, $B_{1,n}$ represents the Adomian polynomial for nonlinear term. The above equations can be obtain that

$$\begin{array}{cc}\hfill \mathcal{L}\left[\sum _{n=0}^{\infty }{S}_n\left(t\right)\right]=& \frac{1}{s}\tilde{S}(0,r)+\frac{1}{s^{\alpha }}\mathcal{L}\left[\psi (t,\sum _{n=0}^{\infty }{S}_n\left(t\right))\right]\hfill \\ \hfill \mathcal{L}\left[\sum _{n=0}^{\infty }{I}_n\left(t\right)\right]=& \frac{1}{s}\tilde{I}(0,r)+\frac{1}{s^{\alpha }}\mathcal{L}\left[\rho (t,\sum _{n=0}^{\infty }{I}_n\left(t\right))\right]\hfill \\ \hfill \mathcal{L}\left[\sum _{n=0}^{\infty }{R}_n\left(t\right)\right]=& \frac{1}{s}\tilde{R}(0,r)+\frac{1}{s^{\alpha }}\mathcal{L}\left[\mathsf{{\rm Y}}(t,\sum _{n=0}^{\infty }{R}_n\left(t\right))\right].\hfill \end{array}$$

Taking inverse LT, we have

$$\begin{array}{cc}\hfill \sum _{n=0}^{\infty }{S}_n\left(t\right)=& \tilde{S}(0,r)+{\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}\left[\psi (t,\sum _{n=0}^{\infty }{S}_n\left(t\right))\right]\right]\hfill \\ \hfill \sum _{n=0}^{\infty }{I}_n\left(t\right)=& \tilde{I}(0,r)+{\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}\left[\rho (t,\sum _{n=0}^{\infty }{I}_n\left(t\right))\right]\right]\hfill \\ \hfill \sum _{n=0}^{\infty }{R}_n\left(t\right)=& \tilde{R}(0,r)+{\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}\left[\mathsf{{\rm Y}}(t,\sum _{n=0}^{\infty }{R}_n\left(t\right))\right]\right].\hfill \end{array}$$

The terms in the parametric form are compared and we have

$$\begin{array}{cc}\hfill {\underline{S}}_0\left(t\right)=& \underline{S}(0,r),{\overline{S}}_0\left(t\right)=\overline{S}(0,r)\hfill \\ \hfill {\underline{I}}_0\left(t\right)=& \underline{I}(0,r),{\overline{I}}_0\left(t\right)=\overline{I}(0,r)\hfill \\ \hfill {\underline{R}}_0\left(t\right)=& \underline{R}(0,\zeta ),{\overline{R}}_0\left(t\right)=\overline{R}(0,\zeta )\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\underline{S}}_1\left(t\right)=& {\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}\left[(1-\tilde{p})\tilde{\pi }-\tilde{\beta }{\underline{S}}_0{\underline{I}}_0-\tilde{\mu }{\underline{S}}_0\right]\right]\hfill \\ \hfill {\overline{S}}_1\left(t\right)=& {\mathcal{L}}^{-1}\left[\frac{1}{s^{\alpha }}\mathcal{L}\left[(1-\tilde{p})\tilde{\pi }-\tilde{\beta }{\overline{S}}_0{\overline{I}}_0-\tilde{\mu }{\overline{S}}_0\right]\right].\hfill \end{array}$$

In light of the aforementioned ideas, it is easy to get the remaining terms. Thus, the generic series solutions are written as follows:

$$\begin{array}{cc}\hfill \underline{S}\left(t\right)=& {\underline{S}}_0\left(t\right)+{\underline{S}}_1\left(t\right)+{\underline{S}}_2\left(t\right)+\dots ,\overline{S}\left(t\right)={\overline{S}}_0\left(t\right)+{\overline{S}}_1\left(t\right)+{\overline{S}}_2\left(t\right)+\dots \hfill \\ \hfill \underline{I}\left(t\right)=& {\underline{I}}_0\left(t\right)+{\underline{I}}_1\left(t\right)+{\underline{I}}_2\left(t\right)+\dots ,\overline{I}\left(t\right)={\overline{I}}_0\left(t\right)+{\overline{I}}_1\left(t\right)+{\overline{I}}_2\left(t\right)+\dots \hfill \\ \hfill \underline{R}\left(t\right)=& {\underline{R}}_0\left(t\right)+{\underline{R}}_1\left(t\right)+{\underline{R}}_2\left(t\right)+\dots ,\overline{R}\left(t\right)={\overline{R}}_0\left(t\right)+{\overline{R}}_1\left(t\right)+{\overline{R}}_2\left(t\right)+\dots \hfill \end{array}$$

Remark 1.

By using the fixed point theorem and Banach contraction principle, the prescribed model has one solution. In addition, the numerical findings of the fuzzy Laplace transform based on the Adomian decomposition enable the comprehension of the physical behavior of a childhood disease model.

6. Numerical Simulation Results and Discussions

This section provides a numerical example showing the effectiveness of the proposed approach using various parameter values. To find the solution to the FFDEs, a range of numerical and analytical methods can be used. For finding the numerical outcomes, we used MATLAB 2017b. We simulate the numerical results by using different fractional order $\alpha$ = 0.2, 0.4, 0.6, 0.8 and 1. The initial conditions are taken as $S\left(0\right)=1$, $I\left(0\right)=0.5$, and $R\left(0\right)=0$.

From the graphical results it is clear that the result obtained by using the proposed method is very efficient. Furthermore, the present method is also shown to be capable of accurately predicting the behavior of the variables in the region under consideration. As shown in Figure 2 and Figure 3, various compartments exhibit a wide range of dynamics. We effectively utilized various fractional order values, considering uncertainties, to enhance the robustness of our study. By accounting for uncertainties, we strengthened the reliability of our findings, contributing to a more thorough and impactful study. As the susceptible individual value declines, there is a corresponding increase in the infected individual, resulting in the spread of infection at varying rates influenced by distinct fractional orders. From these figures, we can easily observe that the proposed fractional-order method is more efficient in the SIR epidemic model for childhood diseases.

7. Conclusions

This research delved into the intricate dynamics of the SIR model, specifically focusing on its implications for the healthcare system. To capture the nuanced behavior of childhood diseases, a novel SIR epidemic model is formulated, leveraging the Caputo derivative fractional-order method. The model’s robustness and singular characteristics are rigorously investigated and confirmed through fixed point theory, establishing the uniqueness and existence of a solution. In order to gain a deeper insight into the dynamic structures inherent in childhood diseases, the study employs two powerful analytical tools: fuzzy Laplace transform and Adomian decomposition transform. By using a fuzzy fractional differential equation with Laplace transformations and their inverses, the numerical results have been obtained for the compartments of the addressed system.