A Material Allocation Model for Public Health Emergency under a Multimodal Transportation Network by Considering the Demand Priority and Psychological Pain

Abstract

In a public health emergency, residents urgently require a large number of rescue materials for treatment or protection. These rescue materials are usually located far from the emergency area. The government must organize rescue materials transportation by selecting suitable transport modes. Thus, we propose a material allocation model for public health emergencies under a multimodal transportation network to determine the best rescue material supply route. In this model, we set the demand priorities according to the emergency degrees to decide the transportation sequence. Meanwhile, we introduce the psychological pain cost brought by the rescue material shortage into the proposed model to trade off the priority and fairness of demand. Having compared it to the research literature, this is the first study that considers multiple categories of materials, absolute pain costs, relative pain costs and demand priority under multimodal transportation. The research problem is formulated into an integer programming model, and we develop a modified genetic algorithm to solve it. A set of numerical examples are conducted to test the performance of the proposed algorithm, and to investigate features and applications of the proposed model. The results indicate that the modified genetic algorithm performs better in the calculation examples at different scales. For small-scale instances, the algorithm produces consistent results with Gurobi. As the instance size increases, Gurobi fails to find the optimal solution within 1800 s, while this algorithm is able to find the optimal solution within an acceptable time frame. Additionally, when dealing with large-scale instances, the algorithm exhibits a significant advantage in terms of runtime. Sensitivity analysis of key factors indicate that (1) Adjusting the relative pain cost coefficient can make the best trade-off between fairness, economy and timeliness; (2) Compared with a single mode of transport, multimodal transport can reduce the psychological pain cost and the logistics cost; (3) Improving the loading and unloading capacity of nodes can reduce the delivery time of materials and the psychological pain cost of residents, but the influence of other factors and cost-effectiveness need to be considered.

1. Introduction

In public health emergencies, the supply of rescue materials has a significant impact on the efficiency of rescue and epidemic control. Local rescue supply cannot meet the demand of residents during severe outbreak, such as COVID-19. Consequently, the government must organize the transportation of rescue materials far from the epidemic area to address the material shortage. To ensure the rapid and extensive supply of rescue materials, multiple modes of transportation should be used. How to optimize the route for multimodal transportation is a key challenge in material allocation tasks. Previous studies have addressed this challenge by proposing various models and structures. For example, Maghfiroh et al. [1] proposed a multi-modal distribution model considering land, air and ship within a three-tier relief network. Chen et al. [2] proposed a three-tier multimodal transport network structure for the cross-regional dispatch of emergency supplies. The objective of these studies was to minimize rescue time and maximize rescue utility. However, in the context of public health emergencies, material allocation should consider the demand priority for curbing the spread of the epidemic effectively. Tofighi et al. [3] determined the priority of demand points based on the degree of earthquake damage and social conditions. In the case of shortage of relief resources, demand points with higher priorities were assigned first. Zhu et al. [4] used the tolerable pain duration of victims during transportation to characterize the rescue priority of victims with different degrees of injury. They constructed an emergency rescue path model that considered the same and different degrees of injury. Considering the psychological pain and fairness of affected individuals is a crucial aspect of humanitarian relief operations, especially from the perspective of the psychological state of the affected people. Cotes et al. [5] proposed a facility siting model with prepositioned supplies. Their model specifically takes into account the cost of deprivation, an estimate used to quantify the human suffering caused by scarcity. Jamali et al. [6] proposed a stochastic programming model considering different scenarios to weigh relief costs, deprivation costs and carbon emissions in humanitarian logistics. The cost of deprivation was affected by the severity of the different injuries of the patients, aiming to strike a balance between different aspects of sustainability. These studies highlight the importance of considering the psychological pain cost in the rescue material allocation to alleviate the psychological trauma of the affected people and improve the rescue efficiency.

To the best of our knowledge, there have been no studies focusing on the trade-off between psychological pain cost and the demand priority in the allocation of rescue material. Therefore, this paper formulates a mixed integer programming model, which takes the psychological pain costs and material allocation costs as the decision-making objectives. The psychological pain costs are divided into absolute and relative pain costs. The absolute pain cost is an economic valuation of the psychological pain of those affected by a public health emergency without rescue material supply. The relative pain cost is expressed by the absolute value of the deviation between the two absolute pain costs, characterizing the fairness and timeliness in rescue operations. To highlight the priority requirements of emergency rescue, we introduce demand priority to represent the urgency of different epidemic areas that affect the material allocation sequence. To solve the proposed model, we have developed an improved genetic algorithm. A set of case studies is conducted to illustrate the influence of the demand priority and psychological pain on the rescue material allocation. This study can provide theoretical guidance and decision-making support for emergency supplies in public health emergencies, ultimately improving the efficiency of emergency rescue efforts.

The rest of this paper is organized as follows: Section 2 reviews the literature related to the problem of rescue material allocation. Section 3 proposes the mixed integer programming model for the rescue material allocation problem. Section 4 presents a modified genetic algorithm to solve the proposed model. Section 5 conducts case studies to evaluate the performance of the solution algorithm and draw managerial insights. Section 6 applies the proposed model and algorithm to a real case. Finally, Section 7 concludes the paper and discusses the direction for future research.

2. Literature Review

The allocation of emergency materials is an indispensable part of responding to public health emergencies, natural disasters and other emergencies. In the field of emergency material allocation, early research focused on single-level logistics networks, where emergency materials are distributed from the distribution center to the demand. For example, Hu et al. [7] considered the situation of dispatching from a single emergency material supply point to multiple emergency points and explored the application of container intermodal transportation in the distribution of emergency materials to optimize the path of the emergency material supply chain. In contrast, Zhang et al. [8] considered the dispatching of multiple emergency warehouses to multiple emergency points and minimized the total time of material dispatching as the goal. Abounacer et al. [9] further studied the multi-objective siting–transportation problem for disaster response, aiming to determine the number, location and tasks of distribution centers and optimize material distribution. Lyu et al. [10] focused on the shortage of materials at multiple supply points and multiple disaster-affected points in the early post-disaster period, taking into account efficiency and fairness, and built an emergency material distribution model to efficiently solve the problem of emergency material allocation under scarcity. Zhu et al. [11] considered the heterogeneous psychological pain of the affected people in post-disaster emergency rescue and constructed a dynamic scheduling model of emergency supplies with two levels of heterogeneous behavior. These studies focused on the single-level allocation of emergency materials from different perspectives. However, the multi-level allocation of emergency materials is common in real emergencies, and it is necessary to consider the decision-making coordination between multiple levels to obtain a reasonable distribution scheme of emergency materials.

Research on multi-level emergency material allocation has gradually attracted attention in recent years. In this type of network, emergency materials need to be transported from the central warehouse to the distribution center, and then delivered to the demand point. Such a multi-level material allocation problem makes it more complicated to optimize the transportation routes and quantities of emergency materials. Tofighi et al. [3] studied the problem of a two-stage humanitarian logistics network design, including central warehouses, local distribution centers and demand points, and developed a two-stage scenario planning approach. This method involves determining the location of the central warehouse and the local distribution center in the first stage, and developing relief plans according to different situations in the second stage. At the same time, Pradhananga et al. [12] considered the deprivation cost caused by the delay in the delivery of emergency supplies and proposed an integrated three-level network model of emergency preparation, emergency supplies distribution and response to ensure the efficient distribution of supplies. Noham et al. [13] studied the two-level humanitarian supply chain design problem, considering pre-disaster and post-disaster scenarios, where the optimal warehouse location was determined before the disaster and the distribution of materials at the demand point is determined after the disaster to improve the performance of the entire supply chain. Song et al. [14] considered the waiting situation of emergency vehicles in the emergency distribution centers, and proposed a multi-material, multi-level distribution emergency material allocation plan optimization model to determine whether vehicles need to wait. Wang et al. [15] proposed a three-level distribution network dynamic allocation model of emergency supplies with multiple collection and distribution points, multiple distribution centers and multiple disaster points by introducing the proportion of material demand shortage into the exponential utility function to measure fairness. It aims to consider efficiency and fairness in the multi-stage distribution of large-scale disaster emergency relief materials, and further reduce costs. While these studies provide new ideas and methods for multi-level emergency material scheduling, further research is needed considering the real emergency. For example, Erbeyoğlu et al. [16] proposed a two-level relief network design model under humanitarian logistics to achieve feasible, efficient and equitable post-disaster distribution plans under different disaster scenarios. Shan et al. [17] studied the cross-regional distribution of center–distribution and center–demand point three-level dynamic material dispatching network considering factors such as timeliness differences, geographical dispersion and capital consumption of emergency materials across regions. Kawase et al. [18] study multi-level relief stock allocation strategies in humanitarian logistics, posing a dynamic stochastic optimization problem.

Considering the requirements for efficient allocation and cost of rescue materials in emergencies, multimodal transportation is used to transport emergency materials based on the characteristics and complementarities of different transportation modes. Thus, optimizing the allocation routes in a multimodal transportation network should consider the coordination and conversion between different transportation modes, as well as factors such as transportation costs and speeds of different transportation modes. Xiong et al. [19] conducted a comprehensive study that considered time window constraints, road damage and mixed loading of various emergency materials. They focused on the multi-level location routing problem of multimodal transportation distribution of emergency materials after the earthquake, to achieve the timely and fair distribution of emergency materials. On this basis, Ning T. et al. [20] proposed a two-stage joint transportation method of medical supplies considering capacity constraints. In the first stage, temporary transfer points are determined, and the construction of a “helicopter-vehicle” joint transportation network structure for medical supplies is considered; The second stage determines the transport routes based on clustering; effectively reducing the number of vehicles. To further optimize the scheduling strategy, Zhang et al. [21] established a two-tier optimal scheduling model for emergency supplies considering multimodal transport. The upper-level model considered multimodal transport and aimed at the shortest transportation time; the lower-level model emphasized the fairness in emergency material distribution, aiming to minimize the variance in material allocation at each demand point, ensuring the timeliness and fairness of emergency material dispatch. Additionally, Gao et al. [22] studied the site selection-combined transportation problem of large-scale emergency material deployment after an earthquake, taking into account timeliness and fairness, and considering the coordinated combined transportation of emergency materials by road, aviation and railway. Furthermore, Li et al. [23] established a multimodal transport hub-radiation comprehensive emergency rescue material transportation network to determine the location of candidate hub nodes and transportation plans for different modes of transportation. This made it possible to ensure the timely guarantee of basic living materials and minimize the transportation cost of the transportation company. To address uncertainties, Liu et al. [24] comprehensively considered the dual uncertainties of demand and transportation environment and established an optimization model for the multimodal transportation of emergency supplies with the goal of maximum reliability. The aim is to deliver emergency supplies to their destinations on time and reliably.

Early studies primarily focused on optimizing rescue operations in terms of timeliness and cost-effectiveness. However, in recent years, more and more studies have turned their focus on humanitarian logistics and consider the psychological conditions of the affected people. They introduce the economic value valuation of the psychological pain caused by the disaster-affected people’s inability to obtain materials into the objective function. For example, Cotes et al. [5] incorporated the loss caused by people’s inability to obtain life-sustaining materials as deprivation costs into the decision-making target, and developed a facility siting model with transportation costs, inventory costs, fixed costs of facilities and deprivation costs as targets. Considering the dynamic features, Zhu et al. [25] used risk perception theory and fairness aversion function to quantify the risk perception satisfaction and distribution fairness of the disaster victims regarding the delivery time and quantity of emergency supplies and constructed a multi-stage scheduling model based on psychological perception for emergency supplies allocation, aiming to improve the satisfaction of the disaster victims with the rescue outcomes. Zhu et al. [26] constructed the relative deprivation cost based on the deprivation cost of disaster victims as one of the decision objectives. They studied the dynamic allocation problem of emergency supplies considering fairness to mitigate the trauma of disaster victims and enhanced the rescue fairness by alleviating the psychological trauma of disaster victims. Moreover, Zhang et al. [27] measured the loss of disaster victims waiting for emergency supplies using the deprivation cost function. They integrated emergency facility location, emergency supplies reserve and allocation based on scenarios, to reduce human suffering during and after disasters. Gong et al. [28] considered the psychological factors of disaster victims under an uncertain environment and proposed to construct a risk perception function to describe the psychological risk perception degree of disaster victims for obtaining relief supplies. They developed a multi-period dynamic allocation optimization decision model for emergency supplies, so that decision-makers can choose their attitude toward cost and psychological loss of disaster victims. It is worth noting that Gao et al. [22] proposed to construct a pain cost function to depict the psychological pain degree of disaster victims, with the minimum psychological pain cost and emergency logistics cost of disaster victims as the objective. They constructed a multi-objective programming model for emergency supplies allocation location and intermodal transport. On this basis, Khodaee et al. [29] proposed a humanitarian supply chain model for vaccine distribution during the COVID-19 pandemic, regarded the human injury degree caused by the inability to obtain vaccines and other key items in critical situations such as deprivation function and included them in the decision objectives, with transportation cost, shortage cost, deprivation cost and holding cost as objectives, to minimize human suffering and death toll. Sun et al. [30] took the total deprivation cost and total operation cost caused by delayed access to medical services as objectives and studied a scenario-based robust optimization model, which integrated medical facility location, casualty transportation and material allocation. The objective was to save lives and alleviate human suffering.

However, most of the existing studies on the allocation of emergency supplies are on natural disasters, and there are relatively few studies on the allocation of emergency supplies in the context of public health emergencies. Considering the damage to facilities and roads caused by natural disaster emergencies and the uncertainty of material demand due to the uncertainty of the number of people affected by the disaster, most of the studies on the allocation of natural disaster-related emergency materials consider the stochasticity and uncertainty of some of the parameters in the scheduling process, and there are more studies on the vehicle routing problem and the site selection-routing problem, among others. Meanwhile, the existing literature mainly focuses on the reduction in the cost or time of emergency supplies allocation and the improvement of subjective and objective fairness, and there are fewer studies on the portrayal and reduction of the psychological pain of the disaster victims under the complex rescue scenarios. They have underestimated the combined effects of demand prioritization and psychological distress on the distribution of supplies. Thus, this paper introduces both the demand priority and psychological pain into the multi-type rescue materials allocation under a multimodal transportation network to trade off the priority and fairness of the demand. The aim of our study is to design optimal transportation routes that minimize the total cost of emergency material allocation, including the average psychological pain cost of the affected residents, transportation cost, loading cost and transfer cost. To illustrate the shortcomings of this study and our contribution,

Table 1. Comparison between the related literature and this paper.

Authors and Year	The Number of Distribution Levels	Type of Problem	Multi-Modal Transport	Psychological Pain Cost	Demand Priorities	Multi-Type Materials	Solution Method
Zhang et al. (2012) [8]	One	Allocation					Heuristic algorithm based linear programming
Abounacer et al. (2014) [9]	One	Location–Allocation				√	Epsilon-constraint method
Tofighi et al. (2016) [3]	One	Allocation			√	√	Differential evolution (DE) algorithm
Noham et al. (2018) [13]	One	Location–Allocation					Heuristic algorithm based on Tabu-search
Cotes et al. (2019) [5]	Two	Location		√		√	CPLEX
Zhu et al. (2019) [4]	One	Routing		√	√		Meta-heuristic algorithm based on the ant colony optimization
Xiong et al. (2019) [19]	Two	Allocation	√			√	Hybrid heuristic algorithm
Zhu et al. (2020) [11]	One	Allocation		√			Genetic algorithm
Erbeyoğlu et al. (2020) [16]	Two	Allocation				√	Logic-based Benders decomposition approach
Ning et al. (2021) [20]	Two	Location- Routing	√			√	Quantum bacterial foraging (QBF) algorithm
Gao et al. (2022) [22]	One	Allocation	√	√		√	Genetic algorithm
Khodaee et al. (2022) [29]	Two	Allocation		√			CPLEX
Li et al. (2022) [23]	Two	Allocation	√			√	Grey wolf optimization algorithm
This study	Two	Allocation	√	√	√	√	Modified genetic algorithm

provides a comparative table of modeling studies of emergency supplies allocation.

3. Model Formulation

3.1. Problem Statement

When a public health emergency occurs, it is necessary to transport the multi-type rescue materials from the supply warehouses in different locations to the epidemic area through the transfer centers. In the epidemic area, there are a number of emergency points whose demands for rescue materials are known.

The demands of each emergency point must be satisfied by only one transfer center. These transfer centers are used to collect various types of rescue materials that are transported from different supply warehouses via trains, trucks or airplanes. Subsequently, the packaged materials are distributed to the emergency point by trucks. Each supply warehouse and transfer center has a fixed storage capacity and transfer capacity for rescue materials. In the process of the material allocation shown in Figure 1, the loading sequence in supply warehouses or transfer centers is determined based on the demand priority. The mode selection and volume size of the transportation will be influenced by both logistics and psychological pain costs. The objective of this allocation problem is to determine the best mode and volume of transportation and the corresponding assignments between the transfer centers and emergency points so as to minimize the total cost, including the psychological pain costs, transportation costs, loading costs and transfer costs.

3.2. Notation List

In this section, the meanings of notations used in this paper are described. Notation explanations are given in

Table 2. Notations explanation.

Notation	Description
$I$	Set of supply warehouses, let $i\in I$
$J$	Set of transfer centers, let $j\in J$
$K$	Set of emergency points, let $k\in K$
$N$	Set of material types, let $n\in N$
$M$	Set of transportation modes, let $m\in M,m=1$ indicates train, $m=2$ indicates airplane, $m=3$ indicates truck
$c_{mn}$	The unit transportation cost of material $n$ by transportation mode $m$
$d_{ijm}$	The distance from supply warehouse $i$ to transfer center $j$ by transportation mode $m$
$d_{jk}$	The distance from the transfer center $j$ to emergency point
$v_m$	The average speed of transportation mode $m$
${\gamma }_i$	The loading capacity per unit time of supply warehouse $i$
${\gamma }_j$	The transfer capacity per unit time of transfer center $j$
$O_{mi}$	The number of transportation mode $m$ for supply warehouse $i$
$O_j$	The number of trucks for transfer center $j$
$o_m$	The loading capacity of one vehicle for transportation mode $m$
${\lambda }_k$	The demand priority of emergency point $k$
$h_i$	The unit cost of loading in supply warehouse $i$
$g_j$	The unit transfer cost of transfer center $j$
$Q_{ni}$	The storage capacity of material $n$ in supply warehouse $i$
$R_j$	The transfer capacity of transfer center $j$
$q_{nk}$	The demand of emergency point $k$ for material $n$
${\theta }_{nk}$	The minimum satisfaction rate of emergency point $k$ for material $n$
$T_{mnij}^0$	The departure time of material $n$ from supply warehouse $i$ to transfer center $j$ by transportation mode $m$
$T_{mnij}^1$	The arrival time of material $n$ from supply warehouse $i$ to transfer center $j$ by transportation mode $m$
$T_{nj}^2$	The average completion time of unloading material $n$ in transfer center $j$
$T_{njk}^3$	The average departure time of material $n$ from transfer center $j$ to emergency point $k$
$T_{nk}$	The average departure time of material $n$ from transfer center $j$ to emergency point $k$
$T_n^{\max }$	The maximum delivery time for material $n$
$BigM$	extreme large number
$w_{mnij}$	Transportation volume of material $n$ from supply warehouse $i$ to transfer center $j$ by transportation mode $m$
$w_{njk}$	Transportation volume of material $n$ from transfer center $j$ to emergency point $k$ by trucks
$y_{mnij}$	0–1 variable, when it is equal to 1, it means that material $n$ is transported from supply warehouse $i$ to transfer center $j$ through transportation mode $m$; otherwise, there is no this assignment
$y_{njk}$	0–1 variable, when it is equal to 1, it means that material $n$ is distributed from transfer center $j$ to emergency point $k$; otherwise, there is no this assignment

.

3.3. Cost Component Quantification

In the material allocation problem, the unsatisfied demand at emergency points results in a potential cost, i.e., the psychological pain cost. In the meantime, the transport of rescue materials also incurs the corresponding transportation cost, loading cost and transfer cost. These costs constitute the total cost of the material allocation problem together.

The psychological pain cost includes two components: absolute pain cost and relative pain cost. The former measures the pain, cold, hunger and other pain perceptions caused by not being able to obtain relief supplies in time. On the other hand, the relative pain cost measures the pain caused by differences in the arrival time and distribution of rescue materials. Gao et al. [22] proposed two functions considering psychological factors of disaster victims to describe their psychological pain perception. Based on these two functions, we formulate the absolute pain cost and the relative pain cost, respectively.

The function of the absolute pain cost $A_{nk}$ for emergency point $k$ due to the lack of material is shown as follows:

$$h_n(t)=a_n\exp (b_{n}t)$$

(1)

$$A_{nk}={\displaystyle \sum _{j\in J}{w}_{njk}}{h}_{nk}(T_{nk})+(q_{nk}-{\displaystyle \sum _{j\in J}{w}_{njk}})h_n(\underset{k\in \mathrm{k}}{\max }{T}_{nk})$$

(2)

where $h_n$ is the cost of material scarcity per unit, and $t$ is the duration of material scarcity; $a_n$ and $b_n$ are coefficients, which changes with the type of materials. The cost of scarcity is the economic value of human suffering caused by a lack of access to rescue materials. Thus, the cost of scarcity is a function of the duration of scarcity and the socioeconomic characteristics of the individual. Scarcity costs are characterized by (1) monotonicity. Scarcity costs increase with the duration of scarcity. (2) Convexity. The cost of scarcity increases more and more rapidly as the time of scarcity increases. (3) Nonlinearity. Nonlinearity is a natural consequence of human response to shortages of life-sustaining supplies [31].

The relative pain cost $R_{{nkk}^{\prime }}$ between emergency points $k\in K$ and $k^{\prime }\in K$ for material $n$ is formulated by

$$R_{{nkk}^{\prime }}=\left|A_{nk}-A_{n{k}^{\prime }}\right|,\forall k,k^{\prime }\in K$$

(3)

The psychological pain cost of affected residents $F$, including the average absolute pain cost and relative pain cost, is formulated as follows:

$$F={\displaystyle \sum _{n\in N}{\displaystyle \sum _{k\in K}{A}_{nk}}}+\alpha {\displaystyle \sum _{n\in N}{\displaystyle \sum _{k\in K}{\displaystyle \sum _{k\in K^{\prime }}{R}_{{nkk}^{\prime }}}}}$$

(4)

where $\alpha$ is the relative pain cost coefficient.

The total transportation cost is expressed as

$$Z1={\displaystyle \sum _{m\in M}{\displaystyle \sum _{n\in N}{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{w}_{mnij}}}}{d}_{ij}{c}_{mn}}+{\displaystyle \sum _{n\in N}{\displaystyle \sum _{j\in J}{\displaystyle \sum _{k\in K}{w}_{njk}}{d}_{jk}{c}_{3n}}}$$

(5)

The first term represents the transportation cost from the supply warehouse to the transfer center, and the second term represents the transportation cost from the transfer center to the emergency point.

The total loading at the supply warehouses is expressed as

$$Z2={\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\displaystyle \sum _{n\in N}{\displaystyle \sum _{m\in M}{h}_i{w}_{mnij}}}}}$$

(6)

The total transfer cost at the transfer centers is expressed as

$$Z3={\displaystyle \sum _{n\in N}{\displaystyle \sum _{j\in J}{\displaystyle \sum _{k\in K}{g}_j{w}_{njk}}}}$$

(7)

The total logistics cost of rescue materials, denoted by $Z$, is formulated as

$$Z=Z1+Z2+Z3$$

(8)

3.4. Delivery Time Formula

We study the rescue material allocation problem in a multi-level supply network. This network includes three-level nodes, i.e., supply warehouses, transfer centers and emergency points, and two-level transportation, i.e., from a supply warehouse to a transfer center and from a transfer center to an emergency point. The arrival time of materials at the demand point is considered as the key factor. The average delivery time $T_{nk}$ denotes the time that material $n$ arrives at emergency point $k$. $T_{nk}$ mainly includes four parts time shown in Figure 2, i.e., the loading time at the supply warehouse, the transportation time from the supply warehouse to the transfer center, the transfer time at the transfer center and the transportation time from the transfer center to the emergency point.

$T_{mnij}^0$ denotes the loading time of material $n$ which is transported to transfer center $j$ by transportation mode $m$ at supply warehouse $i$. The loading sequence of rescue materials is determined by the priority of transfer centers. The priority of transfer center $j$ is formulated by ${\displaystyle \sum _{k\in K}{\lambda }_k}{\displaystyle \sum _{n\in N}{w}_{njk}}$, denoted as $\phi$. This section assumes that $\Phi ({\phi }^{\prime },\phi )$ is judgment function, if the value of ${\phi }^{\prime }$ corresponding to transfer center $j^{\prime }$ is greater than the value of $\phi$ corresponding to transfer center $j$; then, the loading priority of the material flowing to transfer center $j^{\prime }$ is higher than that of the material corresponding to transfer center $j$, and at this time, the value of $\Phi ({\phi }^{\prime },\phi )$ is equal to 1, and otherwise it is equal to 0. Thus, the formula of $T_{mnij}^0$ and $\Phi ({\phi }^{\prime },\phi )$ is as follows:

$$\Phi ({\phi }^{\prime },\phi )=\left\{\begin{array}{c}\begin{array}{cc}1\hfill & if{\phi }^{\prime }>\phi \end{array}\\ \begin{array}{cc}0\hfill & if{\phi }^{\prime }\le \phi \end{array}\end{array}\right.$$

(9)

$$T_{mnij}^0=\frac{\{{\displaystyle \sum _{j^{\prime }\in J}\Phi ({\displaystyle \sum _{k\in K}{\lambda }_k{\displaystyle \sum _{n\in N}{w}_{{nkk}^{\prime }},{\displaystyle \sum _{k\in K}{\lambda }_k{\displaystyle \sum _{n\in N}{w}_{njk}}}}})}{w}_{mni{j}^{\prime }}\}+w_{mnij}}{{\gamma }_i}$$

(10)

$T_{mnij}^1$ denotes the arrival time of materials $n$ from the supply point $i$ to the transfer center $j$ by transportation mode $m$, which is formulated by

$$T_{mnij}^1=T_{mnij}^0+d_{ijm}{y}_{mnij}/v_m$$

(11)

$T_{nj}^2$ demotes the average time for material $n$ when all of material $n$ complete unloading at transfer center $j$, which is formulated by

$$T_{nj}^2=\frac{{\displaystyle \sum _{m\in M}{\displaystyle \sum _{i\in I}\{T_{mnij}^1+w_{mnij}/{\gamma }_j\}}}}{‖M‖‖I‖}$$

(12)

$T_{njk}^3$ denotes the departure time of material $n$ from transfer center $j$ to emergency point $k$. The loading sequence of rescue materials is determined by the priority of emergency points. Thus, the formula of $T_{njk}^3$ is as follows:

$$T_{njk}^3=T_{nj}^2+\frac{\left\{{\displaystyle \sum _{k^{\prime }\in K}\Phi ({\lambda }_{k^{\prime }}{\displaystyle \sum _{n\in N}{w}_{{nkk}^{\prime }},{\lambda }_k{\displaystyle \sum _{n\in N}{w}_{njk}}})}{w}_{nj{k}^{\prime }}\right\}+w_{njk}}{{\gamma }_j}$$

(13)

$T_{nk}$ denotes the time for material $n$ to arrive at the emergency point $k$ and is formulated by

$$T_{nk}={\displaystyle \sum _{j\in J}(}{T}_{njk}^3+d_{jk}{y}_{njk}/v_3)$$

(14)

3.5. Material Allocation Model

This paper proposes a material allocation model for public health emergency under a multimodal transportation network by considering the demand priority and psychological pain. The model formulations are as follows:

$$\min H=F+Z$$

(15)

Subject to

$${\displaystyle \sum _{j\in J}{w}_{mn,ij}}\le Q_{n,i};\forall n\in N,i\in I$$

(16)

$${\displaystyle \sum _{m\in M}}{\displaystyle \sum _{n\in N}}{\displaystyle \sum _{i\in I}{w}_{m,n,ij}}={\displaystyle \sum _{n\in N}}{\displaystyle \sum _{k\in K}{w}_{n,jk}}\le R_j,\forall j\in J$$

(17)

$${\displaystyle \sum _{m\in M}}{\displaystyle \sum _{i\in I}{w}_{m,n,ij}}={\displaystyle \sum _{k\in K}{w}_{n,jk}},\forall j\in J,\forall n\in N$$

(18)

$${\displaystyle \sum _{j\in J}{w}_{n,jk}}\le q_{n,k},\forall k\in K,\forall n\in N$$

(19)

$${\displaystyle \sum _{j\in J}{w}_{n,jk}}\ge q_{n,k}\ast {\theta }_{n,k},\forall k\in K,\forall n\in N$$

(20)

$${\displaystyle \sum _{j\in J}}[{\displaystyle \sum _{n\in N}{w}_{m,n,ij}}/o_m]\le O_{m,i},\forall i\in I,\forall m\in M$$

(21)

$${\displaystyle \sum _{k\in K}}[{\displaystyle \sum _{n\in N}{w}_{n,jk}}/o_3]\le O_j,\forall j\in J$$

(22)

$$T_{n,k}\le T_n^{\max }$$

(23)

$$w_{m,n,ij}\le BigM{y}_{m,n,ij},w_{m,n,ij}\ge y_{m,n,ij},\forall i\in I,j\in J,m\in M,n\in N$$

(24)

$$w_{n,jk}\le BigM{y}_{n,jk},w_{n,jk}\ge y_{n,jk},\forall j\in J,k\in K,n\in N$$

(25)

$$y_{n^{\prime },jk}=y_{n,jk},\forall n,n^{\prime }\in N,j\in J,k\in K$$

(26)

$${\displaystyle \sum _{j\in J}{y}_{n,jk}}=1,\forall n\in N,k\in K$$

(27)

$$y_{m,n,ij},y_{n,jk}\in \left\{0,1\right\},\forall m\in M,\forall i\in I,\forall j\in J,\forall k\in K,\forall n\in N$$

(28)

$$w_{m,n,ij},w_{n,jk}\in N,\forall m\in M,\forall i\in I,\forall j\in J,\forall k\in K,\forall n\in N$$

(29)

Equation (15) indicates the minimization of the average psychological pain cost of the affected people and the total logistics cost of rescue materials; Equation (16) indicates that the demand of all emergency points for material $n$ does not exceed the storage capacity of material $n$ in the supply warehouse; Equation (17) indicates that the total amount of materials flowing from the supply warehouses to each transfer center is equal to the total amount of materials flowing from the transfer center to emergency points, and the total amount of materials flowing from the transfer center to emergency points does not exceed the material capacity of the transfer center; Equation (18) indicates that the total amount of materials received by the transfer center is equal to the total amount of materials flowing to emergency points; Equation (19) indicates that the quantity of received material at the emergency point does not exceed the actual material demand of the emergency point; Equation (20) indicates that the quantity of received material at the emergency point must exceed the minimum material demand of the emergency point; Equation (21) indicates that the number of vehicles by the supply warehouse for transportation mode $m$ does not exceed the maximum available quantity; Equation (22) indicates that the number of vehicles by the transfer center does not exceed the maximum available quantity; Equation (23) indicates that the time for material $n$ to reach emergency point $k$ should not exceed the maximum delivery time; Equations (24) and (25) indicate the correspondence between decision variables; Equations (26) and (27) indicate that the emergency point can only be served by one transfer center; Equations (28) and (29) define the domain of decision variables.

4. Modified Genetic Algorithm

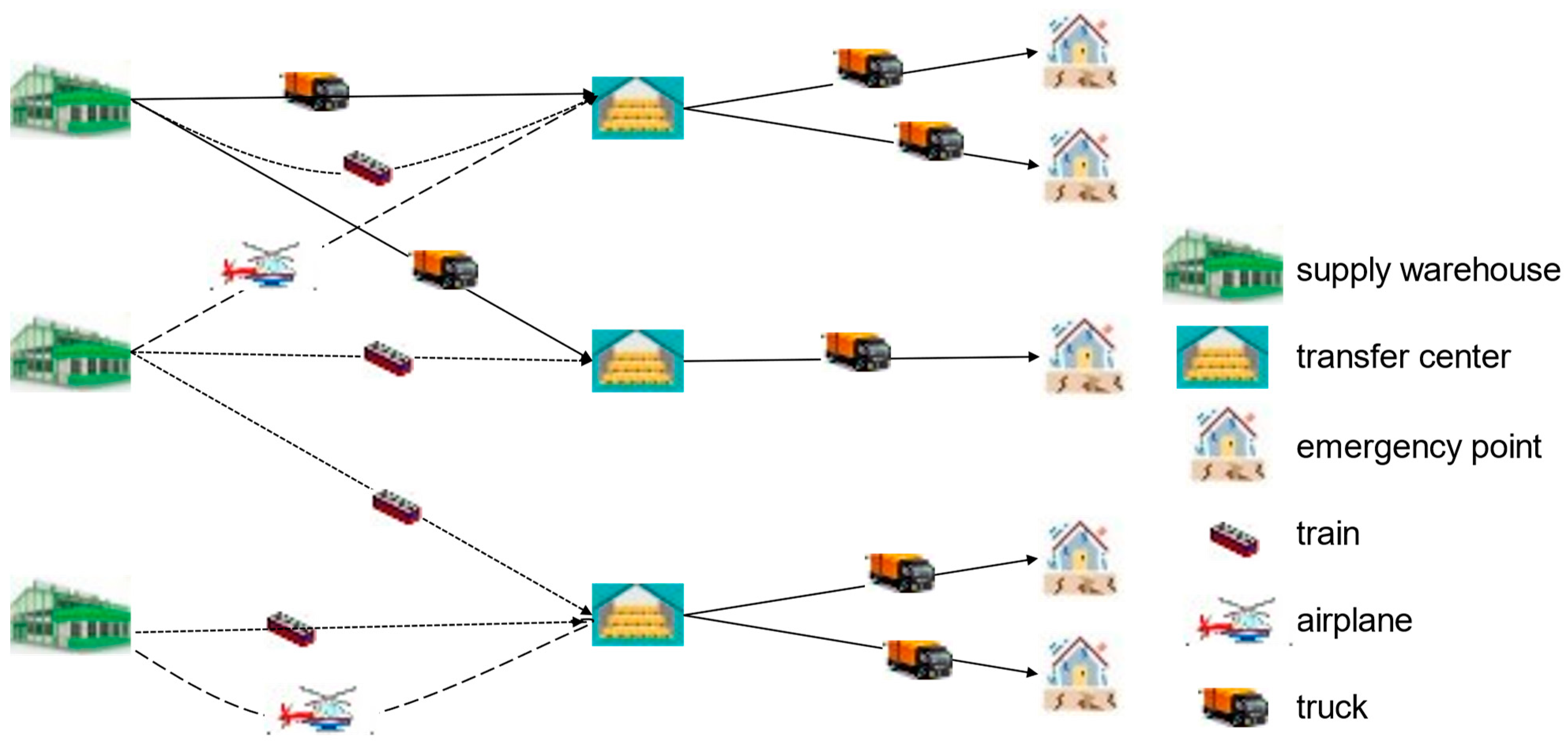
Our proposed model addresses the allocation and transportation problem of emergency materials for multiple categories within the network including multiple supply warehouses, multiple transfer centers and multiple emergency points. The scheduling network is complex and involves a large number of variables, posing significant challenges for solving the difficult problem to solve.

Genetic algorithms are intelligent optimization algorithms that apply Darwin’s natural evolutionary rule of “survival of the fittest” to solve computational problems. Compared with other algorithms, the genetic algorithm has a strong global search ability, can search for the optimal solution in a large-scale solution space and is suitable for solving complex optimization problems. In addition, the genetic algorithm is encoded in a more flexible way and is able to represent a variety of complex solution spaces. In this paper, the flowchart of the modified genetic algorithm for solving the proposed model of allocation of emergency materials is shown in Figure 3.

(1) Parameter Initialization: The input parameters of the genetic algorithm in this model mainly include relevant parameters such as the supply and demand of materials, emergency priorities of emergency points and more. Additionally, the algorithm parameters mainly include population size, number of iterations, crossover rate and mutation rate among others.

(2) Chromosome Coding: The chromosome coding method in this paper is as follows: In the emergency material dispatching model, it is assumed that the number of supply warehouses, transfer centers, emergency points and material types are n1, n2, n3 and n4, respectively, and the number of transportation methods is M = 3. The chromosome is divided into two segments. The first segment represents the quantity of materials allocated from the supply warehouse to the transfer center. It adopts the decimal four-dimensional encoding method. ($m,n,i,j$) represents the gene index, where $i$ represents the index of the supply warehouse, and $j$ represents the transfer center index, $n$ represents the material type index, and $m$ represents the transport mode index. Chromosome ($m,n,i,j$) indicates the quantity of emergency supplies $n$ allocated to transfer center $j$ by supply warehouse $i$ using transportation mode $m$, and contains n1 × n2 × n4 × M genes in total. The second paragraph indicates the quantity of materials allocated from the transfer center to the emergency point, and adopts the decimal three-dimensional coding method. ($n,j,k$) represents the gene index, where $j$ represents the index of the transfer center, $n$ represents the index of the material type and $k$ represents the emergency point index. Chromosome ($n,j,k$) indicates the number of emergency supplies $n$ allocated to emergency point $k$ by transfer center $j$, including n2 × n3 × n4 genes in total.

(3) Population Initialization: Since the chromosomes generated when the population is initialized are usually random, this paper adjusts the initialized chromosomes so that the chromosomes generated through initialization meet the constraints in the scheduling model.

(4) Fitness Function: Fitness indicates the degree of adaptation of an individual to the environment. The genetic algorithm selects the new generation of individuals mainly based on the chromosomal fitness function value to realize the selection of the best and the worst, and the chromosomal genes with high fitness function are inherited to the next generation of individuals. In this algorithm, all the individuals in each generation are sorted according to the fitness value, and then the newly generated individuals are replaced by the next ones in the original population. The objective function of the model in this paper is to minimize the suffering cost of disaster victims and the minimum total cost of emergency supplies deployment. After converting the objective function into a single objective function, set the fitness function to the reciprocal of the transformed objective function. The smaller the value of the objective function, the larger the value of the fitness function.

$$fitness=\frac{1}{{\omega }_1\min (F)+{\omega }_2\min (Z)}$$

(5) Select operation: The mutated chromosomes were selected using the roulette method. First calculate the probability of each chromosome being selected as $p(x)=\frac{fitness(x)}{{\displaystyle \sum fitness(x)}}$, ${\displaystyle \sum fitness(x)}$ which is the cumulative fitness of the chromosome. Randomly generate any decimal, judge from the first chromosome and the first chromosome whose cumulative probability is greater than or equal to the decimal is the chromosome that performs the mutation operation.

(6) Cross-operation: The genetic algorithm usually performs a crossover operation on two bodies. However, due to the violation of the demand constraint of the research problem and the inflow and outflow equality constraints of the transfer center, it is not feasible to perform crossover on two bodies. In order to avoid the problems of the above-mentioned common crossover strategy, the crossover operation used in this algorithm is to exchange two random position indices on the second segment of the chromosome in a selected individual, and then adjust the first segment of the chromosome to meet the constraints. The crossover strategy is shown in Figure 4. The basic rule of crossover is to randomly select two individuals $chrom(n,j_2,k_1)$ and $chrom(n,j_3,k_3)$ that serve different emergency points from different transfer centers, exchange the two different transfer centers to obtain new individuals $chrom(n,j_3,k_1)$ and $chrom(n,j_2,k_3)$, and then adjust the first segment of the chromosome so that the constraints are satisfied.

(7) Mutation Operation: For the structural settings of the three-dimensional gene fragment and the four-dimensional gene fragment in this paper, the mutation operation will produce a large number of infeasible solutions. Therefore, according to the design rules of the non-completely random mutation operator in the genetic algorithm, the chromosome after each mutation is guaranteed to be optimal by designing the mutation operator. This algorithm randomly selects a location for the first segment of the chromosome to mutate the transport mode. The mutation strategy is shown in Figure 5. For the second segment of the chromosome, a transfer center $j_2$ is randomly selected that is different from the transfer center $j_3$, reducing the allocation of transfer centers $j_2$. A part of the emergency materials $n$ for the emergency point $k_1$ is added to the emergency materials $n$ distributed by the transfer center $j_3$ to the emergency point $k_3$. Due to the limitation of the minimum satisfaction rate of material supply and demand, the exchange quantity is not completely random but subject to certain constraints. $aa$, seen in equation (30) includes $\min q(n,k)$, which is the minimum satisfaction, $q(n,k)$, which is the demand, $Q(1,n)$, which is the total supply of materials $n$ and $ff(1,n)$, which is the total distribution of materials $n$. The mutation strategy is shown in Figure 6.

$$\begin{array}{l}aa=\min (q(n,k_1)-\min q(n,k_1),chrom(m,n,j_2,k_1)-\min q(n,k_1),\\ q(n,k_3),-\min q(n,k_3),chrom(m,n,j_3,k_3)-\min q(n,k_3),Q(1,n)-ff(1,n))\end{array}$$

(30)

(8) Elimination of Infeasible Solutions: The model needs to meet the constraints of the number of vehicles and the throughput of the transfer center. Individuals that do not meet the above constraints will be eliminated.

(9) Termination Principle: According to the set maximum number of iterations, when iteration reaches the maximum number of generations, calculation is terminated, and the scheme produced by the chromosome with the largest fitness value is selected as the optimal solution.

The whole model solution framework is given in Algorithm 1.

Algorithm 1: Modified Genetic Algorithm

Input: All parameter values involved in the model.

Output: Material distribution transportation program and objective function value.

1. Fit←zeros (populationSize, 1)% Store the fitness value for each individual 2. Chrom1←zeros (M,N,I,J, populationSize)% Storing each individual 3. Chrom2←zeros (N,J,K, populationSize)

4. for n←1 to populationSize 5.  flag←false 6.  While not flag do 7.   Chrom1, Chrom2←Initialize()

8.   flag←isfeasible (Chrom1, Chrom2)

9.    End 10.  Obj←calculateObj ()

11.  Fit←1/Obj

12. End 13. maxF←0% Record the optimal fitness value 14. bestsolution1←zeros (M,N,I,J)% Record the optimal solution 15. bestsolution2←zeros (N,J,K) 16. gen←1 17. solution←zeros (1,maxGen)% Record the optimal objective function value for each generation 18. Ns←populationSize *Ps

19. while gen < = maxGen do

20.  Fit←calculateFitness (Chrom1, Chrom2)

21.  If max(Fit) > maxF

22.   bestsolution1←Chrom1

23.   bestsolution2←Chrom2 24.   maxF←max (Fit) 25.   solution←1/maxF

26.  End 27.  Sort(Fit, Chrom1,Chrom2)

28.  Selchrom1, Selchromy1←Selection (Chrom1, Chrom2,Ns)

29.  Selchrom1, Selchromy1←Cross (Selchrom1, Selchromy1)

30.  Selchrom1, Selchromy1←Mutation (Selchrom1, Selchromy1)

31.  StoreNewIndividuals (Chrom1, Chrom2, Selchrom1, Selchromy1)

32.  gen←gen + 1

33. end

34. return bestsolution1, bestsolution2, solution

5. Numerical Analysis

In this section, a series of numerical experiments are conducted to test the performance of the proposed model and algorithm. Taking the 2008 Wenchuan Earthquake as the context, we use the relevant data obtained from the China Earthquake Administration (Beijing, China) for the location information of emergency points, including 69 emergency points, three supply warehouses and three transfer centers. The distribution of all nodes is shown in Figure 7. The modified genetic algorithm is coded in Matlab 2023b, the Gurobi10.0.1 optimizer is coded in Python 3.10 (Python, Wilmington, DE, USA) and runs on a computer with a processor of Intel^® Core™ i5-12500H CPU @ 2.50GHz (Intel, Santa Clara, CA, USA), a memory of 16 GB and an operating system of Windows 11-x64 (Redmond, WA, USA). In this case, when solving with Gurobi, we used its default run settings, and Gurobi uses the branch-and-bound method for solving by default.

5.1. Data Introduction

In this scenario, two types of rescue materials $N$ are considered: medicines and masks. The nodes in the experimental network are real cities, and the distance between each node $d_{ijm}$, $d_{jk}$ is estimated by the Vincenty formula according to the latitude and longitude, depicted in Figure 7. The demand of each emergency point $q_{nk}$ is randomly distributed in the range [10, 9000], and the priority of the emergency points ${\lambda }_k$ is randomly distributed in the range [0, 0.5]. Additionally, reasonable assumptions are made about the storage capacity of materials $Q_{ni}$ based on demand. The settings of supply warehouses, transfer centers and emergency points are shown in Appendix A. The calculation scenario involves three modes of transportation, and the relevant data are shown in Appendix A. The minimum satisfaction rate ${\theta }_{nk}$ of medicines and masks for each emergency point is 0.7. The unit material shortage cost parameters are set as $a_1$ = 0.2, $a_2$ = 0.02, $b_1$ = 0.1, $b_2$ = 0.01. The relative pain cost coefficient $\alpha$ is 0.5, and the maximum time window $T_n^{\max }$ is set to [20, 40]. This paper constructs six sets of numerical example data for algorithm performance analysis, including 5 emergency points, 10 emergency points, 20 emergency points, 40 emergency points, 50 emergency points and 69 emergency points. The corresponding material supply $Q_{ni}$ is set to 90% of the demand. The time at which rescue materials start to be transported from supply warehouses is set to 0:00. The genetic algorithm parameters are set as follows: population size Num = 50, crossover probability P1 = 0.8, mutation probability P2 = 0.8, the maximum iteration G = 300 for examples including 5, 10, 20, 40 and 50 emergency points, the maximum iteration G = 500 for the example including 69 emergency points.

5.2. Algorithm Performance Analysis

To evaluate the algorithm performance, this subsection contrasts the solutions derived from the modified genetic algorithm with those attained using Gurobi 10.0.1 solver. Six groups of scenarios are solved by the algorithm and Gurobi. Each scenario is solved 10 times using the algorithm. Gurobi’s execution time is capped at 1800 s. The results are shown in

Table 3. The solution results of the proposed algorithm and Gurobi.

$\mathit{K}$	Modified Genetic Algorithm						GUROBI
	Psychological Pain Cost	Logistics Cost	Total Cost (Best)	Average	Standard Deviation	Running Time (s)	Total Cost	GAP (%)	Running Time (s)
5	1995	14,813	16,808	16,872	36	22	16,808	0.0	10
10	4049	29,211	33,260	33,316	41	51	33,260	0.0	295
20	31,724	58,192	89,916	89,997	49	274	92,920	12.5	1800
40	209,107	183,603	392,710	392,785	63	431	441,247	21.3	1800
50	954,931	218,152	1,173,083	1,173,197	123	524	N/A	N/A	1800
69	1,454,256	243,544	1,697,800	1,698,307	318	946	N/A	N/A	1800

.

In the table, we can observe that, for small-scale instances $(5\le K\le 10)$, the algorithm produces consistent results with Gurobi. As the instance size increases $(20\le K\le 40)$, Gurobi can only find feasible solutions within 1800 s. When $K\ge 50$, Gurobi is unable to find feasible solutions within the specified time limit. From the perspective of solution time, although Gurobi has a shorter runtime when $K=5$, the algorithm exhibits a clear advantage in terms of runtime as the problem size increases. All the instances can be solved by the proposed algorithm within an acceptable time although the computational time is increasing with the scale of instances. In all instances, the algorithm consistently achieves an average value within 1% difference from the optimal solution, with a small standard deviation. This indicates that the algorithm can consistently produce stable solutions that are close to the optimal solution across multiple runs. Figure 8 shows the convergence curves of different instances. In this figure, the improved genetic algorithm has good convergence when solving instances with different emergency points. Additionally, most instances can obtain the optimal solutions within 250 iterations. Thus, the proposed algorithm has strong performance in solving the proposed model.

Furthermore, we also see that all the costs are increasing with the increase in the scenario scale. However, the increasing trend is different. For example, the increase trend is approximately linear for the logistic cost, but is exponential for the psychological pain cost. Meanwhile, the proportion of psychological pain cost in the total cost is gradually increasing. This indicates that the logistics cost is stable and linearly related to the scale of emergencies. However, the psychological pain cost will see a dramatic increase when the scale of emergencies is large. For the instance of 69 emergency points, the proportion of psychological pain cost in the total cost is more than 80%. These results mean that the government should organize the emergency rescue rapidly to control the scale of the emergency and reduce the potential cost (for example, the psychological pain cost of residents), even if this will result in additional logistics or material costs.

5.3. Analysis of Solution Results

To verify the effectiveness of the model, we conducted an analysis of 20 emergency points. The transportation volume, satisfaction rate and delivery time of materials are shown in

Table 4. The solution results from the proposed model.

Emergency Points	Transfer Centers	Transportation Volume (Box)		Satisfaction Rate (%)		Delivery Time (h)
		Medicine	Mask	Medicine	Mask	Medicine	Mask
K27	J2	126	622	99.2%	100.0%	6.35	19.15
K7	J2	79	901	100.0%	100.0%	8.06	18.21
K23	J2	86	568	88.7%	70.0%	7.20	20.49
K12	J3	86	908	100.0%	83.0%	7.84	18.39
K18	J1	92	677	100.0%	97.8%	6.84	21.61
K26	J1	285	1773	100.0%	100.0%	6.49	16.50
K50	J1	168	692	100.0%	100.0%	7.14	19.15
K42	J2	473	1242	100.0%	70.1%	7.07	18.39
K44	J3	25	949	71.4%	100.0%	6.74	15.11
K19	J2	135	1413	100.0%	88.9%	6.41	15.74
K64	J3	21	270	70.0%	100.0%	8.80	19.67
K62	J2	85	250	100.0%	70.2%	7.23	20.68
K41	J1	519	1377	96.6%	100.0%	5.68	14.03
K37	J1	148	1158	100.0%	100.0%	6.71	20.83
K36	J2	66	845	71.0%	88.9%	6.38	18.48
K31	J2	90	297	100.0%	100.0%	6.32	18.63
K20	J1	62	951	100.0%	100.0%	6.32	19.32
K39	J2	168	568	100.0%	70.0%	5.75	16.30
K58	J1	487	1772	100.0%	100.0%	5.85	17.28
K17	J3	1611	2545	77.8%	81.2%	7.88	17.41

. Additionally, the psychological pain cost and the logistics cost are equal to CNY 31,724 and CNY 58,192, respectively.

In Table 4, we observe that the material satisfaction rate of some emergency points is less than 1, and the material satisfaction rate of all emergency points is greater than 0.7, which meets the requirements of the minimum material satisfaction rate (>0.7) in the calculation scenario. This indicates that the total supply of medicines and masks is less than the total demand, and the allocation system is in a state of material shortage. Considering delivery time, the average delivery time for medicines is shorter than that for masks. This is because the demand for masks at the emergency points is greater than the demand for medicines. The delivery time of materials to emergency points is affected by transportation volume of the materials, demand priority and distance between nodes. For example, for K36 and K39, the medicines are transferred through J2, the transportation volume is 66 and 168 boxes, respectively, the demand priority is 0.1197 and 0.1986, respectively, and the delivery time of materials is 6.38 and 5.75 h, respectively. This ensures that materials are delivered to affected areas with high urgency in priority. These results mean that the government should take measures as soon as possible to increase the supply of materials to meet the needs of emergency points. In addition, the government should reasonably establish demand priorities, and give priority to transporting materials to emergency points with high demand to ensure that materials can reach the affected area in time. Figure 9 shows the mode of transportation from supply warehouses to transfer centers. The transportation system adopts the combined transportation of the train, airplane and truck. The train has great advantages in rescue due to its low transportation cost and large transportation volume. Airplane transportation is fast, and truck transportation plays an important role in the material distribution process due to its flexibility. Multimodal transport can make full use of the advantages of different means of transportation, minimize transportation time and cost, and improve transportation efficiency. Thus, the established model can meet the material demand of the affected area and ensure the timely arrival of materials. In actual rescue, decision-makers should rationally allocate emergency materials, effectively arrange transportation capacity input, and improve the fairness and timeliness of emergency materials allocation as much as possible to strengthen emergency material security, reduce negative psychological emotions of residents and improve rescue efficiency.

5.4. Sensitivity Analysis

To evaluate the impact of the parameters on the results, a sensitivity analysis is performed on the relative pain cost coefficient, transportation modes and node loading and unloading capacity. These parameters are affected by many complex real-world factors, such as the construction of nodes, the severity of crises and the attitude of decision makers. We choose 20 emergency points as samples and explore their impact on the objective function by setting a series of values. The results of this analysis are shown in Figure 10, Figure 11 and Figure 12.

According to Figure 10, the psychological pain cost is decreasing gradually with the increase in relative pain cost coefficient, and the logistics cost and the total cost are increasing gradually. However, the absolute pain cost fluctuates less. This indicates that, as the degree of influence of relative pain costs increases, the difference in the delivery time and the transportation volume of materials at emergency points decreases. Simultaneously, this results in additional logistics or material costs. Therefore, decision-makers can achieve their goals by determining their preferences and choosing optimal values for the importance of different objectives, taking into account restrictions in terms of delivery time and budget.

According to Figure 11, the psychological pain cost is the highest and the logistics cost is the lowest for train transportation mode, while air transportation mode shows the opposite result. Truck transportation mode lies between them. The total cost of multimodal transportation mode is lower than the other three single transportation modes. These results indicate the role and impact of different transportation modes in the allocation of rescue materials. Due to the slow speed and low cost of train transportation, although it saves in logistics cost, it delays the delivery time of materials and increases the waiting and anxiety of the residents. Airplane transportation shows the opposite result. Truck transportation has certain advantages in terms of speed and cost, but it is also limited by factors such as road conditions and distances, and there is a certain degree of instability. Multimodal transportation makes full use of the benefits of various transportation modes, considering the balance of speed and cost, achieving the rapid and low-cost allocation of materials, improving the rescue effect and reducing the cost of suffering. Therefore, in the decision-making of emergency material allocation, multimodal transportation should be preferred, and the synergistic effect of various transportation modes should be used to achieve the purpose of reducing costs and improving rescue efficiency.

According to

Table 5. Node loading capacity and corresponding loading cost.

Loading and unloading capacity (box/h)	600	800	1000	1200	1400	1600
Loading and unloading cost (CNY/box)	0.46	0.62	0.76	0.93	1.09	1.24

and Figure 12, the average delivery time and the psychological pain cost are gradually decreasing, and the total cost and the logistics cost are gradually increasing with the improvement in the loading and unloading capacity of supply warehouses and transfer centers. However, the rate of change in the average delivery time and the psychological pain cost have gradually slowed down and will eventually stabilize. This indicates that the delivery time is not only affected by the loading and unloading capacity of nodes, but also by factors such as vehicle capacity, transportation volume of materials and distance. Therefore, the government can shorten the delivery time and improve the response speed of emergency rescue by improving the loading and unloading capacity of nodes, but it needs to pay attention to the influence of other factors.

6. Case Analysis

6.1. Background Information

In this section, the domestic COVID-19 outbreak in 2020 in the Hubei Province is applied for case analysis. The data for the emergency points are the daily epidemic data of Hubei Province published by the Wuhan Health Commission and the Hubei Provincial Bureau of Statistics. The calculation of demand and priority of emergency points are based on Xing [32]. The data for supply warehouses and transfer centers are based on reasonable assumptions based on the actual situation of the epidemic. We still select two types of materials, medicines and masks, and take Xi’an, Zhengzhou and Hefei, the neighboring capital cities of Hubei Province, as the supply warehouses for emergency rescue materials in Hubei Province. Wuchang Station, Xiangyang Station and Yichang East Station serve as transfer centers for emergency rescue supplies in Hubei Province. Taking the cities and autonomous counties under the jurisdiction of Hubei Province as Wuhan, Huangshi, Xiangyang, Shiyan, Yichang, Jingzhou, Jingmen, Xianning, Xiaogan, Huanggang, Suizhou, Enshi, Xiantao, Tianmen, Ezhou City and Qianjiang City are the emergency points. We construct an emergency rescue supply network consisting of three supply warehouses, three transfer centers and 16 emergency points. The relevant data are shown in Appendix B. The rest of the parameters and operating environment are the same as those in Section 5.

6.2. Results Analysis

The computational results of the case study are reported in this section. The case can be solved by the proposed algorithm within 237 s. The psychological pain cost and the logistics cost are equal to CNY 7571 and CNY 37,823, respectively. The solution results of case analysis are shown in

Table 6. The solution results of case analysis.

Emergency Points	Transfer Centers	Transportation Volume (Box)		Satisfaction Rate (%)		Delivery Time (h)
		Medicine	Mask	Medicine	Mask	Medicine	Mask
Wuhan	Wuchang Railway Station	615	3139	100.0%	100.0%	5.93	15.59
Huangshi	Wuchang Railway Station	25	485	71.4%	70.1%	7.01	21.49
Xiangyang	Xiangyang Railway Station	48	1376	90.6%	86.5%	4.85	16.79
Shiyan	Xiangyang Railway Station	20	666	71.4%	70.0%	6.45	19.03
Yichang	Yichang East Railway Station	27	1098	71.1%	94.7%	6.78	19.16
Jingzhou	Yichang East Railway Station	37	1560	71.2%	100.0%	7.66	18.71
Jingmen	Yichang East Railway Station	31	811	72.1%	100.0%	7.79	22.32
Xianning	Wuchang Railway Station	24	714	72.7%	100.0%	6.90	20.28
Xiaogan	Wuchang Railway Station	70	1263	70.0%	91.7%	6.75	19.36
Huanggang	Wuchang Railway Station	115	1578	100.0%	89.0%	6.71	18.00
Suizhou	Xiangyang Railway Station	34	436	70.8%	70.1%	6.27	19.26
Enshi	Yichang East Railway Station	13	949	100.0%	100.0%	9.07	22.63
Xiantao	Wuchang Railway Station	10	300	76.9%	70.1%	7.09	20.80
Tianmen	Wuchang Railway Station	9	250	75.0%	70.0%	7.55	21.52
Ezhou	Wuchang Railway Station	25	208	89.3%	70.0%	6.79	21.47
Qianjiang	Wuchang Railway Station	3	190	100.0%	70.1%	7.71	22.61

.

Analyzing Table 6, rescue materials are transported to emergency points with high priority. For instance, for Wuchang, which experiences the most severe epidemic situation, the greatest demand for supplies and the highest priority, its material satisfaction rate is higher than that of Huangshi and the delivery time of material is shorter than that of Huangshi even if the demand for materials is greater. Figure 13 displays the route of each supply warehouse to the transfer centers regarding the used transportation mode and the assignment of each transfer center to the emergency points. For instance, when the COVID-19 outbreak occurred, Wuchang was used to collect two types of rescue materials that were transported from Xi’an, Zhengzhou and Hefei by trains, trucks or airplanes, and then distribute materials to Wuhan, Huangshi, Xianning, Xiaogan, Huanggang, Xiantao, Tianmen, Ezhou and Qianjiang by trucks.

The model aims to achieve the goal of reducing the budget and the suffering of the population, which is the most important of the various objective functions of the humanitarian relief logistics problem. Among these, equitable distribution is more important under conditions of scarcity. Especially in the case of public health emergencies, the amount of available relief supplies is generally smaller than the total demand, and if equitable distribution is not taken into account in the mathematical model, there may be a situation in which some emergency relief points are completely ignored while others are fully met, thus harming the welfare of the population, which is very important for crisis management decision-makers, and this shows the importance of equitable distribution in the allocation of relief importance in the distribution of supplies.

7. Conclusions

In this paper, we propose a multimodal transportation optimization research method for the allocation of emergency rescue materials that considers the psychological pain cost and the demand priority of emergency points. To highlight the requirements of timeliness, fairness and economy, we take the psychological pain cost of residents and the logistics cost of emergency materials as the decision-making targets. To characterize the rescue priority more accurately, we determine the node loading order by setting the urgency. Then, we construct an emergency allocation model to improve the rescue effectiveness and design a modified genetic algorithm for solving the model. Taking the Wenchuan earthquake as the background, we solve different instances to verify the effectiveness of our proposed algorithm. It was found that, for small-scale instances $(5\le K\le 10)$, the algorithm produces consistent results with Gurobi. As the instance size increases $(20\le K\le 40)$, Gurobi can only find feasible solutions within 1800 s. When $K\ge 50$, Gurobi is unable to find feasible solutions within the specified time limit. The algorithm has a significant advantage in terms of runtime for large-scale instances. Our model can help to better determine the route of material supply in the public health emergency, thereby alleviating residents’ psychological pain and reducing budgets. We also conducted sensitivity analysis to observe the influence of relative pain cost coefficient, transportation modes and loading and unloading capacity of nodes on the objective function. Moreover, the model and algorithm have been applied successfully to the 2020 Wuhan COVID-19 outbreak.

There are some limitations in the research on emergency material allocation discussed in this paper. For example, this study only considers the static emergency material allocation problem. Future research could incorporate supply and demand dynamics. Another important idea is that future research can employ the model to actual emergency rescue scenarios, so as to verify its practicability and continuously improve the model. Specifically, we can try to incorporate the psychological pain cost and demand priority into the optimization decision-making of relief material supply routes under public health emergencies, so as to achieve more effective disaster relief. In addition, further exploration can be conducted on the trade-off between psychological pain cost and demand priority in the allocation of rescue materials through multi-objective optimization, as well as the development of new measurement methods for psychological pain cost.