Analysis of Meshfree Galerkin Methods Based on Moving Least Squares and Local Maximum-Entropy Approximation Schemes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Local Maximum Entropy Approximation
2.2. Moving Least Squares Approximation
2.3. Blending Algorithm for MLS
3. Numerical Examples
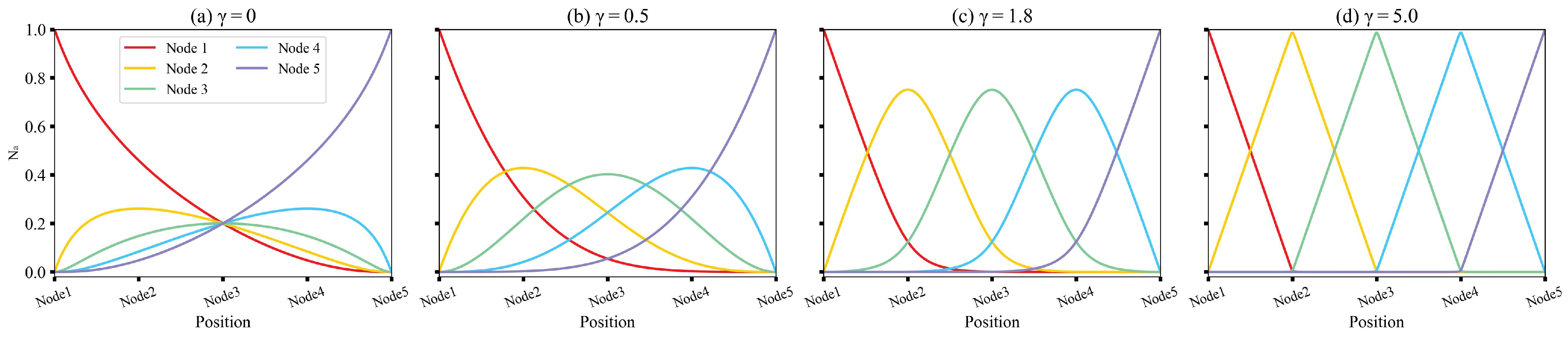
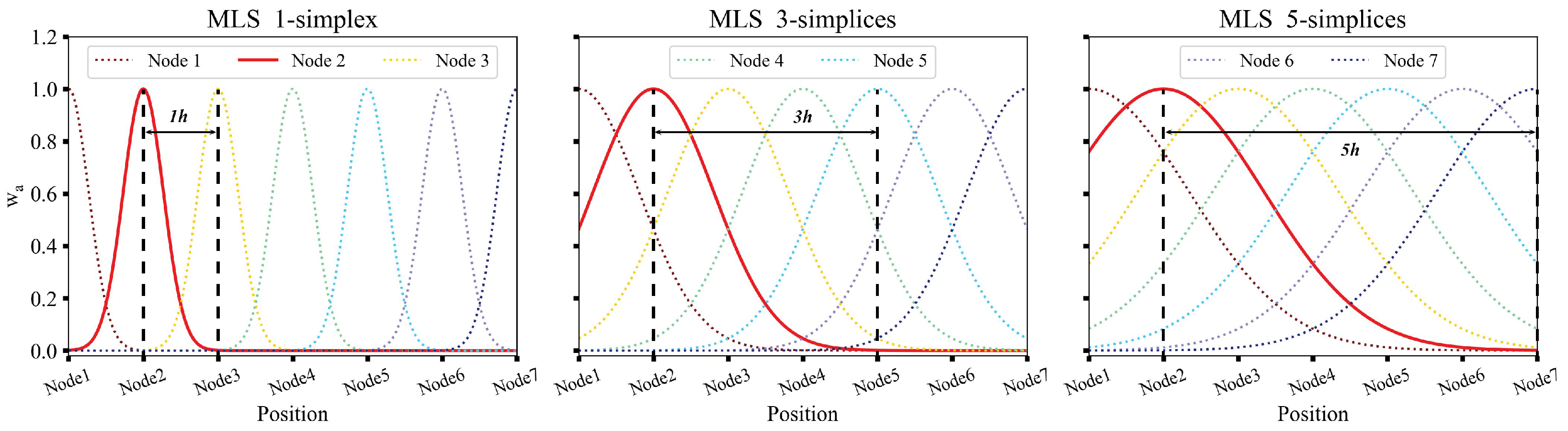
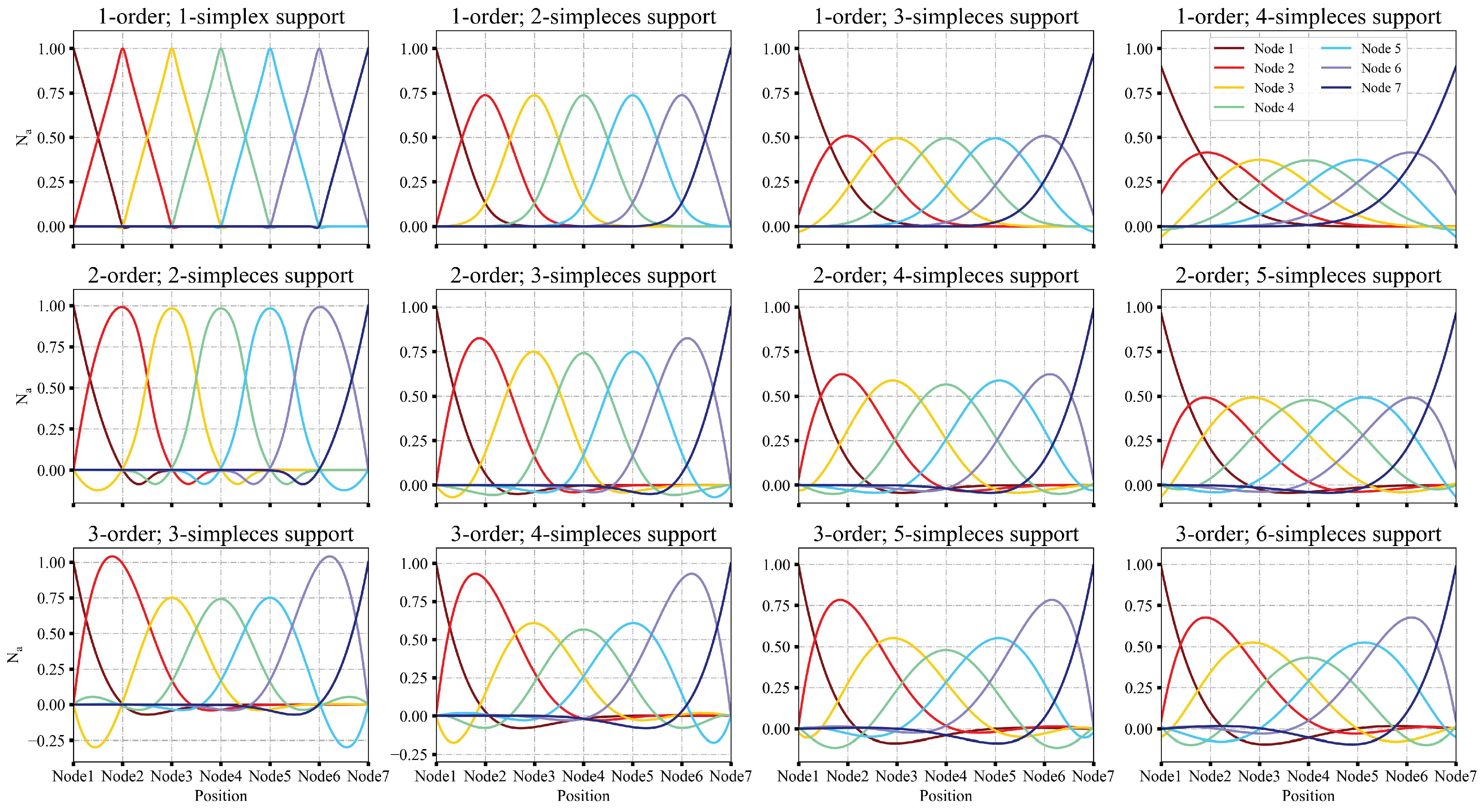
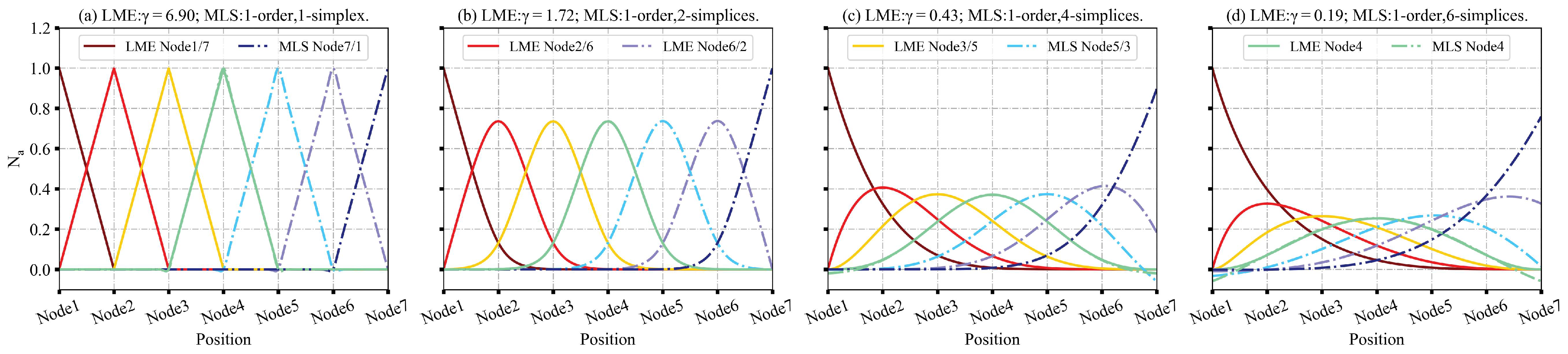
3.1. LME and MLS Shape Functions in 1D
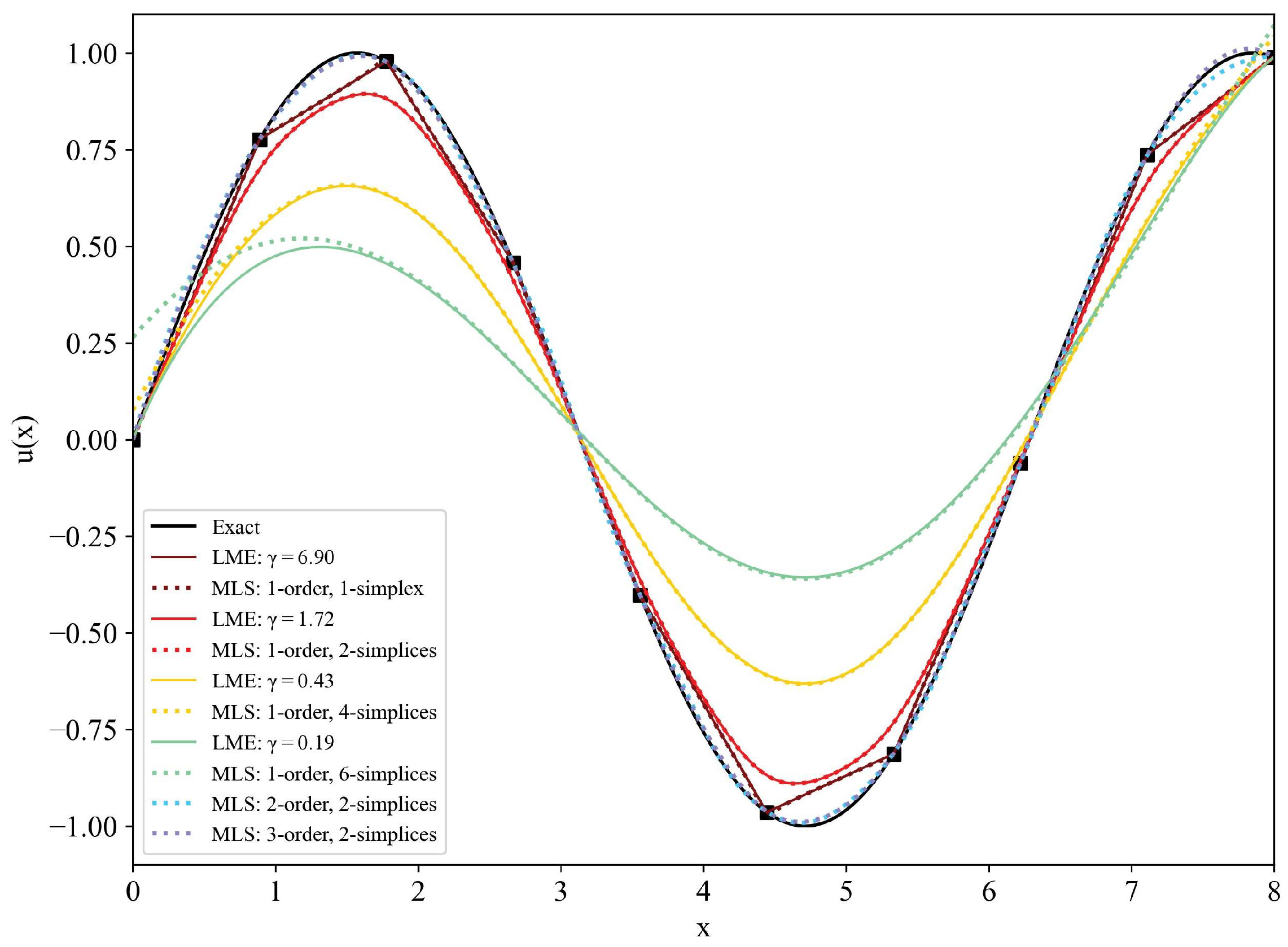
3.2. Approximation of Sine Function in 1D
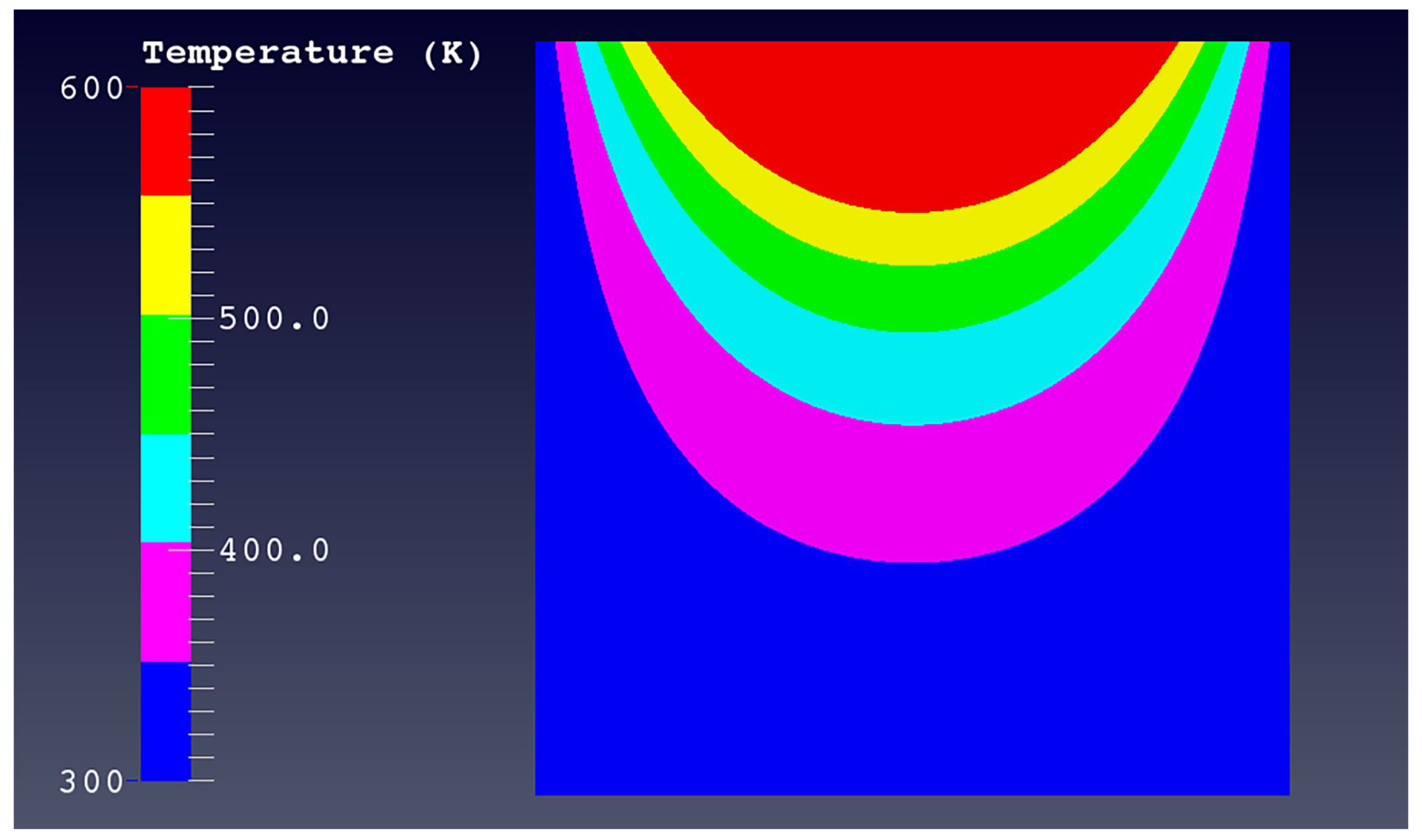
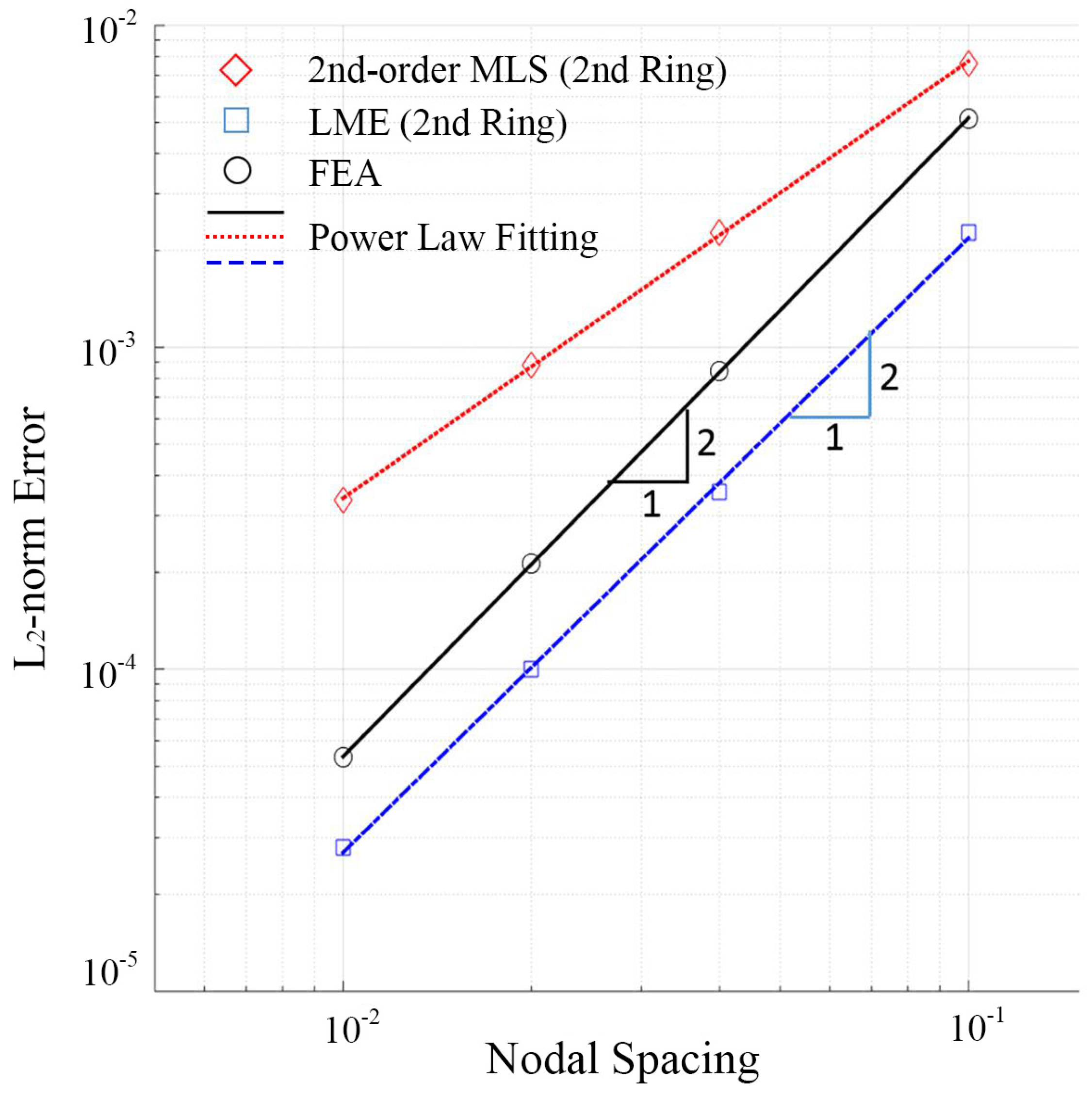
3.3. Thermal Problem with Dirichlet Boundary Conditions
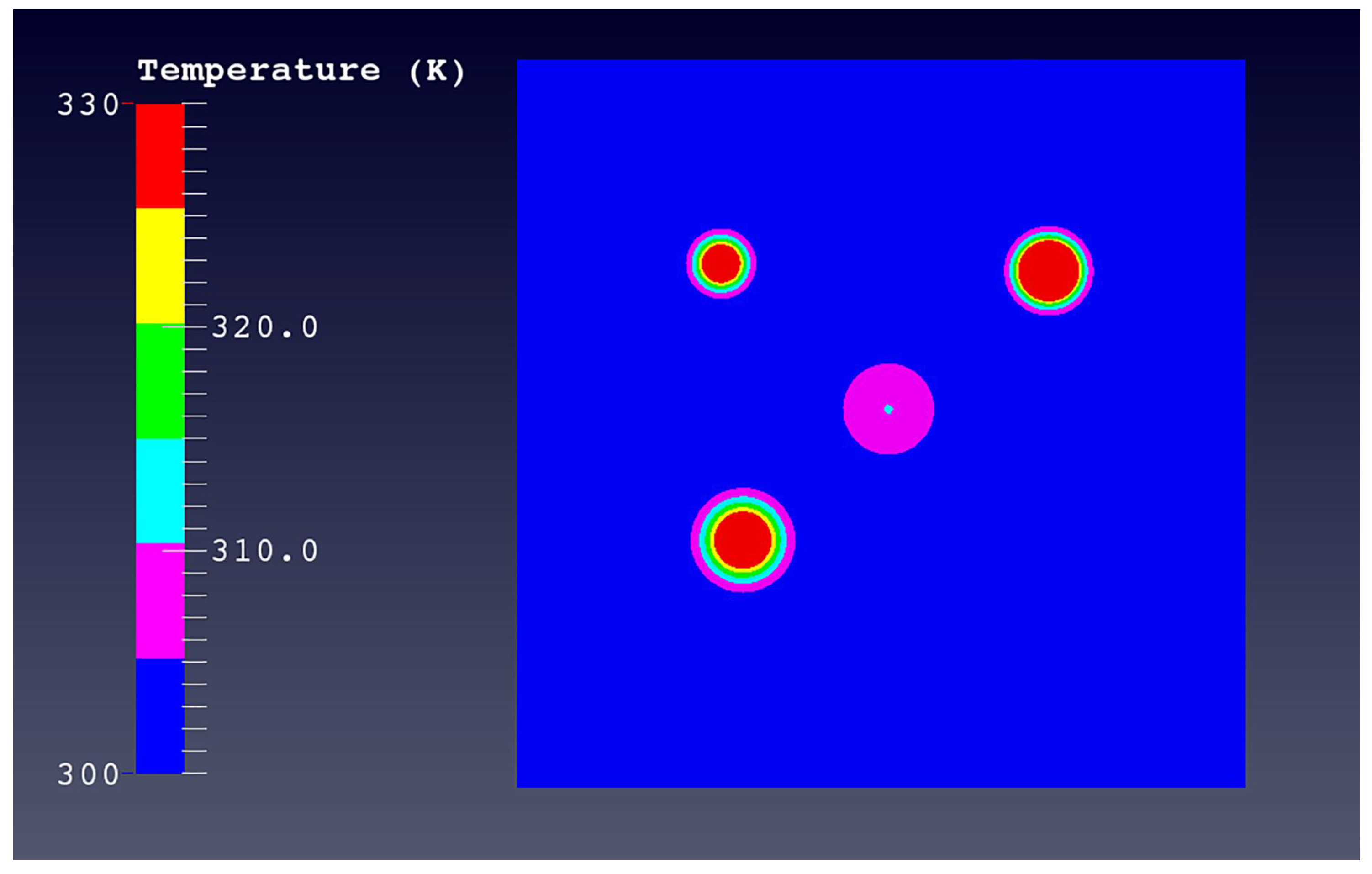
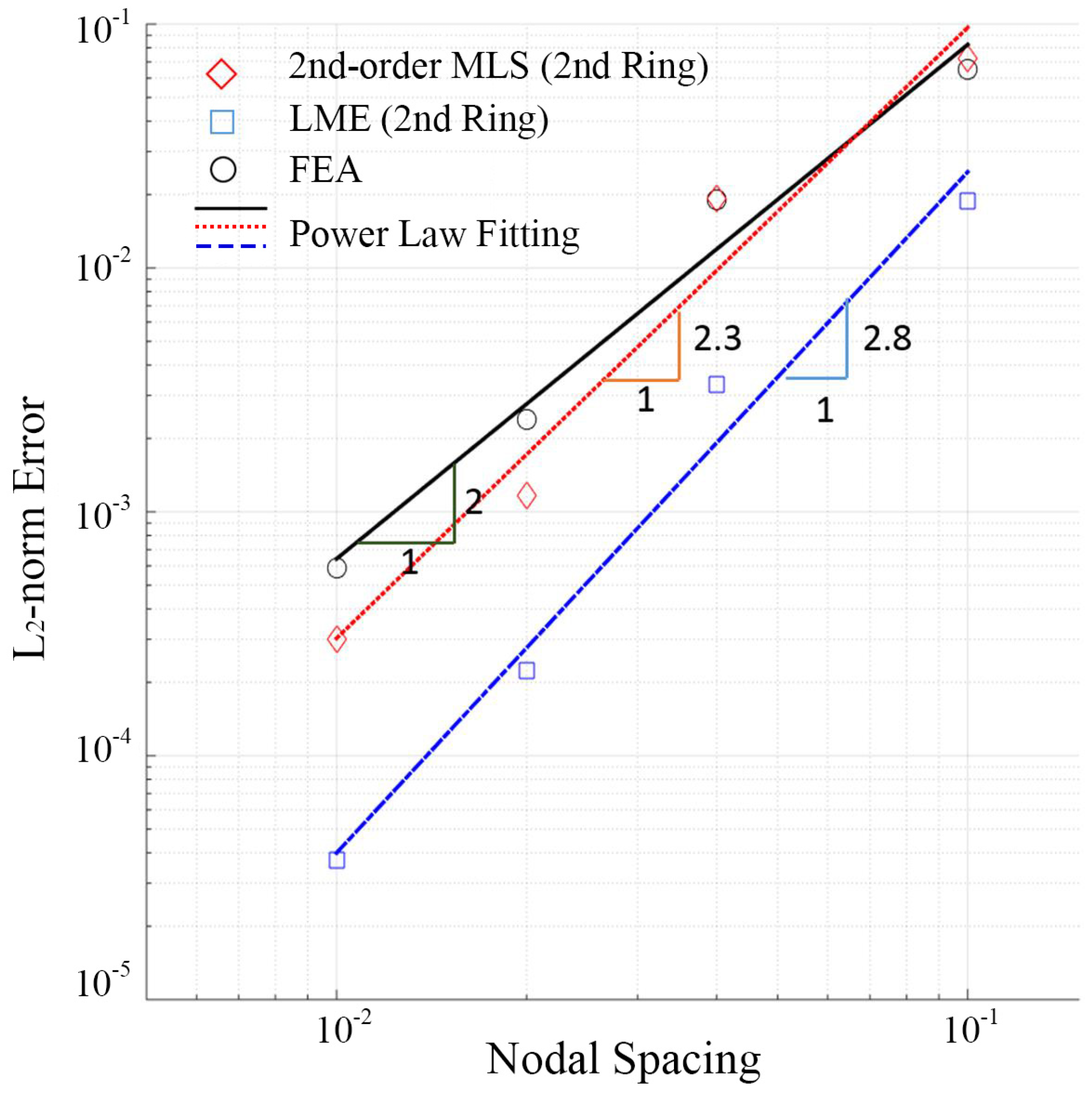
3.4. Thermal Problem with Heat Sources
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Belytschko, T.; Krongauz, Y.; Organ, D.; Fleming, M.; Krysl, P. Meshless methods: An overview and recent developments. Comput. Methods Appl. Mech. Eng. 1996, 139, 3–47. [Google Scholar] [CrossRef]
- Liu, G. An overview on meshfree methods: For computational solid mechanics. Int. J. Comput. Methods 2016, 13, 1630001. [Google Scholar] [CrossRef]
- Chen, J.S.; Hillman, M.; Chi, S.W. Meshfree methods: Progress made after 20 years. J. Eng. Mech. 2017, 143, 04017001. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Singapore, 2003. [Google Scholar]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Dolbow, J.; Belytschko, T. An introduction to programming the meshless Element F reeGalerkin method. Arch. Comput. Methods Eng. 1998, 5, 207–241. [Google Scholar] [CrossRef]
- Liu, W.K.; Jun, S.; Zhang, Y.F. Reproducing kernel particle methods. Int. J. Numer. Methods Fluids 1995, 20, 1081–1106. [Google Scholar] [CrossRef]
- Sulsky, D.; Chen, Z.; Schreyer, H.L. A particle method for history-dependent materials. Comput. Methods Appl. Mech. Eng. 1994, 118, 179–196. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Z.; Liu, Y. The Material Point Method: A Continuum-Based Particle Method for Extreme Loading Cases; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Braun, J.; Sambridge, M. A numerical method for solving partial differential equations on highly irregular evolving grids. Nature 1995, 376, 655–660. [Google Scholar] [CrossRef]
- Sukumar, N.; Moran, B.; Belytschko, T. The natural element method in solid mechanics. Int. J. Numer. Methods Eng. 1998, 43, 839–887. [Google Scholar] [CrossRef]
- Sukumar, N.; Moran, B.; Yu Semenov, A.; Belikov, V. Natural neighbour Galerkin methods. Int. J. Numer. Methods Eng. 2001, 50, 1–27. [Google Scholar] [CrossRef]
- Li, B.; Habbal, F.; Ortiz, M. Optimal transportation meshfree approximation schemes for fluid and plastic flows. Int. J. Numer. Methods Eng. 2010, 83, 1541–1579. [Google Scholar] [CrossRef]
- Wang, H.; Liao, H.; Fan, Z.; Fan, J.; Stainier, L.; Li, X.; Li, B. The Hot Optimal Transportation Meshfree (HOTM) method for materials under extreme dynamic thermomechanical conditions. Comput. Methods Appl. Mech. Eng. 2020, 364, 112958. [Google Scholar] [CrossRef]
- Johnson, G.R.; Beissel, S.R. Normalized smoothing functions for SPH impact computations. Int. J. Numer. Methods Eng. 1996, 39, 2725–2741. [Google Scholar] [CrossRef]
- Randles, P.; Libersky, L. Smoothed particle hydrodynamics: Some recent improvements and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 375–408. [Google Scholar] [CrossRef]
- Belytschko, T.; Krongauz, Y.; Dolbow, J.; Gerlach, C. On the completeness of meshfree particle methods. Int. J. Numer. Methods Eng. 1998, 43, 785–819. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703. [Google Scholar] [CrossRef]
- Lancaster, P.; Salkauskas, K. Surfaces generated by moving least squares methods. Math. Comput. 1981, 37, 141–158. [Google Scholar] [CrossRef]
- Nayroles, B.; Touzot, G.; Villon, P. Generalizing the finite element method: Diffuse approximation and diffuse elements. Comput. Mech. 1992, 10, 307–318. [Google Scholar] [CrossRef]
- Ghoneim, A.Y. A smoothed particle hydrodynamics-phase field method with radial basis functions and moving least squares for meshfree simulation of dendritic solidification. Appl. Math. Model. 2020, 77, 1704–1741. [Google Scholar] [CrossRef]
- Salehi, R.; Dehghan, M. A generalized moving least square reproducing kernel method. J. Comput. Appl. Math. 2013, 249, 120–132. [Google Scholar] [CrossRef]
- Spandan, V.; Lohse, D.; de Tullio, M.D.; Verzicco, R. A fast moving least squares approximation with adaptive Lagrangian mesh refinement for large scale immersed boundary simulations. J. Comput. Phys. 2018, 375, 228–239. [Google Scholar] [CrossRef]
- Sibson, R. A vector identity for the Dirichlet tessellation. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1980; Volume 87, pp. 151–155. [Google Scholar]
- Sibson, R. A brief description of natural neighbour interpolation. In Interpreting Multivariate Data; John Wiley & Sons: New York, NY, USA, 1981; pp. 21–36. [Google Scholar]
- Belikov, V.; Ivanov, V.; Kontorovich, V.; Korytnik, S.; Semenov, A.Y. The non-Sibsonian interpolation: A new method of interpolation of the values of a function on an arbitrary set of points. Comput. Math. Math. Phys. 1997, 37, 9–15. [Google Scholar]
- Belikov, V.V.; Semenov, A.Y. Non-Sibsonian interpolation on arbitrary system of points in Euclidean space and adaptive isolines generation. Appl. Numer. Math. 2000, 32, 371–387. [Google Scholar] [CrossRef]
- Chinesta, F.; Cescotto, S.; Cueto, E.; Lorong, P. Natural Element Method for the Simulation of Structures and Processes; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Sukumar, N.; Moran, B. C1 natural neighbor interpolant for partial differential equations. Numer. Methods Partial. Differ. Equ. 1999, 15, 417–447. [Google Scholar] [CrossRef]
- Alfaro, I.; Bel, D.; Cueto, E.; Doblare, M.; Chinesta, F. Three-dimensional simulation of aluminium extrusion by the α-shape based natural element method. Comput. Methods Appl. Mech. Eng. 2006, 195, 4269–4286. [Google Scholar] [CrossRef]
- Sukumar, N. Construction of polygonal interpolants: A maximum entropy approach. Int. J. Numer. Methods Eng. 2004, 61, 2159–2181. [Google Scholar] [CrossRef]
- Bompadre, A.; Schmidt, B.; Ortiz, M. Convergence analysis of meshfree approximation schemes. SIAM J. Numer. Anal. 2012, 50, 1344–1366. [Google Scholar] [CrossRef]
- Rosolen, A.; Millán, D.; Arroyo, M. On the optimum support size in meshfree methods: A variational adaptivity approach with maximum-entropy approximants. Int. J. Numer. Methods Eng. 2010, 82, 868–895. [Google Scholar] [CrossRef]
- González, D.; Cueto, E.; Doblaré, M. A higher order method based on local maximum entropy approximation. Int. J. Numer. Methods Eng. 2010, 83, 741–764. [Google Scholar] [CrossRef]
- Arroyo, M.; Ortiz, M. Local maximum-entropy approximation schemes: A seamless bridge between finite elements and meshfree methods. Int. J. Numer. Methods Eng. 2006, 65, 2167–2202. [Google Scholar] [CrossRef]
- Fan, J.; Liao, H.; Wang, H.; Hu, J.; Chen, Z.; Lu, J.; Li, B. Local maximum-entropy based surrogate model and its application to structural reliability analysis. Struct. Multidiscip. Optim. 2018, 57, 373–392. [Google Scholar] [CrossRef]
- Fan, J.; Yuan, Q.; Jing, F.; Xu, H.; Wang, H.; Meng, Q. Adaptive local maximum-entropy surrogate model and its application to turbine disk reliability analysis. Aerospace 2022, 9, 353. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, H.; Scott, V.; Li, B. Numerical analysis of oblique hypervelocity impact damage to space structural materials by ice particles in cryogenic environment. Acta Astronaut. 2022, 195, 392–404. [Google Scholar] [CrossRef]
- Fan, Z.; Liao, H.; Jiang, H.; Wang, H.; Li, B. A dynamic adaptive eigenfracture method for failure in brittle materials. Eng. Fract. Mech. 2021, 244, 107540. [Google Scholar] [CrossRef]
- Navas, P.; Rena, C.Y.; Li, B.; Ruiz, G. Modeling the dynamic fracture in concrete: An eigensoftening meshfree approach. Int. J. Impact Eng. 2018, 113, 9–20. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Phipps, M.; Li, B. Numerical and experimental study of hot pressing technique for resin-based friction composites. Compos. Part A Appl. Sci. Manuf. 2022, 153, 106737. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, H.; Chen, L.; Gomez, H.; Li, B.; Cao, C. A meshfree phase-field model for simulating the sintering process of metallic particles for printed electronics. Eng. Comput. 2023, 1–17. [Google Scholar] [CrossRef]
- Sukumar, N.; Wright, R. Overview and construction of meshfree basis functions: From moving least squares to entropy approximants. Int. J. Numer. Methods Eng. 2007, 70, 181–205. [Google Scholar] [CrossRef]
- Rajan, V. Optimality of the Delaunay triangulation in Rd. Discret. Comput. Geom. 1994, 12, 189–202. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Belytschko, T.; Krongauz, Y.; Fleming, M.; Organ, D.; Liu, W.K.S. Smoothing and accelerated computations in the element free Galerkin method. J. Comput. Appl. Math. 1996, 74, 111–126. [Google Scholar] [CrossRef]
- Huerta, A.; Fernández-Méndez, S. Enrichment and coupling of the finite element and meshless methods. Int. J. Numer. Methods Eng. 2000, 48, 1615–1636. [Google Scholar] [CrossRef]
- Fernández-Méndez, S.; Huerta, A. Imposing essential boundary conditions in mesh-free methods. Comput. Methods Appl. Mech. Eng. 2004, 193, 1257–1275. [Google Scholar] [CrossRef]
- Sulsky, D.; Zhou, S.J.; Schreyer, H.L. Application of a particle-in-cell method to solid mechanics. Comput. Phys. Commun. 1995, 87, 236–252. [Google Scholar] [CrossRef]
- Joldes, G.R.; Chowdhury, H.A.; Wittek, A.; Doyle, B.; Miller, K. Modified moving least squares with polynomial bases for scattered data approximation. Appl. Math. Comput. 2015, 266, 893–902. [Google Scholar] [CrossRef]
- Tey, W.Y.; Che Sidik, N.A.; Asako, Y.; Muhieldeen, M.W.; Afshar, O. Moving least squares method and its improvement: A concise review. J. Appl. Comput. Mech. 2021, 7, 883–889. [Google Scholar]
- Matinfar, M.; Pourabd, M. Modified moving least squares method for two-dimensional linear and nonlinear systems of integral equations. Comput. Appl. Math. 2018, 37, 5857–5875. [Google Scholar] [CrossRef]


| Dimension | k |
|---|---|
| 1D | |
| 2D | |
| 3D |
| Approximation | Approximation | ||
|---|---|---|---|
| MLS: 1-order, 1-simplex | 0.0203 | LME: | 0.0205 |
| MLS: 1-order, 2-simplices | 0.0448 | LME: | 0.0451 |
| MLS: 1-order, 3-simplices | 0.1742 | LME: | 0.1744 |
| MLS: 1-order, 4-simplices | 0.4094 | LME: | 0.4171 |
| MLS: 1-order, 5-simplices | 0.7210 | LME: | 0.7226 |
| MLS: 1-order, 6-simplices | 1.0615 | LME: | 1.0918 |
| MLS: 2-order, 2-simplices | 0.0015 | ||
| MLS: 3-order, 2-simplices | 0.0006 |
| i | ||||
|---|---|---|---|---|
| 1 | 10 | 180 | ||
| 2 | 50 | 450 | ||
| 3 | 100 | 800 | ||
| 4 | 50 | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Wang, H.; Li, B. Analysis of Meshfree Galerkin Methods Based on Moving Least Squares and Local Maximum-Entropy Approximation Schemes. Mathematics 2024, 12, 494. https://doi.org/10.3390/math12030494
Yang H, Wang H, Li B. Analysis of Meshfree Galerkin Methods Based on Moving Least Squares and Local Maximum-Entropy Approximation Schemes. Mathematics. 2024; 12(3):494. https://doi.org/10.3390/math12030494
Chicago/Turabian StyleYang, Hongtao, Hao Wang, and Bo Li. 2024. "Analysis of Meshfree Galerkin Methods Based on Moving Least Squares and Local Maximum-Entropy Approximation Schemes" Mathematics 12, no. 3: 494. https://doi.org/10.3390/math12030494
APA StyleYang, H., Wang, H., & Li, B. (2024). Analysis of Meshfree Galerkin Methods Based on Moving Least Squares and Local Maximum-Entropy Approximation Schemes. Mathematics, 12(3), 494. https://doi.org/10.3390/math12030494






