Cluster Size Intelligence Prediction System for Young Women’s Clothing Using 3D Body Scan Data
Abstract
:1. Introduction
- (1)
- We introduced body shape classification to refine the body size prediction model, enhancing the accuracy of prediction data and offering more intuitive visual expression.
- (2)
- We developed an intelligent prediction system that allows designers or users to measure only four basic body dimensions (waist, hip, bust circumference, and height). With the assistance of the intelligent system, it predicts 28 other body sizes and shape categories. This simplifies the operational complexity for the personnel involved and improves the efficiency of prediction.
- The other sections of this paper are organized as follows, as illustrated in Figure 1:
- Section 4 analyzes human body size data.
- Section 5 deduces typical body types based on cluster analysis.
- Section 6 constructs a body size prediction algorithm combined with linear regression. Following this, we introduce our independently developed intelligent prediction system and the clothing design cases completed using this system.
- Section 7 is the discussion.
- Section 8 provides a summary and outlook for this research.

2. Related Work
2.1. Human Body Size Prediction Research
2.2. Body Type Research
3. Methods
3.1. 3D Body Measurement
3.2. Calculation of Minimum Sample Size
3.3. Methods and Processes
- Step 1:
- Step 2:
- Step 3:
4. Analysis
4.1. Percentile Analysis
4.2. Factor Analysis
4.3. K-Means Analysis
5. Cluster Analysis
5.1. Cluster Analysis
5.2. Cluster Description
5.2.1. Type 1: Rectangular Body Shape
5.2.2. Type 2: Pear-Shaped Body
5.2.3. Type 3: Standard Inverted Trapezoid Body
5.2.4. Type 4: Thin Hourglass Shape Body
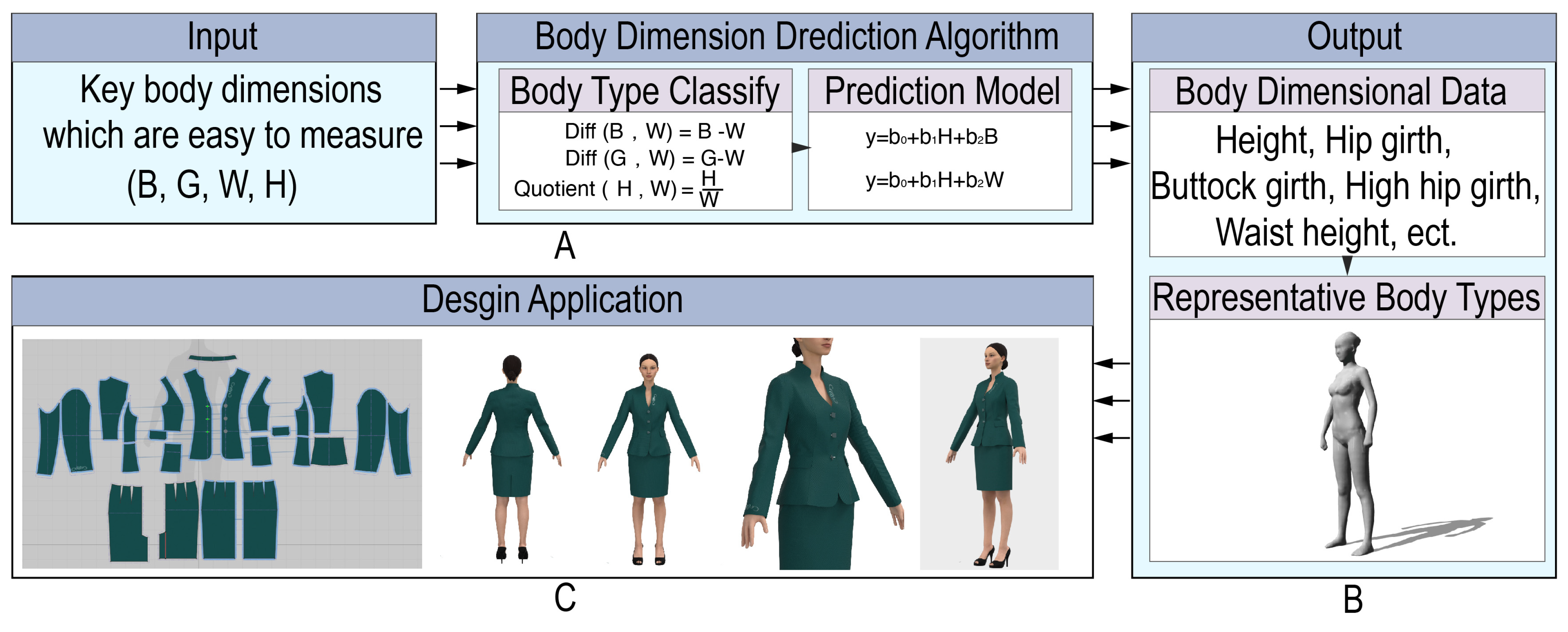
6. A Data-Driven Cluster Size Intelligence Prediction System
6.1. Development of the Prediction Model
6.2. Intelligent Prediction System
6.3. Design Application
7. Discussion
- (1)
- We combined circumference difference classification and trait value classification methods to perform K-means cluster analysis on the 3D human models and 62 key body dimensions of 220 young women from Central China. This led to the identification of four typical body shapes: rectangular, pear-shaped, standard inverted trapezoidal, and thin hourglass. The analysis showed that the pear-shaped body exhibits the thinnest profile in the Bust to waist area from the side, while the thin hourglass shape presents a more pronounced hourglass curve in this region. Additionally, it was found that the thin hourglass shape has a more ideal waist–height ratio. These findings further validate the effectiveness of the chosen clustering indicators and methods.
- (2)
- By combining body shape classification with size prediction algorithms, we developed a series of size prediction models. These models established specific regression equations for each of the four different body shapes, thereby enhancing the accuracy of the prediction models. In the study, body size data of 20 young women were randomly extracted from the total sample. The validation results showed that the error rate of indicators remained below 5%, proving the effectiveness and accuracy of the model.
- (3)
- To enhance the practicality and user-friendliness of the method, the research team developed an intelligent body size prediction system. This system simplifies the user input process, requiring users to provide only four key indicators. The system then automatically determines the body type and, based on the determination and prediction model, outputs 28 body size data. This streamlined process reduces the burden on designers and users in size calculation.
- (4)
- In the validation process for practical application cases, we selected the uniform of the Hunan Provincial Electric Power Company’s business hall in China as the application scenario. This practice demonstrated the significant impact of accurately predicting and determining the body types of different populations in the process of market segmentation on clothing design. With the aid of the system, we applied design thinking to make detailed adjustments to the uniforms for the four body types. One example was enhancing the waistline to optimize the waist proportions for the pear-shaped group, thereby improving the aesthetic appeal of the wearing effect.
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cordier, F.; Seo, H.; Magnenat-Thalmann, N. Made-to-measure technologies for an online clothing store. IEEE Comput. Graph. Appl. 2003, 23, 38–48. [Google Scholar] [CrossRef]
- Lu, J.M.; Wang, M.J.J. Automated anthropometric data collection using 3D whole body scanners. Expert Syst. Appl. 2008, 35, 407–414. [Google Scholar] [CrossRef]
- Makhanya, B.P.; Mabuza, D.C. Body cathexis and fit preferences of young South African women of different body shapes and ethnicity. Int. J. Fash. Des. Technol. Educ. 2020, 13, 173–180. [Google Scholar] [CrossRef]
- Wu, G.; Liu, S.; Wu, X.; Ding, X. Research on lower body shape of late pregnant women in Shanghai area of China. Int. J. Ind. Ergon. 2015, 46, 69–75. [Google Scholar] [CrossRef]
- Heinz, G.; Peterson, L.J.; Johnson, R.W.; Kerk, C.J. Exploring relationship in body dimensions. J. Stat. Educ. 2003, 11, 1–13. [Google Scholar] [CrossRef]
- Xu, B.; Lin, S.; Chen, T. 3D measurement of human body for apparel mass-customization. Videometrics Opt. Methods 3D Shape Meas. 2000, 4309, 26–33. [Google Scholar]
- Štěpánek, L.; Dlouhá, J.; Martinková, P. Item Difficulty Prediction Using Item Text Features: Comparison of Predictive Performance across Machine-Learning Algorithms. Mathematics 2023, 11, 4104. [Google Scholar] [CrossRef]
- Wang, L.; Lee, T.J.; Bavendiek, J.; Eckstein, L. A data-driven approach towards the full anthropometric measurements prediction via Generalized Regression Neural Networks. Appl. Soft Comput. 2021, 109, 107551. [Google Scholar] [CrossRef]
- Galada, A.; Baytar, F. Developing a prediction model for improving bifurcated garment fit for mass customization. Int. J. Cloth. Sci. Technol. 2023, 35, 397–418. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Xing, Y.; Yang, Y.; Liu, K. Estimating human body dimensions using RBF artificial neural networks technology and its application in activewear pattern making. Appl. Sci. 2019, 9, 1140. [Google Scholar] [CrossRef]
- Lin, S.; Shen, T.; Guo, W. Evolution and emerging trends of kansei engineering: A visual analysis based on citespace. IEEE Access 2021, 9, 111181–111202. [Google Scholar] [CrossRef]
- Id, C.S.; Giacone, L.; Staub, K.; Bender, N.; Siegrist, M. Drawings or 3D models: Do illustration methods matter when assessing perceived body size and body dissatisfaction. PLoS ONE 2021, 16, e0261645. [Google Scholar]
- Song, H.K.; Ashdown, S.P. Female Apparel Consumers’ Understanding of Body Size and Shape: Relationship Among Body Measurements, Fit Satisfaction, and Body Cathexis. Cloth. Text. Res. J. 2013, 31, 143–156. [Google Scholar] [CrossRef]
- Li, Z.; Su, J.; Wu, Z. Calculating method of characteristics girth of young female body by 3-D scanning data. J. Text. Res. 2017, 38, 110–114. [Google Scholar]
- Kolose, S.; Stewart, T.; Hume, P.; Tomkinson, G.R. Prediction of military combat clothing size using decision trees and 3D body scan data. Appl. Ergon. 2021, 95, 103435. [Google Scholar] [CrossRef] [PubMed]
- Parker, C.J.; Hayes, S.G.; Brownbridge, K.; Parker, C.J.; Hayes, S.G.; Brownbridge, K. Assessing the female figure identification technique’ s reliability as a body shape classification system. Ergonomics 2021, 68, 1035–1051. [Google Scholar] [CrossRef] [PubMed]
- Park, W.; Park, S. Body shape analyses of large persons in South Korea. Ergonomics 2013, 56, 692–706. [Google Scholar] [CrossRef] [PubMed]
- Ye, W.; Kuang, H.; Lai, X.; Li, J. A Multi-View Approach for Regional Parking Occupancy Prediction with Attention Mechanisms. Mathematics 2023, 11, 4510. [Google Scholar] [CrossRef]
- Chan, A.P.; Fan, J.; Yu, W.M. Prediction of men’s shirt pattern based on 3D body measurements. Int. J. Cloth. Sci. Technol. 2005, 17, 100–108. [Google Scholar] [CrossRef]
- Liu, Z.; Li, J.; Chen, G.; Lu, G. Predicting detailed body sizes by feature parameters. Int. J. Cloth. Sci. Technol. 2014, 26, 118–130. [Google Scholar] [CrossRef]
- Zanwar, D.R.; Zanwar, H.D.; Shukla, H.M.; Deshpande, A.A. Prediction of Anthropometric Dimensions Using Multiple Linear Regression and Artificial Neural Network Models. J. Inst. Eng. India C 2023, 104, 307–314. [Google Scholar] [CrossRef]
- Liu, K.; Zhu, C.; Tao, X.; Bruniaux, P.; Zeng, X. Parametric design of garment pattern based on body dimensions. Int. J. Ind. Ergon. 2019, 72, 212–221. [Google Scholar] [CrossRef]
- Meyer, P.; Birregah, B.; Beauseroy, P.; Grall, E.; Lauxerrois, A. Missing body measurements prediction in fashion industry: A comparative approach. Fash. Text. 2023, 10, 37. [Google Scholar] [CrossRef]
- Rativa, D.; Fernandes, B.J.T.; Roque, A. Height and Weight Estimation from Anthropometric Measurements Using Machine Learning Regressions. IEEE J. Transl. Eng. Health Med. 2018, 6, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Bartol, K.; Bojanić, D.; Petković, T.; Peharec, S.; Pribanić, T. Linear Regression vs. Deep Learning: A Simple Yet Effective Baseline for Human Body Measurement. Sensors 2022, 22, 1885. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.G.B.; Zhong, Z. Classification of young women’s waist-abdomen-hip shapesdriven by front and lateral morphological characteristics. J. Silk 2020, 57, 48–53. [Google Scholar]
- Anderson-Connell, L.J.; Ulrich, P.V.; Brannon, E.L. A consumer-driven model for mass customization in the apparel market. J. Fash. Mark. Manag. 2002, 6, 240–258. [Google Scholar] [CrossRef]
- Shishoo, L.R. International journal of clothing science and technology—Editorial. Int. J. Cloth. Sci. Technol. 2006, 18, 220–224. [Google Scholar]
- Wang, J.; Li, X.; Pan, L.; Zhang, C. Parametric 3D modeling of young women’s lower bodies based on shape classification. Int. J. Ind. Ergon. 2021, 84, 103142. [Google Scholar] [CrossRef]
- Kolose, S.; Stewart, T.; Hume, P.; Tomkinson, G.R. Cluster size prediction for military clothing using 3D body scan data. Appl. Ergon. 2021, 96, 103487. [Google Scholar] [CrossRef]
- Pandarum, R.; Harlock, S.C.; Hunter, L.; Leaf, G.A.V. A normative method for the classification and assessment of women’s 3-D scanned morphotypes. Int. J. Cloth. Sci. Technol. 2021, 33, 421–433. [Google Scholar] [CrossRef]
- Tullis, T.; Albert, B. Measuring the User Experience: Collecting, Analyzing, and Presenting Usability Metrics; Machine Press: Beijing, China, 2009; p. 24. [Google Scholar]
- GB/T 1335.2-2008; Standard Sizing Systems for Garments-Women. Standardization Administration of China: Beijing, China, 2008.
- Deng, M.; Liu, Y.; Chen, L. AI-driven innovation in ethnic clothing design: An intersection of machine learning and cultural heritage. Electron. Res. Arch. 2023, 31, 5793–5814. [Google Scholar] [CrossRef]
- Yu, L.; Xin, G.; Gang, W.; Zhang, Q.; Qiong, S.; Guoju, X. Heavy metal contamination and source in arid agricultural soil in central Gansu Province, China. J. Environ. Sci. 2008, 20, 607–612. [Google Scholar]
- Veenman, C.J.; Reinders, M.J.T.; Backer, E. A maximum variance cluster algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1273–1280. [Google Scholar] [CrossRef]








| Measurement Site/Percentile | 5th | 10th | 50th | 90th | 95th |
|---|---|---|---|---|---|
| Height (cm) | 150.145 | 152.4 | 161.8 | 172.3 | 173.91 |
| Maximum Shoulder Width (cm) | 34.8 | 35.3 | 37.4 | 40.13 | 40.765 |
| Bust Circumference (cm) | 73.675 | 76.67 | 82.35 | 89.56 | 91.83 |
| Bust Width (cm) | 24.2 | 24.8 | 26.4 | 28.76 | 29.3 |
| Waist Circumference (cm) | 57.935 | 58.97 | 64.7 | 71.65 | 73.6 |
| Hip Girth (cm) | 81.54 | 83.61 | 88.6 | 95.05 | 97.35 |
| Hip Width (cm) | 30.1 | 30.74 | 33.2 | 35.1 | 35.6 |
| Factor 1: Height and Length Factors | Loadings | Factor 2: Girth and Width Factors | Loadings | Factor 3: Shoulder and Neck Factors | Loadings |
|---|---|---|---|---|---|
| Height | 0.959 | Wrist Girth | 0.631 | Mid Neck Circumference | 0.839 |
| Neck Height | 0.968 | Bust girth | 0.767 | Shoulder Width | 0.539 |
| Anterior Neck Height | 0.964 | Underbust Circumference | 0.711 | Right Shoulder Width | 0.846 |
| Scapular Height | 0.903 | Waistline Start | 0.850 | Left Shoulder Slope | 0.792 |
| Right Arm Length | 0.861 | High Waist Circumference | 0.882 | Right Shoulder Slope | 0.849 |
| Left Arm Length | 0.857 | Waist Circumference | 0.879 | ||
| Breast Height | 0.956 | Belly Girth | 0.919 | ||
| Waist Height | 0.975 | Maximum Belly Circumference | 0.836 | ||
| Right Waist Side Seam | 0.971 | Max Hip Girth | 0.922 | ||
| Abdominal Height | 0.982 | Hip Girth | 0.885 | ||
| Maximum Abdominal Height | 0.984 | Thigh Circumference | 0.862 | ||
| Hip Peak Height | 0.980 | Thigh Girth | 0.717 | ||
| Trochanter Height | 0.922 | Hip Breadth | 0.520 | ||
| Hip Breadth Height | 0.978 | Right Thigh Circumference | 0.809 | ||
| Left Side Seam Length | 0.955 | Thigh Width | 0.668 | ||
| Right Side Seam Length | 0.957 | Knee Width | 0.620 | ||
| Left Inseam Length | 0.976 | Calf Width | 0.793 | ||
| Right Inseam Length | 0.954 |
| Body Shape Characteristic Indicators | Body Shape Characteristic Variables | Formula |
|---|---|---|
| Tall and Thin Indicators | Body-to-bust Ratio | |
| Body-to-Waist Ratio | Tall and Thin Index = Height/Circumference of Each Part | |
| Body-to-Hip Ratio | ||
| Girth Indicators | Bust-Waist Difference | Girth Index = Difference in Circumference of Each Part |
| Hip-Waist Difference | ||
| Bust-Abdomen Difference | ||
| Waist-Abdomen Difference | ||
| Hip-Abdomen Difference | ||
| Shoulder and Neck Indicators | Shoulder-Waist Difference | Shoulder and Neck Index = Distance from Shoulder Blade to Central Axis and Difference in Distance from Each Part to Central Axis |
| Body Type Code | Bust-Waist Difference (Mean) | Range | Hip-Waist Difference (Mean) | Range | Body-to-Waist Ratio (Mean) | Range |
|---|---|---|---|---|---|---|
| Body Type 1 | 12.88 | 6.40–19.7 | 18.10 | 9.6–22.4 | 2.33 | 1.97–2.77 |
| Body Type 2 | 15.34 | 10.2–18.7 | 26.14 | 23.1–31.7 | 2.54 | 2.21–3.01 |
| Body Type 3 | 17.65 | 14.2–21.9 | 22.03 | 15.8–24.2 | 2.46 | 1.80–2.86 |
| Body Type 4 | 21.99 | 18.9–32.0 | 26.54 | 21.2–34.2 | 2.64 | 2.27–3.10 |
| Body Type Classification Code | Thoracolumbar Difference (cm) | Number of Samples (Person) | Percentage of Samples (%) |
|---|---|---|---|
| Other | >25 | 12 | 6.452 |
| Y | 19–24 | 77 | 41.398 |
| A | 14–18 | 66 | 35.484 |
| B | 9–13 | 30 | 16.129 |
| C | 4–8 | 1 | 0.538 |
| Item | Abbr. | Definition |
|---|---|---|
| Height | H | The vertical distance measured from the crown to the soles of feet with the subject standing upright and the feet together without wearing shoes |
| Waist girth | W | The length of measurement around the most prominent part of abdomen horizontally |
| Hip girth | G | The length of measurement around the fullest part of hip horizontally |
| Bust girth | B | The length of measurement around the fullest part of bust horizontally |
| Control Part/Body Type | Body Type 1 (Rectangular) | Body Type 2 (Pear) | Body Type 3 (Standard Inverted Trapezoid) | Body Type 4 (Thin Hourglass) |
|---|---|---|---|---|
| Height (H) | ||||
| Neck Height | 0.865H + 0.004B − 3.949 | 0.812H − 0.04B + 8.125 | 0.865H − 0.004B − 3.037 | 0.842H − 0.002B + 0.419 |
| Bust Height | 0.776H − 0.086B − 3.637 | 0.779H − 0.026B − 8.244 | 0.806H − 0.013B − 13.017 | 0.807H + 0.077B − 20.826 |
| Waist Height | 0.734H − 0.019B − 17.089 | 0.696H − 0.029B − 10.252 | 0.734H + 0.026B − 20.158 | 0.718H + 0.068B − 21.87 |
| Arm Length | 0.473H + 0.011B − 23.132 | 0.389H + 0.049B − 14.128 | 0.402H − 0.025B − 9.469 | 0.336H + 0.028B − 3.552 |
| Bust (B) | ||||
| Neck Circumference | −0.04H + 0.212B + 19.551 | −0.035H + 0.215B + 18.382 | 0.037H + 0.238B + 4.71 | 0.023H + 0.144B + 14.199 |
| Waist Circumference | 0.074H + 0.866B − 13.742 | −0.034H + 0.938B − 4.835 | −0.027H + 0.875B − 2.918 | −0.008H + 0.654B + 8.845 |
| Neck Width | 0H + 0.077B + 3.981 | 0.015H + 0.032B + 5.087 | 0.008H + 0.061B + 3.838 | 0.007H + 0.025B + 6.932 |
| Shoulder Width | −0.006H + 0.103B + 29.978 | 0.044H + 0.231B + 11.731 | 0.063H + 0.211B + 9.88 | 0.079H + 0.245B + 4.044 |
| Bust Width | 0.042H + 0.248B − 0.329 | −0.075H + 0.142B + 26.689 | −0.019H + 0.25B + 8.937 | −0.007H + 0.28B + 3.938 |
| Waist Width | 0.071H + 0.285B − 9.407 | 0.014H + 0.305B − 2.775 | −0.044H + 0.261B + 9.03 | 0.011H + 0.207B + 3.712 |
| Neck Thickness | −0.017H + 0.148B + 0.02 | 0.007H + 0.09B + 0.801 | −0.004H + 0.078B + 3.738 | 0.021H + 0.044B + 2.392 |
| Bust Thickness | 0.003H + 0.344B − 7.054 | 0.018H + 0.264B − 3.456 | −0.007H + 0.283B − 0.507 | −0.004H + 0.264B + 0.203 |
| Waist Thickness | −0.025H + 0.229B + 3.315 | −0.002H + 0.272B − 4.409 | −0.04H + 0.304B − 0.935 | −0.014H + 0.208B + 1.076 |
| Control Part/Body Type | Body Type 1 (Rectangular) | Body Type 2 (Pear) | Body Type 3 (Standard Inverted Trapezoid) | Body Type 4 (Thin Hourglass) |
|---|---|---|---|---|
| Height (H) | ||||
| Waist Height | 0.735H − 0.012W − 18.027 | 0.697H − 0.062W − 8.856 | 0.736H + 0.019W − 19.538 | 0.718H + 0.115W − 23.372 |
| Hip Height | 0.688H + 0.13W − 39.559 | 0.594H + 0.023W − 18.319 | 0.648H − 0.036W − 22.009 | 0.631H + 0.008W − 23.158 |
| Leg Length | 0.672H + 0.084W − 41.37 | 0.611H − 0.042W − 23.876 | 0.644H − 0.151W − 21.619 | 0.608H − 0.058W − 22.623 |
| Waist (W) | ||||
| Hip Girth | 0.059H + 0.902W + 15.454 | 0.092H + 0.874W + 19.347 | 0.00003529H + 0.877W + 30.087 | 0.128H + 0.846W + 14.983 |
| Thigh Girth | 0.224H + 0.501W − 21.683 | 0.051H + 0.655W + 0.264 | 0.025H + 0.572W + 7.912 | 0.012H + 0.749W + 1.613 |
| Waist Width | 0.047H + 0.329W − 4.834 | 0.023H + 0.342W − 2.007 | −0.036H + 0.294W + 10.16 | 0.013H + 0.32W + 0.706 |
| Hip Width | 0.071H + 0.288W + 0.194 | 0.013H + 0.276W + 13.911 | 0.011H + 0.232W + 15.355 | 0.107H + 0.261W − 1.132 |
| Thigh Width | 0.012H + 0.154W + 3.08 | −0.044H + 0.194W + 10.478 | 0.004H + 0.19W + 2.498 | −0.018H + 0.196W + 6.45 |
| Knee Width | 0.006H + 0.095W + 3.414 | −0.018H + 0.105W + 7.193 | −0.007H + 0.152W + 1.945 | −0.005H + 0.073W + 7.213 |
| Calf Width | 0H + 0.055W + 6.526 | −0.013H + 0.127W + 4.35 | −0.008H + 0.121W + 3.84 | 0.006H + 0.115W + 2.195 |
| Neck Thickness | −0.029H + 0.146W + 3.913 | 0.013H + 0.074W + 2.335 | −0.001H + 0.083W + 4.335 | 0.022H + 0.052W + 2.614 |
| Bust Thickness | −0.022H + 0.233W + 8.906 | 0.035H + 0.194W + 2.29 | 0.004H + 0.289W + 2.276 | 0.006H + 0.26W + 4.641 |
| Waist Thickness | −0.045H + 0.28W + 5.931 | 0.01H + 0.265W − 1.782 | −0.031H + 0.347W + 0.116 | −0.012H + 0.332W − 2.482 |
| Hip Thickness | 0.014H + 0.233W + 3.337 | 0.015H + 0.25W + 2.822 | −0.011H + 0.306W + 2.738 | −0.009H + 0.305W + 3.337 |
| Thigh Thickness | 0.049H + 0.132W − 1.636 | 0.007H + 0.184W + 2.51 | −0.004H + 0.187W + 3.745 | 0.008H + 0.241W − 0.767 |
| Knee Thickness | 0.036H + 0.041W + 2.646 | 0.005H + 0.079W + 5.577 | 0.021H + 0.115W + 0.363 | 0.035H + 0.178W − 5.332 |
| Calf Thickness | 0.01H + 0.019W + 7.418 | 0.011H + 0.104W + 2.203 | 0.01H + 0.117W + 1.269 | 0.015H + 0.07W + 3.715 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Z.; Lin, S.; Wang, Z. Cluster Size Intelligence Prediction System for Young Women’s Clothing Using 3D Body Scan Data. Mathematics 2024, 12, 497. https://doi.org/10.3390/math12030497
Tan Z, Lin S, Wang Z. Cluster Size Intelligence Prediction System for Young Women’s Clothing Using 3D Body Scan Data. Mathematics. 2024; 12(3):497. https://doi.org/10.3390/math12030497
Chicago/Turabian StyleTan, Zhengtang, Shuang Lin, and Zebin Wang. 2024. "Cluster Size Intelligence Prediction System for Young Women’s Clothing Using 3D Body Scan Data" Mathematics 12, no. 3: 497. https://doi.org/10.3390/math12030497
APA StyleTan, Z., Lin, S., & Wang, Z. (2024). Cluster Size Intelligence Prediction System for Young Women’s Clothing Using 3D Body Scan Data. Mathematics, 12(3), 497. https://doi.org/10.3390/math12030497






