Discounting the Distant Future: What Do Historical Bond Prices Imply about the Long-Term Discount Rate?
Abstract
:1. Introduction
2. The Process of Discounting in Continuous Time
2.1. The General Framework
2.2. The Ornstein–Uhlenbeck Process
2.3. Adding Risk Aversion
3. Empirical Results
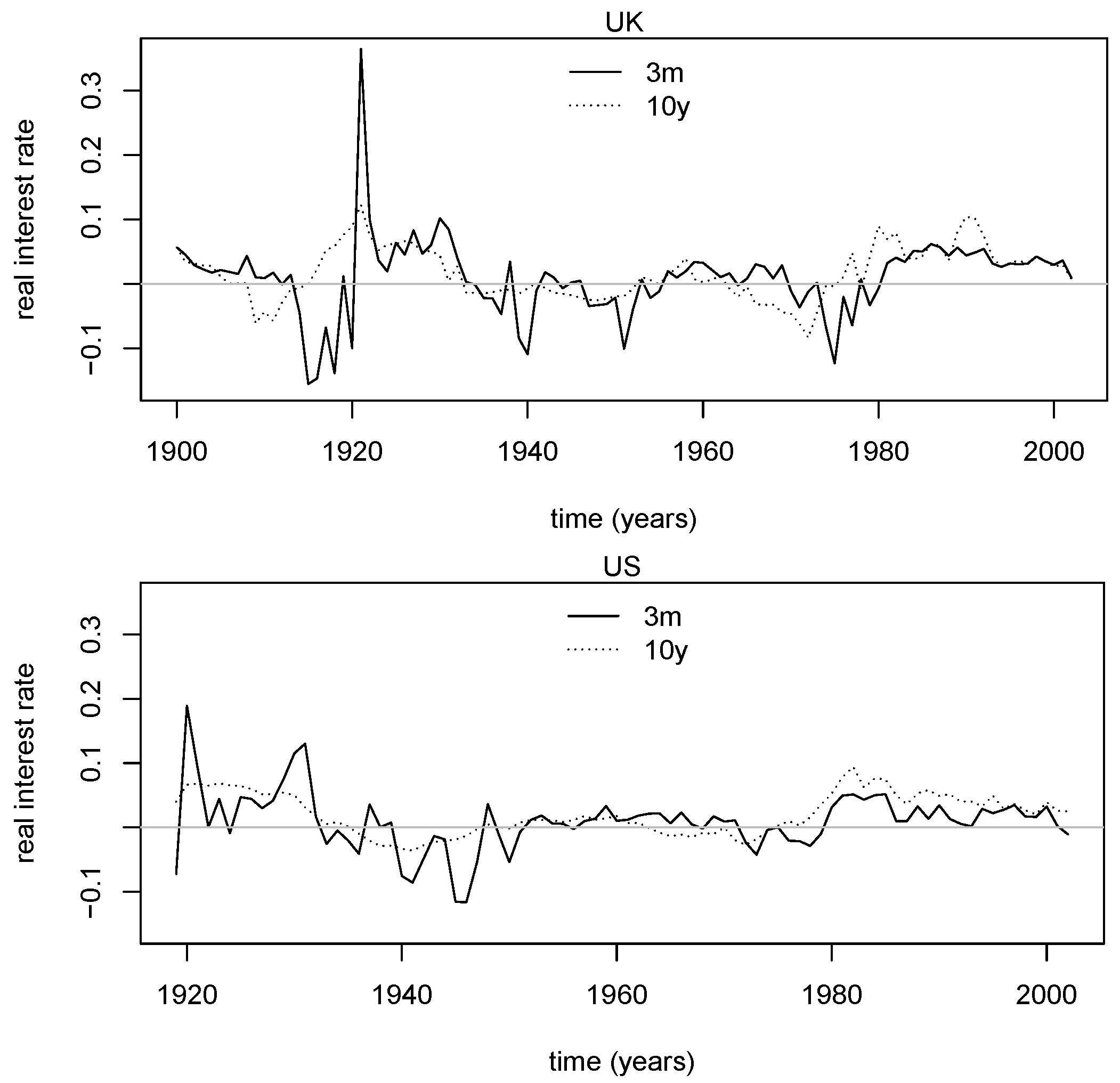
3.1. Estimation of Real Interest Rates
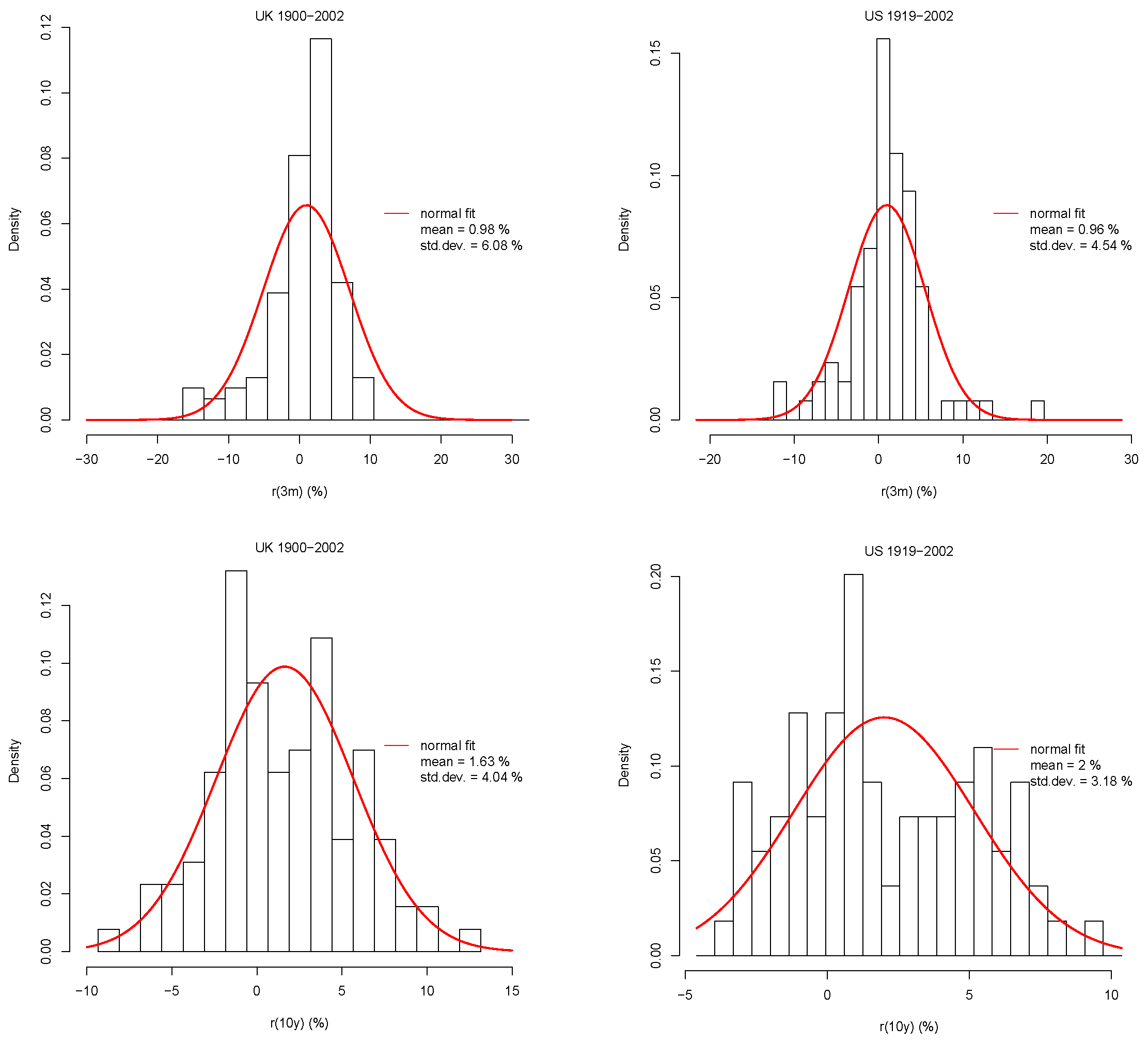
3.2. Empirical Properties of the Data
3.3. Parameter Estimation
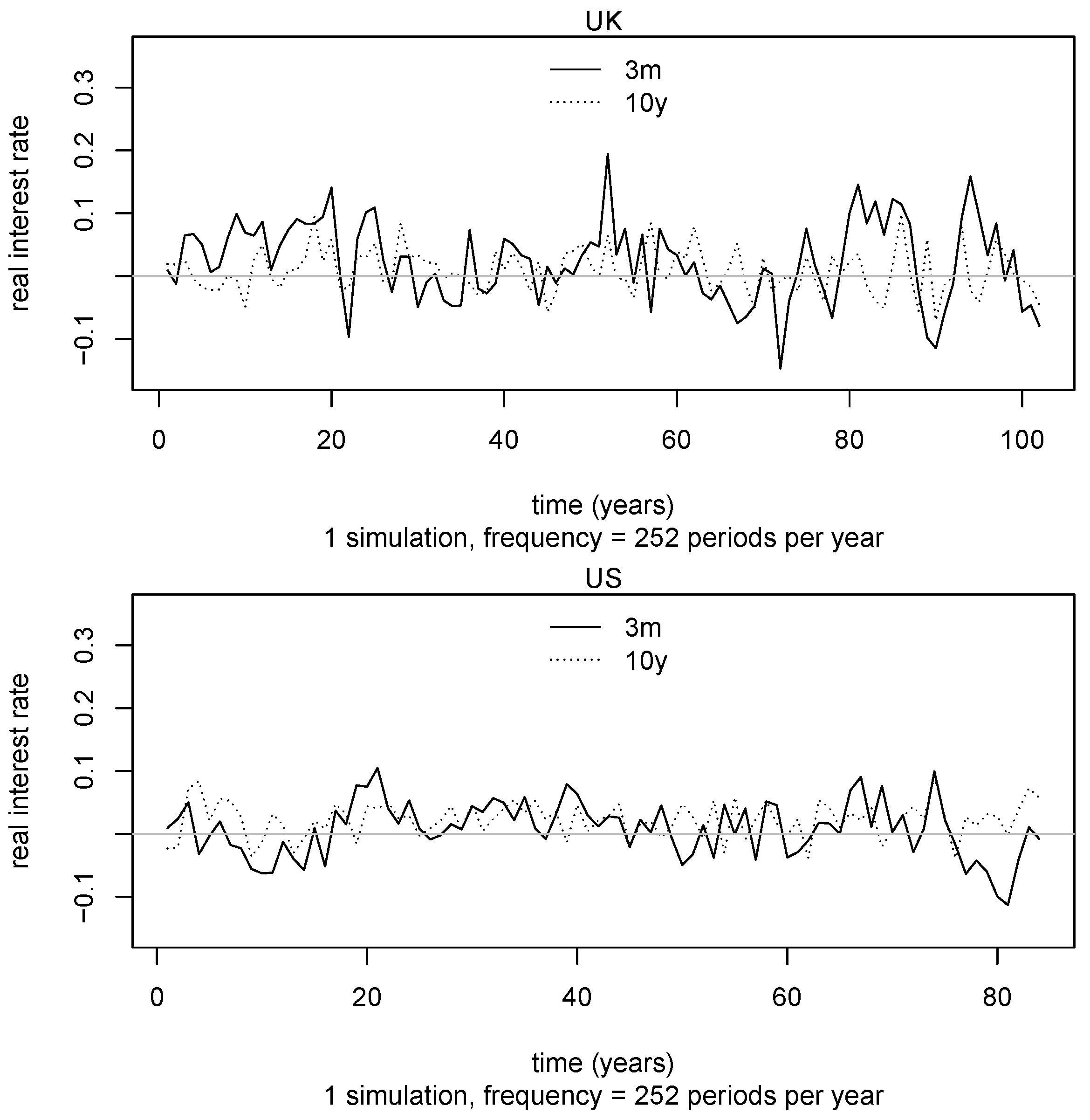
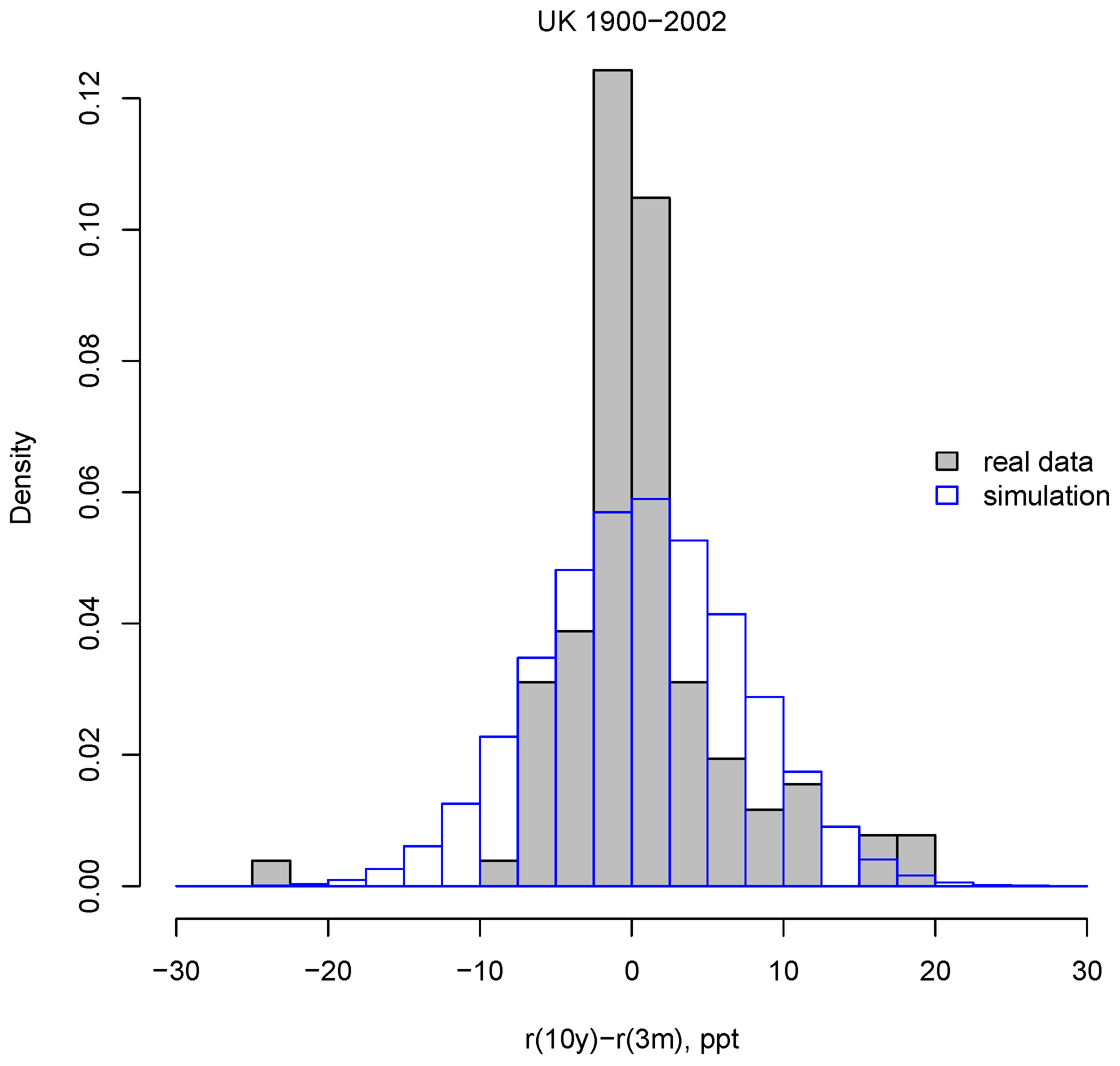
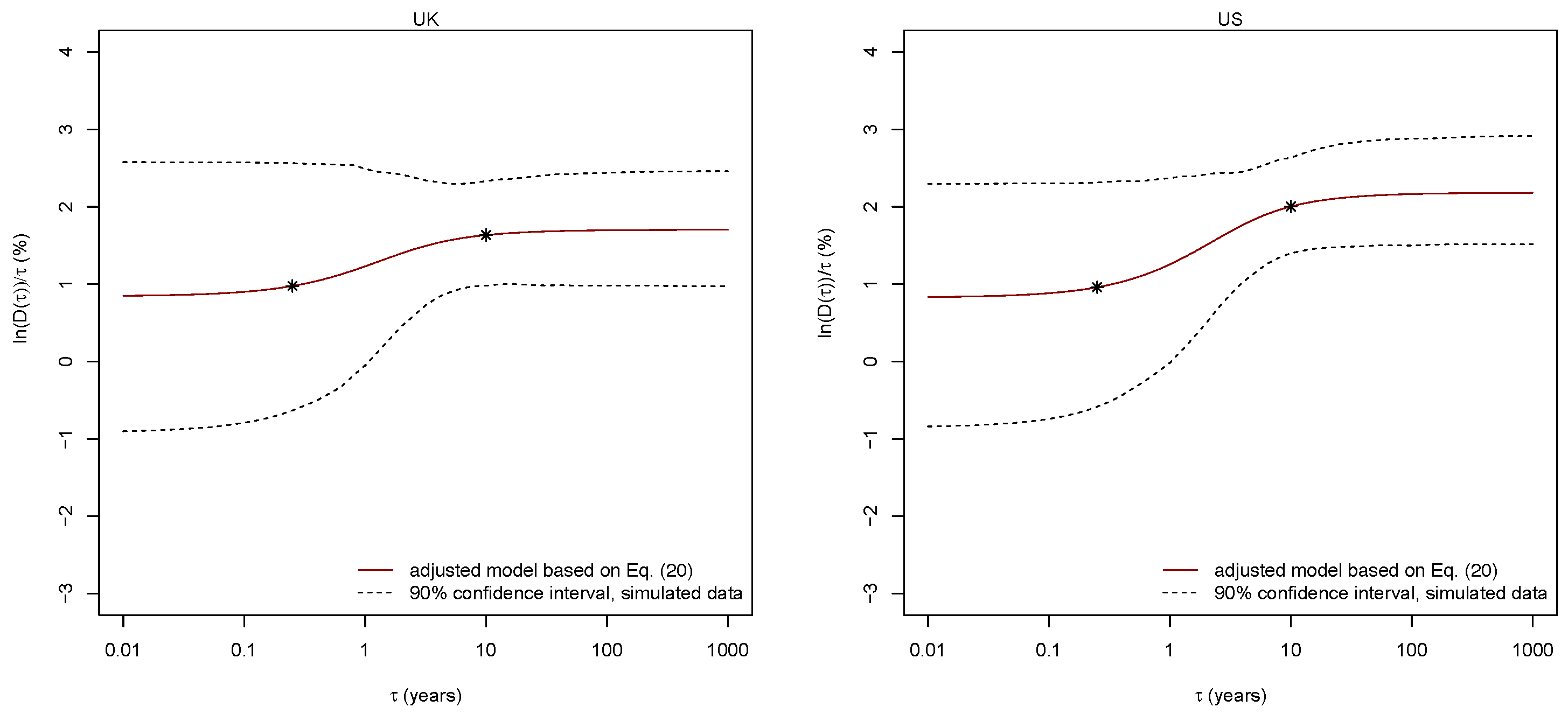
3.4. Contrasting the Model with Data
3.5. Estimating Confidence Intervals
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| OU | Ornstein–Uhlenbeck |
| FPE | Fokker–Planck Equation |
| Probability Density Function | |
| CIR | Cox–Ingersoll–Ross |
| CPI | Consumer Price Index |
| UK | United Kingdom |
| US | United States |
| IID | Independent and Identically Distributed |
Appendix A. Discount Function for the Ornstein-Uhlenbeck Model
Appendix A.1. Negative Rates
Appendix A.2. Rates Below the Long-Run Rate
Appendix B. Real and Nominal Rates—The Market Price of Risk
Appendix B.1. Nominal Rates
Appendix B.2. Inflation Rates
Appendix B.3. The Market Price of Risk
Appendix C. Parameter Estimation and Uncertainties
Appendix C.1. Parameter Estimation
Appendix C.2. Correcting for the Bias Using 3-Month Rates Sampled at Annual Frequency
- Estimate parameters using the historical 3-month and 10-year data as described in the main text.
- Simulate the instantaneous process (which we approximate as a daily process) using the parameters inferred in step (1) to generate a simulated time series whose length matches that of the real data (roughly 100 years for the UK and 80 years for the US).
- Construct simulated 3-month and 10-year time series based on Equation (20) with and , using the time series for from step 1 as the initial condition for each time t.
- Estimate m, k, and on the simulated 3-month series (sampled at annual frequency).
- Repeat steps (2–4) for a 1000 times and compute the average value of each parameter under the estimation process of step (4). This yields systematic shifts in the parameters relative to those estimated on the historical data, making it clear that the estimation process is biased.
- Correct for this bias by adjusting the parameters of the instantaneous process by the magnitude of the average shift, so that the estimation process for the simulated 3-month bond time series roughly matches the values estimated from the historical series.
References
- World Economic Forum. This Is What the Climate Crisis Is Costing Economies Around the World. 29 November 2023. Available online: https://www.weforum.org/agenda/2023/11/climate-crisis-cost-global-economies/ (accessed on 6 February 2024).
- Stern, N. The Economics of Climate Change: The Stern Review; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Dasgupta, P. Human Well-Being and the Natural Environment; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Nordhaus, W.D. A Question of Balance; Yale University Press: New Haven, CT, USA, 2008. [Google Scholar]
- Arrow, K.J.; Cropper, M.L.; Gollier, C.; Groom, B.; Heal, G.M.; Newell, R.G.; Nordhaus, W.D.; Pindyck, R.S.; Pizer, W.A.; Portney, P.R.; et al. Determining benefits and costs for future generations. Science 2013, 341, 349–350. [Google Scholar] [CrossRef]
- Nordhaus, W.D. The Stern Review on the economics of climate change. J. Econ. Lit. 2007, 45, 687–702. [Google Scholar] [CrossRef]
- Nordhaus, W.D. Critical assumptions in the Stern Review on Climate Change. Science 2007, 317, 201–202. [Google Scholar] [CrossRef]
- Dasgupta, P. Comments on the Stern Review’s Economics of Climate Change; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Mendelsohn, R.O. A critique of the Stern report. Regulation 2006, 29, 42–46. [Google Scholar]
- Weitzman, M.L. A review on the Stern Review on the economics of climate change. J. Econ. Lit. 2007, 45, 703–724. [Google Scholar] [CrossRef]
- World Resources Institute. Better Growth, Better Climate: The New Climate Economy Report. The Synthesis Report. 2014. Available online: https://sustainabledevelopment.un.org/content/documents/1595TheNewClimateEconomyReport.pdf (accessed on 6 February 2024).
- Stern, N. Ethics, Equity and the Economics of Climate Change. Paper 1: Science and Philosophy. Econ. Philos. 2014, 30, 397–444. [Google Scholar] [CrossRef]
- Stern, N. Ethics, Equity and the Economics of Climate Change. Paper 2: Economics and Politics. Econ. Philos. 2014, 30, 445–501. [Google Scholar] [CrossRef]
- Drupp, M.A.; Freeman, M.C.; Groom, B.; Nesje, F. Discounting disentangled. Am. Econ. J. Econ. Policy 2018, 10, 109–134. [Google Scholar] [CrossRef]
- Ramsey, F.P. A mathematical theory of saving. Econ. J. 1928, 38, 543–559. [Google Scholar] [CrossRef]
- Arrow, K.J.; Cropper, M.L.; Gollier, C.; Groom, B.; Heal, G.M.; Newell, R.G.; Nordhaus, W.D.; Pindyck, R.S.; Pizer, W.A.; Portney, P.R.; et al. How should benefits and costs be discounted in an intergenerational context? The views of an expert panel. Tech. Rep. Resour. Future 2012, 2012, 12–53. [Google Scholar] [CrossRef]
- Weitzman, M.L. Why the far-distant future should be discounted at its lowest possible rate? J. Environ. Econ. Manag. 1998, 36, 201–208. [Google Scholar] [CrossRef]
- Gollier, C.; Koundouri, P.; Pantelidis, T. Declining discount rates: Economic justifications and implications for the long-run policy. Econ. Policy 2008, 23, 757–795. [Google Scholar] [CrossRef]
- Freeman, M.; Groom, B. How uncertain are we about the certainty-equivalent long-term social discount rate? J. Environ. Econ. Manag. 2016, 79, 152–168. [Google Scholar] [CrossRef]
- Dybvig, P.; Ingersoll, J.; Ross, S. Long forward and zero-coupon rates can never fall. J. Bus. 1996, 60, 1–25. [Google Scholar] [CrossRef]
- Vasicek, O. An equilibrium characterization of the terms structure. J. Fin. Econ. 1977, 5, 177–188. [Google Scholar] [CrossRef]
- Litterman, R.; Scheinkman, J.; Weiss, L. Volatility and the yield curve. J. Fixed Income 1991, 1, 49–53. [Google Scholar] [CrossRef]
- Newell, R.; Pizer, N. Discounting the Distant Future: How much do uncertain rates increase valuations? J. Environ. Econ. Manag. 2003, 46, 52–71. [Google Scholar] [CrossRef]
- Groom, B.; Koundouri, P.; Panopoulou, P.; Pantelidis, T. Discounting distant future: How much selection affect the certainty equivalent rate. J. Appl. Econom. 2007, 22, 641–656. [Google Scholar] [CrossRef]
- Freeman, M.C.; Groom, B.; Panopoulou, E.; Pantelidis, T. Declining discount rates and the fisher effect. Inflated past, discounted future? J. Environ. Econ. Manag. 2015, 73, 32–49. [Google Scholar] [CrossRef]
- Duffie, D. Dynamic Asset Pricing Theory; Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Brigo, D.; Mercurio, F. Interest Rate Models—Theory and Practice; Springer: Berlin, Germany, 2006. [Google Scholar]
- Piazzesi, M. Affine term structure models. In The Handbook of Financial Econometrics; Sahala, Y.A., Hansen, L.P., Eds.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Mamon, R. Three ways to solve bond prices in the Vasicek model. J. Appl. Math. Decis. Sci. 2004, 8, 1–14. [Google Scholar] [CrossRef]
- Davidson, I.; Song, X.; Tippett, M. Time varying costs of capital and the expected present value of future cash flows. Eur. J. Financ. 2015, 21, 129–146. [Google Scholar] [CrossRef]
- Perelló, J.; Montero, M.; Masoliver, J.; Farmer, J.D.; Geanakoplos, J. Statistical analysis and stochastic interest rate modeling for valuing the future with implications in climate change mitigation. J. Stat. Mech. 2020, 2020, 043210. [Google Scholar] [CrossRef]
- Masoliver, J.; Montero, M.; Perelló, J. Valuing the future under random structural conditions: Non-stationary models for discounting. 2024, in preparation. in preparation. 2024. [Google Scholar]
- Masoliver, J.; Montero, M.; Perelló, J. Jump-Diffusion Models for Valuing the Future: Discounting under Extreme Situation. Mathematics 2021, 9, 1589. [Google Scholar] [CrossRef]
- Montero, M.; Perelló, J.; Masoliver, J. Valuing the distant future under stochastic resettings: The effect on discounting. J. Phys. A 2022, 55, 464001. [Google Scholar] [CrossRef]
- Masoliver, J.; Montero, M.; Perelló, J.; Farmer, J.D.; Geanakoplos, J. Valuing the Future and Discounting in Random Environments: A Review. Entropy 2022, 24, 496. [Google Scholar] [CrossRef] [PubMed]
- Gollier, C. Discounting with fat-tailed economic growth. J. Risk Uncertain. 2008, 37, 171–186. [Google Scholar] [CrossRef]
- Cox, J.C.; Ingersoll, J.E.; Ross, S.A. A re-examination of the traditional hypothesis about the term structure of interest rates. J. Financ. 1981, 36, 769–799. [Google Scholar]
- Gilles, C.; Leroy, S.F. A note on the local expectation hypothesis. J. Financ. 1986, 41, 975–979. [Google Scholar]
- Farmer, J.D.; Geanakoplos, J.; Masoliver, J.; Montero, M.; Perelló, J. Value of the future: Discounting in random environments. Phys. Rev. E 2015, 91, 052816. [Google Scholar] [CrossRef]
- Cox, J.C.; Ingersoll, J.E.; Ross, S.A. A theory of the term structure of interest rates. Econometrica 1985, 53, 385–407. [Google Scholar] [CrossRef]
- Soergel, B.; Kriegler, E.; Weindl, I.; Rauner, S.; Dirnaichner, A.; Ruhe, C.; Hofmann, M.; Bauer, N.; Bertram, C.; Bodirsky, B.; et al. A sustainable development pathway for climate action within the UN 2030 Agenda. Nat. Clim. Change 2021, 11, 656–664. [Google Scholar] [CrossRef]
- Giglio, S.; Kelly, B.; Stroebel, J. Climate finance. Annu. Rev. Financ. Econ. 2021, 13, 15–36. [Google Scholar] [CrossRef]
- Stroebel, J.; Wurgler, J. What do you think about climate finance? J. Financ. Econ. 2021, 142, 487–498. [Google Scholar] [CrossRef]
- Bauer, M.D.; Rudebusch, G.D. The rising cost of climate change: Evidence from the bond market. Rev. Econ. Stat. 2023, 105, 1255–1270. [Google Scholar] [CrossRef]
- Stern, N. A time for action on climate change and a time for change in economics. Econ. J. 2022, 132, 1259–1289. [Google Scholar] [CrossRef]
- Stern, N.; Stiglitz, J.; Taylor, C. The economics of immense risk, urgent action and radical change: Towards new approaches to the economics of climate change. J. Econ. Methodol. 2021, 29, 181–216. [Google Scholar] [CrossRef]
- Giglio, S.; Maggiori, M.; Stroebel, J. Very long-run discount rates. Q. J. Econ. 2015, 130, 1. [Google Scholar] [CrossRef]
- Giglio, S.; Maggiori, M.; Stroebel, J. No-bubble conditions:model-free test in housing markets. Econometrica 2016, 84, 1047–1091. [Google Scholar] [CrossRef]
- Giglio, S.; Maggiori, M.; Rao, K.; Stroebel, J.; Weber, A. Climate change and long-run discount rates: Evidence from real estate. Rev. Financ. Stud. 2021, 34, 3527–3571. [Google Scholar] [CrossRef]
- Sukono; Ibrahim, R.A.; Saputra, M.P.A.; Hidayat, Y.; Juahir, H.; Prihanto, I.G.; Halim, N.B.A. Modeling Multiple-Event Catastrophe Bond Prices Involving the Trigger Event Correlation, Interest, and Inflation Rates. Mathematics 2022, 10, 4685. [Google Scholar] [CrossRef]
- Li, M.; Trencher, G.; Asuka, J. The clean energy claims of BP, Chevron, ExxonMobil and Shell: A mismatch between discourse, actions and investments. PLoS ONE 2022, 17, e0263596. [Google Scholar] [CrossRef]
- Creutzig, F.; Kapmeier, F. Engage, don’t preach: Active learning triggers climate action. Energy Res. Soc. Sci. 2020, 70, 101779. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Matczak, P.; Otto, I.M.; Otto, P.E. From “atmosfear” to climate action. Environ. Sci. Policy 2020, 105, 75–83. [Google Scholar] [CrossRef]
- Vicens, J.; Bueno-Guerra, N.; Gutiérrez-Roig, M.; Gracia-Lázaro, C.; Gómez-Gardeñes, J.; Perelló, J.; Sánchez, A.; Moreno, Y.; Duch, J. Resource heterogeneity leads to unjust effort distribution in climate change mitigation. PLoS ONE 2018, 13, e0204369. [Google Scholar] [CrossRef]
- Weitzman, M.L. Gamma discounting. Am. Econ. Rev. 2001, 91, 260–271. [Google Scholar] [CrossRef]
- Buła, R.; Foltyn-Zarychta, M. Declining Discount Rates for Energy Policy Investments in CEE EU Member Countries. Energies 2023, 16, 321. [Google Scholar] [CrossRef]
- Suwanmalai, W.; Zaby, S. How Do Life Insurers Respond to a Prolonged Low Interest Rate Environment? A Literature Review. Risks 2022, 10, 155. [Google Scholar] [CrossRef]
- Fregonara, E.; Ferrando, D.G. The Discount Rate in the Evaluation of Project Economic-Environmental Sustainability. Sustainability 2023, 15, 2467. [Google Scholar] [CrossRef]
- Magnus, W.; Oberhettinger, F.; Soni, R.P. Formulas and Theorems for the Special Functions of Mathematical Physics; Springer: Berlin, Germany, 1966. [Google Scholar]
- Masoliver, J. Random Processes, First-Passage and Escape; World Scientific: Singapore, 2018. [Google Scholar]

| Country | Time Series | Frequency | From | To | # Records |
|---|---|---|---|---|---|
| UK | 3-month Treasury bills | monthly | 31 December 1900 | 31 December 2012 | 113 |
| UK | 10-year bonds | annual | 31 December 1694 | 31 December 2012 | 309 |
| UK | inflation index | annual | 31 December 1694 | 31 December 2012 | 309 |
| US | 3-month Treasury bills | monthly | 31 January 1920 | 30 October 2012 | 93 |
| US | 10-year bonds | annual | 31 December 1820 | 30 October 2012 | 183 |
| US | inflation index | annual | 31 December 1820 | 30 October 2012 | 183 |
| Country | Min | Max | k | Min | Max | Min | Max | ||
|---|---|---|---|---|---|---|---|---|---|
| UK | |||||||||
| US | 0.3 |
| Country | m | 5% | 95% | k | 5% | 95% | 5% | 95% | q | 5% | 95% | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| UK | ||||||||||||
| US | 0.36 |
| Country | 3-Month (Data) | 3-Month (Model) | 10-Year (Data) | 10-Year (Model) |
|---|---|---|---|---|
| UK | 32% | 43% | 38% | 34% |
| US | 32% | 42% | 30% | 26% |
| Country | 5% | 95% | |
|---|---|---|---|
| UK | |||
| US |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farmer, J.D.; Geanakoplos, J.; Richiardi, M.G.; Montero, M.; Perelló, J.; Masoliver, J. Discounting the Distant Future: What Do Historical Bond Prices Imply about the Long-Term Discount Rate? Mathematics 2024, 12, 645. https://doi.org/10.3390/math12050645
Farmer JD, Geanakoplos J, Richiardi MG, Montero M, Perelló J, Masoliver J. Discounting the Distant Future: What Do Historical Bond Prices Imply about the Long-Term Discount Rate? Mathematics. 2024; 12(5):645. https://doi.org/10.3390/math12050645
Chicago/Turabian StyleFarmer, J. Doyne, John Geanakoplos, Matteo G. Richiardi, Miquel Montero, Josep Perelló, and Jaume Masoliver. 2024. "Discounting the Distant Future: What Do Historical Bond Prices Imply about the Long-Term Discount Rate?" Mathematics 12, no. 5: 645. https://doi.org/10.3390/math12050645
APA StyleFarmer, J. D., Geanakoplos, J., Richiardi, M. G., Montero, M., Perelló, J., & Masoliver, J. (2024). Discounting the Distant Future: What Do Historical Bond Prices Imply about the Long-Term Discount Rate? Mathematics, 12(5), 645. https://doi.org/10.3390/math12050645









