Design and Real-Time Implementation of a Cascaded Model Predictive Control Architecture for Unmanned Aerial Vehicles
Abstract
:1. Introduction
2. Kinematics
- Standard quadrotor structure.
- The structure is perfectly rigid.
- The center of mass of the quadrotor coincides with the origin of the body frame.
- Aerodynamics and other complex phenomena that are difficult to model are ignored.
- The quadrotor is hovering.
3. Control Strategy
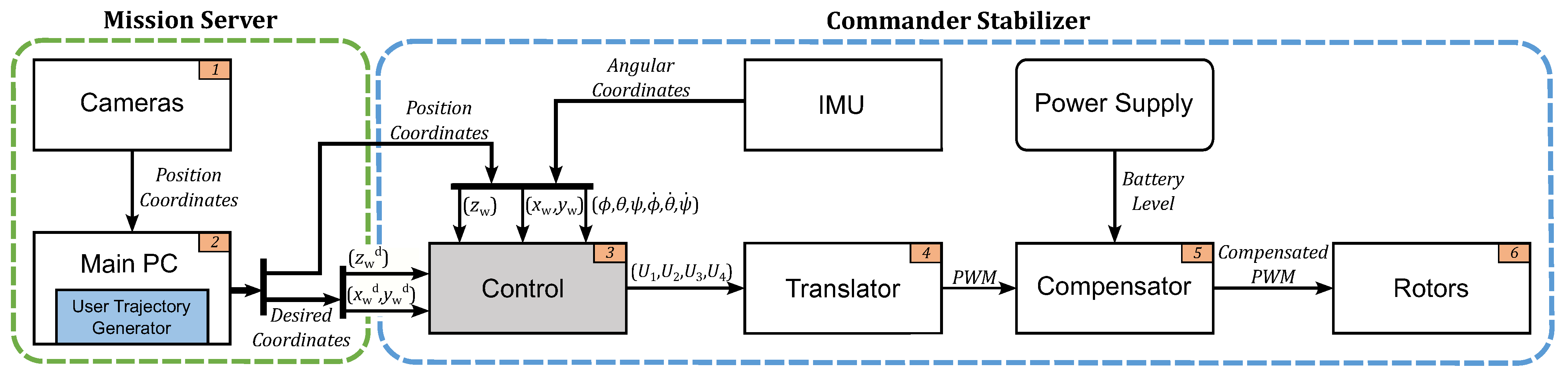
4. Quadrotor Control Structure
- The camera system provides the linear and yaw positions of the quadrotor, while the IMU of the quadrotor sends the angular status.
- The trajectory generator commands the desired position in the inertial frame . These will be the references for translational control.
- The implemented cascaded control structures, PIV, and MPC receive the desired and actual position and rotational coordinates to compute .
- Once all the control actions are calculated, the transformation matrix provided by Quanser® is used to change the control inputs to pulse-width modulation (PWM).
- Most of the quadrotors in real-world implementations are powered by batteries [45]. Here, the reduction in power supply, named battery drainage, occurs gradually [46,47]. Therefore, the control performance of the drone is affected [48]. For this reason, we designed a compensation subsystem by measuring the altitude and battery voltage rate of change. Hence, a relationship between the PWM and the necessary battery level to reach hover position was obtained.
- The rotors receive their compensated PWM control signal.
4.1. PIV Controller Design
- The position PIV controller obtains the desired positions from the trajectory generator while the motion tracking system provides the actual position of the drone. Here, the thrust input and the angular reference of the angular PIV are computed as follows:
- Then, the angular PIV receives the desired angular positions , the actual angular positions , and the actual angular velocities . These are processed to compute the reference angular velocities of the PIV velocities, which are saturated with a minimum and a maximum rate of −45° and 45°, respectively.
- The angular PIV velocity gathers the desired angular velocities , the actual angular velocities , and the actual angular accelerations . Then, it computes the optimal angular torques ; this is performed by considering the thrust input computed in step (a).
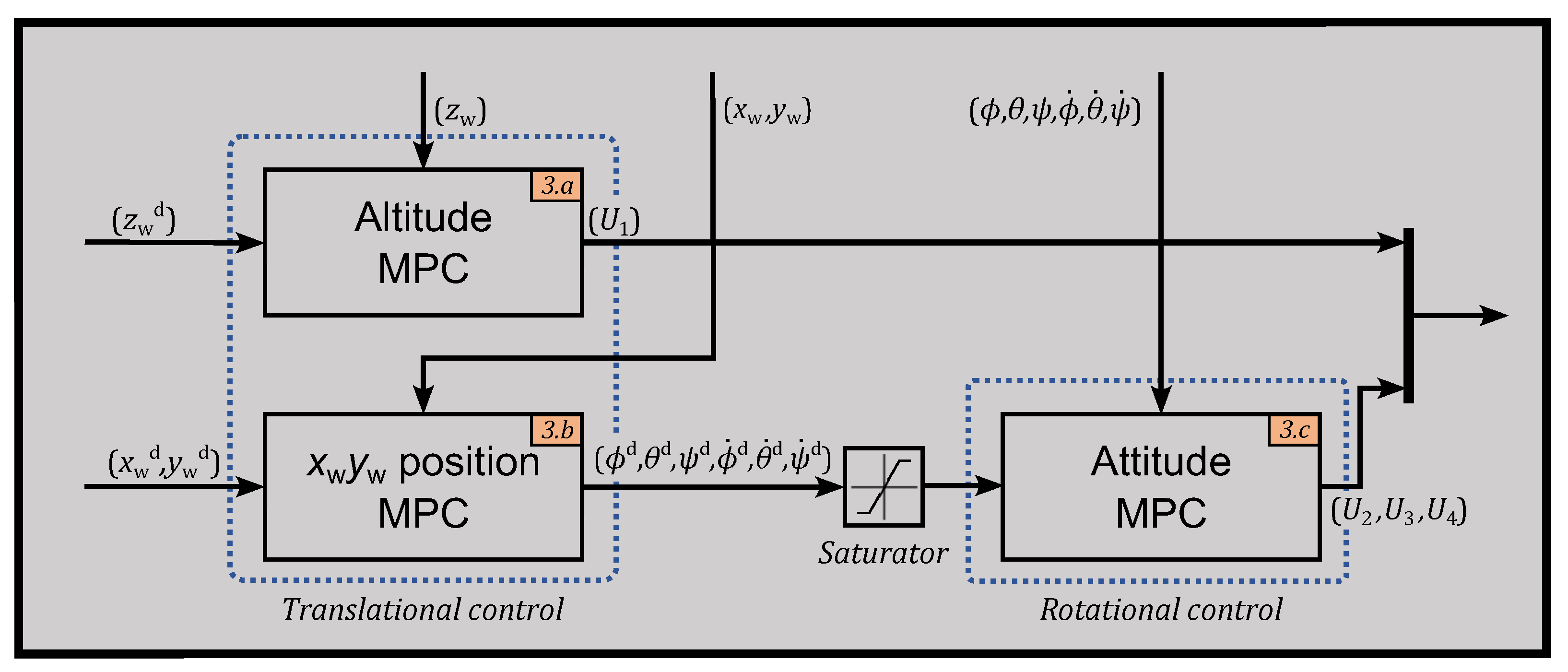
4.2. MPC Controller Design
- The altitude controller obtains the reference from the trajectory generator while the motion tracking system provides the actual position of the drone. Here, the thrust input is computed.
- On the other hand, and accelerations depend directly on the rotation of the drone. Thus, the dynamics are dependent, and the controllers must be related. This relation is described in the dynamical models (29), (30), where it is shown that the product between gravity and the respective angle gives a linear displacement. Then, the output of the MPC algorithm is saturated with a minimum and maximum of −45° and 45°, respectively, and the desired angles are sent to the attitude controller.
- The attitude MPC receives the following: from the motion tracking system, the angular positions and the angular velocities ; and from the MPC algorithm, the saturated orientation references . Then, the attitude MPC uses this information to obtain the optimal angular torques ; factoring into the calculations the thrust input computed in step (a).
5. Real-Time Implementation
5.1. Experimental Setup
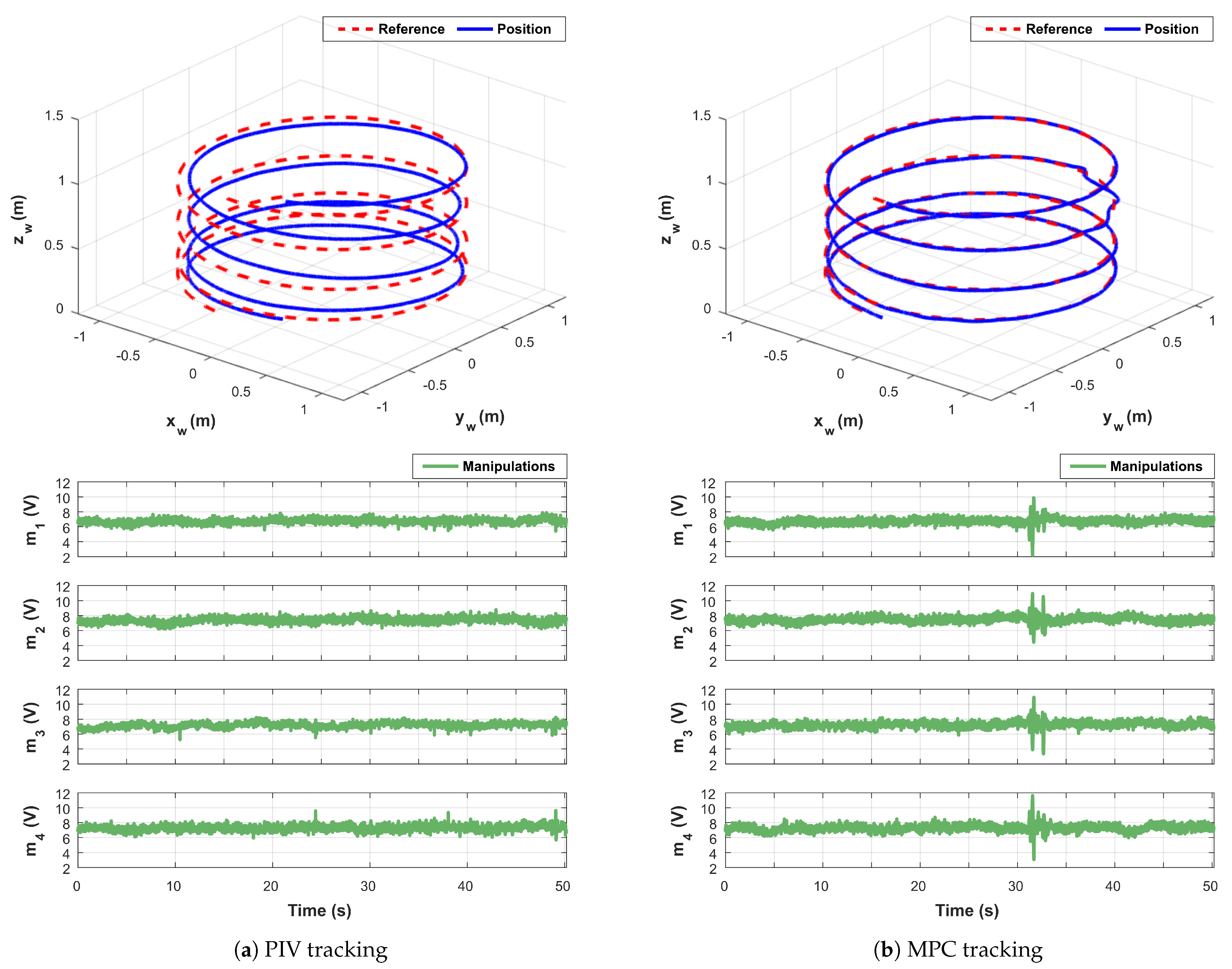
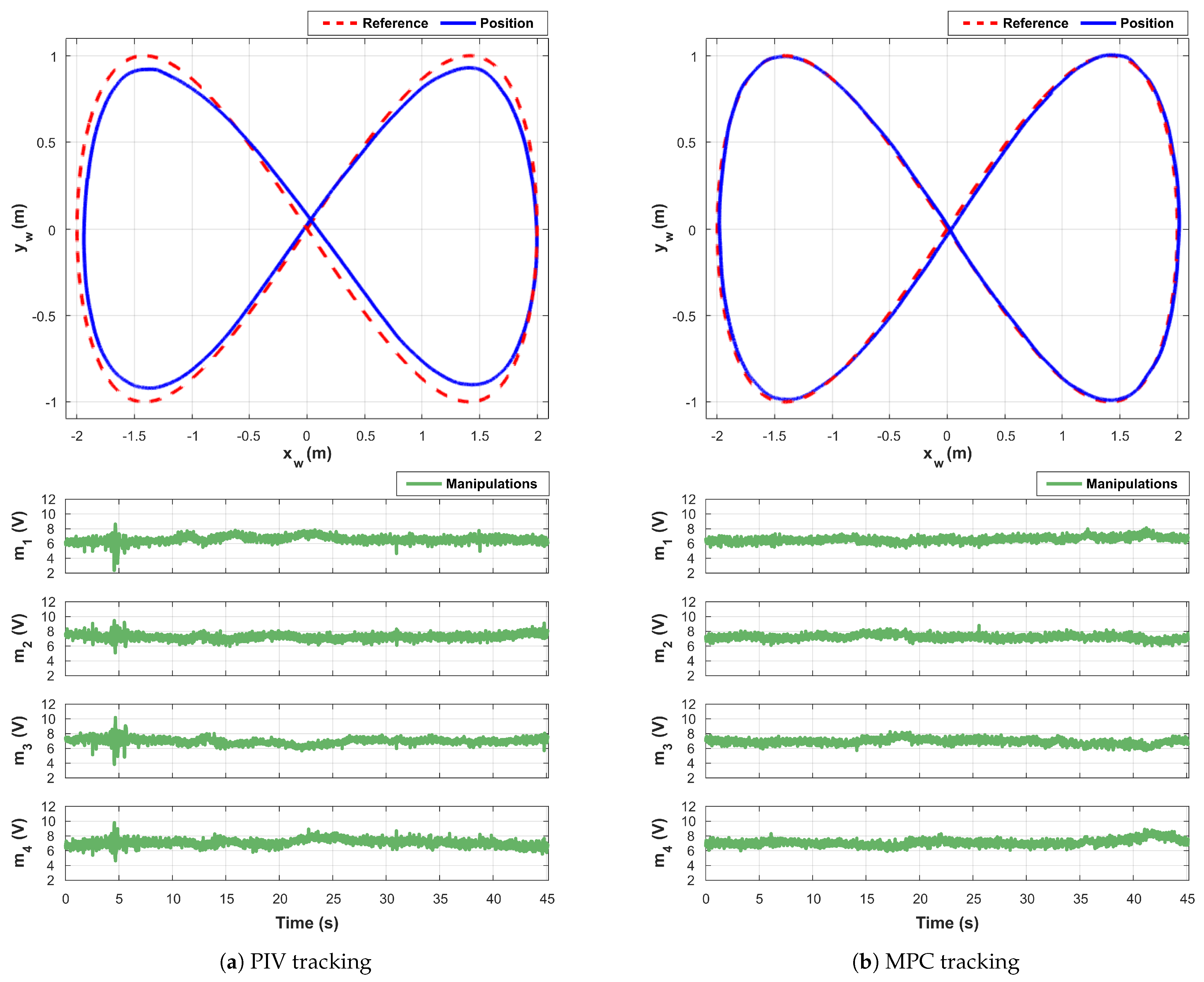
5.2. Experimental Results
- Scenario 1. Helicoidal trajectory;
- Scenario 2. Lemniscate trajectory;
- Scenario 3. Wind disturbance rejection.
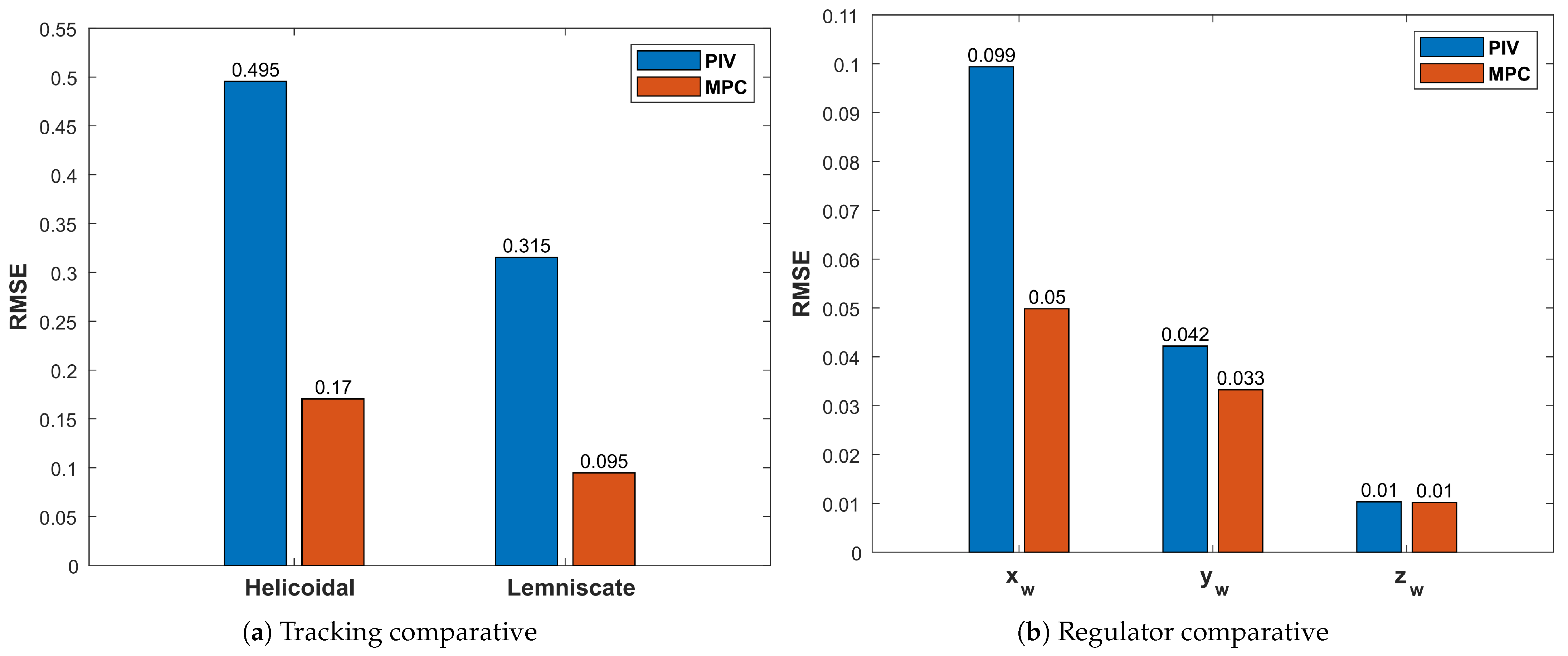
5.2.1. Scenario 1: Helicoidal Trajectory
5.2.2. Scenario 2: Lemniscate Trajectory
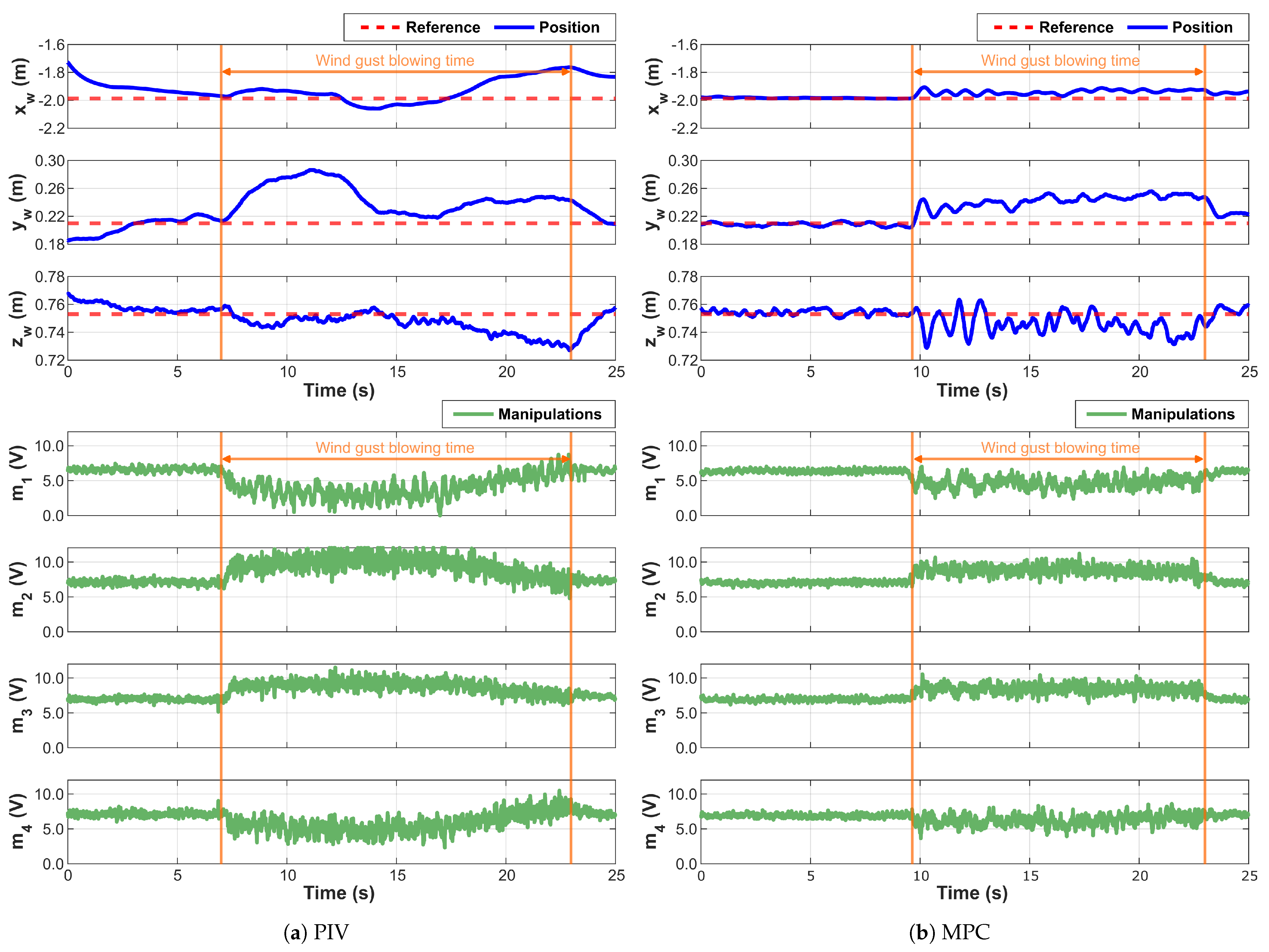
5.2.3. Scenario 3: Disturbance Rejection
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Idrissi, M.; Salami, M.; Annaz, F. A review of quadrotor unmanned aerial vehicles: Applications, architectural design and control algorithms. J. Intell. Robot. Syst. 2022, 104, 22. [Google Scholar] [CrossRef]
- Al Tahtawi, A.R.; Yusuf, M. Low-cost quadrotor hardware design with PID control system as flight controller. TELKOMNIKA (Telecommun. Comput. Electron. Control.) 2019, 17, 1923–1930. [Google Scholar] [CrossRef]
- Shakeel, T.; Arshad, J.; Jaffery, M.H.; Rehman, A.U.; Eldin, E.T.; Ghamry, N.A.; Shafiq, M. A Comparative Study of Control Methods for X3D Quadrotor Feedback Trajectory Control. Appl. Sci. 2022, 12, 9254. [Google Scholar] [CrossRef]
- Rinaldi, M.; Primatesta, S.; Guglieri, G. A comparative study for control of quadrotor uavs. Appl. Sci. 2023, 13, 3464. [Google Scholar] [CrossRef]
- Chovancová, A.; Fico, T.; Duchoň, F.; Dekan, M.; Chovanec, L.; Dekanova, M. Control methods comparison for the real quadrotor on an innovative test stand. Appl. Sci. 2020, 10, 2064. [Google Scholar] [CrossRef]
- Benaddy, A.; Bouzi, M.; Labbadi, M. Comparison of the different control strategies for Quadrotor Unmanned Aerial Vehicle. In Proceedings of the 2020 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 9–11 June 2020; pp. 1–6. [Google Scholar]
- Kang, C.; Park, B.; Choi, J. Scheduling PID attitude and position control frequencies for time-optimal quadrotor waypoint tracking under unknown external disturbances. Sensors 2021, 22, 150. [Google Scholar] [CrossRef] [PubMed]
- Nazin, A.; Alazki, H.; Poznyak, A. Robust Tracking as Constrained Optimization by Uncertain Dynamic Plant: Mirror Descent Method and ASG—Version of Integral Sliding Mode Control. Mathematics 2023, 11, 4112. [Google Scholar] [CrossRef]
- Bøhn, E.; Gros, S.; Moe, S.; Johansen, T.A. Reinforcement learning of the prediction horizon in model predictive control. IFAC-PapersOnLine 2021, 54, 314–320. [Google Scholar] [CrossRef]
- Veksler, A.; Johansen, T.A.; Borrelli, F.; Realfsen, B. Dynamic positioning with model predictive control. IEEE Trans. Control Syst. Technol. 2016, 24, 1340–1353. [Google Scholar] [CrossRef]
- Mohamed, O.; Wang, J.; Al-Duri, B.; Lu, J.; Gao, Q.; Xue, Y.; Liu, X. Predictive control of coal mills for improving supercritical power generation process dynamic responses. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 1709–1714. [Google Scholar]
- Polisano, F.; Ryals, A.D.; Pannocchia, G.; Landi, A. MPC based optimization applied to treatment of HCV infections. Comput. Methods Programs Biomed. 2021, 210, 106383. [Google Scholar] [CrossRef]
- Bardaro, G.; Bascetta, L.; Ceravolo, E.; Farina, M.; Gabellone, M.; Matteucci, M. MPC-based control architecture of an autonomous wheelchair for indoor environments. Control Eng. Pract. 2018, 78, 160–174. [Google Scholar] [CrossRef]
- Skjong, E.; Johansen, T.A.; Molinas, M. Distributed control architecture for real-time model predictive control for system-level harmonic mitigation in power systems. ISA Trans. 2019, 93, 231–243. [Google Scholar] [CrossRef] [PubMed]
- Carlet, P.G.; Toso, F.; Favato, A.; Bolognani, S. A speed and current cascade Continuous Control Set Model Predictive Control architecture for synchronous motor drives. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 5682–5688. [Google Scholar]
- Palmieri, A.; Rosini, A.; Procopio, R.; Bonfiglio, A. An MPC-sliding mode cascaded control architecture for PV grid-feeding inverters. Energies 2020, 13, 2326. [Google Scholar] [CrossRef]
- Kumar, P.; Rawlings, J.B.; Carrette, P. Modeling proportional–integral controllers in tracking and economic model predictive control. J. Process Control 2023, 122, 1–12. [Google Scholar] [CrossRef]
- Benotsmane, R.; Vásárhelyi, J. Towards optimization of energy consumption of tello quad-rotor with mpc model implementation. Energies 2022, 15, 9207. [Google Scholar] [CrossRef]
- Xue, R.; Dai, L.; Huo, D.; Xie, H.; Sun, Z.; Xia, Y. Compound tracking control based on MPC for quadrotors with disturbances. J. Frankl. Inst. 2022, 359, 7992–8013. [Google Scholar] [CrossRef]
- Eskandarpour, A.; Sharf, I. A constrained error-based MPC for path following of quadrotor with stability analysis. Nonlinear Dyn. 2020, 99, 899–918. [Google Scholar] [CrossRef]
- Westenberger, J.; De Wagter, C.; de Croon, G.C. Efficient Bang-Bang Model Predictive Control for Quadcopters. Unmanned Syst. 2022, 10, 395–405. [Google Scholar] [CrossRef]
- Schlagenhauf, J.; Hofmeier, P.; Bronnenmeyer, T.; Paelinck, R.; Diehl, M. Cascaded nonlinear mpc for realtime quadrotor position tracking. IFAC-PapersOnLine 2020, 53, 7026–7032. [Google Scholar] [CrossRef]
- Nan, F.; Sun, S.; Foehn, P.; Scaramuzza, D. Nonlinear MPC for quadrotor fault-tolerant control. IEEE Robot. Autom. Lett. 2022, 7, 5047–5054. [Google Scholar] [CrossRef]
- Hanover, D.; Foehn, P.; Sun, S.; Kaufmann, E.; Scaramuzza, D. Performance, precision, and payloads: Adaptive nonlinear mpc for quadrotors. IEEE Robot. Autom. Lett. 2021, 7, 690–697. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, D.; Hu, J.; Pan, Q. Nonlinear model predictive control-based guidance algorithm for quadrotor trajectory tracking with obstacle avoidance. J. Syst. Sci. Complex. 2021, 34, 1379–1400. [Google Scholar] [CrossRef]
- Pereira, J.C.; Leite, V.J.; Raffo, G.V. Nonlinear model predictive control on SE (3) for quadrotor aggressive maneuvers. J. Intell. Robot. Syst. 2021, 101, 1–15. [Google Scholar] [CrossRef]
- Kamel, M.A.; Hafez, A.T.; Yu, X. A review on motion control of unmanned ground and aerial vehicles based on model predictive control techniques. J. Eng. Sci. Mil. Technol. 2018, 2, 10–23. [Google Scholar]
- Wang, S.; Polyakov, A.; Zheng, G. Generalized homogenization of linear controllers: Theory and experiment. Int. J. Robust Nonlinear Control 2021, 31, 3455–3479. [Google Scholar] [CrossRef]
- Lambert, P.; Reyhanoglu, M. Observer-based sliding mode control of a 2-DOF helicopter system. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 2596–2600. [Google Scholar]
- Mendez, A.P.; Whidborne, J.F.; Chen, L. Wind Preview-Based Model Predictive Control of Multi-Rotor UAVs Using LiDAR. Sensors 2023, 23, 3711. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Hu, S.; Damaren, C.; Luo, L.; Liu, B. Trajectory Planning with Collision Avoidance for Multiple Quadrotor UAVs Using DMPC. Int. J. Aeronaut. Space Sci. 2023, 24, 1403–1417. [Google Scholar] [CrossRef]
- Landolfi, E.; Natale, C. An adaptive cascade predictive control strategy for connected and automated vehicles. Int. J. Adapt. Control Signal Process. 2023, 37, 2725–2751. [Google Scholar] [CrossRef]
- Sajjadi, S.; Mehrandezh, M.; Janabi-Sharifi, F. A Cascaded and Adaptive Visual Predictive Control Approach for Real-Time Dynamic Visual Servoing. Drones 2022, 6, 127. [Google Scholar] [CrossRef]
- Xu, Z.; Fan, L.; Qiu, W.; Wen, G.; He, Y. A Robust Disturbance-Rejection Controller Using Model Predictive Control for Quadrotor UAV in Tracking Aggressive Trajectory. Drones 2023, 7, 557. [Google Scholar] [CrossRef]
- Quanser. Qdrone—Quanser. 2020. Available online: https://www.quanser.com/products/qdrone (accessed on 6 May 2020).
- Alaiwi, Y.; Mutlu, A. Modelling, simulation and implementation of autonomous unmanned quadrotor. Mach. Technol. Mater. 2018, 12, 320–325. [Google Scholar]
- Kapnopoulos, A.; Alexandridis, A. A cooperative particle swarm optimization approach for tuning an MPC-based quadrotor trajectory tracking scheme. Aerosp. Sci. Technol. 2022, 127, 107725. [Google Scholar] [CrossRef]
- Islam, M.; Okasha, M.; Idres, M. Dynamics and control of quadcopter using linear model predictive control approach. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 270, p. 012007. [Google Scholar]
- Yan, D.; Zhang, W.; Chen, H. Design of a multi-constraint formation controller based on improved MPC and consensus for quadrotors. Aerospace 2022, 9, 94. [Google Scholar] [CrossRef]
- Roy, R.; Islam, M.; Sadman, N.; Mahmud, M.A.P.; Gupta, K.D.; Ahsan, M.M. A Review on Comparative Remarks, Performance Evaluation and Improvement Strategies of Quadrotor Controllers. Technologies 2021, 9, 37. [Google Scholar] [CrossRef]
- Saeed, A.S.; Younes, A.B.; Islam, S.; Dias, J.; Seneviratne, L.; Cai, G. A review on the platform design, dynamic modeling and control of hybrid UAVs. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 806–815. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Wang, K.; Lu, Y. A survey of modelling and identification of quadrotor robot. Abstr. Appl. Anal. 2014, 2014, 320526. [Google Scholar] [CrossRef]
- Alamir, M. A Pragmatic Story of Model Predictive Control: Self Contained Algorithms and Case-Studies; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2013. [Google Scholar]
- Chen, K.; Zhu, Z.; Zeng, X.; Wang, J. Distributed Observers for State Omniscience with Stochastic Communication Noises. Mathematics 2023, 11, 1997. [Google Scholar] [CrossRef]
- Liu, Z.; Yuan, C.; Zhang, Y. Active fault-tolerant control of unmanned quadrotor helicopter using linear parameter varying technique. J. Intell. Robot. Syst. 2017, 88, 415–436. [Google Scholar] [CrossRef]
- Mehmet, E. Neural network assisted computationally simple pid control of a quadrotor UAV. IEEE Trans. Ind. Inform. 2011, 7, 354–361. [Google Scholar]
- Efe, M.Ö. Battery power loss compensated fractional order sliding mode control of a quadrotor UAV. Asian J. Control 2012, 14, 413–425. [Google Scholar] [CrossRef]
- Pi, C.H.; Hu, K.C.; Cheng, S.; Wu, I.C. Low-level autonomous control and tracking of quadrotor using reinforcement learning. Control Eng. Pract. 2020, 95, 104222. [Google Scholar] [CrossRef]
- Alkomy, H.; Shan, J. Vibration reduction of a quadrotor with a cable-suspended payload using polynomial trajectories. Nonlinear Dyn. 2021, 104, 3713–3735. [Google Scholar] [CrossRef]
- Labbadi, M.; Chatri, C.; Boubaker, S.; Kamel, S. Fixed-Time Controller for Altitude/Yaw Control of Mini-Drones: Real-Time Implementation with Uncertainties. Mathematics 2023, 11, 2703. [Google Scholar] [CrossRef]
- Aliyari, M.; Wong, W.K.; Bouteraa, Y.; Najafinia, S.; Fekih, A.; Mobayen, S. Design and implementation of a constrained model predictive control approach for unmanned aerial vehicles. IEEE Access 2022, 10, 91750–91762. [Google Scholar] [CrossRef]
- Utkin, A.V.; Utkin, V.A.; Krasnova, S.A. Synthesis of a Control System for a Waste Heat Boiler with Forced Circulation under Restrictions on Control Actions. Mathematics 2022, 10, 2397. [Google Scholar] [CrossRef]


| MPC Methodology | |
|---|---|
| Input: | Actual states of the quadrotor and desired values |
| Output: | Optimal manipulation |
| 1 | Define the LTI mathematical model of the physical system in state space representation |
| 2 | Define the sampling time and discretize the state space representation |
| 3 | Set the sampling instants N for the prediction horizon |
| 4 | Compute the matrices , and used to represent the N-step-ahead prediction map for LTI systems |
| 5 | Define weight matrices and |
| 6 | Determine the saturations |
| 7 | Compute the online matrices and |
| 8 | Obtain the control law and apply to the system the first control input of the best control input sequence |
| QDrone 2 Parameters | ||
|---|---|---|
| Dimensions | 50 × 50 × 15 cm | - |
| Mass | 1500 g | - |
| Max. Payload | 300 g | - |
| 2100 | - | |
| Max. Continuous Current | 25 A | - |
| Effective motor speed constant | ||
| RPM | Voltage-to-angular velocity offset | |
| RPM | Angular velocity-to-force offset | |
| Motor force constant | ||
| N | Motor force offset | |
| Motor thrust–torque constant | ||
| PIV Parameters | Position PIV | Angular PIV | Angular Vel. PIV |
|---|---|---|---|
| - | - | ||
| MPC Parameters | Altitude MPC | Position MPC | Attitude MPC |
|---|---|---|---|
| matrix | 10 | ||
| matrix | |||
| Prediction horizon N | 10 | 10 | 15 |
| Sample time k |
| Quadrotor | Start | End |
|---|---|---|
| Under PIV | 7.005 s | 22.965 s |
| Under MPC | 9.645 s | 23 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borbolla-Burillo, P.; Sotelo, D.; Frye, M.; Garza-Castañón, L.E.; Juárez-Moreno, L.; Sotelo, C. Design and Real-Time Implementation of a Cascaded Model Predictive Control Architecture for Unmanned Aerial Vehicles. Mathematics 2024, 12, 739. https://doi.org/10.3390/math12050739
Borbolla-Burillo P, Sotelo D, Frye M, Garza-Castañón LE, Juárez-Moreno L, Sotelo C. Design and Real-Time Implementation of a Cascaded Model Predictive Control Architecture for Unmanned Aerial Vehicles. Mathematics. 2024; 12(5):739. https://doi.org/10.3390/math12050739
Chicago/Turabian StyleBorbolla-Burillo, Patricio, David Sotelo, Michael Frye, Luis E. Garza-Castañón, Luis Juárez-Moreno, and Carlos Sotelo. 2024. "Design and Real-Time Implementation of a Cascaded Model Predictive Control Architecture for Unmanned Aerial Vehicles" Mathematics 12, no. 5: 739. https://doi.org/10.3390/math12050739
APA StyleBorbolla-Burillo, P., Sotelo, D., Frye, M., Garza-Castañón, L. E., Juárez-Moreno, L., & Sotelo, C. (2024). Design and Real-Time Implementation of a Cascaded Model Predictive Control Architecture for Unmanned Aerial Vehicles. Mathematics, 12(5), 739. https://doi.org/10.3390/math12050739










