The Application of the Modified Lindstedt–Poincaré Method to Solve the Nonlinear Vibration Problem of Exponentially Graded Laminated Plates on Elastic Foundations
Abstract
:1. Introduction
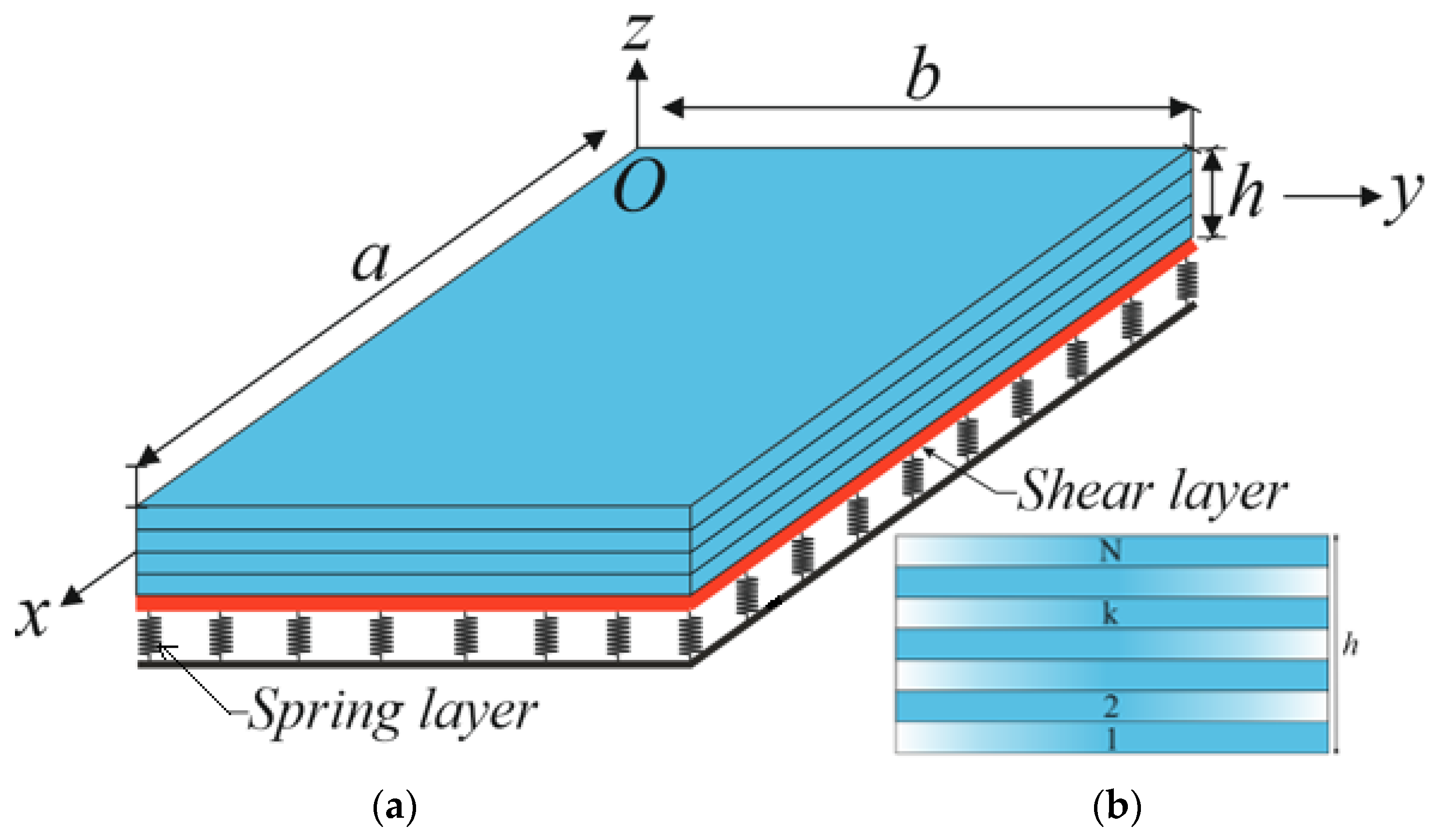
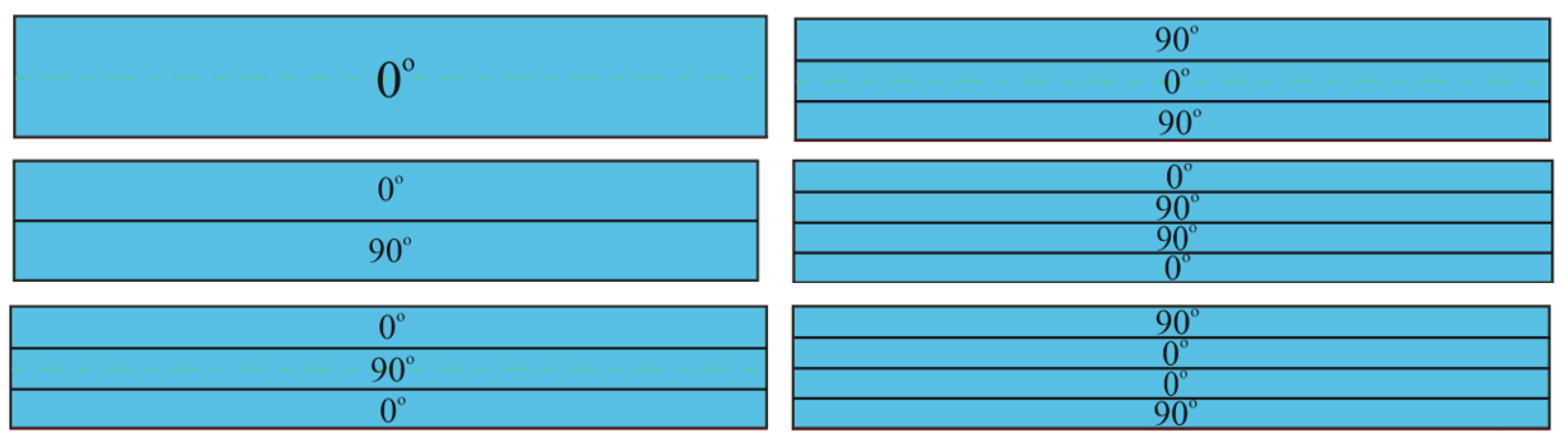
2. Modeling of Laminated Plates Composed of EGOLs
3. Governing Equations
4. Solution Method
5. Results and Discussion
5.1. Comparative Examples
5.2. Nonlinear Analysis in Elastic Media
- (a)
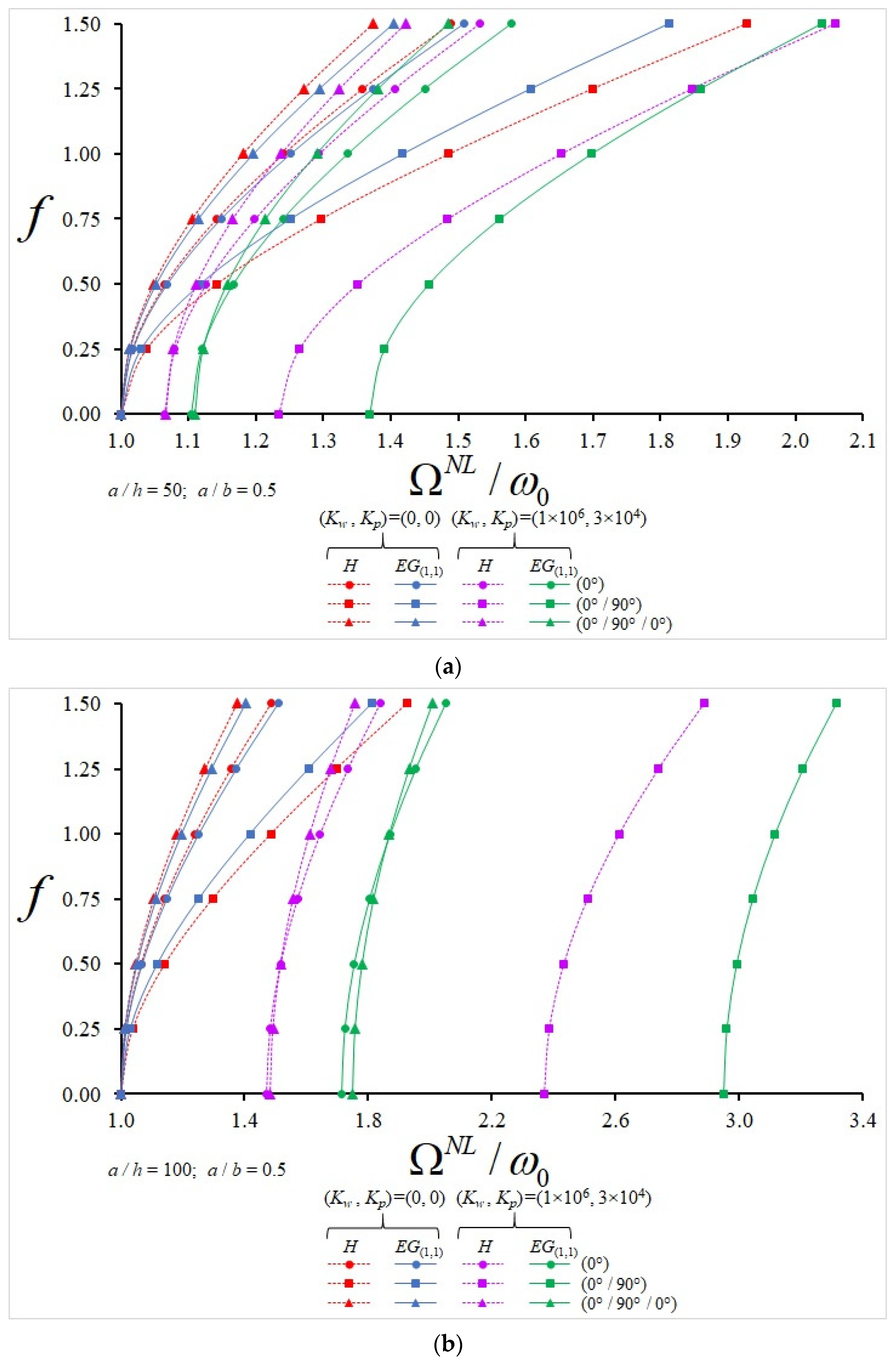
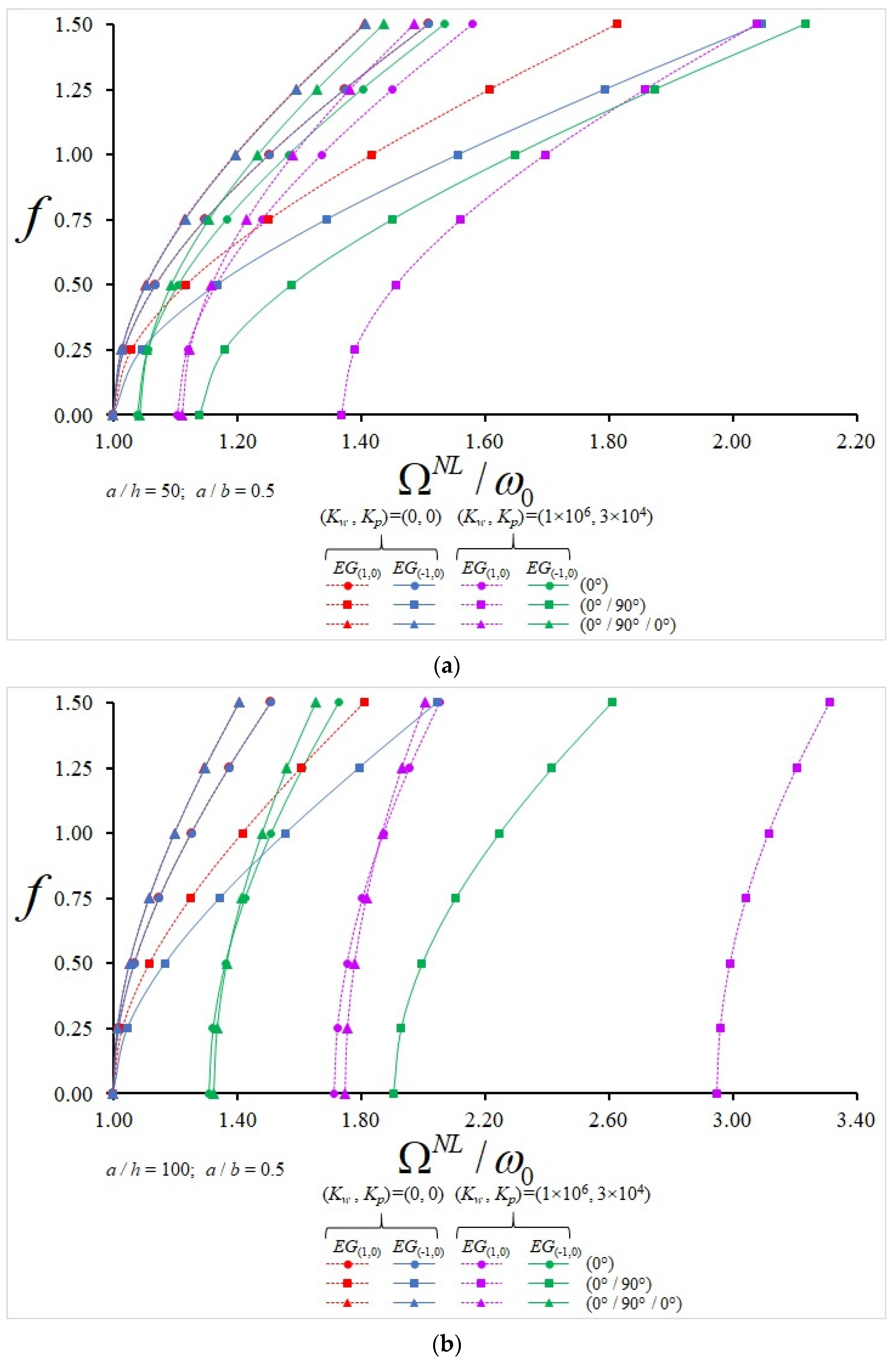
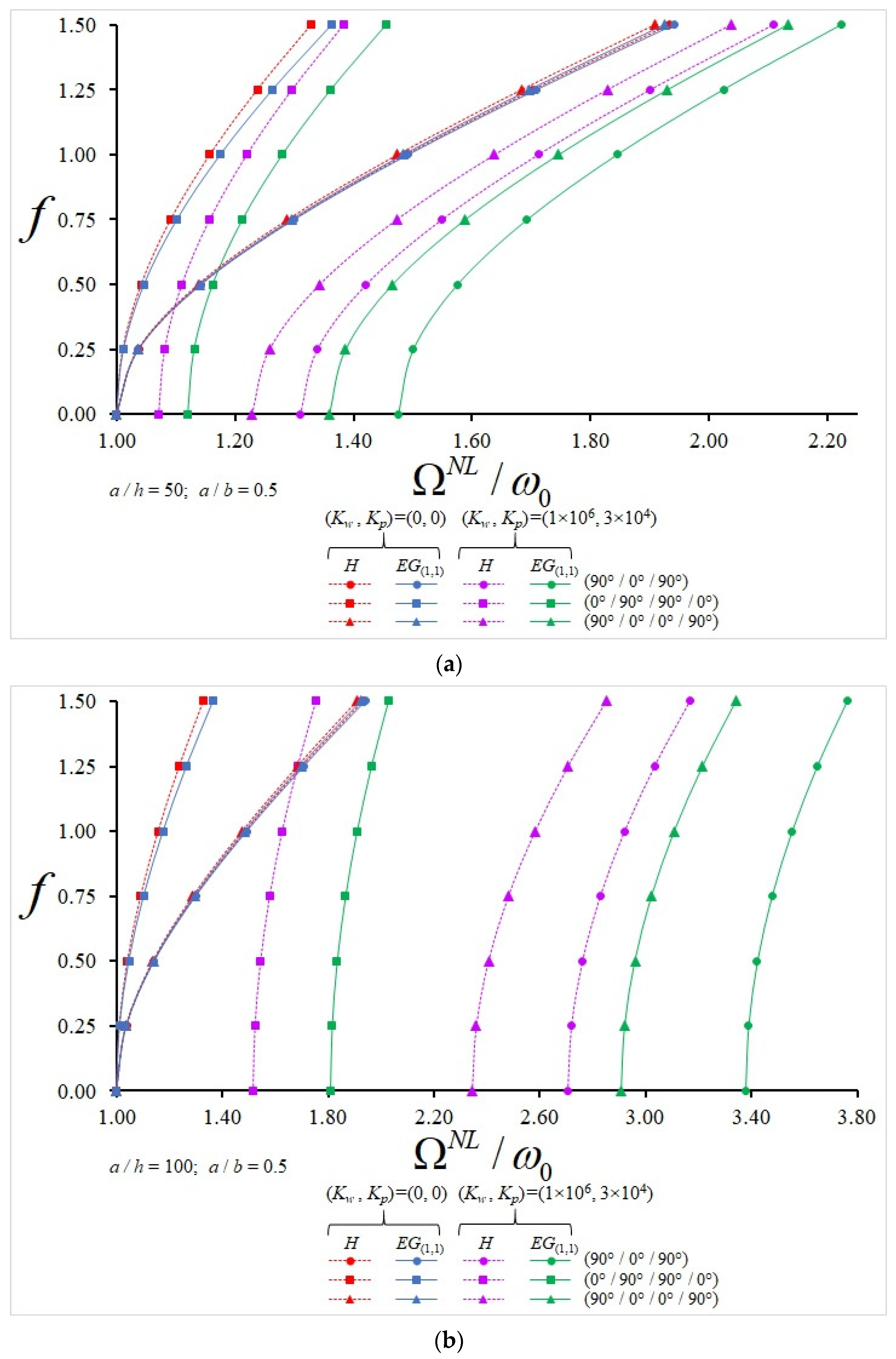
- At a/h = 50 and f = 0.25, the influences of EG(1.0) and EG(−1.0) profiles on the NLF/LF ratio for plates with (0°/90°) alignment are 9.92% and (−6.75%); in the plates arranged in (0°/90°/0°), those effects are 4.17% and (−2.07%); in the plates arranged in (0°/90°/90°/0°), those influences are 4.64% and (−2.18%); in the plates arranged in (90°/0°/90°), those influences are 12.17% and (−8.1%); and in the plates arranged in (90°/0°/0°/90°), those effects are 10.15% and (−6.4%), respectively.
- (b)
- At a/h = 50 and f = 1.5, the influences of EG(1.0) and EG(−1.0) profiles on the NLF/LF ratio for plates with (0°/90°) alignment are (−0.96%) and 2.86%; in the plates arranged in (0°/90°/0°), those influences are 4.37% and 0.97%; in the plates arranged in (0°/90°/90°/0°), those influences are 5.17% and 1.11%; in the plates arranged in (90°/0°/90°), those effects are 5.4% and (−2.6%); and in the plates arranged in (90°/0°/0°/90°), those effects are 4.71% and (−1.65%), respectively.
- (c)
- At a/h = 100 and f = 0.25, the influences of EG(1.0) and EG(−1.0) profiles on the NLF/LF ratio for plates with (0°/90°) alignment are 24.1% and (−19.2%); in the plates arranged in (0°/90°/0°), those influences are 17.68% and (−10.5%); in the plates arranged in (0°/90°/90°/0°), those effects are 18.9% and (−10.6%); in the plates arranged in (90°/0°/90°), those influences are 24.65% and (−18.51%); and in the plates arranged in (90°/0°/0°/90°), those effects are 23.8% and (−17.2%), respectively.
- (d)
- At a/h = 100 and f = 1.5, the influences of EG(1.0) and EG(−1.0) profiles on the NLF/LF ratio for plates with (0°/90°) alignment are 14.85% and (−9.58%); in the plates arranged in (0°/90°/0°), those effects are 14.2% and (−5.93%); in the plates arranged in (0°/90°/90°/0°), those effects are 15.9% and (−6.3%); in the plates arranged in (90°/0°/90°), those effects are 18.75% and (−12.94%); and in the plates arranged in (90°/0°/0°/90°), those influences are 17.15% and (−11%), respectively (see Figure 3, Figure 4, Figure 5 and Figure 6).
6. Conclusions
- (a)
- The NL frequency values increase when f and a/b ratios increase in cases with and without ground, in all alignments and layers and in exponentially graded orthotropic material profiles;
- (b)
- In the homogeneous orthotropic and exponentially graded orthotropic material cases, increasing f supports the increase in the NL frequency but also reveals that the ground effect makes the NL frequency values significant enough to be considered;
- (c)
- Since each of the EG(1,1), EG(1,0) and EG(−1,0) profiles has their own unique effects on the NL frequency, separate evaluation and interpretation must be made for each profile.
- (d)
- NL frequency values of laminated plates consisting of EG(−1.0) profile layers are higher than the values of the homogeneous case and are lower in other exponentially graded orthotropic material profiles;
- (e)
- The effect of exponential graduation profiles on the NL frequency changes when the layer layout or number of layers changes;
- (f)
- Taking the ground into account reduces the influence of the layer arrangement on the NL frequency;
- (g)
- As the model effect on NL frequency values of laminated plate consisting of layers with exponentially graded orthotropic material profiles is compared among themselves, the most significant effect occurs in the plate with the EG(−1.0) profile;
- (h)
- The ground weakens the influence of EG profiles and layer arrangement on the NL frequency;
- (i)
- Although the NLF/LF ratio increases when the f increases in plates starting from (0°/…) or (90°/…) array layers, in cases with and without ground, that ratio increases more clearly in some aligned plates in the case with a ground;
- (j)
- In the case without a ground, the influences of exponentially graded orthotropic material profiles on the NLF/LF ratio are weak at small values of f, while those effects increase for all alignments with the subsequent increase in f and show a more significant increase in plates with alignments starting with (0°/…), which are independent of the a/h ratio;
- (k)
- In the presence of ground effect, when the a/h ratio increases for the selected f, the effect of exponentially graded orthotropic material profiles on the NLF/LF ratio increases significantly depending on the layer arrangement and number and shows a more significant increase in plates with alignments starting with (90°/…);
- (l)
- In the case of without the ground, when f increases for the selected a/h, the influence of exponentially graded orthotropic material profiles on the NLF/LF ratio increases, whereas in the presence of the ground, those effects decrease, although they are much more pronounced;
- (m)
- When the NLF/LF ratio of exponentially graded orthotropic material-profiled plates with different alignments consisting of two, three and four layers on the ground is compared with the single-layer plate (0°), the alignment effects become evident with the increase in f;
- (n)
- In all layered plates, the influence of the soil on the NLF/LF ratio decreases significantly as f increases, while the increase in the a/h increases that effect significantly.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ambartsumian, S.A. Theory of Anisotropic Plates; Strength, Stability, Vibration; Technomic Publishing Company: Stamford, CT, USA, 1964. [Google Scholar]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, 2nd ed.; CRC Press: New York, NY, USA, 2004. [Google Scholar]
- Pan, E. Exact solution for functionally graded anisotropic elastic composite laminates. J. Compos. Mater. 2003, 37, 1903–1920. [Google Scholar] [CrossRef]
- Ootao, Y.; Tanigawa, Y. Three-dimensional solution for transient thermal stresses of an orthotropic functionally graded rectangular plate. Compos. Struct. 2007, 80, 10–20. [Google Scholar] [CrossRef]
- Zenkour, A. Bending responses of an exponentially graded simply-supported elastic/viscoelastic/elastic sandwich plate. Acta Mech. Solida Sin. 2011, 24, 250–261. [Google Scholar] [CrossRef]
- Fazzolari, F.A.; Carrera, E. Advanced variable kinematics Ritz and Galerkin formulations for accurate buckling and vibration analysis of anisotropic laminated composite plates. Compos. Struct. 2011, 94, 50–67. [Google Scholar] [CrossRef]
- Fazzolari, F.A.; Carrera, E. Thermo-mechanical buckling analysis of anisotropic multilayered composite and sandwich plates by using refined variable-kinematics theories. J. Therm. Stresses 2013, 36, 321–350. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Tarantino, A.M. Natural frequency analysis of functionally graded orthotropic cross-ply plates based on the finite element method. Math. Computat. Appl. 2019, 24, 52. [Google Scholar] [CrossRef]
- Zhang, J.H.; Ullah, S.; Zhong, Y. Accurate free vibration solutions of orthotropic rectangular thin plates by straightforward finite integral transform method. Arch. Appl. Mech. 2020, 90, 353–368. [Google Scholar] [CrossRef]
- Krysko, A.V.; Awrejcewicz, J.; Bodyagina, K.S.; Krysko, V.A. Mathematical modeling of planar physically nonlinear inhomogeneous plates with rectangular cuts in the three-dimensional formulation. Acta Mech. 2021, 232, 4933–4950. [Google Scholar] [CrossRef]
- Hachemi, M. Layer-wise solutions for variable stiffness composite laminated sandwich plate using curvilinear fibers. Mech. Adv. Mater. Struct. 2022, 29, 5460–5477. [Google Scholar] [CrossRef]
- Dat, N.D.; Quan, T.Q.; Duc, N.D. Vibration analysis of auxetic laminated plate with magneto-electro-elastic face sheets subjected to blast loading. Compos. Struct. 2022, 280, 114925. [Google Scholar]
- Singh, A.; Naskar, S.; Kumarı, P.; Mukhopadhyay, T. Viscoelastic free vibration analysis of in-plane functionally graded orthotropic plates integrated with piezoelectric sensors: Time-dependent 3D analytical solutions. Mech. Syst. Signal Process. 2023, 184, 109636. [Google Scholar] [CrossRef]
- Simões, T.M.; Ribeiro, P.; Conceição, A.C. Maximisation of bending and membrane frequencies of vibration of variable stiffness composite laminated plates by a genetic algorithm. J. Vib. Eng. Tech. 2023, in press. [Google Scholar] [CrossRef]
- Ribeiro, P.; Akhavan, H. Non-linear vibrations of variable stiffness composite laminated plates. Compos. Struct. 2012, 94, 2424–2432. [Google Scholar] [CrossRef]
- Gupta, A.; Pradyumna, S. Geometrically nonlinear dynamic analysis of variable stiffness composite laminated and sandwich shell panels. Thin Wall. Struct. 2022, 173, 109021. [Google Scholar] [CrossRef]
- Ribeiro, P.; Antunes, A.M.; Akhavan, H.; Rodrigues, J.D. Non-linear forced vibrations of variable stiffness plates on elastic supports. Mech. Adv. Mater. Struct. 2023, 30, 4246–4263. [Google Scholar] [CrossRef]
- Alimoradzadeh, M.; Tornabene, F.; Dimitri, R. Nonlinear axial-lateral coupled vibration of functionally graded-fiber reinforced composite laminated (FG-FRCL) beams subjected to aero-thermal loads. Int. J. Non-Lin. Mech. 2024, 159, 104612. [Google Scholar] [CrossRef]
- Pasternak, P.L. On a New Method of Analysis of an Elastic Foundation by Means of Two Foundation Constants; State Publishing House of Literature on Construction and Architecture: Moscow, Russia, 1954; Volume 1, pp. 1–56. (In Russian) [Google Scholar]
- Tornabene, F. Free vibrations of anisotropic doubly-curved shells and panels of revolution with a free-form meridian resting on Winkler-Pasternak elastic foundations. Compos. Struct. 2011, 94, 186–206. [Google Scholar] [CrossRef]
- Haciyev, V.C.; Sofiyev, A.H.; Kuruoglu, N. Free bending vibration analysis of thin bidirectionally exponentially graded orthotropic rectangular plates resting on two-parameter elastic foundations. Compos. Struct. 2018, 184, 372–377. [Google Scholar] [CrossRef]
- Zenkour, A.M. Trigonometric solution for an exponentially graded thick plate resting on elastic foundations. Arch. Mech. Eng. 2018, 65, 193–208. [Google Scholar]
- Zenkour, A.M.; Alghanmi, R.A. Bending of exponentially graded plates integrated with piezoelectric fiber-reinforced composite actuators resting on elastic foundations. Euro. J. Mech. A-Solids 2019, 75, 461–471. [Google Scholar] [CrossRef]
- Sobhy, M.; Zenkour, A.M. A comprehensive study on the size-dependent hygrothermal analysis of exponentially graded microplates on elastic foundations. Mech. Adv. Mater. Struct. 2020, 27, 816–830. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Zenkour, A.M. A Quasi-3D refined theory for the vibration of functionally graded plates resting on visco-Winkler-Pasternak foundations. Mathematics 2022, 10, 716. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Turan, F.; Kadioglu, F.; Aksogan, O.; Hui, D. Influences of two-parameter elastic foundations on nonlinear free vibration of anisotropic shallow shell structures with variable parameters. Meccanica 2022, 57, 401–414. [Google Scholar] [CrossRef]
- Song, Y.Y.; Li, Q.H.; Xue, K. An analytical method for vibration analysis of arbitrarily shaped non-homogeneous orthotropic plates of variable thickness resting on Winkler-Pasternak foundation. Compos. Struct. 2022, 296, 115885. [Google Scholar] [CrossRef]
- Jena, S.K.; Chakraverty, S.; Manesh, V.; Harursampath, D. Free vibration of functionally graded beam embedded in Winkler-Pasternak elastic foundation with geometrical uncertainties using symmetric Gaussian fuzzy number. Euro. Phys. J. Plus 2022, 137, 399. [Google Scholar] [CrossRef]
- Jena, S.K.; Chakraverty, S.; Manesh, V.; Harursampath, D.; Sedighi, H.M. A novel numerical approach for the stability of nanobeam exposed to hygro-thermo-magnetic environment embedded in elastic foundation. ZAMM-J. Appl. Math. Mech. Z. Für Angew. Math. Und Mech. 2022, 102, e202100380. [Google Scholar] [CrossRef]
- Melaibari, A.; Mohamed, S.A.; Assie, A.E.; Shanab, R.A.; Eltaher, M.A. Static response of 2D FG porous plates resting on elastic foundation using midplane and neutral surfaces with movable constraints. Mathematics 2022, 10, 4784. [Google Scholar] [CrossRef]
- Melaibari, A.; Mohamed, S.A.; Assie, A.E.; Shanab, R.A.; Eltaher, M.A. Free vibration characteristics of bidirectional graded porous plates with elastic foundations using 2D-DQM. Mathematics 2023, 11, 46. [Google Scholar] [CrossRef]
- Zaoui, F.Z.; Ouinas, D.; Achour, B.; Touahmia, M.; Boukendakdji, M.; Latifee, E.R.; Enamur, R.R.; Al-Naghi, A.A.A.; Ahmed, A.A.; Olay, J.A.V. Mathematical approach for mechanical behaviour analysis of FGM plates on elastic foundation. Mathematics 2022, 10, 4764. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, S.J.; Saran, V.H.; Harsha, S.P. Vibration response of the exponential functionally graded material plate with variable thickness resting on the orthotropic Pasternak foundation. Mech. Based Des. Struct. Mach. 2023, in press. [Google Scholar] [CrossRef]
- Tornabene, F.; Viscoti, M.; Dimitri, R. General boundary conditions implementation for the static analysis of anisotropic doubly-curved shells resting on a Winkler foundation. Compos. Struct. 2023, 322, 117198. [Google Scholar] [CrossRef]
- Volmir, A.S. The Nonlinear Dynamics of Plates and Shells; Science Edition: Moscow, Russia, 1972. [Google Scholar]
- He, J.H. Modified Lindstedt-Poincare methods for some strongly non-linear oscillations Part I: Expansion of a constant. Int. J. Non-Lin. Mech. 2002, 37, 309–314. [Google Scholar] [CrossRef]
- Hashemi, S.; Jafari, A.A. An analytical solution for nonlinear vibrations analysis of functionally graded plate using modified Lindstedt–Poincare method. Int. J. Appl. Mech. 2020, 1201, 2050003. [Google Scholar] [CrossRef]
- Althubiti, S. Nonlinear third-order differential equations with distributed delay: Some new oscillatory solutions. J. King Saud Univ.-Sci. 2023, 35, 102730. [Google Scholar] [CrossRef]
- Singha, M.K.; Daripa, R. Nonlinear vibration and dynamic stability analysis of composite plates. J. Sound Vib. 2009, 328, 541–554. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, D.; Shi, X. A modified solution for the free vibration analysis of moderately thick orthotropic rectangular plates with general boundary conditions, internal line supports and resting on elastic foundation. Meccanica 2016, 51, 1985–2017. [Google Scholar] [CrossRef]
- Zhong, R.; Wang, Q.; Tang, J.; Shuai, C.; Liang, Q. Vibration characteristics of functionally graded carbon nanotube reinforced composite rectangular plates on Pasternak foundation with arbitrary boundary conditions and internal line supports. Curved Layer. Struct. 2018, 5, 10–34. [Google Scholar] [CrossRef]

| Isotropic Single-Layer Plate (0°) | Laminated Orthotropic Plate with (0°/90°/0°/90°/0°) | |||
|---|---|---|---|---|
| f | Present Study | Singha and Daripa [39] | Present Study | Singha and Daripa [39] |
| 0.4 | 1.02024 | 1.02049 | 1.04105 | 1.04169 |
| 0.8 | 1.07835 | 1.07959 | 1.15441 | 1.15823 |
| 1.2 | 1.16808 | 1.17249 | 1.32014 | 1.33111 |
| Methods | Wave Number | ||
|---|---|---|---|
| Wang et al. [40] | 3.3400 | 5.9287 | 5.9287 |
| Zhong et al. [41] | 3.3417 | 5.9289 | 5.9289 |
| Present study | 3.3406 | 5.9329 | 5.9329 |
| a/b = 0.5 | a/b = 1.0 | a/b = 1.5 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| f | (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) |
| 0.25 | 0.526 | 0.270 | 0.515 | 0.566 | 0.393 | 0.566 | 0.658 | 0.665 | 0.694 |
| 0.5 | 0.551 | 0.297 | 0.534 | 0.591 | 0.428 | 0.591 | 0.684 | 0.727 | 0.742 |
| 1 | 0.642 | 0.386 | 0.602 | 0.681 | 0.546 | 0.681 | 0.780 | 0.936 | 0.911 |
| 1.5 | 0.770 | 0.501 | 0.700 | 0.809 | 0.700 | 0.810 | 0.919 | 1.207 | 1.138 |
| f | (90°/0°/ 90°) | (0°/90°/ 90°/0°) | (90°/0°/ 0°/90°) | (90°/0° /90°) | (0°/90°/ 90°/0°) | (90°/0°/ 0°/90°) | (90°/0°/ 90°) | (0°/90°/ 90°/0°) | (90°/0° /0°/90°) |
| 0.25 | 0.230 | 0.494 | 0.273 | 0.566 | 0.566 | 0.566 | 1.185 | 0.757 | 1.145 |
| 0.5 | 0.254 | 0.510 | 0.299 | 0.591 | 0.591 | 0.591 | 1.228 | 0.813 | 1.182 |
| 1 | 0.331 | 0.566 | 0.388 | 0.681 | 0.681 | 0.681 | 1.388 | 1.005 | 1.322 |
| 1.5 | 0.430 | 0.650 | 0.502 | 0.810 | 0.810 | 0.810 | 1.619 | 1.261 | 1.526 |
| for | |||||||||
| f | (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) |
| 0.25 | 0.655 | 0.474 | 0.646 | 0.721 | 0.595 | 0.721 | 0.844 | 0.849 | 0.872 |
| 0.5 | 0.675 | 0.489 | 0.661 | 0.741 | 0.618 | 0.741 | 0.864 | 0.899 | 0.911 |
| 1 | 0.751 | 0.549 | 0.717 | 0.814 | 0.705 | 0.815 | 0.942 | 1.075 | 1.053 |
| 1.5 | 0.863 | 0.635 | 0.801 | 0.924 | 0.830 | 0.925 | 1.060 | 1.317 | 1.255 |
| f | (90°/0°/ 90°) | (0°/90°/ 90°/0°) | (90°/0°/ 0°/90°) | (90°/0° /90°) | (0°/90°/ 90°/0°) | (90°/0°/ 0°/90°) | (90°/0°/ 90°) | (0°/90°/ 90°/0°) | (90°/0° /0°/90°) |
| 0.25 | 0.452 | 0.629 | 0.475 | 0.721 | 0.721 | 0.721 | 1.297 | 0.923 | 1.261 |
| 0.5 | 0.465 | 0.641 | 0.491 | 0.741 | 0.741 | 0.741 | 1.337 | 0.969 | 1.295 |
| 1 | 0.511 | 0.687 | 0.550 | 0.815 | 0.815 | 0.815 | 1.485 | 1.135 | 1.423 |
| 1.5 | 0.580 | 0.758 | 0.636 | 0.925 | 0.925 | 0.925 | 1.703 | 1.367 | 1.615 |
| a/b = 0.5 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) | |||||||||||||
| f | EG (1,1) | EG (1,0) | EG (−1,0) | EG (1,1) | EG (1,0) | EG (−1,0) | EG (1,1) | EG (1,0) | EG (−1,0) | EG (1,1) | EG (1,0) | EG (−1,0) | EG (1,1) | EG (1,0) | EG (−1,0) | EG (1,1) | EG (1,0) | EG (−1,0) |
| 0.25 | 0.514 | 0.408 | 0.673 | 0.260 | 0.207 | 0.361 | 0.496 | 0.394 | 0.651 | 0.710 | 0.564 | 0.778 | 0.554 | 0.441 | 0.531 | 0.697 | 0.554 | 0.759 |
| 0.5 | 0.539 | 0.429 | 0.707 | 0.283 | 0.225 | 0.402 | 0.515 | 0.410 | 0.676 | 0.729 | 0.579 | 0.808 | 0.565 | 0.449 | 0.560 | 0.711 | 0.565 | 0.780 |
| 1.0 | 0.632 | 0.502 | 0.829 | 0.359 | 0.285 | 0.537 | 0.586 | 0.466 | 0.769 | 0.800 | 0.636 | 0.916 | 0.607 | 0.483 | 0.663 | 0.764 | 0.607 | 0.863 |
| 1.5 | 0.762 | 0.606 | 0.999 | 0.459 | 0.365 | 0.706 | 0.688 | 0.547 | 0.903 | 0.906 | 0.720 | 1.072 | 0.671 | 0.533 | 0.806 | 0.845 | 0.672 | 0.984 |
| f | (90°/0°/90°) | (0°/90°/90°/0°) | (90°/0°/0°/90°) | (90°/0°/90°) | (0°/90°/90°/0°) | (90°/0°/0°/90°) | ||||||||||||
| 0.25 | 0.226 | 0.179 | 0.296 | 0.472 | 0.375 | 0.619 | 0.266 | 0.212 | 0.349 | 0.539 | 0.428 | 0.489 | 0.680 | 0.541 | 0.732 | 0.557 | 0.443 | 0.523 |
| 0.5 | 0.249 | 0.197 | 0.327 | 0.489 | 0.388 | 0.641 | 0.293 | 0.233 | 0.384 | 0.549 | 0.436 | 0.508 | 0.692 | 0.550 | 0.750 | 0.570 | 0.454 | 0.547 |
| 1.0 | 0.325 | 0.258 | 0.427 | 0.549 | 0.436 | 0.720 | 0.381 | 0.303 | 0.500 | 0.588 | 0.467 | 0.578 | 0.736 | 0.585 | 0.819 | 0.621 | 0.493 | 0.634 |
| 1.5 | 0.423 | 0.336 | 0.556 | 0.637 | 0.506 | 0.835 | 0.495 | 0.393 | 0.649 | 0.647 | 0.514 | 0.679 | 0.803 | 0.639 | 0.922 | 0.696 | 0.553 | 0.757 |
| f | a/b = 1.0 | |||||||||||||||||
| (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) | |||||||||||||
| 0.25 | 0.553 | 0.439 | 0.725 | 0.388 | 0.309 | 0.514 | 0.547 | 0.434 | 0.718 | 0.788 | 0.626 | 0.851 | 0.682 | 0.543 | 0.681 | 0.783 | 0.623 | 0.845 |
| 0.5 | 0.578 | 0.459 | 0.758 | 0.422 | 0.335 | 0.563 | 0.572 | 0.454 | 0.752 | 0.806 | 0.641 | 0.880 | 0.702 | 0.558 | 0.718 | 0.801 | 0.637 | 0.874 |
| 1 | 0.670 | 0.532 | 0.878 | 0.538 | 0.428 | 0.721 | 0.664 | 0.528 | 0.874 | 0.874 | 0.695 | 0.985 | 0.778 | 0.618 | 0.848 | 0.869 | 0.691 | 0.982 |
| 1.5 | 0.800 | 0.636 | 1.049 | 0.692 | 0.550 | 0.924 | 0.795 | 0.632 | 1.047 | 0.977 | 0.777 | 1.140 | 0.891 | 0.708 | 1.026 | 0.973 | 0.774 | 1.138 |
| f | (90°/0°/90°) | (0°/90°/90°/0°) | (90°/0°/0°/90°) | (90°/0°/90°) | (0°/90°/90°/0°) | (90°/0°/0°/90°) | ||||||||||||
| 0.25 | 0.547 | 0.434 | 0.718 | 0.544 | 0.433 | 0.714 | 0.544 | 0.433 | 0.714 | 0.783 | 0.623 | 0.845 | 0.782 | 0.622 | 0.842 | 0.782 | 0.622 | 0.842 |
| 0.5 | 0.572 | 0.454 | 0.752 | 0.570 | 0.453 | 0.747 | 0.570 | 0.453 | 0.747 | 0.801 | 0.637 | 0.874 | 0.800 | 0.636 | 0.871 | 0.800 | 0.636 | 0.871 |
| 1.0 | 0.664 | 0.528 | 0.874 | 0.663 | 0.527 | 0.870 | 0.663 | 0.527 | 0.870 | 0.869 | 0.691 | 0.982 | 0.869 | 0.691 | 0.978 | 0.869 | 0.691 | 0.978 |
| 1.5 | 0.795 | 0.632 | 1.047 | 0.794 | 0.632 | 1.042 | 0.794 | 0.632 | 1.042 | 0.973 | 0.774 | 1.138 | 0.973 | 0.773 | 1.134 | 0.973 | 0.773 | 1.134 |
| f | a/b = 1.5 | |||||||||||||||||
| (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) | |||||||||||||
| 0.25 | 0.643 | 0.511 | 0.842 | 0.670 | 0.532 | 0.854 | 0.674 | 0.536 | 0.886 | 0.924 | 0.734 | 0.994 | 0.943 | 0.749 | 1.004 | 0.946 | 0.752 | 1.031 |
| 0.5 | 0.669 | 0.532 | 0.878 | 0.738 | 0.587 | 0.928 | 0.723 | 0.575 | 0.951 | 0.942 | 0.749 | 1.024 | 0.992 | 0.789 | 1.068 | 0.981 | 0.780 | 1.088 |
| 1 | 0.767 | 0.610 | 1.006 | 0.968 | 0.769 | 1.176 | 0.892 | 0.709 | 1.174 | 1.014 | 0.807 | 1.136 | 1.173 | 0.933 | 1.289 | 1.111 | 0.884 | 1.288 |
| 1.5 | 0.908 | 0.721 | 1.190 | 1.263 | 1.004 | 1.499 | 1.118 | 0.889 | 1.473 | 1.124 | 0.894 | 1.302 | 1.427 | 1.134 | 1.589 | 1.300 | 1.034 | 1.565 |
| f | (90°/0°/90°) | (0°/90°/90°/0°) | (90°/0°/0°/90°) | (90°/0°/90°) | (0°/90°/90°/0°) | (90°/0°/0°/90°) | ||||||||||||
| 0.25 | 1.141 | 0.907 | 1.497 | 0.735 | 0.584 | 0.963 | 1.095 | 0.871 | 1.436 | 1.320 | 1.049 | 1.587 | 0.990 | 0.787 | 1.099 | 1.281 | 1.018 | 1.530 |
| 0.5 | 1.186 | 0.943 | 1.557 | 0.791 | 0.629 | 1.037 | 1.135 | 0.902 | 1.488 | 1.359 | 1.080 | 1.644 | 1.032 | 0.821 | 1.164 | 1.315 | 1.045 | 1.580 |
| 1.0 | 1.351 | 1.074 | 1.776 | 0.984 | 0.782 | 1.290 | 1.282 | 1.019 | 1.681 | 1.506 | 1.197 | 1.853 | 1.187 | 0.944 | 1.394 | 1.443 | 1.148 | 1.762 |
| 1.5 | 1.590 | 1.264 | 2.090 | 1.240 | 0.986 | 1.626 | 1.495 | 1.188 | 1.961 | 1.723 | 1.370 | 2.156 | 1.407 | 1.119 | 1.710 | 1.636 | 1.300 | 2.031 |
| a/h = 50 | a/h = 75 | a/h = 100 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| f | (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) |
| 0.25 | 1.017 | 1.038 | 1.012 | 1.017 | 1.038 | 1.012 | 1.017 | 1.038 | 1.012 |
| 0.5 | 1.065 | 1.142 | 1.048 | 1.065 | 1.142 | 1.048 | 1.065 | 1.142 | 1.048 |
| 1 | 1.241 | 1.486 | 1.181 | 1.241 | 1.486 | 1.181 | 1.241 | 1.486 | 1.181 |
| 1.5 | 1.488 | 1.928 | 1.375 | 1.488 | 1.928 | 1.375 | 1.488 | 1.928 | 1.375 |
| f | (90°/0°/ 90°) | (0°/90°/ 90°/0°) | (90°/0°/ 0°/90°) | (90°/0° /90°) | (0°/90°/ 90°/0°) | (90°/0°/ 0°/90°) | (90°/0°/ 90°) | (0°/90°/ 90°/0°) | (90°/0° /0°/90°) |
| 0.25 | 1.037 | 1.011 | 1.036 | 1.037 | 1.011 | 1.036 | 1.037 | 1.011 | 1.036 |
| 0.5 | 1.142 | 1.042 | 1.137 | 1.142 | 1.042 | 1.137 | 1.142 | 1.042 | 1.137 |
| 1 | 1.489 | 1.158 | 1.474 | 1.489 | 1.158 | 1.474 | 1.489 | 1.158 | 1.474 |
| 1.5 | 1.933 | 1.328 | 1.908 | 1.933 | 1.328 | 1.908 | 1.933 | 1.328 | 1.908 |
| for | |||||||||
| f | (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) |
| 0.25 | 1.080 | 1.264 | 1.077 | 1.216 | 1.686 | 1.219 | 1.483 | 2.385 | 1.492 |
| 0.5 | 1.126 | 1.351 | 1.111 | 1.257 | 1.752 | 1.249 | 1.517 | 2.432 | 1.517 |
| 1 | 1.293 | 1.653 | 1.238 | 1.409 | 1.994 | 1.362 | 1.645 | 2.612 | 1.612 |
| 1.5 | 1.532 | 2.059 | 1.423 | 1.631 | 2.341 | 1.533 | 1.839 | 2.886 | 1.759 |
| f | (90°/0°/ 90°) | (0°/90°/ 90°/0°) | (90°/0°/ 0°/90°) | (90°/0° /90°) | (0°/90°/ 90°/0°) | (90°/0°/ 0°/90°) | (90°/0°/ 90°) | (0°/90°/ 90°/0°) | (90°/0° /0°/90°) |
| 0.25 | 1.338 | 1.081 | 1.258 | 1.869 | 1.233 | 1.672 | 2.718 | 1.525 | 2.360 |
| 0.5 | 1.421 | 1.110 | 1.342 | 1.929 | 1.259 | 1.736 | 2.760 | 1.545 | 2.406 |
| 1 | 1.712 | 1.220 | 1.638 | 2.152 | 1.356 | 1.974 | 2.920 | 1.626 | 2.583 |
| 1.5 | 2.110 | 1.383 | 2.037 | 2.481 | 1.505 | 2.315 | 3.170 | 1.751 | 2.852 |
| a/h = 50 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) | |||||||
| f | EG(1,1), EG(1,0) | EG(−1,0) | EG(1,1), EG(1,0) | EG(−1,0) | EG(1,1), EG(1,0) | EG(−1,0) | EG(1,1), EG(1,0) | EG(−1,0) | EG(1,1), EG(1,0) | EG(−1,0) | EG(1,1), EG(1,0) | EG(−1,0) |
| 0.25 | 1.018 | 1.018 | 1.030 | 1.046 | 1.013 | 1.014 | 1.120 | 1.056 | 1.390 | 1.179 | 1.122 | 1.055 |
| 0.5 | 1.069 | 1.069 | 1.118 | 1.167 | 1.052 | 1.053 | 1.167 | 1.106 | 1.456 | 1.288 | 1.158 | 1.093 |
| 1 | 1.252 | 1.252 | 1.418 | 1.557 | 1.197 | 1.198 | 1.337 | 1.284 | 1.698 | 1.650 | 1.290 | 1.234 |
| 1.5 | 1.509 | 1.509 | 1.813 | 2.046 | 1.405 | 1.407 | 1.580 | 1.535 | 2.039 | 2.117 | 1.486 | 1.437 |
| f | (90°/0°/90°) | (0°/90°/90°/0°) | (90°/0°/0°/90°) | (90°/0°/90°) | (0°/90°/90°/0°) | (90°/0°/0°/90°) | ||||||
| 0.25 | 1.037 | 1.039 | 1.012 | 1.012 | 1.037 | 1.037 | 1.501 | 1.230 | 1.131 | 1.057 | 1.386 | 1.177 |
| 0.5 | 1.142 | 1.146 | 1.047 | 1.047 | 1.140 | 1.140 | 1.575 | 1.321 | 1.162 | 1.091 | 1.465 | 1.269 |
| 1 | 1.493 | 1.498 | 1.175 | 1.176 | 1.484 | 1.483 | 1.845 | 1.636 | 1.280 | 1.215 | 1.745 | 1.585 |
| 1.5 | 1.941 | 1.947 | 1.363 | 1.364 | 1.925 | 1.924 | 2.224 | 2.055 | 1.454 | 1.398 | 2.133 | 2.003 |
| a/h = 75 | ||||||||||||
| f | (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) | ||||||
| 0.25 | 1.018 | 1.018 | 1.030 | 1.046 | 1.013 | 1.014 | 1.333 | 1.144 | 2.002 | 1.448 | 1.347 | 1.148 |
| 0.5 | 1.069 | 1.069 | 1.118 | 1.167 | 1.052 | 1.053 | 1.372 | 1.189 | 2.049 | 1.538 | 1.377 | 1.183 |
| 1 | 1.252 | 1.252 | 1.418 | 1.557 | 1.197 | 1.198 | 1.519 | 1.357 | 2.227 | 1.851 | 1.490 | 1.314 |
| 1.5 | 1.509 | 1.509 | 1.813 | 2.046 | 1.405 | 1.407 | 1.737 | 1.597 | 2.497 | 2.278 | 1.662 | 1.507 |
| f | (90°/0°/90°) | (0°/90°/90°/0°) | (90°/0°/0°/90°) | (90°/0°/90°) | (0°/90°/90°/0°) | (90°/0°/0°/90°) | ||||||
| 0.25 | 1.037 | 1.039 | 1.012 | 1.012 | 1.037 | 1.037 | 2.249 | 1.595 | 1.375 | 1.159 | 1.983 | 1.458 |
| 0.5 | 1.142 | 1.146 | 1.047 | 1.047 | 1.140 | 1.140 | 2.300 | 1.667 | 1.401 | 1.189 | 2.039 | 1.533 |
| 1 | 1.493 | 1.498 | 1.175 | 1.176 | 1.484 | 1.483 | 2.492 | 1.926 | 1.499 | 1.304 | 2.249 | 1.803 |
| 1.5 | 1.941 | 1.947 | 1.363 | 1.364 | 1.925 | 1.924 | 2.784 | 2.292 | 1.651 | 1.476 | 2.561 | 2.180 |
| a/h = 100 | ||||||||||||
| f | (0°) | (0°/90°) | (0°/90°/0°) | (0°) | (0°/90°) | (0°/90°/0°) | ||||||
| 0.25 | 1.018 | 1.018 | 1.030 | 1.046 | 1.013 | 1.014 | 1.724 | 1.322 | 2.960 | 1.927 | 1.756 | 1.336 |
| 0.5 | 1.069 | 1.069 | 1.118 | 1.167 | 1.052 | 1.053 | 1.754 | 1.362 | 2.991 | 1.996 | 1.779 | 1.366 |
| 1 | 1.252 | 1.252 | 1.418 | 1.557 | 1.197 | 1.198 | 1.872 | 1.510 | 3.116 | 2.246 | 1.868 | 1.481 |
| 1.5 | 1.509 | 1.509 | 1.813 | 2.046 | 1.405 | 1.407 | 2.053 | 1.729 | 3.314 | 2.609 | 2.008 | 1.654 |
| f | (90°/0°/90°) | (0°/90°/90°/0°) | (90°/0°/0°/90°) | (90°/0°/90°) | (0°/90°/90°/0°) | (90°/0°/0°/90°) | ||||||
| 0.25 | 1.037 | 1.039 | 1.012 | 1.012 | 1.037 | 1.037 | 3.388 | 2.215 | 1.813 | 1.363 | 2.922 | 1.955 |
| 0.5 | 1.142 | 1.146 | 1.047 | 1.047 | 1.140 | 1.140 | 3.422 | 2.267 | 1.833 | 1.389 | 2.960 | 2.011 |
| 1 | 1.493 | 1.498 | 1.175 | 1.176 | 1.484 | 1.483 | 3.554 | 2.464 | 1.909 | 1.488 | 3.109 | 2.224 |
| 1.5 | 1.941 | 1.947 | 1.363 | 1.364 | 1.925 | 1.924 | 3.764 | 2.760 | 2.030 | 1.641 | 3.342 | 2.539 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avey, M.; Tornabene, F.; Aslanova, N.M.; Sofiyev, A.H. The Application of the Modified Lindstedt–Poincaré Method to Solve the Nonlinear Vibration Problem of Exponentially Graded Laminated Plates on Elastic Foundations. Mathematics 2024, 12, 749. https://doi.org/10.3390/math12050749
Avey M, Tornabene F, Aslanova NM, Sofiyev AH. The Application of the Modified Lindstedt–Poincaré Method to Solve the Nonlinear Vibration Problem of Exponentially Graded Laminated Plates on Elastic Foundations. Mathematics. 2024; 12(5):749. https://doi.org/10.3390/math12050749
Chicago/Turabian StyleAvey, Mahmure, Francesco Tornabene, Nigar Mahar Aslanova, and Abdullah H. Sofiyev. 2024. "The Application of the Modified Lindstedt–Poincaré Method to Solve the Nonlinear Vibration Problem of Exponentially Graded Laminated Plates on Elastic Foundations" Mathematics 12, no. 5: 749. https://doi.org/10.3390/math12050749
APA StyleAvey, M., Tornabene, F., Aslanova, N. M., & Sofiyev, A. H. (2024). The Application of the Modified Lindstedt–Poincaré Method to Solve the Nonlinear Vibration Problem of Exponentially Graded Laminated Plates on Elastic Foundations. Mathematics, 12(5), 749. https://doi.org/10.3390/math12050749







