Scalable Learning for Spatiotemporal Mean Field Games Using Physics-Informed Neural Operator
Abstract
:1. Introduction
2. Preliminaries
2.1. Spatiotemporal Mean Field Games (ST-MFGs)
- 1.
- State is the agent’s position at time t. .
- 2.
- Action is the velocity of the agent at position x at time t. The optimal velocity evolves as time progresses.
- 3.
- Cost is the congestion cost depending on agents’ action u and population density ρ.
- 4.
- Value function is the minimum cost of the generic agent starting from position x at time t. are partial derivatives of with respect to , respectively. denotes the terminal cost.
2.2. Physics-Informed Neural Operator (PINO)
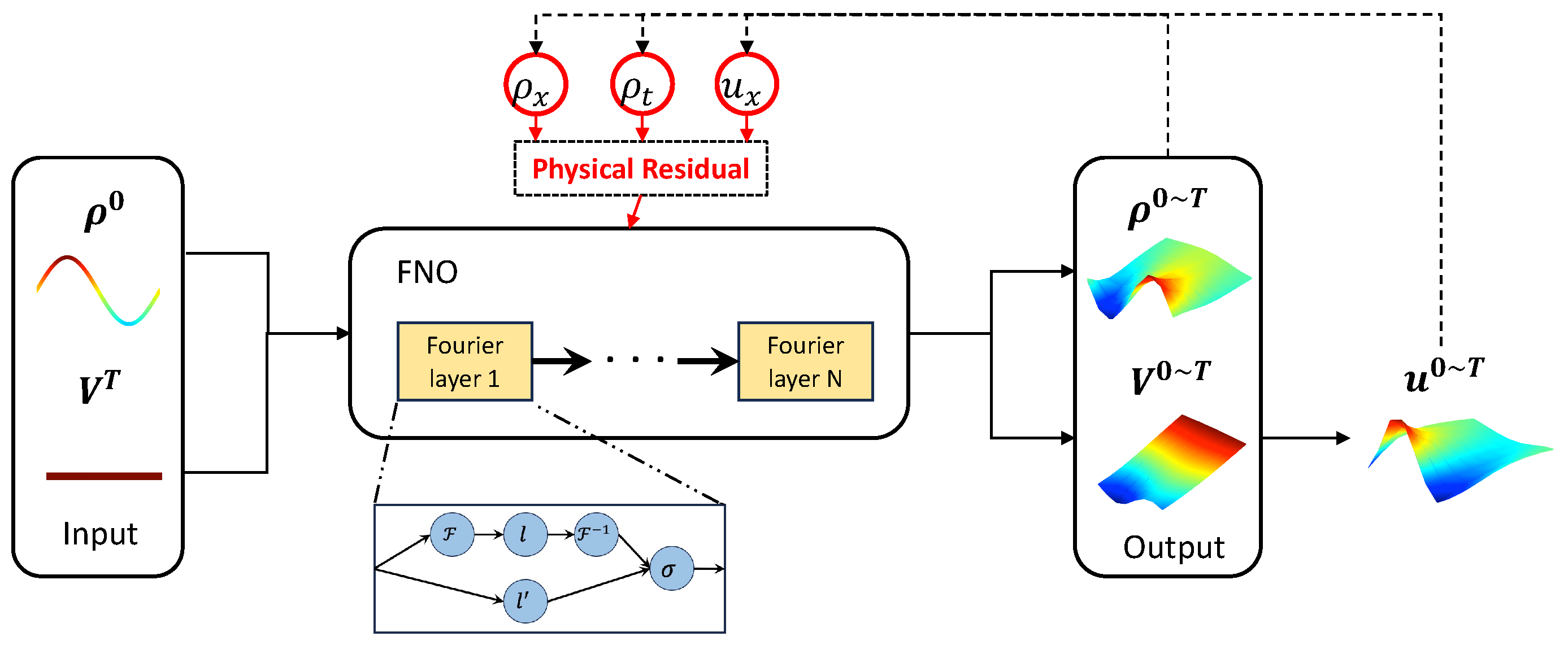
3. Learning ST-MFGs via PINOs
3.1. FPK Module
3.2. HJB Module
4. Solution Approach
| Algorithm 1 PINO for ST-MFG |
|
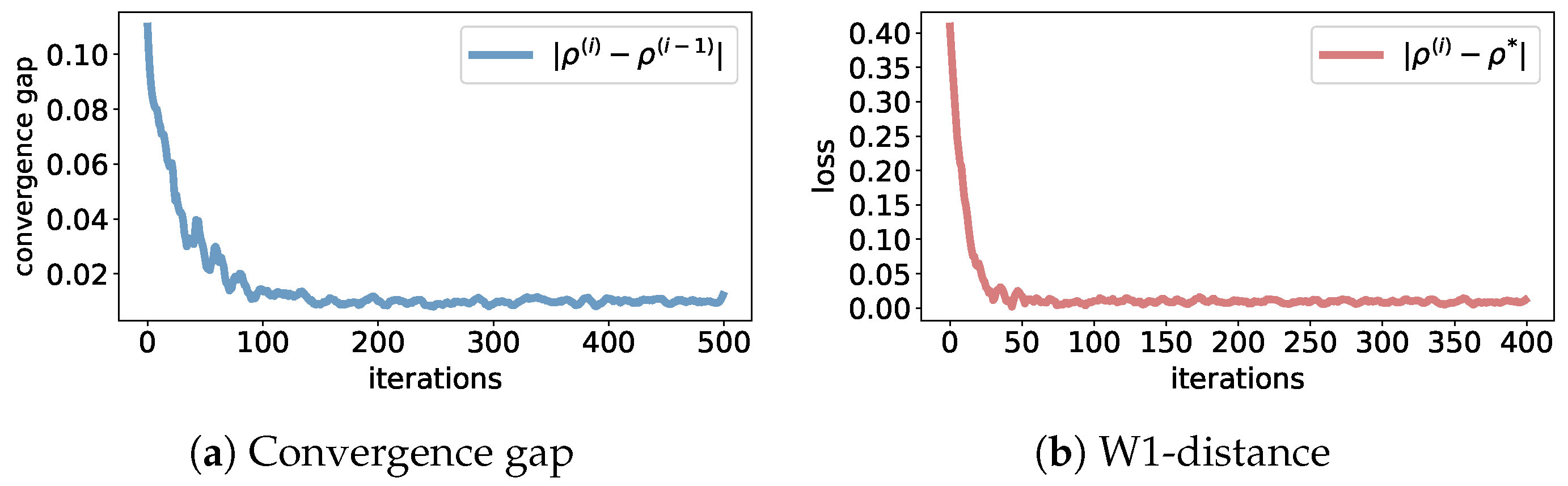
5. Numerical Experiments
- ST-MFG1: The cost function is
- 2.
- ST-MFG2: The Lighthill–Whitham–Richards model is a traditional traffic flow model where the driving objective is to maintain some desired speed. The cost function iswhere, is an arbitrary desired speed function with respect to density . It is straightforward to find that the analytical solution of the LWR model is , which means that at MFE, vehicles maintain the desired speed on roads.
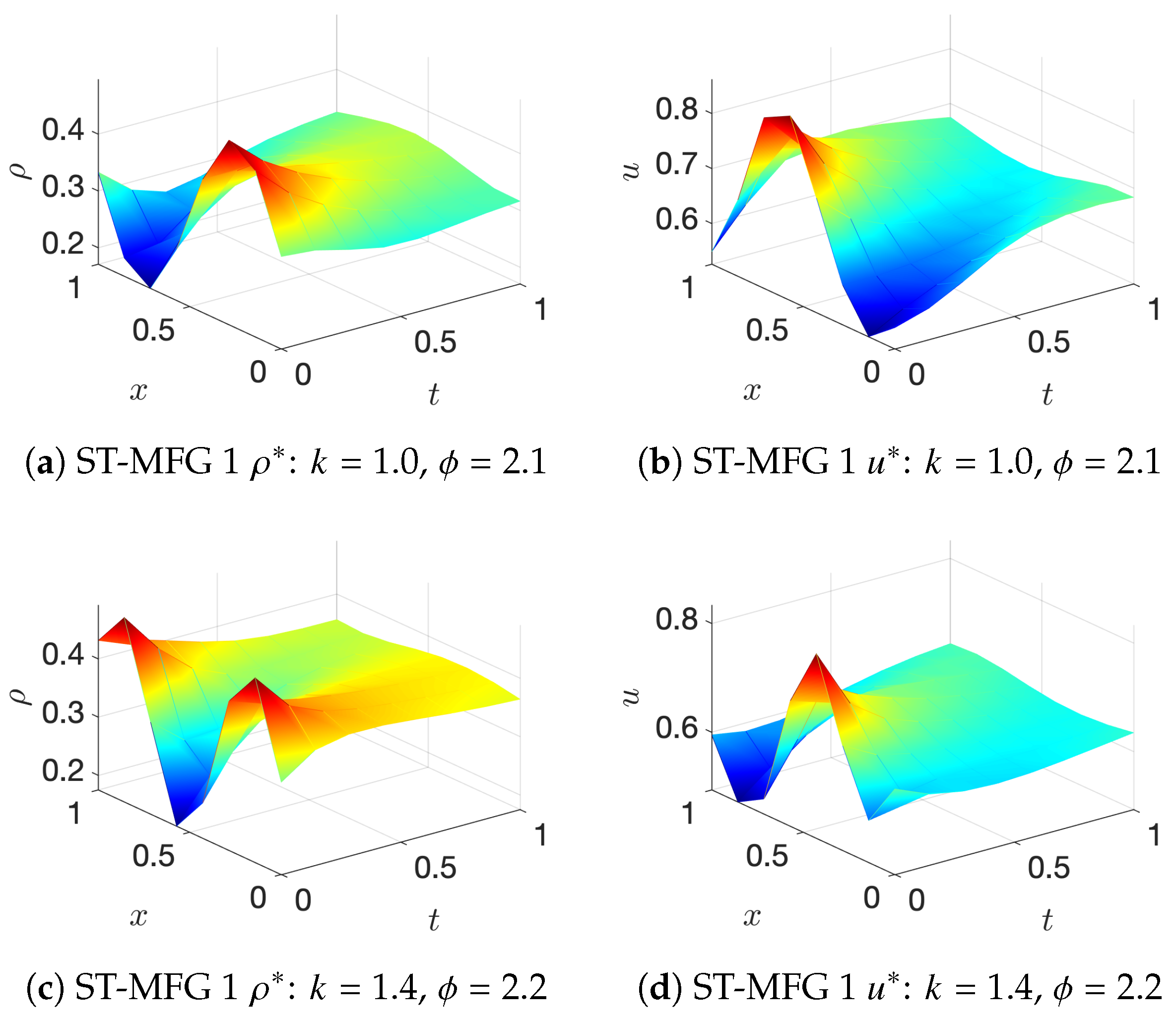
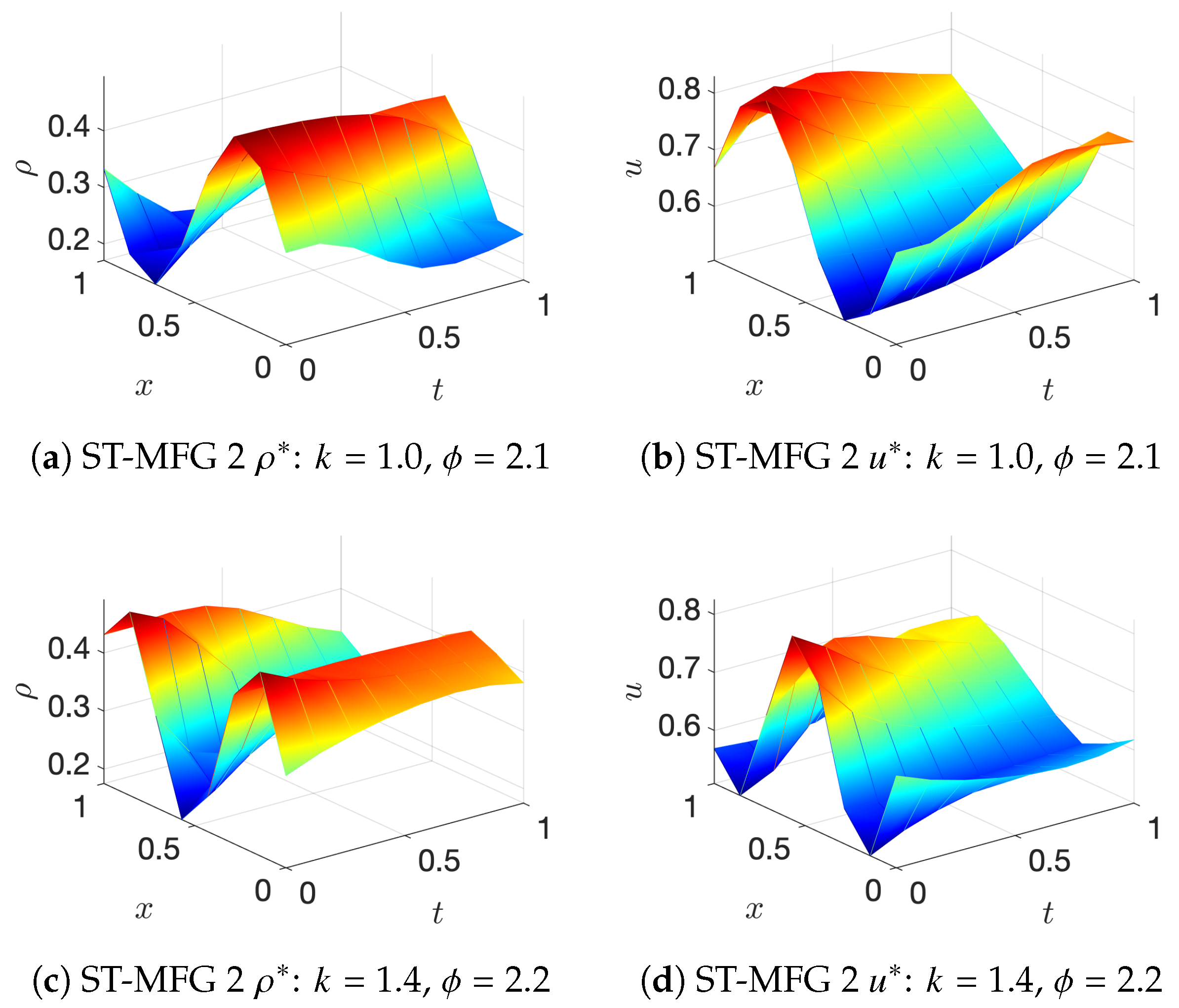
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Mo, Z.; Fu, Y.; Di, X. PI-NeuGODE: Physics-Informed Graph Neural Ordinary Differential Equations for Spatiotemporal Trajectory Prediction. In Proceedings of the 23rd International Conference on Autonomous Agents and Multiagent Systems, AAMAS, London, UK, 29 May–2 June 2023. [Google Scholar]
- Di, X.; Shi, R.; Mo, Z.; Fu, Y. Physics-Informed Deep Learning for Traffic State Estimation: A Survey and the Outlook. Algorithms 2023, 16, 305. [Google Scholar] [CrossRef]
- Shi, R.; Mo, Z.; Di, X. Physics-informed deep learning for traffic state estimation: A hybrid paradigm informed by second-order traffic models. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 540–547. [Google Scholar]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier neural operator for parametric partial differential equations. arXiv 2020, arXiv:2010.08895. [Google Scholar]
- Thodi, B.T.; Ambadipudi, S.V.R.; Jabari, S.E. Learning-based solutions to nonlinear hyperbolic PDEs: Empirical insights on generalization errors. arXiv 2023, arXiv:2302.08144. [Google Scholar]
- Li, Z.; Zheng, H.; Kovachki, N.; Jin, D.; Chen, H.; Liu, B.; Azizzadenesheli, K.; Anandkumar, A. Physics-informed neural operator for learning partial differential equations. arXiv 2021, arXiv:2111.03794. [Google Scholar] [CrossRef]
- Lasry, J.M.; Lions, P.L. Mean field games. Jpn. J. Math. 2007, 2, 229–260. [Google Scholar] [CrossRef]
- Huang, M.; Malhamé, R.P.; Caines, P.E. Large population stochastic dynamic games: Closed-loop McKean-Vlasov systems and the Nash certainty equivalence principle. Commun. Inf. Syst. 2006, 6, 221–252. [Google Scholar]
- Cardaliaguet, P. Notes on Mean Field Games; Technical Report; Stanford University: Stanford, CA, USA, 2010. [Google Scholar]
- Cardaliaguet, P. Weak solutions for first order mean field games with local coupling. In Analysis and Geometry in Control Theory and Its Applications; Springer: Cham, Switzerland, 2015; pp. 111–158. [Google Scholar]
- Kizilkale, A.C.; Caines, P.E. Mean Field Stochastic Adaptive Control. IEEE Trans. Autom. Control. 2013, 58, 905–920. [Google Scholar] [CrossRef]
- Yin, H.; Mehta, P.G.; Meyn, S.P.; Shanbhag, U.V. Learning in Mean-Field Games. IEEE Trans. Autom. Control 2014, 59, 629–644. [Google Scholar] [CrossRef]
- Yang, J.; Ye, X.; Trivedi, R.; Xu, H.; Zha, H. Deep Mean Field Games for Learning Optimal Behavior Policy of Large Populations. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Elie, R.; Perolat, J.; Laurière, M.; Geist, M.; Pietquin, O. On the convergence of model free learning in mean field games. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 7143–7150. [Google Scholar]
- Perrin, S.; Laurière, M.; Pérolat, J.; Geist, M.; Élie, R.; Pietquin, O. Mean Field Games Flock! The Reinforcement Learning Way. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI-21), Virtual, 19–26 August 2021. [Google Scholar]
- Mguni, D.; Jennings, J.; de Cote, E.M. Decentralised learning in systems with many, many strategic agents. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Subramanian, S.; Taylor, M.; Crowley, M.; Poupart, P. Decentralized Mean Field Games. In Proceedings of the AAAI Conference on Artificial Intelligence, Palo Alto, CA, USA, 22 February–1 March 2022. [Google Scholar]
- Chen, X.; Liu, S.; Di, X. Learning Dual Mean Field Games on Graphs. In Proceedings of the 26th European Conference on Artificial Intelligence, ECAI, Krakow, Poland, 30 September–4 October 2023. [Google Scholar]
- Reisinger, C.; Stockinger, W.; Zhang, Y. A fast iterative PDE-based algorithm for feedback controls of nonsmooth mean-field control problems. arXiv 2022, arXiv:2108.06740. [Google Scholar]
- Cao, H.; Guo, X.; Laurière, M. Connecting GANs, MFGs, and OT. arXiv 2021, arXiv:2002.04112. [Google Scholar]
- Ruthotto, L.; Osher, S.J.; Li, W.; Nurbekyan, L.; Fung, S.W. A machine learning framework for solving high-dimensional mean field game and mean field control problems. Proc. Natl. Acad. Sci. USA 2020, 117, 9183–9193. [Google Scholar] [CrossRef] [PubMed]
- Carmona, R.; Laurière, M. Convergence Analysis of Machine Learning Algorithms for the Numerical Solution of Mean Field Control and Games I: The Ergodic Case. SIAM J. Numer. Anal. 2021, 59, 1455–1485. [Google Scholar] [CrossRef]
- Germain, M.; Mikael, J.; Warin, X. Numerical resolution of McKean-Vlasov FBSDEs using neural networks. Methodol. Comput. Appl. Probab. 2022, 24, 2557–2586. [Google Scholar] [CrossRef]
- Chen, X.; Liu, S.; Di, X. A Hybrid Framework of Reinforcement Learning and Physics-Informed Deep Learning for Spatiotemporal Mean Field Games. In Proceedings of the 22nd International Conference on Autonomous Agents and Multiagent Systems, AAMAS ’23, London, UK, 29 May–2 June 2023. [Google Scholar]
- Huang, K.; Di, X.; Du, Q.; Chen, X. A game-theoretic framework for autonomous vehicles velocity control: Bridging microscopic differential games and macroscopic mean field games. Discret. Contin. Dyn. Syst. D 2020, 25, 4869–4903. [Google Scholar] [CrossRef]
- Huang, K.; Chen, X.; Di, X.; Du, Q. Dynamic driving and routing games for autonomous vehicles on networks: A mean field game approach. Transp. Res. Part C Emerg. Technol. 2021, 128, 103189. [Google Scholar] [CrossRef]
- Guo, X.; Hu, A.; Xu, R.; Zhang, J. Learning Mean-Field Games. In Proceedings of the Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Perrin, S.; Perolat, J.; Laurière, M.; Geist, M.; Elie, R.; Pietquin, O. Fictitious Play for Mean Field Games: Continuous Time Analysis and Applications. In Proceedings of the 34th International Conference on Neural Information Processing Systems, NIPS’20, Virtual, 6–12 December 2020. [Google Scholar]
- Lauriere, M.; Perrin, S.; Girgin, S.; Muller, P.; Jain, A.; Cabannes, T.; Piliouras, G.; Perolat, J.; Elie, R.; Pietquin, O.; et al. Scalable Deep Reinforcement Learning Algorithms for Mean Field Games. In Proceedings of the 39th International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; Volume 162, pp. 12078–12095. [Google Scholar]

| PINO | RL-PIDL | Pure-PIDL | ||
|---|---|---|---|---|
| Memory (Number of NNs) | 1 | 48 | 32 | |
| Time (s) | ST-MFG 1 | |||
| ST-MFG 2 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Chen, X.; Di, X. Scalable Learning for Spatiotemporal Mean Field Games Using Physics-Informed Neural Operator. Mathematics 2024, 12, 803. https://doi.org/10.3390/math12060803
Liu S, Chen X, Di X. Scalable Learning for Spatiotemporal Mean Field Games Using Physics-Informed Neural Operator. Mathematics. 2024; 12(6):803. https://doi.org/10.3390/math12060803
Chicago/Turabian StyleLiu, Shuo, Xu Chen, and Xuan Di. 2024. "Scalable Learning for Spatiotemporal Mean Field Games Using Physics-Informed Neural Operator" Mathematics 12, no. 6: 803. https://doi.org/10.3390/math12060803
APA StyleLiu, S., Chen, X., & Di, X. (2024). Scalable Learning for Spatiotemporal Mean Field Games Using Physics-Informed Neural Operator. Mathematics, 12(6), 803. https://doi.org/10.3390/math12060803







