Optimizing the Economic Order Quantity Using Fuzzy Theory and Machine Learning Applied to a Pharmaceutical Framework
Abstract
:1. Introduction
2. Methodology
2.1. Foundational Concepts and Assumptions
- (i)
- The inventory model focuses on a specific product involving a single vendor and a single customer.
- (ii)
- Demand for the product remains constant over time.
- (iii)
- Shortages are not allowed in the inventory system.
- (iv)
- The lead time, denoted as L, is composed of independent components.
- (v)
- The vendor acceptance of payment delays from the customer results in cost savings for the customer by reducing the annual cost of order processing.
- (vi)
- The model assumes an infinite time horizon.
- [Addition] , with weights , for .
- [Subtraction] , with weights , for .
- [Multiplication] , with for . Consequently, for a scalar and a PFN , the scalar multiplication is defined as , for , and , for .
- [Division] . It is important to note that a PFN is divisible by only when is a non-null PFN with non-zero components.
- [Exponentiation] , where k is a real number.
2.2. Optimization Model Framework
- n: is a positive integer representing the total quantity of drug shipments made by a vendor to a purchaser in a batch;
- J: is the size of drug lots per production run, influencing both production scheduling and inventory level;
- U: is the buyer hourly processing fee for drug orders, impacting cost efficiency of the supply chain.
- F: is the transportation cost per drug shipment;
- : is the price of vendor pharmacy unit stock holdings;
- : is the cost of annual drug unit holdings per item;
- : is the shipping processing time for initial orders;
- P: is the purchase price of a drug unit;
- : is the setup cost per vendor production run.
2.3. Solution Methods and Model Formulation
2.4. Cost Function and Optimal Solution
2.5. Integrated Inventory Model for Fuzzy Production Quantity
3. Results
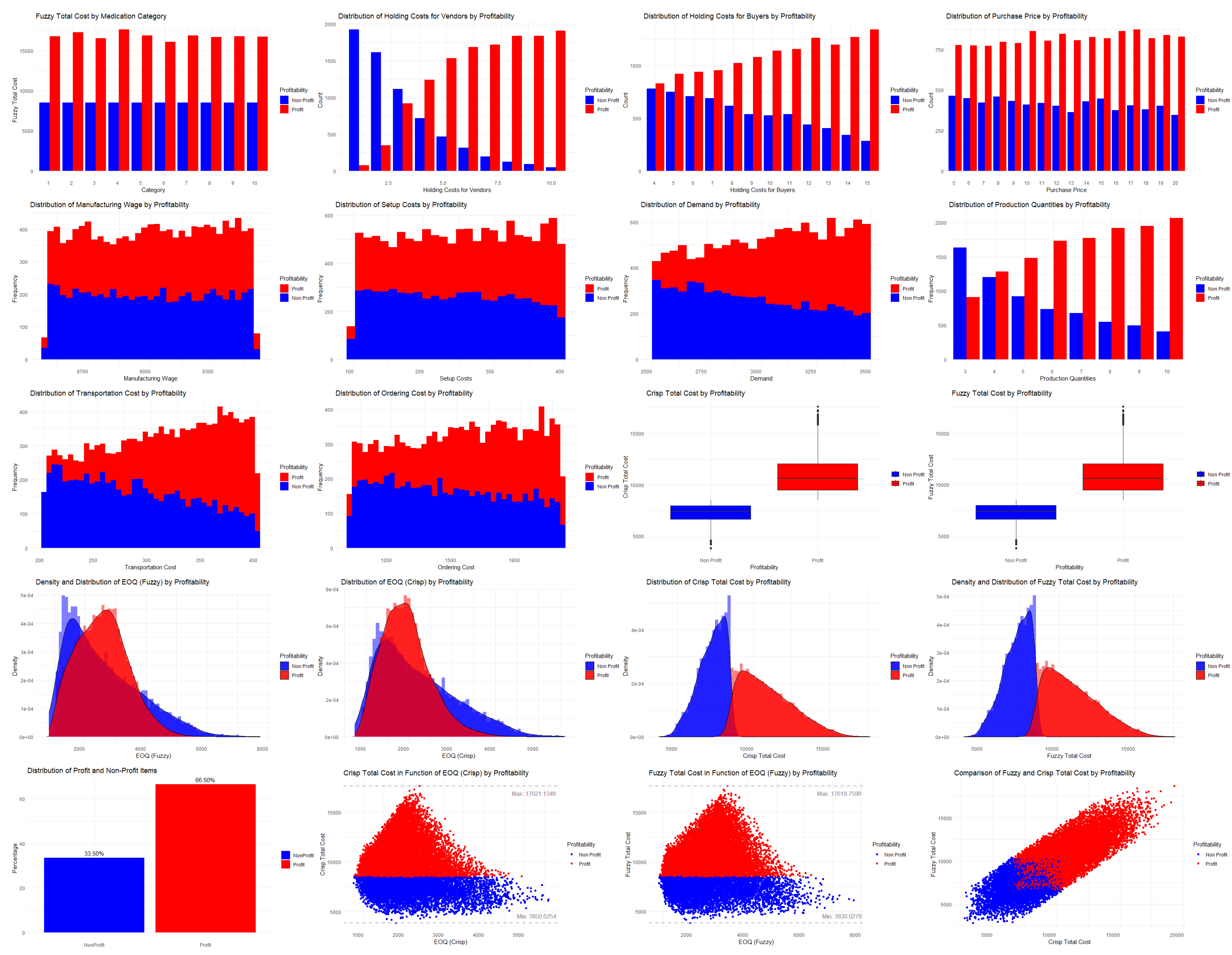
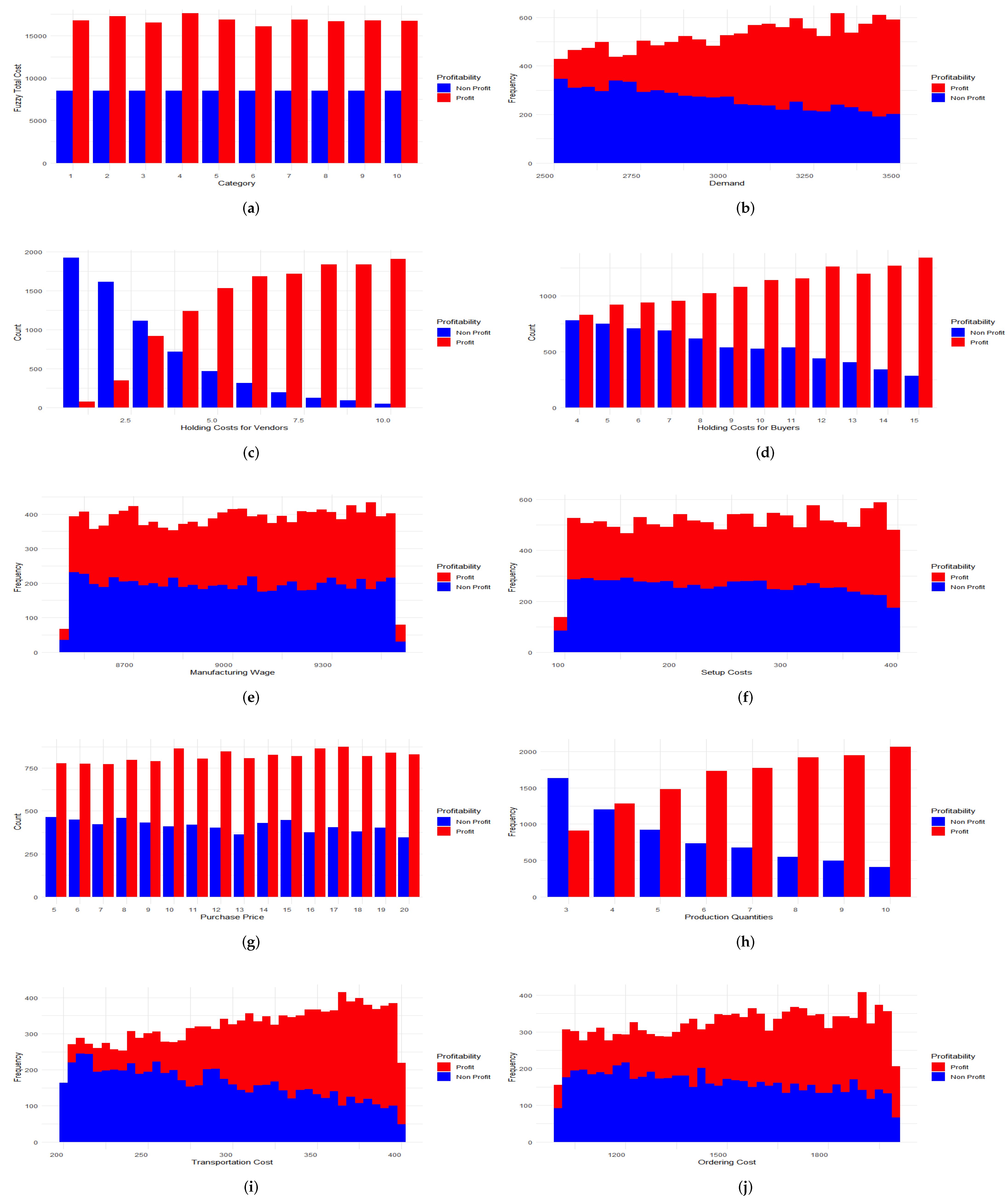
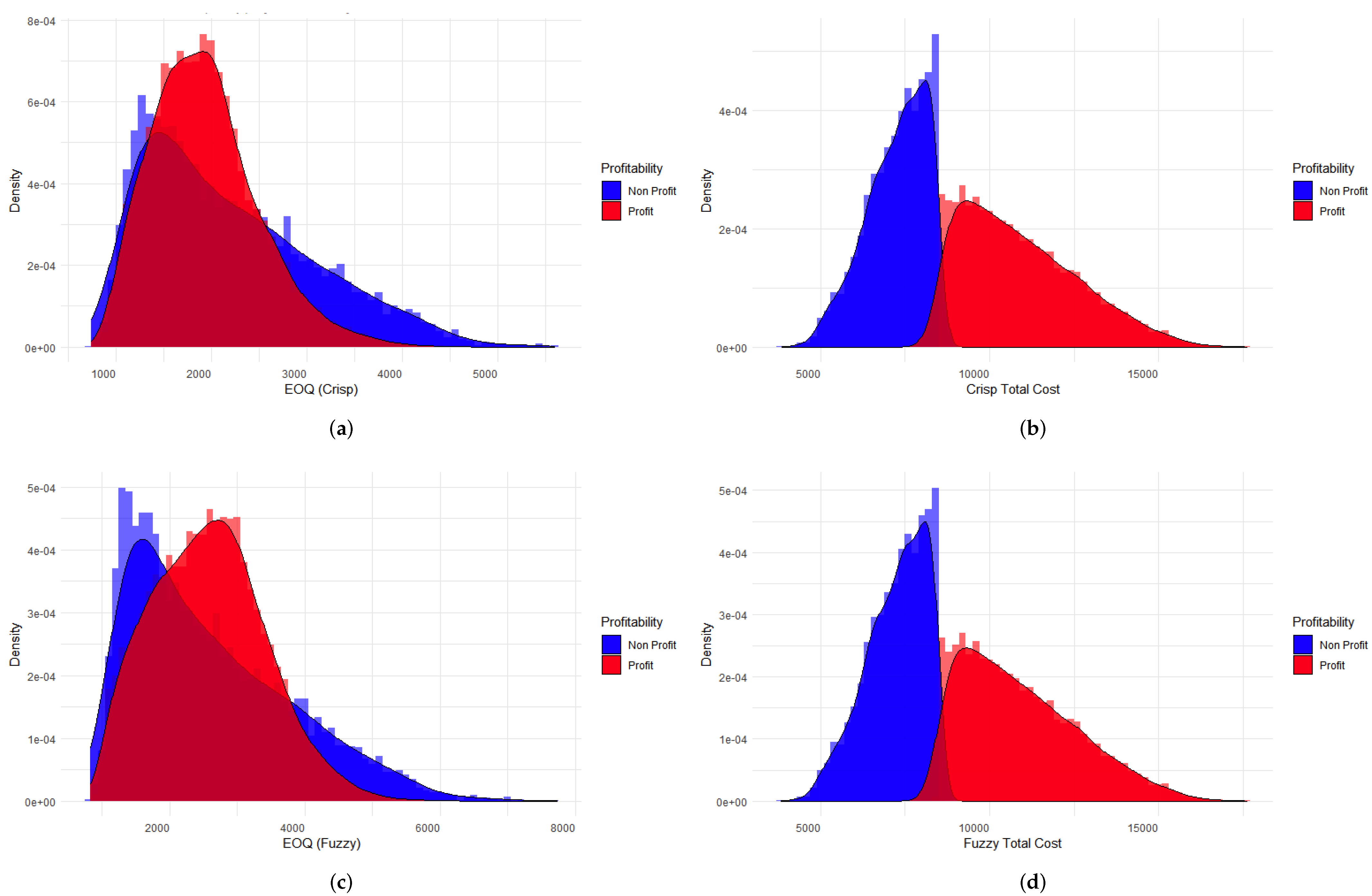
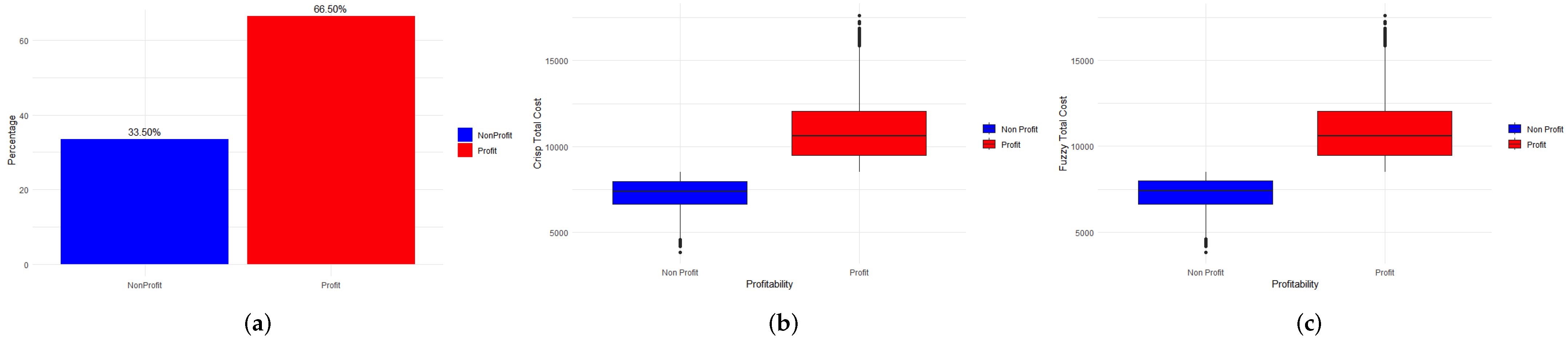
3.1. Simulation Using Machine Learning Techniques
- [Creation of the dataset] We began by compiling a comprehensive dataset that reflects a variety of scenarios within the pharmaceutical supply chain, including demand data, production costs, and other pertinent parameters.
- [Fuzzification of parameters] Key parameters in the dataset were fuzzified, which involved transforming deterministic (crisp) values into fuzzy numbers to better represent uncertainties and variabilities inherent in the supply chain.
- [Conversion to ARFF] The dataset, now containing fuzzy parameters, was converted into the ARFF for compatibility with the Weka software, facilitating the subsequent machine learning analysis.
- [Classification with NB] The dataset was then processed using the NB classifier, which categorizes supply chain scenarios into ‘profitable’ and ‘non-profitable’, aiding in the assessment of the feasibility of these scenarios.
- [Defuzzification process] After classification, a defuzzification process was employed, which converts the fuzzy results back into crisp values for a clearer interpretation.
- [Analysis of results] The outcomes of the classification and defuzzification were thoroughly analyzed to evaluate the model accuracy and its potential applicability in the real-world pharmaceutical supply chain management.
3.2. Evaluation of the Integrated Inventory Model
- [Class difficulty] Complexity of classifying different categories.
- [Correctly classified incidents] Percentage of correctly identified instances (accuracy).
- [Difficulty improvement] How much the classifier simplifies classification.
- [Kappa statistic] Agreement between model predictions and observed classifications.
- [K&B information score] Classifier capability in discerning underlying data structures based on the Kononenko and Bratko (K&B) indicator [75].
- [Mean error] Mean difference between predicted and observed values.
- [Misclassified incidents] Instances incorrectly identified by the classifier.
- [Root-mean-squared error] Aggregate measure of the error magnitude.
- [Total number of occurrences] Total instances evaluated by the classifier.
- [False positive (FP) rate] Proportion of non-profitable scenarios incorrectly classified as profitable.
- [F-measure] Harmonic mean of precision and recall, balancing the two.
- [Matthews correlation coefficient (MCC)] Robust measure considering true and false positives and negatives, particularly helpful for imbalanced datasets.
- [Precision] Accuracy in identifying profitable scenarios.
- [PRC area] Value of the precision–recall curve used for imbalanced class distribution.
- [Recall] Measure to capture all observed profitable scenarios.
- [ROC area] Value of the receiver operating characteristic curve assessing the trade-off between the TP and FP rates.
- [True positive (TP) rate] Proportion of profitable scenarios correctly identified.
3.3. Visualization of the Results in the Weka Software
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goyal, S.K. An integrated inventory model for a single supplier-single customer problem. Int. J. Prod. Res. 1976, 15, 107–111. [Google Scholar] [CrossRef]
- Goyal, S.K. Economic order quantity under conditions of permissible delay in payments. J. Oper. Res. Soc. 1985, 36, 335–338. [Google Scholar] [CrossRef]
- Rojas, F.; Leiva, V.; Huerta, M.; Martin-Barreiro, C. Lot-size models with uncertain demand considering its skewness/kurtosis and stochastic programming applied to hospital pharmacy with sensor-related COVID-19 data. Sensors 2021, 21, 5198. [Google Scholar] [CrossRef]
- Chand, S.; Ward, J. A note on economic order quantity under conditions of permissible delay in payments. J. Oper. Res. Soc. 1987, 38, 83–84. [Google Scholar]
- Gupta, U.K. A comment on economic order quantity under conditions of permissible delay in payments. J. Oper. Res. Soc. 1988, 39, 322–323. [Google Scholar]
- Chung, K.J. A theorem on the determination of economic order quantity under conditions of permissible delay in payments. Comput. Oper. Res. 1998, 25, 49–52. [Google Scholar] [CrossRef]
- Chung, K.J.; Huang, C.K. An ordering policy with allowable shortage and permissible delay in payments. Appl. Math. Model. 2009, 33, 2518–2525. [Google Scholar] [CrossRef]
- Chang, H.J.; Hung, C.H.; Dye, C.Y. An inventory model for deteriorating item with linear trend demand under the condition of permissible delay in payments. Prod. Plan. Control. 2001, 12, 274–282. [Google Scholar] [CrossRef]
- Rojas, F.; Leiva, V.; Wanke, P.; Marchant, C. Optimization of contribution margins in food services by modeling independent component demand. Colomb. J. Stat. 2015, 38, 1–30. [Google Scholar] [CrossRef]
- Teng, T.J. On the economic order quantity under conditions of permissible delay in payments. J. Oper. Res. Soc. 2002, 53, 915–918. [Google Scholar] [CrossRef]
- Huang, H.; Shin, S.W. Retailer’s pricing and lot sizing for exponentially deteriorating products under the condition of permissible delay in payments. Comput. Oper. Res. 1997, 24, 539–547. [Google Scholar]
- Huang, Y.F. Optimal retailer’s ordering policies in the EOQ model under trade credit financing. J. Res. Soc. 2003, 54, 1011–1015. [Google Scholar] [CrossRef]
- Wanke, P.; Ewbank, H.; Leiva, V.; Rojas, F. Inventory management for new products with triangularly distributed demand and lead-time. Comput. Oper. Res. 2016, 69, 97–108. [Google Scholar] [CrossRef]
- Park, K.S. Fuzzy set theoretic interpretation of economic order quantity. IEEE Trans. Syst. Man, Cybern. Smc 1987, 17, 1082–1084. [Google Scholar] [CrossRef]
- Rojas, F.; Wanke, P.; Leiva, V.; Huerta, M.; Martin-Barreiro, C. Modeling inventory cost savings and supply chain success factors: A hybrid robust compromise multi-criteria approach. Mathematics 2022, 10, 2911. [Google Scholar] [CrossRef]
- Rojas, F.; Leiva, V.; Wanke, P.; Lillo, C.; Pascual, J. Modeling lot-size with time-dependent demand based on stochastic programming and case study of drug supply in Chile. PLoS ONE 2019, 14, e0212768. [Google Scholar] [CrossRef] [PubMed]
- Huerta, M.; Leiva, V.; Rojas, F.; Wanke, P.; Cabezas, X. A methodology for consolidation effects of inventory management with serially dependent random demand. Processes 2023, 11, 2008. [Google Scholar] [CrossRef]
- Palanivelu, K.U.B.; Leiva, V.; Dhandapani, P.B.; Castro, C. On fuzzy and crisp solutions of a novel fractional pandemic model. Fractal Fract. 2023, 7, 528. [Google Scholar]
- Rangasamy, M.; Alessa, N.; Dhandapani, P.B.; Loganathan, K. Dynamics of a novel IVRD pandemic model of a large population over a long time with efficient numerical methods. Symmetry 2022, 14, 1919. [Google Scholar] [CrossRef]
- Kalpana, U.; Balaganesan, P.; Renuka, J.; Dumitru, B.; Dhandapani, P.B. On the decomposition and analysis of novel simultaneous SEIQR epidemic model. AIMS Math. 2023, 10, 5918–5933. [Google Scholar]
- Sebatjane, M.; Adetunji, O. A four-echelon supply chain inventory model for growing items with imperfect quality and errors in quality inspection. Ann. Oper. Res. 2024, in press. [CrossRef]
- Alamri, O.A. Sustainable supply chain model for defective growing items (fishery) with trade credit policy and fuzzy learning effect. Axioms 2023, 12, 436. [Google Scholar] [CrossRef]
- Alamri, O.A.; Jayaswal, M.K.; Khan, F.A.; Mittal, M. An EOQ Model with Carbon Emissions and Inflation for Deteriorating Imperfect Quality Items under Learning Effect. Sustainability 2022, 14, 1365. [Google Scholar] [CrossRef]
- Chang, H.C. An application of fuzzy sets to the EOQ model with imperfect quality items. Comput. Oper. Res. 2004, 31, 2079–2092. [Google Scholar] [CrossRef]
- Rani, S.; Ali, R.; Agarwal, A. Fuzzy inventory model for new and refurbished deteriorating items with cannibalization in green supply chain. Int. J. Syst. Sci. Oper. Logist. 2022, 9, 22–38. [Google Scholar]
- Wee, H.M.; Yu, J.; Chen, M.C. Optimum inventory model for items with imperfect quality and shortage backordering. Omega 2007, 35, 7–11. [Google Scholar] [CrossRef]
- Rajeswari, S.; Sugapriya, C.; Nagarajan, D.; Kavikumar, J. Optimization in fuzzy economic order quantity model involving pentagonal fuzzy parameter. Int. J. Fuzzy Syst. 2022, 24, 44–56. [Google Scholar] [CrossRef]
- Jayaswal, M.K.; Mittal, M.; Alamri, O.A.; Khan, F.A. Learning EOQ Model with Trade-Credit Financing Policy for Imperfect Quality Items under Cloudy Fuzzy Environment. Mathematics 2022, 10, 246. [Google Scholar] [CrossRef]
- Banerjee, A. A joint economic lot size model for purchase and vendor. Decis. Sci. 1986, 17, 292–311. [Google Scholar] [CrossRef]
- Chen, S.K. Operations on fuzzy numbers with function principle. Tamkang J. Mang. Sci. 1985, 6, 13–26. [Google Scholar]
- Zhao, H.; Jiang, Y.; Yang, Y. Robust and Sparse Portfolio: Optimization Models and Algorithms. Mathematics 2023, 11, 4925. [Google Scholar] [CrossRef]
- Kotz, S.; Leiva, V.; Sanhueza, A. Two new mixture models related to the inverse Gaussian distribution. Methodol. Comput. Appl. Probab. 2010, 12, 199–212. [Google Scholar] [CrossRef]
- Kalaiarasi, K.; Sumathi, M.; Mary Henrietta, H. Optimizing EOQ using geometric programming with varying fuzzy numbers by applying Python. J. Crit. Rev. 2020, 7, 596–603. [Google Scholar]
- Kalaiarasi, K.; Soundaria, R.; Kausar, N.; Agarwal, P.; Aydi, H.; Alsamir, H. Optimization of the average monthly cost of an EOQ inventory model for deteriorating items in machine learning using Python. Therm. Sci. 2021, 2, S347–S358. [Google Scholar] [CrossRef]
- Chen, S.H.; Hsieh, C.H. Optimization of fuzzy inventory models. In Proceedings of the IEEE SMC99 Conference, Tokyo, Japan, 12–15 October 1999; Volume 1, pp. 240–244. [Google Scholar]
- Dong, Y.; Xu, K. A supply chain model of vendor managed inventory. Transp. Res. Part Logist. Transp. Rev. 2002, 38, 75–95. [Google Scholar] [CrossRef]
- Marquès, G.; Thierry, C.; Lamothe, J.; Gourc, D. A review of vendor managed inventory (VMI): From concept to processes. Prod. Plan. Control. 2010, 21, 547–561. [Google Scholar] [CrossRef]
- Lotfi, R.; MohajerAnsari, P.; Nevisi, M.M.S.; Afshar, M.; Davoodi, S.M.R.; Ali, S.S. A viable supply chain by considering vendor-managed-inventory with a consignment stock policy and learning approach. Results Eng. 2024, 21, 101609. [Google Scholar] [CrossRef]
- Silva, R.; Tarigan, Z.; Siagian, H. The influence of supplier competency on business performance through supplier integration, vendor-managed inventory, and supply chain collaboration in Fuel Station: An evidence from Timor Leste. Uncertain Supply Chain. Manag. 2024, 12, 207–220. [Google Scholar] [CrossRef]
- Rahman, M.Z.; Akbar, M.A.; Leiva, V.; Tahir, A.; Riaz, M.T.; Martin-Barreiro, C. An intelligent health monitoring and diagnosis system based on the internet of things and fuzzy logic for cardiac arrhythmia COVID-19 patients. Comput. Biol. Med. 2023, 154, 106583. [Google Scholar] [CrossRef]
- Rangasamy, M.; Chesneau, C.; Martin-Barreiro, C.; Leiva, V. On a novel dynamics of SEIR epidemic models with a potential application to COVID-19. Symmetry 2022, 14, 1436. [Google Scholar] [CrossRef]
- Rahman, M.Z.U.; Akbar, M.A.; Leiva, V.; Martin-Barreiro, C.; Imran, M.; Riaz, M.T.; Castro, C. An IoT-fuzzy intelligent approach for holistic management of COVID-19 patients. Heliyon 2024, 10, e22454. [Google Scholar] [CrossRef] [PubMed]
- Taylan, O.; Alkabaa, A.S.; Alqabbaa, H.S.; Pamukcu, E.; Leiva, V. Early prediction in classification of cardiovascular diseases with machine learning, neuro-fuzzy and statistical methods. Biology 2023, 12, 1179. [Google Scholar] [CrossRef] [PubMed]
- Kuppusamy, V.; Shanmugasundaram, M.; Dhandapani, P.B.; Martin-Barreiro, C.; Cabezas, X.; Leiva, V.; Castro, C. Addressing a decision problem through a bipolar Pythagorean fuzzy approach: A novel methodology with application in digital marketing. Heliyon 2024, 10, e23991. [Google Scholar] [CrossRef]
- Mittal, M.; Jain, V.; Pandey, J.T.; Jain, M.; Dem, H. Optimizing Inventory Management: A Comprehensive Analysis of Models Integrating Diverse Fuzzy Demand Functions. Mathematics 2024, 12, 70. [Google Scholar] [CrossRef]
- Alshammari, O.; Kchaou, M.; Jerbi, H.; Ben Aoun, S.; Leiva, V. A fuzzy design for a sliding mode observer-based control scheme of Takagi-Sugeno Markov jump systems under imperfect premise matching with bio-economic and industrial applications. Mathematics 2022, 10, 3309. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Klir, G.J.; Yuan, B. Fuzzy Sets and Fuzzy Logic: Theory and Applications; Prentice Hall: Hoboken, NJ, USA, 1995. [Google Scholar]
- Zimmermann, H.J. Fuzzy Set Theory—and Its Applications; Kluwer Academic Publishers: Boston, MA, USA, 2001. [Google Scholar]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems: Theory and Applications; Academic Press: Cambridge, MA, USA, 1980. [Google Scholar]
- Nguyen, H.T.; Walker, E.A. A First Course in Fuzzy Logic; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Ghaznavi, M.; Soleimani, F.; Hoseinpoor, N. Parametric Analysis in Fuzzy Number Linear Programming Problems. Int. J. Fuzzy Syst. 2016, 18, 463–477. [Google Scholar] [CrossRef]
- Kaufmann, A.; Gupta, M.M. Introduction to Fuzzy Arithmetic Theory and Applications; Van Nostrand Reinhold: New York, NY, USA, 1985. [Google Scholar]
- Khan, I.U.; Ahmad, T.; Maan, N. A simplified novel technique for solving fully fuzzy linear programming problems. J. Optim. Theory Appl. 2013, 159, 536–546. [Google Scholar] [CrossRef]
- Mordeson, J.N.; Nair, P.S. Fuzzy Mathematics: An Introduction for Engineers and Scientists; Physica-Verlag: Heidelberg, Germany, 2001. [Google Scholar]
- Bede, B. The Mathematics of Fuzzy Sets and Fuzzy Logic; Springer: Berlin, Germany, 2007. [Google Scholar]
- Panda, A.; Pal, M. A study on pentagonal fuzzy number and its corresponding matrices. Pac. Sci. Rev. Humanit. Soc. Sci. 2015, 1, 131–139. [Google Scholar] [CrossRef]
- Mondal, S.P.; Mandal, M. Pentagonal fuzzy number, its properties and application in fuzzy equation. Future Comput. Inform. J. 2017, 2, 110–117. [Google Scholar] [CrossRef]
- Taha, H.A. Operations Research; Prentice-Hall: Englewood Cliffs, NJ, USA, 1997. [Google Scholar]
- Bazaraa, M.S.; Sherali, H.D.; Shetty, C.M. Nonlinear Programming: Theory and Algorithms; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Luenberger, D.G. Optimization by Vector Space Methods; John Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]
- Hillier, F.S.; Lieberman, G.J. Introduction to Operations Research; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Nagar, H.; Surana, P. Fuzzy inventory model for deteriorating item by using signed distance method in which inventory parameters are treated as Pfn. Indian J. Appl. Res. 2015, 7, 628–634. [Google Scholar]
- Atanassov, K.T. Fuzzy Sets and Their Applications to Cognitive and Decision Processes; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Kacprzyk, J.; Fedrizzi, M. Fuzzy Sets, Decision Making, and Expert Systems; Kluwer Academic Publishers: Boston, MA, USA, 1986. [Google Scholar]
- Taylor, B.W. Introduction to Management Science; Pearson: New York, NY, USA, 2019. [Google Scholar]
- Nahmias, S. Production and Operations Analysis; McGraw-Hill/Irwin: New York, NY, USA, 2009. [Google Scholar]
- Silver, E.A.; Pyke, D.F.; Peterson, R. Inventory Management and Production Planning and Scheduling; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Ritha, W.; Kalaiarasi, R.; Jun, Y.B. Optimization of fuzzy integrated vendor–buyer inventory models. Ann. Fuzzy Math. Inform. 2011, 2, 239–257. [Google Scholar]
- Kausar, N.; Munir, M.; Agarwal, P.; Kalaiarasi, K. The characterization of fuzzy and anti fuzzy Ideals in AG-groupoid. Thai J. Math. 2022, 20, 653–667. [Google Scholar]
- Kalaiarasi, K.; Henrietta, H.M.; Sumathi, M. Determining the efficient optimal order quantity for an Inventory model with varying fuzzy components. J. Algebr. Stat. 2022, 6, 653–667. [Google Scholar]
- Kalaiarasi, K.; Nasreen Kausar, P.; Kousar, S.; Pamucar, D.; Ide, N.A.D. Economic order quantity model-based optimized fuzzy nonlinear dynamic mathematical schemes. Comput. Intell. Neurosci. 2022, 2022, 3881265. [Google Scholar]
- Aykroyd, R.G.; Leiva, V.; Ruggeri, F. Recent developments of control charts, identification of big data sources and future trends of current research. Technol. Forecast. Soc. Chang. 2019, 144, 221–232. [Google Scholar] [CrossRef]
- Kononenko, I.; Bratko, I. Information-based evaluation criterion for classifier’s performance. Mach. Learn. 1991, 6, 67–80. [Google Scholar] [CrossRef]


| Notation | Description |
|---|---|
| D | Drug demand on an annual basis |
| F | Fixed drug transportation costs per shipment |
| Price of vendor pharmacy unit stock holdings | |
| Cost of drug annual unit holdings per item | |
| I | Bearing expense per drug per year |
| J | Size of drug lots per production run |
| Drug shipping processing time for initial orders | |
| L | Lead time |
| n | A positive integer representing the total number of drug shipments |
| made by a vendor to a purchaser in a batch | |
| P | Purchase price of a drug unit |
| R | Drug manufacturing wage () |
| Drug vendor setup costs per production run | |
| t | Allowable drug holding in account settlement |
| U | Buyer hourly processing fee for drug orders |
| Metric | Value | |
|---|---|---|
| Absolute | Relative | |
| Class difficulty|Order 0 (baseline) | 18,137.94 bits | 0.92 bits/instance |
| Class difficulty|Model (NB) | 2860.54 bits | 0.15 bits/instance |
| Correctly classified incidents | 18,910 | 95.91% |
| Difficulty improvement | 15,277.41 bits | 0.77 bits/instance |
| Kappa statistic | 0.91 | - |
| K&B information score | - | 87.91% |
| Mean error | 0.05 | 12.25% |
| Misclassified incidents | 806 | 4.09% |
| Root-mean-squared error | 0.17 | 36.01% |
| Total number of occurrences | 19,716 | 100% |
| Class | TP Rate | FP Rate | Precision | Recall | F-Measure | MCC | ROC Area | PRC Area |
|---|---|---|---|---|---|---|---|---|
| Non-Profit | 0.981 | 0.052 | 0.905 | 0.981 | 0.941 | −0.912 | 0.995 | 0.988 |
| Profit | 0.948 | 0.019 | 0.990 | 0.948 | 0.969 | 0.912 | 0.995 | 0.997 |
| Weighted Average | 0.959 | 0.030 | 0.961 | 0.959 | 0.959 | 0.912 | 0.995 | 0.994 |
| Class | Predicted Non-Profit | Predicted Profit |
|---|---|---|
| Observed Non-Profit | TN (6478) | FP (127) |
| Observed Profit | FN (679) | TP (12,432) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalaichelvan, K.; Ramalingam, S.; Dhandapani, P.B.; Leiva, V.; Castro, C. Optimizing the Economic Order Quantity Using Fuzzy Theory and Machine Learning Applied to a Pharmaceutical Framework. Mathematics 2024, 12, 819. https://doi.org/10.3390/math12060819
Kalaichelvan K, Ramalingam S, Dhandapani PB, Leiva V, Castro C. Optimizing the Economic Order Quantity Using Fuzzy Theory and Machine Learning Applied to a Pharmaceutical Framework. Mathematics. 2024; 12(6):819. https://doi.org/10.3390/math12060819
Chicago/Turabian StyleKalaichelvan, Kalaiarasi, Soundaria Ramalingam, Prasantha Bharathi Dhandapani, Víctor Leiva, and Cecilia Castro. 2024. "Optimizing the Economic Order Quantity Using Fuzzy Theory and Machine Learning Applied to a Pharmaceutical Framework" Mathematics 12, no. 6: 819. https://doi.org/10.3390/math12060819
APA StyleKalaichelvan, K., Ramalingam, S., Dhandapani, P. B., Leiva, V., & Castro, C. (2024). Optimizing the Economic Order Quantity Using Fuzzy Theory and Machine Learning Applied to a Pharmaceutical Framework. Mathematics, 12(6), 819. https://doi.org/10.3390/math12060819









