Loss-Averse Supply Chain Coordination with a Revenue-Sharing Contract

Abstract

As economic fluctuations and market uncertainty intensify, supply chain members face enormous challenges. To explore the role of revenue-sharing contracts in supply chain members with different risk preferences, we study the risk-averse two-stage supply chain coordination in a revenue-sharing contract under three different scenarios: the supplier is risk-averse and the retailer is risk-neutral, or the retailer is risk-averse and the supplier is risk-neutral, or both are risk-averse. We find that the revenue-sharing contract mechanism allows the supplier to offer a lower wholesale price, effectively bearing part of the retailer’s cost risk. In return, the retailer compensates the supplier with a larger portion of their revenue, and the lower wholesale price also stimulates the retailer’s desire to order more products. In addition, risk aversion always reduces the optimal order quantity in the supply chain. Interestingly, when the retailer’s risk aversion level is low, the supplier charges a higher wholesale price under the risk-averse supply chain than that under the risk-neutral supply chain. However, if the retailer’s risk aversion level is high enough, the supplier should charge a lower price to stimulate the retailer under the risk-averse supply chain to retain the order size to maintain the channel profit.

1. Background

The 2020 COVID-19 pandemic has already greatly impacted global economic and social development, through issues such as global trade stagnation, supply chain coordination issues, and business closures [1]. Now, the world has moved into the post-epidemic era. It seems that the peak period of the epidemic has passed, while repeated small-intensity epidemics and the continuous mutation of the virus are still a realistic situation [2], which will bring uncertainty in market demand and the risk of supply chains. Correspondingly, it greatly increases the risk for supply chain members. This has made companies increasingly vigilant about business risks, investment, and expansion behavior, keeping low inventories to control costs to avoid risks, even if business decision-makers realize that these behaviors may sometimes bring more profits [3,4]. These behaviors are often viewed as loss-averse, which is one of the key characteristics of prospect theory [5]; that is, people are more sensitive to losses than to equal revenue. A survey conducted by McKinsey on 1500 executives from 90 countries showed that regardless of the size of the company, managers exhibit extreme levels of risk aversion [6]. In particular, retailers with fewer funds and smaller scales have a much smaller ability to bear risks than manufacturers in the supply chain, who are normally loss-averse. This contradicts the current market environment and existing research that sets supply chain members as loss-neutral [7].

Therefore, in the current complex market with the various risks and uncertainties, how to effectively coordinate the supply chain is an important topic [8,9]. Many scholars have verified that the revenue-sharing contract is an important means to effectively coordinate a decentralized supply chain in a risk-neutral setting. Large distribution platforms such as Apple App Store and Google Games adopt the unified revenue-sharing contract to interact with developers of all sales applications, in which the platform retain 30% of the sales application revenue, while developers receive 70% [10]. On Amazon.com, sellers pay a certain percentage of the sales price and fixed fees to the platform to obtain platform support [11]. Although the importance and practicality of revenue-sharing contracts have been recognized in supply chain management, the loss avoidance behavior of supply chain members has not been fully considered in revenue-sharing contracts. Research based on loss-neutral behavior setting may not be able to analyze the supply chain coordination problem when supply chain members have different risk preferences under the current demand uncertainty. The decisions of supply members are often influenced by behavioral preferences, which affect the profits of the enterprise and supply chain. Therefore, to supplement this gap, we study loss-averse supply chain coordination with a revenue-sharing contract.

Some of the following literature is similar to the topic of our article. Jammerneg et al. [12] compared the supply chain profits and the optimal order quantities when suppliers had different risk preferences in the newsvendor problem while considering the role of wholesale price contracts. Liu et al. [13] analyzed the impact of the option contract on optimal decision making in a humanitarian supply chain (HSC) consisting of a humanitarian agency and a loss-averse supplier. Yi et al. [14] constructed a maritime supply chain with one port and two carriers under a wholesale price contact and two-tariff contract, and analyzed how risk-averse behavior and contract unobservability impact the pricing and contract preference. Liu et al. [15] investigated the coordination of both the supplier-led and the retailer-led supply chains with a risk-neutral supplier and a risk-averse retailer under an option contract. Zhang et al. [16] established a risk-averse supply chain revenue-sharing contract model under supplier dominance, proving the importance of member dominance in supply chain coordination.

Although the above-mentioned scholars have studied the coordination of different contracts on the supply chain with loss-averse suppliers, a few considered the game scenario of the loss-averse retailer, while the retailer is normally more sensitive to risk than the supplier based on the research of [7]. Precious few studies have compared the performance and equilibrium results of supply chains composed of suppliers and retailers with different risk preferences under contract coordination. Meanwhile, few have discussed the interaction between profit-sharing factors and risk preference levels in the above research. Therefore, to supplement this gap, we study risk-averse two-stage supply chain coordination in a revenue-sharing contract under three different scenarios: the supplier is risk-averse and the retailer is risk-neutral, or the retailer is risk-averse and the supplier is risk-neutral, or both are risk-averse. We hope to answer the following questions:

• What are the equilibrium decisions in the game?
• Could the revenue sharing coordinate the supply chain under three different scenarios? And how?
• If yes, what are the effects of loss aversion on the two sides’ optimal decisions under the three game scenarios? And at the same time, does maximizing utility align with maximizing profits?
• How do risk aversion levels and revenue-sharing factors interact with each other under the three scenarios?

To answer the above questions, we follow the following research procedure. In the first step, we analyze the optimal wholesale prices and order quantities under the centralized and decentralized game model with the revenue-sharing contract through constructing a supply chain system consisting of a single supplier and a single retailer. In the second step, based on this, we consider the loss avoidance behavior of the supplier or the retailer and establish three different game scenarios, namely, the game scenarios NA, AN, and AA. The game scenario NA represents a supply chain system consisting of a risk-neutral supplier and a risk-averse retailer; the game scenario AN represents a supply chain system consisting of a risk-averse supplier and a risk-neutral retailer; the game scenario AA represents a supply chain system consisting of a risk-averse supplier and a risk-averse retailer. In the third step, we compare and analyze the decisions and parameters. The major contributions of this work can be summarized as follows:

• It introduces decision-makers’ loss aversion into traditional supply chain revenue-sharing contracts, modifying the “economic man” assumption of suppliers or retailers to reduce prediction errors.
• It is based on game theory and explores the coordination process and equilibrium analysis between the retailer and the supplier, enriching the research on behavioral supply chains, and providing analytical methods and a theoretical basis for supply chain coordination research and enterprise management.
• We extend equilibrium decision analysis to show the impact of loss-averse behavior on the revenue-sharing contract.

The rest of the paper is as follows: In Section 2, we review the related literature to identify the research gap and position our study. In Section 3, we construct a benchmark model to analyze the equilibrium outcome under the revenue-sharing contract. In Section 4, we consider three risk-averse game scenarios under the revenue-sharing contracts in the supply chain. In Section 5, we conduct the numerical analysis. In Section 6, we conclude this paper and provide suggestions for further research. Proofs of all lemmas and propositions are provided in Appendix A.

2. Literature Review

Our work brings together streams of research on supply chain coordination (Section 2.1), supply chain contracts (Section 2.2), and loss aversion (Section 2.3). Although there is a relatively rich body of research in these three areas, combined and comparative analyses of the three aspects are relatively rare. We review the closely related literature in the three areas and then summarize the differences between our work and the others, as well as highlight our research objective and contributions.

2.1. Supply Chain Coordination

Entering the 21st century, many scholars have focused their research on supply chain management in the field of supply chain coordination. There is a widely accepted definition of supply chain coordination, which is a mechanism in which the total profit of all members in a decentralized system is equal to the profit of the centralized system [17]. The purpose of supply chain coordination is to achieve the integration and optimization of supply chain members so that the optimal decisions are value-oriented towards maximizing the overall benefits of the supply chain. When the supply chain is uncoordinated, that is, due to members pursuing maximum self-interest without the goal of optimizing overall interests, it can lead to information asymmetry between upstream and downstream, a trust crisis between the cooperating parties, and low operational efficiency of the supply chain. Malone [18] divided coordination mechanisms into information coordination and contract coordination, with the former involving cost information sharing and demand information sharing.

A supply chains with a single manufacturer and a single retailer is the typical setting in previous studies, in which the retailer faces random demand with a cumulative distribution function $F(·)$ and an exogenous retail price, and a supply contract between the manufacturer and the retailer determines the transfer payments, such as the wholesale price. The retailer decides on the order quantity q, and the manufacturer decides on the wholesale price w [19,20,21]. The signing of supply chain contracts for both parties aligns their goals with the profit maximization of the supply chain system to avoid an uncoordinated situation; adjusting the contract parameters can improve the profits and system efficiency of all participants [22].

Therefore, more and more scholars have confirmed that supply chain contracts can coordinate the supply chain effectively [20,23].

2.2. Supply Chain Contracts

Pasternack [24], one of the earliest scholars to propose the concept of supply chain coordination, believed that appropriate contracts could coordinate the supply chain and provided some conceptual models of basic supply chain contracts, including revenue-sharing contracts, which provided a theoretical basis for subsequent supply chain research. Our study is based on previous research on coordinating supply chains through contracts in intensifying market uncertainty.

Corbett and De Groote [25] proposed that revenue-sharing mechanisms could effectively coordinate supply chains and improve efficiency through a comparative analysis of one-to-one and one-to-many structures in a two-tier supply chain system under a revenue-sharing contract. Dana and Spier [26] compared revenue-sharing and wholesale-price contracts in the supply chain, finding that revenue-sharing contracts are valuable tools for solving coordination problems caused by vertical separation, uncertain demand, and downstream competition. Hou et al. [27] studied a two-stage supply chain system affected by inventory levels on product delivery periods and found that using revenue-sharing contracts in a bargaining mode can achieve supply chain coordination. Zhang et al. [28] compared the impact of repurchase contracts and revenue-sharing contracts on the optimal decision making of companies, considering the opportunity cost of capital and supply chain performance. Du et al. [29] studied a two-stage supply chain system composed of two competing suppliers and a retailer, exploring non-cooperative games in a dual channel and finding that cooperation is only achievable under revenue-sharing contract coordination. Liu and Yan [30] analyzed a three-stage supply chain system in the electronics industry with recycling and reuse, finding that coordination through revenue-sharing contracts can achieve a win–win situation for all parties.

Revenue-sharing contracts are the most common means of supply chain coordination. Reviewing the existing literature on revenue-sharing contracts, we found that there is a lack of research incorporating behavioral factors into revenue-sharing contract mechanisms. From this perspective, our study aims to provide reference and insights for the field of supply chain contracts.

2.3. Loss Aversion

Simon [31] proposed the concept of “bounded rationality”, asserting that psychological factors influence decisions and judgments involving humans. Loss aversion has long been a focus in social sciences. Zhang et al. [32] proved that a supply chain system involving a loss-averse retailer can be coordinated through a buyback contract. Shen et al. [33] studied the newsvendor problem under a recourse option, considering loss aversion in spot price fluctuations, and compared the loss avoidance ordering behavior in this contract with the loss avoidance ordering behavior in wholesale price contracts. Ma et al. [34] established a loss-averse newsvendor model with two ordering opportunities and market information updating. Zhou et al. [35] analyzed order strategies with returns in supply chains involving loss-averse retailers, exploring changes in optimal order quantities under different loss aversion factors. Li et al. [36] considered a dual-channel supply chain consisting of a risk-neutral supplier and a risk-averse retailer and verified that the dual-channel supply chain could be coordinated by a similar improved risk-sharing contract. Vipin and Amit [37] show that loss aversion improves the rationality prediction of utility models and establishes coordination of a supply chain with a loss-averse retailer in the newsvendor under the recourse option. Zhu et al. [38] proposed a decision-making model considering the CVaR measure in the dual-channel supply chain. Bai et al. [39] constructed a two-stage supply chain comprising a single manufacturer and a single retailer and compared the revenue-sharing contract and the two-part tariff contract proposed to coordinate the manufacturer-led decentralized system, and found that the former cannot coordinate the supply chain, while the latter can do it only if the retailer is risk-averse. Zhang et al. [16] characterize coordinating contracts that result in Pareto-optimal actions in a setting of risk-averse agents.

Previous research has mainly focused on studying rational decision-makers and designing contracts for these decision-makers in different environments. The few studies on loss-averse supply chain coordination mainly focus on upstream loss-averse behavior, with less comparison between downstream and different loss aversion combination models. In this article, we focus on bounded rational decision-makers under revenue-sharing contracts to expand existing research. We summarize the contributions of our work compared to the related works in

Table 1. Gap between the existing literature and our research.

Paper	Supply Chain Coordination	Revenue-Sharing Contract	Loss-Averse Supplier	Loss-Averse Retailer	Optimal Wholesale Price	Optimal Order Quantity
Zhou et al. (2014) [35]	✓		✓	✓	✓
Hu et al. (2016) [7]	✓	✓		✓		✓
Li et al. (2016) [36]	✓			✓		✓
Liu et al. (2020) [15]	✓			✓		✓
Bai et al. (2020) [39]	✓	✓		✓	✓
Zhang et al. (2022) [16]	✓	✓	✓			✓
Liu et al. (2023) [13]	✓		✓			✓
Yi et al. (2023) [14]	✓			✓
This paper	✓	✓	✓	✓	✓	✓

.

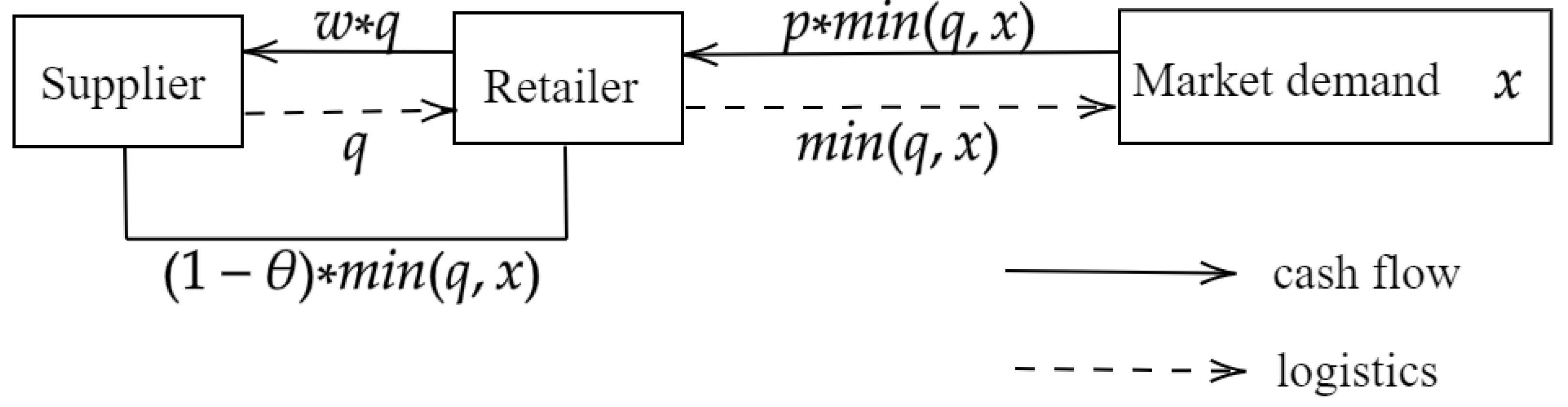
3. Benchmark Model

In the benchmark model, we construct a game model between a risk-neutral supplier and a risk-neutral retailer under a revenue-sharing contract. Meanwhile, we compare and analyze the results of centralized decision making and decentralized decision making. In the model the information about the product between manufacturers and retailers is set to be completely symmetrical. The market demand for products is x, which is a non-negative, continuous random variable with a cumulative distribution function $F\left(x\right)$ that is derivable and continuously increasing. When $x>0$, $F\left(x\right)>0,f\left(x\right)>0,F\left(0\right)>0$, and $F^{-1}\left(x\right)$ is the inverse function of $F\left(x\right)$, $\overline{F}\left(x\right)=1-F\left(x\right)$ [19,20,21]. The unit salvage value of unsold products in the supply chain is v. The retailer and the supplier make decisions simultaneously based on maximizing expected profits. According to Figure 1, the retailer decides the order quantity q from the supplier based on market demand before the period of sales. Meanwhile, the supplier makes two decisions, one is to make a production decision based on the order quantities of the retailer and the other is to sell products to the retailer at a wholesale price of w. After negotiations, the supplier and retailer sign a revenue-sharing contract, in which the retailer shares the portion $\varphi$$0<\varphi <1$ of the total sales revenue and gives the supplier a portion $1-\varphi$. When $q_r^{*}=q_{sc}^{*}$, it means that the contract can effectively coordinate the supply chain system, where $q_r^{*}$ represents the retailer’s order quantity and $q_{sc}^{*}$ represents the optimal order quantity of the supply chain. At this point, a Pareto improvement exists, ensuring that the profits of each party are at least not lower than those of uncoordinated cases.

The definitions of the symbols can be found in

Table 2. Definitions of symbols.

Symbol	Description
Parameters:
x	The market demand
$F\left(x\right)$	The cumulative distribution function of demand
$f\left(x\right)$	The probability density function of demand
c	Unit production cost of goods
p	Unit sales price of goods
v	Unit salvage value
$\varphi$	Revenue share for the retailer
${\lambda }_i$	Loss avoidance coefficient, i = r, s represents retailer, supplier, respectively
Decision variables:
w	Wholesale price per unit of goods
q	Order quantity of products
Revenue functions:
${\pi }_r$	The revenue of the retailer
${\pi }_s$	The revenue of the supplier
${\pi }_{sc}$	Total revenue of the supply chain

. The event sequence is shown in Figure 1.

Centralized and Decentralized Decision Models

In this subsection, according to the model description given above, we construct the profits function of the retailer and the supplier and the total. The expected profit for the retailers is

$${\pi }_r=\left(\varphi (p-v)\right)\ast S\left(q\right)-(w-\varphi v)q$$

(1)

In which the first part $\left(\varphi \right(p-v\left)\right)*S\left(q\right)$ represents the expected sales revenue of the retailer, and the second part $(w-\varphi v)q$ represents the cost that retailers pay to purchase products from suppliers under the revenue-sharing contract.

The expected profit for the supplier is

$${\pi }_s=(w+(1-\varphi )v-c)q+(1-\varphi )(p-v)S\left(q\right)$$

(2)

In which the first part $(w+(1-\varphi )v-c)q$ represents the net profit of the supplier from selling products, and the second part $(1-\varphi )(p-v)S\left(q\right)$ represents the profit sharing that the supplier receives from the retailer under the revenue-sharing contract.

Correspondingly, the expected profit for the supply chain is

$${\pi }_{sc}={\pi }_r+{\pi }_s=(p-v)S\left(q\right)-(c-v)q$$

(3)

In Equations (1)–(3), $S\left(q\right)={\int }_0^{q}xf\left(x\right)d\left(x\right)+{\int }_q^{\infty }qf\left(x\right)dx=Q-{\int }_0^{q}F\left(x\right)dx$ represents the sales volume equation of products. Solving the above optimization function, we obtain the following lemma.

Lemma 1.

A global optimal order quantity exists for the total profit of the supply chain, which maximizes the overall profit of the supply chain. At this time, the order quantity is

$$q_{sc}^{*}=F^{-1}\left(\frac{p-c}{p-v}\right)$$

(4)

In centralized decision making, each member aims to maximize the profit of the supply chain, which may be consistent with maximizing its revenue. Supply chain members can sign agreements based on the revenue-sharing contract mechanism, aligning their order quantity with the optimal order quantity of the supply chain so that supply chain coordination can be achieved. Next, we consider decentralized decision making, where the retailer is within reasonable limits and prioritizes self-profit. At this point, the order quantity decided by the retailer is the quantity that maximizes their profit, namely, $q_r^{*}=arg{max}_q\left[{\pi }_r\right]$. Solving the above optimization function, we obtain the following lemma.

Lemma 2.

(i) 

Under decentralized decision making, the retailer’s profit maximizes at an optimal order quantity,$q_r^{*}$. At this time, the order quantity is

$$q_r^{*}=F^{-1}\left(\frac{\varphi p-w}{\varphi (p-v)}\right)$$

(5)

(ii) 

When the supplier’s wholesale price $w^{*}=\varphi c$, the supply chain is coordinated under the revenue-sharing contract, i.e., $q_r^{*}=q_{sc}^{*}$.

According to Lemmas 1 and 2, we know that under the coordination of a revenue-sharing contract, the supplier often offers the retailer a wholesale price lower than the production cost ($\varphi \in (0,1)$). In compensation, the retailer shares a portion $(1-\varphi )$ of their total revenue with the supplier. Based on the optimal order quantity and wholesale price, we can obtain Proposition 1.

Proposition 1.

The optimal order quantity $q_{sc}^{*}$ for the supply chain decreases with the unit production cost c and increases with the sales price p; the retailer’s optimal order quantity $q_r^{*}$ increases with the revenue-sharing coefficient ϕ and the sales price p, but decreases with the wholesale price w.

When the wholesale price is high, the retailer reduces order size; conversely, when market conditions are favorable and the sales price or revenue-sharing coefficient increases, retailers increase order quantities.

4. Loss Aversion Model

In the benchmark model, we assume that both the supplier and the retailer are risk-neutral. However, decision-makers often exhibit loss aversion, especially when the economy is in a downturn. Therefore, we consider the loss-averse behavior of supply chain members in the model. We adjust the revenue-sharing contract model to study the supply chain coordination and outcomes under the influence of loss-averse behavior. Differing from previous studies that only considered a loss-averse supplier or retailer, we construct three game scenarios in the model to compare the impact of the revenue-sharing contract on loss avoidance among different members: a game model consisting of a risk-neutral supplier and a loss-averse retailer ($NA$); a game model consisting of a loss-averse supplier and a risk-neutral retailer ($AN$); and a game model consisting of a loss-averse supplier and a loss-averse retailer ($AA$). We compare the optimal order quantity of the retailer and the wholesale price of the supplier under different scenarios.

4.1. The NA Scenario

In the NA game scenario, we consider the risk-neutral supplier and the loss-averse retailer. First, we analyze the retailer’s optimal order quantity; then, by combining this with the centralized decision making optimal order quantity, we optimize and analyze the coordination of the supply chain under the revenue-sharing mechanism and the relationship between the retailer’s optimal order quantity and various parameters.

The retailer’s profit function is

$${\pi }_r=\{\begin{array}{c}\varphi (p-v)x+(w-\varphi v)q,x\le q\\ (\varphi p-w)q,x>q\end{array}$$

(6)

Based on this equation, the retailer’s break-even point is $x_r\left(q\right)=\frac{(w-\varphi v)}{\varphi (p-v)}q$, that is, the order quantity of the retailer meets the market demand. Correspondingly, the expected utility of the loss-averse retailer is

$${\tilde{\pi }}_r=(\varphi p-w)q-{\lambda }_r\varphi (p-v){\int }_0^{x_r\left(q\right)}F\left(x\right)dx-\varphi (p-v){\int }_{x_r\left(q\right)}^{q}F\left(x\right)dx$$

(7)

In the NA scenario, the supplier is risk-neutral, with their profit equation being as in (2). And the expected profit for the supply chain is

$$\begin{array}{ccc}\hfill {\tilde{\pi }}_{scr}& ={\tilde{\pi }}_r+{\pi }_s\hfill & \\ & =(p-c)q-(1-\Phi )(p-v){\int }_0^{q}F\left(x\right)dx-{\lambda }_r\varphi (p-v){\int }_0^{x_r\left(q\right)}F\left(x\right)dx\hfill \\ & -\varphi (p-v){\int }_{x_r\left(q\right)}^{q}F\left(x\right)dx\hfill \end{array}$$

Proposition 2.

Under the NA scenario, when using a revenue-sharing contract for coordination, we conclude that:

(i) 

Under decentralized decision making, there exists a unique optimal order quantity $q_r^{NA}$ that maximizes the expected profit of the loss-averse retailer, $q_r^{NA}=F^{-1}\left(\frac{\varphi p-w}{\varphi (p-v)}-\frac{\left({\lambda }_r-1\right)(w-\varphi v)}{\varphi (p-v)}F\left(x_r\left(q_r^{NA}\right)\right)\right)$. And $q_r^{NA}<q_r^{*}$ means the retailer’s optimal order quantity when loss-averse is lower than when risk-neutral.

(ii) 

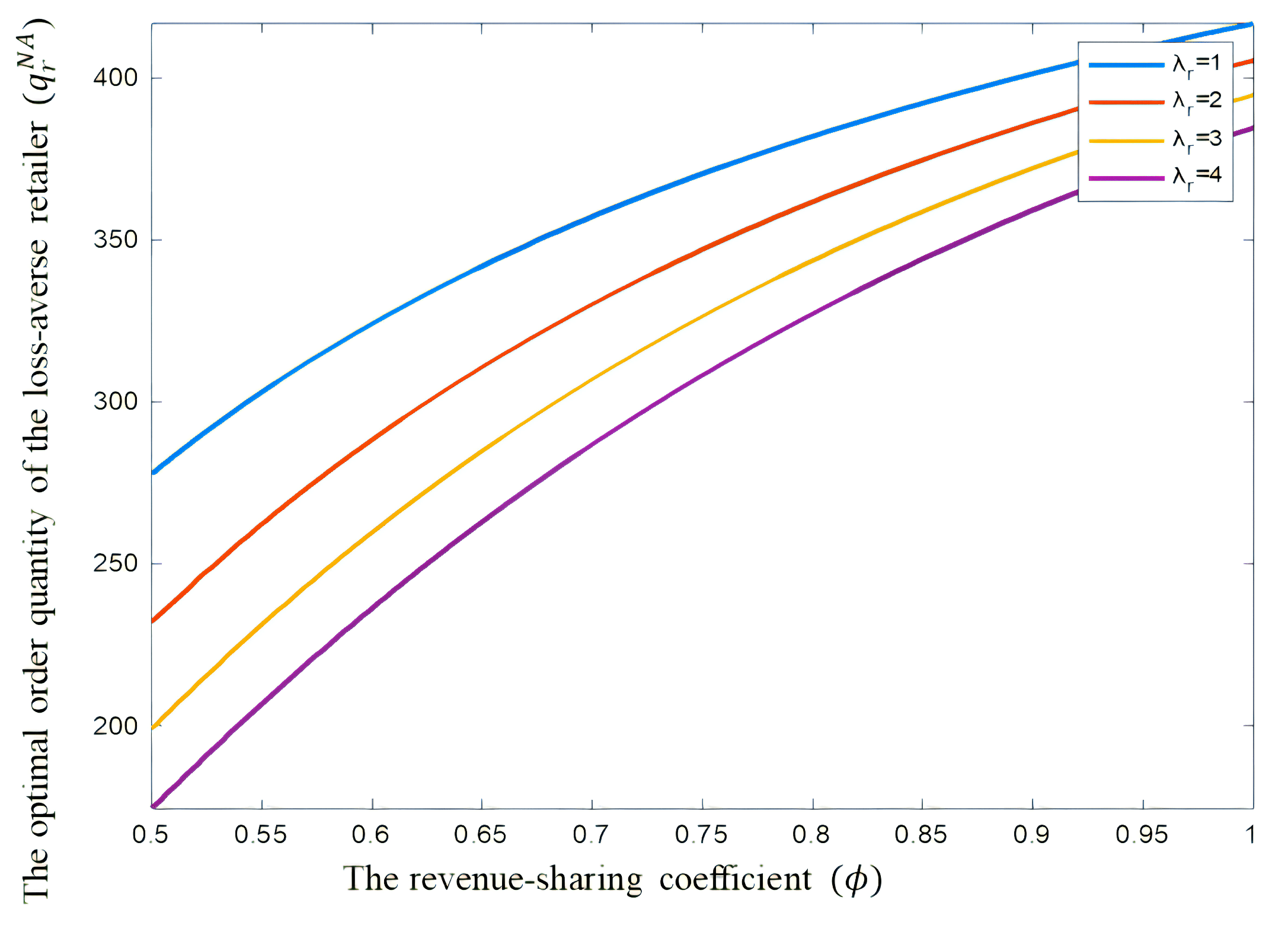
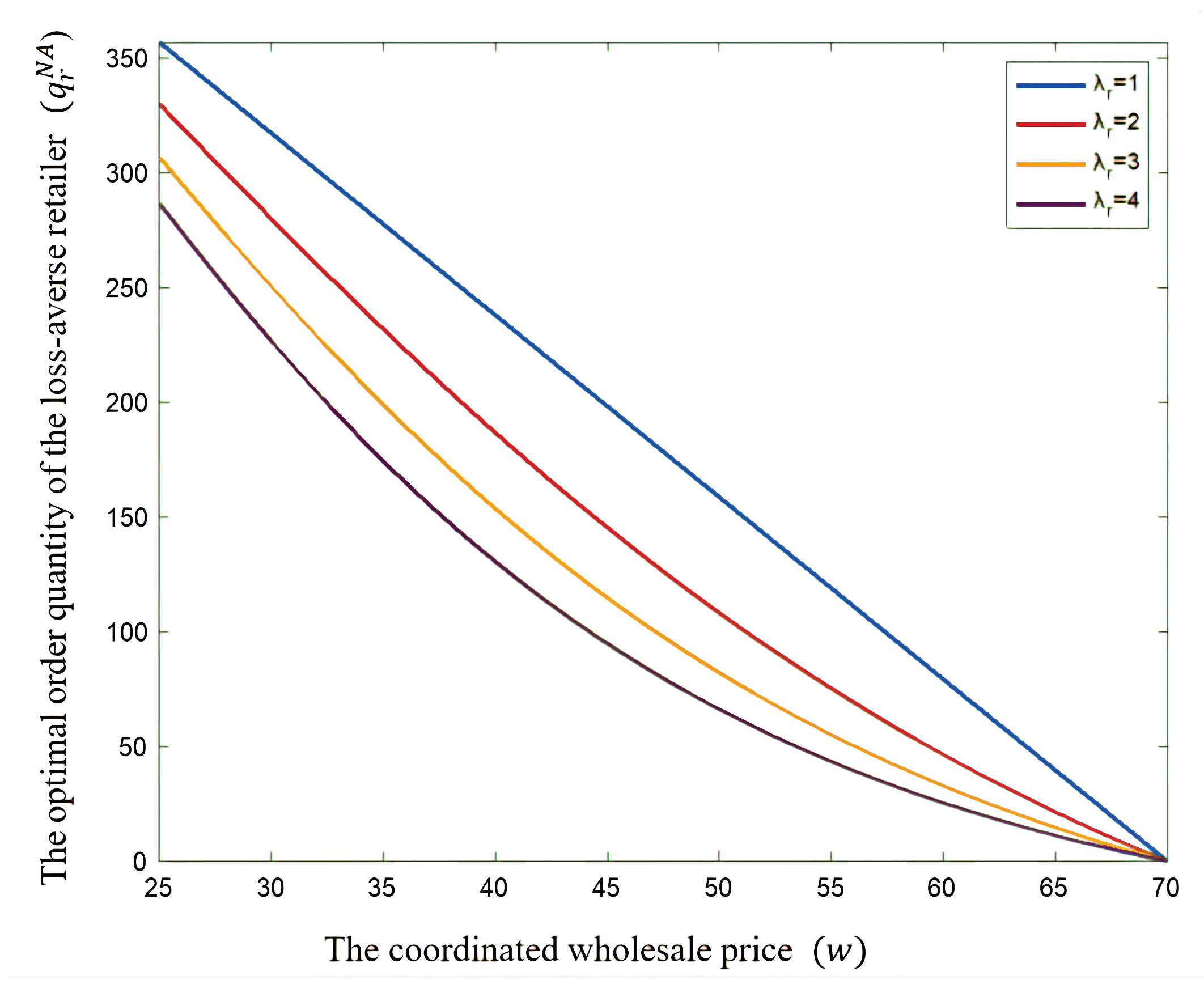
When ${\lambda }_r=1$, $q_r^{NA}=q_r^{*}=F^{-1}\left(\frac{\varphi p-w}{\varphi (p-v)}\right)$, meaning the loss-averse retailer’s optimal order quantity equals their risk-neutral optimal order quantity. Thus, when ${\lambda }_r>1$, it indicates the retailer’s loss-averse attitude, leading to a reduction in order quantity. The optimal order quantity $q_r^{NA}$ decreases with the supplier’s wholesale price w and the loss aversion coefficient ${\lambda }_r$ but increases with the revenue-sharing coefficient ϕ. In a revenue-sharing contract, the loss-averse retailer’s expected utility function ${\tilde{\pi }}_r$ decreases with the supplier’s wholesale price w and the loss aversion coefficient ${\lambda }_r$.

(iii) 

Under centralized decision making, the retailer’s optimal order quantity is $q_{sc}^{NA}=F^{-1}\left(\frac{p-c}{p-v}-\right.$ $\left.\frac{\left({\lambda }_r-1\right)(w-\varphi v)F\left(x_r\left(q_{sc}^{NA}\right)\right)}{p-v}\right)$.

(iv) 

The supply chain is coordinated when $w^{NA}$ and ${\varphi }^{NA}$ satisfy the set

$$\begin{array}{cc}\hfill w& =\varphi c-(1-\varphi )\left({\lambda }_r-1\right)(w-\varphi v)F\left(x_r(q_{sc}^{NA}\right),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill q_{sc}^{NA}& =F^{-1}\left(\frac{p-c}{p-v}-\frac{\left({\lambda }_r-1\right)(w-\varphi v)F\left(x_r\left(q_{sc}^{NA}\right)\right)}{p-v}\right);\hfill \end{array}$$

(9)

moreover, $w^{NA}<w^{*}$.

According to Proposition 2 (i), when the retailer perceives economic losses as having a greater negative impact, the revenue-sharing contract mechanism can still coordinate the supply. When the supplier raises the wholesale price to pursue higher profits, the utility of the retailer decreases, along with the marginal profit utility. The retailer takes on higher risk, and thus, appropriately reduces the order quantity. When the loss aversion coefficient increases, indicating the retailer has a greater concern about loss effects, they convey their loss aversion to the supply chain by reducing the order quantity, consequently reducing the profit of the supply chain. Thus, supply chain coordination is harder.

According to Proposition 2 (ii), when the supply chain reaches a coordinated state, the wholesale price will be lower than in a supply chain system with a risk-neutral retailer. Although the retailer’s risk-averse psychology does not cause supply chain imbalance, it reduces the order quantity, and under the same conditions, the coordinated wholesale price is lower than the risk-neutral supply chain system to stimulate the retailer to retain the order size.

Under decentralized equilibrium decision making, the order quantity increases with the revenue-sharing coefficient and decreases with the wholesale price and the loss aversion factor. When the revenue-sharing contract coordinates the supply chain, the retailer conveys their loss aversion to the supply chain by reducing the order quantity. The coordinated wholesale price decreases with the increase in the loss aversion coefficient. However, the retailer reducing the order quantity drives suppliers to increase wholesale prices to maximize profits. Regardless of how suppliers increase wholesale prices, under the revenue-sharing contract, the coordinated wholesale prices of the supply chain will be lower than those in the benchmark model. The revenue-sharing contract mechanism allows the supplier to offer a lower wholesale price, effectively bearing part of the retailer’s cost risk. In return, the retailer compensates the supplier with a larger portion of their revenue, and the lower wholesale price also encourages the retailer to order more products.

4.2. The AN Scenario

In the AN game scenario, we consider a loss-averse supplier and a risk-neutral retailer by observing and comparing the optimal order quantity under the decentralized and centralized model with the revenue-sharing contract. Then, we discuss whether the revenue-sharing coefficient and wholesale price can coordinate the supply chain. And we analyze the decision variable w and various coefficients under equilibrium decisions.

We assume that the retailer is risk-neutral, with their expected profit function as in (1). The profit function of the loss-averse supplier is

$${\pi }_s=\left\{\begin{array}{c}(w+(1-\varphi \left)v\right)q+(1-\varphi )(p-v)x-cq,x\le q\\ (w+(1-\varphi )p-c)q,x>q\end{array}\right.$$

(10)

The supplier’s break-even point is $x_s\left(q\right)=\frac{(c-w-(1-\varphi \left)v\right)}{(1-\varphi )(p-v)}q$, and the expected profit function of the loss-averse supplier is

$${\tilde{\pi }}_s=(w+(1-\varphi )p-c)q-{\lambda }_s(1-\varphi )(p-v){\int }_0^{x_s\left(q\right)}F\left(x\right)dx-(1-\varphi )(p-v){\int }_{x_s\left(q\right)}^{q}F\left(x\right)dx$$

(11)

The profit function of the supply chain is as follows:

$$\begin{array}{ccc}\hfill {\tilde{\pi }}_{scs}& ={\pi }_r+{\tilde{\pi }}_s\hfill & \\ & =(p-c)q-\varphi (p-v){\int }_0^{q}F\left(x\right)dx-{\lambda }_r(1-\varphi )(p-v){\int }_0^{x_s\left(q\right)}F\left(x\right)dx\hfill \\ & -(1-\varphi )(p-v){\int }_{x_s\left(q\right)}^{q}F\left(x\right)dx\hfill \end{array}$$

Proposition 3.

Under the AN scenario, adopting a revenue-sharing contract for coordinating the supply chain:

(i) 

Under centralized decision making, $q_{sc}^{AN}=F^{-1}\left(\frac{p-c}{p-v}-\frac{\left({\lambda }_s-1\right)(c-w-(1-\varphi )v)F\left(x_s\left(q_{sc}^{NA}\right)\right)}{p-v}\right)$; under decentralized decision making, $q_r^{AN}=F^{-1}\left(\frac{\varphi p-w}{\varphi (p-v)}\right)$.

(ii) 

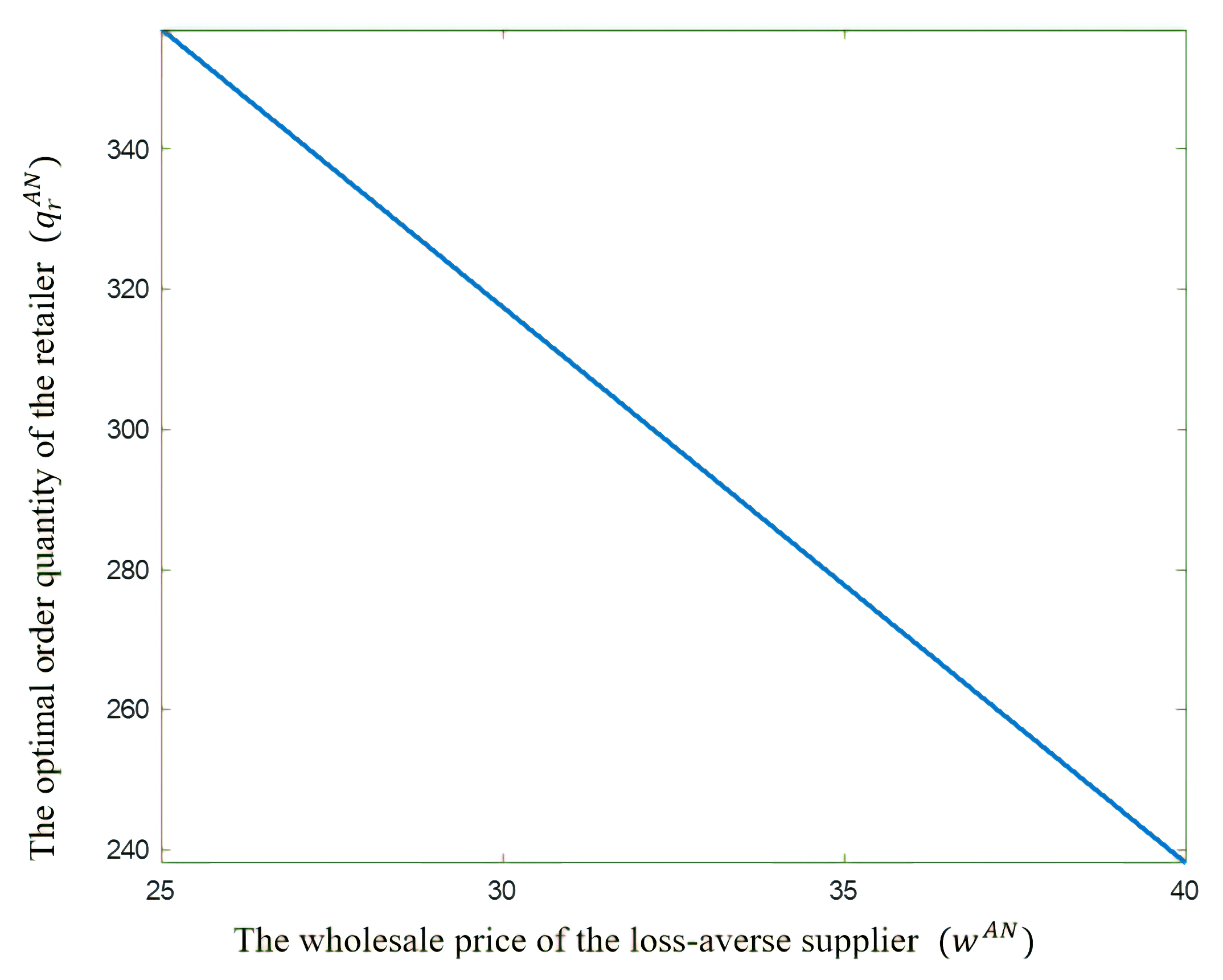
When ${\lambda }_s=1$, $q_{sc}^{AN}=F^{-1}\left(\frac{p-c}{p-v}\right),q_{sc}^{AN}=q_r^{*}$. When ${\lambda }_s>1$, it indicates the supplier is loss-averse, and thus, $q_{sc}^{AN}<q_r^{*},w^{AN}>w^{*}$.

(iii) 

Under decentralized decision making, the risk-neutral retailer’s optimal order quantity $q_r^{AN}$ decreases with the wholesale price w but increases with the revenue-sharing coefficient ϕ. When ϕ satisfies $q+\frac{(c-w)\left({\lambda }_s-1\right)x_s}{(1-\varphi )}\mathrm{F}\left(x_s\right)+(1-\varphi )(p-v)F\left(x\right)>{\lambda }_s(p-v){\int }_0^{x_s}F\left(x\right)dx+(p-v){\int }_{x_s}^{q}F\left(x\right)dx$, ${\tilde{\pi }}_s$ decreases with ϕ; otherwise, ${\tilde{\pi }}_s$ increases with ϕ.

(iv) 

The supply chain system can be effectively coordinated when $w^{AN}$ and ${\varphi }^{AN}$ satisfy the set

$$\begin{array}{cc}\hfill q_{sc}^{AN}& =F^{-1}\left(\frac{p-c}{p-v}-\frac{\left({\lambda }_s-1\right)(c-w-(1-\varphi )v)F\left(x_s\left(q_{sc}^{AN}\right)\right)}{p-v}\right),\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill w^{AN}& =\varphi c+\varphi \left({\lambda }_s-1\right)(c-w-(1-\varphi )v)F\left(x_s\left(q_{sc}^{AN}\right)\right).\hfill \end{array}$$

(13)

From Proposition 3, under the AN scenario, the revenue-sharing contract still can coordinate the supply chain. The loss-averse supplier conveys their loss aversion to the supply chain by offering a higher wholesale price than the coordinated wholesale price in the benchmark model. This leads to a reduction in the order quantity. This means that under contract coordination, the supplier undertakes the risk with the retailer due to upstream raw material instability or market risk being weakened, leading the retailer to reduce their order quantity to protect their profit.

Thus, if the supplier wants to keep the order quantity from the retailer, the supplier needs to overcome the impact of their loss aversion by lowering the wholesale price or offering a higher revenue-sharing coefficient to benefit the retailer. The more the supplier fears loss, the lower their expected profit, reducing the efficiency of supply chain operations. This disrupts the linear relationship between the expected profits of the supply chain members and the supply chain system. The expected profit of the loss-averse supplier decreases with an increase in the profit-sharing coefficient under certain conditions.

4.3. The AA Scenario

In the AA scenario, we assume that both the supplier and the retailer are risk-averse decision-makers. By comparing the optimal order quantity $q_r^{AA}$ under the decentralized model with the optimal order quantity $q_{sc}^{AA}$ under the centralized model, we analyze whether the revenue-sharing contract can still coordinate the supply chain.

When the supplier and retailer exhibit loss-averse behavior, the expected profit functions for the supplier and retailer are, respectively,

$${\tilde{\pi }}_s=(w+(1-\varphi )p-c)q-{\lambda }_s(1-\varphi )(p-v){\int }_0^{x_s\left(q\right)}F\left(x\right)dx-(1-\varphi )(p-v){\int }_{x_s\left(q\right)}^{q}F\left(x\right)dx$$

(14)

$${\tilde{\pi }}_r=(\varphi p-w)q-{\lambda }_r\varphi (p-v){\int }_0^{x_r\left(q\right)}F\left(x\right)dx-\varphi (p-v){\int }_{x_r\left(q\right)}^{q}F\left(x\right)dx$$

(15)

Expected profit of the loss-averse supply chain system:

$$\begin{array}{ccc}\hfill {\tilde{\pi }}_{sca}& ={\tilde{\pi }}_s+{\tilde{\pi }}_r\hfill & \\ & =(p-c)q-{\lambda }_r\varphi (p-v){\int }_0^{x_r\left(q\right)}F\left(x\right)dx-\Phi (p-v){\int }_{x_r\left(q\right)}^{q}F\left(x\right)dx\hfill \\ & -{\lambda }_s(1-\varphi )(p-v){\int }_0^{x_s\left(q\right)}F\left(x\right)dx-(1-\varphi )(p-v){\int }_{x_s\left(q\right)}^{q}F\left(x\right)dx\hfill \end{array}$$

Proposition 4.

Under the AA, we can conclude that:

(i) 

Under decentralized decision making, $q_r^{AA}=F^{-1}\left(\frac{\varphi p-w}{\varphi (p-v)}-\frac{\left({\lambda }_r-1\right)(w-\varphi v)}{\varphi (p-v)}F\left(x_r\left(q_r^{AA}\right)\right)\right)$; under centralized decision making,

$q_{sc}^{AA}=F^{-1}\left(\frac{p-c}{p-v}-\frac{\left({\lambda }_s-1\right)(c-w-(1-\varphi )v)F\left(x_s\left(q_{sc}^{AA}\right)\right)}{p-v}-\frac{\left({\lambda }_r-1\right)(w-\varphi v)F\left(x_r\left(q_{sc}^{AA}\right)\right)}{p-v}\right)$.

(ii) 

When ${\lambda }_s\ge 1+\left({\lambda }_r-1\right)\frac{\left(F\left(x_r\right)+x_{r}f\left(x_r\right)\right)}{\left(F\left(x_s\right)+x_{s}f\left(x_s\right)\right)}$, the optimal order quantity $q_{sc}^{AA}$ increases with the supplier’s wholesale price w; otherwise, it is negatively correlated.

(iii) 

When ${\lambda }_s>1+\left({\lambda }_r-1\right)\frac{\left(vF\left(x_r\right)+x_{r}f\left(x_r\right)\frac{w(p-v)}{\varphi }\right)}{\left(vF\left(x_s\right)+x_{s}f\left(x_s\right)\frac{(c-w)(p-v)}{1-\varphi }\right)}$, $q_{sc}^{AA}$ decreases with the revenue-sharing coefficient ϕ; otherwise, $q_{sc}^{AA}$ increases with the revenue-sharing coefficient ϕ.

(iv) 

The supply chain is coordinated if $w^{AA}$ and ${\varphi }^{AA}$ satisfy the set

$$\begin{array}{c}\hfill F\left(q_{sc}^{AA}\right)=\frac{p-c}{p-v}-\frac{\left({\lambda }_s-1\right)(c-w-(1-\varphi )v)F\left(x_s\left(q_{sc}^{AA}\right)\right)}{p-v}-\frac{\left({\lambda }_r-1\right)(w-\varphi v)F\left(x_r\left(q_{sc}^{AA}\right)\right)}{p-v};\end{array}$$

(16)

$$\begin{array}{c}\hfill w=\varphi c+\varphi \left({\lambda }_s-1\right)(c-w-(1-\varphi )v)F\left(x_s\left(q_{sc}^{AA}\right)\right)-(1-\varphi )\left({\lambda }_r-1\right)(w^{AA}-\varphi v)F\left(x_r\left(q_{sc}^{AA}\right)\right).\end{array}$$

(17)

Proposition 4 indicates that revenue-sharing contracts can still coordinate the supply chain when both suppliers and retailers are loss-averse. When the loss aversion factor is relatively high, the optimal order quantity decreases with the revenue-sharing coefficient.

5. Comparison and Sensitivity Analysis

5.1. Comparison

Comparing the NA, AN, and AA game scenarios, although the loss-averse behaviors of the supplier and retailer have different impacts on the supply chain, the results show that the revenue-sharing contract can still coordinate the supply chain.

Proposition 5.

Under a revenue-sharing contract, comparing the NA, AN, and AA game scenarios and benchmark model, we can obtain:

(i) 

The optimal wholesale price satisfies the relationship

$\begin{array}{l}{\lambda }_r\ge 1+\frac{\left({\lambda }_s-1\right)\left(c-w^{AA}-(1-\varphi )v\right)F\left(x_s\left(q_{sc}^{AA}\right)\right)}{(1-\varphi )\left(w^{AA}-\varphi v\right)F\left(x_r\left(q_{sc}^{AA}\right)\right)},w^{AN}>w^{*}>w^{AA}>w^{NA};\\ 1<{\lambda }_r<1+\frac{\left({\lambda }_s-1\right)\left(c-w^{AA}-(1-\varphi )v\right)F\left(x_s\left(q_{sc}^{AA}\right)\right)}{(1-\varphi )\left(w^{AA}-\varphi v\right)F\left(x_r\left(q_{sc}^{AA}\right)\right)},w^{AN}>w^{AA}>w^{*}>w^{NA}.\end{array}$

(ii) 

The optimal order quantity the relationship

$\begin{array}{l}{\lambda }_r>1+\frac{\left({\lambda }_s-1\right)\left(c-w^{AN}-(1-\varphi )v\right)F\left(x_s\left(q_{sc}^{AN}\right)\right)}{\left(w^{NA}-\varphi v\right)F\left(x_s\left(q_{sc}^{NA}\right)\right)},q_{sc}^{*}>q_{sc}^{AN}>q_{sc}^{NA}>q_{sc}^{AA};\\ 1<{\lambda }_r\le 1+\frac{\left({\lambda }_s-1\right)\left(c-w^{AN}-(1-\varphi )v\right)F\left(x_s\left(q_{sc}^{AN}\right)\right)}{\left(w^{NA}-\varphi v\right)F\left(x_s\left(q_{sc}^{NA}\right)\right)},q_{sc}^{*}>q_{sc}^{NA}>q_{sc}^{AN}>q_{sc}^{AA}.\end{array}$

The commonality of the three supply chain revenue-sharing contract models with different member loss avoidance behaviors is that the coordination goal of the three models is to make the revenue of retailers under decentralized decision making equal to that under centralized decision making. The risk-neutral supply chain always reduces the order quantity. The optimal order quantity under the risk-neutral supply chain is always higher than that under the risk-averse supply chain. When the retailer’s risk aversion level is high, the optimal order quantity in the supply chain with the risk-averse retailer is higher than that with the risk-averse supplier. Since the retailer burdens more risk in the supply chain, the supplier charges the lowest wholesale price under the supply chain with the risk-averse retailer but charges the highest wholesale price under the supply chain with the risk-averse supplier. When the retailer’s risk-averse level is low, the supplier charges a higher wholesale price under the risk-averse supply chain than that under the risk-neutral supply chain. However, if the retailer’s risk aversion level is high enough (${\lambda }_r\ge 1+\frac{\left({\lambda }_s-1\right)\left(c-w^{AA}-(1-\varphi )v\right)F\left(x_s\left(q_{sc}^{AA}\right)\right)}{(1-\varphi )\left(w^{AA}-\varphi v\right)F\left(x_r\left(q_{sc}^{AA}\right)\right)}$), the supplier should charge a lower price to stimulate the retailer under the risk-averse supply chain to retain the order quantity to maintain the profit.

5.2. Numerical Analysis in the NA Scenario

In this section, we conduct a numerical study to illustrate the theoretical results discussed above and further analyze the effects of some key parameters. Referring to [7,39,40], we assume that the product market demand X follows a uniform distribution $U(0,500)$, the unit production cost is $c=40$, the market selling price per unit is $p=100$, the revenue-sharing coefficient in the contract is $\varphi =0.7$, and the residual value per unit product is $v=10$. When the retailer and the supplier both are risk-neutral and make decisions simultaneously, the optimal wholesale price under the coordination of the revenue-sharing contract is $w^{*}=28$. The following will analyze the impact of the loss aversion factor on the optimal decisions and profits of members under the NA and AN game scenarios.

When the retailer is loss-averse, if the unit wholesale price remains at $w^{*}=28$, the revenue-sharing contract cannot coordinate the supply chain. Therefore, based on Proposition 2, we set the unit wholesale price as $w^{MA}=25$, at which point the optimal order quantity under decentralization equals that under centralization. With the coordinated wholesale price unchanged, we observe how optimal decisions and profits in the centralized model change when the loss aversion factor of the retailer ${\lambda }_r$ varies from 1 to 4, as shown in

Table 3. The impact of the loss avoidance factor ${\lambda }_r$ on optimal order quantity and profit.

${\mathit{\lambda }}_{\mathit{r}}$	${\mathit{q}}_{\mathit{r}}^{\mathbf{NA}}$	${\mathit{q}}_{\mathbf{sc}}^{\mathbf{NA}}$	${\tilde{\mathit{\pi }}}_{\mathit{r}}$	${\mathit{\pi }}_{\mathit{s}}$	${\mathit{\pi }}_{\mathit{s}}\mathit{c}$
1	330	330	16,090.7	5337.8	21,428.5
2	307	307	14,854	4935	19,758
3	286	286	13,806	4581	18,387
4	269	269	12,894.3	4291.4	17,170.7

.

From Table 3, it is evident that as the loss aversion coefficient of the retailer ${\lambda }_r$ increases, both the retailer’s optimal order quantity $q_s{c}^{NA}$ under the centralization and the retailer’s optimal order quantity $q_r^{NA}$ under the decentralization decrease with the rise in the loss aversion coefficient. However, the optimal order quantities for retailers under centralized and decentralized decision making are equal with the coordination of the revenue-sharing contract. And the profits of all supply chain members diminish as the loss factor of the retailer increases. To more intuitively observe the changes, we set different loss aversion coefficients to compare the relationship between the corresponding order quantity, allocation coefficient $\varphi$, and the wholesale price $w^{NA}$. We illustrate the change in supply chain members’ profits with the variation in the retailer’s loss aversion coefficient ${\lambda }_r$ in Figure 2, Figure 3 and Figure 4.

In Figure 2, we describe the relationship between the retailer’s optimal order quantity $q_r^{*}$ and the revenue-sharing coefficient $\varphi$ at different loss aversion coefficients ${\lambda }_r$. We observe that the retailer’s order quantity increases with the revenue-sharing coefficient. When the loss aversion coefficient increases, if retailers want to maintain their optimal order quantity, they need a higher revenue-sharing coefficient; similarly, if the revenue-sharing coefficient is stable, then as the loss aversion increases, the order quantity will decrease.

In Figure 3, we show the relationship between the equilibrium order quantity and equilibrium wholesale price under the retailer’s loss aversion coefficient. From the figure, it is clear that the wholesale price increases as the order quantity decreases; this is not affected by changes in loss aversion factors. When the wholesale price remains constant, as the loss aversion coefficient increases, the retailer’s optimal order quantity becomes lower; similarly, when the retailer’s optimal order quantity remains unchanged, and the loss aversion coefficient increases, the wholesale price correspondingly decreases.

From Figure 4, it is evident that the revenue of each member in the supply chain and the supply chain system decreases as the retailer’s loss aversion coefficient increases. The retailer’s expected revenue decreases at the fastest rate, followed by the supply chain system, and the expected revenue of the supplier decreases the slowest. The rate of change of these profit curves also slows down as the loss aversion coefficient increases. Since the total profit of the system equals the sum of both profits, we find that as the retailer’s loss aversion behavior increases, the retailer’s expected revenue occupies a smaller proportion of the total system revenue.

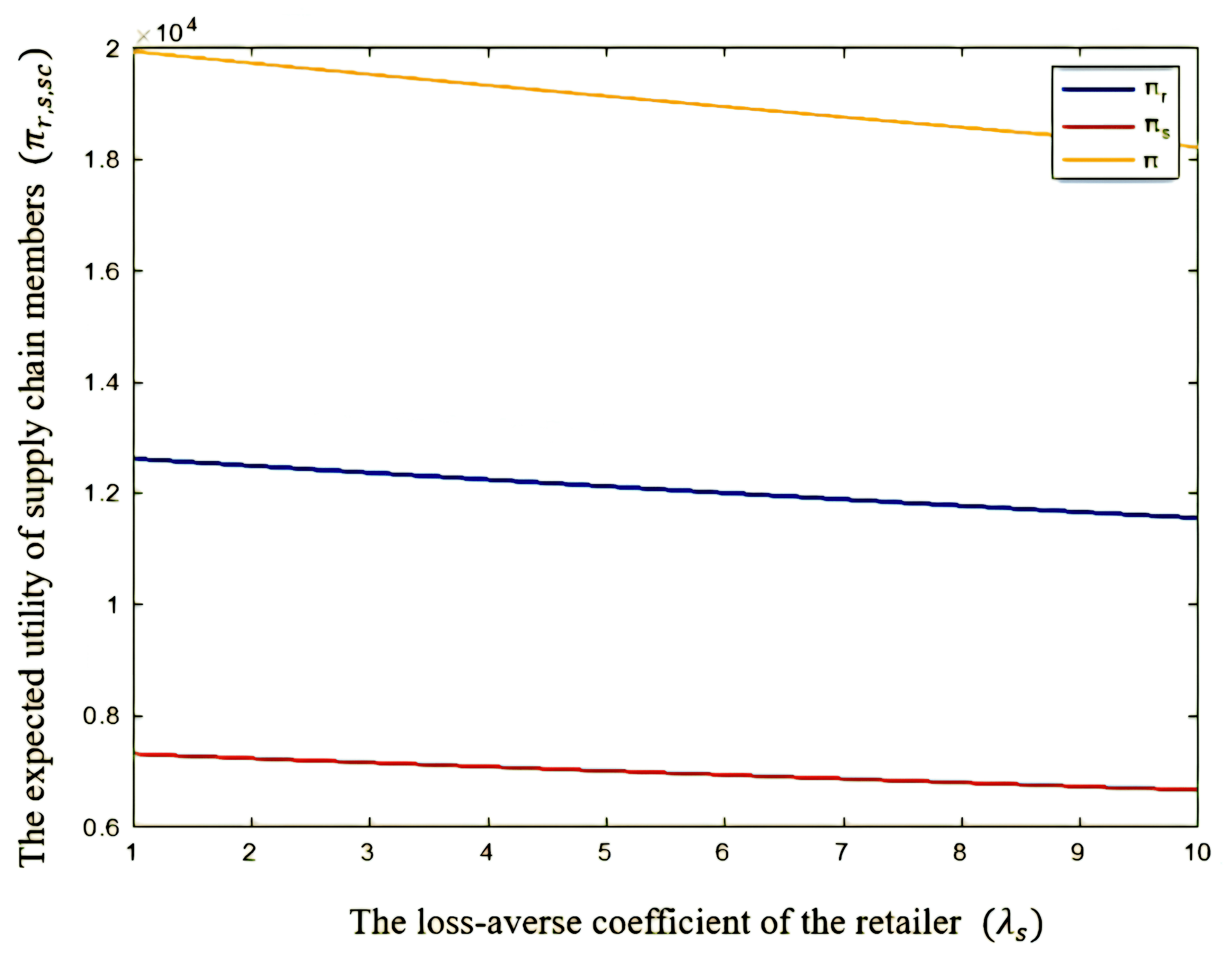
5.3. Numerical Analysis in the AN Scenario

In this section, as in the numerical analysis of the NA scenario, we refer to [7,39,40] and set the supplier’s wholesale price at $w^{AN}=29$; the other parameters are as shown in

Table 4. Impact of the loss avoidance factor ${\lambda }_s$ on optimal order quantity and profit.

${\mathit{\lambda }}_{\mathit{s}}$	${\mathit{q}}_{\mathit{r}}^{\mathbf{AN}}$	${\mathit{q}}_{\mathbf{sc}}^{\mathbf{AN}}$	${\tilde{\mathit{\pi }}}_{\mathit{r}}$	${\mathit{\pi }}_{\mathit{s}}$	${\mathit{\pi }}_{\mathit{s}}\mathit{c}$
1	317	317	7331.1	12,781.6	20,112.7
2	302	302	7185.4	12,437.6	19,623
3	284	284	7024.1	12,174.6	19,198.7
4	263	263	6890.3	11,940.8	18,831.1

.

From Table 4, it is observed that the retailer’s order quantity under decentralization and centralization decreases is equal and decreases with the increase in the supplier’s loss aversion coefficient when the wholesale price is constant. The expected revenue of all system members diminishes as the supplier’s loss aversion increases. To delve deeper into the relationship between the supplier’s loss aversion factor and the retailer’s order quantity, we analyzed the relationship between the risk-neutral retailer’s optimal order quantity in a decentralized decision-making model and the revenue-sharing coefficient, as well as the wholesale price, along with the curve of how the system members’ expected revenue varies with the supplier’s loss aversion coefficient, as shown in Figure 5, Figure 6 and Figure 7.

As shown in Figure 5, in a supply chain system with a loss-averse supplier and a risk-neutral retailer, members make decisions simultaneously under the decentralized model. The relationship between risk-neutral retailer’s optimal order quantity and the revenue-sharing coefficient is positive. The relationship between a risk-neutral retailer’s optimal order quantity and the wholesale price of the loss-averse supplier is negative. Compared with $w^{AN}$, we find that when there is a revenue contract in the supply chain, the coordinated wholesale price $w^{*}$ is an increasing function of the supplier’s loss aversion coefficient and a decreasing function of the revenue-sharing coefficient. If the revenue-sharing coefficient remains constant and the supplier’s loss aversion coefficient increases, the coordinated wholesale price also increases, leading to a decrease in the retailer’s order quantity.

From Figure 7, we notice that as the supplier’s loss aversion coefficient increases, the expected revenue of all members in the system gradually decreases. Therefore, we can conclude that in a supply chain composed of a loss-averse supplier and a risk-neutral retailer, the system can still be effectively coordinated by the revenue-sharing contract. In decentralization, the risk-neutral retailer’s order quantity is not affected by the supplier’s loss aversion factor. After the revenue-sharing contract coordinates the supply chain, the relationship between the retailer’s order quantity, the revenue-sharing coefficient, and the wholesale price remains unchanged, while the supplier conveys their loss aversion to the system by raising the wholesale price. At this time, the ability of the revenue-sharing contract to assume downstream risk is weakened, leading the retailer to reduce their order quantity in pursuit of maximum utility, thereby verifying the conclusion of Proposition 3.

6. Conclusions

6.1. Results Summary

Through the above analysis, we can conclude that revenue-sharing contracts effectively mitigate the risks brought to supply chain members during economic operations, making the study of revenue-sharing contracts under loss aversion factors practically significant. Based on [7,15], we also considered the scenario of loss-averse suppliers in the supply chain.

We study the risk-averse two-stage supply chain coordination in a revenue-sharing contract under three different scenarios: the supplier is risk-averse and the retailer is risk-neutral, or the retailer is risk-averse and the supplier is risk-neutral, or both are risk-averse. Therefore, we can answer the questions in Section 1. Firstly, we found that the revenue-sharing contract can always coordinate the supply chain under the three different scenarios through the revenue-sharing coefficient. Secondly, the optimal wholesale price of the supplier in a supply chain system with a risk-neutral supplier and a loss-averse retailer under a revenue-sharing contract is always lower than those of suppliers in a supply chain system with a loss-averse supplier and risk-neutral retailers under a revenue-sharing contract, regardless of risk factors. Thirdly, in a supply chain system with a loss-averse supplier and a loss-averse retailer under a revenue-sharing contract, regardless of risk factors, the optimal order quantity of retailers is always the lowest in the three game scenarios. Meanwhile, as the loss factor increases, the optimal order quantity of the retailer in the supply chain with the loss-averse supplier and the risk-neutral retailer will gradually exceed that of the retailer in the supply chain composed of the risk-neutral supplier and the loss-averse retailer under the revenue-sharing contract. Finally, the revenue-sharing coefficient increase can stimulate retailers to order more products and reduce the impact of loss aversion on retailers. When the loss aversion coefficient increases, retailers will reduce the order quantity to protect their revenue, resulting in the expected utility of all members and a supply chain system decrease.

The theoretical and numerical results yield the above observations, which highlight the contributions of this work. We extended the equilibrium analysis between the loss-averse retailer and the loss-averse supplier and the research on risk appetite in supply chain management, and fully explored the impact of loss aversion behavior on revenue-sharing contracts.

6.2. Managerial Implications

Based on the above, we provide the following practical recommendations. At first, the loss-averse behavior of supply chain members will increase operating costs. Therefore, recognizing one’s own and other members’ loss-averse characteristics is vital in guiding practical decisions effectively. Secondly, revenue-sharing contracts can effectively improve the impact of loss aversion. Therefore, enhancing the application and rational selection of supply chain contracts is imperative. Thirdly, it enhances the accuracy of information transmission between enterprises and promotes information sharing. As seen from the analysis of the two-tier loss aversion supply chain system, when members exhibit loss-averse characteristics, they express their loss aversion through certain behaviors, and accurate decision making can only occur when the corresponding party has this risk attitude. Enhancing information accuracy can be achieved through information sharing, joint market forecasting, ensuring the authenticity and effectiveness of transmitted information, etc. Accurate communication helps enterprises to avoid more potential risks and improve the operational efficiency of the supply chain system. Finally, companies can adopt big data analysis to predict the loss aversion behavior of upstream and downstream enterprises and take preventive measures in time. And can establish a decentralized trust mechanism among system members through blockchain technology, enhancing the traceability and transparency of the system.

6.3. Limitations and Further Study

While this work adds to the growing literature on supply chain management by integrating risk preferences into the models in a fuzzy environment, there are also certain limitations due to some assumptions. Firstly, to simplify calculations, we only considered the situation of a single supplier and retailer in the supply chain. Reality will be more complex than this. Secondly, loss avoidance can not only be introduced into the supply chain system based on prospect theory but also through the methods of the“CVaR value” and “mean variance”; the behavioral factors are multifaceted. This article only introduces loss avoidance as a reference factor, without discussing the impact of others. Thirdly, this article only analyzes the impact of loss avoidance behavior factors on members’ expected utility and balanced decision making, without establishing the prevention and correction mechanisms for the systemic damage caused by loss avoidance. Based on the above limitations, we can expand in the following areas in the future.

• Considering more complex network-like supply chain structures.
• Comparing the impact of different loss avoidance methods on the supply chain system, other behavioral and preference factors can also be added to separately or jointly affect the revenue-sharing contract mechanism.
• Developing effective measures to address the loss avoidance behavior of enterprises, guiding system members to make optimal decisions.