Influence of Homo- and Hetero-Junctions on the Propagation Characteristics of Love Waves in a Piezoelectric Semiconductor Semi-Infinite Medium
Abstract
:1. Introduction
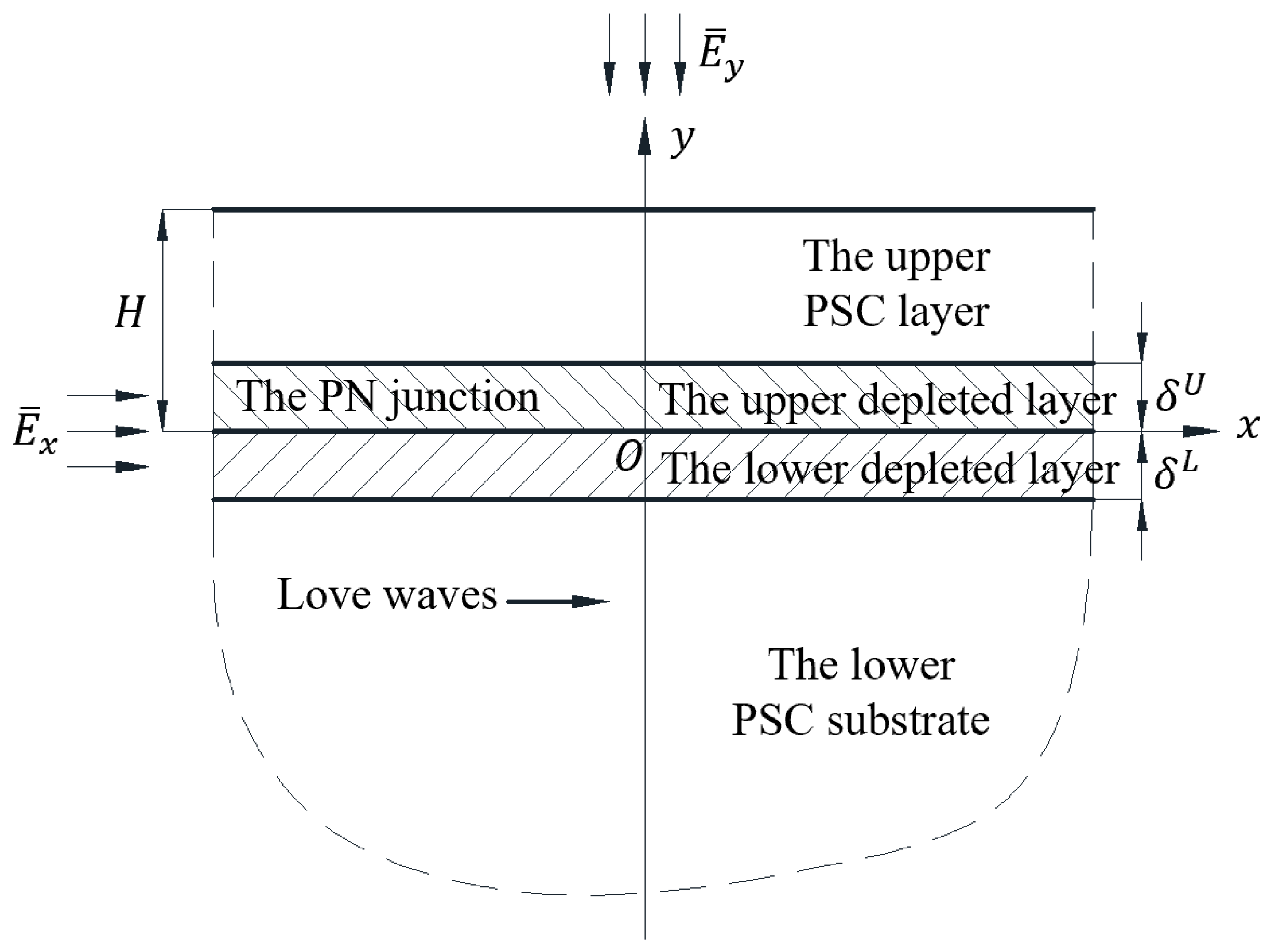
2. Problem Formulation and Basic Equations
3. The First Equivalent Mathematical Model
4. The Second Equivalent Mathematical Model
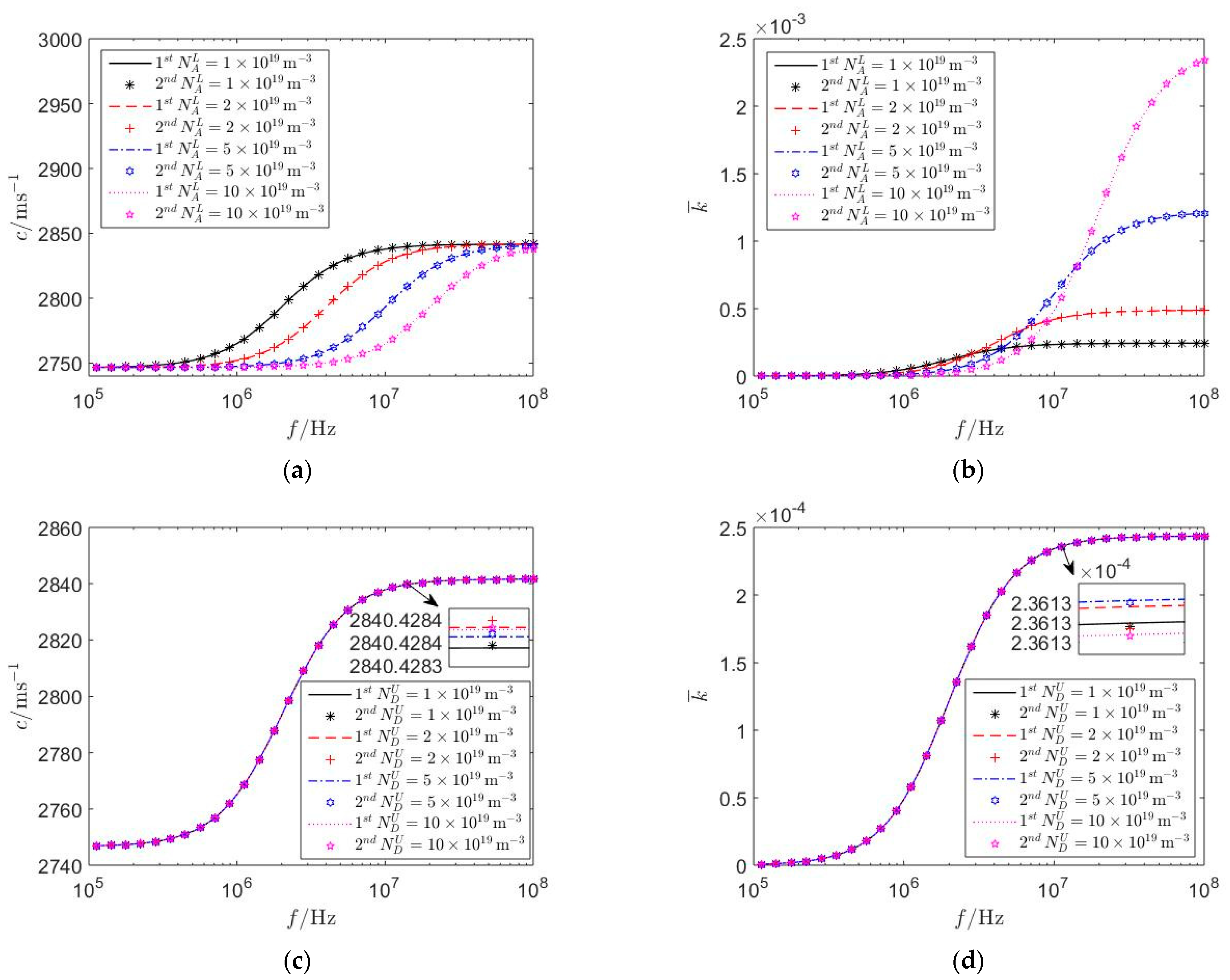
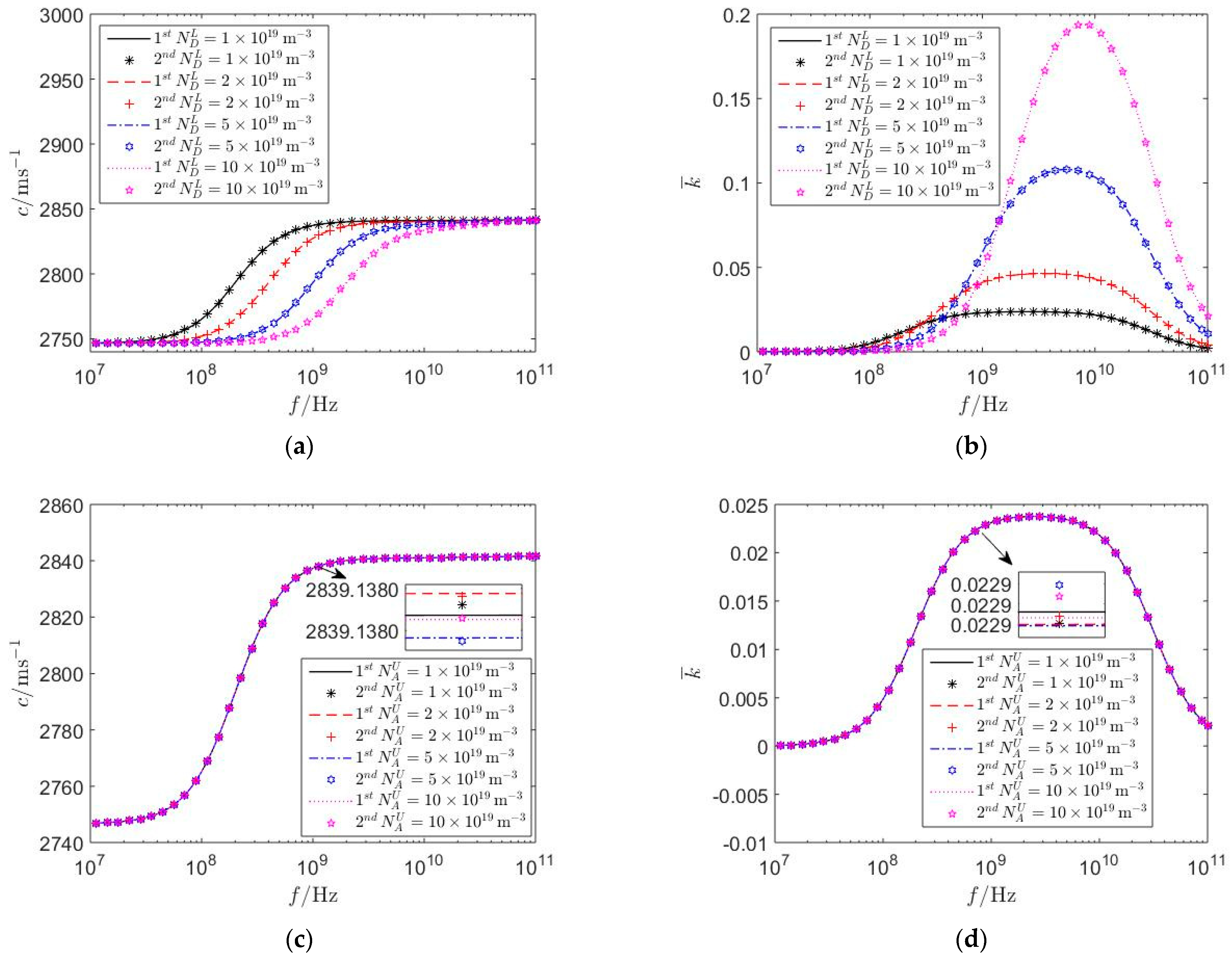
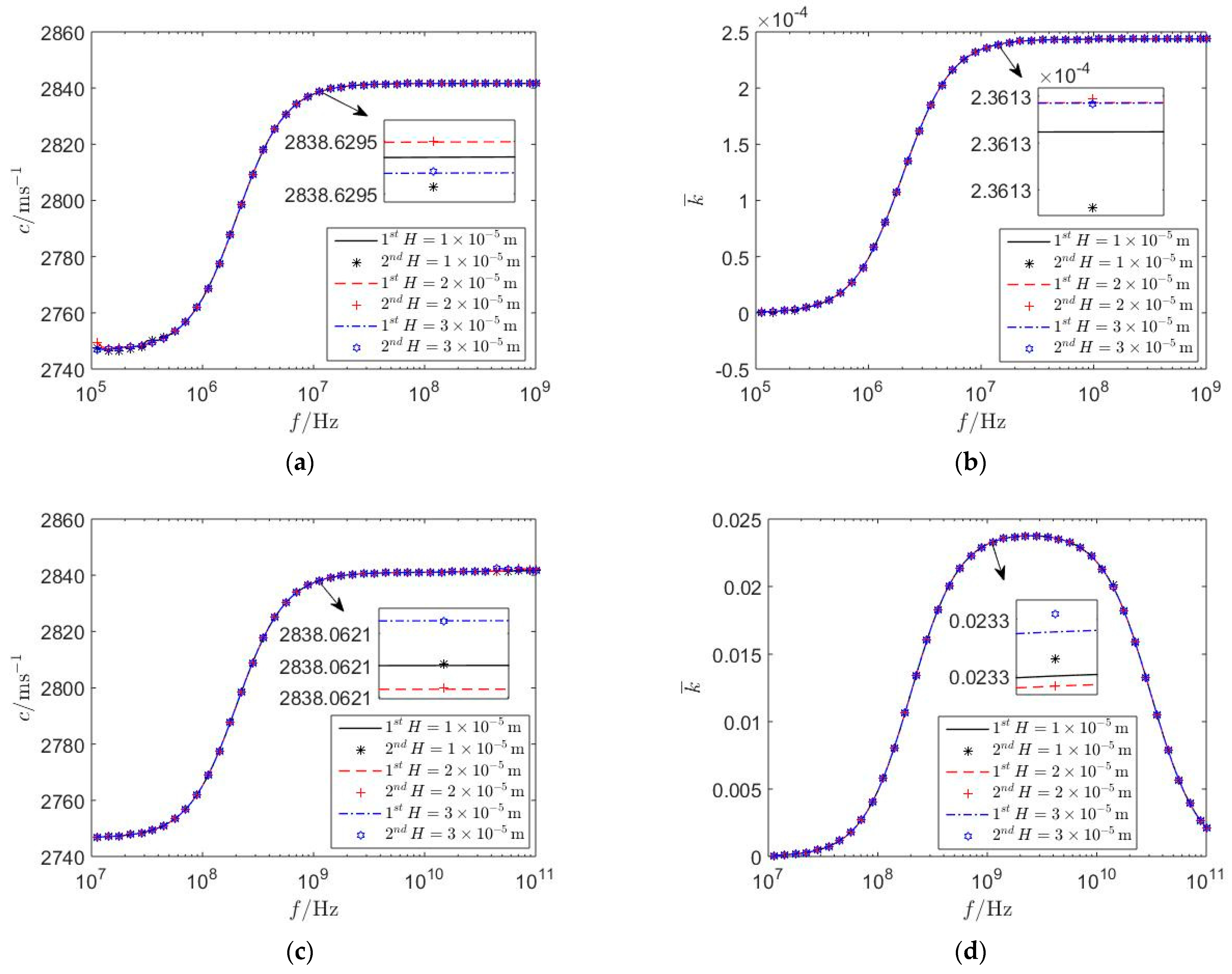
5. Numerical Results and Discussion
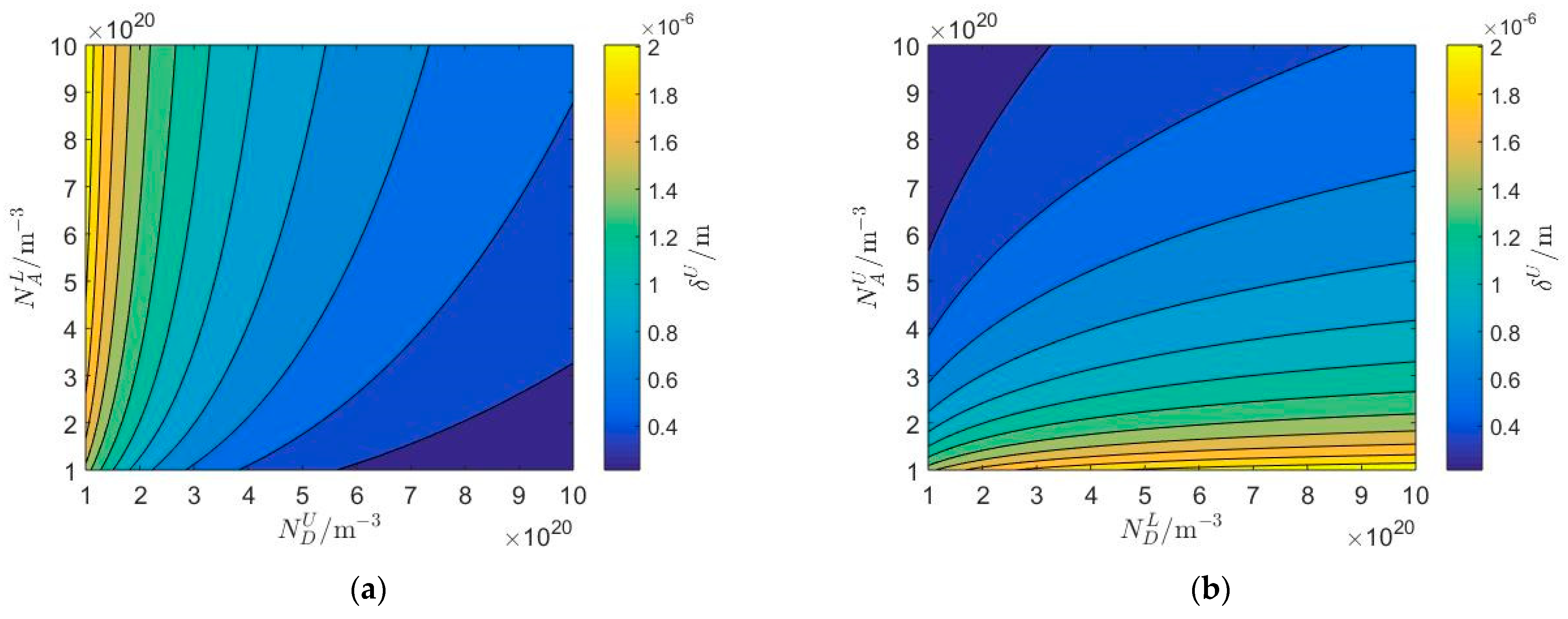
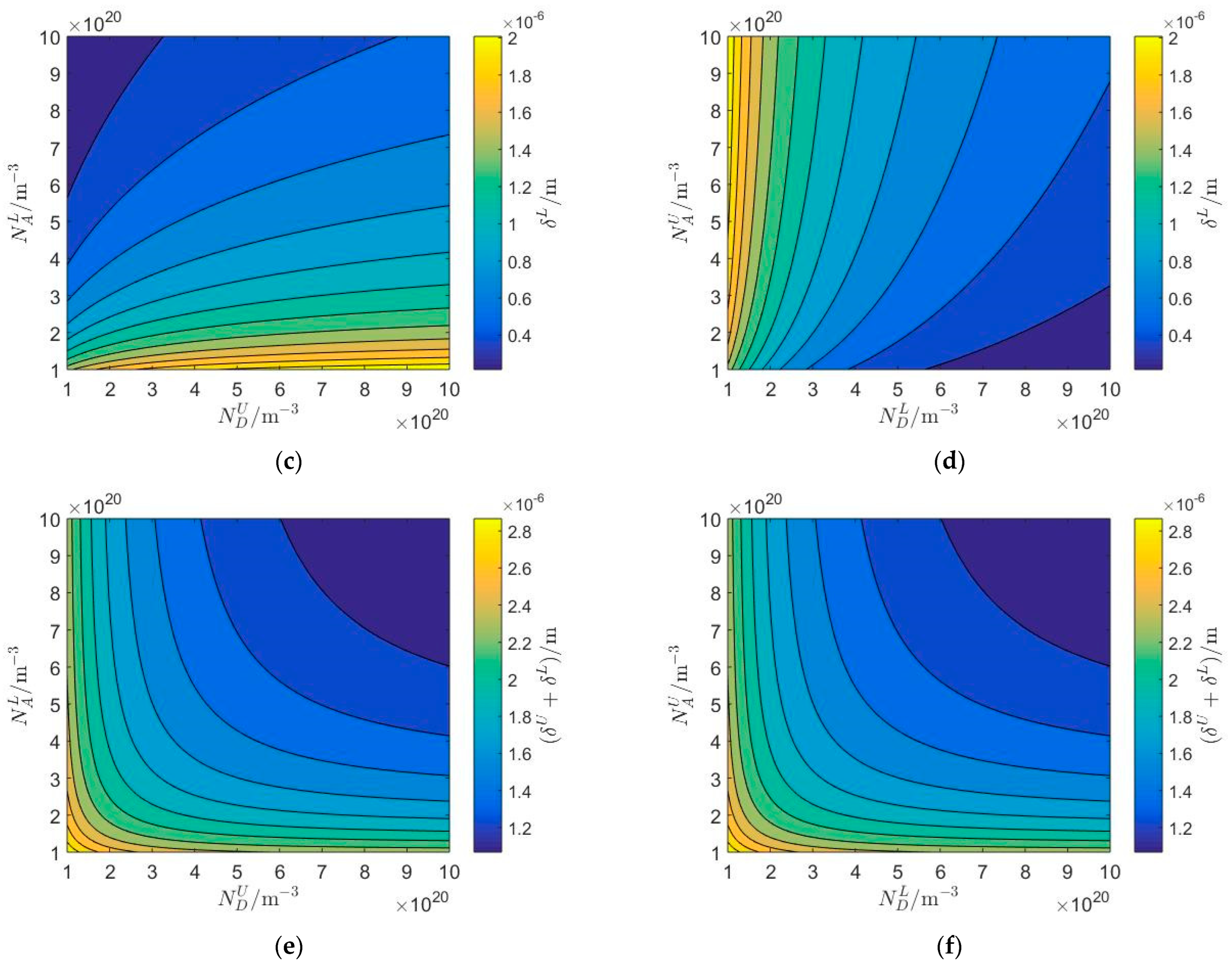
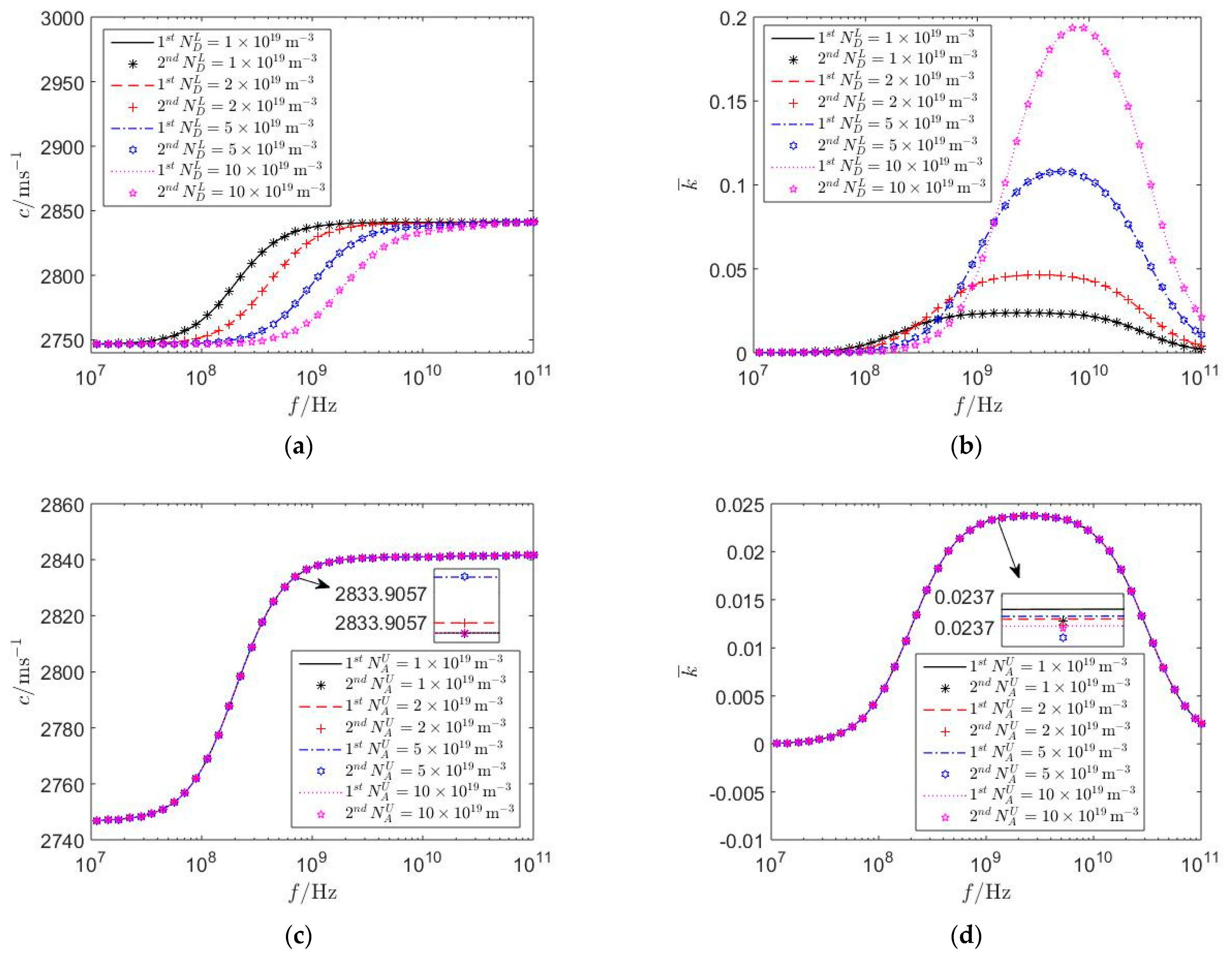
5.1. The Influence of Homo-Junctions
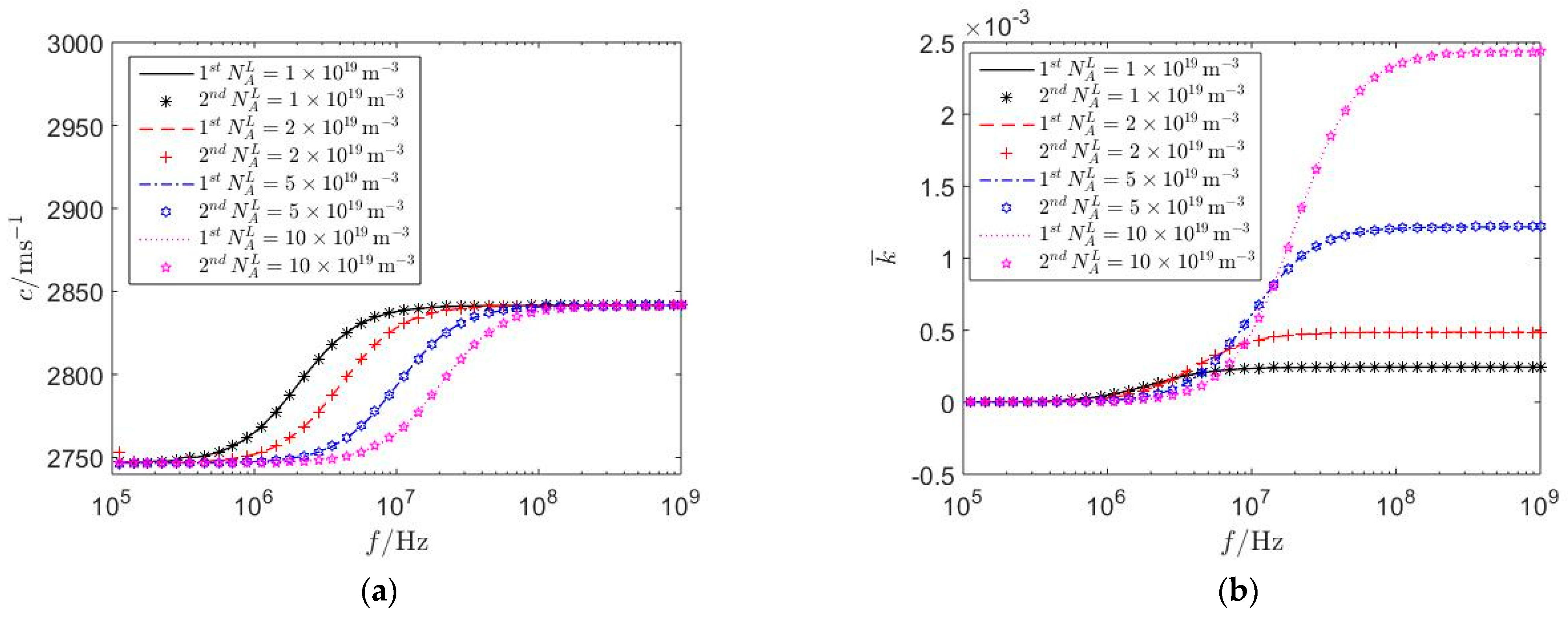
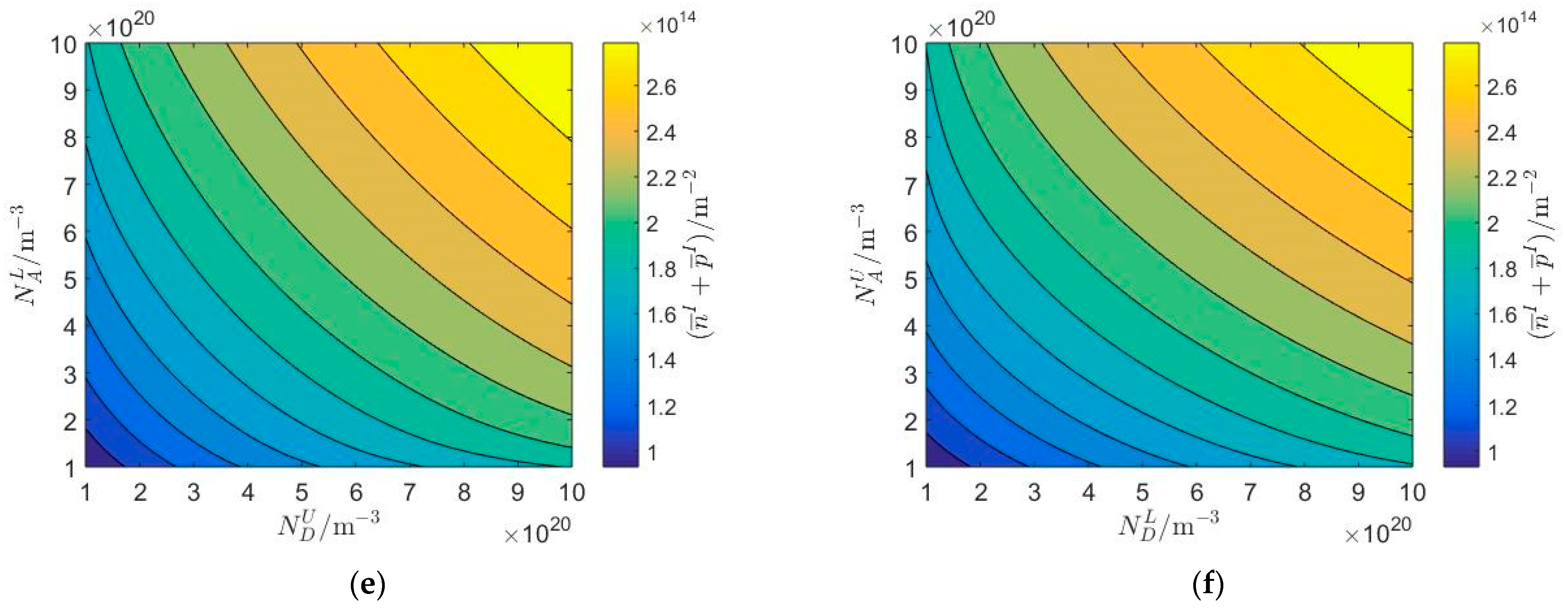
5.2. The Influence of Hetero-Junctions
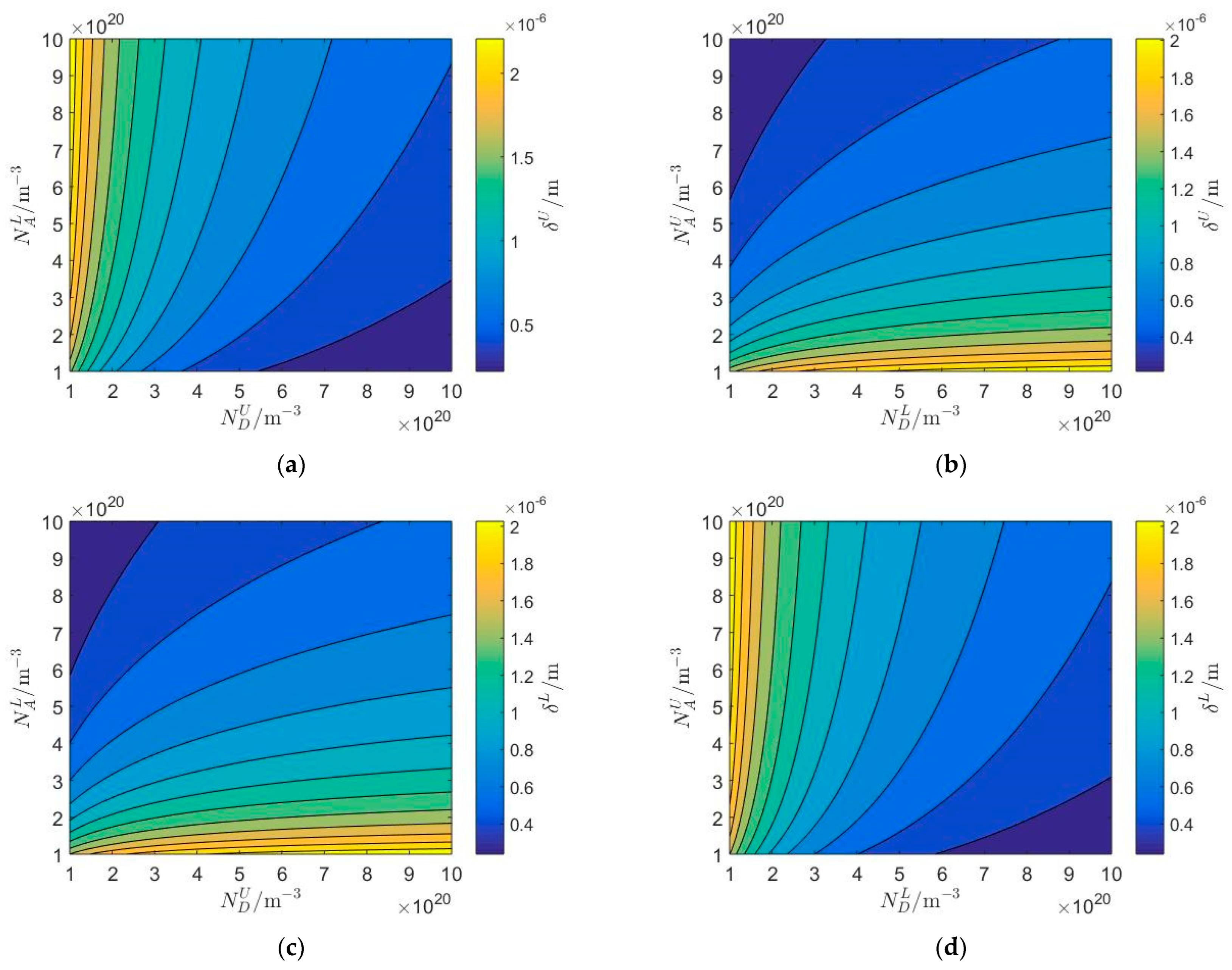
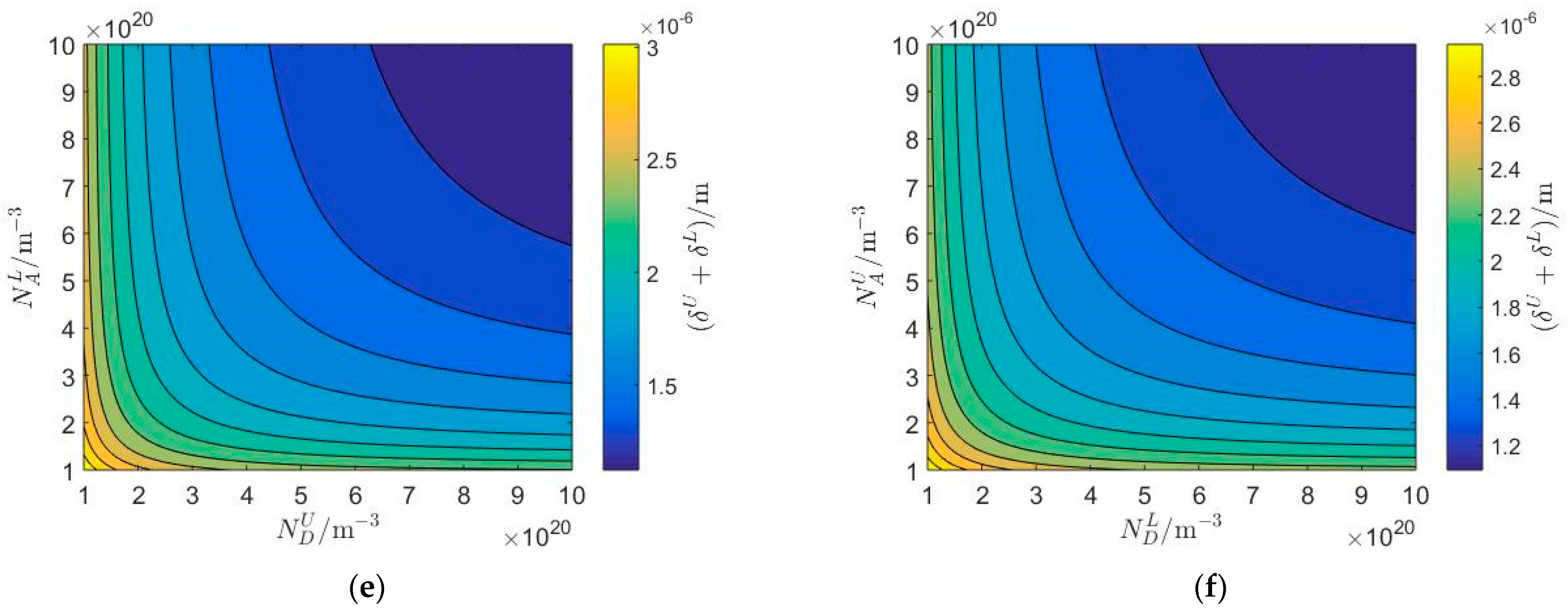
5.3. The Influence of the Thickness of the Upper PSC Layer and Biasing Electric Fields
6. Concluding Remarks
- The electrical imperfect characteristics of homo- and hetero-junctions are closely related to the piezoelectric and semiconductor effect of the upper PSC layer and lower PSC substrate, while independent of the electrical surface boundary conditions, acceptor and donor concentrations, thickness of the upper PSC layer, and biasing electric fields in the PSC semi-infinite medium.
- The variations of the type and combination of PSC materials can dramatically change the electrical imperfect characteristics of PN junctions, which might increase the complexity of the numerical values of interface characteristic lengths.
- As the acceptor and donor concentrations and thickness of the upper PSC layer increase, homo- and hetero-junctions are closer to electrical imperfect interfaces, and the first mathematical model established in this paper is more applicable, which provides a theoretical basis for the investigation of the propagation surface acoustic waves in PSC materials.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Cheng, R.; Zhang, C.; Yang, J. Thermally Induced Carrier Distribution in a Piezoelectric Semiconductor Fiber. J. Electron. Mater. 2019, 48, 4939–4946. [Google Scholar] [CrossRef]
- Fang, K.; Li, N.; Li, P.; Liu, D.; Qian, Z.; Kolesov, V.; Kuznetsova, I. A convenient approach to tuning the local piezopotential of an extensional piezoelectric semiconductor fiber via composite structure design. Nano Energy 2021, 90, 106626. [Google Scholar] [CrossRef]
- Fang, K.; Li, P.; Qian, Z. Static and Dynamic Analysis of a Piezoelectric Semiconductor Cantilever Under Consideration of Flexoelectricity and Strain Gradient Elasticity. Acta Mechanica Solida Sinica 2021, 34, 673–686. [Google Scholar] [CrossRef]
- Fang, K.; Li, P.; Li, N.; Liu, D.; Qian, Z.; Kolesov, V.; Kuznetsova, I. Model and performance analysis of non-uniform piezoelectric semiconductor nanofibers. Appl. Math. Model. 2022, 104, 628–643. [Google Scholar] [CrossRef]
- Li, D.; Zhang, C.; Zhang, S.; Wang, H.; Chen, W.; Zhang, C. Propagation of terahertz elastic longitudinal waves in piezoelectric semiconductor rods. Ultrasonics 2023, 132, 106964. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Li, S.; Zhang, C.; Chen, W. Propagation characteristics of shear horizontal waves in piezoelectric semiconductor nanoplates incorporating surface effect. Int. J. Mech. Sci. 2023, 247, 108201. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Zhang, S.; Yang, G.; Gao, C.; Zhou, C.; Zhang, C.; Zhang, P. One step synthesis of ZnO nanoparticles from ZDDP and its tribological properties in steel-aluminum contacts. Tribol. Int. 2020, 141, 105890. [Google Scholar] [CrossRef]
- Lozano, H.; Catalan, G.; Esteve, J.; Domingo, N.; Murillo, G. Non-linear nanoscale piezoresponse of single ZnO nanowires affected by piezotronic effect. Nanotechnology 2021, 32, 025202. [Google Scholar] [CrossRef]
- Yan, X.; Li, G.; Wang, Z.; Yu, Z.; Wang, K.; Wu, Y. Recent progress on piezoelectric materials for renewable energy conversion. Nano Energy 2020, 77, 105180. [Google Scholar] [CrossRef]
- Pan, C.; Zhai, J.; Wang, Z. Piezotronics and piezo-phototronics of third generation semiconductor nanowires. Chem. Rev. 2019, 119, 9303–9359. [Google Scholar] [CrossRef]
- Tu, S.; Guo, Y.; Zhang, Y.; Hu, C.; Zhang, T.; Ma, T.; Huang, H. Piezocatalysis and piezo-photocatalysis: Catalysts classification and modification strategy, reaction mechanism, and practical application. Adv. Funct. Mater. 2020, 30, 2005158. [Google Scholar] [CrossRef]
- Liang, X.; Ding, C.; Zhu, X.; Zhou, J.; Chen, C.; Guo, X. Visualization study on stress evolution and crack propagation of jointed rock mass under blasting load. Eng. Fract. Mech. 2024, 296, 109833. [Google Scholar] [CrossRef]
- Fan, S.; Yang, W.; Hu, Y. Adjustment and control on the fundamental characteristics of a piezoelectric PN junction by mechanical-loading. Nano Energy 2018, 52, 416–421. [Google Scholar] [CrossRef]
- Yang, W.; Fan, S.; Liang, Y.; Hu, Y. Prestress-loading effect on the current–voltage characteristics of a piezoelectric p–n junction together with the corresponding mechanical tuning laws. Beilstein J. Nanotechnol. 2019, 10, 1833–1843. [Google Scholar] [CrossRef]
- Yang, W.; Liu, J.; Hu, Y. Mechanical tuning methodology on the barrier configuration near a piezoelectric PN interface and the regulation mechanism on I–V characteristics of the junction. Nano Energy 2021, 81, 105581. [Google Scholar] [CrossRef]
- Yang, W.; Hong, R.; Wang, Y.; Hu, Y. Efiects of mechanical loadings on the performance of a piezoelectric hetero-junction. Appl. Math. Mech. 2022, 43, 615–626. [Google Scholar] [CrossRef]
- Liang, C.; Zhang, C.; Chen, W.; Yang, J. Effects of Magnetic Fields on PN Junctions in Piezomagnetic–Piezoelectric Semiconductor Composite Fibers. Int. J. Appl. Mech. 2020, 8, 2050085. [Google Scholar] [CrossRef]
- Cheng, R.; Zhang, C.; Chen, W.; Yang, J. Temperature Effects on PN Junctions in Piezoelectric Semiconductor Fibers with Thermoelastic and Pyroelectric Couplings. J. Electron. Mater. 2020, 19, 3140–3148. [Google Scholar] [CrossRef]
- Guo, X.; Wang, Y.; Xu, C.; Wei, Z.; Ding, C. Influence of Homo- and Hetero-Junctions on the Propagation Characteristics of Radially Propagated Cylindrical Surface Acoustic Waves in a Piezoelectric Semiconductor Semi-Infinite Medium. Mathematics 2024, 12, 145. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, W.; Yang, Y.; Zeng, X.; Hu, Y. A mechanically induced artificial potential barrier and its tuning mechanism on performance of piezoelectric PN junctions. Nano Energy 2022, 92, 106741. [Google Scholar] [CrossRef]
- Fang, K.; Li, P.; Li, N.; Liu, D.; Qian, Z.; Kolesov, V.; Kuznetsova, I. Impact of PN junction inhomogeneity on the piezoelectric fields of acoustic waves in piezo-semiconductive fibers. Ultrasonics 2022, 120, 106660. [Google Scholar] [CrossRef]
- Xu, C.; Wei, P.; Wei, Z.; Guo, X. Shear horizontal wave in a p-type Si substrate covered with a piezoelectric semiconductor n-type ZnO layer with consideration of PN heterojunction effects. Acta Mech. 2023, 235, 735–750. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Ian Murdoch, A. A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 1975, 57, 291–323. [Google Scholar] [CrossRef]
- Murdoch, A.I. The propagation of surface waves in bodies with material boundaries. J. Mech. Phys. Solids 1976, 24, 137–146. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Ian Murdoch, A. Surface stress in solids. Int. J. Solids Struct. 1978, 14, 431–440. [Google Scholar] [CrossRef]
- Tian, R.; Liu, J.; Pan, E.; Wang, Y. SH waves in multilayered piezoelectric semiconductor plates with imperfect interfaces. Eur. J. Mech./A Solids 2020, 81, 103961. [Google Scholar] [CrossRef]
- Kumar, S.; Kumari, R.; Singh, A.K. Love wave on a flexoelectric piezoelectric-viscoelastic stratified structure with dielectrically conducting imperfect interface. J. Acoust. Soc. Am. 2023, 154, 3615–3626. [Google Scholar] [CrossRef]
- Karpfinger, F.; Gurevich, B.; Bakulin, A. Modeling of wave dispersion along cylindrical structures using the spectral method. J. Acoust. Soc. Am. 2008, 124, 859. [Google Scholar] [CrossRef]
- Li, K.; Jing, S.; Yu, J.; Zhang, X.; Zhang, B. The Complex Rayleigh Waves in a Functionally Graded Piezoelectric Half-Space: An Improvement of the Laguerre Polynomial Approach. Materials 2020, 13, 2320. [Google Scholar] [CrossRef]
- Li, K.; Jing, S.; Yu, J.; Zhang, B. Complex Rayleigh Waves in Nonhomogeneous Magneto-Electro-Elastic Half-Spaces. Materials 2021, 14, 1011. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Wang, Y.; Xu, C.; Wei, Z.; Ding, C. Influence of the Schottky Junction on the Propagation Characteristics of Shear Horizontal Waves in a Piezoelectric Semiconductor Semi-Infinite Medium. Mathematics 2024, 12, 560. [Google Scholar] [CrossRef]
- Yang, J.S.; Zhou, H.G. Wave propagation in a piezoelectric ceramic plate sandwiched between two semiconductor layers. Int. J. Appl. Electromagn. Mech. 2005, 22, 97–109. [Google Scholar] [CrossRef]
- Gu, C.; Jin, F. Shear-horizontal surface waves in a half-space of piezoelectric semiconductors. Philos. Mag. Lett. 2015, 95, 92–100. [Google Scholar] [CrossRef]
- Jiao, F.; Wei, P.; Zhou, X.; Zhou, Y. The dispersion and attenuation of the multi-physical fields coupled waves in a piezoelectric semiconductor. Ultrasonics 2019, 92, 68–78. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Wang, Y.; Xu, C.; Wei, Z.; Ding, C. Influence of Homo- and Hetero-Junctions on the Propagation Characteristics of Love Waves in a Piezoelectric Semiconductor Semi-Infinite Medium. Mathematics 2024, 12, 1075. https://doi.org/10.3390/math12071075
Guo X, Wang Y, Xu C, Wei Z, Ding C. Influence of Homo- and Hetero-Junctions on the Propagation Characteristics of Love Waves in a Piezoelectric Semiconductor Semi-Infinite Medium. Mathematics. 2024; 12(7):1075. https://doi.org/10.3390/math12071075
Chicago/Turabian StyleGuo, Xiao, Yilin Wang, Chunyu Xu, Zibo Wei, and Chenxi Ding. 2024. "Influence of Homo- and Hetero-Junctions on the Propagation Characteristics of Love Waves in a Piezoelectric Semiconductor Semi-Infinite Medium" Mathematics 12, no. 7: 1075. https://doi.org/10.3390/math12071075





