Sparse Estimation for Hamiltonian Mechanics
Abstract
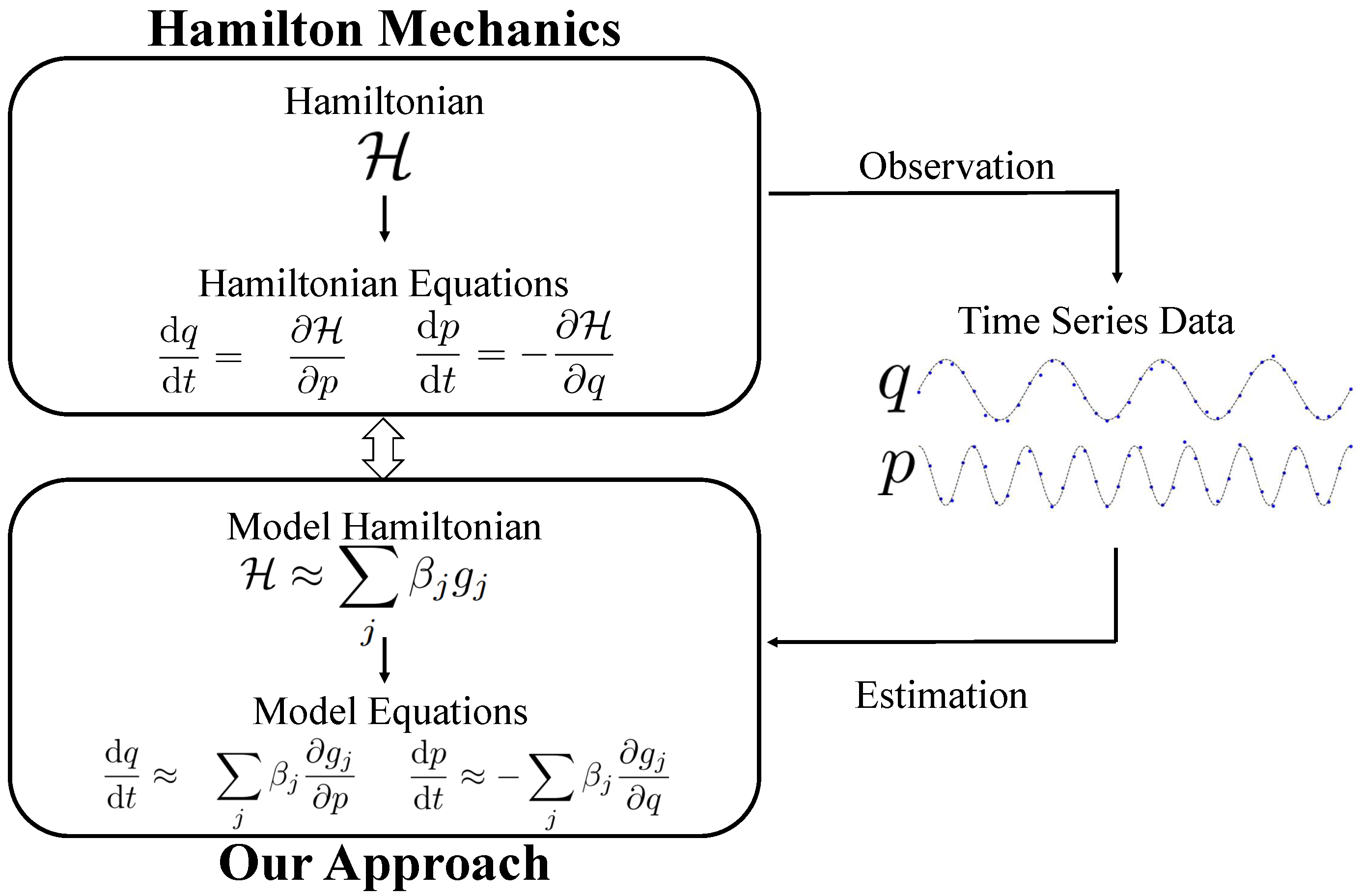
:1. Introduction
2. Methods
2.1. Hamiltonian Mechanics
2.2. Sparse Estimation for Dynamical Systems
2.3. Proposed Method
3. Results
3.1. Duffing Oscillator
3.2. Rayleigh–Bénard Convection
3.3. Robustness
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LSM | Least Squares Method |
| LASSO | Least Absolute Shrinkage and Selection operator |
Appendix A. Notation for Mathematical Symbols
| Symbol | Description |
|---|---|
| t | time |
| y | state variable |
| state variable for momenta | |
| state variable for coordinates | |
| observed value of | |
| observed value of | |
| n | degrees of freedom |
| derivative of state variable | |
| derivative of state variable for momentum | |
| derivative of state variable for coordinate | |
| observed value of | |
| observed value of | |
| j-th basis function | |
| m | total number of basis functions |
| coefficients for terms in governing equations | |
| coefficient for terms in Hamiltonian | |
| hyperparameter of norm regularization | |
| parameters of the Duffing oscillator | |
| parameters of Rayleigh–Bénard convection |
Appendix B. Code for Proposed Method
| Algorithm A1 Pseudo-code of the proposed method |
|
References
- Ghadami, A.; Epureanu, B.I. Data-driven prediction in dynamical systems: Recent developments. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2022, 380, 20210213. [Google Scholar] [CrossRef] [PubMed]
- Leylaz, G.; Wang, S.; Sun, J.Q. Identification of nonlinear dynamical systems with time delay. Int. J. Dyn. Control 2022, 10, 13–24. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Y.; Fang, H.; Ding, H. Data-driven discovery of linear dynamical systems from noisy data. Sci. Chin. Technol. Sci. 2024, 67, 121–129. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Kamrava, S.; Bai, T.; Sahimi, M. Machine learning in geo- and environmental sciences: From small to large scale. Adv. Water Resour. 2020, 142, 103619. [Google Scholar] [CrossRef]
- Geer, A.J. Learning earth system models from observations: Machine learning or data assimilation? Philos. Trans. R. Ser. A Math. Phys. Eng. Sci. 2021, 379, 20200089. [Google Scholar] [CrossRef] [PubMed]
- Omori, T.; Kuwatani, T.; Okamoto, A.; Hukushima, K. Bayesian inversion analysis of nonlinear dynamics in surface heterogeneous reactions. Phys. Rev. E 2016, 94, 033305. [Google Scholar] [CrossRef]
- Oyanagi, R.; Kuwatani, T.; Omori, T. Exploration of nonlinear parallel heterogeneous reaction pathways through Bayesian variable selection. Eur. Phys. J. B 2021, 94, 42. [Google Scholar] [CrossRef]
- Agostini, L. Exploration and prediction of fluid dynamical systems using auto-encoder technology. Phys. Fluids 2020, 32, 067103. [Google Scholar] [CrossRef]
- Yu, C.; Bi, X.; Fan, Y. Deep learning for fluid velocity field estimation: A review. Ocean Eng. 2023, 271, 113693. [Google Scholar] [CrossRef]
- Balaji, J.; Al Abdullah, M.S.A.A. On data-driven sparse sensing and linear estimation of fluid flows. Sensors 2020, 20, 3752. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Shen, M. Fusion-based event-triggered H∞ State estimation of networked autonomous surface vehicles with measurement outliers and cyber-attacks. IEEE Trans. Intell. Transp. Syst. 2024, 1–11. [Google Scholar] [CrossRef]
- Course, K.; Nair, P.B. State estimation of a physical system with unknown governing equations. Nature 2023, 622, 261–267. [Google Scholar] [CrossRef] [PubMed]
- Ching, J.; Beck, J.L.; Porter, K.A. Bayesian state and parameter estimation of uncertain dynamical systems. Probab. Eng. Mech. 2006, 21, 81–96. [Google Scholar] [CrossRef]
- Niven, R.K.; Mohammad-Djafari, A.; Cordier, L.; Abel, M.; Quade, M. Bayesian identification of dynamical systems. Proceedings 2019, 33, 33. [Google Scholar]
- Fuentes, R.; Nayek, R.; Gardner, P.; Dervilis, N.; Rogers, T.; Worden, K.; Cross, E.J. Equation discovery for nonlinear dynamical systems: A Bayesian viewpoint. Mech. Syst. Signal Process. 2020, 154, 107528. [Google Scholar] [CrossRef]
- Inoue, H.; Hukushima, K.; Omori, T. Estimating distributions of parameters in nonlinear state space models with replica exchange particle marginal Metropolis-Hastings method. Entropy 2022, 24, 115. [Google Scholar] [CrossRef] [PubMed]
- Linden, N.J.; Kramer, B.; Rangamani, P. Bayesian parameter estimation for dynamical models in systems biology. PLoS Comput. Biol. 2023, 19, e1011041. [Google Scholar] [CrossRef]
- Grashorn, J.; Urrea-Quintero, J.; Broggi, M.; Chamoin, L.; Beer, M. Transport map Bayesian parameter estimation for dynamical systems. Proc. Appl. Math. Mech. 2023, 23, e202200136. [Google Scholar] [CrossRef]
- De, S. Uncertainty quantification of locally nonlinear dynamical systems using neural networks. J. Comput. Civ. Eng. 2021, 35, 04021009. [Google Scholar] [CrossRef]
- Rajendra, P.; Brahmajirao, V. Modeling of dynamical systems through deep learning. Biophys. Rev. 2020, 12, 1311–1320. [Google Scholar] [CrossRef]
- Gao, H.; Wang, J.X.; Zahr, M.J. Non-intrusive model reduction of large-scale, nonlinear dynamical systems using deep learning. Phys. D Nonlinear Phenom. 2020, 412, 132614. [Google Scholar] [CrossRef]
- Yin, Y.; Ayed, I.; Bézenac, E.; Baskiotis, N.; Gallinari, P. LEADS: Learning dynamical systems that generalize across environments. Adv. Neural Inf. Process. Syst. 2021, 34, 7561–7573. [Google Scholar]
- Dufera, T.T.; Seboka, Y.C.; Portillo, C.F. Parameter estimation for dynamical systems using a deep neural network. Appl. Comput. Intell. Soft Comput. 2022, 2022, 2014510. [Google Scholar] [CrossRef]
- Cheng, S.; Qiu, M. Observation error covariance specification in dynamical systems for data assimilation using recurrent neural networks. Neural Comput. Appl. 2022, 34, 13149–13167. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [PubMed]
- Mangan, N.M.; Kutz, J.N.; Brunton, S.L.; Proctor, J.L. Model selection for dynamical systems via sparse regression and information criteria. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170009. [Google Scholar] [CrossRef] [PubMed]
- Schaeffer, H.; Tran, G.; Ward, R.; Zhang, L. Extracting structured dynamical systems using sparse optimization with very few samples. Multiscale Model. Simul. 2020, 18, 1435–1461. [Google Scholar] [CrossRef]
- Cortiella, A.; Park, K.-C.; Doostan, A. Sparse identification of nonlinear dynamical systems via reweighted ℓ1-regularized least squares. Comput. Methods Appl. Mech. Eng. 2021, 376, 113620. [Google Scholar] [CrossRef]
- Messenger, D.; Bortz, D. Weak SINDy: Galerkin-based data-driven model selection. Multiscale Model. Simul. 2021, 19, 1474–1497. [Google Scholar] [CrossRef]
- Nayek, R.; Fuentes, R.; Worden, K.; Cross, E.J. On spike-and-slab priors for Bayesian equation discovery of nonlinear dynamical systems via sparse linear regression. Mech. Syst. Signal Process. 2021, 161, 107986. [Google Scholar] [CrossRef]
- Fasel, U.; Kutz, J.N.; Brunton, B.W.; Brunton, S.L. Ensemble-SINDy: Robust sparse model discovery in the low-data, high-noise limit, with active learning and control. Proc. R. Soc. A Math. Phys. Eng. Sci. 2022, 478, 20210904. [Google Scholar] [CrossRef] [PubMed]
- Wentz, J.; Doostan, A. Derivative-based SINDy (DSINDy): Addressing the challenge of discovering governing equations from noisy data. Comput. Methods Appl. Mech. Eng. 2023, 413, 116096. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Millman, K.J.; Mayorov, N.; Nelson, A.R.J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Watanabe, M.; Yoshimura, H. Experimental investigation of Lagrangian coherent structures and lobe dynamics in perturbed Rayleigh-Bénard convection. Fluid Appl. Syst. Fluid Meas. Instrum. 2021, 2, V002T04A001. [Google Scholar]
- Starck, J.L.; Murtagh, F.; Fadili, J.M. Sparse Image and Signal Processing: Wavelets, Curvelets, Morphological Diversity; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]






| Duffing Oscillator | Rayleigh–Bénard Convection | |
|---|---|---|
| Ours | 0.19 | 0.26 |
| LSM | 1.82 | 1.51 |
| LASSO | 1.39 | 2.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Note, Y.; Watanabe, M.; Yoshimura, H.; Yaguchi, T.; Omori, T. Sparse Estimation for Hamiltonian Mechanics. Mathematics 2024, 12, 974. https://doi.org/10.3390/math12070974
Note Y, Watanabe M, Yoshimura H, Yaguchi T, Omori T. Sparse Estimation for Hamiltonian Mechanics. Mathematics. 2024; 12(7):974. https://doi.org/10.3390/math12070974
Chicago/Turabian StyleNote, Yuya, Masahito Watanabe, Hiroaki Yoshimura, Takaharu Yaguchi, and Toshiaki Omori. 2024. "Sparse Estimation for Hamiltonian Mechanics" Mathematics 12, no. 7: 974. https://doi.org/10.3390/math12070974





