Spatial Decay Estimates and Continuous Dependence for the Oldroyd Fluid
Abstract
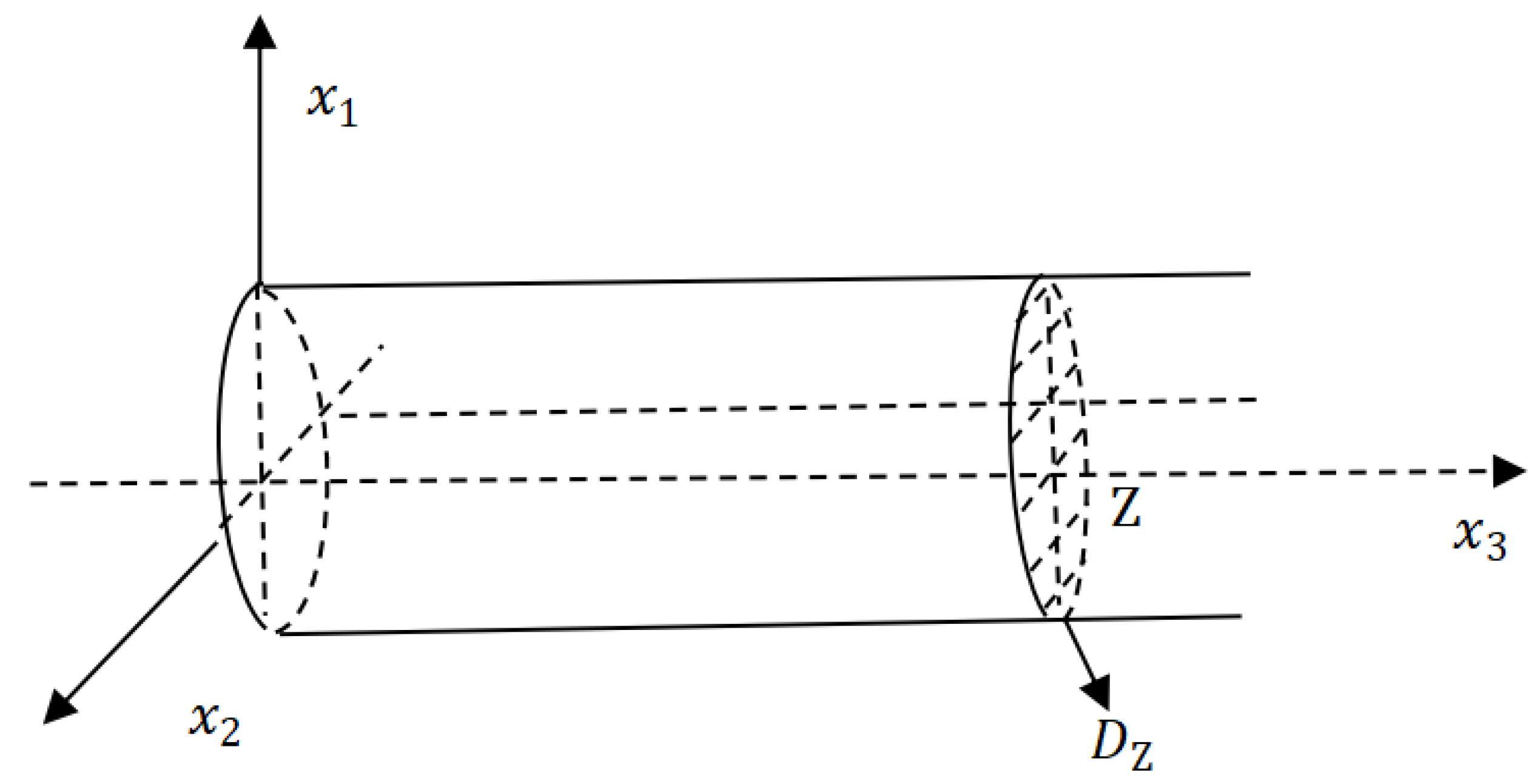
1. Introduction
2. The Main Theorems
3. The Proof of Theorem 1
4. The Proof of Theorem 2
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References and Note
- Straughan, B. Continuous dependence and convergence for a Kelvin-Voigt fluid of order one. Annaidell Univ. Diferrara 2022, 68, 49–61. [Google Scholar] [CrossRef]
- Oskolkov, A.P.; Shadiev, R. Towards a theory of global solvability on [0,∞) of initial-boundary value problems for the equations of motion of Oldroyd and Kelvin-Voigt fluids. J. Math. Sci. 1994, 68, 240–253. [Google Scholar] [CrossRef]
- Christov, I.C.; Jordan, P.M. Maxwell’s “Other” Equations; The Royal Society, Blog: London, UK, 2015. [Google Scholar]
- Keiller, R.A. Spatial decay of steady perturbations of plane Poiseuille flow for the Oldroyd-B equation. J. Non-Newton. Fluid Mech. 1993, 46, 129–142. [Google Scholar] [CrossRef]
- Lozinski, A.; Owens, R.G. An energy estimate for the Oldroyd B model: Theory and applications. J. Non-Newton. Fluid Mech. 2003, 112, 161–176. [Google Scholar] [CrossRef]
- Boley, B. Some observations on Saint-Venant’s principle. Proc. 3rd U.S. Nat. Con 9. Appl. Mech. ASME 1958, 259–264. [Google Scholar]
- Payne, L.E.; Song, J.C. Spatial decay estimates for the Brinkman and Darcy flows in a semi-infinite cylinder. Contin. Mech. Thermodyn. 1997, 9, 175–190. [Google Scholar] [CrossRef]
- Li, Y.F.; Xiao, S.Z.; Chen, X.J. Spatial alternative and stability of type III Thermoelastic equations. Appl. Math. Mech. 2021, 42, 431–440. [Google Scholar]
- Li, Y.F.; Lin, C.H. Spatial Decay for Solutions to 2-D Boussinesq System with Variable Thermal Diffusivity. Acta Appl. Math. 2018, 154, 111–130. [Google Scholar] [CrossRef]
- Quintanilla, R. Some remarks on the fast spatial growth/decay in exterior regions. Z. Angew. Math. Phys. 2019, 70, 83. [Google Scholar] [CrossRef]
- Quintanilla, R.; Racke, R. Spatial behavior in phase-lag heat conduction. Differ. Integral Equ. 2015, 28, 291–308. [Google Scholar] [CrossRef]
- Knops, R.J.; Quintanilla, R. Spatial behaviour in thermoelastostatic cylinders of indefinitely increasing cross-section. J. Elast. 2015, 121, 89–117. [Google Scholar] [CrossRef][Green Version]
- Knops, R.J.; Quintanilla, R. Spatial decay in transient heat conduction for general elongated regions. Q. Appl. Math. 2018, 76, 611–625. [Google Scholar] [CrossRef]
- Chen, W.H. Cauchy problem for thermoelastic plate equations with different damping mechanisms. Commun. Math. Sci. 2020, 18, 429–457. [Google Scholar] [CrossRef]
- Chen, W.H. Decay properties and asymptotic profiles for elastic waves with Kelvin-Voigt damping in 2D. Asymptot. Anal. 2020, 117, 113–140. [Google Scholar] [CrossRef]
- Bofill, F.; Quintanilla, R. Spatial estimates for dynamical problems in several elasticity theories. Richerche Mat. 1998, 46, 425–441. [Google Scholar]
- Liu, Z.; Zheng, S. Exponential stability of the Kirchhoff plate with thermal or viscoelastic damping. Q. Appl. Math. 1997, 3, 551–564. [Google Scholar] [CrossRef]
- Avalos, G.; Lesiecka, I. Exponential stability of an uncontrolled thermoelastic system with varying boundary conditions. Appl. Anal. 1998, 68, 31–49. [Google Scholar]
- Meyvacı, M. Structural stability for a linear system of thermoelastic plate equations. Appl. Math. Comput. 2014, 242, 664–668. [Google Scholar] [CrossRef]
- Quintanilla, R. Convergence and structural stability in thermoelasticity. Appl. Math. Comput. 2003, 135, 287–300. [Google Scholar] [CrossRef]
- Quintanilla, R. Structural stability and continuous dependence of solutions in thermoelasticity of type III. Discret. Contin. Dyn. Syst. B 2001, 1, 463–470. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, Y.W.; Li, Y.F. Convergence result for the thermoelasticity of type III. Appl. Math. Lett. 2013, 26, 97–102. [Google Scholar] [CrossRef][Green Version]
- Liu, Y. Continuous dependence for a thermal convection model with temperature-dependent solubitity. Appl. Math. Comput. 2017, 308, 18–30. [Google Scholar]
- Liu, Y.; Xiao, S.Z.; Lin, Y.W. Continuous dependence for the Brinkman-Forchheimer fluid interfacing with a Darcy fluid in a bounded domain. Math. Comput. Simul. 2018, 150, 66–82. [Google Scholar] [CrossRef]
- Shi, J.C.; Liu, Y. Structural stability for the Forchheimer equations interfacing with a Darcy fluid in a bounded region in R3. Bound. Value Probl. 2021, 46. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, X.L.; Shi, J.C.; Zhi, W.J. Structural stability of the Boussinesq fluid interfacing with a Darcy fluid in a bounded region in R2. Appl. Math. Comput. 2021, 411, 126488. [Google Scholar]
- Hameed, A.A.; Harfash, A.J. Continuous dependence of double diffusive convection in a porous medium with temperature-dependent density. Basrah J. Sci. 2019, 37, 1–15. [Google Scholar]
- Scott, N.L. Continuous dependence on boundary reaction terms in a porous mediu od Darcy type. J. Math. Anal. Appl. 2013, 399, 667–675. [Google Scholar] [CrossRef]
- Scott, N.L.; Straughan, B. Continuous dependence on the reaction terms in porous convection with surface reactions. Q. Appl. Math. 2013, 71, 501–508. [Google Scholar] [CrossRef][Green Version]
- Li, Y.F.; Zeng, P. Continuous dependence on the heat source of 2D large-scale primitive equations in oceanic dynamics. Symmetry 2021, 13, 1961. [Google Scholar] [CrossRef]
- Li, Y.F.; Chen, X.J.; Shi, J.C. Structural stability in resonant penetrative convection in a Brinkman-Forchheimer fluid interfacing with a Darcy fluid. Appl. Math. Optim. 2021, 84, 979–999. [Google Scholar] [CrossRef]
- Li, Y.F.; Xiao, S.Z.; Zeng, P. The applications of some basic mathematical inequalities on the convergence of the primitive equations of moist atmosphere. J. Math. Inequalities 2021, 15, 293–304. [Google Scholar] [CrossRef]
- Li, Y.F.; Xiao, S.Z. Continuous dependence of 2D large scale primitive equtions on the boundary conditions. Appl. Math. 2022, 67, 103–124. [Google Scholar] [CrossRef]
- Ciarletta, M.; Straughan, B.; Tibullo, V. Structural stability for a thermal convection model with temperature-dependent solubility. Nonlinear Anal. Real World Appl. 2015, 22, 34–43. [Google Scholar] [CrossRef]
- Franchi, F.; Straughan, B. Continuous dependence and decay for the Forchheimer equations. Proc. R. Soc. Lond. A 2003, 459, 3195–3202. [Google Scholar] [CrossRef]
- Song, J.C.; Yoon, D.S. Phragmén-Lindelöf type and continuous dependence results in generalized dissipative heat conduction. J. Korean Math. Soc. 1998, 35, 945–960. [Google Scholar]
- Song, J.C. Phragmén—Lindelöf and continuous dependence type results in a Stokes flow. Appl. Math. Mech. 2010, 31, 875–882. [Google Scholar] [CrossRef]
- Li, Y.F.; Lin, C. Continuous dependence for the nonhomogeneous Brinkman-Forchheimer equations in a semi-infinite pipe. Appl. Math. Comput. 2014, 244, 201–208. [Google Scholar] [CrossRef]
- Ladyzhenskaya, O.A.; Solonnikov, V.A. Some problems of vector analysis and generalized formulations of boundary-value problems for the Navier-Stokes equations. Russ. Math. Surv. 1973, 28, 43–82. [Google Scholar] [CrossRef]
- Babuǒska, I.; Aziz, A.K. Survey lectures on the mathematical foundations of the finite element method. In The Mathematical Foundations of the Finite Element Method with Applications to Partial Differential Equations (Proc. Sympos., Univ. Maryland, Baltimore, Md., 1972); Academic Press: New York, NY, USA, 1972; pp. 1–359. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y. Spatial Decay Estimates and Continuous Dependence for the Oldroyd Fluid. Mathematics 2024, 12, 1240. https://doi.org/10.3390/math12081240
Li Y. Spatial Decay Estimates and Continuous Dependence for the Oldroyd Fluid. Mathematics. 2024; 12(8):1240. https://doi.org/10.3390/math12081240
Chicago/Turabian StyleLi, Yuanfei. 2024. "Spatial Decay Estimates and Continuous Dependence for the Oldroyd Fluid" Mathematics 12, no. 8: 1240. https://doi.org/10.3390/math12081240
APA StyleLi, Y. (2024). Spatial Decay Estimates and Continuous Dependence for the Oldroyd Fluid. Mathematics, 12(8), 1240. https://doi.org/10.3390/math12081240





