Robust Consensus Modeling: Concerning Consensus Fairness and Efficiency with Uncertain Costs
Abstract
:1. Introduction
- (1)
- Most of the current research on the fairness of group consensus has been conducted in a deterministic environment, and there is currently a significant gap in the research on consensus efficiency. However, uncertainty factors are widely present and cannot be ignored, and similarly, the impact of the complexity of uncertainty factors on the efficiency and fairness of reaching consensus cannot be ignored.
- (2)
- In most consensus studies, the DMs’ weights tend to be determined individually. In classic GDM models that do not take social networks into account, each DM’s weight is directly determined based on the subjective experience of the moderator, while each DM’s weight is uniquely determined by the trust relationships of the DMs in SNGDM. In real decision making scenarios, differences in the professional skills, educational background, and social experiences of the DMs can directly affect their weights. These factors should also not be ignored in the assignment of weights.
- (1)
- A robust consensus model focusing on fairness and efficiency with uncertain costs is proposed. The proposed model not only introduces the fair utility level to measure the fairness of compensation allocation, but also introduces the opinion adjustment distance to measure the efficiency of reaching consensus. Moreover, this paper constructs four kinds of uncertainty sets to portray the uncertainty of the unit adjustment cost more accurately.
- (2)
- A data-driven method combined with the trust propagation method in social networks is used to determine the DMs’ weights jointly. The data-driven method mainly determines the DMs’ weights (i.e., intrinsic influence) from a large amount of historical data, which mainly reflects differences in the DMs’ social experiences, preferences, and educational backgrounds. The trust propagation determines the DMs’ weights in the social network (i.e., extrinsic influence), which mainly reflects the DMs’ trust degrees in the social network. The combination of the two methods jointly determines the weights, which is more scientific and objective.
- (3)
- The proposed model is applied to the carbon emission reduction negotiation process between the government and enterprises, focusing on analyzing the influence of uncertain parameter levels, DMs’ fair concern behaviors, and other factors on consensus fairness and the efficiency of reaching consensus. The experimental results also verify the rationality and robustness of the proposed model.
2. Preliminaries
2.1. Minimum Adjustment Consensus Model and Consensus Metrics
- (1)
- When 2, . The larger the distance between and , the smaller the consensus level, which is consistent with the actual consensus process.
- (2)
- When , . The larger the distance between and , the smaller the consensus level, which is consistent with actual consensus process.
- (3)
- When 2, the distance between and is too large for the moderator to accept the adjusted opinion.
2.2. Fairness Preference Theory
2.3. Trust Propagation and Aggregation in the Social Network
3. Model Construction
3.1. Determination of Weight
3.2. Fair Utility Level
3.3. Uncertainty in Unit Adjustment Cost
3.4. Robust Consensus Model Considering Fairness and Efficiency
3.4.1. EFCM Based on Box Set
3.4.2. EFCM Based on Ellipsoid Set
3.4.3. EFCM Based on Box–Ellipsoid Set
- and . Moreover, is the dual cone of and .
- In , , . Since the dual paradigm of the second paradigm is itself, holds. In effect, it is a second-order cone.
3.4.4. EFCM Based on Box–Polyhedral Set
- , , and , where , and is the dual cone of .
- and , which implies that = . This is because 1-paradigm numbers and infinity-paradigm numbers are pairwise-paradigm numbers to each other.
4. Simulation
4.1. Numerical Example
4.2. Comparative Analysis
- (1)
- The proposed model in this paper is more efficient and has a lower consensus cost. Take the MACM as an example: The MACM proposed by Dong et al. [52] has a theoretical solution and the total distance of the opinion adjustment is much higher than that of this paper , in other words, the MACM is less efficient in reaching consensus. Moreover, the consensus budget in the MACM is much higher than the EFCM proposed in this paper , reflecting that when the government has a sufficient budget, enterprises may adjust their opinions through multiple rounds of negotiation, which increases the overall negotiation cost, and leads to a lower efficiency of reaching consensus.
- (2)
- The proposed model in this paper is more relevant to the practical GDM scenarios and pays more attention to multiple indicators in the CRP. From the results in Table 2, it is not difficult to find that when there are uncertainties, the fair utility level of enterprise is 0, so enterprise may take non-cooperative measures to hinder the CRP in the actual GDM. In the proposed consensus models (i.e., EFCM-B, EFCM-E, EFCM-BE, EFCM-BP) that consider the uncertain unit adjustment cost, a high fair utility level (i.e., in Section 4.1) for all the enterprises is ensured, as well as the efficiency of the consensus being reached under a limited cost budget.
4.3. Sensitivity Analysis
4.3.1. Sensitivity Analysis of Consensus Cost Budget
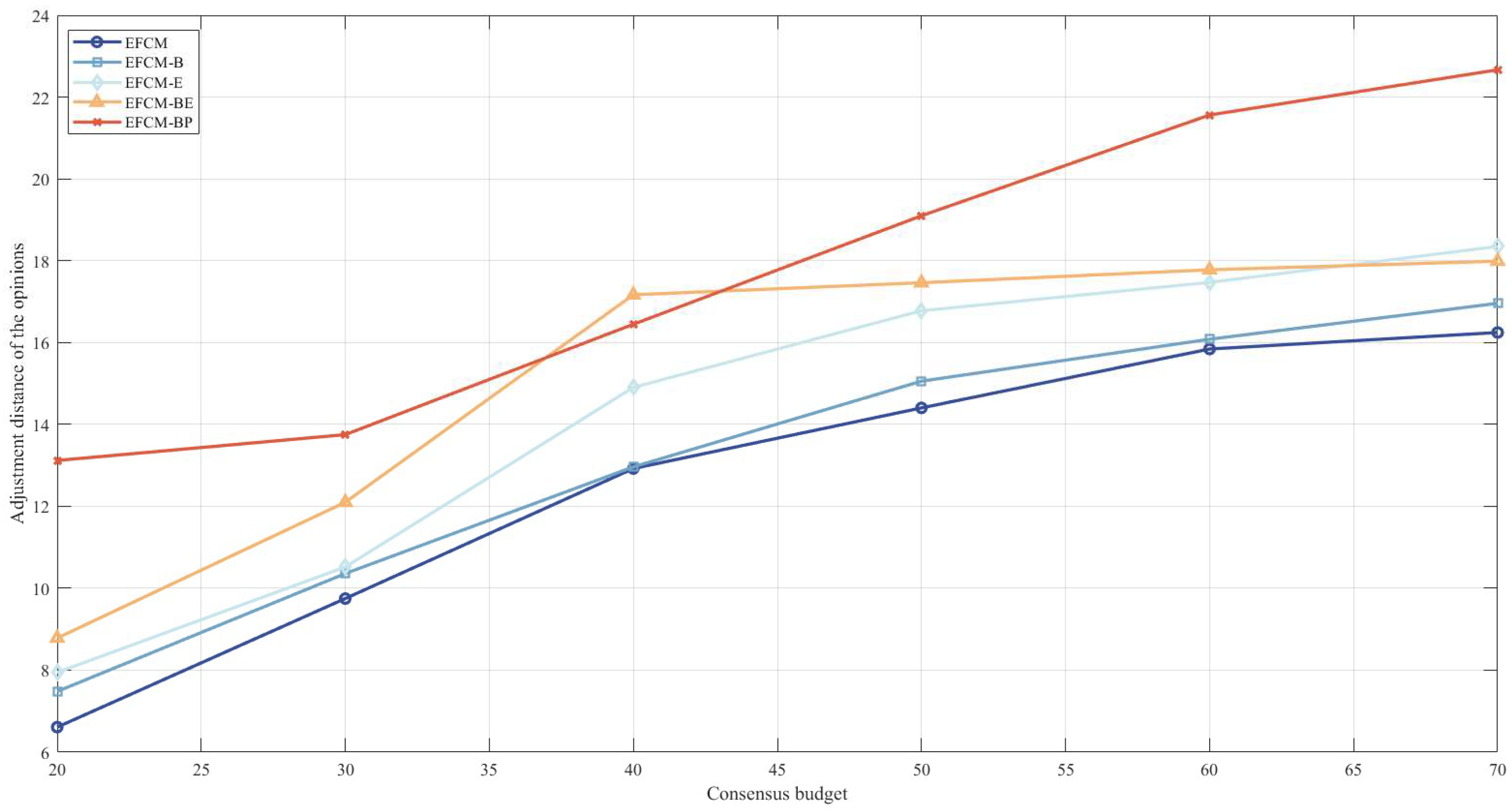
- (1)
- As the consensus budget increases, the efficiency of reaching a consensus decreases (i.e., the adjustment distance of the opinion increases). We argue that enterprises’ pursuits of maximizing their compensation during the negotiation is the reason for this phenomenon. In other words, as the government’s budget increases, enterprises pursue higher compensation gains by constantly revising their opinions, which leads to an overall increase in the adjustment distance of the opinion; in other words, it leads to a decrease in the efficiency of reaching consensus.
- (2)
- The government should set a reasonable consensus budget. When the consensus budget is low, the budget of the EFCM to reach consensus is equal to the government-set budget. With the increase in the consensus budget, the budget of the EFCM to reach consensus becomes closer to the government-set budget. When the government budget is high, increasing the consensus budget, the efficiency of consensus being reached only increases in a small range, indicating that a consensus budget that is too high cannot significantly improve the efficiency of reaching consensus. Therefore, setting an appropriate consensus budget helps to ensure the efficiency of reaching consensus, and it is recommended that the moderator sets a reasonable consensus budget for actual GDM problems.
4.3.2. Sensitivity Analysis of Consensus Threshold
4.3.3. Sensitivity Analysis of Perturbation Cost
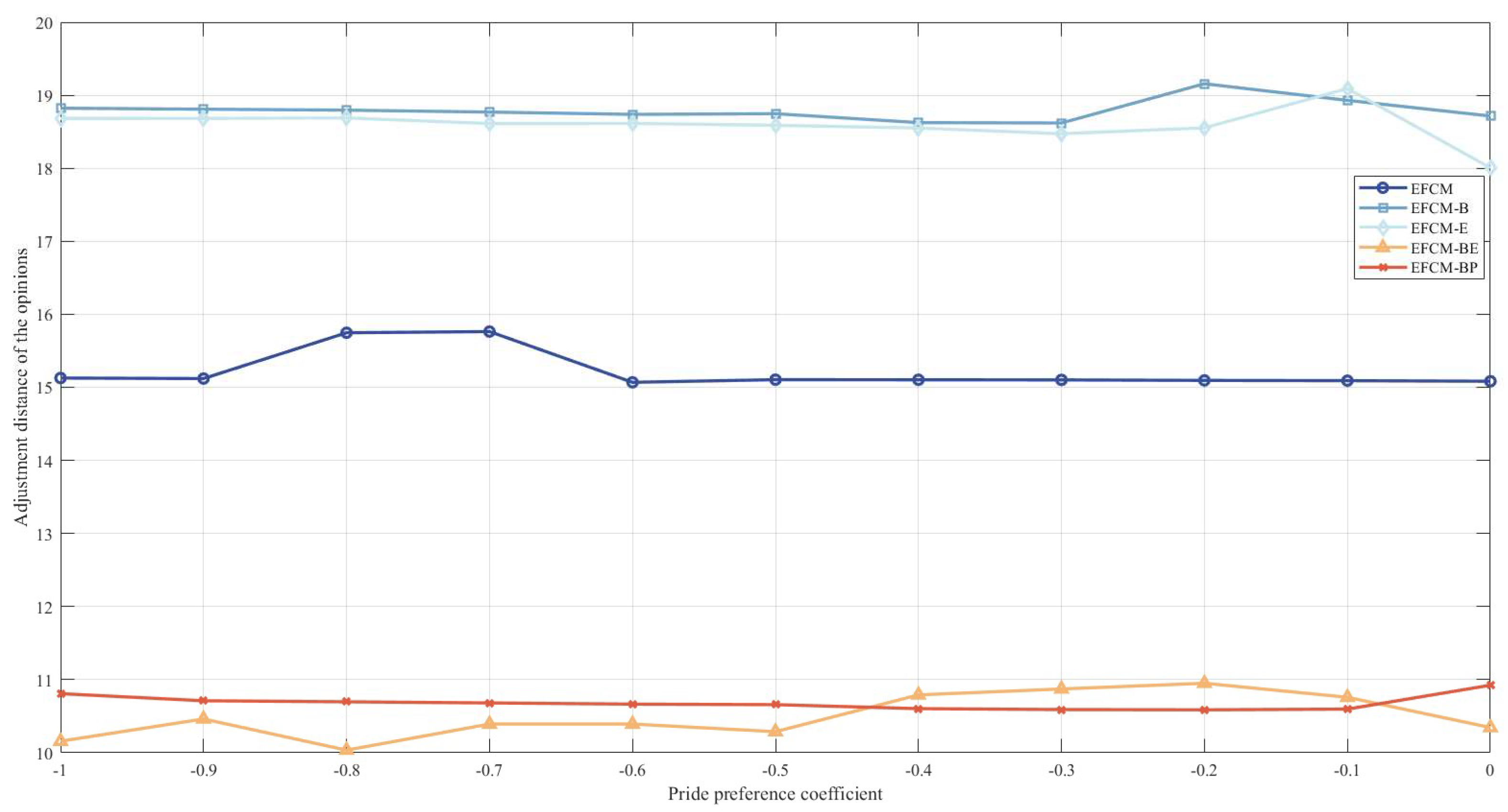
4.3.4. Sensitivity Analysis of Uncertainty Parameter Level
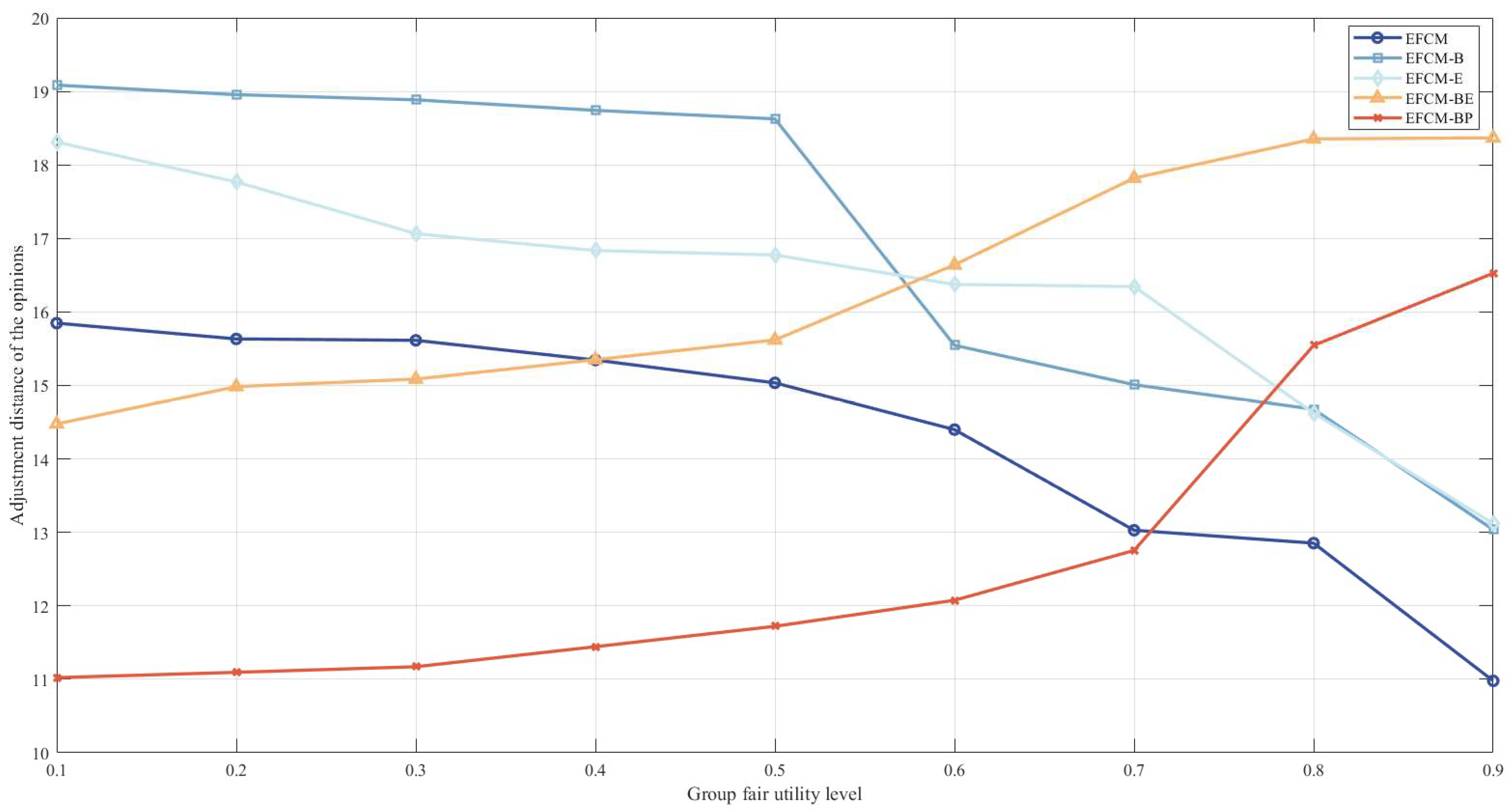
4.3.5. Sensitivity Analysis of Group Fair Utility Level
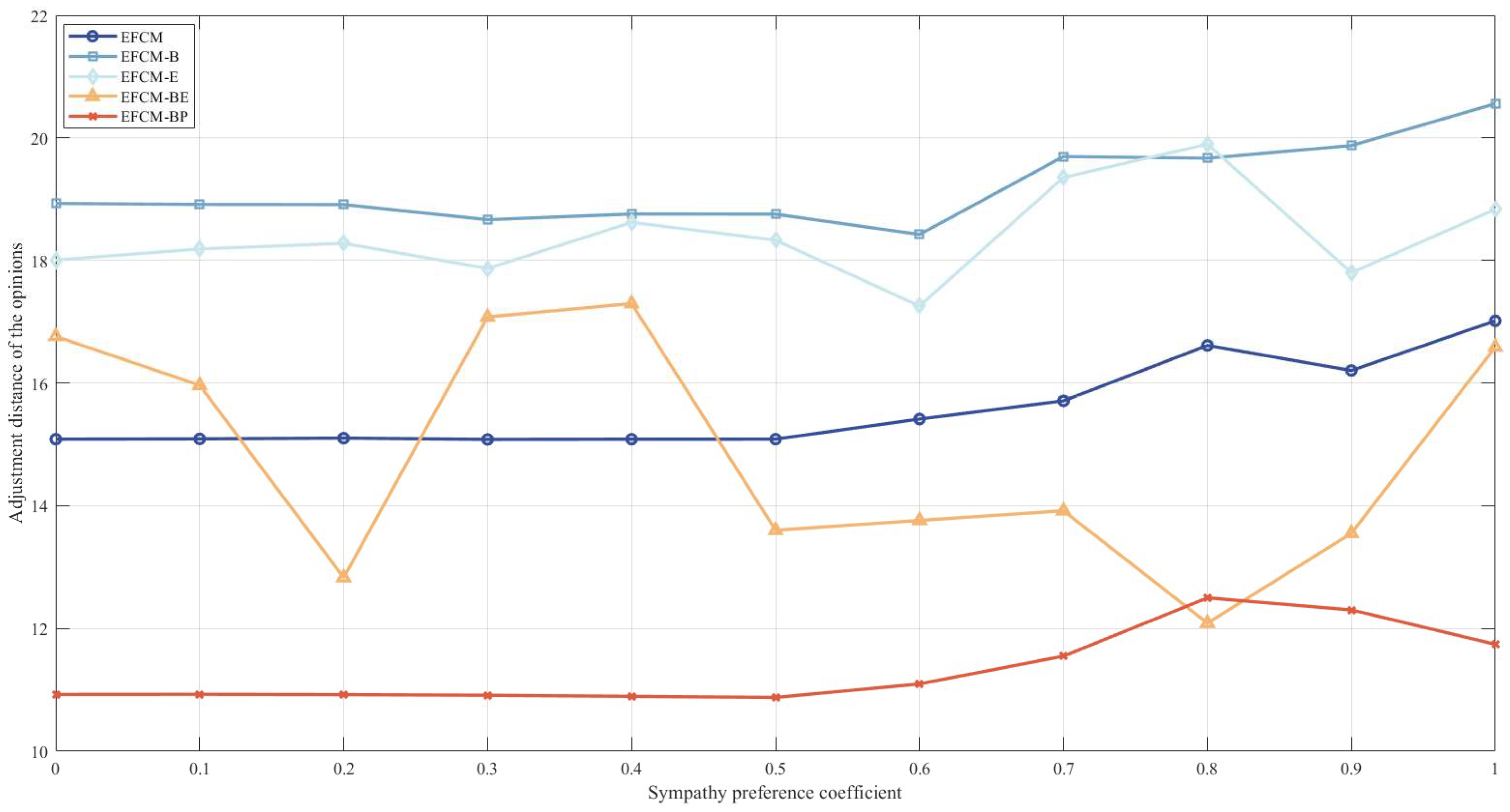
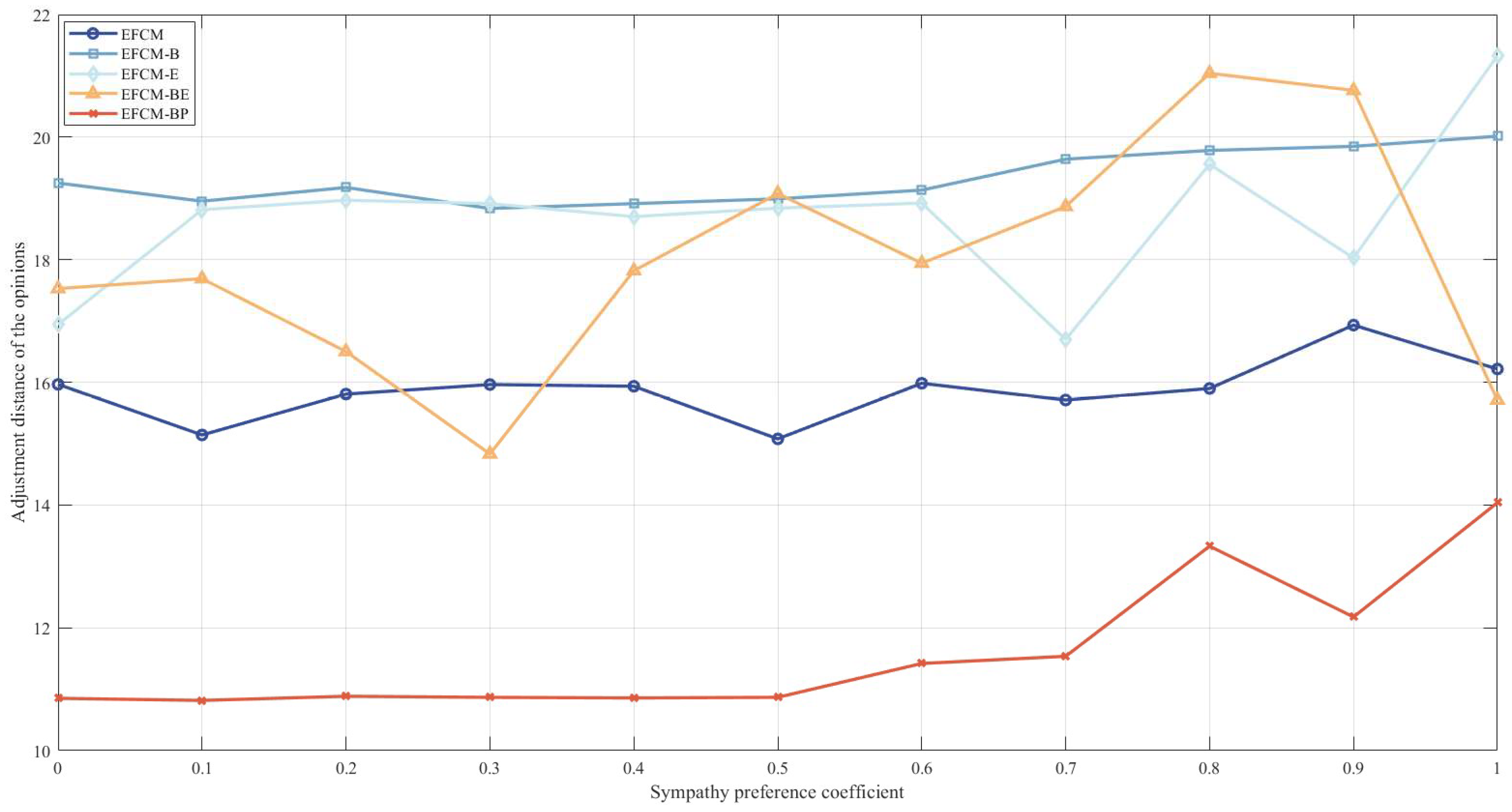
4.3.6. Sensitivity Analysis of Fair Concern Behavior
- (1)
- The jealousy preference of all the DMs has a stronger impact on the efficiency of reaching consensus in the CRP. When the other DMs do not have a jealous preference (i.e., case 1), the adjustment distance of the opinion fluctuates in a small interval as the jealous preference coefficient increases, indicating that the jealous preference behavior of a single DM cannot significantly affect the group’s efficiency of reaching consensus. When other DMs have a full jealousy preference (i.e., case 2), as the jealousy preference coefficient increases, the adjustment distance of the opinion increases, indicating that all the DMs exhibit jealousy preference behavior, which significantly affects the efficiency of reaching consensus.
- (2)
- Secondly, comparing Table 9 and Table 10, whether all the DMs exhibit jealousy preference behavior or not has different effects on the efficiency of reaching consensus. Specifically, in the EFCM, EFCM-B, and EFCM-E, when all the DMs exhibit jealous preference behavior, it increases the adjustment distance of the opinion compared to when a single DM exhibits jealous preference behavior. In other words, when all the DMs exhibit jealous preference behavior, reaching consensus will be less efficient. Conversely, in EFCM-BE and EFCM-BP, when all the DMs exhibit jealousy preference behavior, it leads to a decrease in the adjustment distance of the opinion compared to when a single DM exhibits jealous preference behavior.
5. Conclusions
- (1)
- This paper proposes robust group consensus models focusing on fairness and efficiency, studies how to reach consensus efficiently and fairly under uncertain costs and enriches the theoretical system of group consensus research.
- (2)
- This paper utilizes a data-driven approach combined with the trust transfer method in social networks to jointly determine the weights of the decision makers. Compared with the single method of determining DMs’ weights based on the subjective experience of moderators or the trust degree in social networks in existing studies, the method of determining weights by combining data-driven methods and trust transfer in social networks adopted in this paper is more scientific and objective.
- (1)
- Comparing the MACM proposed by Dong et al. [52] and the robust consensus models proposed by Han et al. [64], the proposed models in this paper have a higher efficiency of reaching consensus and a lower consensus cost. In addition, compared with the above studies, the proposed models in this paper are more relevant to GDM problems and pay more attention to multiple metrics in the CRP.
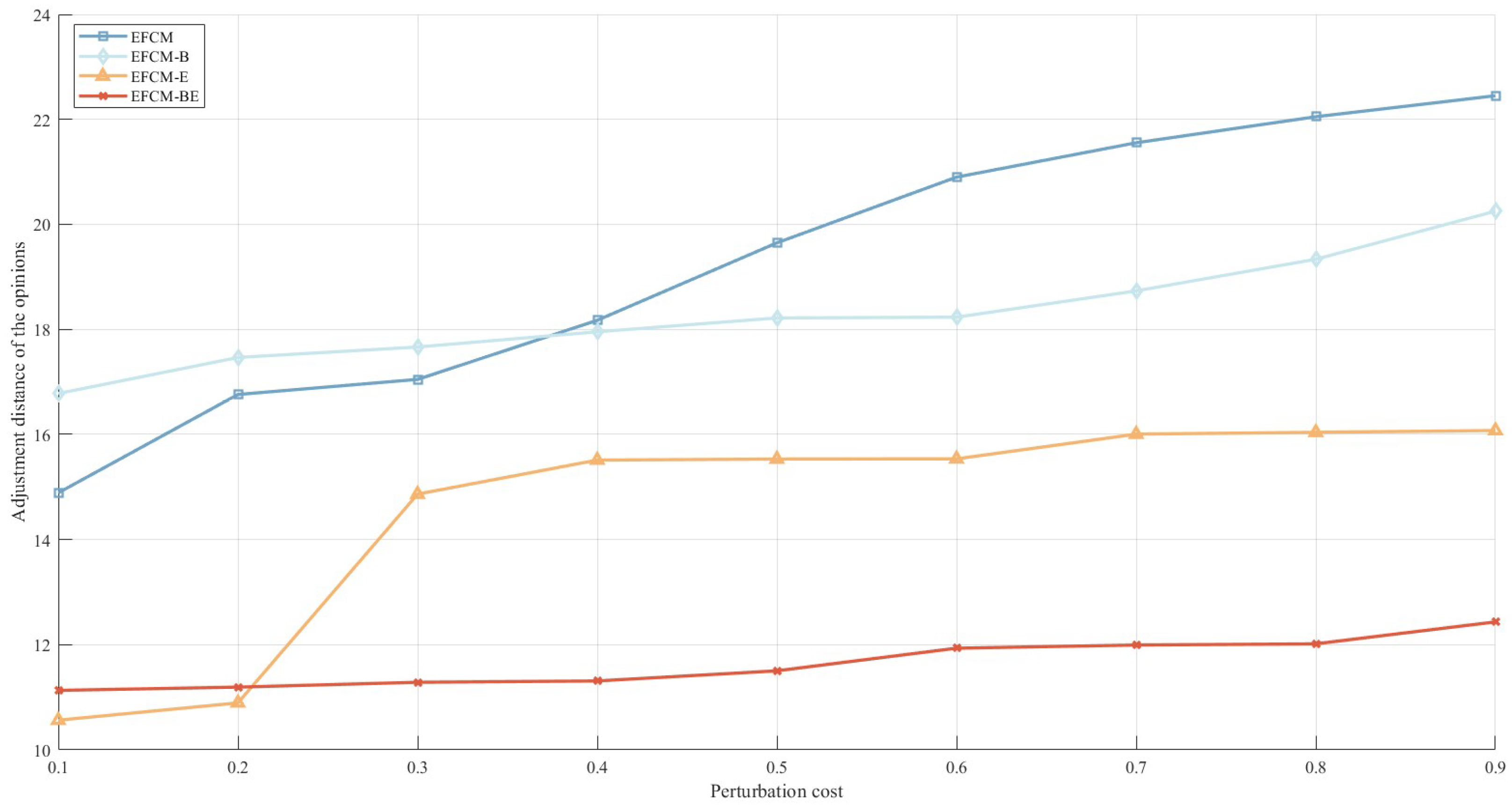
- (2)
- There are differences in the effects of the perturbation cost and uncertainty parameter level on the efficiency of reaching consensus. Specifically, with the increase in the perturbation cost, the adjustment distance of the opinion shows a trend of gradual increase. For the uncertain parameter level, when the uncertainty set is a box set and ellipsoid set, with the increase in the uncertain parameter level, the efficiency of reaching consensus decreases (the adjustment distance of the opinion increases), and when the uncertainty set is a box–ellipsoid set and a box–polyhedron set, with the increase in the uncertainty parameter level, the efficiency of reaching consensus increases (the opinion adjustment distance becomes decreases). Therefore, when faced with GDM of varying complexity, the moderator should choose different uncertainty sets with an appropriate uncertainty parameter level to accurately characterize the uncertainty cost.
- (3)
- Taking the negotiation between the government and enterprises on carbon emission reduction as an example, the government should pay full attention to the fair concern behavior shown by enterprises in the CRP, and mainly avoid DMs’ unreasonable jealousy preference behavior. Furthermore, the government can formulate a reasonable consensus cost budget to ensure a reasonable group fair utility level and the efficiency of reaching consensus.
- (1)
- Only one consensus efficiency measure is used in this paper to construct the consensus model. So, different consensus efficiency measures could be flexibly adopted for future consensus scenarios.
- (2)
- The social network structure considered in this paper is static. However, the connections between individuals may change dynamically in real SNGDM, and the individual weights evolve dynamically as a result. So, it could be possible to study consensus based on the dynamic social network structure in the future.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baucells, M.; Sarin, R.K. Group decisions with multiple criteria. Manag. Sci. 2003, 49, 1105–1118. [Google Scholar] [CrossRef]
- Hochbaum, D.S.; Levin, A. Methodologies and algorithms for group-rankings decision. Manag. Sci. 2006, 52, 1394–1408. [Google Scholar] [CrossRef]
- Wallenius, J.; Dyer, J.S.; Fishburn, P.C.; Steuer, R.E.; Zionts, S.; Deb, K. Multiple criteria decision making, multiattribute utility theory: Recent accomplishments and what lies ahead. Manag. Sci. 2008, 54, 1336–1349. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Dong, Q.; Gong, Z.; Wu, J.; Wu, Z.; Xu, Y.; Zhang, Z.; Dong, Y. Consensus in Group Decision Making: Research Progress and Prospect. J. UESTC 2021, 23, 26–37. [Google Scholar]
- Wu, J.; Chiclana, F.; Herrera-Viedma, E. Trust based consensus model for social network in an incomplete linguistic information context. Appl. Soft Comput. 2015, 35, 827–839. [Google Scholar] [CrossRef]
- Recio-García, J.A.; Quijano, L.; Díaz-Agudo, B. Including social factors in an argumentative model for group decision support systems. Decis. Support Syst. 2013, 56, 48–55. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Cabrerizo, F.J.; Chiclana, F.; Wu, J.; Cobo, M.J.; Konstantin, S. Consensus in group decision making and social networks. Stud. Inform. Control 2017, 26, 259–268. [Google Scholar] [CrossRef]
- Dong, Y.; Zha, Q.; Zhang, H.; Kou, G.; Fujita, H.; Chiclana, F.; Herrera-Viedma, E. Consensus reaching in social network group decision making: Research paradigms and challenges. Knowl.-Based Syst. 2018, 162, 3–13. [Google Scholar] [CrossRef]
- Capuano, N.; Chiclana, F.; Fujita, H.; Herrera-Viedma, E.; Loia, V. Fuzzy group decision making with incomplete information guided by social influence. IEEE Trans. Fuzzy Syst. 2017, 26, 1704–1718. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Alonso, S.; Chiclana, F.; Herrera, F. A consensus model for group decision making with incomplete fuzzy preference relations. IEEE Trans. Fuzzy Syst. 2007, 15, 863–877. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Herrera, F.; Chiclana, F. A consensus model for multiperson decision making with different preference structures. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2002, 32, 394–402. [Google Scholar] [CrossRef]
- Ben-Arieh, D.; Easton, T.; Evans, B. Minimum cost consensus with quadratic cost functions. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2008, 39, 210–217. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. A rational consensus model in group decision making using linguistic assessments. Fuzzy Sets Syst. 1997, 88, 31–49. [Google Scholar] [CrossRef]
- Zhang, H.; Dong, Y.; Chiclana, F.; Yu, S. Consensus efficiency in group decision making: A comprehensive comparative study and its optimal design. Eur. J. Oper. Res. 2019, 275, 580–598. [Google Scholar] [CrossRef]
- Zhang, H.; Kou, G.; Peng, Y. Soft consensus cost models for group decision making and economic interpretations. Eur. J. Oper. Res. 2019, 277, 964–980. [Google Scholar] [CrossRef]
- Gong, Z.; Zhang, H.; Forrest, J.; Li, L.; Xu, X. Two consensus models based on the minimum cost and maximum return regarding either all individuals or one individual. Eur. J. Oper. Res. 2015, 240, 183–192. [Google Scholar] [CrossRef]
- Liu, J.; Chan, F.T.; Li, Y.; Zhang, Y.; Deng, Y. A new optimal consensus method with minimum cost in fuzzy group decision. Knowl.-Based Syst. 2012, 35, 357–360. [Google Scholar] [CrossRef]
- Gong, Z.; Xu, X.; Lu, F.; Li, L.; Xu, C. On consensus models with utility preferences and limited budget. Appl. Soft Comput. 2015, 35, 840–849. [Google Scholar] [CrossRef]
- Gong, Z.; Xu, X.; Zhang, H.; Ozturk, U.A.; Herrera-Viedma, E.; Xu, C. The consensus models with interval preference opinions and their economic interpretation. Omega 2015, 55, 81–90. [Google Scholar] [CrossRef]
- Gong, Z.; Guo, W.; Herrera-Viedma, E.; Gong, Z.; Wei, G. Consistency and consensus modeling of linear uncertain preference relations. Eur. J. Oper. Res. 2020, 283, 290–307. [Google Scholar] [CrossRef]
- Tan, X.; Gong, Z.; Chiclana, F.; Zhang, N. Consensus modeling with cost chance constraint under uncertainty opinions. Appl. Soft Comput. 2018, 67, 721–727. [Google Scholar] [CrossRef]
- Ji, Y.; Li, H.; Zhang, H. Risk-averse two-stage stochastic minimum cost consensus models with asymmetric adjustment cost. Group Decis. Negot. 2022, 31, 261–291. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Qu, S.; Wang, Q.; Luan, D.; Zhao, X. The novel data-driven robust maximum expert mixed integer consensus models under multirole’s opinions uncertainty by considering noncooperators. IEEE Trans. Comput. Soc. Syst. 2022, 10, 3454–3470. [Google Scholar] [CrossRef]
- Gou, X.; Xu, Z.; Liao, H. Group decision making with compatibility measures of hesitant fuzzy linguistic preference relations. Soft Comput. 2019, 23, 1511–1527. [Google Scholar] [CrossRef]
- Li, H.; Ji, Y.; Gong, Z.; Qu, S. Two-stage stochastic minimum cost consensus models with asymmetric adjustment costs. Inf. Fusion 2021, 71, 77–96. [Google Scholar] [CrossRef]
- Ji, Y.; Li, Y.; Wijekoon, C. Robust two-stage minimum asymmetric cost consensus models under uncertainty circumstances. Inf. Sci. 2024, 663, 120279. [Google Scholar] [CrossRef]
- Qu, S.; Han, Y.; Wu, Z.; Raza, H. Consensus modeling with asymmetric cost based on data-driven robust optimization. Group Decis. Negot. 2021, 30, 1395–1432. [Google Scholar] [CrossRef]
- Cabrerizo, F.J.; Morente-Molinera, J.A.; Pedrycz, W.; Taghavi, A.; Herrera-Viedma, E. Granulating linguistic information in decision making under consensus and consistency. Expert Syst. Appl. 2018, 99, 83–92. [Google Scholar] [CrossRef]
- Pérez, I.J.; Cabrerizo, F.J.; Alonso, S.; Herrera-Viedma, E. A new consensus model for group decision making problems with non-homogeneous experts. IEEE Trans. Syst. Man Cybern. Syst. 2013, 44, 494–498. [Google Scholar] [CrossRef]
- Wu, Y.; Dong, Y.; Qin, J.; Pedrycz, W. Flexible linguistic expressions and consensus reaching with accurate constraints in group decision-making. IEEE Trans. Cybern. 2019, 50, 2488–2501. [Google Scholar] [CrossRef]
- Alonso, S.; Pérez, I.J.; Cabrerizo, F.J.; Herrera-Viedma, E. A linguistic consensus model for web 2.0 communities. Appl. Soft Comput. 2013, 13, 149–157. [Google Scholar] [CrossRef]
- Cheng, D.; Cheng, F.; Zhou, Z.; Wu, Y. Reaching a minimum adjustment consensus in social network group decision-making. Inf. Fusion 2020, 59, 30–43. [Google Scholar] [CrossRef]
- Liang, Q.; Liao, X.; Liu, J. A social ties-based approach for group decision-making problems with incomplete additive preference relations. Knowl.-Based Syst. 2017, 119, 68–86. [Google Scholar] [CrossRef]
- Wu, J.; Chiclana, F.; Fujita, H.; Herrera-Viedma, E. A visual interaction consensus model for social network group decision making with trust propagation. Knowl.-Based Syst. 2017, 122, 39–50. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, K.; Liu, X.; Cao, C. A two-stage social trust network partition model for large-scale group decision-making problems. Knowl.-Based Syst. 2019, 163, 632–643. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, X.; Dong, Y.; Herrera, F. Consensus reaching in social network DeGroot Model: The roles of the Self-confidence and node degree. Inf. Sci. 2019, 486, 62–72. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y.; Montes, R.; Herrera, F. Social network group decision making: Managing self-confidence-based consensus model with the dynamic importance degree of experts and trust-based feedback mechanism. Inf. Sci. 2019, 505, 215–232. [Google Scholar] [CrossRef]
- Wu, J.; Chiclana, F. A social network analysis trust–consensus based approach to group decision-making problems with interval-valued fuzzy reciprocal preference relations. Knowl.-Based Syst. 2014, 59, 97–107. [Google Scholar] [CrossRef]
- Adams, J.S. Towards an understanding of inequity. J. Abnorm. Soc. Psychol. 1963, 67, 422. [Google Scholar] [CrossRef]
- Adams, J.S. Inequity in social exchange. In Advances in Experimental Social Psychology; Elsevier: Amsterdam, The Netherlands, 1965; Volume 2, pp. 267–299. [Google Scholar]
- Kacprzyk, J.; Zadrożny, S. On a fairness type approach to consensus reaching support under fuzziness via linguistic summaries. In Proceedings of 2016 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Vancouver, BC, Canada, 24–29 July 2016; pp. 1999–2006. [Google Scholar]
- Świechowski, M.; Kacprzyk, J.; Zadrożny, S. A novel game playing based approach to the modeling and support of consensus reaching in a group of agents. In Proceedings of 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar]
- Zhang, B.; Dong, Y.; Zhang, H.; Pedrycz, W. Consensus mechanism with maximum-return modifications and minimum-cost feedback: A perspective of game theory. Eur. J. Oper. Res. 2020, 287, 546–559. [Google Scholar] [CrossRef]
- Fedrizzi, M.; Brunelli, M. Fair consistency evaluation for reciprocal relations and in group decision making. N. Math. Nat. Comput. 2009, 5, 407–420. [Google Scholar] [CrossRef]
- Fu, C.; Zhou, K.; Xue, M. Fair framework for multiple criteria decision making. Comput. Ind. Eng. 2018, 124, 379–392. [Google Scholar] [CrossRef]
- Kuhlman, C.; Rundensteiner, E. Rank aggregation algorithms for fair consensus. Proc. VLDB Endow. 2020, 13, 2706–2719. [Google Scholar] [CrossRef]
- Boiney, L.G. When efficient is insufficient: Fairness in decisions affecting a group. Manag. Sci. 1995, 41, 1523–1537. [Google Scholar] [CrossRef]
- Du, J.; Liu, S.; Liu, Y. A limited cost consensus approach with fairness concern and its application. Eur. J. Oper. Res. 2022, 298, 261–275. [Google Scholar] [CrossRef]
- Gong, G.; Li, K.; Zha, Q. A maximum fairness consensus model with limited cost in group decision making. Comput. Ind. Eng. 2023, 175, 108891. [Google Scholar] [CrossRef]
- Zhang, R.; Huang, J.; Xu, Y.; Herrera-Viedma, E. Consensus models with aggregation operators for minimum quadratic cost in group decision making. Appl. Intell. 2023, 53, 1370–1390. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Zhao, D.; Zhang, X. A fair consensus adjustment mechanism for large-scale group decision making in term of Gini coefficient. Eng. Appl. Artif. Intell. 2023, 126, 106962. [Google Scholar] [CrossRef]
- Dong, Y.; Xu, Y.; Li, H.; Feng, B. The OWA-based consensus operator under linguistic representation models using position indexes. Eur. J. Oper. Res. 2010, 203, 455–463. [Google Scholar] [CrossRef]
- Bolton, G.E.; Ockenfels, A. ERC: A theory of equity, reciprocity, and competition. Am. Econ. Rev. 2000, 91, 166–193. [Google Scholar] [CrossRef]
- Rabin, M. Incorporating fairness into game theory and economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition, and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Macmillan: London, UK, 1976; Volume 290. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Rosen, K.H. Discrete Mathematics and Its Applications; The McGraw Hill Companies: New York, NY, USA, 2007. [Google Scholar]
- Zhang, H.; Palomares, I.; Dong, Y.; Wang, W. Managing non-cooperative behaviors in consensus-based multiple attribute group decision making: An approach based on social network analysis. Knowl.-Based Syst. 2018, 162, 29–45. [Google Scholar] [CrossRef]
- Victor, P.; Cornelis, C.; De Cock, M.; Herrera-Viedma, E. Practical aggregation operators for gradual trust and distrust. Fuzzy Sets Syst. 2011, 184, 126–147. [Google Scholar] [CrossRef]
- Zadeh, L.A. A computational approach to fuzzy quantifiers in natural languages. In Computational Linguistics; Elsevier: Amsterdam, The Netherlands, 1983; pp. 149–184. [Google Scholar]
- Zhang, Y.; Chen, X.; Pedrycz, W.; Dong, Y. Consensus reaching based on social influence evolution in group decision making. IEEE Trans. Cybern. 2022, 53, 4134–4147. [Google Scholar] [CrossRef] [PubMed]
- Bertsimas, D.; Sim, M. The price of robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Han, Y.; Qu, S.; Wu, Z.; Huang, R. Robust consensus models based on minimum cost with an application to marketing plan. J. Intell. Fuzzy Syst. 2019, 37, 5655–5668. [Google Scholar] [CrossRef]


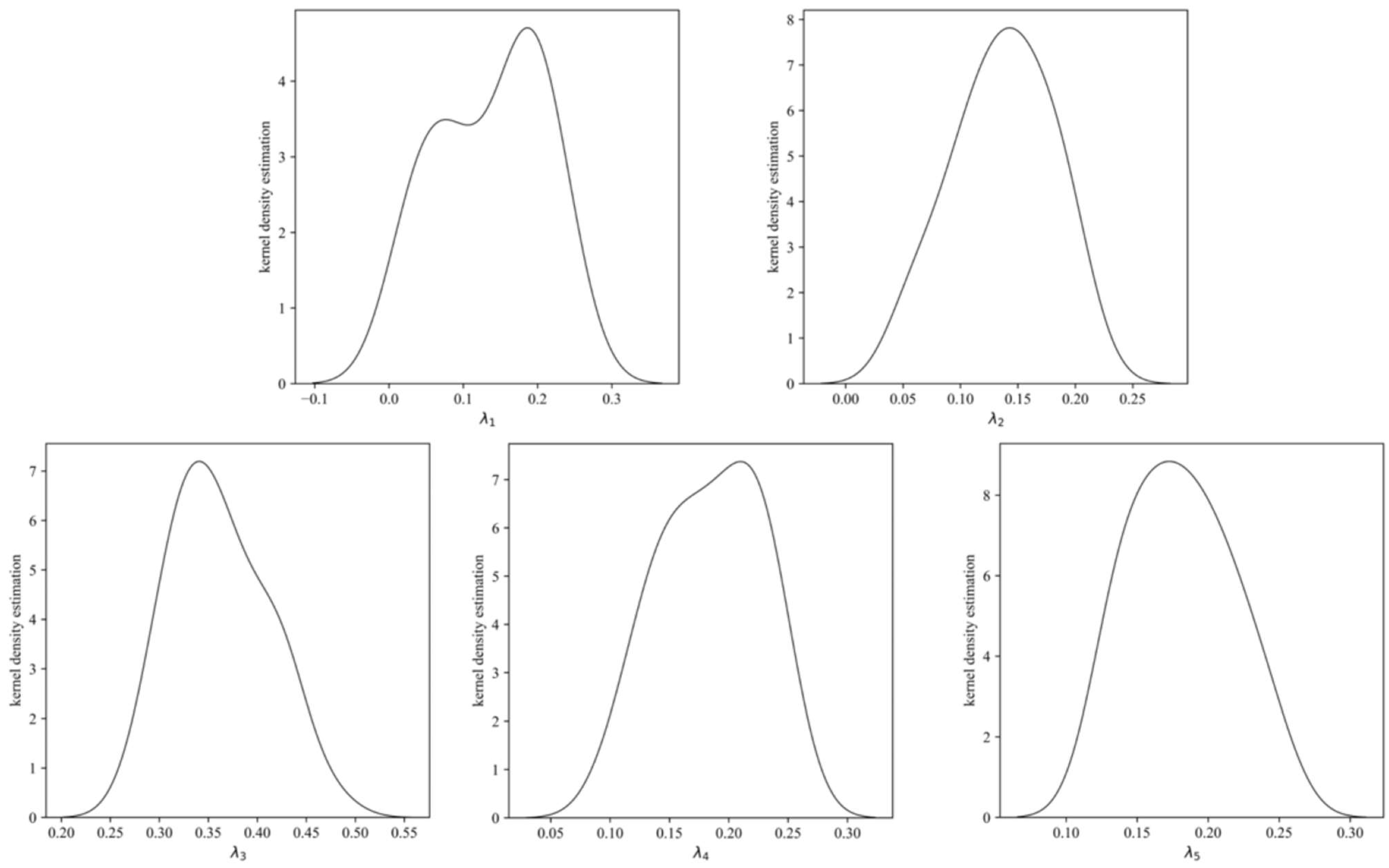





| Efficiency | ||||||||
|---|---|---|---|---|---|---|---|---|
| EFCM | 1.4298 | 0.0682 | 1.3793 | 1.0318 | 1.4222 | 0.8139 | 10.2433 | 24.9232 |
| EFCM-B | 2.1041 | 0.6746 | 0.6621 | 1.579 | 2.1057 | 1.2135 | 9.0152 | 16.0081 |
| EFCM-E | 4.0709 | 1.0934 | 3.3084 | 3.1719 | 4.4799 | 2.4631 | 7.6259 | 21.2987 |
| EFCM-BE | 1.2355 | 0.1515 | 1.5558 | 1.121 | 1.3199 | 0.7095 | 14.0438 | 16.9342 |
| EFCM-BP | 1.9271 | 0.275 | 0.5075 | 1.3518 | 1.931 | 1.1356 | 11.9539 | 23.9909 |
| MCCM-B | 0.7842 | 0 | 0.9461 | 0.4625 | 0.8824 | 77.9413 |
| MCCM-E | 0.787 | 0 | 0.9465 | 0.471 | 0.8834 | 78.8421 |
| 20 | 30 | 40 | 50 | 60 | 70 | |
|---|---|---|---|---|---|---|
| EFCM | 6.6107 | 9.7484 | 12.9206 | 14.3994 | 15.839 | 16.2425 |
| EFCM-B | 7.4818 | 10.358 | 12.9607 | 15.0529 | 16.0787 | 16.9564 |
| EFCM-E | 7.946 | 10.5183 | 14.9001 | 16.7752 | 17.4683 | 18.3472 |
| EFCM-BE | 8.7839 | 12.0972 | 17.165 | 17.4603 | 17.7757 | 17.9875 |
| EFCM-BP | 13.117 | 13.7471 | 16.4441 | 19.0974 | 21.5613 | 22.6664 |
| 20 | 30 | 40 | 50 | 60 | 70 | |
|---|---|---|---|---|---|---|
| EFCM | 20.1207 | 30.0822 | 40.05 | 43.4603 | 48.8724 | 50.0644 |
| EFCM-B | 12.5214 | 19.6475 | 27.2221 | 35.0102 | 43.9578 | 35.6324 |
| EFCM-B | 17.0516 | 25.2726 | 31.8104 | 43.1147 | 42.0282 | 31.6937 |
| EFCM-BE | 20.214 | 30.1506 | 40.2043 | 45.6546 | 39.1401 | 43.4572 |
| EFCM-BP | 20.4165 | 30.0245 | 34.3489 | 48.4952 | 50.0519 | 36.6591 |
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
|---|---|---|---|---|---|---|---|---|---|
| EFCM | 13.0172 | 14.143 | 15.3994 | 15.5407 | 15.6651 | 15.7479 | 15.9805 | 16.1608 | 16.1994 |
| EFCM-B | 15.3161 | 15.5471 | 15.6458 | 15.9569 | 16.2882 | 16.7567 | 16.9575 | 17.1141 | 17.366 |
| EFCM-E | 15.6709 | 16.4858 | 17.1722 | 15.266 | 16.7752 | 15.741 | 16.5135 | 15.4698 | 15.5382 |
| EFCM-BE | 10.1948 | 9.1038 | 11.4718 | 10.4049 | 10.8935 | 8.8979 | 8.9554 | 10.5364 | 9.3254 |
| EFCM-BP | 10.8013 | 10.888 | 11.474 | 12.0162 | 12.0857 | 12.7641 | 12.8721 | 13.3083 | 13.3464 |
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
|---|---|---|---|---|---|---|---|---|---|
| EFCM-B | 14.8867 | 16.7567 | 17.0446 | 18.1708 | 19.6465 | 20.899 | 21.5537 | 22.0501 | 22.4506 |
| EFCM-E | 16.7752 | 17.4627 | 17.6614 | 17.9514 | 18.2154 | 18.2299 | 18.7311 | 19.3342 | 20.2506 |
| EFCM-BE | 10.5635 | 10.8935 | 14.862 | 15.5095 | 15.5284 | 15.5327 | 16.0024 | 16.0374 | 16.0714 |
| EFCM-BP | 11.1307 | 11.1929 | 11.285 | 11.3102 | 11.503 | 11.9331 | 11.9933 | 12.0162 | 12.4327 |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| EFCM-B | 15.5471 | 17.1542 | 18.6913 | 20.1231 | 20.7203 |
| EFCM-E | 16.7752 | 17.0197 | 17.7207 | 18.6869 | 19.4116 |
| EFCM-BE | 13.0068 | 10.8935 | 9.6779 | 9.4527 | 9.2381 |
| EFCM-BP | 16.5269 | 11.6638 | 11.5449 | 11.4584 | 11.4059 |
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
|---|---|---|---|---|---|---|---|---|---|
| EFCM | 15.8481 | 15.6333 | 15.6144 | 15.3462 | 15.0359 | 14.3994 | 13.0294 | 12.854 | 10.9792 |
| EFCM-B | 19.0852 | 18.9557 | 18.8851 | 18.7421 | 18.626 | 15.5471 | 15.0112 | 14.6771 | 13.0382 |
| EFCM-E | 18.3098 | 17.7684 | 17.0651 | 16.8359 | 16.7752 | 16.3747 | 16.3454 | 14.6241 | 13.1201 |
| EFCM-BE | 14.4774 | 14.9848 | 15.0872 | 15.3507 | 15.6197 | 16.6413 | 17.8202 | 18.3536 | 18.3674 |
| EFCM-BP | 11.0231 | 11.0946 | 11.1709 | 11.4438 | 11.7217 | 12.076 | 12.7541 | 15.5456 | 16.5269 |
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| EFCM | 15.0828 | 15.0836 | 15.0824 | 15.0826 | 15.0832 | 15.0833 | 15.0805 | 15.0797 | 15.0804 | 15.0798 | 15.5921 |
| EFCM-B | 18.9297 | 18.9247 | 19.2734 | 19.2315 | 18.7989 | 18.7923 | 18.7793 | 18.7543 | 18.7513 | 18.7393 | 18.7325 |
| EFCM-E | 18.0057 | 18.3617 | 18.4923 | 19.1581 | 17.577 | 18.6388 | 18.6092 | 18.6166 | 18.6382 | 18.5911 | 18.6464 |
| EFCM-BE | 13.764 | 13.2629 | 14.0104 | 14.1305 | 14.1447 | 13.9202 | 13.8389 | 13.3599 | 13.3706 | 14.1217 | 14.2109 |
| EFCM-BP | 10.9244 | 10.9187 | 10.9137 | 10.9049 | 10.8953 | 10.8857 | 10.876 | 10.8662 | 10.8565 | 10.8469 | 10.8376 |
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| EFCM | 12.7218 | 12.851 | 12.912 | 12.929 | 12.965 | 13.029 | 13.166 | 13.469 | 13.706 | 15.239 | 15.291 |
| EFCM-B | 13.1835 | 13.186 | 13.188 | 13.192 | 13.194 | 13.196 | 13.197 | 13.200 | 15.040 | 16.143 | 16.446 |
| EFCM-E | 13.4631 | 13.469 | 13.834 | 14.042 | 14.629 | 16.407 | 16.856 | 16.902 | 16.909 | 17.172 | 17.334 |
| EFCM-BE | 16.2986 | 16.344 | 16.833 | 17.112 | 17.622 | 17.816 | 17.972 | 18.250 | 18.316 | 18.398 | 18.446 |
| EFCM-BP | 11.4241 | 11.92 | 12.076 | 12.082 | 12.168 | 12.30 | 12.53 | 12.567 | 12.597 | 13.782 | 15.146 |
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| EFCM | 15.083 | 15.088 | 15.100 | 15.079 | 15.083 | 15.083 | 15.410 | 15.707 | 16.611 | 16.202 | 17.014 |
| EFCM-B | 18.930 | 18.913 | 18.910 | 18.665 | 18.757 | 18.754 | 18.423 | 19.696 | 19.668 | 19.875 | 20.558 |
| EFCM-E | 18.006 | 18.186 | 18.279 | 17.868 | 18.621 | 18.331 | 17.255 | 19.354 | 19.898 | 17.799 | 18.834 |
| EFCM-BE | 16.759 | 15.961 | 12.828 | 17.077 | 17.295 | 13.599 | 13.760 | 13.916 | 12.086 | 13.550 | 16.587 |
| EFCM-BP | 10.924 | 10.927 | 10.922 | 10.911 | 10.894 | 10.876 | 11.096 | 11.549 | 12.498 | 12.302 | 11.741 |
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| EFCM | 15.965 | 15.140 | 15.806 | 15.961 | 15.933 | 15.076 | 15.982 | 15.708 | 15.897 | 16.931 | 16.215 |
| EFCM-B | 19.250 | 18.954 | 19.177 | 18.835 | 18.914 | 18.992 | 19.134 | 19.640 | 19.782 | 19.849 | 20.014 |
| EFCM-E | 16.941 | 18.815 | 18.969 | 18.914 | 18.702 | 18.839 | 18.923 | 16.698 | 19.557 | 18.026 | 21.330 |
| EFCM-BE | 17.527 | 17.689 | 16.500 | 14.830 | 17.819 | 19.078 | 17.941 | 18.867 | 21.041 | 20.762 | 15.708 |
| EFCM-BP | 10.852 | 10.818 | 10.885 | 10.868 | 10.858 | 10.868 | 11.419 | 11.536 | 13.329 | 12.177 | 14.038 |
| −1 | −0.9 | −0.8 | −0.7 | −0.6 | −0.5 | −0.4 | −0.3 | −0.2 | −0.1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| EFCM | 15.127 | 15.119 | 15.747 | 15.763 | 15.068 | 15.104 | 15.103 | 15.101 | 15.094 | 15.091 | 15.083 |
| EFCM-B | 18.822 | 18.809 | 18.796 | 18.769 | 18.738 | 18.747 | 18.625 | 18.620 | 19.158 | 18.930 | 18.715 |
| EFCM-E | 18.682 | 18.683 | 18.689 | 18.612 | 18.614 | 18.588 | 18.551 | 18.473 | 18.553 | 19.091 | 18.006 |
| EFCM-BE | 10.158 | 10.462 | 10.036 | 10.393 | 10.393 | 10.289 | 10.792 | 10.87 | 10.951 | 10.759 | 10.345 |
| EFCM-BP | 10.809 | 10.712 | 10.697 | 10.682 | 10.666 | 10.659 | 10.604 | 10.591 | 10.588 | 10.597 | 10.924 |
| −1 | −0.9 | −0.8 | −0.7 | −0.6 | −0.5 | −0.4 | −0.3 | −0.2 | −0.1 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| EFCM | 15.497 | 15.871 | 15.858 | 16.078 | 15.823 | 15.733 | 15.493 | 15.837 | 15.423 | 15.387 | 15.828 |
| EFCM-B | 18.676 | 18.916 | 18.702 | 18.676 | 18.713 | 18.721 | 18.721 | 18.730 | 18.453 | 18.948 | 18.850 |
| EFCM-E | 18.861 | 18.408 | 18.631 | 18.883 | 18.411 | 18.534 | 18.616 | 18.763 | 18.696 | 18.985 | 18.590 |
| EFCM-BE | 10.296 | 2.938 | 2.945 | 4.524 | 4.253 | 2.037 | 1.996 | 11.463 | 14.708 | 7.852 | 8.236 |
| EFCM-BP | 10.613 | 10.611 | 10.614 | 10.630 | 10.658 | 10.495 | 10.527 | 10.569 | 10.665 | 10.799 | 10.627 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Liang, H.; Qu, S. Robust Consensus Modeling: Concerning Consensus Fairness and Efficiency with Uncertain Costs. Mathematics 2024, 12, 1266. https://doi.org/10.3390/math12081266
Zhang X, Liang H, Qu S. Robust Consensus Modeling: Concerning Consensus Fairness and Efficiency with Uncertain Costs. Mathematics. 2024; 12(8):1266. https://doi.org/10.3390/math12081266
Chicago/Turabian StyleZhang, Xuyuan, Hailin Liang, and Shaojian Qu. 2024. "Robust Consensus Modeling: Concerning Consensus Fairness and Efficiency with Uncertain Costs" Mathematics 12, no. 8: 1266. https://doi.org/10.3390/math12081266
APA StyleZhang, X., Liang, H., & Qu, S. (2024). Robust Consensus Modeling: Concerning Consensus Fairness and Efficiency with Uncertain Costs. Mathematics, 12(8), 1266. https://doi.org/10.3390/math12081266







