Robust Bias Compensation Method for Sparse Normalized Quasi-Newton Least-Mean with Variable Mixing-Norm Adaptive Filtering
Abstract
:1. Introduction
2. System Models

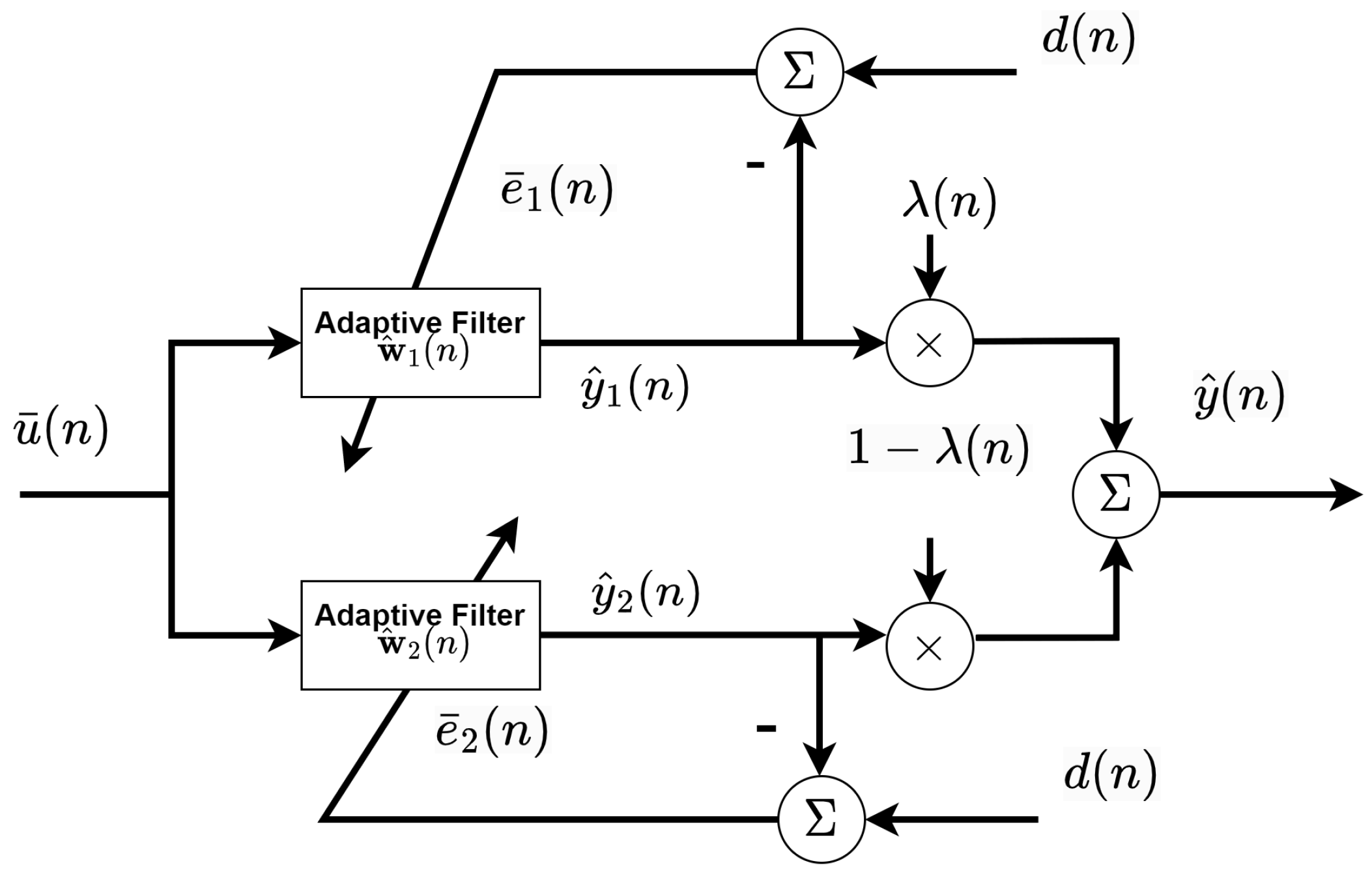
3. Proposed BC-SNQNLM-VMN Adaptive Filtering Algorithm
3.1. Review of SQNLMMN Algorithm [13]
3.2. Normalized SQNLMMN
3.3. Bias Compensation Design
3.4. Variable Mixing Parameter Design
3.5. Robustness Consideration
3.6. Computational Cost Analysis
4. Simulation Results
4.1. Setup
4.2. Results
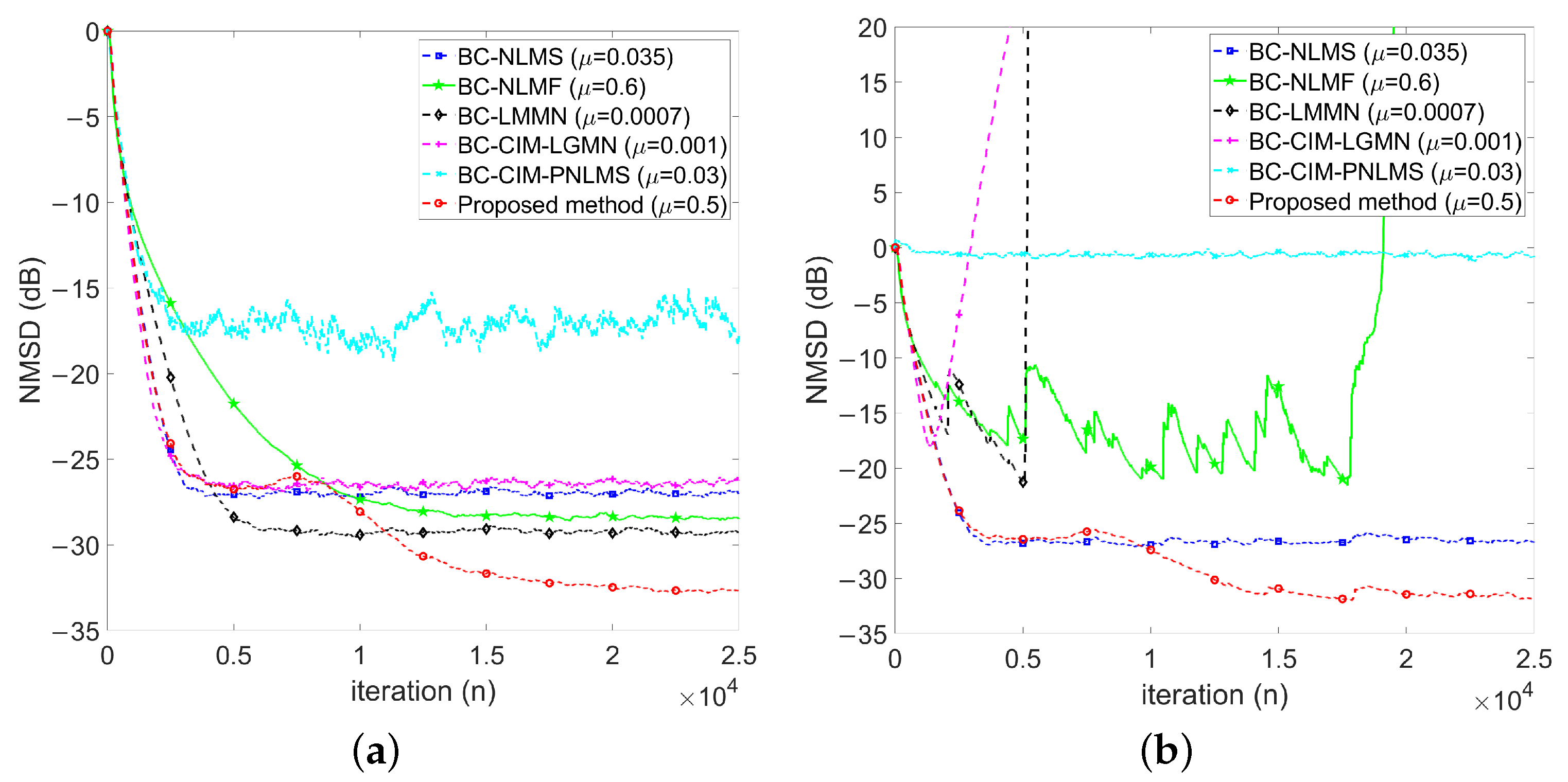
4.2.1. Baseline: No Impulse Noise
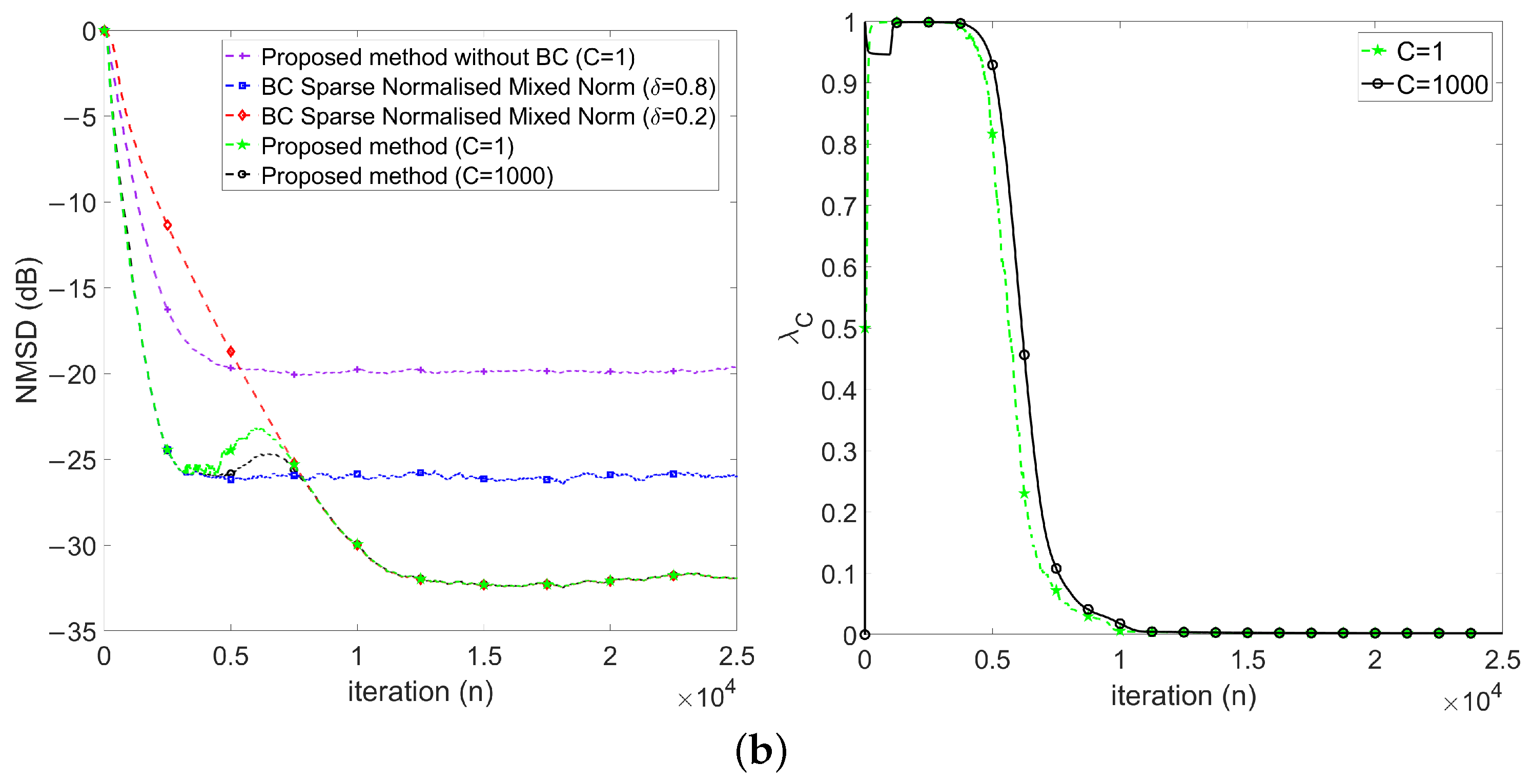
4.2.2. Evaluation of Variable Mixing Parameter Method
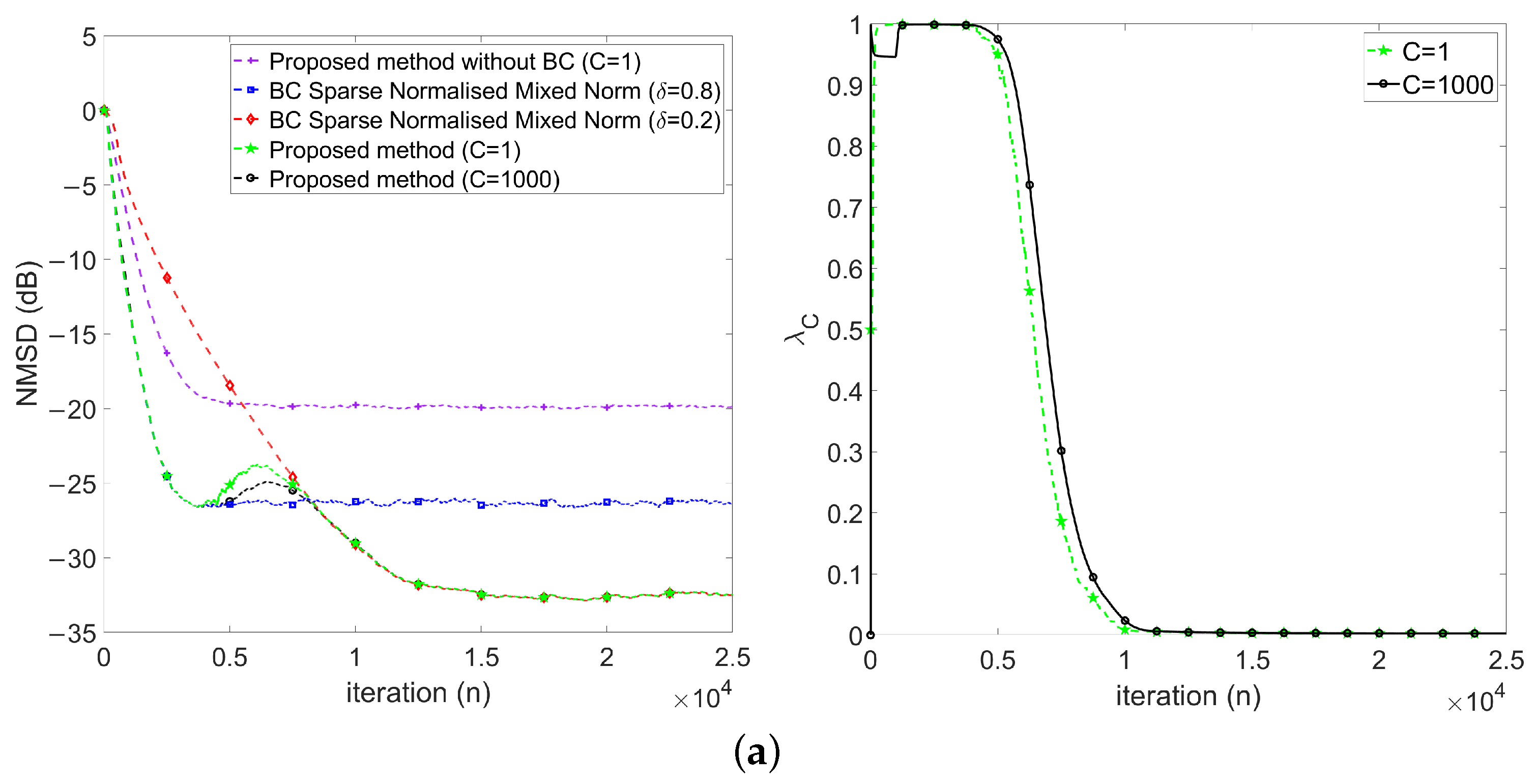
- First, keeps at 1 in the early stage (), which implies the proposed method behaves like .
- Then, decreases gradually during the transient stage (), which implies the proposed method behaves changing from to .
- Finally, keeps around 0 in the steady-state stage ().
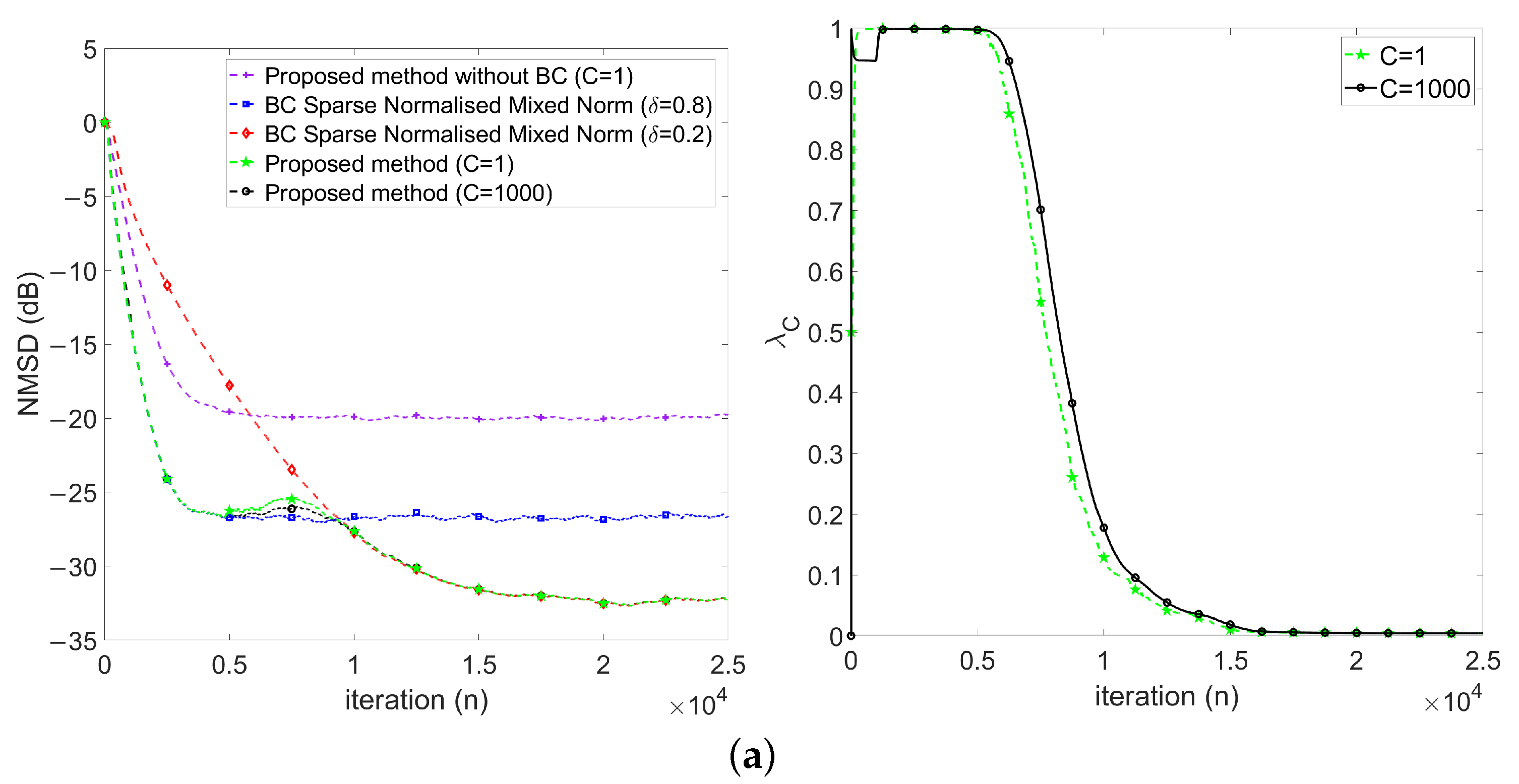
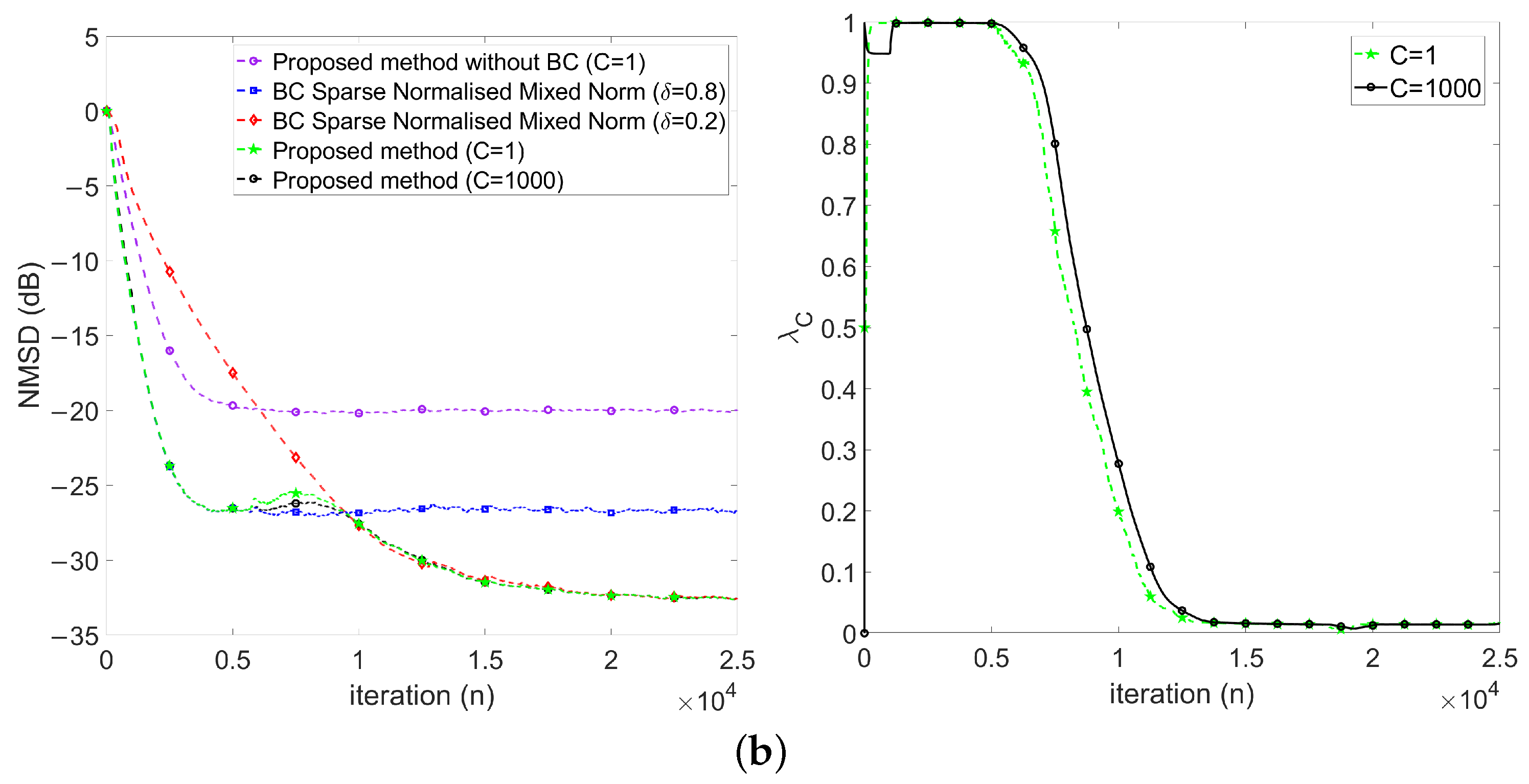
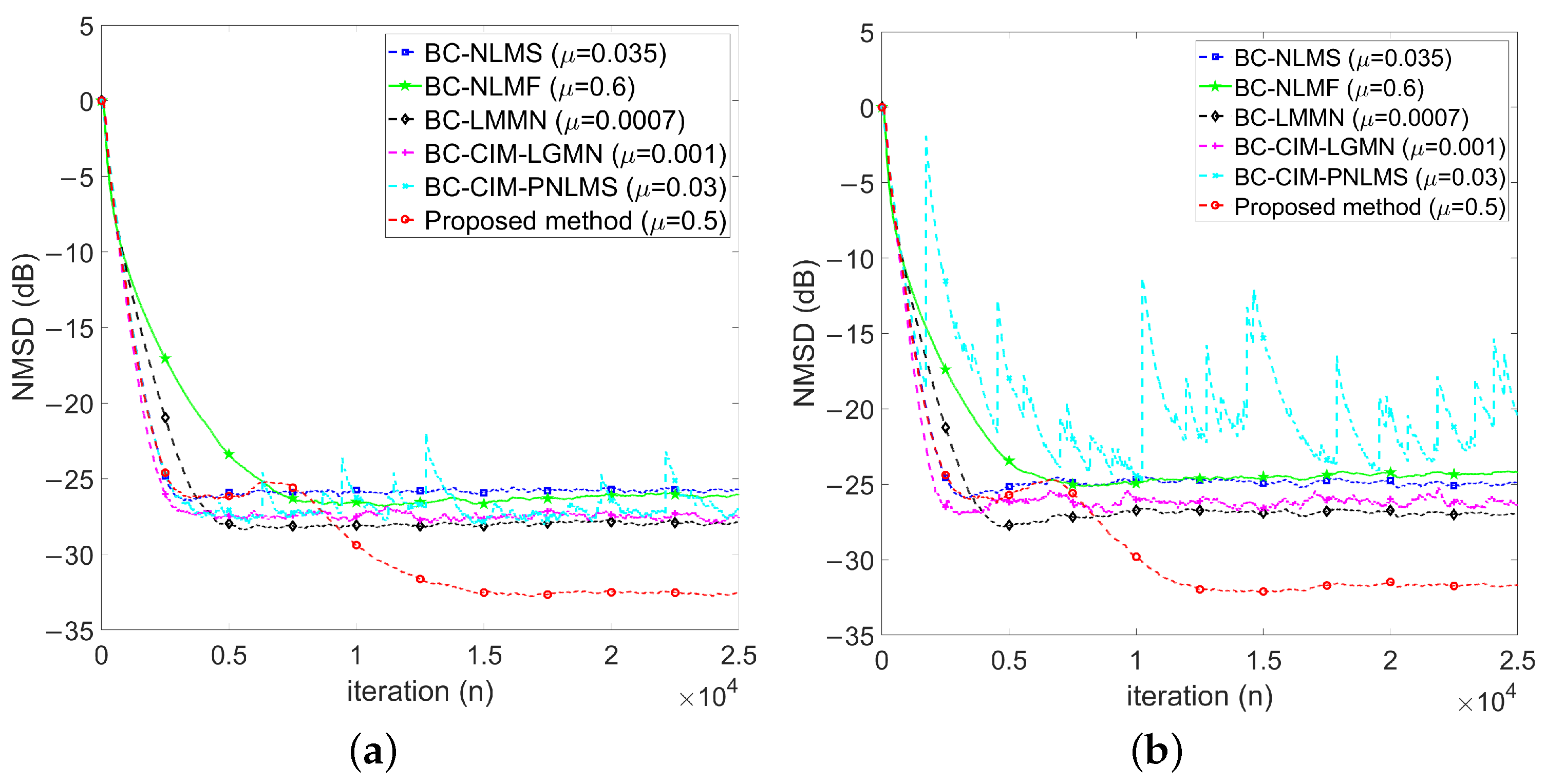
4.2.3. Performance Comparisons in the Presence of Impulse Noise
5. Conclusions and Future Prospects
- The interaction between weight-vector correction term and bias compensation term (see Equation (42)): We have employed a constant scaling factor, , to mitigate the interaction between the weight-vector correction term, , and the bias compensation term, . Nonetheless, devising a dynamic algorithm for adapting would enhance the robustness of bias compensation methods to varying input noise over time or in scenarios involving time-varying unknown systems.
- Extension to general mixed-norm algorithms: While our study focused on and norms, the methodology can be extended to encompass bias compensation in adaptive filtering algorithms utilizing a mix of and norms, where p and q are positive parameters.
- Bias compensation for non-linear adaptive filtering systems: Addressing bias compensation becomes notably intricate in non-linear adaptive filtering systems. A future avenue of research involves developing techniques to estimate biases induced by noisy inputs in such non-linear contexts.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diniz, P.S.R. Adaptive Filtering Algorithms and Practical Implementation, 5th ed.; Springer: New York, NY, USA, 2020. [Google Scholar]
- Tan, G.; Yan, S.; Yang, B. Impulsive Noise Suppression and Concatenated Code for OFDM Underwater Acoustic Communications. In Proceedings of the 2022 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xi’an, China, 25–27 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Yan, S.; Shi, W.; Yang, X.; Guo, Y.; Gulliver, T.A. A Novel Underwater Acoustic Signal Denoising Algorithm for Gaussian/Non-Gaussian Impulsive Noise. IEEE Trans. Veh. Technol. 2021, 70, 429–445. [Google Scholar] [CrossRef]
- Diamant, R. Robust Interference Cancellation of Chirp and CW Signals for Underwater Acoustics Applications. IEEE Access 2018, 6, 4405–4415. [Google Scholar] [CrossRef]
- Ge, F.X.; Zhang, Y.; Li, Z.; Zhang, R. Adaptive Bubble Pulse Cancellation From Underwater Explosive Charge Acoustic Signals. IEEE J. Oceanic Eng. 2011, 36, 447–453. [Google Scholar] [CrossRef]
- Fieve, S.; Portala, P.; Bertel, L. A new VLF/LF atmospheric noise model. Radio Sci. 2007, 42, 1–14. [Google Scholar] [CrossRef]
- Rehman, I.u.; Raza, H.; Razzaq, N.; Frnda, J.; Zaidi, T.; Abbasi, W.; Anwar, M.S. A Computationally Efficient Distributed Framework for a State Space Adaptive Filter for the Removal of PLI from Cardiac Signals. Mathematics 2023, 11, 350. [Google Scholar] [CrossRef]
- Peng, L.; Zang, G.; Gao, Y.; Sha, N.; Xi, C. LMS Adaptive Interference Cancellation in Physical Layer Security Communication System Based on Artificial Interference. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018; pp. 1178–1182. [Google Scholar] [CrossRef]
- Chen, Y.E.; Chien, Y.R.; Tsao, H.W. Chirp-Like Jamming Mitigation for GPS Receivers Using Wavelet-Packet-Transform-Assisted Adaptive Filters. In Proceedings of the 2016 International Computer Symposium (ICS), Chiayi, Taiwan, 15–17 December 2016; pp. 458–461. [Google Scholar] [CrossRef]
- Yu, H.C.; Chien, Y.R.; Tsao, H.W. A study of impulsive noise immunity for wavelet-OFDM-based power line communications. In Proceedings of the 2016 International Conference On Communication Problem-Solving (ICCP), Taipei, Taiwan, 7–9 September 2016; pp. 1–2. [Google Scholar] [CrossRef]
- Chien, Y.R.; Wu, S.T.; Tsao, H.W.; Diniz, P.S.R. Correntropy-Based Data Selective Adaptive Filtering. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 754–766. [Google Scholar] [CrossRef]
- Chien, Y.R.; Xu, S.S.D.; Ho, D.Y. Combined boosted variable step-size affine projection sign algorithm for environments with impulsive noise. Digit. Signal Process. 2023, 140, 104110. [Google Scholar] [CrossRef]
- Maleki, N.; Azghani, M. Sparse Mixed Norm Adaptive Filtering Technique. Circuits Syst. Signal Process. 2020, 39, 5758–5775. [Google Scholar] [CrossRef]
- Shao, M.; Nikias, C. Signal processing with fractional lower order moments: Stable processes and their applications. Proc. IEEE 1993, 81, 986–1010. [Google Scholar] [CrossRef]
- Huang, F.; Song, F.; Zhang, S.; So, H.C.; Yang, J. Robust Bias-Compensated LMS Algorithm: Design, Performance Analysis and Applications. IEEE Trans. Veh. Technol. 2023, 72, 13214–13228. [Google Scholar] [CrossRef]
- Danaee, A.; Lamare, R.C.d.; Nascimento, V.H. Distributed Quantization-Aware RLS Learning With Bias Compensation and Coarsely Quantized Signals. IEEE Trans. Signal Process. 2022, 70, 3441–3455. [Google Scholar] [CrossRef]
- Walach, E.; Widrow, B. The least mean fourth (LMF) adaptive algorithm and its family. IEEE Trans. Inform. Theory 1984, 30, 275–283. [Google Scholar] [CrossRef]
- Balasundar, C.; Sundarabalan, C.K.; Santhanam, S.N.; Sharma, J.; Guerrero, J.M. Mixed Step Size Normalized Least Mean Fourth Algorithm of DSTATCOM Integrated Electric Vehicle Charging Station. IEEE Trans. Ind. Inform. 2023, 19, 7583–7591. [Google Scholar] [CrossRef]
- Papoulis, E.; Stathaki, T. A normalized robust mixed-norm adaptive algorithm for system identification. IEEE Signal Process. Lett. 2004, 11, 56–59. [Google Scholar] [CrossRef]
- Zerguine, A. A variable-parameter normalized mixed-norm (VPNMN) adaptive algorithm. Eurasip J. Adv. Signal Process. 2012, 2012, 55. [Google Scholar] [CrossRef]
- Pimenta, R.M.S.; Petraglia, M.R.; Haddad, D.B. Stability analysis of the bias compensated LMS algorithm. Digital Signal Process. 2024, 147, 104395. [Google Scholar] [CrossRef]
- Jung, S.M.; Park, P. Normalised least-mean-square algorithm for adaptive filtering of impulsive measurement noises and noisy inputs. Electron. Lett. 2013, 49, 1270–1272. [Google Scholar] [CrossRef]
- Jin, Z.; Guo, L.; Li, Y. The Bias-Compensated Proportionate NLMS Algorithm With Sparse Penalty Constraint. IEEE Access 2020, 8, 4954–4962. [Google Scholar] [CrossRef]
- Lee, M.; Park, T.; Park, P. Bias-Compensated Normalized Least Mean Fourth Algorithm for Adaptive Filtering of Impulsive Measurement Noises and Noisy Inputs. In Proceedings of the 2019 12th Asian Control Conference (ASCC), Kitakyushu, Japan, 9–12 June 2019; pp. 220–223. [Google Scholar]
- Vasundhara. Robust filtering employing bias compensated M-estimate affine-projection-like algorithm. Electron. Lett. 2020, 56, 241–243. [Google Scholar] [CrossRef]
- Lee, M.; Park, I.S.; Park, C.e.; Lee, H.; Park, P. Bias Compensated Least Mean Mixed-norm Adaptive Filtering Algorithm Robust to Impulsive Noises. In Proceedings of the 2020 20th International Conference on Control, Automation and Systems (ICCAS), Busan, Republic of Korea, 13–16 October 2020; pp. 652–657. [Google Scholar] [CrossRef]
- Ma, W.; Zheng, D.; Zhang, Z. Bias-compensated generalized mixed norm algorithm via CIM constraints for sparse system identification with noisy input. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 5094–5099. [Google Scholar] [CrossRef]
- Yoo, J.; Shin, J.; Park, P. An Improved NLMS Algorithm in Sparse Systems Against Noisy Input Signals. IEEE Trans. Circuits Syst. Express Briefs 2015, 62, 271–275. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, H. Efficient DOA Estimation Method Using Bias-Compensated Adaptive Filtering. IEEE Trans. Veh. Technol. 2020, 69, 13087–13097. [Google Scholar] [CrossRef]
- Kim, S.R.; Efron, A. Adaptive robust impulse noise filtering. IEEE Transa. Signal Process. 1995, 43, 1855–1866. [Google Scholar] [CrossRef]
- Gu, Y.; Jin, J.; Mei, S. l0 Norm Constraint LMS Algorithm for Sparse System Identification. IEEE Signal Process. Lett. 2009, 16, 774–777. [Google Scholar] [CrossRef]
- Eweda, E. Global Stabilization of the Least Mean Fourth Algorithm. IEEE Trans. Signal Process. 2012, 60, 1473–1477. [Google Scholar] [CrossRef]
- Zheng, Z.; Liu, Z.; Zhao, H. Bias-Compensated Normalized Least-Mean Fourth Algorithm for Noisy Input. Circuits Syst. Signal Process. 2017, 36, 3864–3873. [Google Scholar] [CrossRef]
- Zhao, H.; Zheng, Z. Bias-compensated affine-projection-like algorithms with noisy input. Electron. Lett. 2016, 52, 712–714. [Google Scholar] [CrossRef]
- Arenas-Garcia, J.; Figueiras-Vidal, A.; Sayed, A. Mean-square performance of a convex combination of two adaptive filters. IEEE Trans. Signal Process. 2006, 54, 1078–1090. [Google Scholar] [CrossRef]
- Lu, L.; Zhao, H.; Li, K.; Chen, B. A Novel Normalized Sign Algorithm for System Identification Under Impulsive Noise Interference. Circuits Syst. Signal Process. 2015, 35, 3244–3265. [Google Scholar] [CrossRef]
- Zhou, Y.; Chan, S.C.; Ho, K.L. New Sequential Partial-Update Least Mean M-Estimate Algorithms for Robust Adaptive System Identification in Impulsive Noise. IEEE Trans. Ind. Electron. 2011, 58, 4455–4470. [Google Scholar] [CrossRef]
- Jung, S.M.; Park, P. Stabilization of a Bias-Compensated Normalized Least-Mean-Square Algorithm for Noisy Inputs. IEEE Trans. Signal Process. 2017, 65, 2949–2961. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chien, Y.-R.; Hsieh, H.-E.; Qian, G. Robust Bias Compensation Method for Sparse Normalized Quasi-Newton Least-Mean with Variable Mixing-Norm Adaptive Filtering. Mathematics 2024, 12, 1310. https://doi.org/10.3390/math12091310
Chien Y-R, Hsieh H-E, Qian G. Robust Bias Compensation Method for Sparse Normalized Quasi-Newton Least-Mean with Variable Mixing-Norm Adaptive Filtering. Mathematics. 2024; 12(9):1310. https://doi.org/10.3390/math12091310
Chicago/Turabian StyleChien, Ying-Ren, Han-En Hsieh, and Guobing Qian. 2024. "Robust Bias Compensation Method for Sparse Normalized Quasi-Newton Least-Mean with Variable Mixing-Norm Adaptive Filtering" Mathematics 12, no. 9: 1310. https://doi.org/10.3390/math12091310
APA StyleChien, Y.-R., Hsieh, H.-E., & Qian, G. (2024). Robust Bias Compensation Method for Sparse Normalized Quasi-Newton Least-Mean with Variable Mixing-Norm Adaptive Filtering. Mathematics, 12(9), 1310. https://doi.org/10.3390/math12091310







