Fast Eigenvalue Decomposition of Arrowhead and Diagonal-Plus-Rank-k Matrices of Quaternions
Abstract
:1. Introduction and Definitions
1.1. Quaternions
1.2. Matrices of Quaternions
1.3. Arrowhead and Diagonal-Plus-Rank-k Matrices
1.4. Fast Multiplication and Inverses of Arrow and DPRk Matrices
2. Methods for Eigenvalue Decomposition
2.1. A Quaternion QR Algorithm
| Algorithm 1 Computing all eigenpairs of a quaternion matrix |
|
2.2. Rayleigh Quotient Iterations
2.3. Rayleigh Quotient Iterations with Double Shifts
2.4. Wielandt’s Deflation
2.5. Deflation for Arrow Matrices
2.5.1. Computing the Eigenvectors of Arrow Matrices
2.5.2. Complete Algorithm for Arrow Matrices
- Equation (17) is solved for (the first element of the eigenvector of the larger matrix). The quantity is the last element of the eigenvectors and was stored in the forward pass.
- The first element of the eigenvector of the super-matrix is updated (set to ).
- The last element of the eigenvectors of the super-matrix is updated using (14).
- the absolutely largest eigenvalue and its eigenvector (unchanged from the first run of the RQIds);
- all other eigenvalues and the last elements of their corresponding eigenvectors.
| Algorithm 2 Computing all eigenpairs of an arrow matrix |
|
2.6. Deflation for DPRk Matrices
2.6.1. Computing the Eigenvectors of DPRk Matrices
2.6.2. Complete Algorithm for DPRk Matrices
- The absolutely largest eigenvalue and its eigenvector (unchanged from the first run of the RQIds);
- All other eigenvalues and the first elements of their corresponding eigenvectors.
| Algorithm 3 Computing all eigenpairs of a DPRk matrix |
|
3. Perturbation Theory, Error Analysis and Error Bounds
3.1. Perturbation Theory
3.2. Errors of Basic Operations
3.3. Error Bounds for Algorithms 2 and 3
4. Numerical Results
5. Discussion and Conclusions
- Efficient algorithms for computing eigenvalue decompositions of arrow and DPRk matrices of quaternions;
- The algorithms require arithmetic operations, n being the order of the matrix;
- Algorithms have proven error bounds;
- Experiments demonstrate that the computable residual is a good estimate of actual errors;
- Experiments demonstrate that actual errors are even smaller than predicted by the residuals;
- In all experiments, errors and residuals are of the order of tolerance from Algorithms 2 and 3;
- Experiments demonstrate that Rayleigh Quotient Iteration with double-shifts is efficient for non-Hermitian matrices;
- Algorithms 2 and 3 compare favorably in terms of accuracy and speed to the quaternion QR method for general matrices from Algorithm 1.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bunse-Gerstner, A.; Byers, R.; Mehrmann, V. A quaternion QR algorithm. Numer. Math. 1989, 55, 83–95. [Google Scholar]
- Ahmad, S.S.; Ali, I.; Slapničar, I. Perturbation analysis of matrices over a quaternion division algebra. Electron. Trans. Numer. Anal. 2021, 54, 128–149. [Google Scholar] [CrossRef]
- Baker, A. Right eigenvalues for quaternionic matrices: A topological approach. Linear Algebra Appl. 1999, 286, 303–309. [Google Scholar] [CrossRef]
- Farenick, D.R.; Pidkowich, B.A. The spectral theorem in quaternions. Linear Algebra Appl. 2003, 371, 75–102. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, Q.; Pang, H.K.; Zhao, M. Computing Partial Quaternion Eigenpairs with Quaternion Shift. J. Sci. Comput. 2023, 97, 41:1–41:21. [Google Scholar] [CrossRef]
- Lee, H.C. Eigenvalues and canonical forms of matrices with quaternion coefficients. Proc. R. Irish. Acad. 1949, 52, 253–260. [Google Scholar]
- De Leo, S.; Scolarici, G. Right eigenvalue equation in quaternionic quantum mechanics. J. Phys. A 2000, 33, 2971–2995. [Google Scholar]
- Tisseur, F.; Meerbergen, K. Quadratic eigenvalue problem. SIAM Rev. 2001, 43, 235–286. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 4th ed.; The John Hopkins University Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Najafi, H.S.; Edalatpanah, S.A.; Gravvanis, G.A. An efficient method for computing the inverse of arrowhead matrices. Appl. Math. Lett. 2014, 33, 1–5. [Google Scholar] [CrossRef]
- Jakovčević Stor, N.; Slapničar, I.; Barlow, J.L. Accurate eigenvalue decomposition of real symmetric arrowhead matrices and applications. Linear Algebra Appl. 2015, 464, 62–89. [Google Scholar] [CrossRef]
- Jakovčević Stor, N.; Slapničar, I.; Barlow, J.L. Forward stable eigenvalue decomposition of rank-one modifications of diagonal matrices. Linear Algebra Appl. 2015, 487, 301–315. [Google Scholar] [CrossRef]
- Saad, Y. Numerical Methods for Large Eigenvalue Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2011. [Google Scholar] [CrossRef]
- Watkins, D.S. Unsymmetric Matrix Eigenvalue Techniques. In Handbook of Linear Algebra; Hogben, L., Ed.; CRC Press: Boca Raton, FL, USA, 2014; Chapter 56; pp. 1–12. [Google Scholar] [CrossRef]
- Hamilton, W.R., Sr. Lectures on Quaternions; Hodges and Smith: London, UK, 1853. [Google Scholar]
- Hamilton, W.R., Sr. Elements of Quaternions; Longmans, Green and Co.: London, UK, 1866. [Google Scholar]
- Sudbery, A. Quaternionic analysis. Math. Proc. Camb. Philos. Soc. 1979, 85, 199–225. [Google Scholar] [CrossRef]
- The Julia Language. Version 1.10.2. Available online: http://julialang.org/ (accessed on 9 February 2024).
- Quaternions.jl. Version 0.7.4. Available online: https://github.com/JuliaGeometry/Quaternions.jl (accessed on 9 February 2024).
- Jakovčević Stor, N.; Slapničar, I. Fast multiplication, determinants and inverses of arrowhead and diagonal-plus-rank-one matrices over associative fields. arXiv 2022, arXiv:2212.10966. [Google Scholar]
- Matrix Algorithms for Non-Commutative Associative Algebras. Available online: https://github.com/ivanslapnicar/MANAA/ (accessed on 9 February 2024).
- Joldeş, M.; Muller, J.-M. Algorithms for manipulating quaternions in floating-point arithmetic. In Proceedings of the 2020 IEEE 27th Symposium on Computer Arithmetic (ARITH), Portland, OR, USA, 7–10 June 2020; pp. 48–55. [Google Scholar] [CrossRef]
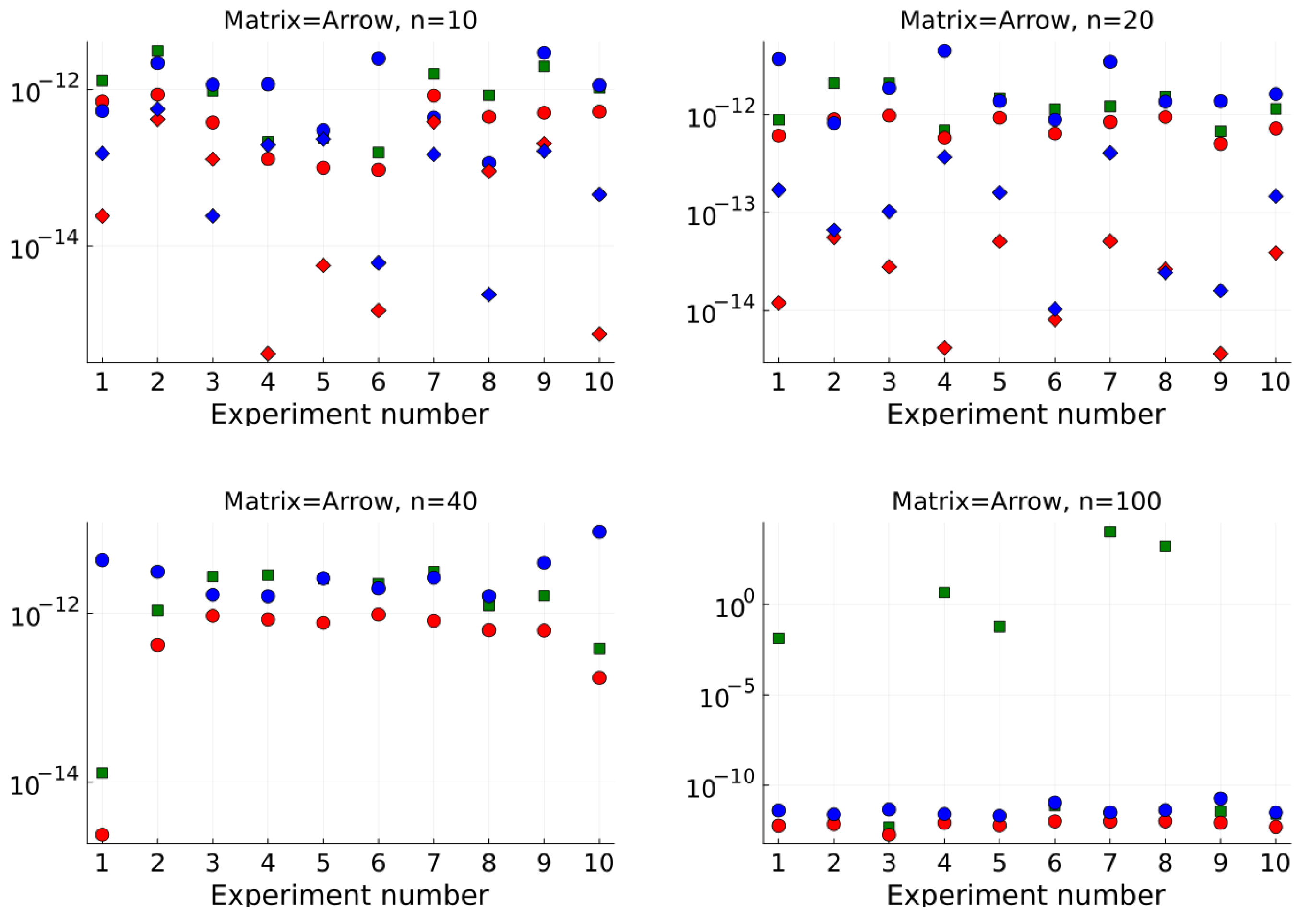
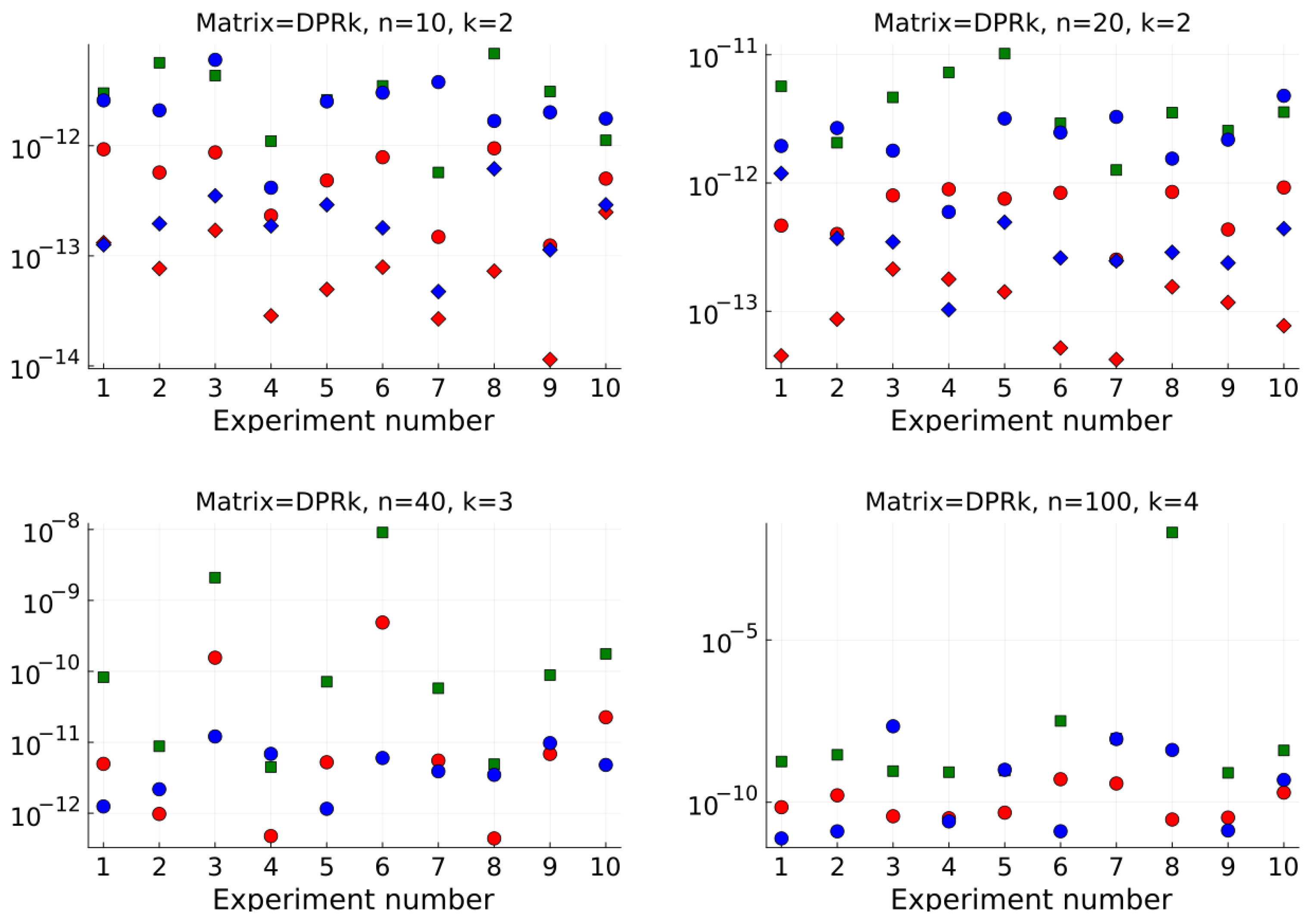
| Mean Number of Iterations per Eigenvalue | Mean Total Running Time (s) | |||
|---|---|---|---|---|
| n | RQIds | n | RQIds | QR |
| 10 | 8 | 10 | 0.00081 | 0.00079 |
| 20 | 9 | 20 | 0.0026 | 0.011 |
| 40 | 16 | 40 | 0.014 | 0.039 |
| 100 | 32 | 100 | 0.17 | 0.47 |
| Mean Number of Iterations per Eigenvalue | Mean Total Running Time (s) | |||||
|---|---|---|---|---|---|---|
| n | k | RQIds | n | k | RQIds | QR |
| 10 | 2 | 7 | 10 | 2 | 0.0018 | 0.00075 |
| 20 | 2 | 9 | 20 | 2 | 0.0077 | 0.011 |
| 40 | 3 | 16 | 40 | 3 | 0.031 | 0.071 |
| 100 | 4 | 27 | 100 | 4 | 0.25 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chaysri, T.; Jakovčević Stor, N.; Slapničar, I. Fast Eigenvalue Decomposition of Arrowhead and Diagonal-Plus-Rank-k Matrices of Quaternions. Mathematics 2024, 12, 1327. https://doi.org/10.3390/math12091327
Chaysri T, Jakovčević Stor N, Slapničar I. Fast Eigenvalue Decomposition of Arrowhead and Diagonal-Plus-Rank-k Matrices of Quaternions. Mathematics. 2024; 12(9):1327. https://doi.org/10.3390/math12091327
Chicago/Turabian StyleChaysri, Thaniporn, Nevena Jakovčević Stor, and Ivan Slapničar. 2024. "Fast Eigenvalue Decomposition of Arrowhead and Diagonal-Plus-Rank-k Matrices of Quaternions" Mathematics 12, no. 9: 1327. https://doi.org/10.3390/math12091327







