Mathematical Dimensional Synthesis of Four-Bar Linkages Based on Cognate Mechanisms
Abstract
1. Introduction
1.1. General Background and Main Significance of the Present Research Work
1.2. Formulation of the Specific Problem of Interest for This Investigation
1.3. Literature Review
1.4. Scope and Contributions of This Investigation
2. Materials and Methods
2.1. Theoretical Background
- (1)
- Links: These are the solid parts of the mechanism that connect to each other to transmit movement. Depending on the number of nodes (connection points between links) the links are classified as binary, ternary, or quaternary.
- (2)
- Joints or rotation pairs: These are the points of connection between two or more links where some movement is allowed between the interconnected links. Reuleaux coined the term lower pair to describe joints with lower contact and the term upper pair to describe joints with point or line contact [19,20,21,22].
- (3)
- Supports: These are the fixed points of the mechanism that provide stability and support to the mechanism.
2.1.1. Determination of Degrees of Freedom
2.1.2. Grashof Method
- (1)
- Class I: They are defined as crank mechanisms where at least one of its links performs a complete rotation.
- (2)
- Class II: They are defined as rocker mechanisms where none of the elements of the quadrilateral performs a complete rotation.
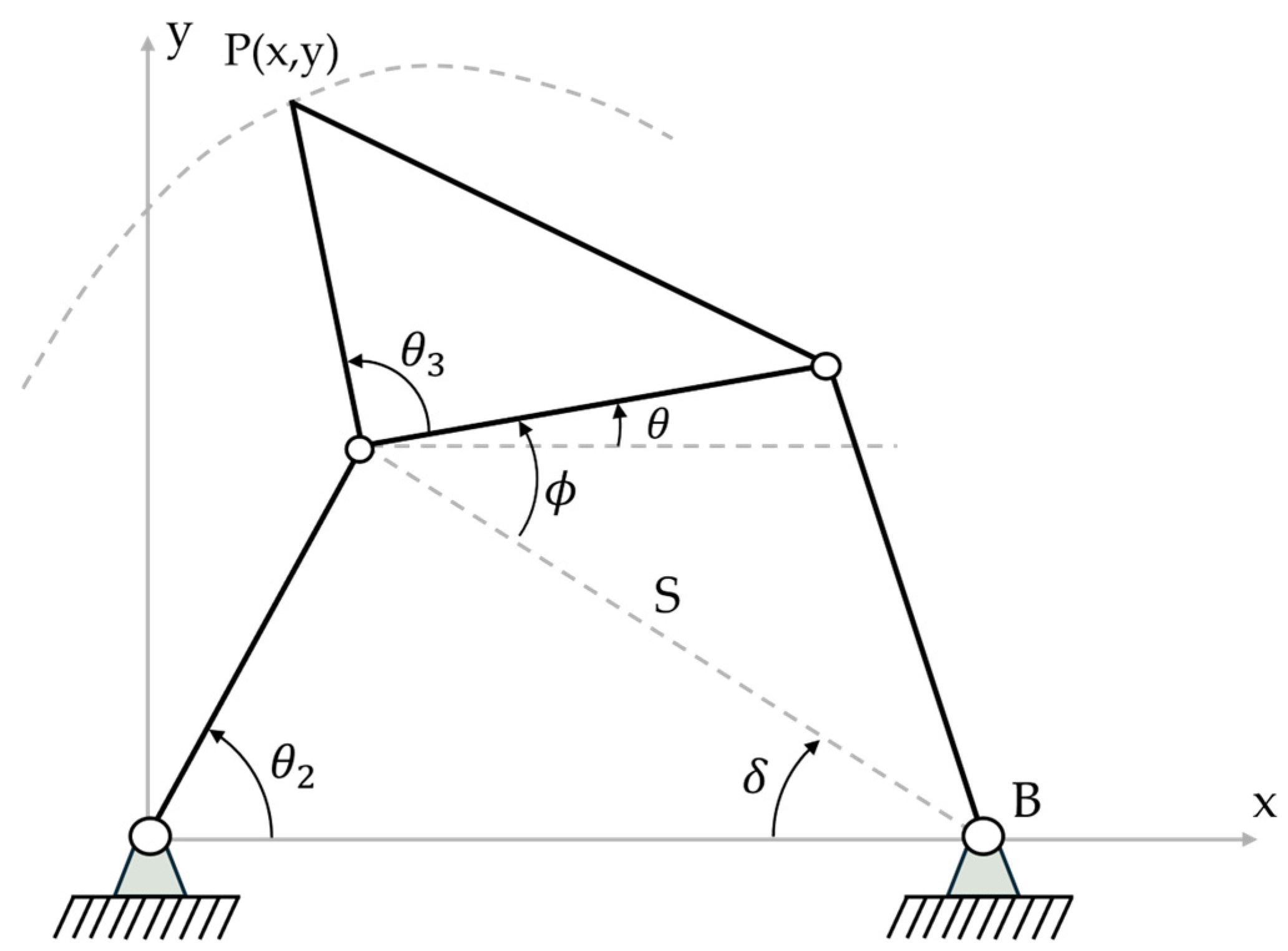
2.1.3. Mechanism Modeling by Natural Coordinates
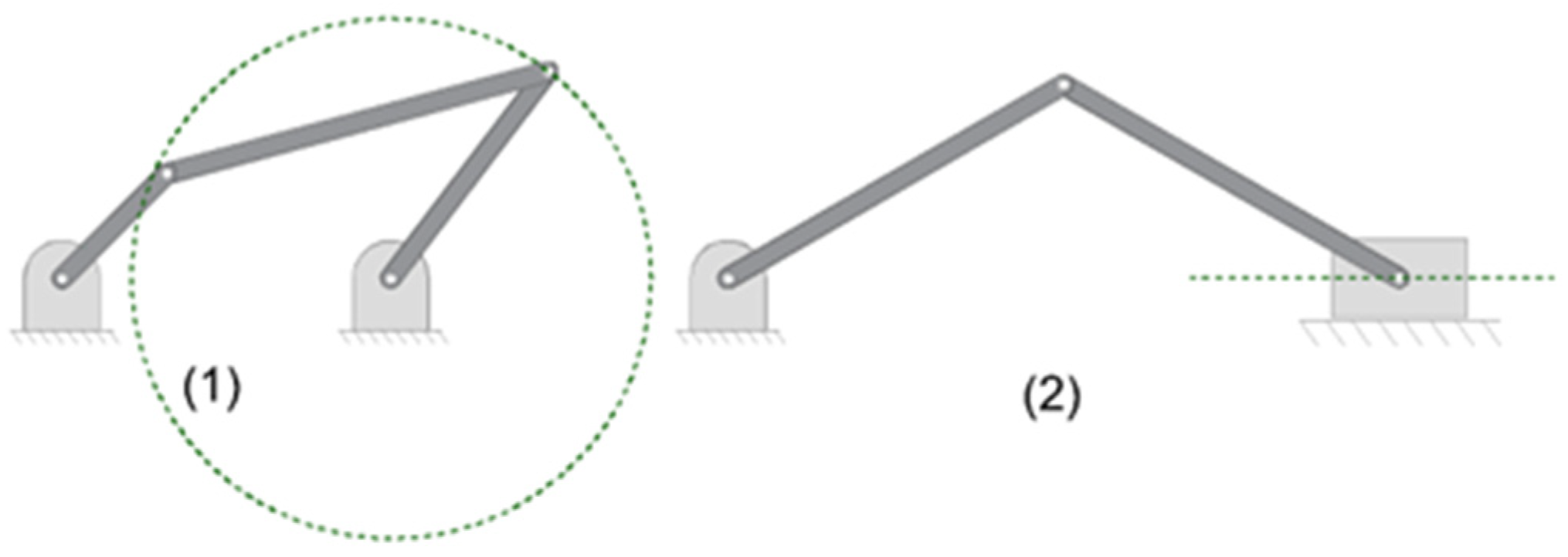
2.1.4. Methods for Constructing Cognate Mechanisms
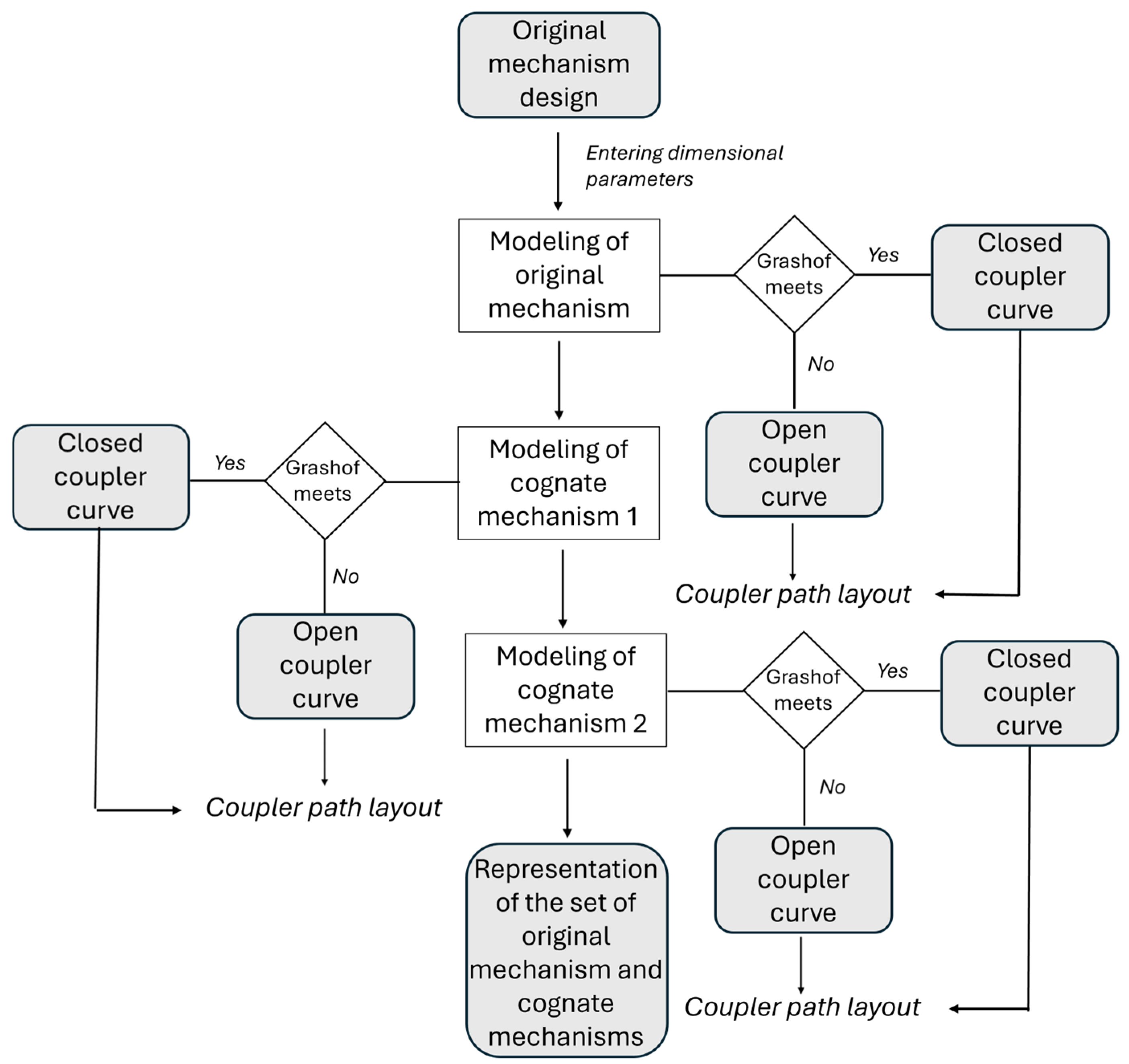
2.2. Proposed Method of Constructing Cognate Mechanisms
- (1)
- Modeling of the four-bar mechanism, classification of this according to whether it complies with Grashof or not, and plotting of the trajectory of the coupling point.
- (2)
- Construction of the cognate mechanism 1, classification based on the Grashof condition, and plotting of the trajectory of the coupling point.
- (3)
- Construction of the cognate mechanism 2, classification based on the Grashof condition, and plotting of the trajectory of the coupling point.
2.2.1. Dimensioning of the Original Mechanism
- (1)
- The separation distance “l” between the supports A and B, expressed in units of length.
- (2)
- The lengths of the links a, b, c, d, and e, expressed in units of length.
- (3)
- The coefficients “t1” and “t2”, whose values are 1 or −1 and indicate the configuration of the mechanism, as shown in Figure 8.
- (4)
- The input angle θ2 expressed in degrees to be able to represent the mechanism in a fixed position.

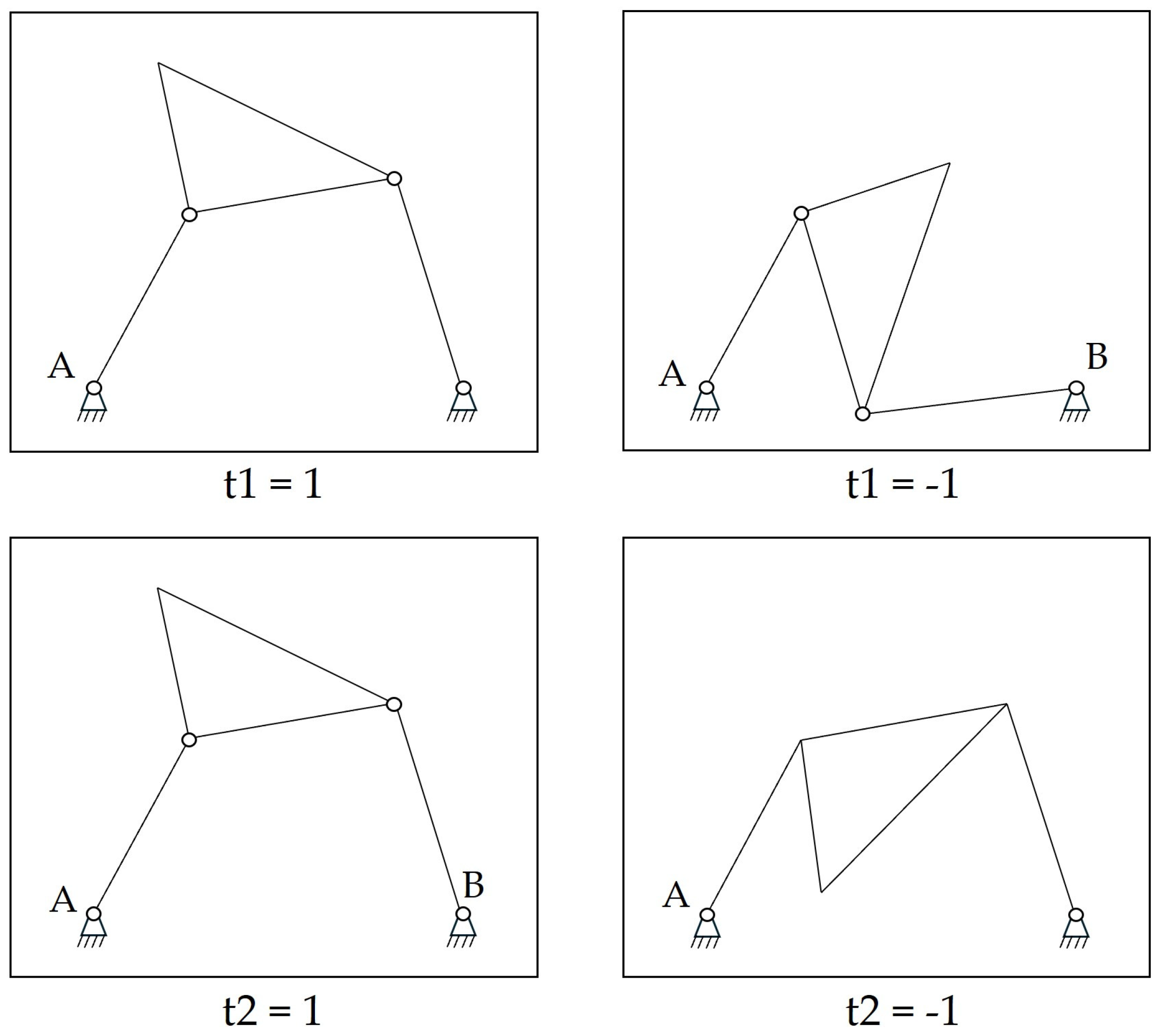
2.2.2. Generation of the Trajectory of Mechanisms
2.2.3. Construction of Cognate Mechanisms
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raven, F.H. Velocity and Acceleration Analysis of Plane and Space Mechanisms by Means of Independent-Position Equations. J. Appl. Mech. 1958, 25, 1–6. [Google Scholar] [CrossRef]
- Lee, W.-T.; Russell, K. Developments in quantitative dimensional synthesis (1970–present): Four-bar path and function generation. Inverse Probl. Sci. Eng. 2018, 26, 1280–1304. [Google Scholar] [CrossRef]
- Pathak, V.K.; Singh, R.; Sharma, A.; Kumar, R.; Chakraborty, D. A Historical Review on the Computational Techniques for Mechanism Synthesis: Developments Up to 2022. Arch. Comput. Methods Eng. 2023, 30, 1131–1156. [Google Scholar] [CrossRef]
- Li, X.; Wei, S.; Liao, Q.; Zhang, Y. A novel analytical method for four-bar path generation synthesis based on Fourier series. Mech. Mach. Theory 2020, 144, 103671. [Google Scholar] [CrossRef]
- Hernández, A.; Muñoyerro, A.; Urízar, M.; Amezua, E. Comprehensive approach for the dimensional synthesis of a four-bar linkage based on path assessment and reformulating the error function. Mech. Mach. Theory 2021, 156, 104126. [Google Scholar] [CrossRef]
- Kang, Y.-H.; Lin, J.-W.; You, W.-C. Comparative Study on the Synthesis of Path-Generating Four-Bar Linkages Using Metaheuristic Optimization Algorithms. Appl. Sci. 2022, 12, 7368. [Google Scholar] [CrossRef]
- Lakshminarayana, K.; Butchi Raju, K.C. Function-cognate mechanisms: General theory and application. Mech. Mach. Theory 1985, 20, 389–397. [Google Scholar] [CrossRef]
- Sherman, S.N.; Hauenstein, J.D.; Wampler, C.W. A General Method for Constructing Planar Cognate Mechanisms. J. Mech. Robot. 2021, 13, 031009. [Google Scholar] [CrossRef]
- Sherman, S.N.; Hauenstein, J.D.; Wampler, C.W. Advances in the Theory of Planar Curve Cognates. J. Mech. Robot. 2022, 14, 031005. [Google Scholar] [CrossRef]
- Wampler, C.W.; Morgan, A.P.; Sommese, A.J. Complete Solution of the Nine-Point Path Synthesis Problem for Four-Bar Linkages. J. Mech. Des. 1992, 114, 153–159. [Google Scholar] [CrossRef]
- Roth, B.; Freudenstein, F. Synthesis of Path-Generating Mechanisms by Numerical Methods. J. Eng. Ind. 1963, 85, 298–304. [Google Scholar] [CrossRef]
- Kramer, S.N.; Sandor, G.N. Selective Precision Synthesis—A General Method of Optimization for Planar Mechanisms. J. Eng. Ind. 1975, 97, 689–701. [Google Scholar] [CrossRef]
- Plecnik, M.M.; McCarthy, J.M. Kinematic synthesis of Stephenson III six-bar function generators. Mech. Mach. Theory 2016, 97, 112–126. [Google Scholar] [CrossRef]
- Baskar, A.; Plecnik, M. Synthesis of Six-Bar Timed Curve Generators of Stephenson-Type Using Random Monodromy Loops. J. Mech. Robot. 2021, 13, 011005. [Google Scholar] [CrossRef]
- Simionescu, P.A.; Smith, M.R. Four- and six-bar function cognates and overconstrained mechanisms. Mech. Mach. Theory 2001, 36, 913–924. [Google Scholar] [CrossRef]
- Han, J.; Liu, W. On the Solution of Eight-Precision-Point Path Synthesis of Planar Four-Bar Mechanisms Based on the Solution Region Methodology. J. Mech. Robot. 2019, 11, 064504. [Google Scholar] [CrossRef]
- Mehdigholi, H.; Akbarnejad, S. Optimization of Watt’s Six-Bar Linkage to Generate Straight and Parallel Leg Motion. Int. J. Adv. Robot. Syst. 2012, 9, 22. [Google Scholar] [CrossRef]
- Starns, G.; Flugrad, D.R. Five-Bar Path Generation Synthesis by Continuation Methods. J. Mech. Des. 1993, 115, 988–994. [Google Scholar] [CrossRef]
- Moon, F.C. Franz Reuleaux: Contributions to 19th century kinematics and theory of machines. Appl. Mech. Rev. 2003, 56, 261–285. [Google Scholar] [CrossRef]
- Reuleaux, F. The Kinematics of Machinery: Outlines of a Theory of Machines; Publications, D., Ed.; Courier Corporation: Mineloa, NY, USA, 2013. [Google Scholar]
- Shiwalkar, P.B.; Ceccarelli, M. History of Planar Linkage Coupler Point Loci for Tracing Special Coupler Curves. In Explorations in the History and Heritage of Machines and Mechanisms. HMM 2024. History of Mechanism and Machine Science, Volume 47; Ceccarelli, M., Aslan Seyhan, I., Eds.; Springer: Cham, Switzerland, 2024; pp. 213–226. [Google Scholar]
- Koetsier, T. A History of Kinematics from Zeno to Einstein; History of Mechanism and Machine Science; Springer Nature: Cham, Switzerland, 2024; Volume 46. [Google Scholar]
- Grübler, M. Die Relativbewegungen von drei und mehr komplanen Ebenen. In Getriebelehre; Springer: Berlin/Heidelberg, Germany, 1917; pp. 55–62. [Google Scholar]
- Grashof, F. Theoretische Maschinenlehre; Leopold Voss: Leipzig, Germany, 1875. [Google Scholar]
- Hartenberg, R.; Danavit, J. Kinematic Synthesis of Linkages; McGraw-Hill: New York, NY, USA, 1964. [Google Scholar]
- Ting, K.-L. Mobility Criteria of Single-Loop N-Bar Linkages. J. Mech. Transm. Autom. Des. 1989, 111, 504–507. [Google Scholar] [CrossRef]
- Mitsi, S. Position analysis in polynomial form of planar mechanisms with a closed chain of the Assur group of class 4 L’analyse de position sous forme polynomiale des mecanismes plans avec une chaine fermee du groupe d’Assur de 4-eme classe. Mech. Mach. Theory 1999, 34, 1195–1209. [Google Scholar] [CrossRef]
- Rojas, N.; Thomas, F. Distance-based position analysis of the three seven-link Assur kinematic chains. Mech. Mach. Theory 2011, 46, 112–126. [Google Scholar] [CrossRef]
- Rojas, N.; Dollar, A.M.; Thomas, F. A unified position analysis of the Dixon and the generalized Peaucellier linkages. Mech. Mach. Theory 2015, 94, 28–40. [Google Scholar] [CrossRef]
- Romero-Núñez, N.N.; Flórez Serrano, E.G. Análisis de posición de un mecanismo de Stephenson tipo I utilizando coordenadas naturales. DYNA 2018, 85, 91–97. [Google Scholar] [CrossRef]
- Soriano-Heras, E.; Blaya-Haro, F.; Molino, C.; de Agustín del Burgo, J.M. Rapid prototyping prosthetic hand acting by a low-cost shape-memory-alloy actuator. J. Artif. Organs 2018, 21, 238–246. [Google Scholar] [CrossRef]
- Soni, A.H.; Harrisberger, L. Roberts’ Cognates of Space Four-Bar Mechanisms With Two General Constraints. J. Eng. Ind. 1969, 91, 123–127. [Google Scholar] [CrossRef]
- Soni, A.H. Coupler cognate mechanisms of certain parallelogram forms of watt’s six-link mechanism. J. Mech. 1970, 5, 203–215. [Google Scholar] [CrossRef]
- Roberts, S. On Three-bar Motion in Plane Space. Proc. Lond. Math. Soc. 1875, s1-7, 14–23. [Google Scholar] [CrossRef]





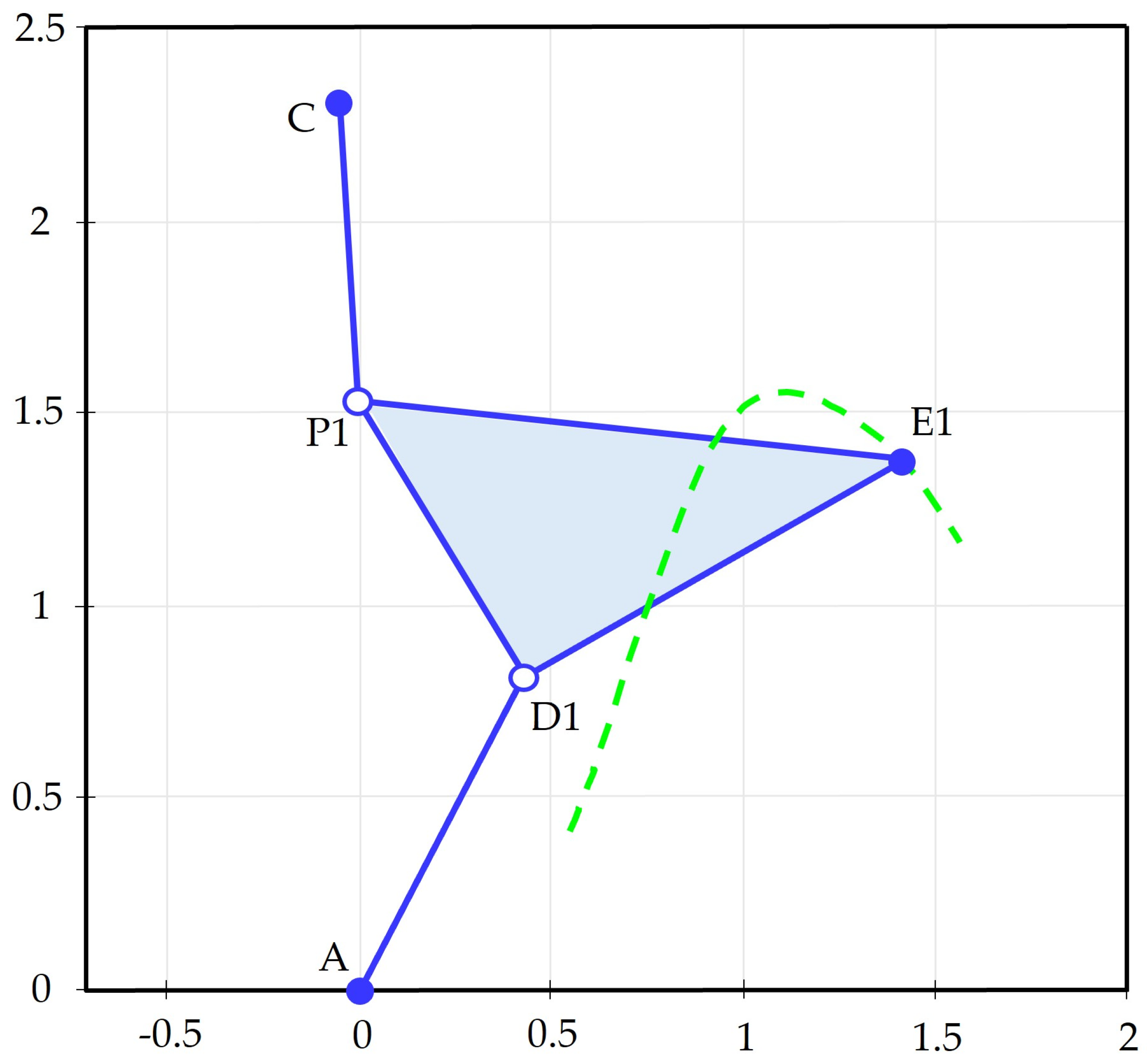


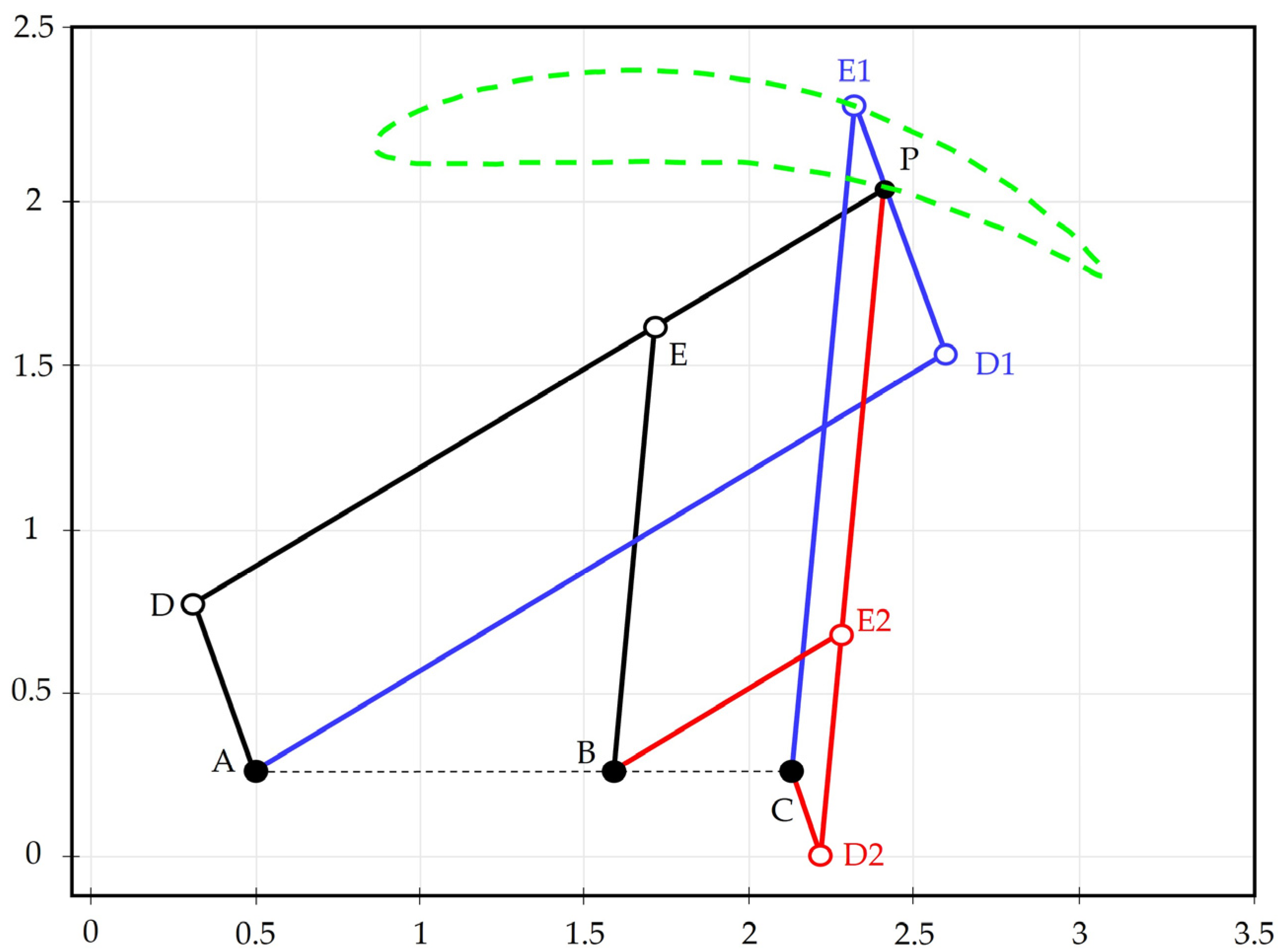
| Dimensional Parameters | |||
|---|---|---|---|
| Parameter | Original Mechanism | Cognate 1 | Cognate 2 |
| A (x, y) | (0, 0) | (0, 0) | - |
| B (x, y) | (l,0) | - | (l, 0) |
| C (x, y) | - | (−0.05, 2.31) | (−0.05, 2.31) |
| l (cm) | 3.10 | - | - |
| a (cm) | 1.13 | 0.92 | 1.43 |
| b (cm) | 1.23 | 1.13 | 1.04 |
| c (cm) | 1.04 | 0.78 | 1.56 |
| d (cm) | 0.92 | 0.84 | 0.78 |
| e (cm) | 1.56 | 1.43 | 1.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soriano-Heras, E.; Pérez-Carrera, C.; Rubio, H. Mathematical Dimensional Synthesis of Four-Bar Linkages Based on Cognate Mechanisms. Mathematics 2025, 13, 11. https://doi.org/10.3390/math13010011
Soriano-Heras E, Pérez-Carrera C, Rubio H. Mathematical Dimensional Synthesis of Four-Bar Linkages Based on Cognate Mechanisms. Mathematics. 2025; 13(1):11. https://doi.org/10.3390/math13010011
Chicago/Turabian StyleSoriano-Heras, Enrique, Carlos Pérez-Carrera, and Higinio Rubio. 2025. "Mathematical Dimensional Synthesis of Four-Bar Linkages Based on Cognate Mechanisms" Mathematics 13, no. 1: 11. https://doi.org/10.3390/math13010011
APA StyleSoriano-Heras, E., Pérez-Carrera, C., & Rubio, H. (2025). Mathematical Dimensional Synthesis of Four-Bar Linkages Based on Cognate Mechanisms. Mathematics, 13(1), 11. https://doi.org/10.3390/math13010011








