A Comparison of Three Real-Time Shortest Path Models in Dynamic Interval Graph
Abstract
1. Introduction
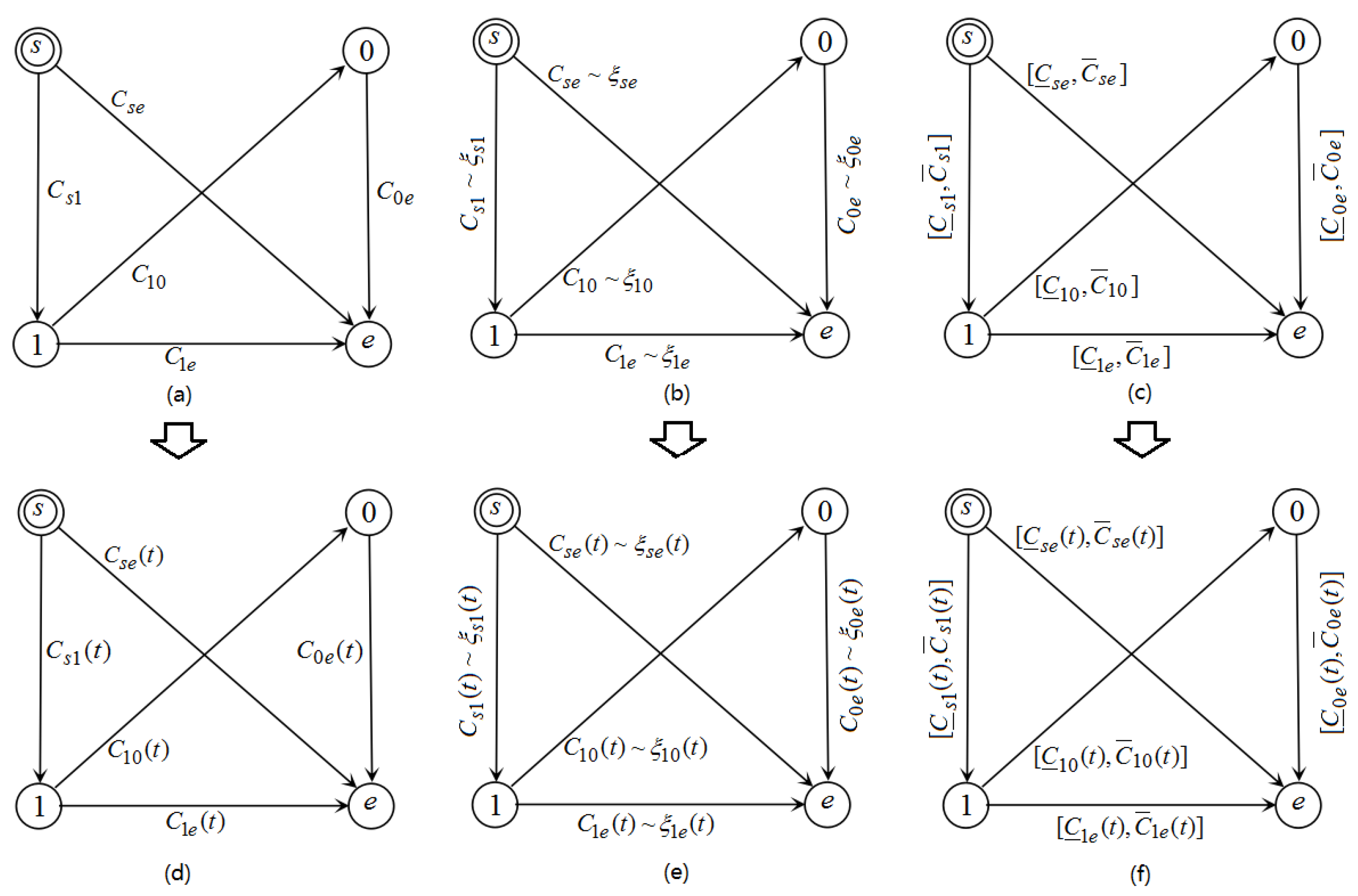
2. Problem Definition
3. DRSP Model in DI Graph
3.1. Problem Description
3.2. Mixed Integer Programming (MIP) Formulations
4. DGRSP Model in DI Graph
4.1. Problem Description
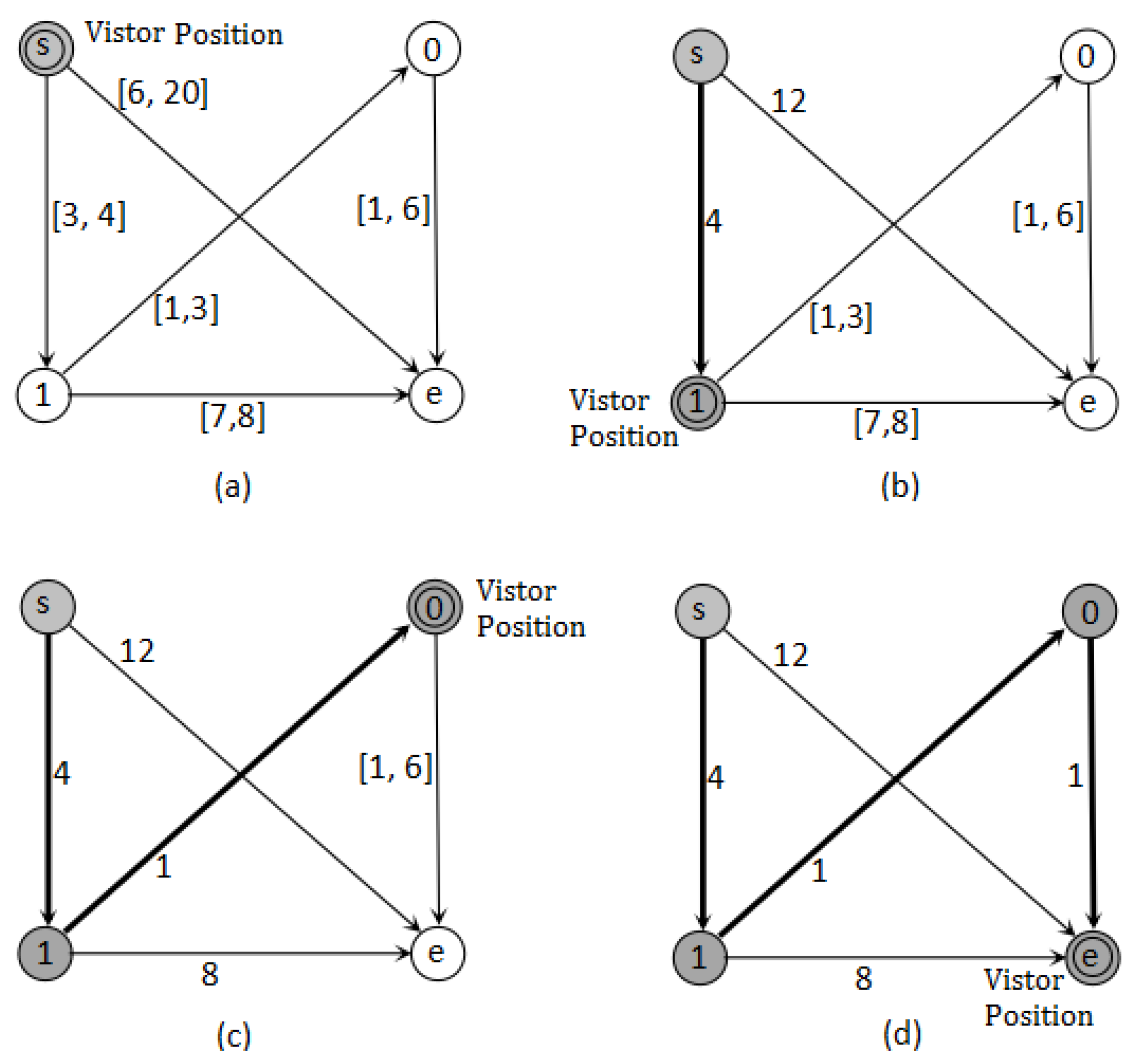
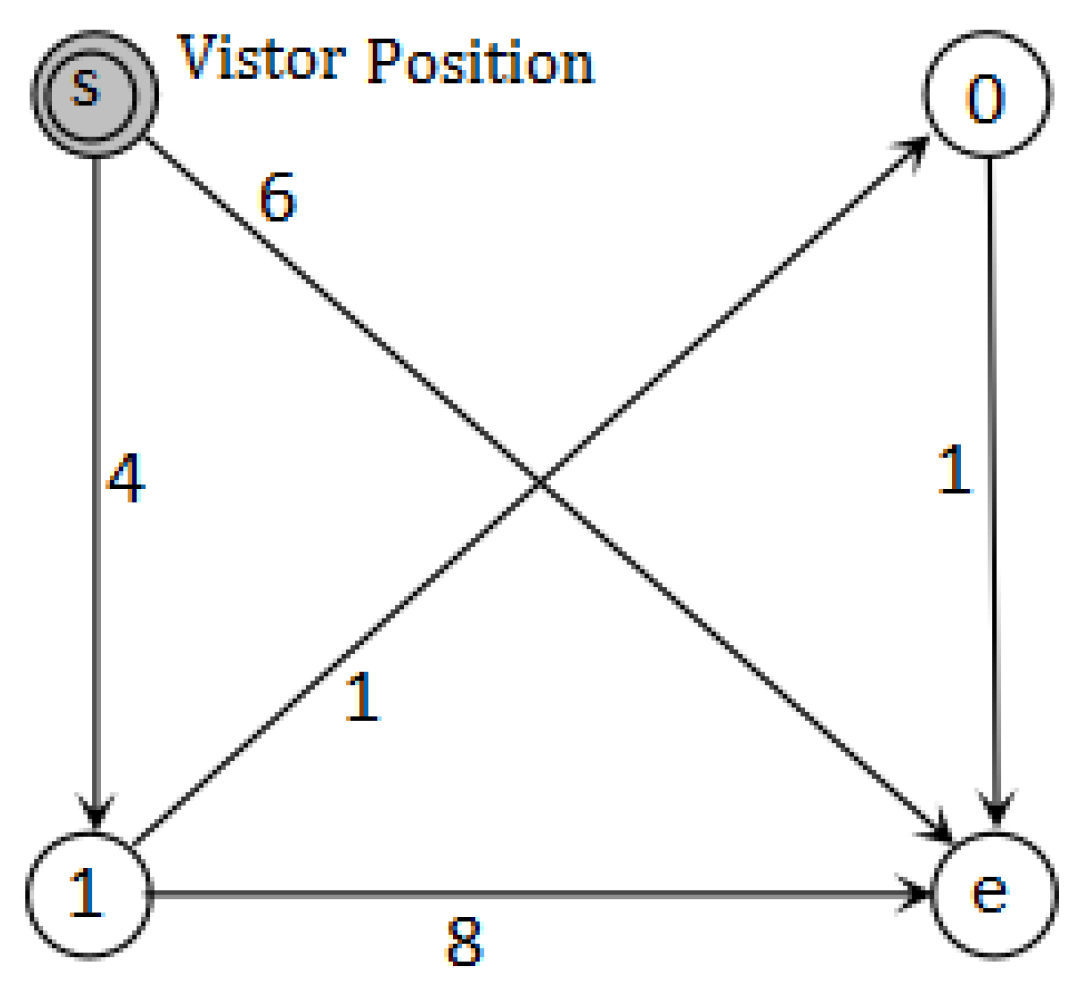
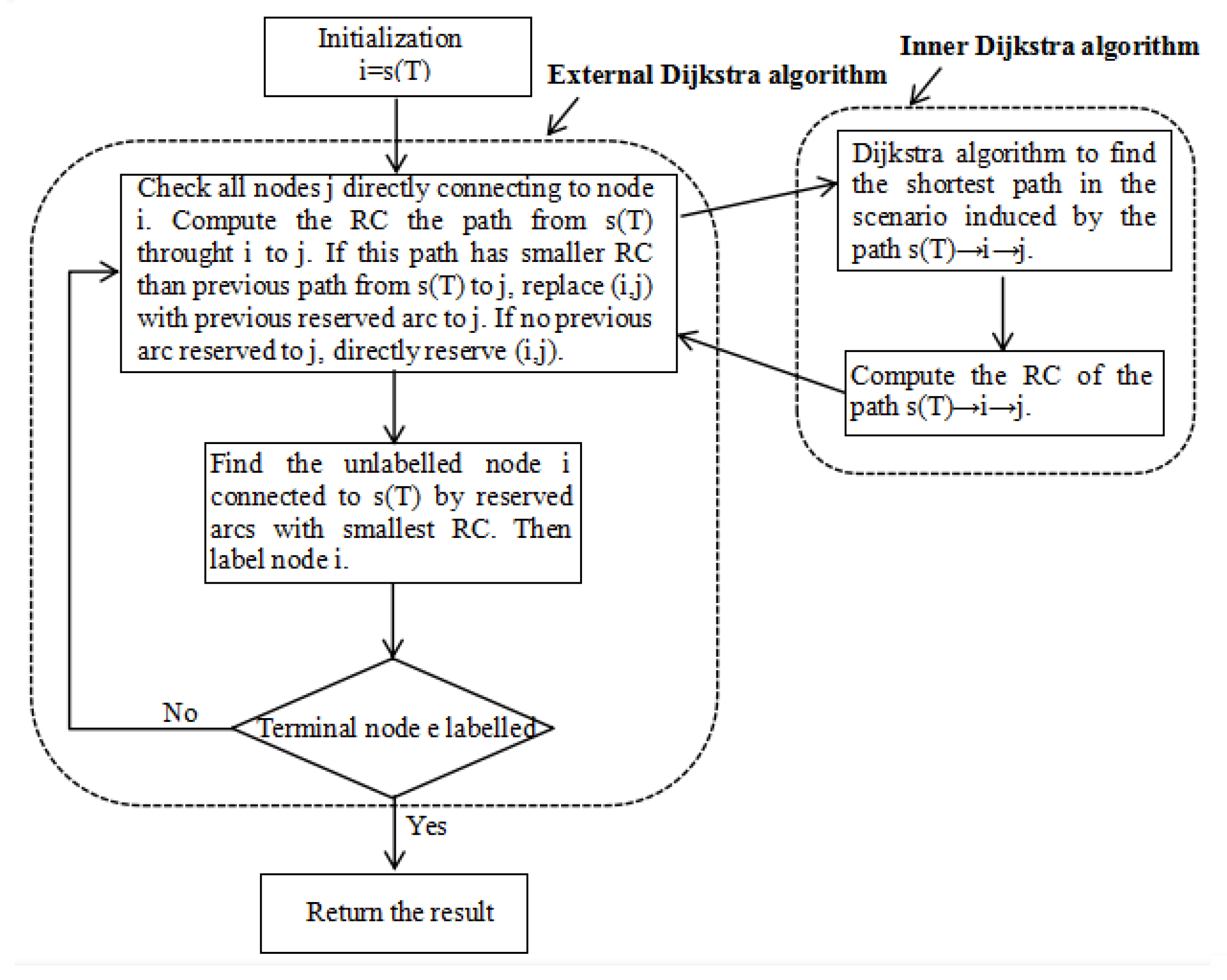
4.2. Nested Dijkstra Algorithm for DGRSP
| Algorithm 1: ND algorithm |
; %Initialization while node e unlabeled do %Terminal check :=a set of unlabeled nodes directly connected to i; for iteration do %Update the RC of nodes in Compute by inner Dijkstra from through i to j; if no previous reserved arc from directly or indirectly to j; then reserve arc ; else then compare with the RC of previous path to j; reserve the smaller one instead of the previous one; end if end :=a set of unlabeled nodes; ; for iteration do %Find unlabeled nodes with min RC if then ; end if end for Label i and reserve the corresponding arc directly or indirectly to ; end return the RC of all nodes and all the reserved arcs; %Final result |
5. DMSP Model in DI Graph
6. Numerical Study
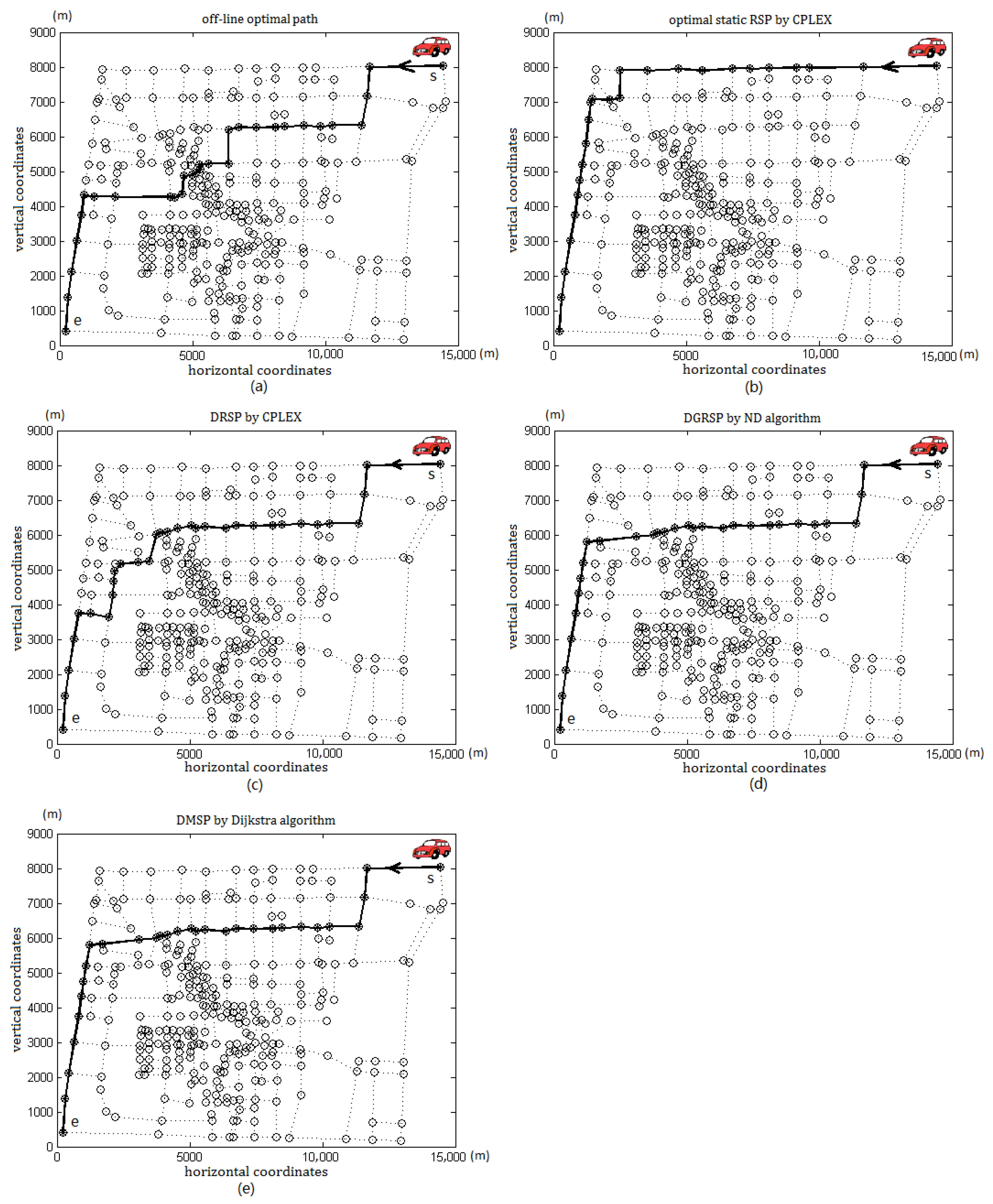
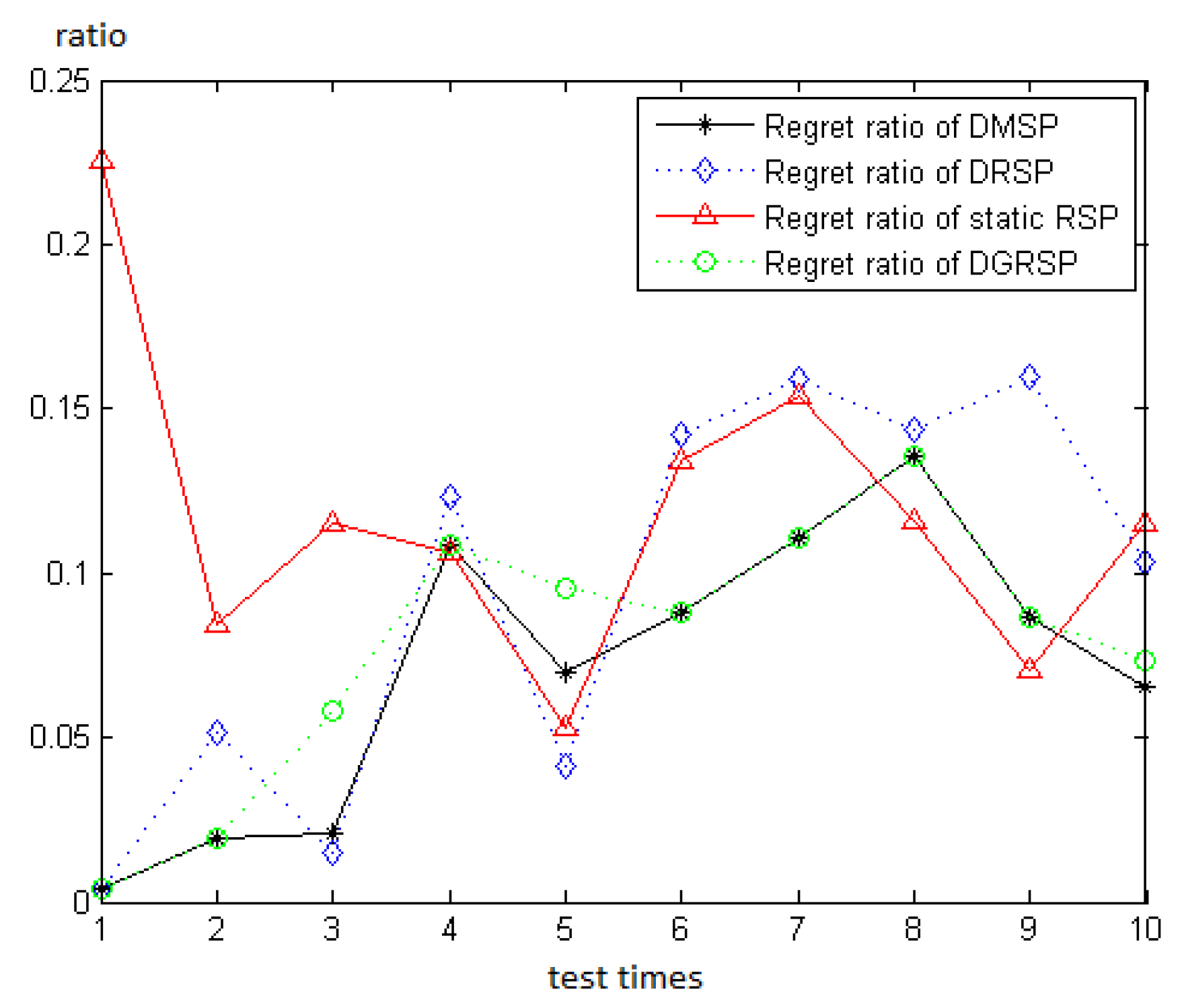
6.1. Real Roads Test
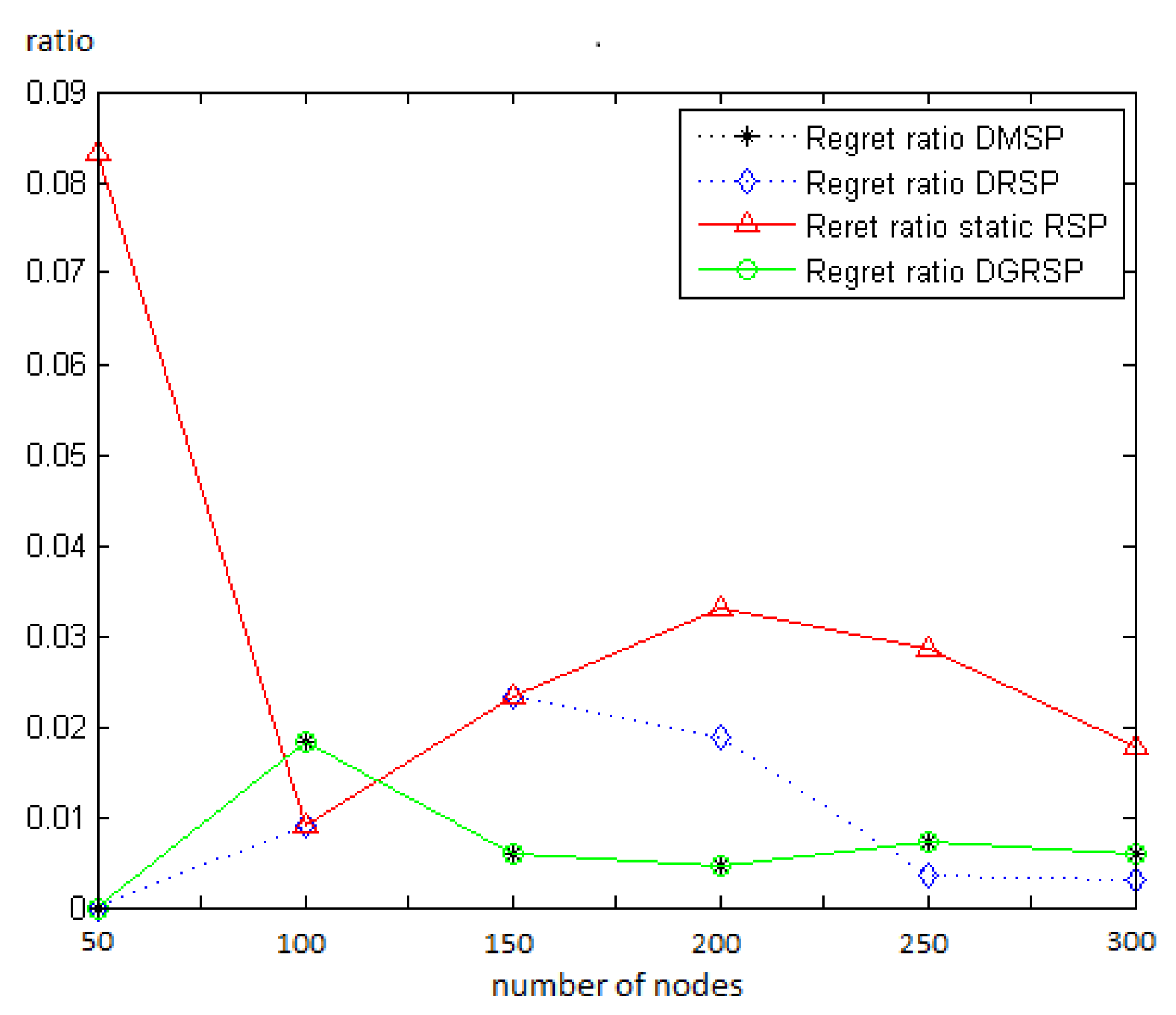
6.2. Generated Network Test
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dijkstra, E.W. A note on two problems in connection with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Floyd, R.W. Algorithm 97: Shortest path. Commun. Acm 1962, 5, 345. [Google Scholar] [CrossRef]
- Bellman, R.E. On a routing problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Ford, L.R., Jr.; Fulkerson, D.R. Flows in Networks; Princeton Univ. Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Himmich, I.; El Hallaoui, I.; Soumis, F. A multiphase dynamic programming algorithm for the shortest path problem with resource constraints. Eur. J. Oper. Res. 2023, 315, 470–483. [Google Scholar] [CrossRef]
- Bahel, E.; Gomez-Rua, M.; Vidal-Puga, J. Stable and weakly additive cost sharing in shortest path problems. J. Math. Econ. 2024, 110, 102921. [Google Scholar] [CrossRef]
- Murchl, J.D. A Fixed Matrix Method for All Shortest Distances in a Directed Graph and for the Inverse Problem. Ph.D. Thesis, University of Karlsruhe, Karlsruhe, Germany, 1970. [Google Scholar]
- Dionne, R. Etude et extension d’un algorithme de Murchland. INFOR Inf. Syst. Oper. Res. 1978, 16, 132–146. [Google Scholar]
- Goto, S.; Sangiovanni-Vincentelli, A. A new shortest path updating algorithm. Networks 1978, 8, 341–372. [Google Scholar] [CrossRef]
- Ramalingam, G.; Reps, T. An incremental algorithm for a generalization of the shortest-path problem. J. Algorithms 1996, 21, 267–305. [Google Scholar] [CrossRef]
- Demetrescu, C.; Frigioni, D.; Marchetti-Spaccamela, A.; Nanni, U. Maintaining shortest paths in digraphs with arbitrary arc weights: An experimental study. In Proceedings of the Algorithm Engineering: 4th International Workshop, WAE 2000 Saarbrücken, Germany, September 5–8, 2000 Proceedings 4; Naher, S., Wagner, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1982, pp. 218–229. [Google Scholar]
- Buriol, L.S.; Resende, M.G.C.; Thorup, M. Speeding up dynamic shortest-path algorithms. INFORMS J. Comput. 2008, 20, 191–204. [Google Scholar] [CrossRef]
- Martin, J. Distribution of time through a directed acyclic network. Oper. Res. 1965, 13, 46–66. [Google Scholar] [CrossRef]
- Frank, H. Shortest paths in probabilistic graphs. Oper. Res. 1969, 17, 583–599. [Google Scholar] [CrossRef]
- Hassin, R.; Zemel, E. On shortest paths in graphs with random weights. Math. Oper. Res. 1985, 10, 557–564. [Google Scholar] [CrossRef]
- Mirchandani, P.B.; Soroush, H. Optimal paths in probabilistic networks: A case with temporary preferences. Comput. Oper. Res. 1985, 12, 365–381. [Google Scholar] [CrossRef]
- Mirchandani, P.B.; Soroush, H.; Angrealtta, G.; Mason, F.; Serafini, P. Routes and flows in stochastic networks. In Stochastics in Combinatorial Optimization; World Scientific Publishing Company: Singapore, 1986; pp. 129–177. [Google Scholar]
- Beigy, H.; Meybodi, M.R. A sampling method based on distributed learning automata for solving stochastic shortest path problem. Knowl.-Based Syst. 2021, 212, 106638. [Google Scholar] [CrossRef]
- Ketkov, S.S.; Prokopyev, O.A.; Burashnikov, E.P. An approach to the distributionally robust shortest path problem. Comput. Oper. Res. 2021, 130, 105212. [Google Scholar] [CrossRef]
- Lee, J.; Joung, S.; Lee, K. A fully polynomial time approximation scheme for the probability maximizing shortest path problem. Eur. J. Oper. Res. 2022, 300, 35–45. [Google Scholar] [CrossRef]
- Song, M.; Cheng, L. A generalized Benders decomposition approach for the mean-standard deviation shortest path problem. Transp. Lett. 2023, 15, 823–833. [Google Scholar] [CrossRef]
- Hall, R. The fastest path through a network with random time-dependent travel times. Transp. Sci. 1986, 20, 182–188. [Google Scholar] [CrossRef]
- Bertsimas, D.; Van Ryzin, G. A stochastic and dynamic vehicle routing problem in the Euclidean plane. Oper. Res. 1991, 39, 601–615. [Google Scholar] [CrossRef]
- Bertsimas, D.; Van Ryzin, G. Stochastic and dynamic vehicle routing in Euclidean plane with multiple capacitated vehicles. Oper. Res. 1993, 41, 60–76. [Google Scholar] [CrossRef]
- Psaraftis, H.; Tsitsiklis, J. Dynamic shortest paths in acyclic networks with Markovian arc costs. Oper. Res. 1993, 41, 91–101. [Google Scholar] [CrossRef]
- Azaron, A.; Kianfar, F. Dynamic shortest path in stochastic dynamic networks: Ship routing problem. Eur. J. Oper. Res. 2003, 144, 138–156. [Google Scholar] [CrossRef]
- Pattanamekar, P.; Park, D.; Rilett, L.R.; Lee, J.; Lee, C. Dynamic and stochastic shortest path in transportation networks with two components of travel time uncertainty. Transp. Res. Part C 2003, 11, 331–354. [Google Scholar] [CrossRef]
- Ojeda Rios, B.H.; Xavier, E.C.; Miyazawa, F.K.; Amorim, P.; Curcio, E.; Santos, M.J. Recent dynamic vehicle routing problems: A survey. Comput. Ind. Eng. 2021, 160, 107604. [Google Scholar] [CrossRef]
- Dias, L.C.; Climaco, J.N. Shortest path problems with partial information: Models and algorithms for detecting dominance. Eur. J. Oper. Res. 2000, 121, 16–31. [Google Scholar] [CrossRef][Green Version]
- Averbakh, I.; Lebedev, V. Interval data minmax regret network optimization problems. Discret. Appl. Math. 2004, 138, 289–301. [Google Scholar] [CrossRef]
- Zielinski, P. The computational complexity of the relative robust shortest path problem with interval data. Eur. J. Oper. Res. 2004, 158, 570–576. [Google Scholar] [CrossRef]
- Karasan, O.E.; Pinar, M.C.; Yaman, H. The Robust Shortest Path Problem with Interval Data; Bilkent University: Ankara, Turkey, 2001. [Google Scholar]
- Montemanni, R.; Gambardella, L.M.; Donati, A.V. A branch and bound algorithm for the robust shortest path problem with interval data. Oper. Res. Lett. 2004, 3, 225–232. [Google Scholar] [CrossRef]
- Montemanni, R.; Gambardella, L.M. The robust shortest path problem with interval data via Benders decomposition. 4OR 2005, 3, 315–328. [Google Scholar] [CrossRef]
- Kasperski, A.; Zielinski, P. An approximation algorithm for interval data minimax regret combinatorial optimization problems. Inf. Process. Lett. 2006, 97, 177–180. [Google Scholar] [CrossRef]
- Catanzaro, D.; Labbe, M.; Salazar-Neumann, M. Reduction approaches for robust shortest path problems. Comput. Oper. Res. 2004, 38, 1610–1619. [Google Scholar] [CrossRef]
- Chassein, A.; Dokka, T.; Goerigk, M. Algorithms and uncertainty sets for data-driven robust shortest path problems. Eur. J. Oper. Res. 2019, 274, 671–686. [Google Scholar] [CrossRef]
- Zhang, C. Problem characterization of unique shortest path routing. Comput. Ind. Eng. 2023, 178, 109110. [Google Scholar] [CrossRef]
- Davoodi, M.; Ghaffari, M. Shortest path problem on uncertain networks: An efficient two phases approach. Comput. Ind. Eng. 2021, 157, 107302. [Google Scholar] [CrossRef]
- Xu, B.; Zhou, X. Dynamic relative robust shortest path problem. Comput. Ind. Eng. 2020, 148, 106651. [Google Scholar] [CrossRef]


| Graphs | Problems | Arc Cost | Search |
|---|---|---|---|
| SD | SP | exact value | static |
| SS | SSP | random variable | static |
| SI | RSP | interval value | static |
| DD | DSP | exact value depending on time | dynamic |
| DS | DSSP | random variable depending on time | dynamic |
| DI | DRSP | interval value depending on time | dynamic |
| Abbr | Full Terms | Abbr | Full Terms |
|---|---|---|---|
| DD | Dynamic and Deterministic | RC | Robust Cost |
| DGRSP | Dynamic Greedy Robust Shortest Path | RD | Robust Deviation |
| DI | Dynamic Interval | RSP | Robust Shortest Path |
| DMSP | Dynamic Mean Shortest Path | RTSP | Real-time Shortest Path |
| DRSP | Dynamic Robust Shortest Path | SD | Static and Deterministic |
| DS | Dynamic and Stochastic | SI | Static and Interval |
| DSP | Dynamic Shortest Path | SP | Shortest Path |
| DSSP | Dynamic Stochastic Shortest Path | SS | Static and Stochastic |
| DVR | Dynamic Vehicle Routing | SSP | Stochastic Shortest Path |
| MIP | Mixed Integer Programming | VR | Vehicle Routing |
| ND | Nested Dijkstra |
| Possible | Maximum Regret Relating to Location in | Final | Final | |||
|---|---|---|---|---|---|---|
| Paths | Node | Node 1 | Node 0 | Node | Cost | Regret |
| {s,e} | 15 | 6 | 6 | 6 | 12 | 6 |
| {s,1,e} | 6 | 6 | 6 | 12 | 6 | |
| {s,1,0,e} | 7 | 0 | ||||
| Test Times | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| optimal | cost | 18,250 | 19,131; | 17,936 | 18,792 | 19,407 | 18,595 | 18,504 | 17,707 | 17,749 | 17,812 | 18,388 |
| time(s) | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | |
| Static RSP | cost | 22,361 | 20,743 | 19,995 | 20,797 | 20,442 | 21,094 | 21,345 | 19,757 | 19,006 | 19,868 | 20,541 |
| regret | 4110 | 1612 | 2058 | 2005 | 1035 | 2499 | 2841 | 2050 | 1257 | 2056 | 2152 | |
| ratio | 22.5% | 8.4% | 11.5% | 10.7% | 5.3% | 13.4% | 15.4% | 11.6% | 7.1% | 11.5% | 11.7% | |
| time(s) | 6.8 | 0.2 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.9 | |
| DRSP | cost | 18,321 | 20,121 | 18,211 | 21,112 | 20,211 | 21,237 | 21,443 | 20,253 | 20,582 | 19,659 | 20,115 |
| regret | 71 | 990 | 275 | 2320 | 804 | 2642 | 2939 | 2546 | 2833 | 1847 | 1727 | |
| ratio | 0.4% | 5.2% | 1.5% | 12.4% | 4.1% | 14.2% | 15.9% | 14.4% | 16.0% | 10.4% | 9.4% | |
| time(s) | 0.5 | 0.5 | 0.5 | 0.5 | 0.6 | 0.6 | 0.6 | 0.5 | 0.8 | 0.6 | 0.6 | |
| DGRSP | cost | 18,321 | 19,505 | 18,983 | 20,836 | 21,257 | 20,236 | 20,558 | 20,110 | 19,286 | 19,124 | 19,822 |
| regret | 71 | 374 | 1047 | 2044 | 1851 | 1641 | 2055 | 2402 | 1537 | 1312 | 1433 | |
| ratio | 0.4% | 2.0% | 5.8% | 10.9% | 9.5% | 8.8% | 11.1% | 13.6% | 8.7% | 7.4% | 7.8% | |
| time(s) | 2.5 | 2.5 | 3.2 | 2.8 | 2.6 | 2.8 | 3.2 | 2.9 | 3.2 | 3.1 | 2.9 | |
| DMSP | cost | 18,321 | 19,505 | 18,306 | 20,836 | 20,762 | 20,236 | 20,558 | 20,110 | 19,286 | 18,983 | 19,690 |
| regret | 71 | 374 | 370 | 2044 | 1355 | 1641 | 2055 | 2402 | 1537 | 1171 | 1302 | |
| ratio | 0.4% | 2.0% | 2.1% | 10.9% | 7.0% | 8.8% | 11.1% | 13.6% | 8.7% | 6.6% | 7.1% | |
| time(s) | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | |
| Number of Nodes | 50 | 100 | 150 | 200 | 250 | 300 | Average | |
|---|---|---|---|---|---|---|---|---|
| optimal | cost | 48 | 109 | 171 | 212 | 281 | 337 | 193 |
| time(s) | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | |
| Static RSP | cost | 52 | 110 | 175 | 219 | 289 | 343 | 218 |
| regret | 4 | 1 | 4 | 7 | 8 | 6 | 5 | |
| ratio | 8.3% | 0.9% | 2.3% | 3.3% | 2.9% | 1.8% | 2.6% | |
| time(s) | 0.6 | 1.2 | 2.7 | 3.9 | 10.0 * | 10.0 * | 4.7 | |
| DRSP | cost | 48 | 110 | 175 | 216 | 282 | 338 | 195 |
| regret | 0 | 1 | 4 | 4 | 1 | 1 | 2 | |
| ratio | 0.0% | 0.9% | 2.3% | 1.9% | 0.3% | 0.3% | 1.0% | |
| time(s) | 0.2 | 0.4 | 0.9 | 1.4 | 5.1 * | 4.0 * | 2.0 | |
| DGRSP | cost | 48 | 111 | 172 | 213 | 283 | 339 | 194 |
| regret | 0 | 2 | 1 | 1 | 2 | 2 | 1 | |
| ratio | 0.0% | 1.8% | 0.6% | 0.5% | 0.7% | 0.6% | 0.5% | |
| time(s) | 0.1 | 0.2 | 0.6 | 1.2 | 2.3 | 3.7 | 1.3 | |
| DMSP | cost | 48 | 111 | 172 | 213 | 283 | 339 | 194 |
| regret | 0 | 2 | 1 | 1 | 2 | 2 | 1 | |
| ratio | 0.0% | 1.8% | 0.6% | 0.5% | 0.7% | 0.6% | 0.5% | |
| time(s) | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | <0.1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, B.; Ji, X.; Cheng, Z. A Comparison of Three Real-Time Shortest Path Models in Dynamic Interval Graph. Mathematics 2025, 13, 134. https://doi.org/10.3390/math13010134
Xu B, Ji X, Cheng Z. A Comparison of Three Real-Time Shortest Path Models in Dynamic Interval Graph. Mathematics. 2025; 13(1):134. https://doi.org/10.3390/math13010134
Chicago/Turabian StyleXu, Bo, Xiaodong Ji, and Zhengrong Cheng. 2025. "A Comparison of Three Real-Time Shortest Path Models in Dynamic Interval Graph" Mathematics 13, no. 1: 134. https://doi.org/10.3390/math13010134
APA StyleXu, B., Ji, X., & Cheng, Z. (2025). A Comparison of Three Real-Time Shortest Path Models in Dynamic Interval Graph. Mathematics, 13(1), 134. https://doi.org/10.3390/math13010134






