Disturbance Observer-Based Dynamic Surface Control for Servomechanisms with Prescribed Tracking Performance
Abstract
1. Introduction
- Frictions, parameter uncertainties, load disturbances, and external disturbances are lumped as an extended state variable, which is estimated using an ESO and compensated in the controller. It solves the requirement for linear parameterization of the unknown nonlinear dynamics in the traditional dynamic surface control and improves the anti-disturbance ability. Furthermore, the parameters of the ESO are designed based on the observer bandwidth only to simplify the parameter tuning;
- A prescribed performance function is employed to achieve the expected transient performance. It is incorporated into the controller design to ensure the tracking error within a prescribed region;
- A novel dynamic surface control combined with the prescribed performance function and an ESO is proposed for a turntable servo system with many unknown disturbances. It fully takes advantage of the low computational complexity of the dynamic surface control and improves the control performance of the control system;
- Furthermore, the conclusion is drawn using Lyapunov theory. Specifically, the proposed design is uniformly ultimately bounded, all signals of the closed-loop control system are bounded, and the estimate error of the ESO and tracking error of the design converge to a small neighborhood around the equilibrium point.
2. Dynamic Model and Problem Description
2.1. Dynamic Model
2.2. Problem Description
2.2.1. Coordinate Transformation
2.2.2. Problem Description
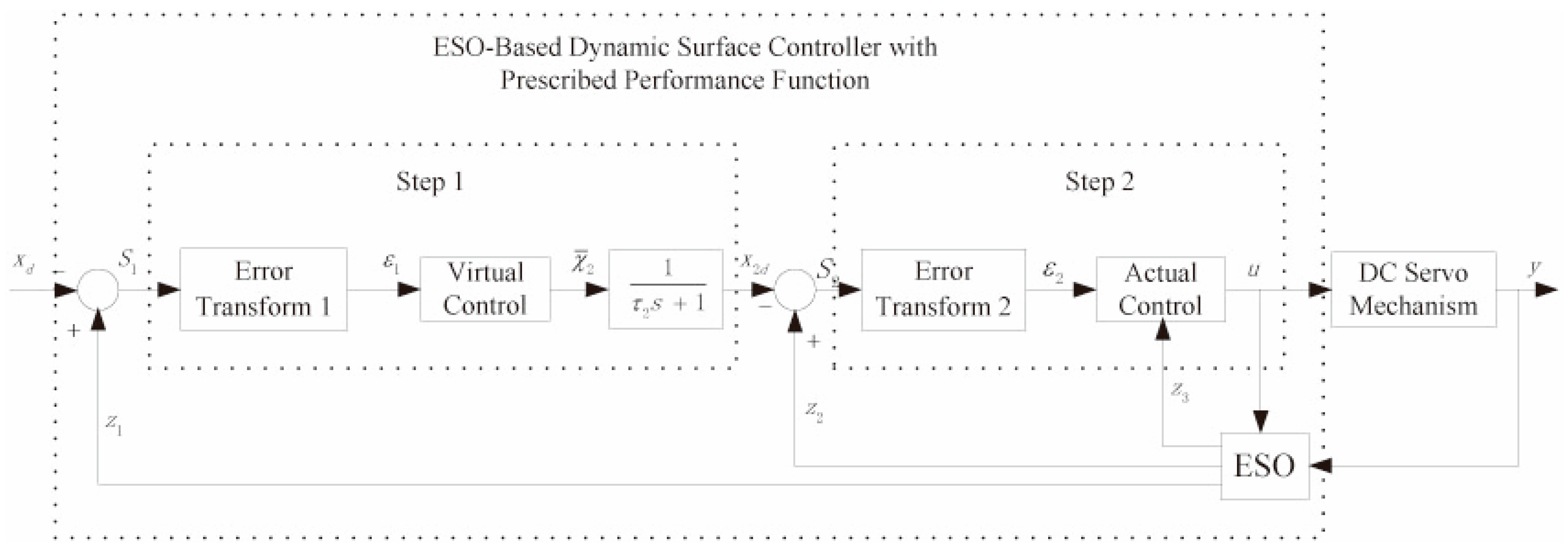
3. Control Strategy
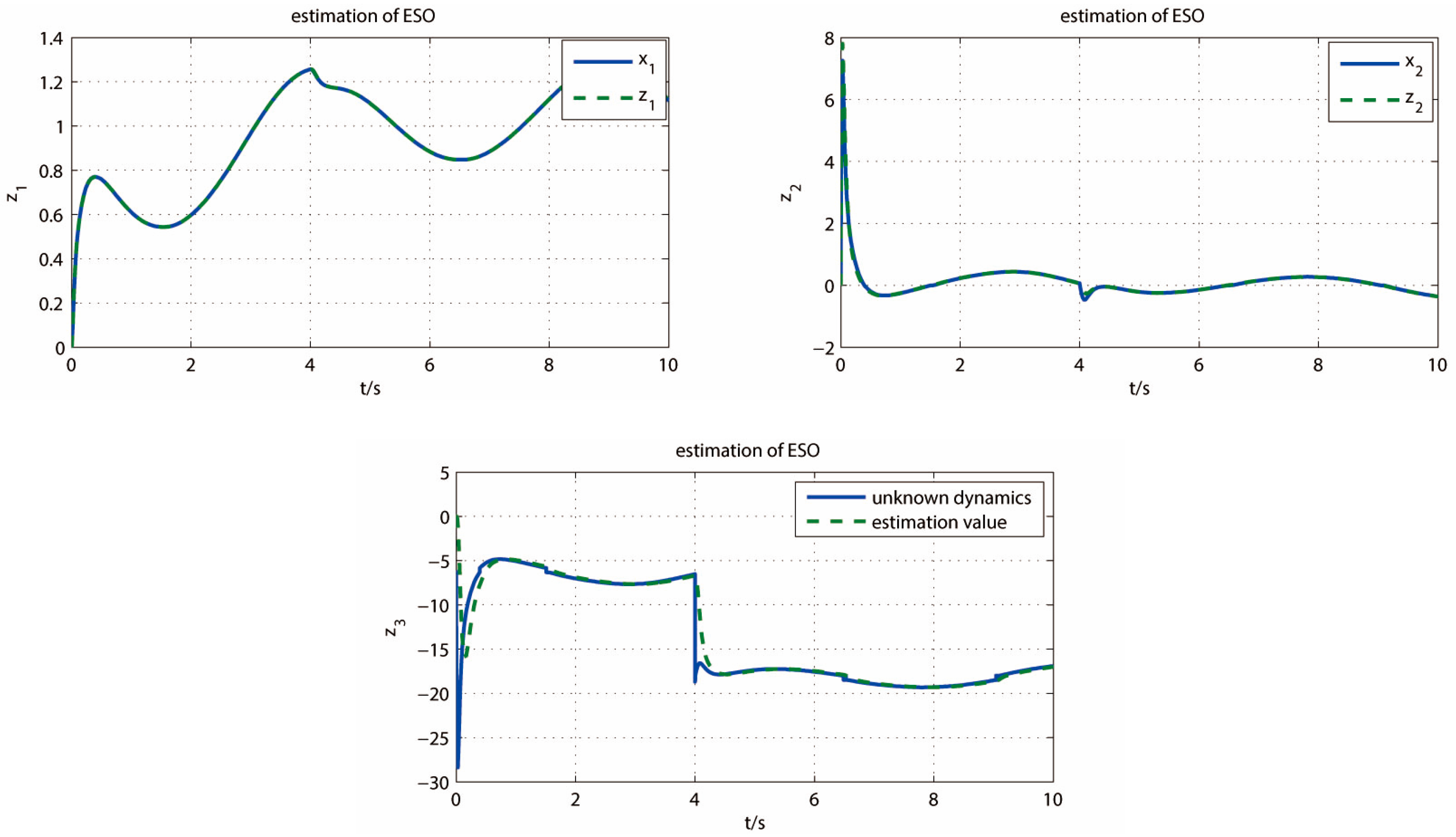
3.1. Extended State Observer Design
3.2. Prescribed Performance Control
- (1)
- It is a smooth strictly increasing function;
- (2)
- ;
- (3)
- and .
3.3. Controller Design
4. Stability Analysis
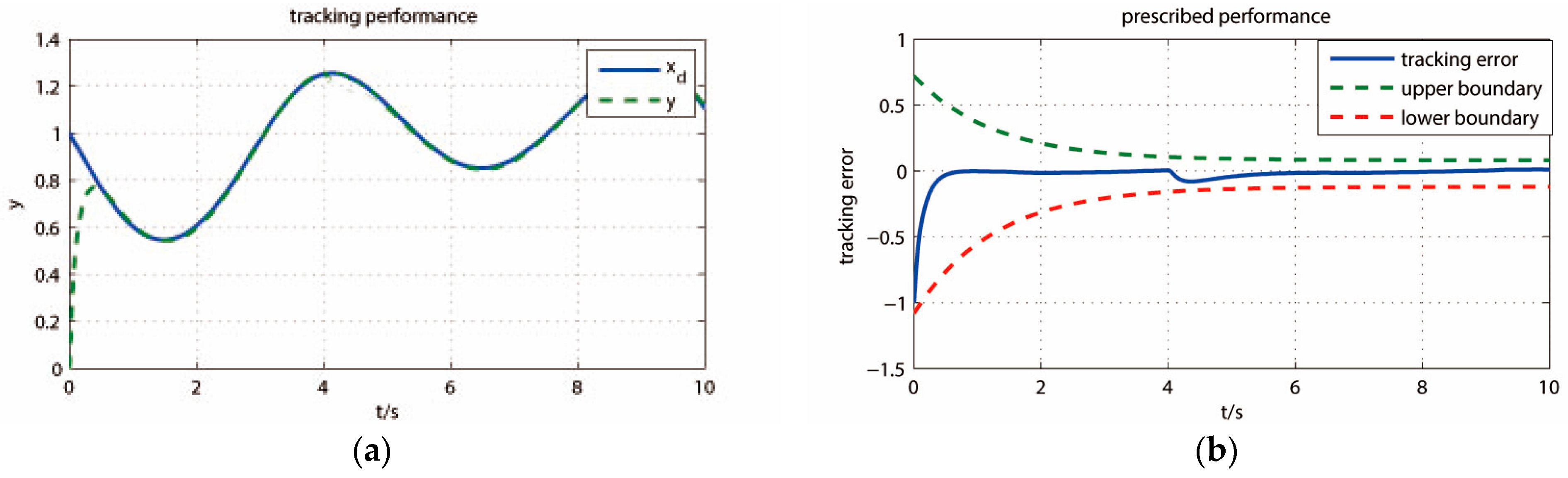
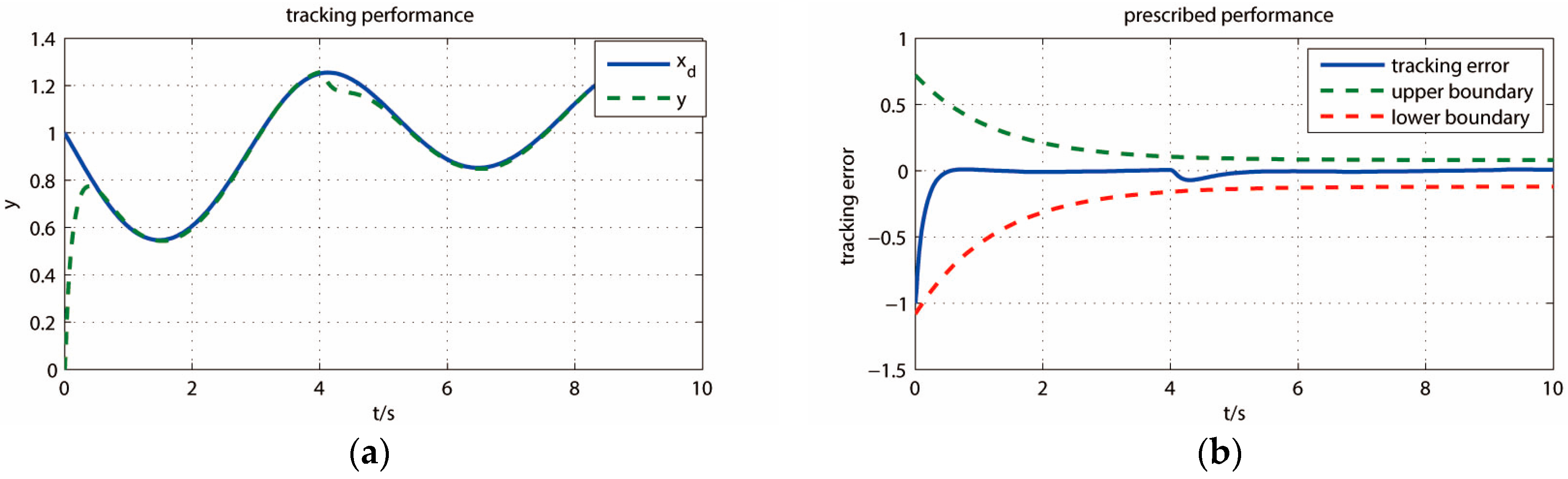
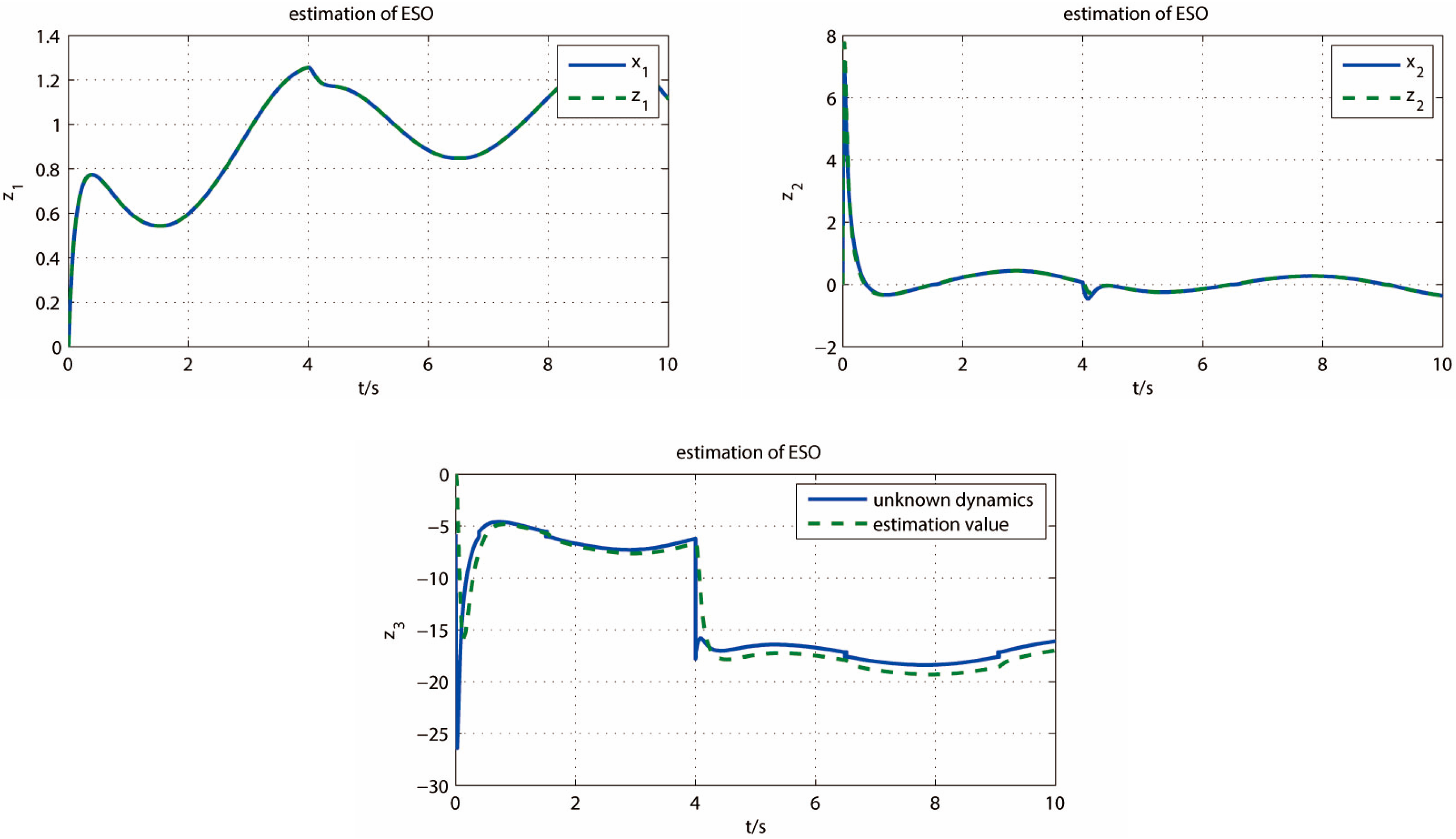
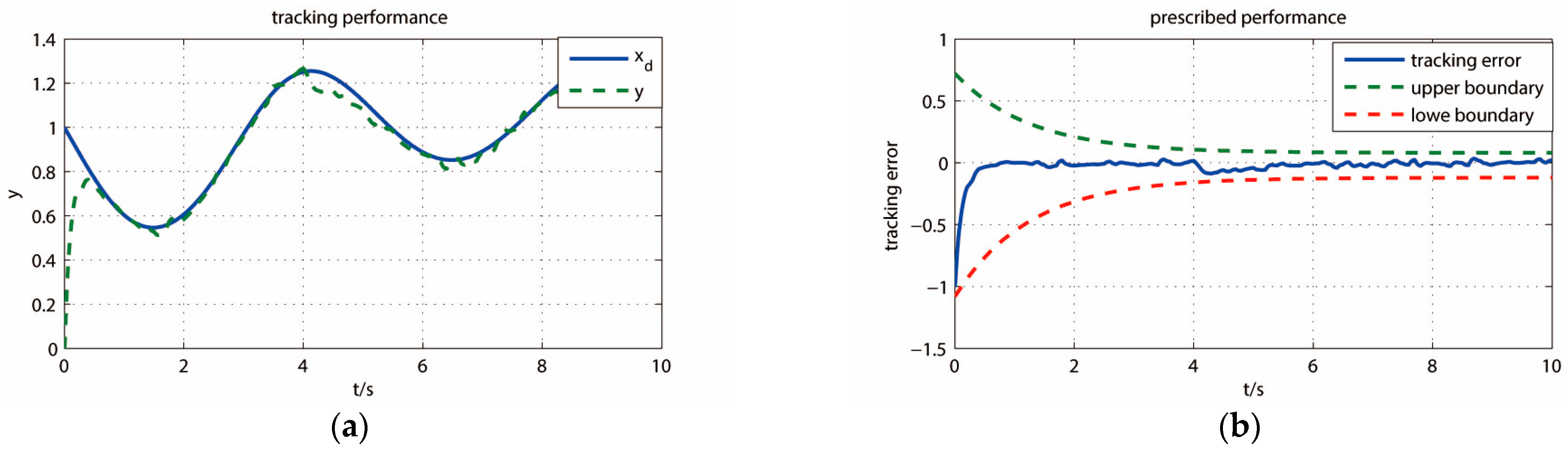
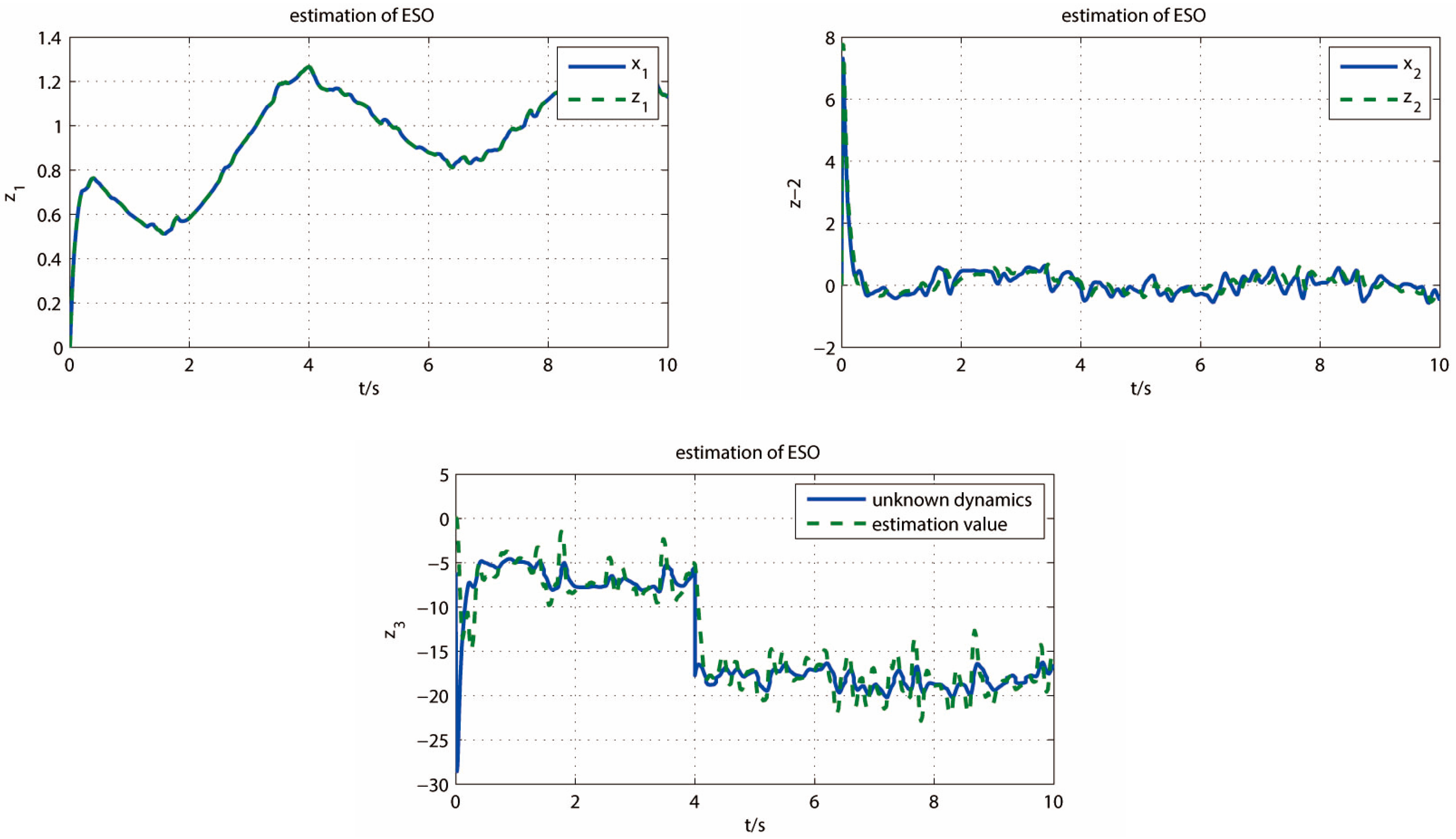
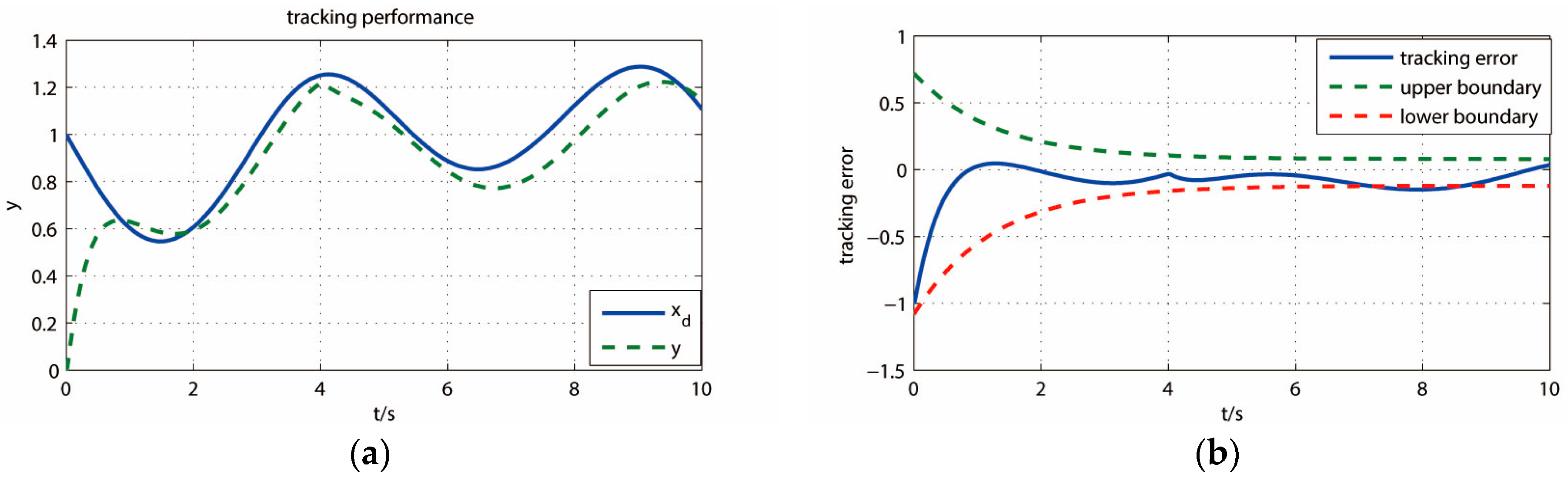
5. Analysis of Simulation Results
5.1. Simulation Experiments of Turntable
5.2. Quantitative Analysis of Control Performance
- (1)
- The maximum absolute value of the tracking error during the steady state period ;
- (2)
- Integrated absolute error ;
- (3)
- Standard deviation of the tracking errors , where ;
- (4)
- Integrated time absolute error ;
- (5)
- Integrated square error , where is the mean value of the error;
- (6)
- Integrated absolute control .
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shaik, R.B.; Rao, B.L.; Rani, D.S. PMBLDC motor (PMBLDCM) with non-linear controller usage in electric. e-Prime—Adv. Electr. Eng. Electron. Energy 2024, 7, 100461. [Google Scholar] [CrossRef]
- Zhang, T.H.; Li, X.W. Integrated Controller Design and Application for CNC Machine Tool Servo Systems Based on Model Reference Adaptive Control and Adaptive Sliding Mode Control. Sensors 2023, 23, 9755. [Google Scholar] [CrossRef]
- Hu, C.; Yao, B.; Wang, Q. Adaptive Robust Precision Motion Control of Systems With Unknown Input Dead-Zones: A Case Study With Comparative Experiments. IEEE Trans. Ind. Electron. 2011, 58, 2454–2464. [Google Scholar] [CrossRef]
- Encalada-Davila, A.; Ellithy, K.M. Optimized PID and NN-based Speed Control of a Load-coupled DC Motor. J. Phys. Conf. Ser. 2024, 2701, 012128. [Google Scholar] [CrossRef]
- Alejandro-Sanjines, U.; Maisincho-Jivaja, A. Adaptive PI Controller Based on a Reinforcement Learning Algorithm for Speed Control of a DC Motor. Biomimetics 2023, 8, 434. [Google Scholar] [CrossRef] [PubMed]
- Awan, A.A.; Khan, U.S.; Awan, A.U.; Hamza, A. Tracking Control and Backlash Compensation in an Inverted Pendulum with Switched-Mode PID Controllers. Appl. Sci. 2024, 14, 10265. [Google Scholar] [CrossRef]
- Kandiban, R.; Arulmozhiyal, R. Design of Adaptive Fuzzy PID Controller for Speed control of BLDC Motor. Int. J. Soft Comput. Eng. 2012, 2, 386–391. [Google Scholar]
- Prabu, M.J.; Poongodi, P.; Premkumar, K. Fuzzy supervised online coactive neuro-fuzzy inference system-based rotor position control of brushless DC motor. IET Power Electron. 2016, 9, 2229–2239. [Google Scholar] [CrossRef]
- Lv, Y.; Ren, X.; Na, J. Online Nash-optimization tracking control of multi-motor driven load system with simplified RL scheme. ISA Trans. 2020, 98, 251–262. [Google Scholar] [CrossRef] [PubMed]
- Subramani, S.; Vijayarangan, K.K. Improved African Buffalo Optimization-Based Takagi–Sugeno–Kang Fuzzy PI Controller for Speed Control in BLDC Motor. Electr. Power Compon. Syst. 2023, 51, 1948–1962. [Google Scholar] [CrossRef]
- Eker, E.; Kayri, M.; Ekinci, S. A new fusion of ASO with SA algorithm and its applications to MLP training and DC motor speed control. Arab. J. Sci. Eng. 2021, 46, 3889–3911. [Google Scholar] [CrossRef]
- Tao, T.; Hua, L.H. Decoupling control of bearingless brushless DC motor using particle swarm optimized neural network inverse system. Meas. Sens. 2024, 31, 100952. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, H.; Yuan, M.; Liang, B.; Li, Y.; Huangfu, Y. Chattering suppression fast terminal sliding mode control for aircraft EMA braking system. IEEE Trans. Transp. Electr. 2021, 7, 1901–1914. [Google Scholar] [CrossRef]
- Wang, T.; Zhao, X.; Jin, H. Robust tracking control for permanent magnet linear servo system using intelligent fractional-order backstepping control. IEEE Trans. Transp. Electr. 2021, 103, 1555–1567. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Ahn, K.K. Output Feedback Robust Tracking Control for a Variable-Speed Pump-Controlled Hydraulic System Subject to Mismatched Uncertainties. Mathematics 2023, 11, 1783. [Google Scholar] [CrossRef]
- Elp, H.E.; Altug, H.; Inan, R. Designing a Brushed DC Motor Driver with a Novel Adaptive Learning Algorithm for the Automotive Industry. Electronics 2024, 13, 4344. [Google Scholar] [CrossRef]
- Jang, M.; Kim, S.; Yoo, B.; Oh, K. A Robust Path Tracking Controller for Autonomous Mobility with Control Delay Compensation Using Backstepping Control. Mathematics 2024, 13, 508. [Google Scholar] [CrossRef]
- Yun, J.N.; Su, J.; Kim, Y.I.; Kim, Y.C. Robust disturbance observer for two-inertia system. IEEE Trans. Ind. Electron. 2013, 60, 2700–2710. [Google Scholar] [CrossRef]
- Canuto, E.; Acuna-Bravo, W.; Molano, A.; Perez, C. Embedded Model Control calls for disturbance modeling and rejection. ISA Trans. 2012, 51, 584–595. [Google Scholar] [CrossRef] [PubMed]
- Szabat, K.; Tran-Van, T.; Kaminski, M. A modified fuzzy Luenberger observer for a two-mass drive system. IEEE Trans. Ind. Inform. 2015, 11, 531–539. [Google Scholar] [CrossRef]
- Yang, X.Y.; Wang, X.J.; Wang, S.P. Finite-time adaptive dynamic surface synchronization control for dual-motor servo systems with backlash and time-varying uncertainties. ISA Trans. 2023, 137, 248–262. [Google Scholar] [CrossRef] [PubMed]
- Han, J.Q. Active Disturbance Rejection Control Technology; National Defence Industry Press: Beijing, China, 2008. [Google Scholar]
- Liu, S.; Liao, H.; Xue, J.J. A non-contact spacecraft architecture with extended stochastic state observer based control for gravity mission. J. Syst. Eng. Electron. 2021, 32, 460–472. [Google Scholar]
- Liu, J.J.; Sun, M.W.; Chen, Z.Q. High AOA decoupling control for aircraft based on ADRC. J. Syst. Eng. Electron. 2020, 31, 393–402. [Google Scholar] [CrossRef]
- Rosas, D.; Alvarez, J.; Cardenas, J.A. Application of the active disturbance rejection control structure to improve the controller performance of uncertain pneumatic actuators. Asian J. Control 2019, 21, 99–113. [Google Scholar]
- Wang, B.; Tang, C.Y.; Yao, Z.N. Trajectory tracking control of unmanned aerial vehicles based on cascaded LADRC design. Syst. Eng. Electron. 2019, 41, 1358–1365. [Google Scholar]
- Nguyen, M.H.; Ahn, K.K. A Finite-Time Disturbance Observer for Tracking Control of Nonlinear Systems Subject to Model Uncertainties and Disturbances. Mathematics 2024, 12, 3512. [Google Scholar] [CrossRef]
- Zhang, G.Z.; Chen, J.; Li, Z.P. Identifier-Based Adaptive Robust Control for Servomechanisms With Improved Transient Performance. IEEE Trans. Ind. Electron. 2010, 57, 2536–2547. [Google Scholar] [CrossRef]
- Liu, X. Technology of Line-of-Sight (LOS) Stabilization for Ship-Based Photoelectric Tracking; University of Chinese Academy of Sciences: Beijing, China, 2013. [Google Scholar]
- Zheng, Q.; Gaol, L.D.; Gao, Z.Q. On Stability Analysis of Active Disturbance Rejection Control for Nonlinear Time-Varying Plants with Unknown Dynamics. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 3501–3506. [Google Scholar]
- Gao, Z.Q. Scaling and Bandwidth-Parameterization Based Controller Tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Chen, X. Active Disturbance Rejection Control Tuning and Its Application to Thermal Processes; Tsinghua University: Beijing, China, 2008. [Google Scholar]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust adaptive control of feedback linearizable mimo nonlinear systems with prescribed performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Na, J.; Chen, Q.; Ren, X.; Guo, Y. Adaptive prescribed performance motion control of servo mechanisms with friction compensation. IEEE Trans. Ind. Electron. 2013, 61, 486–494. [Google Scholar] [CrossRef]
- Wang, S.B.; Ren, X.M.; Na, J. Adaptive dynamic surface control based on fuzzy disturbance observer for drive system with elastic coupling. J. Frankl. Inst. 2016, 353, 1899–1919. [Google Scholar] [CrossRef]
- Hardy, G.; Littlewood, J.E.; Polya, G. Inequalities, 2nd ed.; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Khalil, H. Nonlinear Systems; Prentice-Hall Press: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Wang, F.Y.; Zhang, X.K.; Ren, C.Z.; Gao, H.B.; Chen, C.Q.; Chen, J. Self-stabilization modeling and simulation on ship-sway of a photoelectric tracker. Opto-Electron. Eng. 2005, 32, 11–14. [Google Scholar]
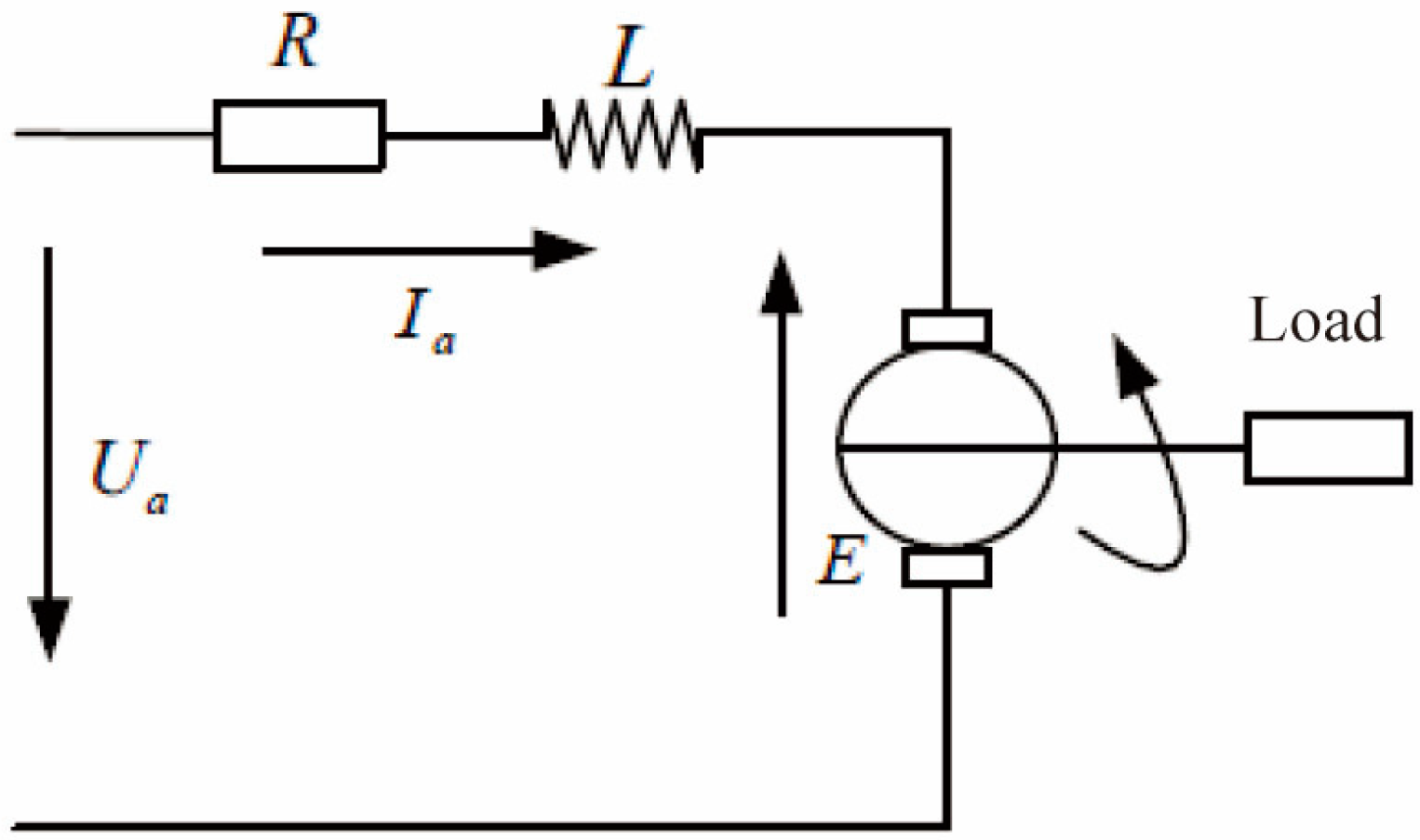

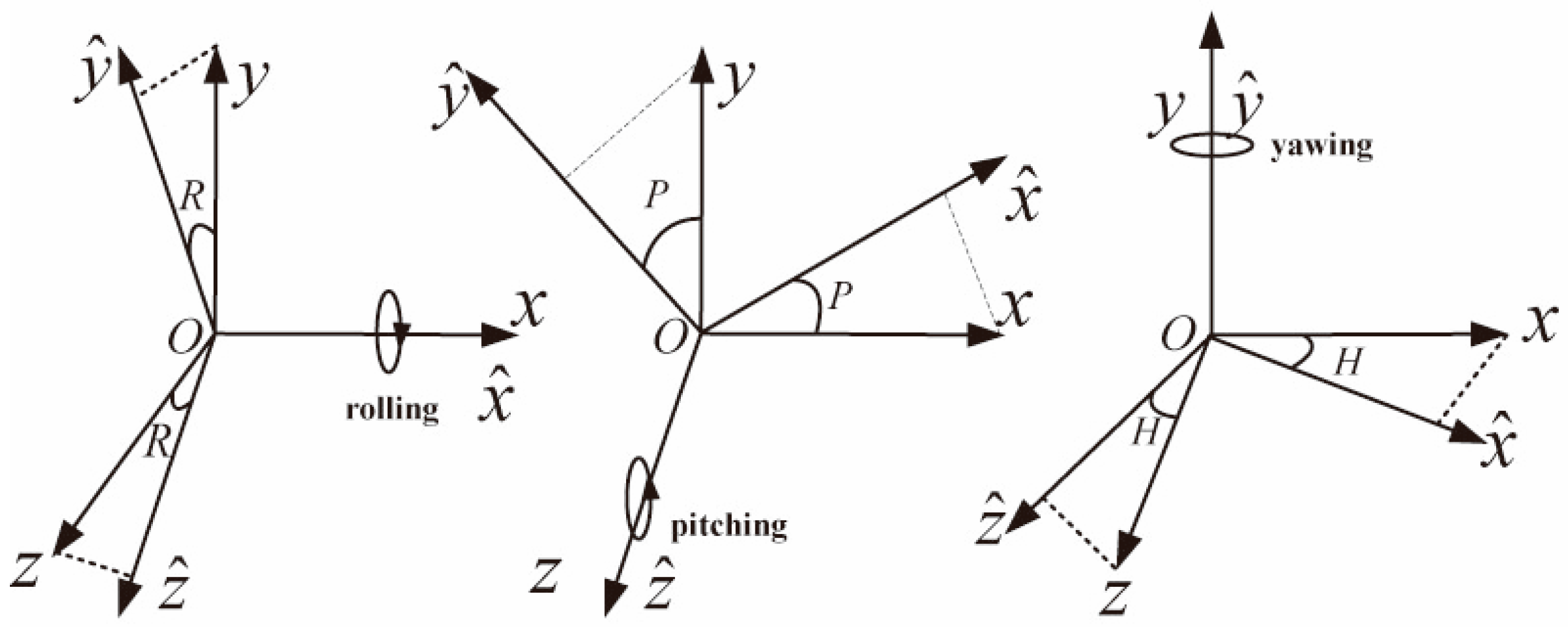
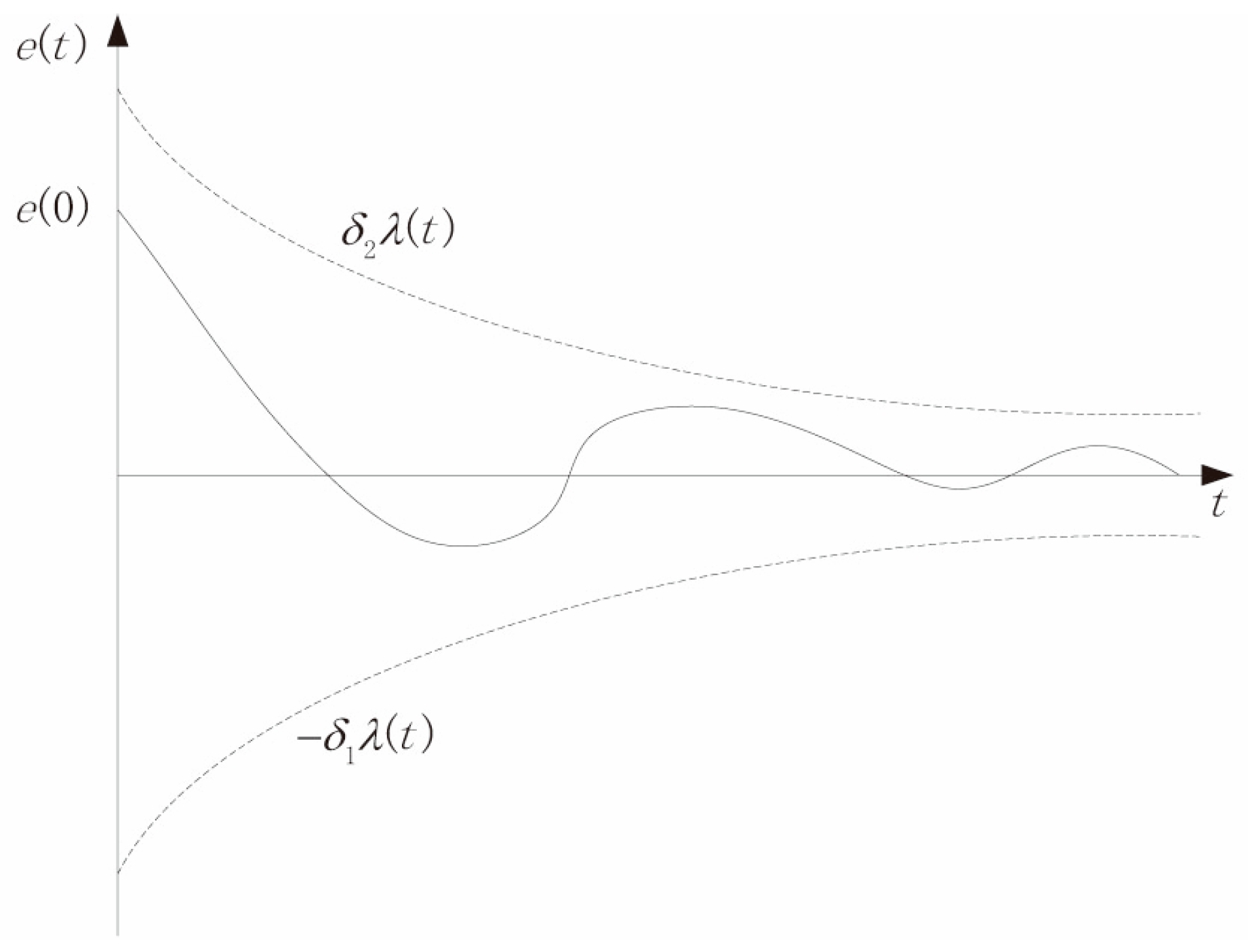
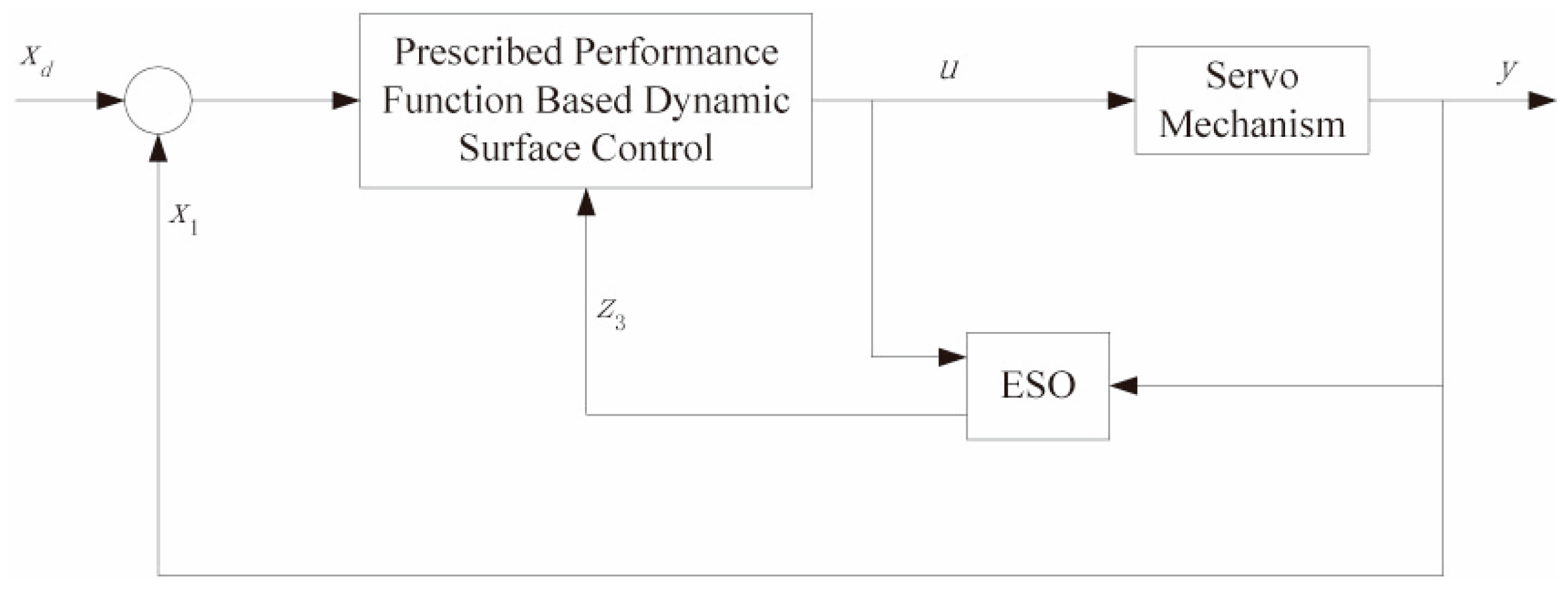

| Motor Type | Azimuth Motor: 200LYX25-DS |
|---|---|
| Armature voltage | 28 V |
| Armature resistance | 2.6 Ω |
| Armature inductance | 5.4 mH |
| Maximum non-load speed | 186 r/m |
| Moment of inertia | 1645.866 × 10–5 kg·m2 |
| Motor torque coefficient | 1.24 N·m/A |
| W | IDSCESO | IDSCESOw | PID | PIDw |
|---|---|---|---|---|
| Me | 0.00684 | 0.01769 | 0.03628 | 0.00093 |
| IAE | 0.21538 | 0.26023 | 0.95133 | 0.97555 |
| σe | 0.08165 | 0.08085 | 0.1345 | 0.1303 |
| ITAE | 0.43855 | 0.68525 | 3.98676 | 3.89386 |
| ISDE | 0.06528 | 0.06523 | 0.15933 | 0.16001 |
| IAU | 6.62932 | 6.88447 | 8.85061 | 8.62583 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Liao, W.; Liu, T.; Zhang, D.; Tao, Y. Disturbance Observer-Based Dynamic Surface Control for Servomechanisms with Prescribed Tracking Performance. Mathematics 2025, 13, 172. https://doi.org/10.3390/math13010172
Zhao X, Liao W, Liu T, Zhang D, Tao Y. Disturbance Observer-Based Dynamic Surface Control for Servomechanisms with Prescribed Tracking Performance. Mathematics. 2025; 13(1):172. https://doi.org/10.3390/math13010172
Chicago/Turabian StyleZhao, Xingfa, Wenhe Liao, Tingting Liu, Dongyang Zhang, and Yumin Tao. 2025. "Disturbance Observer-Based Dynamic Surface Control for Servomechanisms with Prescribed Tracking Performance" Mathematics 13, no. 1: 172. https://doi.org/10.3390/math13010172
APA StyleZhao, X., Liao, W., Liu, T., Zhang, D., & Tao, Y. (2025). Disturbance Observer-Based Dynamic Surface Control for Servomechanisms with Prescribed Tracking Performance. Mathematics, 13(1), 172. https://doi.org/10.3390/math13010172





