Gradient Method with Step Adaptation
Abstract
1. Introduction
- The principle of step adaptation of the gradient method is developed.
- Several step adaptation algorithms are proposed.
- The proposed methods use only one gradient value per iteration.
- A step adaptation method is proposed such that in the case without interference, its iteration costs are either equivalent to the number of iterations or significantly less than the steepest descent method costs.
- The proposed methods were studied under conditions of relative interference on the gradient and their efficiency was established.
- The obtained algorithms converge at a high rate in the case where the radius of the ball of uniformly distributed interference significantly exceeds the norm of the gradient value.
2. Problem Statement and Related Work
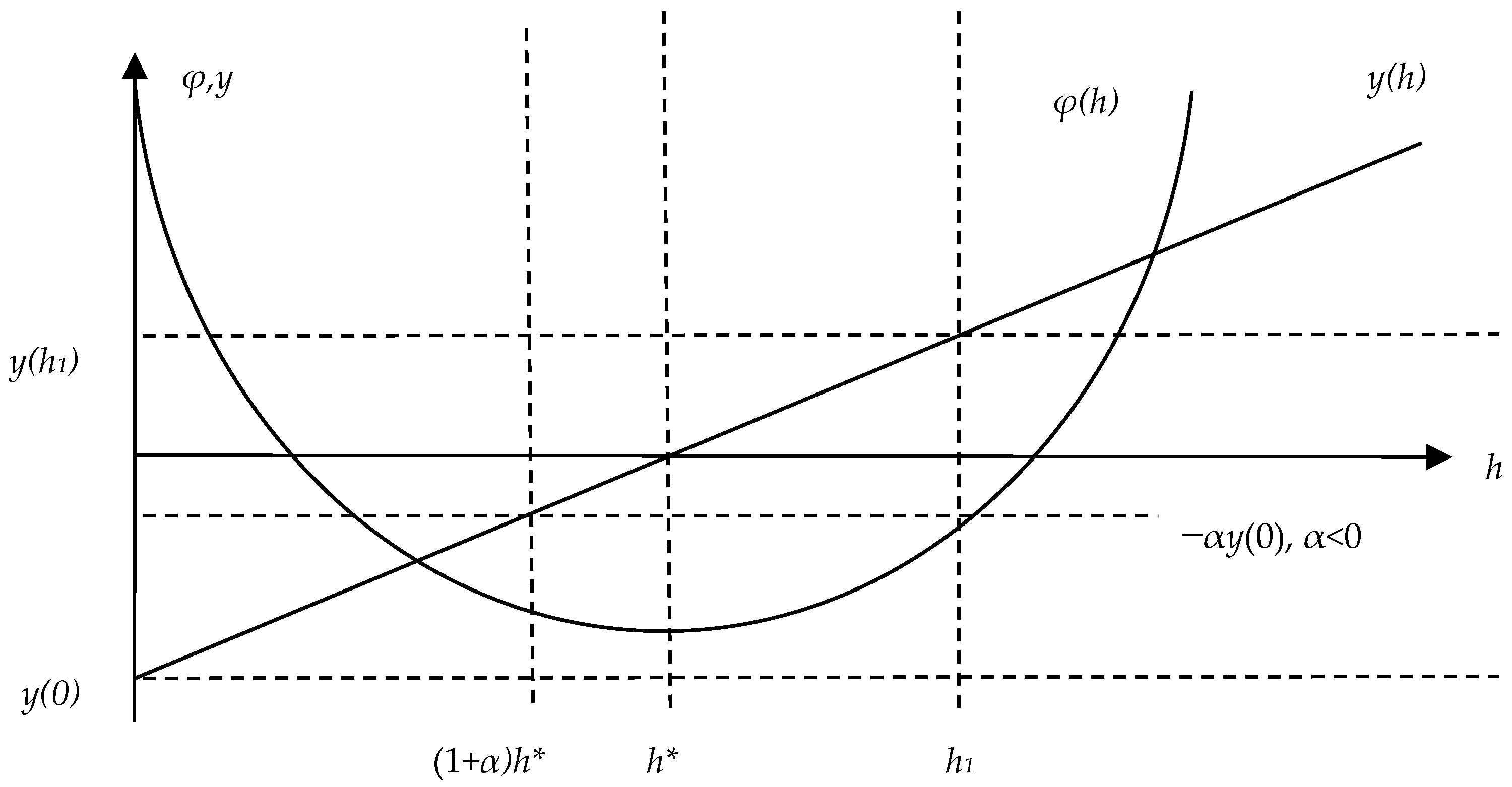
- The step is too large if there is an obtuse angle between adjacent gradients, that is, . Therefore, the step should be reduced.
- If there is an acute angle between adjacent gradients, that is, , then the step is too small, and it should be increased.
3. Algorithms for Step Adaptation in the Gradient Method
| Algorithm 1 (A1(q)) |
| 1. Set q > 1, the search step h0 > 0, the initial point x0. 2. For k = 0,1,2,… do 2.1 Search for new approximation 2.2 If then else . 2.3 Compute the new search step |
| Algorithm 2 (A2(q)) |
| 1. Set q > 1, the search step h0 > 0, the initial point x0. 2. For k = 0,1,2,… do 2.1 Search for new approximation 2.2 If then else . 2.3 Compute the new search step |
4. Algorithms for the Step Adaptation of the Gradient Method with Incomplete Relaxation, Super Relaxation and Mixed Relaxation
| Algorithm 3 (A3(q, α)) |
| 1. Set q > 1, the search step h0 > 0, the initial point x0, parameter α > −1. 2. For k = 0,1,2,… do 2.1 Search for new approximation 2.2 If then else . 2.3 Compute the new search step . |
| Algorithm 4 (A4(q, α)) |
| 1. Set q > 1, the search step h0 > 0, the initial point x0, parameter α > −1. 2. For k = 0,1,2,… do 2.1 Search for new approximation 2.2 If then else . 2.3 Compute the new search step |
| Algorithm 5 (A5(q, α[a, b])) |
| 1. Set q > 1, the search step h0 > 0, the initial point x0, parameters of the segment [a, b] a > −1, b > a. 2. For k = 0,1,2,… do 2.1 Search for new approximation 2.2 Set α ∈ [a, b]. 2.3 If then else . 2.4 Compute the new search step |
5. Convergence Analysis
6. Numerical Experiment
- Evaluate the efficiency of the proposed algorithms and compare their efficiency with the efficiency of the steepest descent method under conditions without interference.
- Determine the effects of convergence acceleration in the proposed methods and identify modifications that have accelerated convergence.
- Study the effect on the convergence rate when applying a gradient of relative interference uniformly distributed on a ball of radius
- Make estimates of the iteration costs given (29).
6.1. Rosenbrock Function
6.2. Quadratic Function
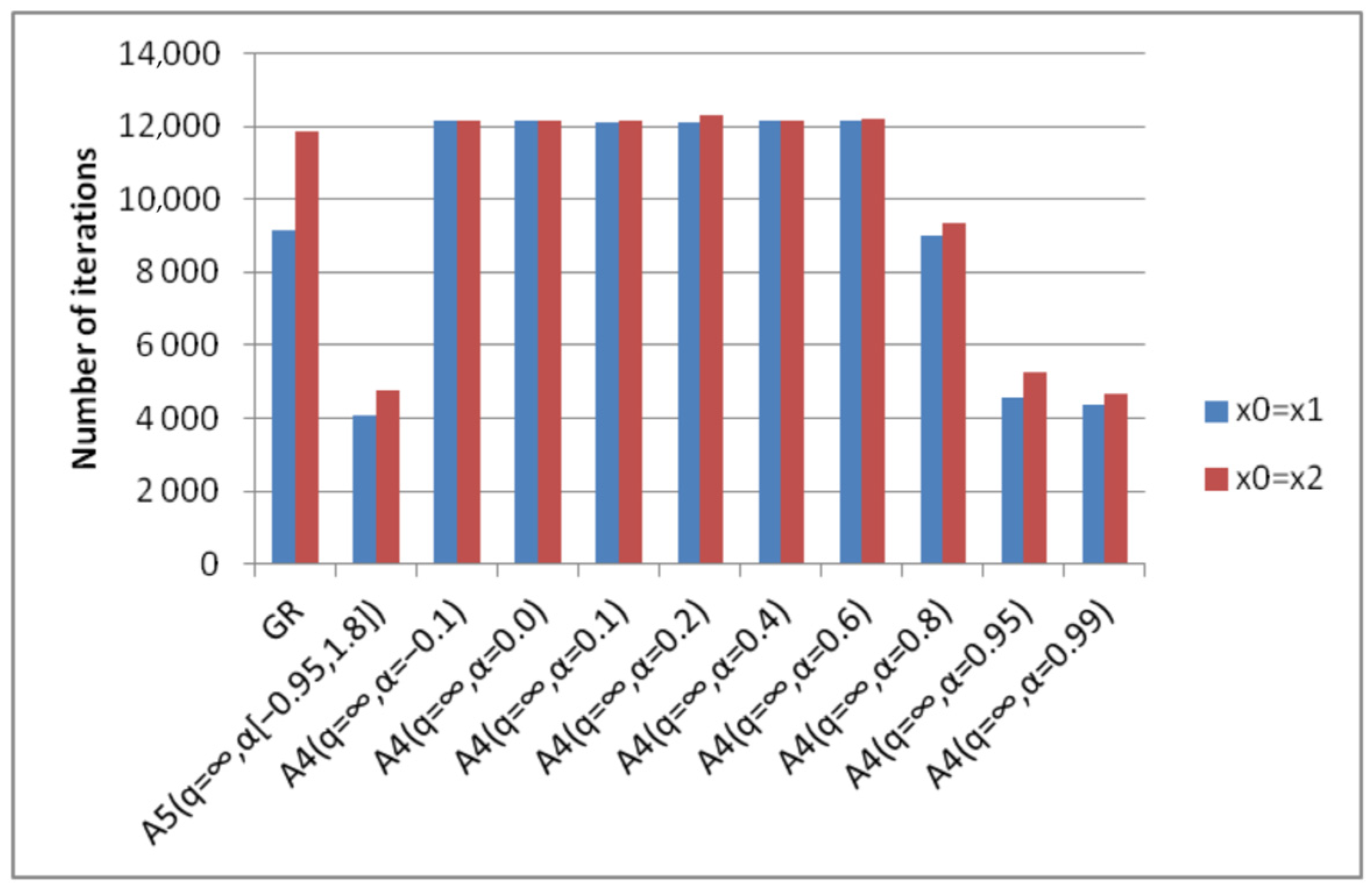
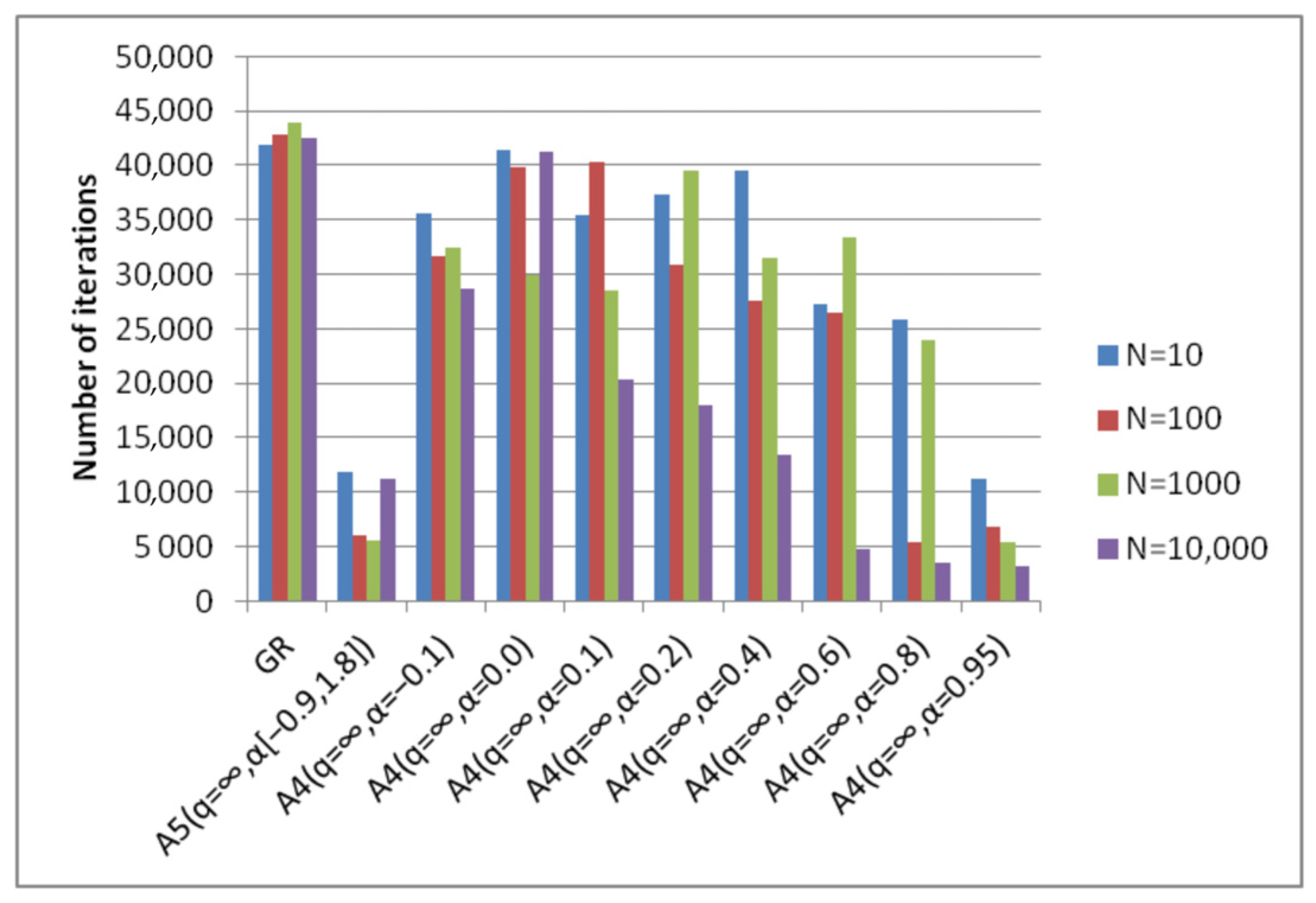
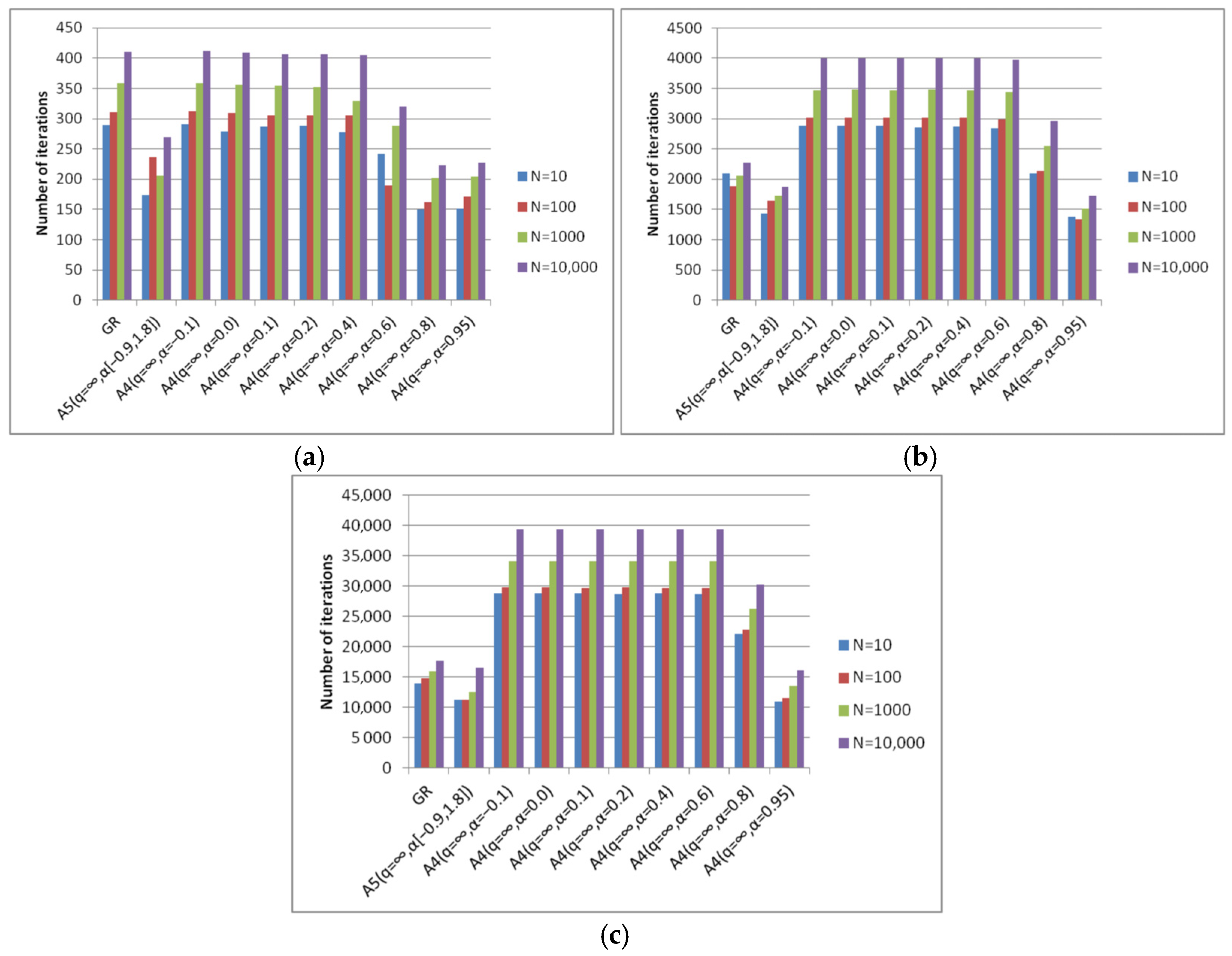
- Algorithm A4(q = ∞, α) achieves good results with different parameters α for different degrees of conditionality. This parameter can only be determined experimentally.
- Algorithm A5(q = ∞, α[a, b]) achieves good results with fixed parameters of the algorithm for different degrees of conditionality. From this point of view, it can be considered universal.
- The best versions of algorithm A4(q = ∞, α) and algorithm A5(q = ∞, α[a, b]) are less expensive in terms of the number of iterations compared to the gradient method.
6.3. Functions with Ellipsoidal Ravine
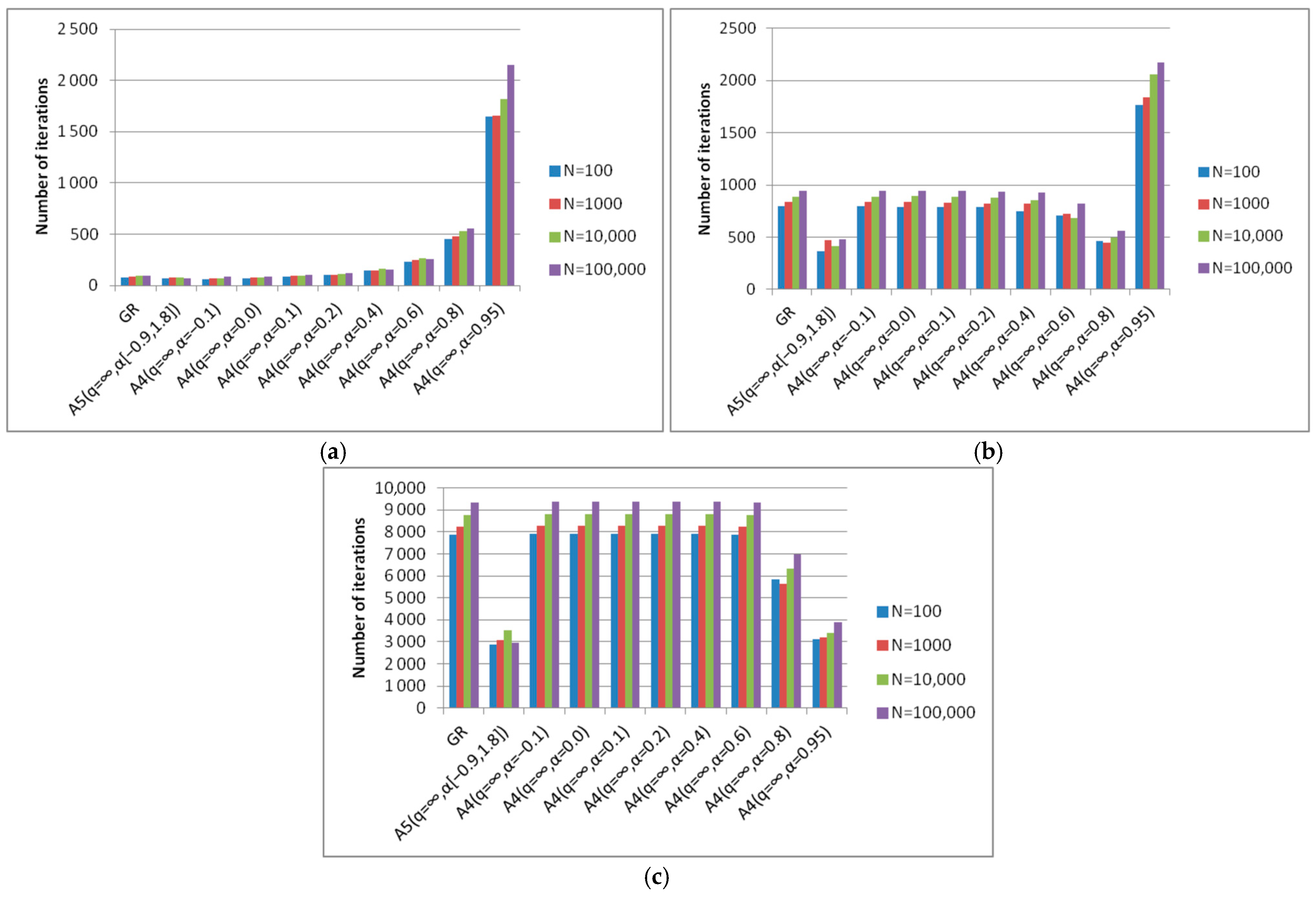
- Algorithm A4(q = ∞, α) achieves good results at α = 0.95 for various degrees of elongation of the level surfaces. This parameter can only be determined experimentally.
- Algorithm A5(q = ∞, α[a, b]) achieves good results with fixed algorithm parameters for various degrees of elongation of the level surfaces. From this point of view, it confirms its universality.
- The best versions of algorithm A4(q = ∞, α) and algorithm A5(q = ∞, α[a, b]) are less expensive in terms of the number of iterations compared to the steepest descent method.
7. Discussion
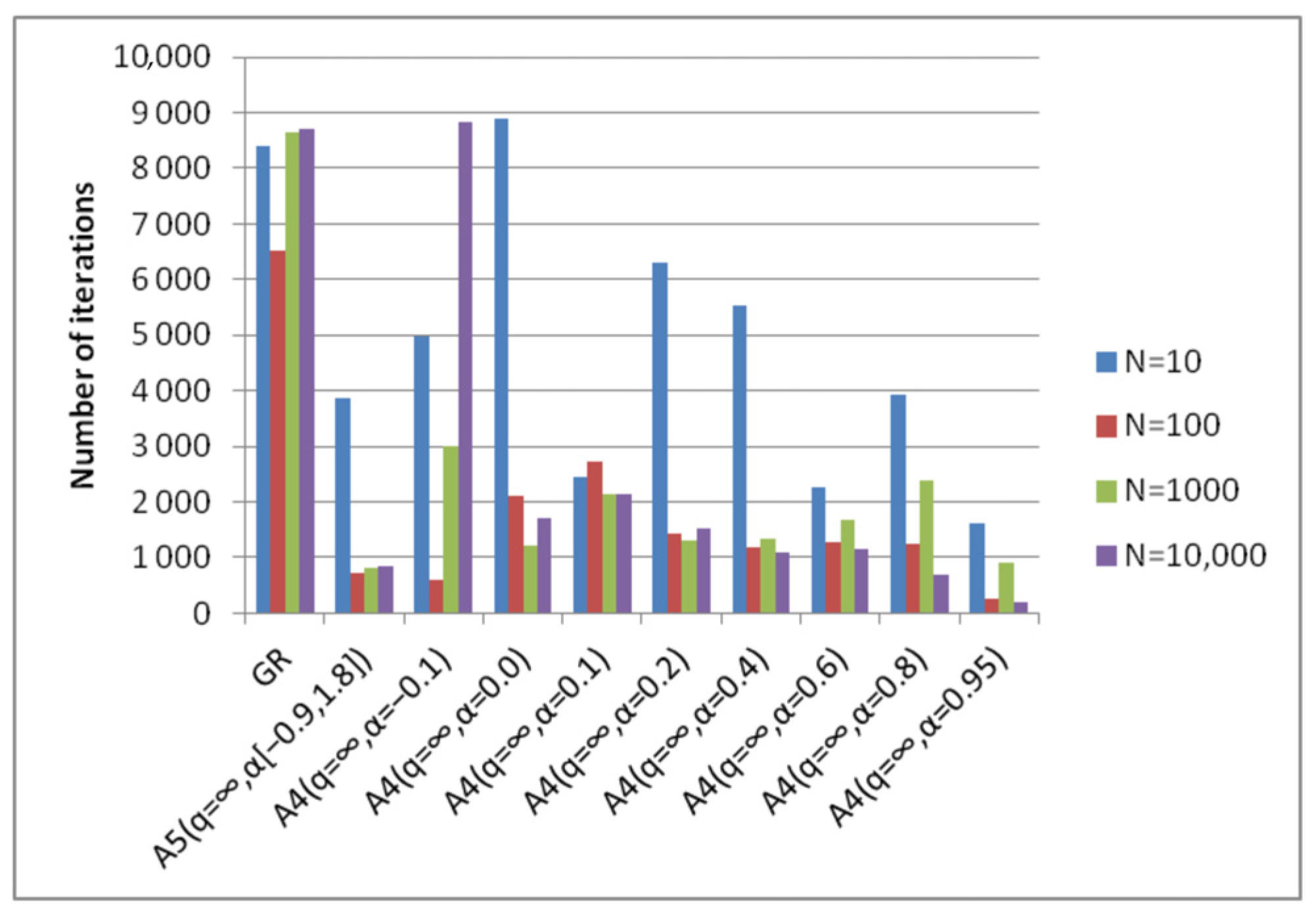
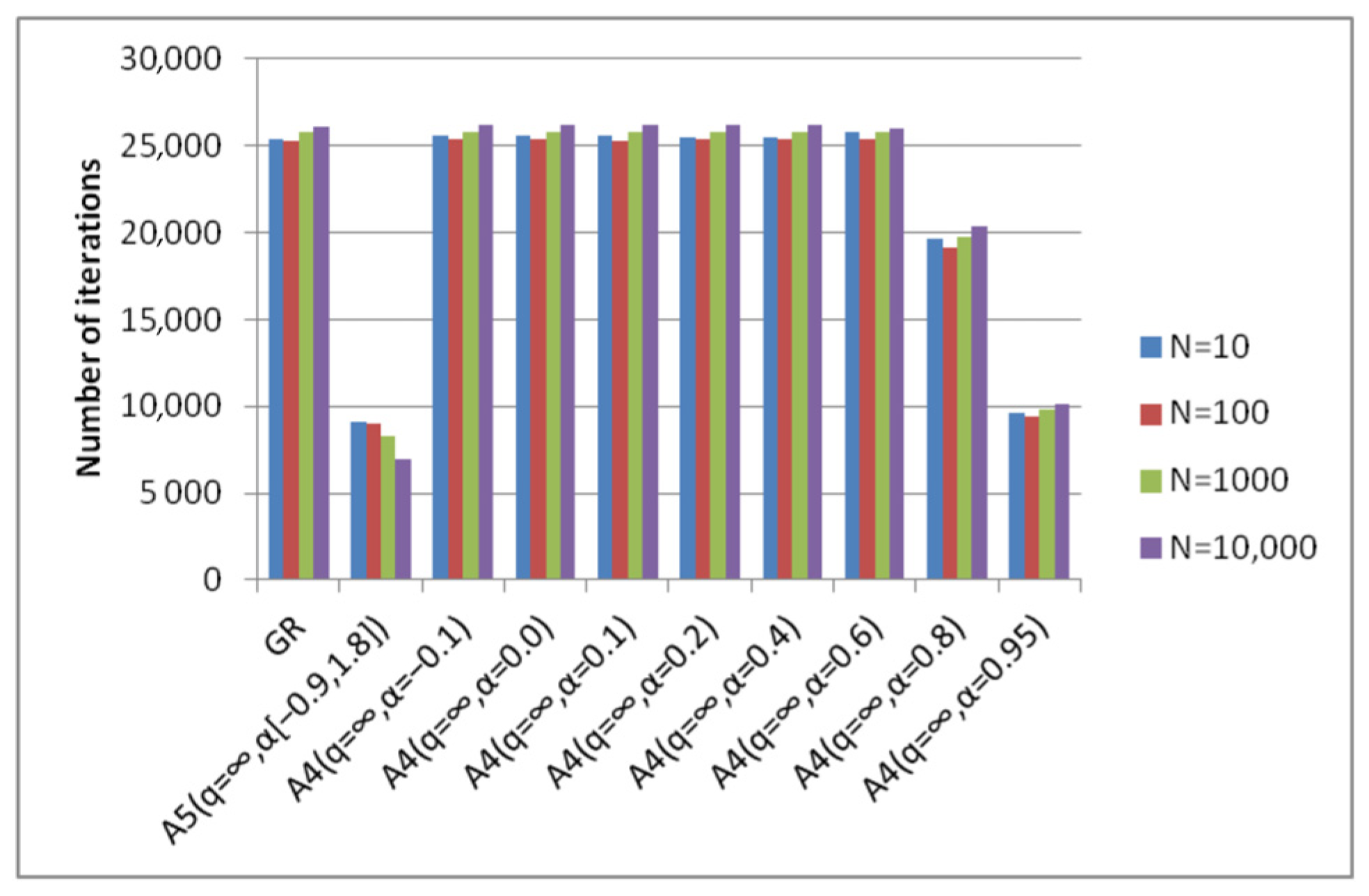
- Algorithm A4(q = ∞, α) achieves the best (minimal) results with different parameters α, which depend on the degree of conditionality of the problem and the choice of the starting point (Figure 19).
- The best results of algorithm A4(q = ∞, α) are either comparable or significantly exceed the results of the steepest descent method in the number of iterations.
- The results of algorithm A5(q = ∞, α[a, b]) with fixed parameters correspond to the results of the optimal algorithm A4(q = ∞, α) (Figure 20). This means that there is no need to preliminarily choose the parameters for the A4(q = ∞, α) algorithm. To obtain optimal results one can use the A5(q = ∞, α[a, b]) algorithm, the parameters of which are fixed.
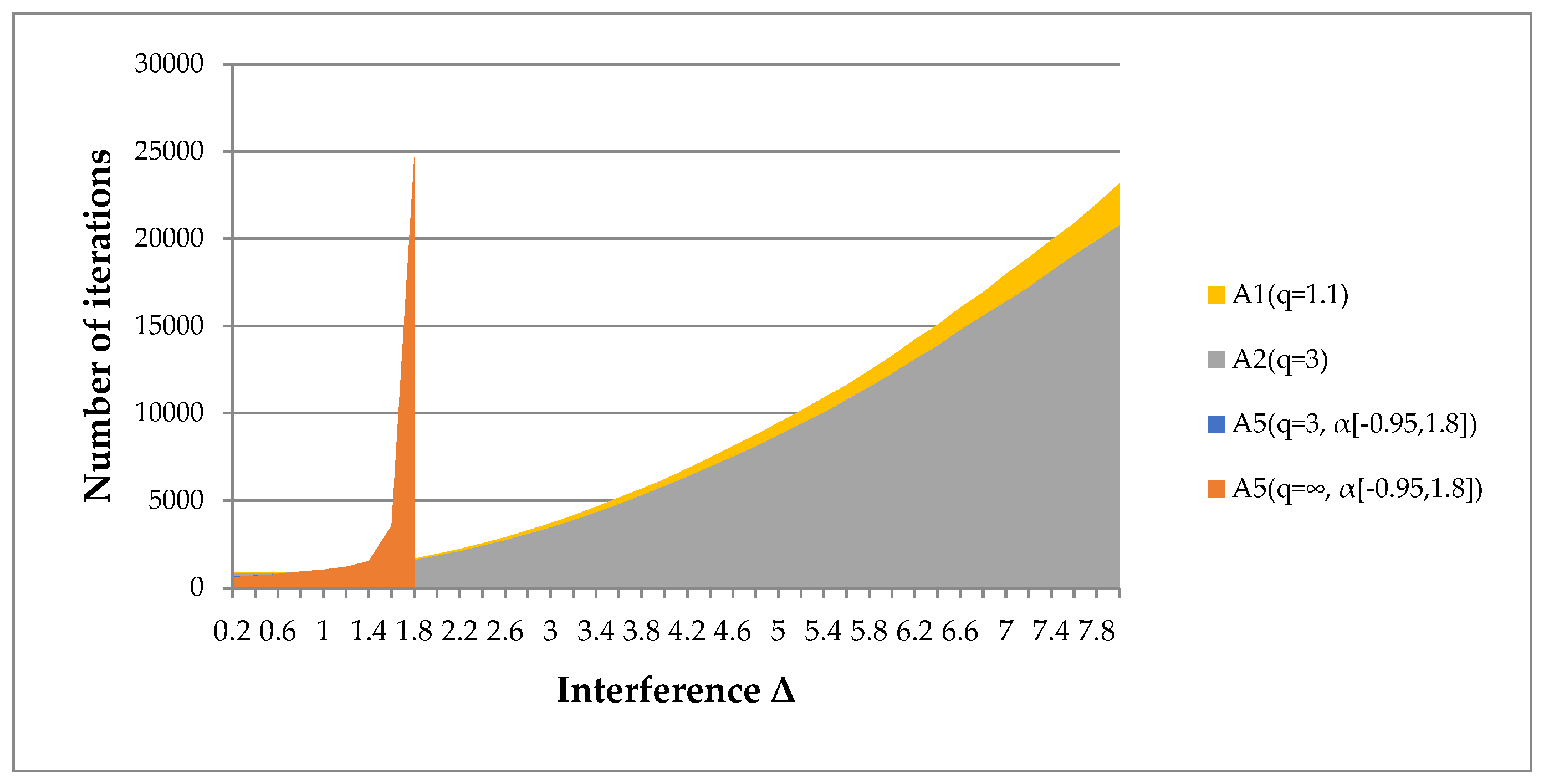
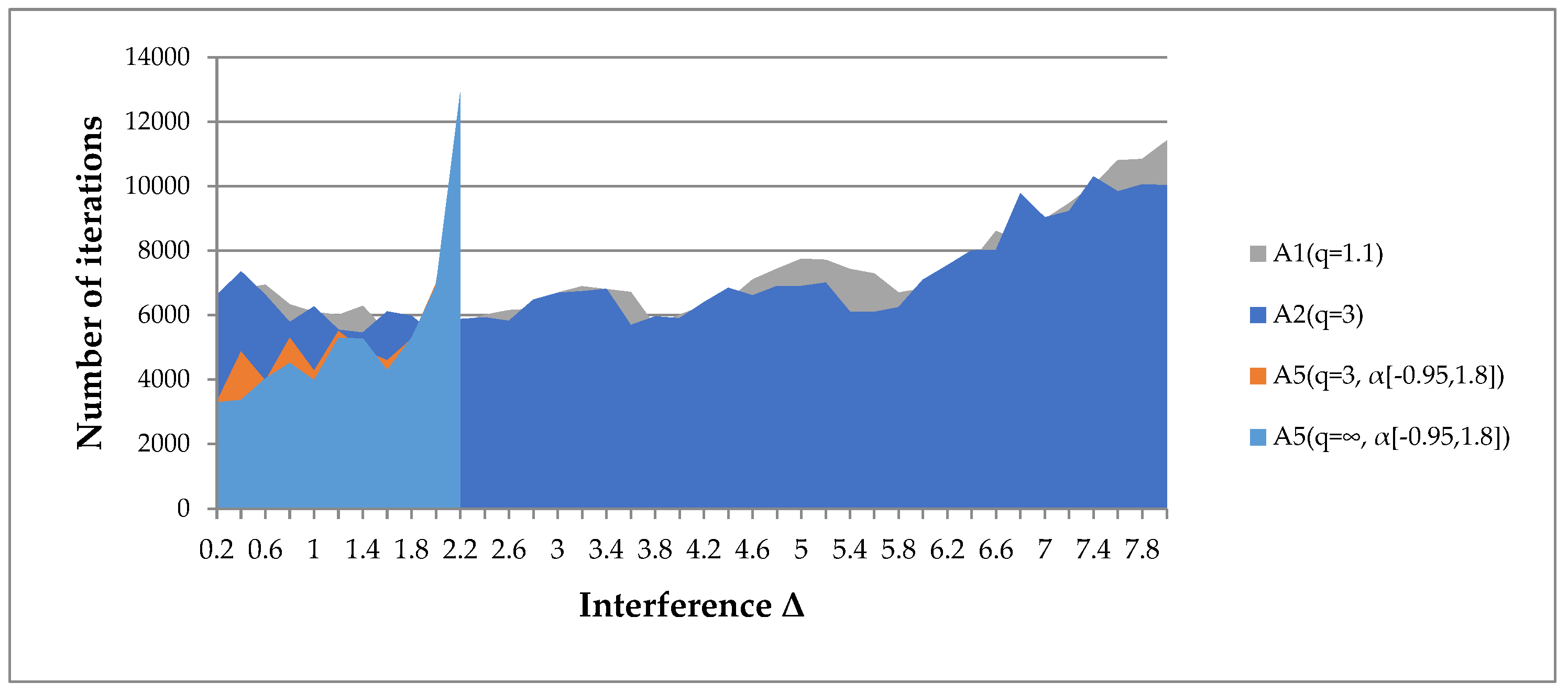
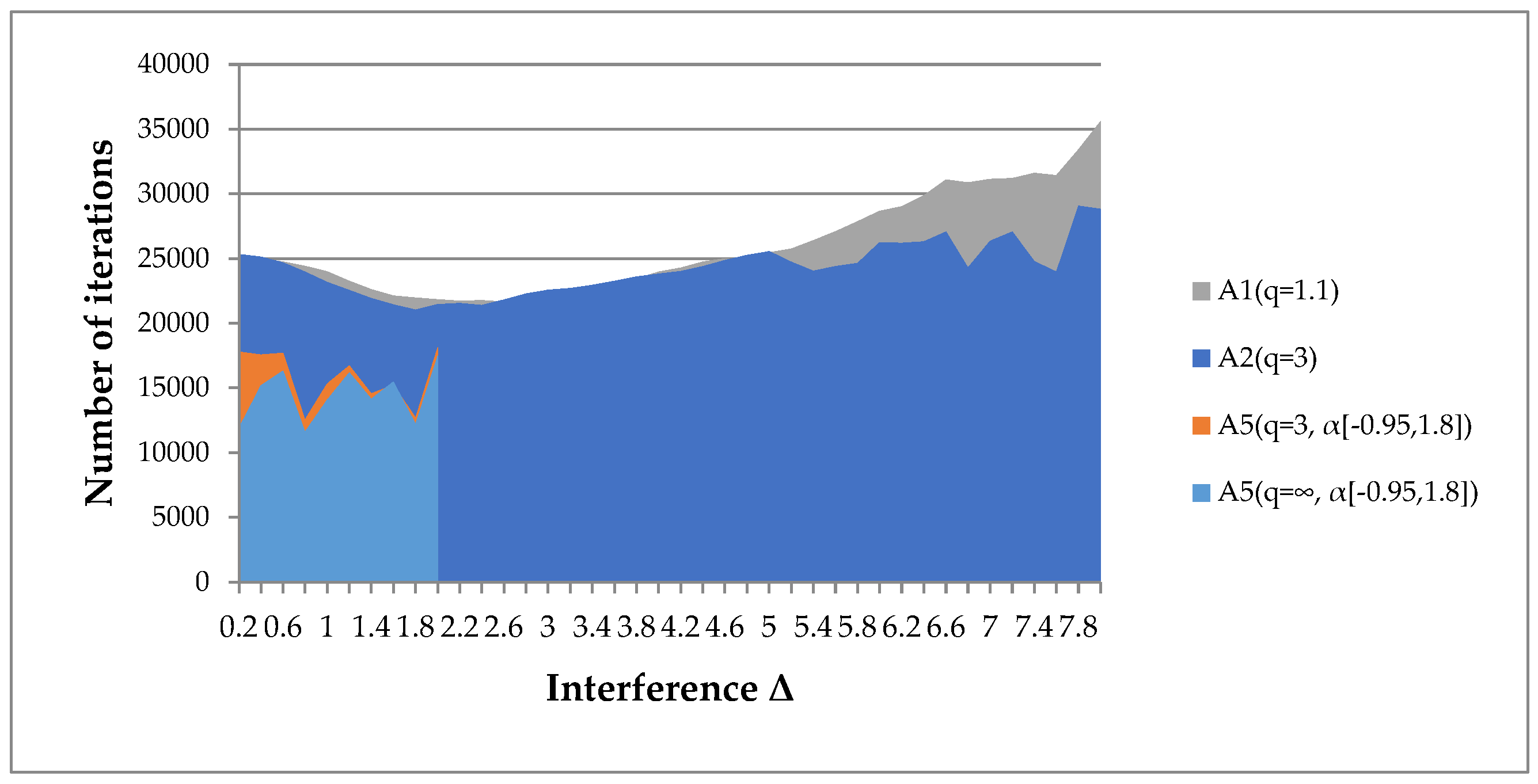
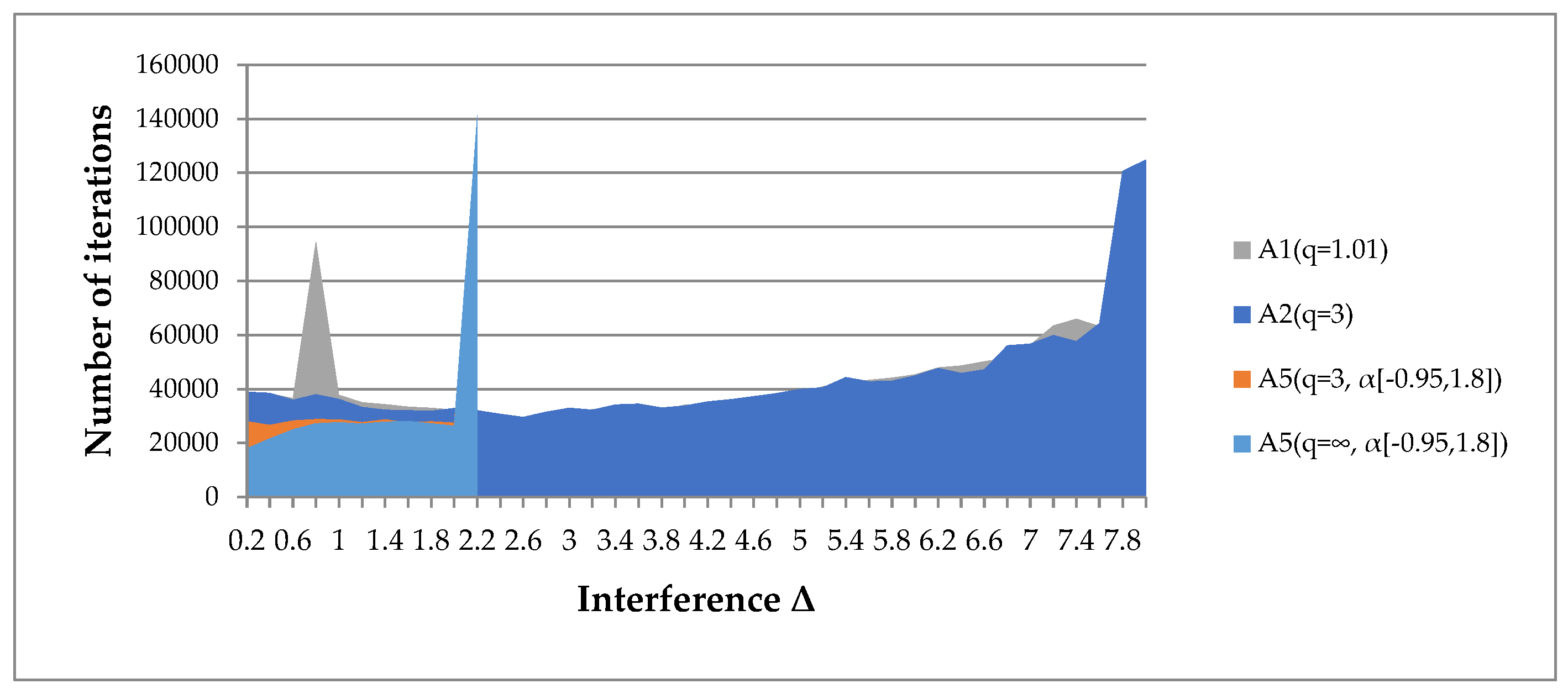
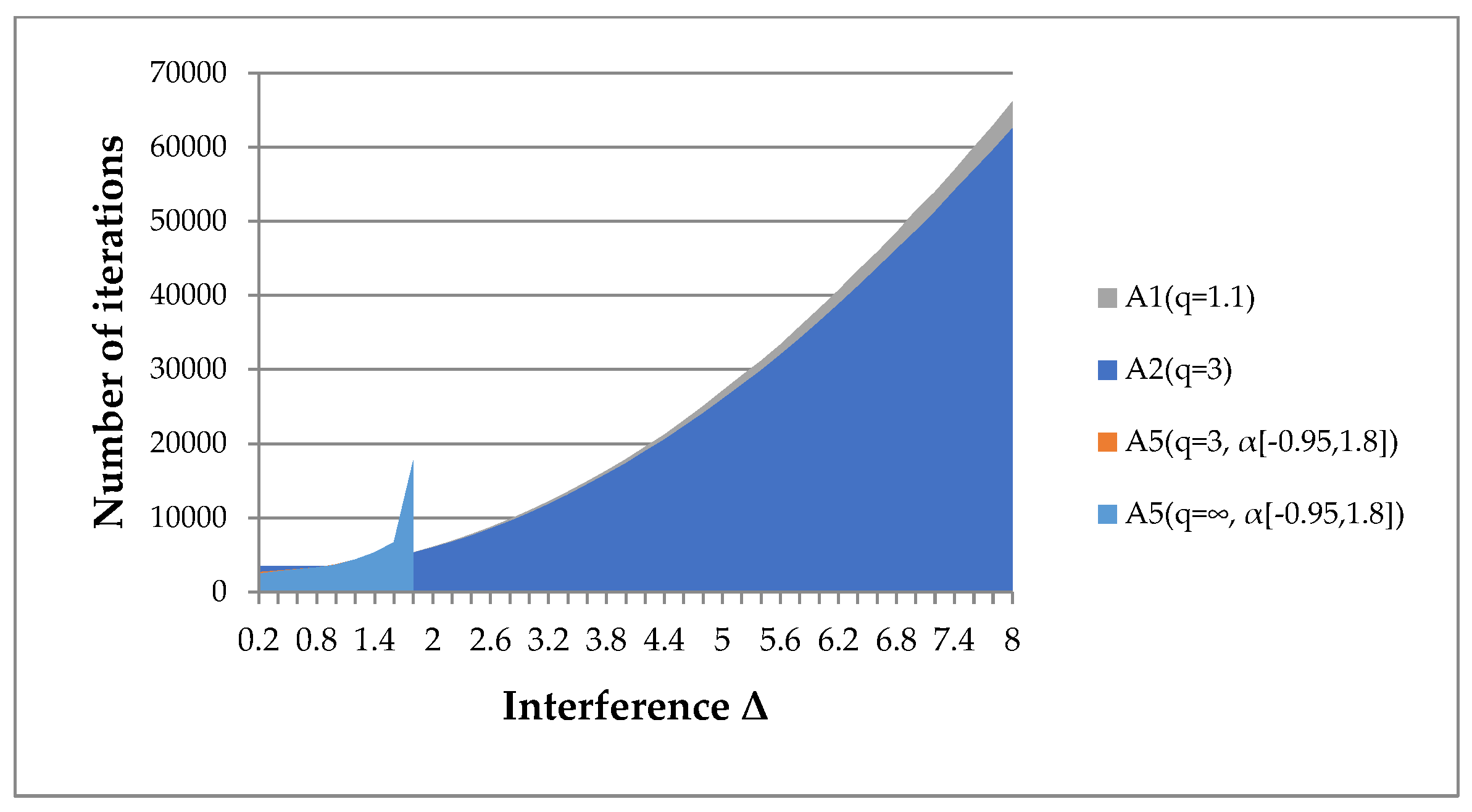
- Algorithm A5(q, α[a, b]) is applicable only for minor interference. However, its results are not always more significant than the results of algorithms A1(q), A2(q).
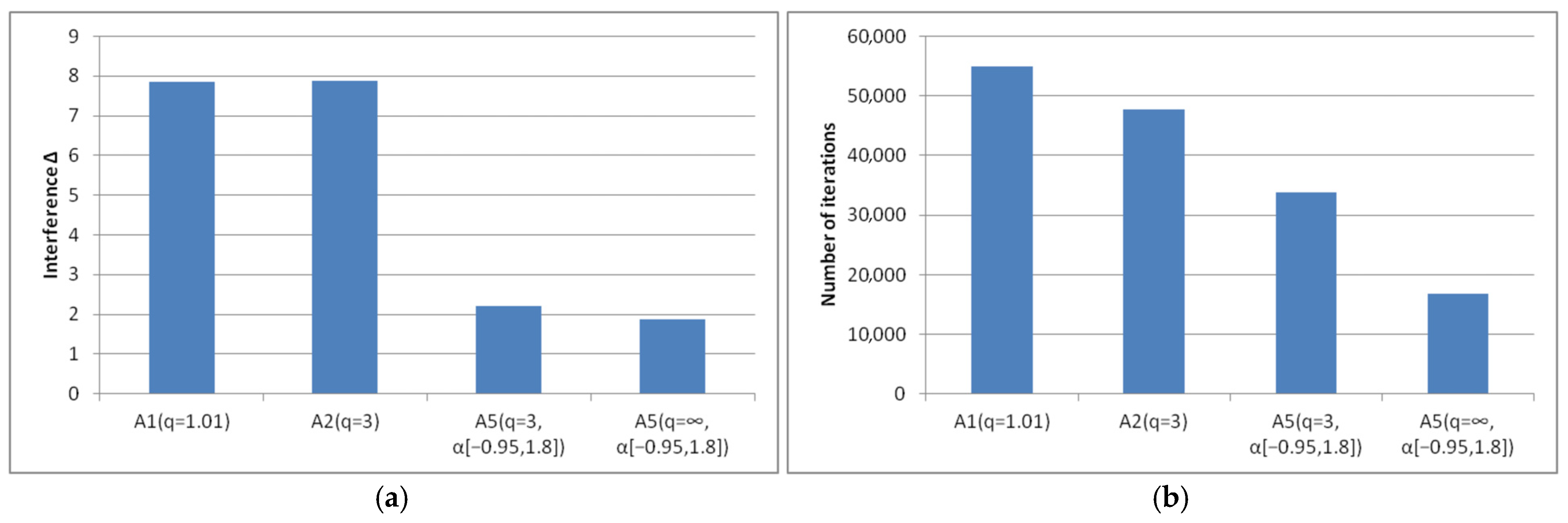
- Algorithms A1(q), A2(q) are applicable for high interference levels. We have given examples where the radius of the interference uniformly distributed in the sphere exceeds the gradient norm by 8 times (Figure 21a).
- The convergence of algorithms A1(q), A2(q) depends on the restrictions imposed on the parameter q (Figure 21b). For smaller values of the parameter q, the algorithms are efficient at a higher interference level. However, the convergence rate slows down. For smaller values of the boundary q, results can be obtained even with a 10-fold excess of the interference radius over the gradient norm.
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| N | GR * | A5(q = ∞, α[a, b]) | A4(q = ∞, α) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.95, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | α = 0.99 | ||
| 2 | 9150 (22,788) | 4077 | 12,152 | 12,149 | 12,122 | 12,105 | 12,144 | 12,134 | 9008 | 4553 | 4391 |
| N | GR * | A5(q = ∞, α[a, b]) | A4(q = ∞, α) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.95, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | α = 0.99 | ||
| 2 | 11,865 (29,610) | 4761 | 12,159 | 12,133 | 12,149 | 12,294 | 12,150 | 12,196 | 9340 | 5263 | 4657 |
| Δ | x1 | x2 | ||||||
|---|---|---|---|---|---|---|---|---|
| A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | |
| α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | |
| q = 1.01 | q = 3 | q = 3 | q = ∞ | q = 1.01 | q = 3 | q = 3 | q = ∞ | |
| 0.2 | 12,184 | 10,722 | 8567 | 5906 | 12,234 | 10,939 | 8637 | 6147 |
| 0.4 | 11,465 | 8439 | 8402 | 6466 | 11,465 | 8541 | 8635 | 5847 |
| 0.6 | 11,023 | 7676 | 8284 | 6561 | 11,092 | 8458 | 8694 | 6696 |
| 0.8 | 11,120 | 8510 | 8721 | 5382 | 10,782 | 9086 | 7935 | 7145 |
| 1 | 10,491 | 10,111 | 9446 | 6121 | 11,269 | 9635 | 12,340 | 7319 |
| 1.2 | 13,315 | 14,285 | 12,368 | 8728 | 10,686 | 7985 | 16,987 | 3271 |
| 1.4 | 20,098 | 15,445 | 19,649 | 16,118 | 18,720 | 18,911 | 34,700 | 9366 |
| 1.6 | 24,043 | 24,570 | 20,621 | 19,482 | 28,600 | 24,022 | 22,241 | 25,043 |
| 1.8 | 34,352 | 29,378 | 33,314 | 157,679 | 44,400 | 32,019 | 41,962 | |
| 2 | 37,942 | 38,146 | 30,051 | 31,477 | 37,510 | 29,335 | ||
| 2.2 | 50,690 | 45,354 | 29,812 | 51,192 | 42,941 | 28,450 | ||
| 2.4 | 66,219 | 47,895 | 35,579 | 89,059 | 51,962 | 35,754 | ||
| 2.6. | 69,348 | 53,748 | 36,969 | 77,062 | 60,003 | 86,217 | ||
| 2.8 | 55,604 | 57,246 | 43,107 | 84,679 | 65,490 | 30,715 | ||
| 3 | 59,616 | 79,305 | 38,298 | 29,050 | 43,264 | 65,511 | ||
| 3.2 | 60,337 | 72,013 | 37,955 | 57,805 | 85,334 | 157,592 | ||
| 3.4 | 64,974 | 69,090 | 14,077 | 64,798 | 94,479 | 122,119 | ||
| 3.6 | 78,793 | 88,460 | 275,656 | 110,826 | 90,339 | 389,925 | ||
| 3.8 | 269,995 | 97,980 | 195,847 | 222,006 | 117,191 | 291,453 | ||
| 4 | 253,321 | 101,563 | 275,651 | 147,051 | 130,206 | |||
| 4.2 | 94,456 | 179,195 | 792,694 | 47,864 | 116,564 | |||
| 4.4 | 24,622 | 197,242 | 21,570 | 128,049 | ||||
| 4.6 | 86,633 | 218,273 | 64,747 | 124,935 | ||||
| 4.8 | 106,416 | 219,263 | 110,989 | 105,653 | ||||
| 5 | 167,580 | 119,307 | 168,840 | 146,901 | ||||
| 5.2 | 204,223 | 42,896 | 196,347 | 214,080 | ||||
| 5.4 | 229,839 | 167,171 | 244,947 | 135,973 | ||||
| 5.6 | 249,466 | 80,196 | 282,396 | 164,611 | ||||
| 5.8 | 285,200 | 280,227 | 285,186 | 272,935 | ||||
| 6 | 308,540 | 144,408 | 429,597 | 461,874 | ||||
| 6.2 | 333,173 | 179,384 | 334,031 | 440,997 | ||||
| 6.4 | 442,650 | 231,839 | 450,688 | 346,296 | ||||
| 6.6 | 506,562 | 150,984 | 562,969 | 335,605 | ||||
| 6.8 | 558,934 | 491,455 | 624,308 | 371,494 | ||||
| 7 | 499,818 | 215,790 | 625,358 | 250,578 | ||||
| 7.2 | 388,358 | 362,532 | 502,964 | 120,357 | ||||
| 7.4 | 379,735 | 247,071 | 568,432 | 730,441 | ||||
| 7.6 | 821,177 | 267,345 | 651,425 | 257,868 | ||||
| 7.8 | 785,639 | 500,870 | 386,720 | 651,424 | ||||
| 8 | 594,816 | 497,469 | 379,943 | 388,342 | ||||
| N | GR * | A5(q = , α[a, b]) | А4(q = , α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 100 | 81 (186) | 71 | 60 | 71 | 90 | 102 | 147 | 230 | 451 | 1652 |
| 1000 | 86 (200) | 82 | 68 | 74 | 95 | 105 | 146 | 247 | 478 | 1656 |
| 10,000 | 91 (214) | 78 | 73 | 78 | 97 | 111 | 162 | 265 | 526 | 1822 |
| 100,000 | 97 (230) | 72 | 84 | 89 | 103 | 122 | 154 | 257 | 556 | 2147 |
| N | GR * | А5(q = , α[a, b]) | А4(q = , α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 100 | 793 (1618) | 364 | 795 | 791 | 792 | 788 | 746 | 704 | 461 | 1764 |
| 1000 | 835 (1708) | 468 | 839 | 837 | 833 | 823 | 819 | 725 | 445 | 1836 |
| 10,000 | 888 (1819) | 413 | 888 | 891 | 886 | 881 | 855 | 686 | 494 | 2061 |
| 100,000 | 944 (1936) | 476 | 947 | 943 | 947 | 937 | 926 | 822 | 561 | 2170 |
| N | GR * | А5(q = , α[a, b]) | А4(q = , α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 100 | 7869 (15,768) | 2874 | 7908 | 7914 | 7912 | 7910 | 7900 | 7858 | 5841 | 3110 |
| 1000 | 8239 (16,514) | 3079 | 8287 | 8277 | 8278 | 8275 | 8264 | 8250 | 5636 | 3202 |
| 10,000 | 8770 (17,582) | 3532 | 8820 | 8821 | 8810 | 8813 | 8806 | 8785 | 6342 | 3391 |
| 100,000 | 9324 (18,697) | 2966 | 9376 | 9371 | 9376 | 9370 | 9362 | 9350 | 7000 | 3881 |
| Δ | fQ(x, [amax = 100]) | fQ(x, [amax = 1000]) | ||||||
|---|---|---|---|---|---|---|---|---|
| A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | |
| α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | |
| q = 1.1 | q = 3 | q = 3 | q = ∞ | q = 1.1 | q = 3 | q = 3 | q = ∞ | |
| 0.2 | 873 | 843 | 647 | 604 | 8234 | 8251 | 6858 | 6618 |
| 0.4 | 874 | 843 | 703 | 678 | 8227 | 8238 | 7320 | 7204 |
| 0.6 | 876 | 846 | 778 | 777 | 8252 | 8278 | 8005 | 8029 |
| 0.8 | 897 | 868 | 898 | 920 | 8499 | 8553 | 8964 | 9028 |
| 1 | 968 | 935 | 1030 | 1037 | 9085 | 9115 | 9982 | 10,030 |
| 1.2 | 1090 | 1043 | 1191 | 1196 | 9989 | 9929 | 11,219 | 11,241 |
| 1.4 | 1245 | 1181 | 1513 | 1518 | 11,181 | 11,020 | 20,713 | 20,795 |
| 1.6 | 1446 | 1358 | 3555 | 3565 | 12,621 | 12,498 | ||
| 1.8 | 1671 | 1580 | 24,613 | 24,677 | 14,340 | 14,253 | ||
| 2 | 1934 | 1822 | 16,243 | 16,155 | ||||
| 2.2 | 2217 | 2089 | 18,380 | 18,282 | ||||
| 2.4 | 2541 | 2395 | 20,647 | 20,540 | ||||
| 2.6. | 2897 | 2714 | 23,195 | 22,954 | ||||
| 2.8 | 3287 | 3063 | 25,941 | 25,606 | ||||
| 3 | 3695 | 3440 | 28,925 | 28,431 | ||||
| 3.2 | 4142 | 3860 | 32,035 | 31,511 | ||||
| 3.4 | 4632 | 4307 | 35,494 | 34,834 | ||||
| 3.6 | 5164 | 4779 | 39,093 | 38,320 | ||||
| 3.8 | 5663 | 5283 | 42,881 | 41,972 | ||||
| 4 | 6216 | 5810 | 46,834 | 45,830 | ||||
| 4.2 | 6828 | 6345 | 50,922 | 49,877 | ||||
| 4.4 | 7445 | 6921 | 55,372 | 54,136 | ||||
| 4.6 | 8095 | 7498 | 59,873 | 58,421 | ||||
| 4.8 | 8748 | 8090 | 64,598 | 62,862 | ||||
| 5 | 9454 | 8715 | 69,391 | 67,532 | ||||
| 5.2 | 10,139 | 9365 | 74,271 | 72,317 | ||||
| 5.4 | 10,897 | 10,018 | 79,538 | 77,524 | ||||
| 5.6 | 11,600 | 10,752 | 85,077 | 82,805 | ||||
| 5.8 | 12,428 | 11,474 | 90,453 | 88,153 | ||||
| 6 | 13,268 | 12,264 | 96,130 | 93,746 | ||||
| 6.2 | 14,206 | 13,060 | 102,006 | 99,503 | ||||
| 6.4 | 15,051 | 13,850 | 108,469 | 105,460 | ||||
| 6.6 | 16,051 | 14,769 | 114,860 | 111,749 | ||||
| 6.8 | 16,927 | 15,580 | 121,053 | 117,931 | ||||
| 7 | 17,956 | 16,385 | 119,322 | 124,245 | ||||
| 7.2 | 18,906 | 17,191 | 126,186 | 130,862 | ||||
| 7.4 | 19,912 | 18,136 | 132,999 | 137,335 | ||||
| 7.6 | 20,884 | 19,041 | 139,836 | 137,335 | ||||
| 7.8 | 21,982 | 19,885 | 147,162 | 143,897 | ||||
| 8 | 23,166 | 20,781 | 153,001 | 150,746 | ||||
| N | GR * | А5(q = , α[a, b]) | А4(q = , α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 10 | 8393 (20,648) | 3861 | 4969 | 8897 | 2442 | 6305 | 5520 | 2275 | 3919 | 1628 |
| 100 | 6505 (16,234) | 724 | 584 | 2105 | 2712 | 1440 | 1186 | 1271 | 1256 | 250 |
| 1000 | 8661 (20,498) | 822 | 3005 | 1215 | 2131 | 1292 | 1326 | 1676 | 2386 | 917 |
| 10,000 | 8715 (21,186) | 847 | 8826 | 1712 | 2153 | 1531 | 1081 | 1161 | 681 | 207 |
| N | GR * | А5(q = , α[a, b]) | А4(q = , α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 10 | 2058 (4547) | 872 | 2022 | 2056 | 2079 | 2027 | 2047 | 2041 | 1516 | 881 |
| 100 | 1547 (3817) | 1672 | 3667 | 3634 | 3579 | 3584 | 3607 | 3666 | 2896 | 1555 |
| 1000 | 5592 (13,929) | 1901 | 5838 | 5879 | 5898 | 5829 | 5937 | 6085 | 4769 | 2873 |
| 10,000 | 2339 (5807) | 1898 | 7323 | 7316 | 6354 | 7463 | 1728 | 5389 | 3923 | 3556 |
| Δ | fEEL(x, [amax = 10, bmax = 10]) | |||
|---|---|---|---|---|
| A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | |
| α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | |
| q = 1.1 | q = 3 | q = 3 | q = ∞ | |
| 0.2 | 6428 | 8070 | 4546 | 3120 |
| 0.4 | 6138 | 7443 | 4364 | 3870 |
| 0.6 | 6389 | 6497 | 4927 | 4468 |
| 0.8 | 6468 | 6175 | 5354 | 4822 |
| 1 | 6390 | 6298 | 4983 | 4723 |
| 1.2 | 6275 | 6507 | 4966 | 5030 |
| 1.4 | 6367 | 6547 | 4619 | 4746 |
| 1.6 | 7473 | 6898 | 5136 | 5063 |
| 1.8 | 7734 | 6466 | 5004 | 4809 |
| 2 | 7625 | 6496 | 6478 | 7026 |
| 2.2 | 7764 | 6417 | 71,359 | 73,154 |
| 2.4 | 7763 | 6709 | ||
| 2.6. | 7598 | 6530 | ||
| 2.8 | 7802 | 6369 | ||
| 3 | 7649 | 6341 | ||
| 3.2 | 7625 | 6372 | ||
| 3.4 | 7515 | 6837 | ||
| 3.6 | 7541 | 6749 | ||
| 3.8 | 7505 | 6536 | ||
| 4 | 7586 | 6476 | ||
| 4.2 | 7749 | 6443 | ||
| 4.4 | 7826 | 6638 | ||
| 4.6 | 7661 | 6821 | ||
| 4.8 | 7777 | 6378 | ||
| 5 | 7393 | 6674 | ||
| 5.2 | 7655 | 6711 | ||
| 5.4 | 7599 | 6783 | ||
| 5.6 | 7265 | 6873 | ||
| 5.8 | 6927 | 7237 | ||
| 6 | 7256 | 7058 | ||
| 6.2 | 7404 | 7237 | ||
| 6.4 | 7605 | 7276 | ||
| 6.6 | 7868 | 7101 | ||
| 6.8 | 7 947 | 7252 | ||
| 7 | 7876 | 7508 | ||
| 7.2 | 8147 | 7722 | ||
| 7.4 | 8420 | 7904 | ||
| 7.6 | 8237 | 7924 | ||
| 7.8 | 8328 | 8067 | ||
| 8 | 8712 | 8239 | ||
| Δ | x2 | x1 | ||||||
|---|---|---|---|---|---|---|---|---|
| A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | |
| α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | |
| q = 1.1 | q = 3 | q = 3 | q = ∞ | q = 1.1 | q = 3 | q = 3 | q = ∞ | |
| 0.2 | 6463 | 6619 | 3324 | 3296 | 3500 | 3558 | 2566 | 1969 |
| 0.4 | 6811 | 7356 | 4862 | 3369 | 3469 | 3502 | 2670 | 2307 |
| 0.6 | 6945 | 6627 | 3963 | 4032 | 3452 | 3478 | 2943 | 2741 |
| 0.8 | 6338 | 5778 | 5297 | 4512 | 3450 | 3461 | 3010 | 2919 |
| 1 | 6102 | 6272 | 4268 | 3980 | 3428 | 3408 | 3191 | 3102 |
| 1.2 | 6009 | 5548 | 5503 | 5287 | 3550 | 3399 | 3243 | 3284 |
| 1.4 | 6286 | 5458 | 4914 | 5281 | 3433 | 3428 | 3529 | 3693 |
| 1.6 | 5480 | 6119 | 4593 | 4288 | 3538 | 3395 | 3396 | 3436 |
| 1.8 | 5462 | 5979 | 5262 | 5293 | 3551 | 3487 | 3363 | 3314 |
| 2 | 5508 | 5375 | 6975 | 6902 | 3769 | 3568 | 3609 | 4003 |
| 2.2 | 5780 | 5876 | 11,733 | 12,909 | 3787 | 3698 | 5778 | 5922 |
| 2.4 | 6006 | 5926 | 3966 | 3810 | ||||
| 2.6. | 6152 | 5823 | 3977 | 3844 | ||||
| 2.8 | 6199 | 6479 | 4625 | 3959 | ||||
| 3 | 6703 | 6696 | 4381 | 4072 | ||||
| 3.2 | 6899 | 6739 | 4835 | 4277 | ||||
| 3.4 | 6809 | 6813 | 4993 | 4440 | ||||
| 3.6 | 6715 | 5691 | 5177 | 4457 | ||||
| 3.8 | 5665 | 5962 | 5316 | 4619 | ||||
| 4 | 6015 | 5901 | 5320 | 4742 | ||||
| 4.2 | 6288 | 6401 | 5498 | 4669 | ||||
| 4.4 | 6468 | 6850 | 5520 | 4886 | ||||
| 4.6 | 7110 | 6609 | 5743 | 4802 | ||||
| 4.8 | 7440 | 6907 | 5827 | 5374 | ||||
| 5 | 7751 | 6903 | 5771 | 5469 | ||||
| 5.2 | 7715 | 7009 | 6210 | 5242 | ||||
| 5.4 | 7432 | 6108 | 6284 | 5316 | ||||
| 5.6 | 7293 | 6097 | 5791 | 5582 | ||||
| 5.8 | 6703 | 6248 | 5923 | 5715 | ||||
| 6 | 6833 | 7096 | 6040 | 5433 | ||||
| 6.2 | 7098 | 7544 | 6314 | 6100 | ||||
| 6.4 | 7660 | 8011 | 6703 | 6387 | ||||
| 6.6 | 8610 | 8026 | 6894 | 5967 | ||||
| 6.8 | 8306 | 9781 | 6684 | 7017 | ||||
| 7 | 8984 | 9033 | 6868 | 6968 | ||||
| 7.2 | 9472 | 9227 | 7161 | 8292 | ||||
| 7.4 | 10,039 | 10,303 | 7202 | 6709 | ||||
| 7.6 | 10,803 | 9840 | 7743 | 6972 | ||||
| 7.8 | 10,844 | 10,057 | 7923 | 9873 | ||||
| 8 | 11,414 | 10,028 | 8267 | 9668 | ||||
| N | GR * | А5(q = , α[a, b]) | А4(q = , α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 10 | 25,334 (61,902) | 9128 | 25,586 | 25,539 | 25,591 | 25,481 | 25,492 | 25,820 | 19,615 | 9624 |
| 100 | 25,237 (61,712) | 9045 | 25,346 | 25,329 | 25,305 | 25,376 | 25,371 | 25,355 | 19,130 | 9430 |
| 1000 | 25,742 (62,524) | 8302 | 25,801 | 25,819 | 25,768 | 25,824 | 25,826 | 25,823 | 19,788 | 9835 |
| 10,000 | 26,125 (64,321) | 6972 | 26,209 | 261,99 | 26,173 | 26,201 | 26,210 | 25,958 | 20,315 | 10,157 |
| Δ | fEEL(x, [amax = 30, bmax = 10]) | |||
|---|---|---|---|---|
| A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | |
| α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | |
| q = 1.1 | q = 3 | q = 3 | q = ∞ | |
| 0.2 | 25,099 | 25,341 | 17,787 | 11,910 |
| 0.4 | 24,972 | 25,119 | 17,560 | 15,195 |
| 0.6 | 24,759 | 24,693 | 17,692 | 16,312 |
| 0.8 | 24,413 | 23,964 | 12,537 | 11,609 |
| 1 | 23,998 | 23,179 | 15,310 | 14,063 |
| 1.2 | 23,250 | 22,544 | 16,715 | 16,184 |
| 1.4 | 22,614 | 21,935 | 14,574 | 14,142 |
| 1.6 | 22,135 | 21,448 | 15,230 | 15,481 |
| 1.8 | 21,966 | 21,038 | 12,699 | 12,213 |
| 2 | 21,828 | 21,469 | 18,127 | 17,482 |
| 2.2 | 21,723 | 21,538 | ||
| 2.4 | 21,771 | 21,396 | ||
| 2.6. | 21,661 | 21,814 | ||
| 2.8 | 22,065 | 22,283 | ||
| 3 | 22,205 | 22,580 | ||
| 3.2 | 22,320 | 22,711 | ||
| 3.4 | 22,289 | 22,945 | ||
| 3.6 | 22,716 | 23,266 | ||
| 3.8 | 23,446 | 23,596 | ||
| 4 | 23,977 | 23,819 | ||
| 4.2 | 24,292 | 24,022 | ||
| 4.4 | 24,747 | 24,399 | ||
| 4.6 | 24,994 | 24,852 | ||
| 4.8 | 24,781 | 25,264 | ||
| 5 | 25,453 | 25,549 | ||
| 5.2 | 25,746 | 24,729 | ||
| 5.4 | 26,405 | 24,031 | ||
| 5.6 | 27,098 | 24,399 | ||
| 5.8 | 27,870 | 24,650 | ||
| 6 | 28,674 | 26,238 | ||
| 6.2 | 29,028 | 26,200 | ||
| 6.4 | 29,874 | 26,299 | ||
| 6.6 | 31,088 | 27,064 | ||
| 6.8 | 30,879 | 24,282 | ||
| 7 | 31,144 | 26,347 | ||
| 7.2 | 31,194 | 27,062 | ||
| 7.4 | 31,607 | 24,769 | ||
| 7.6 | 31,432 | 23,974 | ||
| 7.8 | 33,436 | 29,079 | ||
| 8 | 35,627 | 28,815 | ||
| N | GR * | А5(q = , α[a, b]) | А4(q = , α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 10 | 41,854 (73,933) | 11,819 | 35,579 | 41,396 | 35,471 | 37,251 | 39,603 | 27,322 | 25,806 | 11,276 |
| 100 | 42,888 (74,275) | 5968 | 31,693 | 39,836 | 40,243 | 30,840 | 27,556 | 26,535 | 5382 | 6887 |
| 1000 | 43,867 (78,317) | 5636 | 32,430 | 30,004 | 28,578 | 39,560 | 31,555 | 33,324 | 23,921 | 5343 |
| 10,000 | 42,537 (75,562) | 11,292 | 28,718 | 41,286 | 20,289 | 18,044 | 13,411 | 4721 | 3481 | 3134 |
| N | GR * | А5(q = , α[a, b]) | А4(q = , α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 10 | 19,327 (48,234) | 14,202 | 32,401 | 32,412 | 32,409 | 32,402 | 32,402 | 32,387 | 24,936 | 13,102 |
| 100 | 18,936 (47,183) | 14,427 | 33,407 | 33,410 | 33,408 | 33,318 | 33,398 | 33,396 | 25,724 | 13,528 |
| 1000 | 34,541 (86,318) | 15,549 | 35,864 | 35,917 | 35,944 | 35,727 | 36,008 | 36,288 | 28,274 | 15,046 |
| 10,000 | 25,837 (64,455) | 15,542 | 37,922 | 37,878 | 36,342 | 38,117 | 38,931 | 37,235 | 23,886 | 15,969 |
| Δ | x2 | x1 | ||||||
|---|---|---|---|---|---|---|---|---|
| A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | |
| α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | |
| q = 1.01 | q = 3 | q = 3 | q = ∞ | q = 1.01 | q = 3 | q = 3 | q = ∞ | |
| 0.2 | 37,261 | 39,007 | 28,008 | 18,091 | 33,231 | 33,419 | 23,600 | 16,216 |
| 0.4 | 38,355 | 38,541 | 26,724 | 21,720 | 33,299 | 33,231 | 24,268 | 19,993 |
| 0.6 | 36,569 | 36,039 | 28,297 | 25,003 | 33,241 | 32,905 | 24,610 | 22,325 |
| 0.8 | 94,629 | 38,007 | 28,867 | 27,261 | 32,891 | 32,579 | 24,709 | 23,412 |
| 1 | 37,825 | 36,312 | 28,740 | 27,674 | 32,374 | 31,916 | 25,320 | 24,206 |
| 1.2 | 35,119 | 33,383 | 27,729 | 27,199 | 31,789 | 30,820 | 25,689 | 24,913 |
| 1.4 | 34,335 | 32,358 | 28,724 | 27,925 | 31,176 | 30,068 | 24,969 | 24,793 |
| 1.6 | 33,424 | 32,123 | 27,567 | 28,159 | 30,461 | 29,453 | 24,479 | 24,254 |
| 1.8 | 33,018 | 31,864 | 28,051 | 27,285 | 29,711 | 29,106 | 24,255 | 24,720 |
| 2 | 32,288 | 32,887 | 27,469 | 26,362 | 29,359 | 28,734 | 28,527 | 28,601 |
| 2.2 | 31,293 | 32,121 | 127,756 | 141,449 | 28,950 | 28,555 | 133,978 | 159,208 |
| 2.4 | 29,560 | 30,786 | 28,804 | 28,586 | ||||
| 2.6. | 29,053 | 29,665 | 28,902 | 28,272 | ||||
| 2.8 | 29,282 | 31,642 | 29,397 | 28,963 | ||||
| 3 | 30,602 | 33,052 | 29,036 | 29,448 | ||||
| 3.2 | 32,505 | 32,337 | 29,585 | 29,523 | ||||
| 3.4 | 32,430 | 34,266 | 30,025 | 30,582 | ||||
| 3.6 | 32,912 | 34,555 | 30,618 | 30,898 | ||||
| 3.8 | 32,362 | 33,138 | 30,836 | 31,461 | ||||
| 4 | 34,169 | 33,837 | 31,586 | 32,495 | ||||
| 4.2 | 34,408 | 35,353 | 32,236 | 33,122 | ||||
| 4.4 | 35,033 | 36,173 | 32,768 | 34,311 | ||||
| 4.6 | 37,325 | 37,278 | 34,021 | 34,872 | ||||
| 4.8 | 37,019 | 38,411 | 34,451 | 36,339 | ||||
| 5 | 38,425 | 39,939 | 34,712 | 37,565 | ||||
| 5.2 | 40,954 | 40,611 | 36,631 | 38,074 | ||||
| 5.4 | 42,431 | 44,346 | 36,522 | 39,336 | ||||
| 5.6 | 43,359 | 42,846 | 37,023 | 41,404 | ||||
| 5.8 | 44,149 | 43,068 | 39,175 | 41,123 | ||||
| 6 | 45,440 | 45,009 | 40,235 | 42,563 | ||||
| 6.2 | 47,913 | 47,721 | 41,789 | 43,140 | ||||
| 6.4 | 48,651 | 45,961 | 42,449 | 42,268 | ||||
| 6.6 | 50,238 | 47,260 | 44,234 | 45,318 | ||||
| 6.8 | 51,542 | 56,151 | 45,820 | 45,302 | ||||
| 7 | 56,361 | 56,762 | 49,367 | 46,206 | ||||
| 7.2 | 63,478 | 59,872 | 52,129 | 47,642 | ||||
| 7.4 | 65,989 | 57,709 | 55,812 | 50,892 | ||||
| 7.6 | 63,248 | 64,288 | 59,237 | 60,767 | ||||
| 7.8 | 70,764 | 12,0629 | 69,242 | 58,808 | ||||
| 8 | 72,668 | 124,948 | 66,135 | 54,755 | ||||
| N | GR * | А5(q = , α[a, b]) | А4(q = , α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 10 | 289 (591) | 174 | 291 | 279 | 287 | 288 | 278 | 241 | 150 | 151 |
| 100 | 311 (635) | 236 | 312 | 309 | 306 | 305 | 305 | 190 | 162 | 171 |
| 1000 | 358 (729) | 206 | 359 | 356 | 354 | 352 | 329 | 288 | 202 | 204 |
| 10,000 | 411 (835) | 269 | 412 | 409 | 407 | 406 | 405 | 320 | 223 | 227 |
| N | GR * | А5(q = , α[a, b]) | А4(q = , α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 10 | 2104 (4789) | 1431 | 2883 | 2882 | 2879 | 2862 | 2868 | 2845 | 2095 | 1382 |
| 100 | 1878 (4363) | 1643 | 3016 | 3021 | 3017 | 3019 | 3010 | 2993 | 2142 | 1335 |
| 1000 | 2059 (4811) | 1719 | 3466 | 3477 | 3474 | 3475 | 3472 | 3444 | 2552 | 1515 |
| 10,000 | 2267 (5331) | 1877 | 3998 | 4006 | 4003 | 4004 | 4004 | 3977 | 2966 | 1727 |
| N | GR * | А5(q = , α[a, b]) | А4(q = , α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 10 | 14,019 (34,549) | 11,329 | 28,788 | 28,782 | 28,783 | 28,763 | 28,781 | 28,769 | 22,130 | 11,040 |
| 100 | 14,785 (36,151) | 11,293 | 29,777 | 29,776 | 29,769 | 29,775 | 29,766 | 29,759 | 22,891 | 11,554 |
| 1000 | 15,958 (39,107) | 12,489 | 34,124 | 34,122 | 34,115 | 34,121 | 34,119 | 34,105 | 26,240 | 13,563 |
| 10,000 | 17,636 (43,300) | 16,481 | 39,386 | 39,384 | 39,378 | 39,384 | 39,380 | 39,375 | 30,278 | 16,122 |
| Δ | fQ^2(x, [amax = 1000]) | fQ^2(x, [amax = 10,000]) | ||||||
|---|---|---|---|---|---|---|---|---|
| A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | |
| α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | |
| q = 1.1 | q = 3 | q = 3 | q = ∞ | q = 1.1 | q = 3 | q = 3 | q = ∞ | |
| 0.2 | 3452 | 3465 | 2651 | 2453 | 33,790 | 34,023 | 26,031 | 22,973 |
| 0.4 | 3452 | 3459 | 2875 | 2782 | 33,756 | 33,927 | 27,882 | 26,563 |
| 0.6 | 3451 | 3451 | 3078 | 3036 | 33,701 | 33,801 | 29,704 | 29,109 |
| 0.8 | 3468 | 3463 | 3294 | 3276 | 33,693 | 33,719 | 31,545 | 31,256 |
| 1 | 3580 | 3567 | 3720 | 3659 | 34,041 | 33,998 | 33,506 | 33,427 |
| 1.2 | 3826 | 3812 | 4371 | 4353 | 35,222 | 35,226 | 38,304 | 38,566 |
| 1.4 | 4211 | 4192 | 5342 | 5314 | 37,552 | 37,519 | 47,043 | 46,838 |
| 1.6 | 4724 | 4691 | 6698 | 6693 | 40,786 | 40,792 | 56,293 | 56,151 |
| 1.8 | 5329 | 5289 | 17,758 | 17,770 | 44,952 | 44,909 | 242,613 | 275,452 |
| 2 | 6057 | 5974 | 50,041 | 49,760 | ||||
| 2.2 | 6865 | 6742 | 55,762 | 55,277 | ||||
| 2.4 | 7770 | 7596 | 62,273 | 61,395 | ||||
| 2.6. | 8740 | 8529 | 69,538 | 68,166 | ||||
| 2.8 | 9839 | 9553 | 77,268 | 75,707 | ||||
| 3 | 10,969 | 10,663 | 86,043 | 83,887 | ||||
| 3.2 | 12,180 | 11,837 | 95,119 | 92,698 | ||||
| 3.4 | 13,525 | 13,124 | 104,769 | 102,139 | ||||
| 3.6 | 14,912 | 14,504 | 115,146 | 112,302 | ||||
| 3.8 | 16,354 | 15,912 | 125,313 | 122,981 | ||||
| 4 | 17,914 | 17,370 | 136,547 | 134,183 | ||||
| 4.2 | 19,566 | 18,980 | 148,435 | 145,973 | ||||
| 4.4 | 21,214 | 20,566 | 161,241 | 158,268 | ||||
| 4.6 | 23,088 | 22,306 | 174,628 | 171,257 | ||||
| 4.8 | 25,059 | 24,091 | 188,113 | 184,685 | ||||
| 5 | 27,136 | 26,017 | 202,016 | 198,775 | ||||
| 5.2 | 29,175 | 27,933 | 217,963 | 213,433 | ||||
| 5.4 | 31,189 | 29,910 | 233,419 | 228,438 | ||||
| 5.6 | 33,379 | 32,004 | 249,645 | 244,233 | ||||
| 5.8 | 35,822 | 34,176 | 266,880 | 260,484 | ||||
| 6 | 38,209 | 36,466 | 284,429 | 277,197 | ||||
| 6.2 | 40,653 | 38,781 | 294,631 | |||||
| 6.4 | 43,332 | 41,217 | ||||||
| 6.6 | 45,830 | 43,705 | ||||||
| 6.8 | 48,444 | 46,221 | ||||||
| 7 | 51,438 | 48,728 | ||||||
| 7.2 | 53,950 | 51,308 | ||||||
| 7.4 | 56,921 | 54,157 | ||||||
| 7.6 | 60,000 | 56,912 | ||||||
| 7.8 | 62,919 | 59,614 | ||||||
| 8 | 66,154 | 62,535 | ||||||
| N | GR * | A5(q = ∞, α[a, b]) | A4(q = ∞, α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 10 | 475 (951) | 272 | 459 | 478 | 476 | 464 | 441 | 221 | 253 | 843 |
| 100 | 488 (979) | 305 | 480 | 484 | 482 | 472 | 477 | 303 | 271 | 874 |
| 1000 | 533 (1073) | 321 | 534 | 535 | 529 | 524 | 514 | 418 | 248 | 898 |
| 10,000 | 579 (1172) | 363 | 590 | 583 | 584 | 572 | 582 | 489 | 319 | 996 |
| N | GR * | А5(q = , α[a, b]) | А4(q = , α) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α ∈ [−0.9, 1.8] | α = −0.1 | α = 0.0 | α = 0.1 | α = 0.2 | α = 0.4 | α = 0.6 | α = 0.8 | α = 0.95 | ||
| 10 | 4718 (11,463) | 1790 | 4781 | 4772 | 4776 | 4767 | 4755 | 4353 | 3490 | 864 |
| 100 | 4796 (11,348) | 2101 | 4852 | 4846 | 4840 | 4849 | 4843 | 4824 | 3550 | 1798 |
| 1000 | 5222 (12,372) | 2328 | 5276 | 5274 | 5271 | 5263 | 5261 | 5246 | 3941 | 2298 |
| 10,000 | 5682 (13,901) | 2570 | 5802 | 5801 | 5763 | 5798 | 5780 | 5750 | 4258 | 2562 |
| Δ | fR(x, [amax = 100]) | fR(x, [amax = 1000]) | ||||||
|---|---|---|---|---|---|---|---|---|
| A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | A1(q) | A2(q) | A5(q, α[a, b]) | A5(q, α[a, b]) | |
| α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | α = 0.0 | α = 0.0 | α ∈ [−0.95, 1.8] | α ∈ [−0.95, 1.8] | |
| q = 1.1 | q = 3 | q = 3 | q = ∞ | q = 1.1 | q = 3 | q = 3 | q = ∞ | |
| 0.2 | 535 | 538 | 425 | 373 | 5228 | 5276 | 4012 | 3599 |
| 0.4 | 537 | 539 | 447 | 437 | 5223 | 5271 | 4340 | 4174 |
| 0.6 | 537 | 538 | 482 | 477 | 5213 | 5259 | 4588 | 4511 |
| 0.8 | 552 | 552 | 527 | 527 | 5225 | 5265 | 4873 | 4826 |
| 1 | 599 | 591 | 587 | 587 | 5387 | 5412 | 5239 | 5203 |
| 1.2 | 672 | 657 | 679 | 679 | 5747 | 5758 | 5712 | 5692 |
| 1.4 | 774 | 747 | 850 | 850 | 6315 | 6308 | 6383 | 6371 |
| 1.6 | 901 | 857 | 1541 | 1542 | 7069 | 7042 | 8801 | 8805 |
| 1.8 | 1047 | 992 | 7986 | 7934 | ||||
| 2 | 1214 | 1140 | 9064 | 8986 | ||||
| 2.2 | 1392 | 1300 | 10,306 | 10,175 | ||||
| 2.4 | 1598 | 1478 | 11,627 | 11,488 | ||||
| 2.6. | 1827 | 1676 | 13,103 | 12,917 | ||||
| 2.8 | 2062 | 1892 | 14,756 | 14,507 | ||||
| 3 | 2350 | 2123 | 16,519 | 16,199 | ||||
| 3.2 | 2630 | 2381 | 18,372 | 17,988 | ||||
| 3.4 | 2948 | 2654 | 20,363 | 19,950 | ||||
| 3.6 | 3246 | 2942 | 22,582 | 22,027 | ||||
| 3.8 | 3557 | 3241 | 24,705 | 24,211 | ||||
| 4 | 3931 | 3566 | 27,056 | 26,490 | ||||
| 4.2 | 4330 | 3904 | 29,433 | 28,891 | ||||
| 4.4 | 4729 | 4262 | 32,155 | 31,422 | ||||
| 4.6 | 5105 | 4618 | 34,719 | 34,101 | ||||
| 4.8 | 5567 | 4995 | 37,581 | 36,837 | ||||
| 5 | 6053 | 5371 | 40,432 | 39,688 | ||||
| 5.2 | 6525 | 5812 | 43,607 | 42,683 | ||||
| 5.4 | 7057 | 6268 | 46,818 | 45,809 | ||||
| 5.6 | 7560 | 6729 | 50,183 | 49,014 | ||||
| 5.8 | 8104 | 7190 | 53,747 | 52,398 | ||||
| 6 | 8688 | 7608 | 57,493 | 55,898 | ||||
| 6.2 | 9356 | 8090 | 61,392 | 59,515 | ||||
| 6.4 | 9945 | 8612 | 65,251 | 63,122 | ||||
| 6.6 | 10,547 | 9166 | 69,389 | 66,927 | ||||
| 6.8 | 11,186 | 9769 | 73,205 | 70,865 | ||||
| 7 | 11,874 | 10,325 | 77,342 | 74,619 | ||||
| 7.2 | 12,552 | 10,877 | 81,762 | 78,900 | ||||
| 7.4 | 13,176 | 11,458 | 86,101 | 82,977 | ||||
| 7.6 | 13,946 | 12,045 | 90,935 | 87,288 | ||||
| 7.8 | 14,670 | 12,640 | 95,621 | 91,805 | ||||
| 8 | 15,483 | 13,282 | 100,846 | 96,240 | ||||
Appendix B
| Designation | Meaning |
|---|---|
| hk | Step of minimization method |
| h* | Optimal step |
| gk, ∇f | Gradient of a function |
| f* | Optimal function value |
| (. , .) | Scalar product |
| Vector norm | |
| sk | New direction for minimization |
| zk | Step change |
| α, q | Step adaptation parameters |
| Δ | Interference level |
| N | Dimension |
References
- Lyu, F.; Xu, X.; Zha, X. An adaptive gradient descent attitude estimation algorithm based on a fuzzy system for UUVs. Ocean Eng. 2022, 266, 113025. [Google Scholar] [CrossRef]
- Rivas, J.M.; Gutierrez, J.J.; Guasque, A.; Balbastre, P. Gradient descent algorithm for the optimization of fixed priorities in real-time systems. J. Syst. Archit. 2024, 153, 103198. [Google Scholar] [CrossRef]
- Silaa, M.; Bencherif, A.; Barambones, O. A novel robust adaptive sliding mode control using stochastic gradient descent for PEMFC power system. Int. J. Hydrogen Energy 2023, 48, 17277–17292. [Google Scholar] [CrossRef]
- Li, S.; Wang, J.; Zhang, H.; Feng, Y.; Lu, G.; Zhai, A. Incremental accelerated gradient descent and adaptive fine-tuning heuristic performance optimization for robotic motion planning. Expert Syst. Appl. 2024, 243, 122794. [Google Scholar] [CrossRef]
- Zhao, W.; Huang, H. Adaptive stepsize estimation based accelerated gradient descent algorithm for fully complex-valued neural networks. Expert Syst. Appl. 2024, 236, 121166. [Google Scholar] [CrossRef]
- Chen, H.; Natsuaki, R.; Hirose, A. Polarization-aware prediction of mobile radio wave propagation based on complex-valued and quaternion neural networks. IEEE Access 2022, 10, 66589–66600. [Google Scholar] [CrossRef]
- Zeng, Z.; Sun, J.; Han, Z.; Hong, W. SAR automatic target recognition method based on multi-stream complex-valued networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5228618. [Google Scholar] [CrossRef]
- Ke, T.; Hwang, J.; Guo, Y.; Wang, X.; Yu, S. Unsupervised hierarchical semantic segmentation with multiview cosegmentation and clustering transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 2571–2581. [Google Scholar]
- Li, C.; Yao, K.; Wang, J.; Diao, B.; Xu, Y.; Zhang, Q. Interpretable generative adversarial networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2022. [Google Scholar]
- Polyak, B.T. Gradient methods for the minimisation of functional. USSR Comput. Math. Math. Phys. 1963, 3, 864–878. [Google Scholar] [CrossRef]
- Polyak, B.T. Introduction to Optimization; Optimization Software: New York, NY, USA, 1987. [Google Scholar]
- Nesterov, Y. Introductory Lectures on Convex Optimization; Kluwer Academic Publisher: Boston, MA, USA, 2004. [Google Scholar]
- Lojasiewicz, S. Une propriété topologique des sous-ensembles analytiques réels. Les Équations Aux Dérivées Partielles 1963, 117, 87–89. [Google Scholar]
- Karimi, H.; Nutini, J.; Schmidt, M. Linear convergence of gradient and proximal-gradient methods under the Polyak- Lojasiewicz condition. In Proceedings of the Machine Learning and Knowledge Discovery in Databases Conference, Riva del Garda, Italy, 19–23 September 2016; p. 795811. [Google Scholar]
- Yue, P.; Fang, C.; Lin, Z. On the lower bound of minimizing Polyak-Lojasiewicz functions. In Proceedings of the 36th Annual Conference on Learning Theory, Bangalore, India, 12–15 July 2023; pp. 2948–2968. [Google Scholar]
- Stonyakin, F.; Kuruzov, I.; Polyak, B. Stopping rules for gradient methods for nonconvex problems with additive noise in gradient. J. Optim. Theory Appl. 2023, 198, 531–551. [Google Scholar] [CrossRef]
- Devolder, O. Exactness, Inexactness and Stochasticity in First-Order Methods for Largescale Convex Optimization. Ph.D. Thesis, CORE UCLouvain, Louvain-la-Neuve, Belgium, 2013. [Google Scholar]
- d’Aspremont, A. Smooth optimization with approximate gradient. SIAM J. Optim. 2008, 19, 11711183. [Google Scholar] [CrossRef]
- Vasin, A.; Gasnikov, A.; Spokoiny, V. Stopping Rules for Accelerated Gradient Methods with Additive Noise in Gradient; Preprint No. 2812; WIAS: Berlin, Germany, 2021. [Google Scholar] [CrossRef]
- Nesterov, Y. Universal gradient methods for convex optimization problems. Math. Program. Ser. A 2015, 152, 381–404. [Google Scholar] [CrossRef]
- Puchinin, S.; Stonyakin, F. Gradient-Type Method for Optimization Problems with Polyak-Lojasiewicz Condition: Relative Inexactness in Gradient and Adaptive Parameters Setting. arXiv 2023, arXiv:2307.14101. [Google Scholar]
- Wang, Q.; Su, F.; Dai, S.; Lu, X.; Liu, Y. AdaGC: A Novel Adaptive Optimization Algorithm with Gradient Bias Correction. Expert Syst. Appl. 2024, 256, 124956. [Google Scholar] [CrossRef]
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Ablaev, S.; Beznosikov, A.; Gasnikov, A.; Dvinskikh, D.; Lobanov, A.; Puchinin, S.; Stonyakin, F. About Some Works of Boris Polyak on Convergence of Gradient Methods and Their Development. arXiv 2023, arXiv:2311.16743. [Google Scholar]
- Loizou, N.; Vaswani, S.; Laradji, I.; Lacoste-Julien, S. Stochastic Polyak step-size for SGD: An adaptive learning rate for fast convergence. In Proceedings of the 24th International Conference on Artificial Intelligence and Statistics (AISTATS-2021), Virtual, 13–15 April 2021; PMLR. Volume 130, pp. 1306–1314. [Google Scholar] [CrossRef]
- Hazan, E.; Kakade, S. Revisiting the Polyak Step Size. arXiv 2019, arXiv:1905.00313. [Google Scholar]
- Orvieto, A.; Lacoste-Julien, S.; Loizou, N. Dynamics of SGD with stochastic Polyak stepsizes: Truly adaptive variants and convergence to exact solution. In Advances in Neural Information Processing Systems; Koyejo, S., Mohamed, S., Agarwal, A., Belgrave, D., Cho, K., Oh, A., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2022; Volume 35, pp. 26943–26954. [Google Scholar]
- Jiang, X.; Stich, S.U. Adaptive SGD with Polyak stepsize and Line-search: Robust Convergence and Variance Reduction. In Proceedings of the 37th Conference on Neural Information Processing Systems (NeurIPS 2023), New Orleans, LA, USA, 10–16 December 2023; pp. 1–29. [Google Scholar]
- Berrada, L.; Zisserman, A.; Kumar, M.P. Training neural networks for and by interpolation. In Proceedings of the 37th International Conference on Machine Learning (ICML’20), Virtual, 13–18 July 2020; PMLR. Volume 119. [Google Scholar]
- Prazeres, M.; Oberman, A.M. Stochastic Gradient Descent with Polyak’s Learning Rate. J. Sci. Comput. 2021, 89, 25. [Google Scholar] [CrossRef]
- Rolinek, M.; Martius, G. L4: Practical loss-based stepsize adaptation for deep learning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS 2018), Montreal, QC, Canada, 3–8 December 2018; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31, pp. 6434–6444. [Google Scholar]
- Gower, R.; Defazio, A.; Rabbat, M. Stochastic Polyak Stepsize with a Moving Target. arXiv 2021, arXiv:2106.11851. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Orabona, F.; Pál, D. Scale-Free Algorithms for Online Linear Optimization. In Algorithmic Learning Theory; Chaudhuri, K., Gentile, C., Zilles, S., Eds.; ALT 2015, Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9355. [Google Scholar] [CrossRef]
- Vaswani, S.; Laradji, I.; Kunstner, F.; Meng, S.Y.; Schmidt, M.; Lacoste-Julien, S. Adaptive Gradient Methods Converge Faster with Over-Parameterization (But You Should Do a Line-Search). arXiv 2020, arXiv:2006.06835. [Google Scholar]
- Vaswani, S.; Mishkin, A.; Laradji, I.; Schmidt, M.; Gidel, G.; Lacoste-Julien, S. Painless Stochastic Gradient: Interpolation, Line-Search, and Convergence Rates. arXiv 2019, arXiv:1905.09997. [Google Scholar]
- Reddi, S.J.; Kale, S.; Kumar, S. On the convergence of Adam and beyond. In Proceedings of the 6th International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Tan, C.; Ma, S.; Dai, Y.-H.; Qian, Y. Barzilai-Borwein step size for stochastic gradient descent. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 685–693. [Google Scholar]
- Chen, J.; Zhou, D.; Tang, Y.; Yang, Z.; Cao, Y.; Gu, Q. Closing the Generalization Gap of Adaptive Gradient Methods in Training Deep Neural Networks. arXiv 2018, arXiv:1806.06763. [Google Scholar]
- Ward, R.; Wu, X.; Bottou, L. AdaGrad stepsizes: Sharp convergence over nonconvex landscapes. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR. Volume 97, pp. 6677–6686. [Google Scholar]
- Xie, Y.; Wu, X.; Ward, R. Linear convergence of adaptive stochastic gradient descent. In Proceedings of the 33 International Conference on Artificial Intelligence and Statistics, Online, 26–28 August 2020; PMLR. Volume 108, pp. 1475–1485. [Google Scholar]
- Li, X.; Orabona, F. On the convergence of stochastic gradient descent with adaptive stepsizes. In Proceedings of the 22 International Conference on Artificial Intelligence and Statistics (AISTATS) 2019, Naha, Japan, 16–18 April 2019; Volume 89, pp. 983–992. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Polyak, B.T. Some methods of speeding up the convergence of iteration methods. USSR Comp. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Tieleman, T.; Hinton, G. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA Neural Netw. Mach. Learn. 2012, 4, 26. [Google Scholar]
- Dozat, T. Incorporating Nesterov Momentum into Adam. In Proceedings of the ICLR 2016 workshop, San Juan, Puerto Rico, 2–4 May 2016; Available online: https://openreview.net/forum?id=OM0jvwB8jIp57ZJjtNEZ (accessed on 16 December 2024).
- Liu, L.; Jiang, H.; He, P.; Chen, W.; Liu, X.; Gao, J.; Han, J. On the Variance of the Adaptive Learning Rate and Beyond. arXiv 2019, arXiv:1908.03265. [Google Scholar]
- Dauphin, Y.; Vries, H.D.; Bengio, Y. RMSProp and Equilibrated Adaptive Learning Rates for Non-Convex Optimization. arXiv 2015, arXiv:1502.04390v1. [Google Scholar]
- Yousefian, F.; Nedic, A.; Shanbhag, U. On stochastic gradient and subgradient methods with adaptive steplength sequences. Automatica 2012, 48, 56–67. [Google Scholar] [CrossRef]
- Wu, X.; Ward, R.; Bottou, L. WNGrad: Learn the Learning Rate in Gradient Descent. arXiv 2018, arXiv:1803.02865. [Google Scholar]
- Levy, K.Y.; Yurtsever, A.; Cevher, V. Online Adaptive Methods, Universality and Acceleration. arXiv 2018, arXiv:1809.02864. [Google Scholar]
- He, C.; Zhang, Y.; Zhu, D.; Cao, M.; Yang, Y. A mini-batch algorithm for large-scale learning problems with adaptive step size. Digit. Signal Process. 2023, 143, 104230. [Google Scholar] [CrossRef]
- Zhuang, J.; Tang2, T.; Ding, Y.; Tatikonda, S.; Dvornek, N.; Papademetris, X.; Duncan, J. AdaBelief Optimizer: Adapting Stepsizes by the Belief in Observed Gradients. In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, BC, Canada, 6–12 December 2020; Volume 33, pp. 1–12. [Google Scholar]
- Zou, W.; Xia, Y.; Cao, W. AdaDerivative optimizer: Adapting step-sizes by the derivative term in past gradient information. Eng. Appl. Artif. Intell. 2023, 119, 105755. [Google Scholar] [CrossRef]
- Gaudioso, M.; Giallombardo, G.; Miglionico, G.; Vocaturo, E. Classification in the multiple instance learning framework via spherical separation. Soft Comput. 2020, 24, 5071–5077. [Google Scholar] [CrossRef]
- Astorino, A.; Fuduli, A.; Gaudioso, M. A Lagrangian Relaxation Approach for Binary Multiple Instance Classification. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2662–2671. [Google Scholar] [CrossRef] [PubMed]
- Fuduli, A.; Gaudioso, M.; Khalaf, W.; Vocaturo, E. A heuristic approach for multiple instance learning by linear separation. Soft Comput. 2022, 26, 3361–3368. [Google Scholar] [CrossRef]
- Kuruzov, I.A.; Stonyakin, F.S.; Alkousa, M.S. Gradient-type methods for optimization problems with Polyak–Lojasiewicz condition: Early stopping and adaptivity to inexactness parameter. In Advances in Optimization and Applications; Olenev, N., Evtushenko, Y., Jaćimović, M., Khachay, M., Malkova, V., Pospelov, I., Eds.; OPTIMA 2022, Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2022; Volume 1739, pp. 18–32. [Google Scholar]


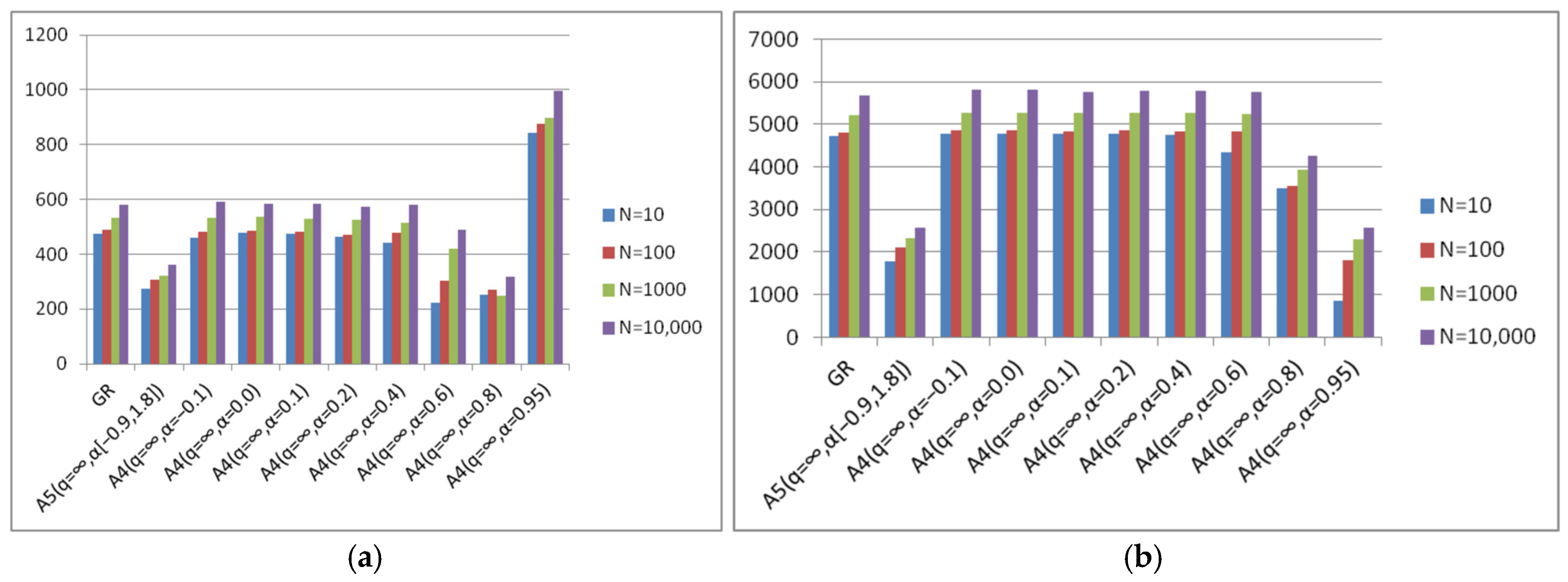
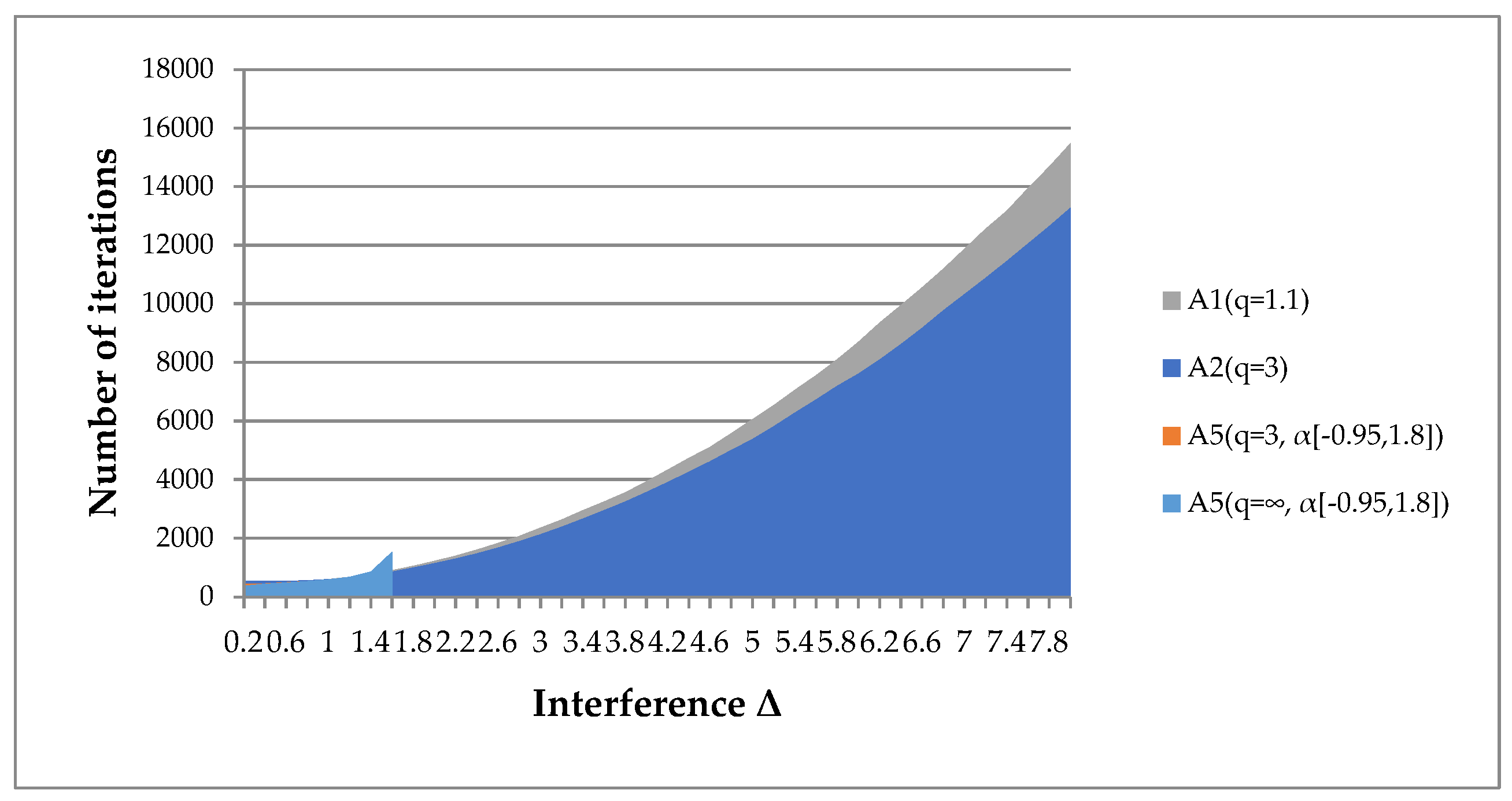

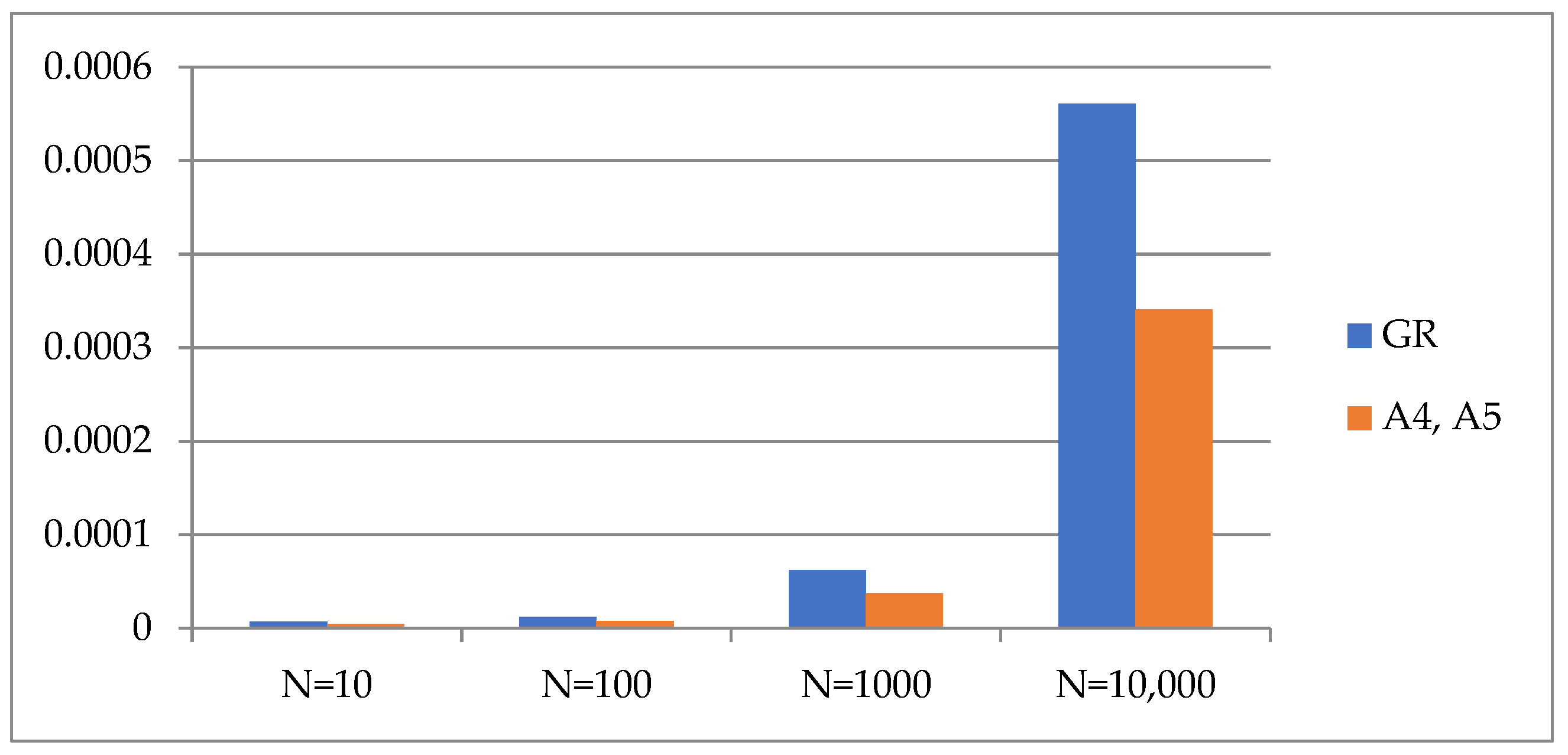

| Function | N = 10 | N = 100 | N = 1000 | N = 10,000 | ||||
|---|---|---|---|---|---|---|---|---|
| GR | A4, A5 | GR | A4, A5 | GR | A4, A5 | GR | A4, A5 | |
| fQ(x, [amax = 1000]) | - | - | 2.018 × 10−5 | 1.083 × 10−5 | 9.341 × 10−5 | 3.258 × 10−5 | 8.446 × 10−4 | 3.236 × 10−4 |
| fEEL(x, [amax = 10, bmax = 10]) | 6.782 × 10−6 | 4.400 × 10−6 | 1.174 × 10−5 | 7.592 × 10−6 | 6.195 × 10−5 | 3.738 × 10−5 | 5.610 × 10−4 | 3.409 × 10−4 |
| fEELX(x, [amax = 100]) | 4.632 × 10−6 | 3.006 × 10−6 | 9.637 × 10−6 | 6.233 × 10−6 | 6.971 × 10−5 | 4.116 × 10−5 | 6.050 × 10−4 | 3.973 × 10−4 |
| fQ^2(x, [amax = 100]) | 5.554 × 10−6 | 4.556 × 10−6 | 1.026 × 10−5 | 1.011 × 10−5 | 1.079 × 10−4 | 5.624 × 10−5 | 1.302 × 10−3 | 5.873 × 10−4 |
| fR(x, [amax = 100]) | 2.345 × 10−5 | 1.426 × 10−5 | 6.288 × 10−5 | 3.306 × 10−5 | 2.910 × 10−4 | 1.472 × 10−4 | 3.099 × 10−3 | 1.640 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krutikov, V.; Tovbis, E.; Gutova, S.; Rozhnov, I.; Kazakovtsev, L. Gradient Method with Step Adaptation. Mathematics 2025, 13, 61. https://doi.org/10.3390/math13010061
Krutikov V, Tovbis E, Gutova S, Rozhnov I, Kazakovtsev L. Gradient Method with Step Adaptation. Mathematics. 2025; 13(1):61. https://doi.org/10.3390/math13010061
Chicago/Turabian StyleKrutikov, Vladimir, Elena Tovbis, Svetlana Gutova, Ivan Rozhnov, and Lev Kazakovtsev. 2025. "Gradient Method with Step Adaptation" Mathematics 13, no. 1: 61. https://doi.org/10.3390/math13010061
APA StyleKrutikov, V., Tovbis, E., Gutova, S., Rozhnov, I., & Kazakovtsev, L. (2025). Gradient Method with Step Adaptation. Mathematics, 13(1), 61. https://doi.org/10.3390/math13010061






