Persistent Topological Laplacians—A Survey
Abstract
1. Introduction
2. Mathematical Preliminaries
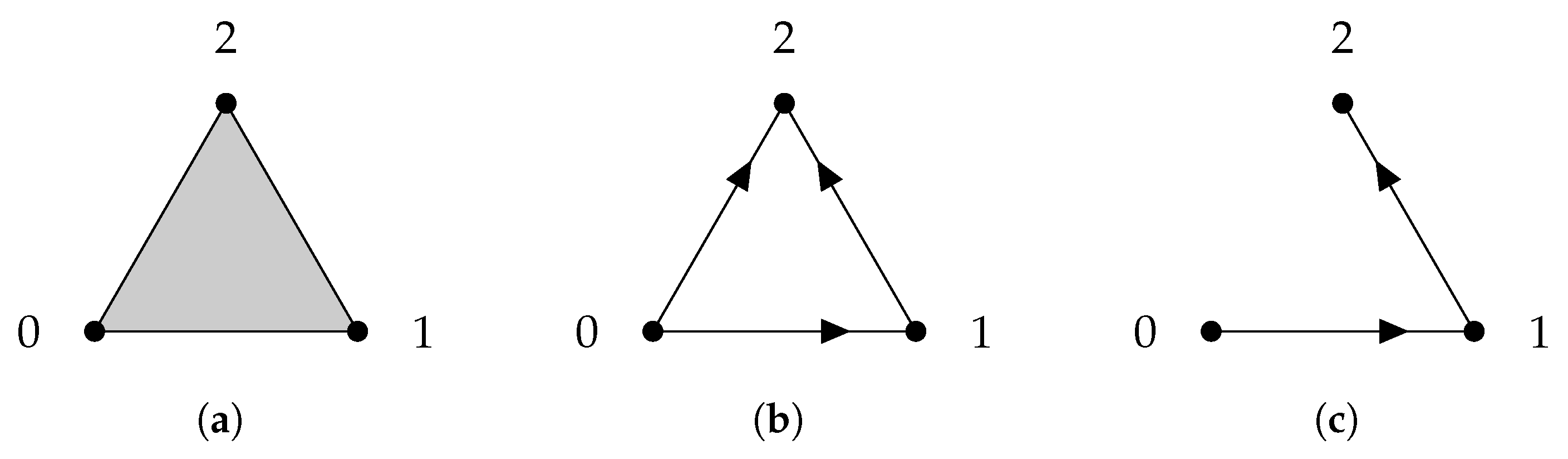
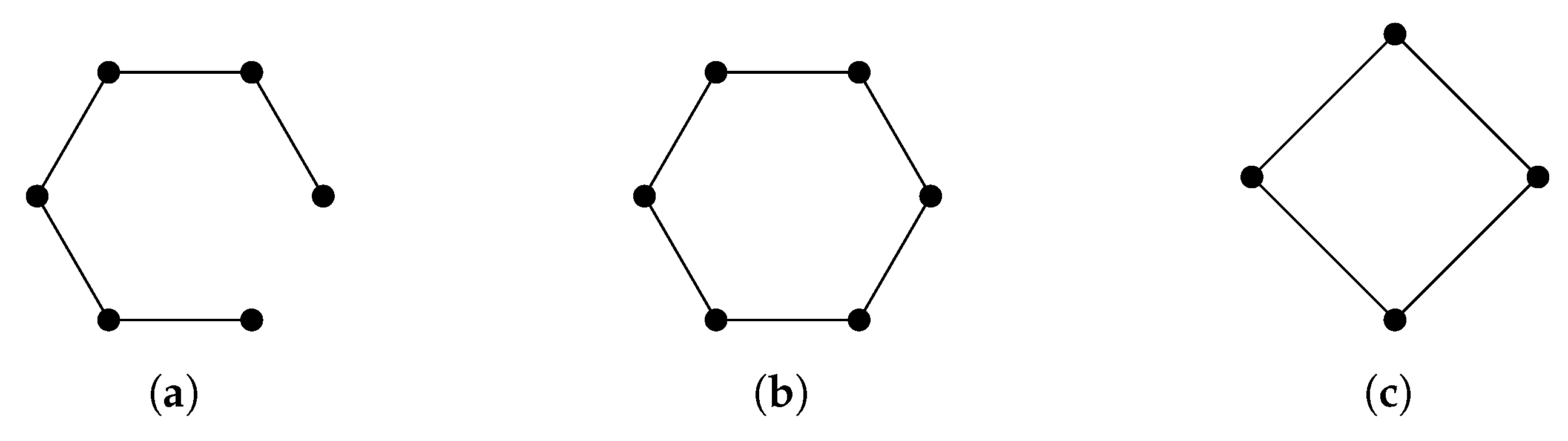
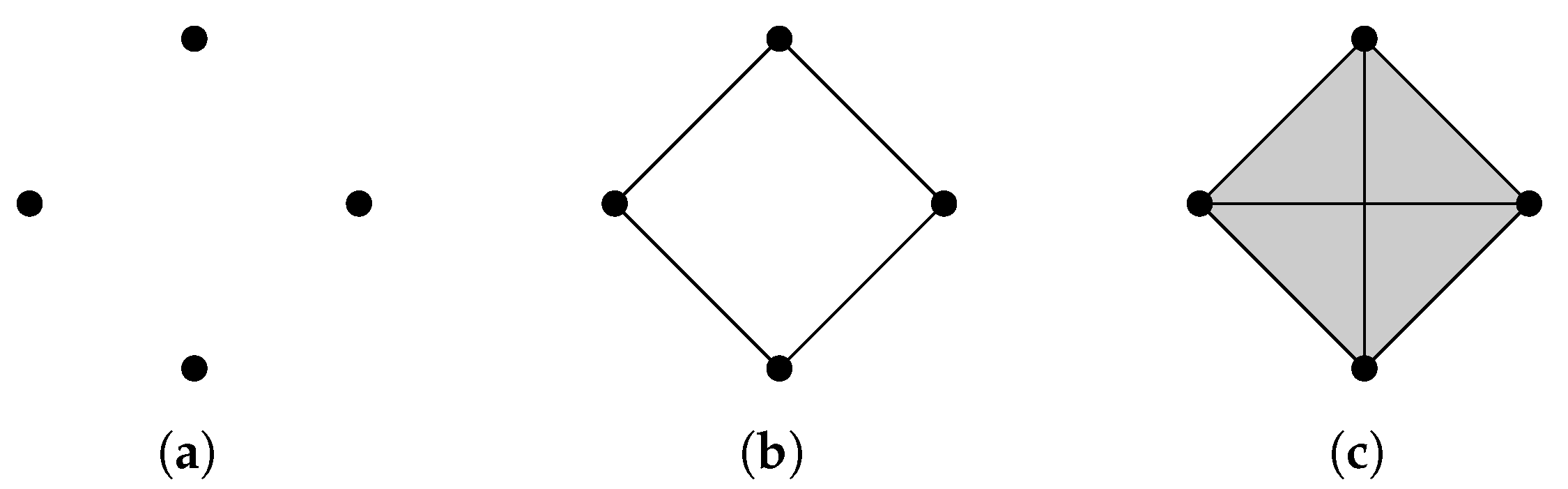
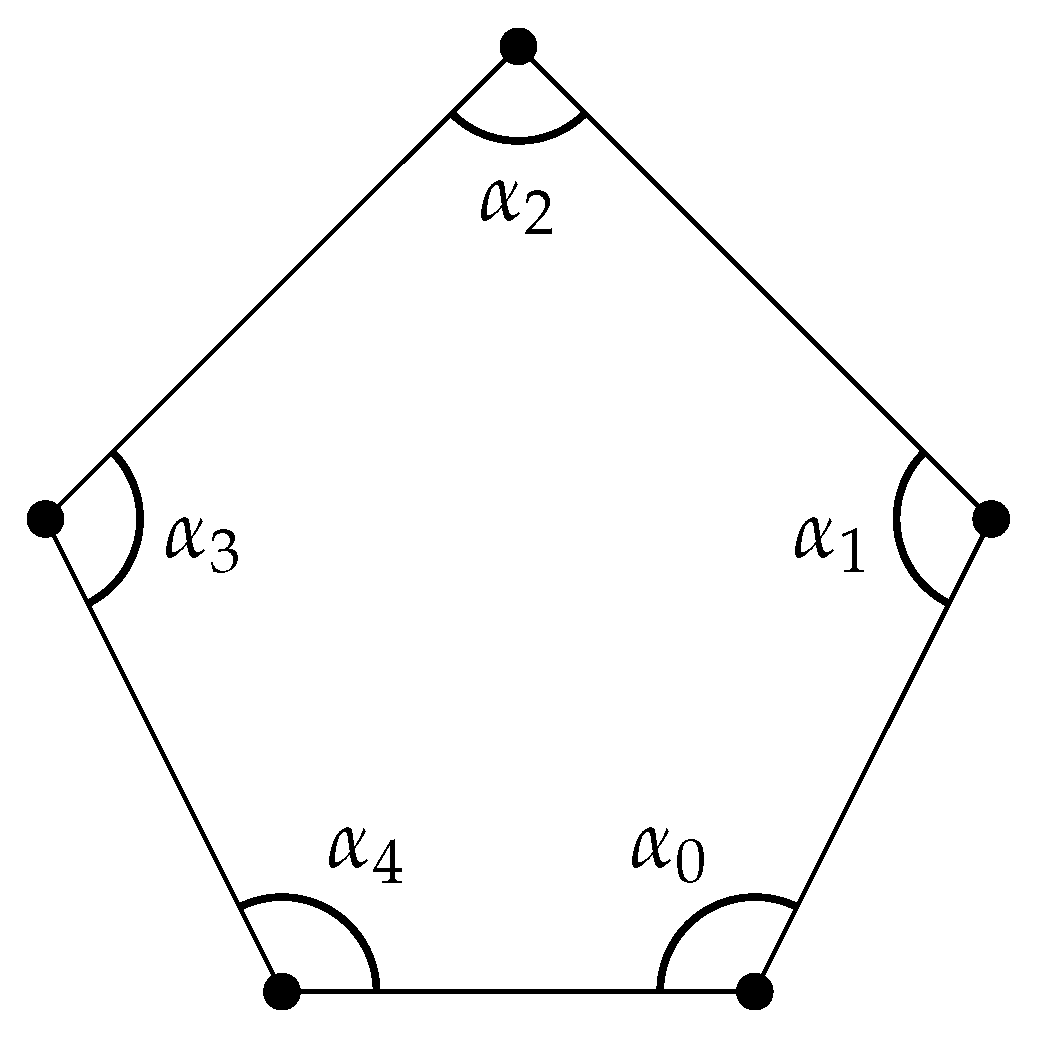
2.1. Simplicial Complexes and Homology


2.2. Combinatorial Laplacians
2.3. Filtration and Persistent Homology

3. Persistent (Combinatorial) Laplacians
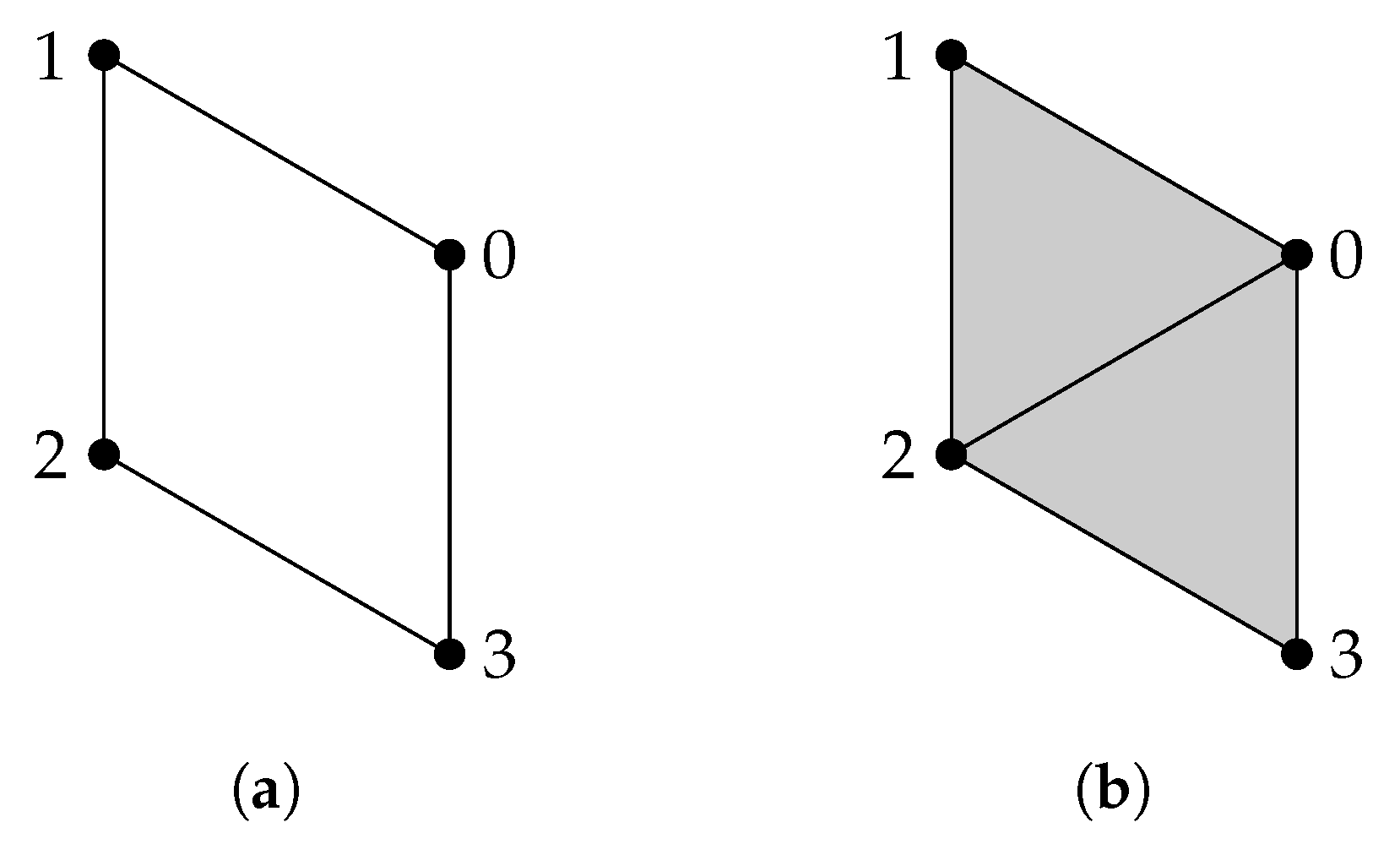
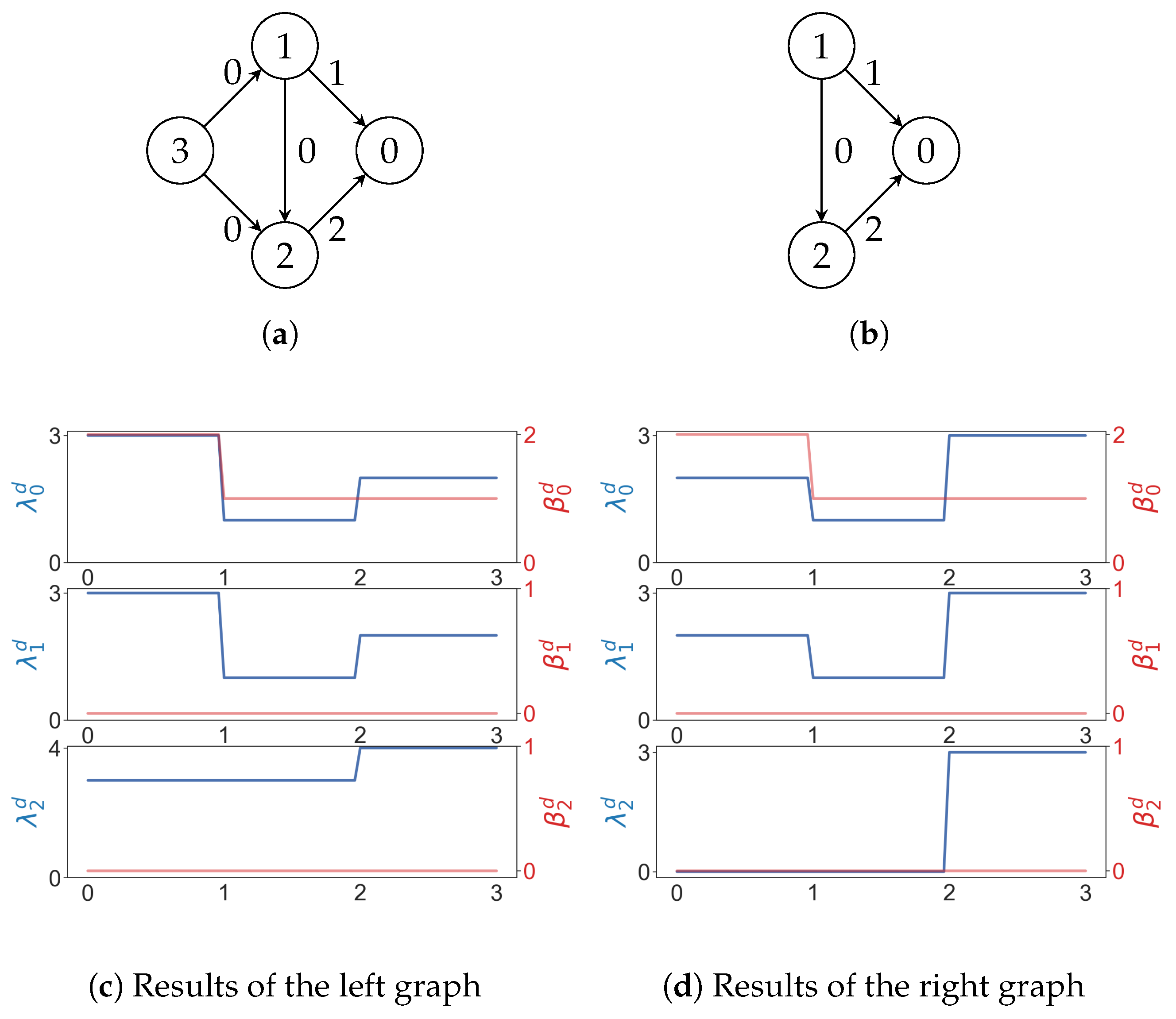
3.1. Persistent Laplacians

3.2. Matrix Representations of a (Persistent) Laplacian








3.3. Eigenvectors of a Laplacian
4. Generalizations of (Persistent) Laplacians
4.1. Differential Graded Inner Product Spaces

4.2. Persistent Laplacians for Simplicial Maps

4.3. Weighted Simplicial Complexes

4.4. Cellular (Co)Sheaves


4.5. Path Homology, Flag Homology, and Digraphs

4.6. Hypergraphs and Hyperdigraphs
4.7. Persistent Dirac Operators


4.8. Mayer Homology

5. Conclusions and Outlook
5.1. Persistent Topological Laplacians Versus Topological Data Analysis
5.2. Limitations of Persistent Topological Laplacians
5.3. Future Works
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Edelsbrunner, H.; Harer, J. Persistent homology—A survey. Contemp. Math. 2008, 453, 257–282. [Google Scholar]
- Zomorodian, A.; Carlsson, G. Computing persistent homology. Discret. Comput. Geom. 2005, 33, 249–274. [Google Scholar] [CrossRef]
- Ghrist, R. Barcodes: The persistent topology of data. Bull. Am. Math. Soc. 2008, 45, 61–75. [Google Scholar] [CrossRef]
- Adams, H.; Emerson, T.; Kirby, M.; Neville, R.; Peterson, C.; Shipman, P.; Chepushtanova, S.; Hanson, E.; Motta, F.; Ziegelmeier, L. Persistence images: A stable vector representation of persistent homology. J. Mach. Learn. Res. 2017, 18, 1–35. [Google Scholar]
- Xia, K.; Wei, G.W. Multidimensional persistence in biomolecular data. J. Comput. Chem. 2015, 36, 1502–1520. [Google Scholar] [CrossRef]
- Bubenik, P. Statistical topological data analysis using persistence landscapes. J. Mach. Learn. Res. 2015, 16, 77–102. [Google Scholar]
- Bae, W.; Yoo, J.; Chul Ye, J. Beyond deep residual learning for image restoration: Persistent homology-guided manifold simplification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 145–153. [Google Scholar]
- Clough, J.R.; Byrne, N.; Oksuz, I.; Zimmer, V.A.; Schnabel, J.A.; King, A.P. A topological loss function for deep-learning based image segmentation using persistent homology. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 8766–8778. [Google Scholar] [CrossRef]
- Dabaghian, Y.; Mémoli, F.; Frank, L.; Carlsson, G. A topological paradigm for hippocampal spatial map formation using persistent homology. PLoS Comput. Biol. 2012, 8, e1002581. [Google Scholar] [CrossRef]
- Townsend, J.; Micucci, C.P.; Hymel, J.H.; Maroulas, V.; Vogiatzis, K.D. Representation of molecular structures with persistent homology for machine learning applications in chemistry. Nat. Commun. 2020, 11, 3230. [Google Scholar] [CrossRef]
- Cang, Z.; Wei, G.W. TopologyNet: Topology based deep convolutional and multi-task neural networks for biomolecular property predictions. PLoS Comput. Biol. 2017, 13, e1005690. [Google Scholar] [CrossRef]
- Cang, Z.; Wei, G.W. Integration of element specific persistent homology and machine learning for protein-ligand binding affinity prediction. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2914. [Google Scholar] [CrossRef] [PubMed]
- Gameiro, M.; Hiraoka, Y.; Izumi, S.; Kramar, M.; Mischaikow, K.; Nanda, V. A topological measurement of protein compressibility. Jpn. J. Ind. Appl. Math. 2015, 32, 1–17. [Google Scholar] [CrossRef]
- Kovacev-Nikolic, V.; Bubenik, P.; Nikolić, D.; Heo, G. Using persistent homology and dynamical distances to analyze protein binding. Stat. Appl. Genet. Mol. Biol. 2016, 15, 19–38. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Barthel, S.D.; Dłotko, P.; Moosavi, S.M.; Hess, K.; Smit, B. Quantifying similarity of pore-geometry in nanoporous materials. Nat. Commun. 2017, 8, 15396. [Google Scholar] [CrossRef]
- Xia, K.; Feng, X.; Tong, Y.; Wei, G.W. Persistent homology for the quantitative prediction of fullerene stability. J. Comput. Chem. 2015, 36, 408–422. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, D.; Chen, X.; Li, T.; Wei, G.W.; Pan, F. Topological representations of crystalline compounds for the machine-learning prediction of materials properties. Npj Comput. Mater. 2021, 7, 28. [Google Scholar] [CrossRef]
- Horak, D.; Maletić, S.; Rajković, M. Persistent homology of complex networks. J. Stat. Mech. Theory Exp. 2009, 2009, P03034. [Google Scholar] [CrossRef]
- Nguyen, D.D.; Cang, Z.; Wei, G.W. A review of mathematical representations of biomolecular data. Phys. Chem. Chem. Phys. 2020, 22, 4343–4367. [Google Scholar] [CrossRef]
- Nguyen, D.D.; Cang, Z.; Wu, K.; Wang, M.; Cao, Y.; Wei, G.W. Mathematical deep learning for pose and binding affinity prediction and ranking in D3R Grand Challenges. J. Comput.-Aided Mol. Des. 2019, 33, 71–82. [Google Scholar] [CrossRef]
- Chen, J.; Wang, R.; Wang, M.; Wei, G.W. Mutations strengthened SARS-CoV-2 infectivity. J. Mol. Biol. 2020, 432, 5212–5226. [Google Scholar] [CrossRef]
- Papamarkou, T.; Birdal, T.; Bronstein, M.M.; Carlsson, G.E.; Curry, J.; Gao, Y.; Hajij, M.; Kwitt, R.; Lio, P.; Di Lorenzo, P.; et al. Position: Topological Deep Learning is the New Frontier for Relational Learning. In Proceedings of the Forty-first International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024. [Google Scholar]
- Lieutier, A. Talk: Persistent Harmonic Forms. 2014. Available online: https://project.inria.fr/gudhi/files/2014/10/Persistent-Harmonic-Forms.pdf (accessed on 11 January 2024).
- Wang, R.; Nguyen, D.D.; Wei, G.W. Persistent spectral graph. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3376. [Google Scholar] [CrossRef] [PubMed]
- Chung, F.R. Spectral Graph Theory; American Mathematical Soc.: Providence, RI, USA, 1997; Volume 92. [Google Scholar]
- Horak, D.; Jost, J. Spectra of combinatorial Laplace operators on simplicial complexes. Adv. Math. 2013, 244, 303–336. [Google Scholar] [CrossRef]
- Butler, S.; Chung, F. Small spectral gap in the combinatorial Laplacian implies Hamiltonian. Ann. Comb. 2010, 13, 403–412. [Google Scholar] [CrossRef]
- Eckmann, B. Harmonische funktionen und randwertaufgaben in einem komplex. Comment. Math. Helv. 1944, 17, 240–255. [Google Scholar] [CrossRef]
- Desbrun, M.; Kanso, E.; Tong, Y. Discrete differential forms for computational modeling. In Proceedings of the ACM SIGGRAPH 2006 Courses: Special Interest Group on Computer Graphics and Interactive Techniques Conference Massachusetts, Boston, MA, USA, 30 July–3 August 2006; pp. 39–54. [Google Scholar]
- Dodziuk, J. Finite-difference approach to the Hodge theory of harmonic forms. Am. J. Math. 1976, 98, 79–104. [Google Scholar] [CrossRef]
- Arnold, D.N.; Falk, R.S.; Winther, R. Finite element exterior calculus, homological techniques, and applications. Acta Numer. 2006, 15, 1–155. [Google Scholar] [CrossRef]
- Bhatia, H.; Norgard, G.; Pascucci, V.; Bremer, P.T. The Helmholtz-Hodge decomposition—A survey. IEEE Trans. Vis. Comput. Graph. 2012, 19, 1386–1404. [Google Scholar] [CrossRef]
- Lim, L.H. Hodge laplacians on graphs. Siam Rev. 2020, 62, 685–715. [Google Scholar] [CrossRef]
- Ribando-Gros, E.; Wang, R.; Chen, J.; Tong, Y.; Wei, G.W. Combinatorial and Hodge Laplacians: Similarities and Differences. SIAM Rev. 2024, 66, 575–601. [Google Scholar] [CrossRef]
- Jiang, X.; Lim, L.H.; Yao, Y.; Ye, Y. Statistical ranking and combinatorial Hodge theory. Math. Program. 2011, 127, 203–244. [Google Scholar] [CrossRef]
- Ma, W.; Morel, J.M.; Osher, S.; Chien, A. An L 1-based variational model for Retinex theory and its application to medical images. In Proceedings of the CVPR 2011, Colorado Springs, CO, USA, 20–25 June 2011; IEEE: New York, NY, USA, 2011; pp. 153–160. [Google Scholar]
- Xu, Q.; Huang, Q.; Jiang, T.; Yan, B.; Lin, W.; Yao, Y. HodgeRank on random graphs for subjective video quality assessment. IEEE Trans. Multimed. 2012, 14, 844–857. [Google Scholar] [CrossRef]
- Hirani, A.N. Discrete Exterior Calculus; California Institute of Technology: Pasadena, CA, USA, 2003. [Google Scholar]
- Tong, Y.; Lombeyda, S.; Hirani, A.N.; Desbrun, M. Discrete multiscale vector field decomposition. ACM Trans. Graph. (TOG) 2003, 22, 445–452. [Google Scholar] [CrossRef]
- Candogan, O.; Menache, I.; Ozdaglar, A.; Parrilo, P.A. Flows and decompositions of games: Harmonic and potential games. Math. Oper. Res. 2011, 36, 474–503. [Google Scholar] [CrossRef]
- Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric deep learning: Going beyond euclidean data. IEEE Signal Process. Mag. 2017, 34, 18–42. [Google Scholar] [CrossRef]
- Chui, C.K.; Mhaskar, H.; Zhuang, X. Representation of functions on big data associated with directed graphs. Appl. Comput. Harmon. Anal. 2018, 44, 165–188. [Google Scholar] [CrossRef]
- Perea, J.A. Multiscale projective coordinates via persistent cohomology of sparse filtrations. Discret. Comput. Geom. 2018, 59, 175–225. [Google Scholar] [CrossRef]
- Schaub, M.T.; Segarra, S. Flow smoothing and denoising: Graph signal processing in the edge-space. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018; IEEE: New York, NY, USA, 2018; pp. 735–739. [Google Scholar]
- Gao, T.; Brodzki, J.; Mukherjee, S. The geometry of synchronization problems and learning group actions. Discret. Comput. Geom. 2021, 65, 150–211. [Google Scholar] [CrossRef]
- Benson, A.R.; Abebe, R.; Schaub, M.T.; Jadbabaie, A.; Kleinberg, J. Simplicial closure and higher-order link prediction. Proc. Natl. Acad. Sci. USA 2018, 115, E11221–E11230. [Google Scholar] [CrossRef]
- Zhang, M.; Goupil, A.; Hanaf, A.; Wang, T. Distributed harmonic form computation. IEEE Signal Process. Lett. 2018, 25, 1241–1245. [Google Scholar] [CrossRef]
- Kook, W.; Lee, K.J. Simplicial networks and effective resistance. Adv. Appl. Math. 2018, 100, 71–86. [Google Scholar] [CrossRef]
- Ye, K.; Lim, L.H. Cohomology of cryo-electron microscopy. SIAM J. Appl. Algebra Geom. 2017, 1, 507–535. [Google Scholar] [CrossRef]
- Lee, H.; Chung, M.K.; Choi, H.; Kang, H.; Ha, S.; Kim, Y.K.; Lee, D.S. Harmonic holes as the submodules of brain network and network dissimilarity. In Proceedings of the Computational Topology in Image Context: 7th International Workshop, CTIC 2019, Málaga, Spain, 24–25 January 2019; Proceedings 7. Springer: Berlin/Heidelberg, Germany, 2019; pp. 110–122. [Google Scholar]
- Schaub, M.T.; Benson, A.R.; Horn, P.; Lippner, G.; Jadbabaie, A. Random walks on simplicial complexes and the normalized Hodge 1-Laplacian. SIAM Rev. 2020, 62, 353–391. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, R.; Tong, Y.; Wei, G.W. Evolutionary de rham-hodge method. Iscrete Contin. Dyn. Syst.-B 2021, 26, 3785–3821. [Google Scholar] [CrossRef] [PubMed]
- Su, Z.; Tong, Y.; Wei, G.W. Persistent de Rham-Hodge Laplacians in Eulerian representation for manifold topological learning. AIMS Math. 2024, 9, 27438–27470. [Google Scholar] [CrossRef]
- Gülen, A.B.; Mémoli, F.; Wan, Z.; Wang, Y. A generalization of the persistent Laplacian to simplicial maps. arXiv 2023, arXiv:2302.03771. [Google Scholar]
- Liu, J.; Li, J.; Wu, J. The algebraic stability for persistent Laplacians. arXiv 2023, arXiv:2302.03902. [Google Scholar] [CrossRef]
- Mémoli, F.; Wan, Z.; Wang, Y. Persistent Laplacians: Properties, algorithms and implications. SIAM J. Math. Data Sci. 2022, 4, 858–884. [Google Scholar] [CrossRef]
- Jones, B.; Wei, G.W. Persistent directed flag Lpalacians. Found. Data Sci. 2024. [Google Scholar] [CrossRef]
- Wang, R.; Wei, G.W. Persistent path Laplacian. Found. Data Sci. 2023, 5, 26–55. [Google Scholar] [CrossRef]
- Wei, X.; Wei, G.W. Persistent sheaf Laplacians. Found. Data Sci. 2024. [Google Scholar] [CrossRef]
- Liu, X.; Feng, H.; Wu, J.; Xia, K. Persistent spectral hypergraph based machine learning (PSH-ML) for protein-ligand binding affinity prediction. Briefings Bioinform. 2021, 22, bbab127. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Liu, J.; Wu, J.; Wei, G.W. Persistent hyperdigraph homology and persistent hyperdigraph Laplacians. Found. Data Sci. 2023, 5, 558–588. [Google Scholar] [CrossRef] [PubMed]
- Dong, R. A faster algorithm of up persistent laplacian over non-branching simplicial complexes. arXiv 2024, arXiv:2408.16741. [Google Scholar]
- Wang, R.; Zhao, R.; Ribando-Gros, E.; Chen, J.; Tong, Y.; Wei, G.W. HERMES: Persistent spectral graph software. Found. Data Sci. 2020, 3, 67–97. [Google Scholar] [CrossRef] [PubMed]
- Meng, Z.; Xia, K. Persistent spectral–based machine learning (PerSpect ML) for protein-ligand binding affinity prediction. Sci. Adv. 2021, 7, eabc5329. [Google Scholar] [CrossRef]
- Du, H.; Wei, G.W.; Hou, T. Multiscale Topology in Interactomic Network: From Transcriptome to Antiaddiction Drug Repurposing. Briefings Bioinform. 2024, 25, bbae054. [Google Scholar] [CrossRef]
- Cottrell, S.; Wang, R.; Wei, G.W. PLPCA: Persistent Laplacian Enhanced-PCA for Microarray Data Analysis. J. Chem. Inf. Model. 2023, 64, 2405–2420. [Google Scholar] [CrossRef]
- Chen, J.; Woldring, D.R.; Huang, F.; Huang, X.; Wei, G.W. Topological deep learning based deep mutational scanning. Comput. Biol. Med. 2023, 164, 107258. [Google Scholar] [CrossRef]
- Hozumi, Y.; Wei, G.W. Revealing the Shape of Genome Space via K-mer Topology. arXiv 2024, arXiv:2412.20202. [Google Scholar]
- Wei, X.; Chen, J.; Wei, G.W. Persistent topological Laplacian analysis of SARS-CoV-2 variants. J. Comput. Biophys. Chem. 2023, 22, 569. [Google Scholar] [CrossRef]
- Qiu, Y.; Wei, G.W. Persistent spectral theory-guided protein engineering. Nat. Comput. Sci. 2023, 3, 149–163. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Qiu, Y.; Wang, R.; Wei, G.W. Persistent Laplacian projected Omicron BA. 4 and BA. 5 to become new dominating variants. Comput. Biol. Med. 2022, 151, 106262. [Google Scholar] [CrossRef] [PubMed]
- Mayer, W. A new homology theory. Ann. Math. 1942, 43, 370–380. [Google Scholar] [CrossRef]
- Shen, L.; Liu, J.; Wei, G.W. Persistent Mayer homology and persistent Mayer Laplacian. Found. Data Sci. 2024, 6, 584–612. [Google Scholar] [CrossRef]
- Carlsson, G. Topology and data. Bull. Am. Math. Soc. 2009, 46, 255–308. [Google Scholar] [CrossRef]
- Otter, N.; Porter, M.A.; Tillmann, U.; Grindrod, P.; Harrington, H.A. A roadmap for the computation of persistent homology. EPJ Data Sci. 2017, 6, 1–38. [Google Scholar] [CrossRef]
- Pun, C.S.; Lee, S.X.; Xia, K. Persistent-homology-based machine learning: A survey and a comparative study. Artif. Intell. Rev. 2022, 55, 5169–5213. [Google Scholar] [CrossRef]
- Munkres, J.R. Elements of Algebraic Topology; Addison-Wesley Publishing Company, Inc.: London, UK, 1984. [Google Scholar]
- Fiedler, M. Algebraic connectivity of graphs. Czechoslov. Math. J. 1973, 23, 298–305. [Google Scholar] [CrossRef]
- Goldberg, T.E. Combinatorial Laplacians of Simplicial Complexes. Bachelor’s Thesis, Bard College, Annandale-On-Hudson, NY, USA, 2002. [Google Scholar]
- Krishnagopal, S.; Bianconi, G. Spectral detection of simplicial communities via Hodge Laplacians. Phys. Rev. E 2021, 104, 064303. [Google Scholar] [CrossRef]
- Muhammad, A.; Egerstedt, M. Control using higher order Laplacians in network topologies. In Proceedings of the 17th International Symposium on Mathematical Theory of Networks and Systems, Citeseer, Kyoto, Japan, 24–28 July 2006; pp. 1024–1038. [Google Scholar]
- Wei, R.K.J.; Wee, J.; Laurent, V.E.; Xia, K. Hodge theory-based biomolecular data analysis. Sci. Rep. 2022, 12, 9699. [Google Scholar] [CrossRef]
- Baccini, F.; Geraci, F.; Bianconi, G. Weighted simplicial complexes and their representation power of higher-order network data and topology. Phys. Rev. E 2022, 106, 034319. [Google Scholar] [CrossRef] [PubMed]
- Battiloro, C.; Sardellitti, S.; Barbarossa, S.; Di Lorenzo, P. Topological Signal Processing over Weighted Simplicial Complexes. arXiv 2023, arXiv:2302.08561. [Google Scholar]
- Chung, F.R.; Langlands, R.P. A combinatorial Laplacian with vertex weights. J. Comb. Theory Ser. 1996, 75, 316–327. [Google Scholar] [CrossRef]
- Courtney, O.T.; Bianconi, G. Weighted growing simplicial complexes. Phys. Rev. E 2017, 95, 062301. [Google Scholar] [CrossRef]
- Petri, G.; Scolamiero, M.; Donato, I.; Vaccarino, F. Topological strata of weighted complex networks. PloS ONE 2013, 8, e66506. [Google Scholar] [CrossRef]
- Sharma, A.; Moore, T.J.; Swami, A.; Srivastava, J. Weighted simplicial complex: A novel approach for predicting small group evolution. In Proceedings of the Advances in Knowledge Discovery and Data Mining: 21st Pacific-Asia Conference, PAKDD 2017, Jeju, South Korea, 23–26 May 2017; Proceedings, Part I 21. Springer: Berlin/Heidelberg, Germany, 2017; pp. 511–523. [Google Scholar]
- Dawson, R.J.M. Homology of weighted simplicial complexes. Cah. Topol. Géom. Différ. Catég. 1990, 31, 229–243. [Google Scholar]
- Bura, A.; He, Q.; Reidys, C. Weighted Homology of Bi-Structures over Certain Discrete Valuation Rings. Mathematics 2021, 9, 744. [Google Scholar] [CrossRef]
- Bura, A.C.; Dutta, N.S.; Li, T.J.; Reidys, C.M. A computational framework for weighted simplicial homology. arXiv 2022, arXiv:2206.04612. [Google Scholar] [CrossRef]
- Li, T.J.; Reidys, C.M. On Weighted Simplicial Homology. arXiv 2022, arXiv:2205.03435. [Google Scholar]
- Ren, S.; Wu, C. Weighted Simplicial Complexes and Weighted Analytic Torsions. arXiv 2021, arXiv:2103.04252. [Google Scholar]
- Ren, S.; Wu, C.; Wu, J. Weighted persistent homology. Rocky Mt. J. Math. 2018, 48, 2661–2687. [Google Scholar] [CrossRef]
- Wu, C.; Ren, S.; Wu, J.; Xia, K. Weighted (co)homology and weighted laplacian. arXiv 2018, arXiv:1804.06990. [Google Scholar]
- Wu, C.; Ren, S.; Wu, J.; Xia, K. Discrete Morse theory for weighted simplicial complexes. Topol. Its Appl. 2020, 270, 107038. [Google Scholar] [CrossRef]
- Hansen, J.; Ghrist, R. Toward a spectral theory of cellular sheaves. J. Appl. Comput. Topol. 2019, 3, 315–358. [Google Scholar] [CrossRef]
- Shepard, A.D. A Cellular Description of the Derived Category of a Stratified Space. Ph.D. Thesis, Brown University, Providence, RI, USA, 1985. [Google Scholar]
- Curry, J. Sheaves, Cosheaves and Applications. Ph.D. Thesis, University of Pennsylvania, Philadelphia, PA, USA, 2014. [Google Scholar]
- Hansen, J. Laplacians of Cellular Sheaves: Theory and Applications. Ph.D. Thesis, University of Pennsylvania, Philadelphia, PA, USA, 2020. [Google Scholar]
- Robinson, M. Topological Signal Processing; Springer: Berlin/Heidelberg, Germany, 2014; Volume 81. [Google Scholar]
- Robinson, M. Sheaves are the canonical data structure for sensor integration. Inf. Fusion 2017, 36, 208–224. [Google Scholar] [CrossRef]
- Yoon, H.R. Cellular Sheaves and Cosheaves for Distributed Topological Data Analysis. Ph.D. Thesis, University of Pennsylvania, Philadelphia, PA, USA, 2018. [Google Scholar]
- Barbero, F.; Bodnar, C.; de Ocáriz Borde, H.S.; Bronstein, M.; Veličković, P.; Liò, P. Sheaf neural networks with connection laplacians. In Proceedings of the Topological, Algebraic and Geometric Learning Workshops 2022, PMLR, Virtual, 25 February–22 July 2022; pp. 28–36. [Google Scholar]
- Bodnar, C.; Di Giovanni, F.; Chamberlain, B.; Lio, P.; Bronstein, M. Neural sheaf diffusion: A topological perspective on heterophily and oversmoothing in gnns. Adv. Neural Inf. Process. Syst. 2022, 35, 18527–18541. [Google Scholar]
- Gillespie, P.; Maroulas, V.; Schizas, I. Bayesian Sheaf Neural Networks. arXiv 2024, arXiv:2410.09590. [Google Scholar]
- Hansen, J.; Gebhart, T. Sheaf neural networks. arXiv 2020, arXiv:2012.06333. [Google Scholar]
- Hansen, J. A Gentle Introduction to Sheaves on Graphs. Available online: https://jakobhansen.org/publications/gentleintroduction.pdf (accessed on 2 February 2024).
- Robinson, M. How Do We Deal with Noisy Data? Available online: https://www.youtube.com/watch?v=TZpA8E5U4CE (accessed on 3 January 2024).
- Yegnesh, K. Persistence and sheaves. arXiv 2016, arXiv:1612.03522. [Google Scholar]
- Russold, F. Persistent sheaf cohomology. arXiv 2022, arXiv:2204.13446. [Google Scholar]
- Caputi, L.; Riihimäki, H. Hochschild homology, and a persistent approach via connectivity digraphs. J. Appl. Comput. Topol. 2023, 8, 1121–1170. [Google Scholar] [CrossRef]
- Lütgehetmann, D.; Govc, D.; Smith, J.P.; Levi, R. Computing persistent homology of directed flag complexes. Algorithms 2020, 13, 19. [Google Scholar] [CrossRef]
- Masulli, P.; Villa, A.E. The topology of the directed clique complex as a network invariant. SpringerPlus 2016, 5, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Reimann, M.W.; Nolte, M.; Scolamiero, M.; Turner, K.; Perin, R.; Chindemi, G.; Dłotko, P.; Levi, R.; Hess, K.; Markram, H. Cliques of neurons bound into cavities provide a missing link between structure and function. Front. Comput. Neurosci. 2017, 11, 48. [Google Scholar] [CrossRef]
- Grigor’yan, A.; Lin, Y.; Muranov, Y.; Yau, S.T. Homologies of path complexes and digraphs. arXiv 2012, arXiv:1207.2834. [Google Scholar]
- Grigor’yan, A.; Lin, Y.; Muranov, Y.; Yau, S.T. Homotopy Theory for Digraphs. Pure Appl. Math. Q. 2014, 10, 619–674. [Google Scholar] [CrossRef]
- Grigor’yan, A.; Lin, Y.; Muranov, Y.; Yau, S.T. Cohomology of digraphs and (undirected) graphs. Asian J. Math. 2015, 19, 887–932. [Google Scholar] [CrossRef]
- Grigor’yan, A.; Lin, Y.; Muranov, Y.V.; Yau, S.T. Path complexes and their homologies. J. Math. Sci. 2020, 248, 564–599. [Google Scholar] [CrossRef]
- Grigor’yan, A.; Muranov, Y.; Yau, S.T. Homologies of digraphs and Künneth formulas. Commun. Anal. Geom. 2017, 25, 969–1018. [Google Scholar] [CrossRef]
- Lin, Y.; Ren, S.; Wang, C.; Wu, J. Weighted path homology of weighted digraphs and persistence. arXiv 2019, arXiv:1910.09891. [Google Scholar]
- Grigor’yan, A. Advances in path homology theory of digraphs. Not. Int. Consort. Chin. Math. 2022, 10, 61–124. [Google Scholar] [CrossRef]
- Grigor’yan, A.; Jimenez, R.; Muranov, Y.; Yau, S.T. Homology of path complexes and hypergraphs. Topol. Its Appl. 2019, 267, 106877. [Google Scholar] [CrossRef]
- Huntsman, S. Path homology as a stronger analogue of cyclomatic complexity. arXiv 2020, arXiv:2003.00944. [Google Scholar]
- Chowdhury, S.; Huntsman, S.; Yutin, M. Path homologies of motifs and temporal network representations. Appl. Netw. Sci. 2022, 7, 4. [Google Scholar] [CrossRef]
- Chowdhury, S.; Mémoli, F. Persistent path homology of directed networks. In Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, SIAM, New Orleans, LA, USA, 7–10 January 2018; pp. 1152–1169. [Google Scholar]
- Chen, D.; Liu, J.; Wu, J.; Wei, G.W.; Pan, F.; Yau, S.T. Path topology in molecular and materials sciences. J. Phys. Chem. Lett. 2023, 14, 954–964. [Google Scholar] [CrossRef]
- Estrada, E. Path Laplacian matrices: Introduction and application to the analysis of consensus in networks. Linear Algebra Its Appl. 2012, 436, 3373–3391. [Google Scholar] [CrossRef]
- Liu, R.; Liu, X.; Wu, J. Persistent Path-Spectral (PPS) Based Machine Learning for Protein–Ligand Binding Affinity Prediction. J. Chem. Inf. Model. 2023, 63, 1066–1075. [Google Scholar] [CrossRef]
- Gomes, A.; Miranda, D. Path cohomology of locally finite digraphs, Hodge’s theorem and the p-lazy random walk. arXiv 2019, arXiv:1906.04781. [Google Scholar]
- Parks, A.D.; Lipscomb, S.L. Homology and Hypergraph Acyclicity: A Combinatorial Invariant for Hypergraphs; Technical report; Naval Surface Warfare Center: Dahlgren, VA, USA, 1991. [Google Scholar]
- Bressan, S.; Li, J.; Ren, S.; Wu, J. The embedded homology of hypergraphs and applications. Asian J. Math. 2019, 23, 479–500. [Google Scholar] [CrossRef]
- Ausiello, G.; Laura, L. Directed hypergraphs: Introduction and fundamental Algorithms—A survey. Theor. Comput. Sci. 2017, 658, 293–306. [Google Scholar] [CrossRef]
- Thakur, M.; Tripathi, R. Linear connectivity problems in directed hypergraphs. Theor. Comput. Sci. 2009, 410, 2592–2618. [Google Scholar] [CrossRef]
- Ren, S.; Wu, C.; Wu, J. Hodge decompositions for weighted hypergraphs. arXiv 2018, arXiv:1805.11331. [Google Scholar]
- Ren, S.; Wu, J. Stability of persistent homology for hypergraphs. arXiv 2020, arXiv:2002.02237. [Google Scholar]
- Chung, F.R. The Laplacian of a Hypergraph. In Proceedings of the Expanding Graphs, Princeton, NJ, USA, 11–14 May 1992; pp. 21–36. [Google Scholar]
- Emtander, E. Betti numbers of hypergraphs. Commun. Algebra 2009, 37, 1545–1571. [Google Scholar] [CrossRef]
- Hu, S.; Qi, L. The Laplacian of a uniform hypergraph. J. Comb. Optim. 2015, 29, 331–366. [Google Scholar] [CrossRef]
- Jost, J.; Mulas, R. Hypergraph Laplace operators for chemical reaction networks. Adv. Math. 2019, 351, 870–896. [Google Scholar] [CrossRef]
- Muranov, Y.; Szczepkowska, A.; Vershinin, V. Path homology of directed hypergraphs. Homol. Homotopy Appl. 2022, 24, 347–363. [Google Scholar] [CrossRef]
- Myers, A.; Joslyn, C.; Kay, B.; Purvine, E.; Roek, G.; Shapiro, M. Topological Analysis of Temporal Hypergraphs. In Proceedings of the Algorithms and Models for the Web Graph: 18th International Workshop, WAW 2023, Toronto, ON, Canada, 23–26 May 2023; Proceedings. Springer: Berlin/Heidelberg, Germany, 2023; pp. 127–146. [Google Scholar]
- Ameneyro, B.; Maroulas, V.; Siopsis, G. Quantum persistent homology. J. Appl. Comput. Topol. 2024, 8, 1961–1980. [Google Scholar] [CrossRef]
- Ameneyro, B.; Siopsis, G.; Maroulas, V. Quantum Persistent Homology for Time Series. Bull. Am. Phys. Soc. 2023, 68, 387–392. [Google Scholar]
- Bianconi, G. The topological Dirac equation of networks and simplicial complexes. J. Phys. Complex. 2021, 2, 035022. [Google Scholar] [CrossRef]
- Suwayyid, F.; Wei, G.W. Persistent Dirac of paths on digraphs and hypergraphs. Found. Data Sci. 2024, 6, 124–135. [Google Scholar] [CrossRef] [PubMed]
- Suwayyid, F.A.; Wei, G. Persistent Mayer Dirac. J. Phys. Complex. 2024, 5, 045005. [Google Scholar] [CrossRef] [PubMed]
- Wee, J.; Bianconi, G.; Xia, K. Persistent Dirac for molecular representation. Sci. Rep. 2023, 13, 11183. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Shen, L.; Liu, J.; Wei, G.W. Mayer-homology learning prediction of protein-ligand binding affinities. J. Comput. Biophys. Chem. 2024. [Google Scholar] [CrossRef]
- Song, R.; Li, F.; Wu, J.; Lei, F.; Wei, G.W. Multiscale Jones Polynomial and Persistent Jones Polynomial for Knot Data Analysis. arXiv 2024, arXiv:2411.17331. [Google Scholar]
- Shen, L.; Liu, J.; Wei, G.W. Evolutionary Khovanov homology. AIMS Math. 2024, 9, 26139–26165. [Google Scholar] [CrossRef]
- Jones, B.; Wei, G.W. A Khovanov Laplacian for Knots and Links. arXiv 2024, arXiv:2411.18841. [Google Scholar]
- Hofer, C.D.; Kwitt, R.; Niethammer, M. Learning representations of persistence barcodes. J. Mach. Learn. Res. 2019, 20, 1–45. [Google Scholar]
- Gerstenhaber, M.; Voronov, A. Higher operations on the Hochschild complex. Funct. Anal. Appl 1995, 29, 3. [Google Scholar]
- Biran, P.; Cornea, O. A Lagrangian quantum homology. In New Perspectives and Challenges in Symplectic Field Theory; American Mathematical Society: Providence, RI, USA, 2009; Volume 49, pp. 1–44. [Google Scholar]
- Harrington, H.A.; Otter, N.; Schenck, H.; Tillmann, U. Stratifying multiparameter persistent homology. SIAM J. Appl. Algebra Geom. 2019, 3, 439–471. [Google Scholar] [CrossRef]
- Liu, J.; Chen, D.; Wei, G.W. Interaction homotopy and interaction homology. arXiv 2023, arXiv:2311.16322. [Google Scholar]
- Liu, J.; Chen, D.; Wei, G.W. Persistent interaction topology in data analysis. arXiv 2024, arXiv:2404.11799. [Google Scholar]
- Kaji, S.; Sudo, T.; Ahara, K. Cubical ripser: Software for computing persistent homology of image and volume data. arXiv 2020, arXiv:2005.12692. [Google Scholar]
- Wagner, H.; Chen, C.; Vuçini, E. Efficient computation of persistent homology for cubical data. In Topological Methods in Data Analysis and Visualization II: Theory, Algorithms, and Applications; Springer: Berlin/Heidelberg, Germany, 2011; pp. 91–106. [Google Scholar]
- Wang, B.; Wei, G.W. Object-oriented persistent homology. J. Comput. Phys. 2016, 305, 276–299. [Google Scholar] [CrossRef]
- Kauffman, L.H. State models and the Jones polynomial. Topology 1987, 26, 395–407. [Google Scholar] [CrossRef]
- Khovanov, M. A categorification of the Jones polynomial. Duke Math. J. 2000, 101, 359–426. [Google Scholar] [CrossRef]
- Liu, J.; Shen, L.; Wei, G.W. ChatGPT for Computational Topology. Found. Data Sci. 2024, 6, 221–250. [Google Scholar] [CrossRef]
- Chen, D.; Liu, J.; Wei, G.W. Multiscale topology-enabled structure-to-sequence transformer for protein–ligand interaction predictions. Nat. Mach. Intell. 2024, 6, 799–810. [Google Scholar] [CrossRef]




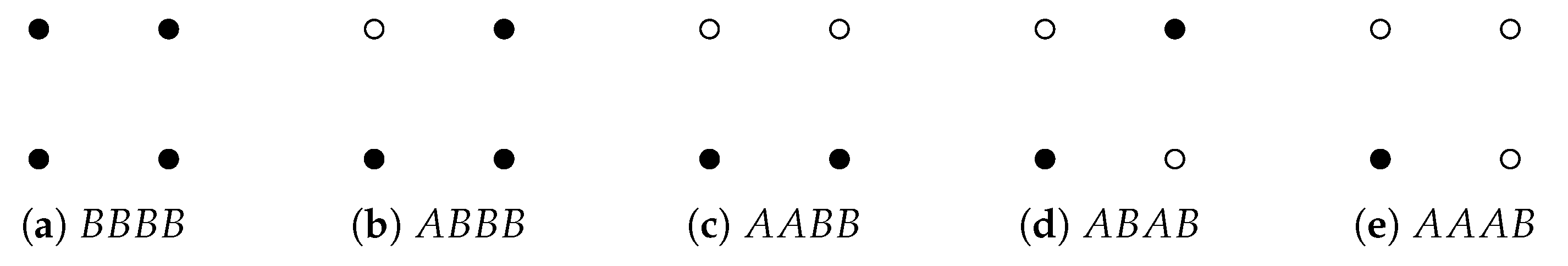


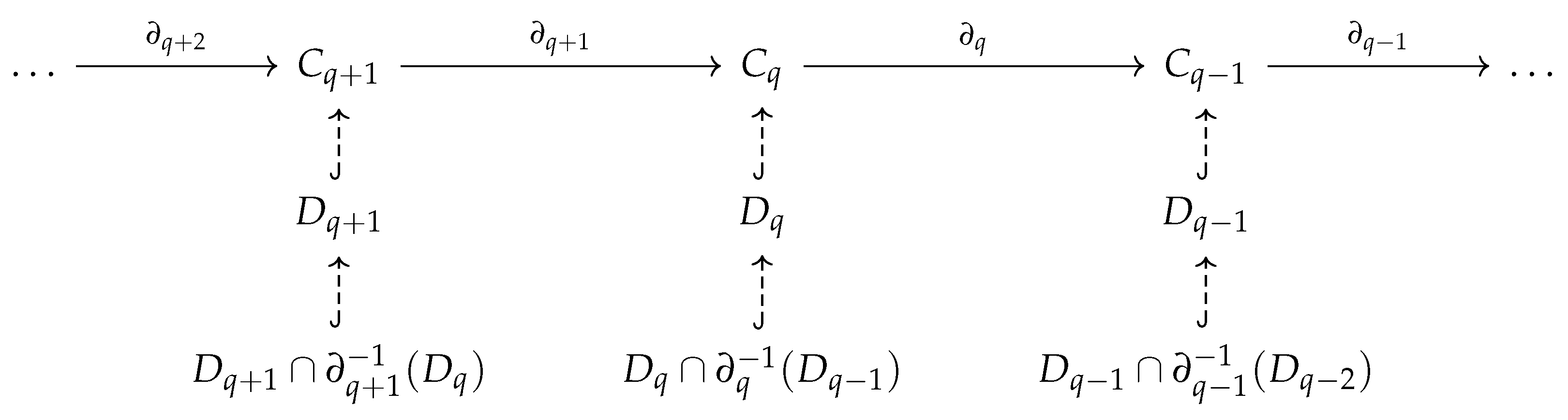
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Wei, G.-W. Persistent Topological Laplacians—A Survey. Mathematics 2025, 13, 208. https://doi.org/10.3390/math13020208
Wei X, Wei G-W. Persistent Topological Laplacians—A Survey. Mathematics. 2025; 13(2):208. https://doi.org/10.3390/math13020208
Chicago/Turabian StyleWei, Xiaoqi, and Guo-Wei Wei. 2025. "Persistent Topological Laplacians—A Survey" Mathematics 13, no. 2: 208. https://doi.org/10.3390/math13020208
APA StyleWei, X., & Wei, G.-W. (2025). Persistent Topological Laplacians—A Survey. Mathematics, 13(2), 208. https://doi.org/10.3390/math13020208






