Analytical Solution for Surrounding Rock Pressure of Deep-Buried Four-Hole Closely Spaced Double-Arch Tunnel
Abstract
:1. Introduction
2. Theoretical Framework
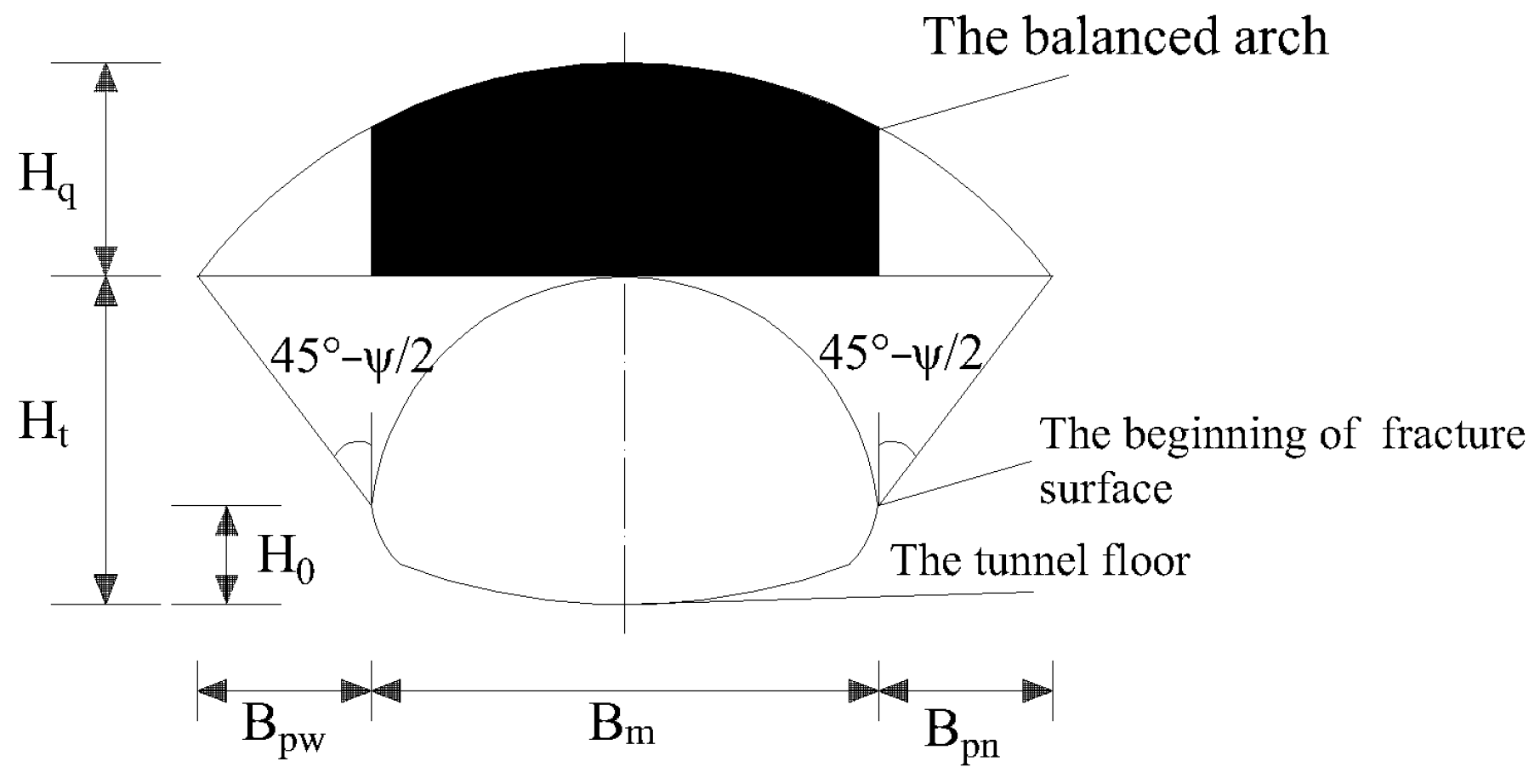
2.1. Calculation Method of Surrounding Rock Pressure of Protodyakonov’s Arch
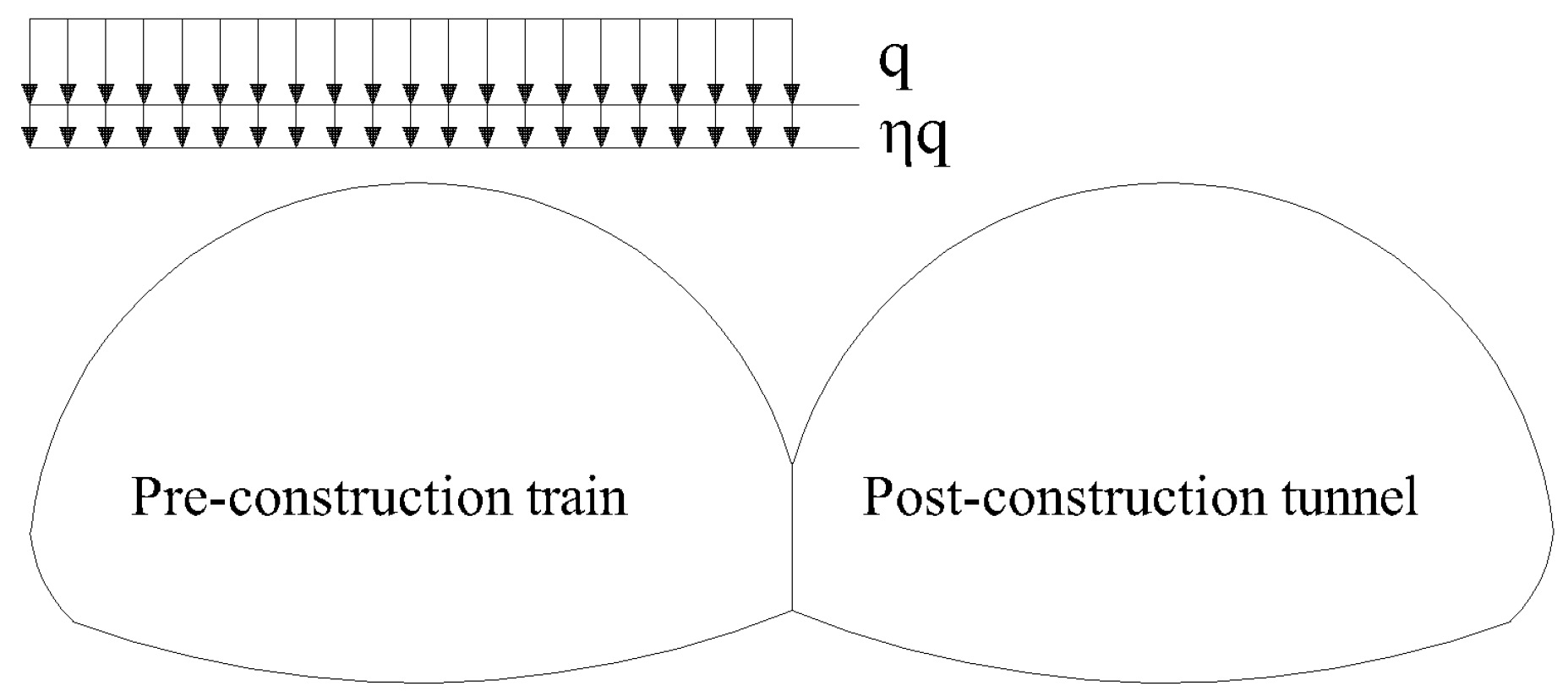
2.2. Process Load Design
2.3. The Calculation Model of Surrounding Rock Pressure
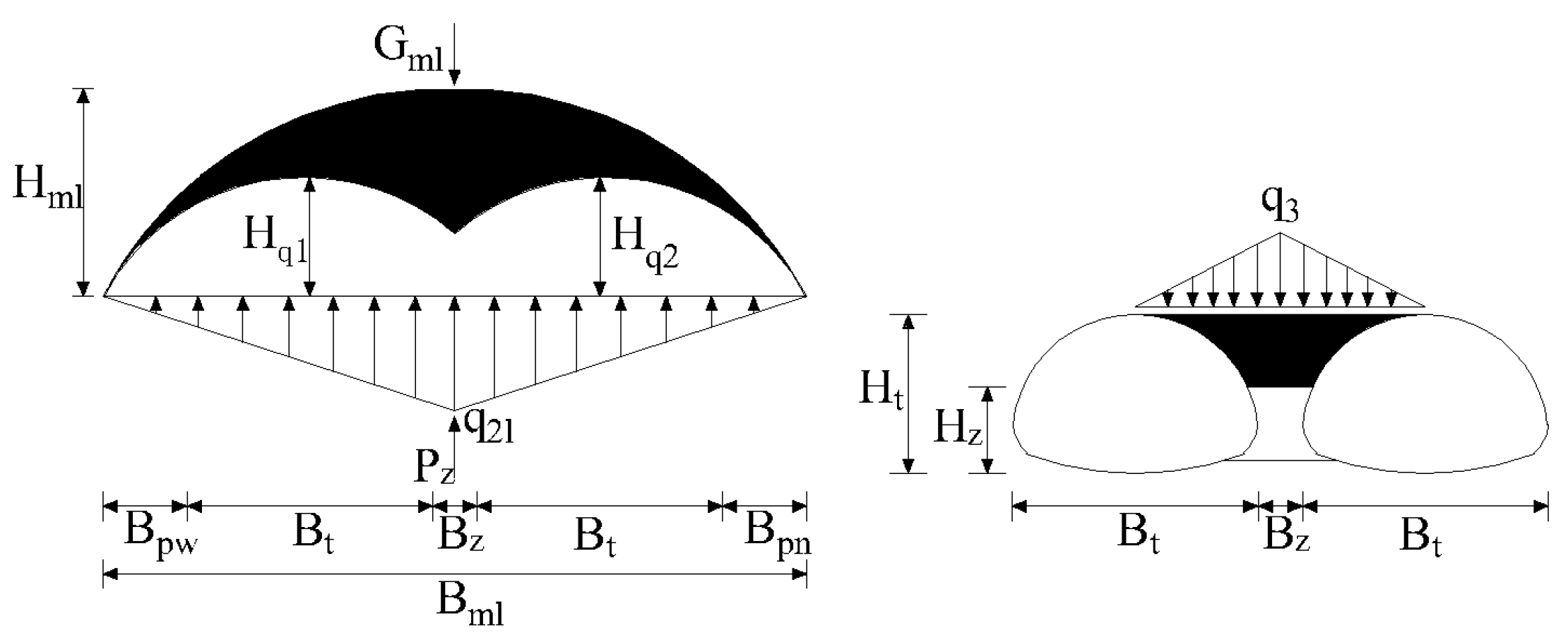
2.3.1. Mechanical Behavior of Continuous Arch
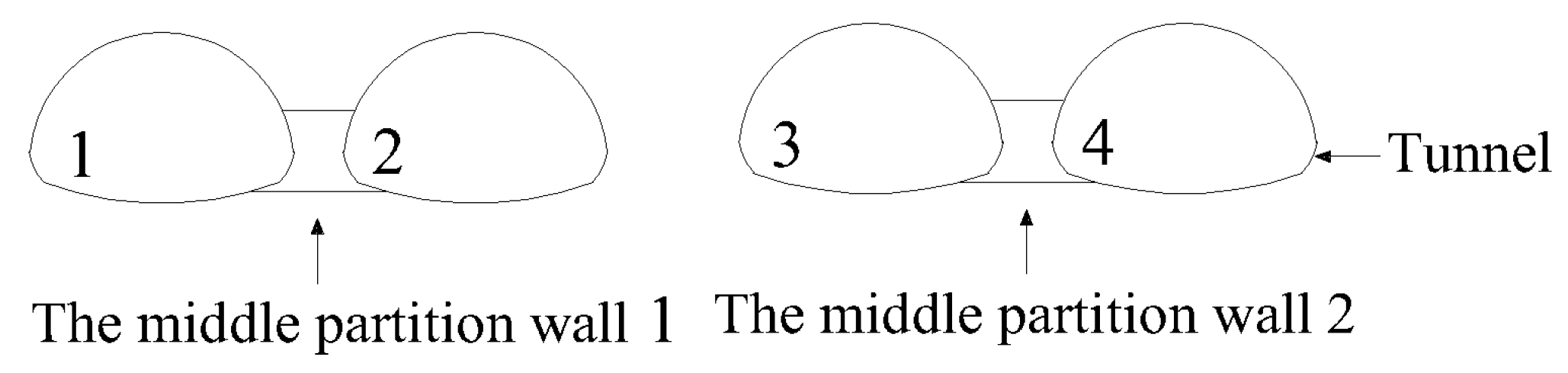
2.3.2. Mechanical Behavior of Closely Spaced
2.3.3. Models and Assumptions
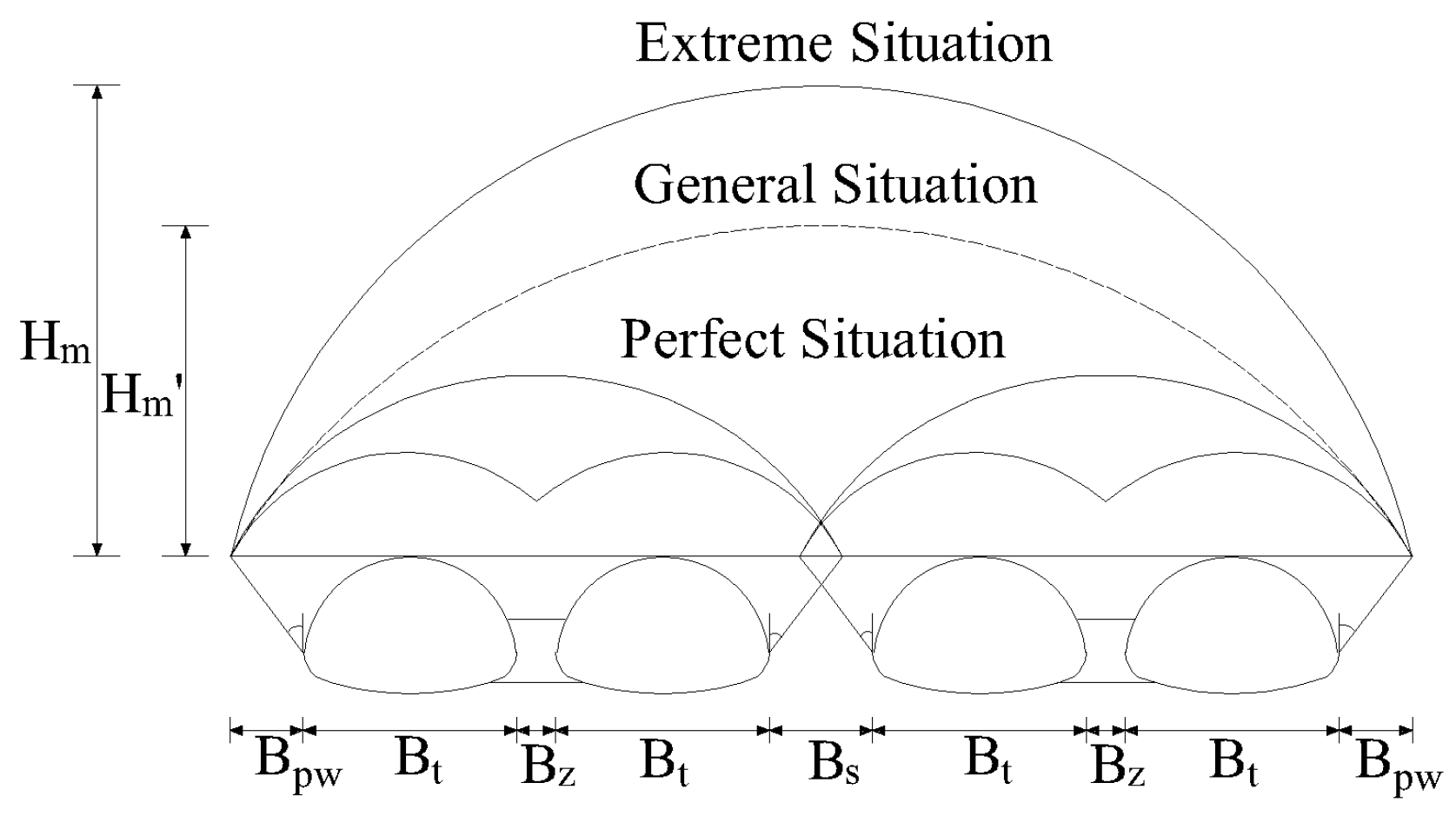
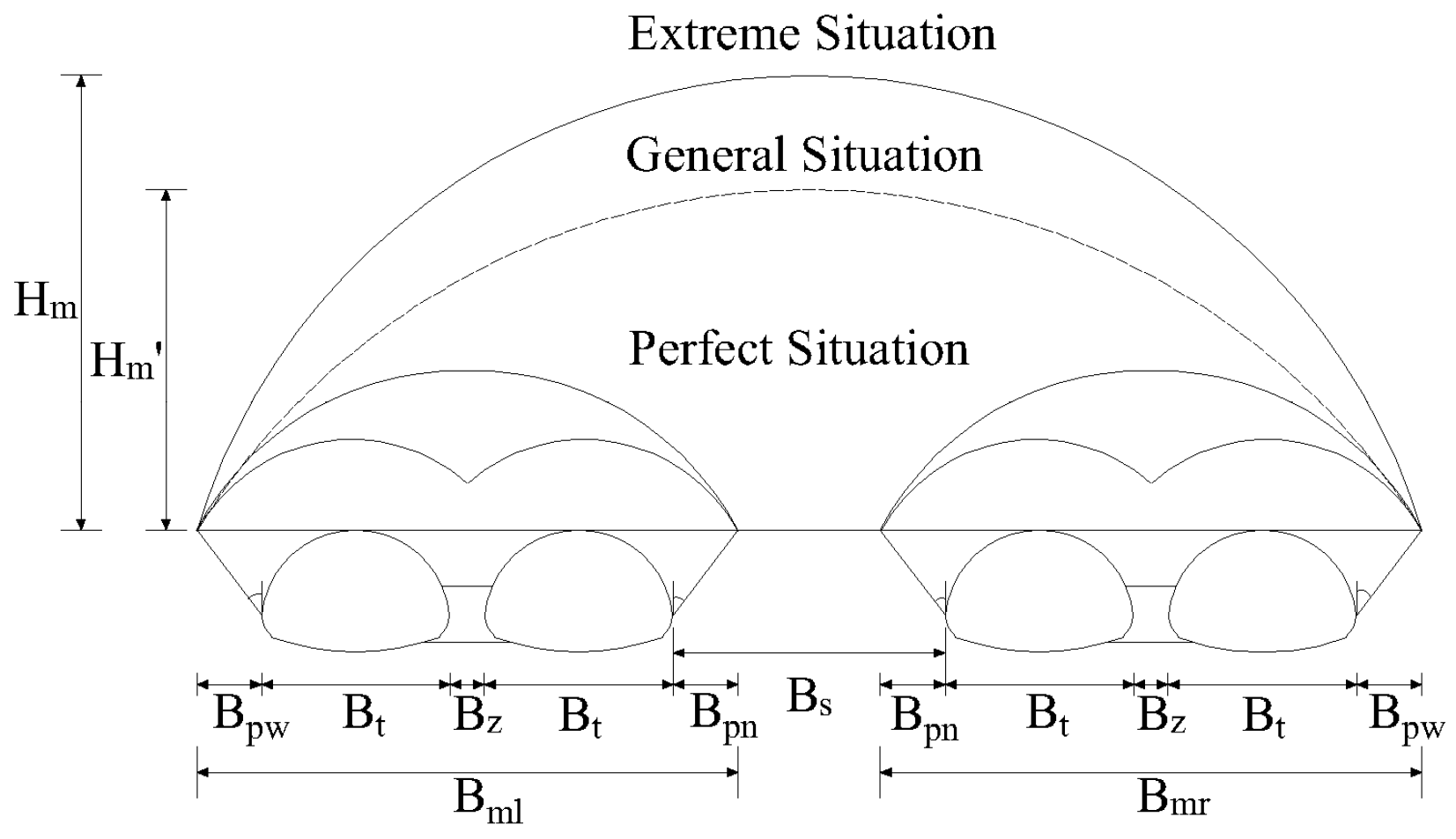
3. Calculation Method
3.1. Assumption of Surrounding Rock Pressure Calculation
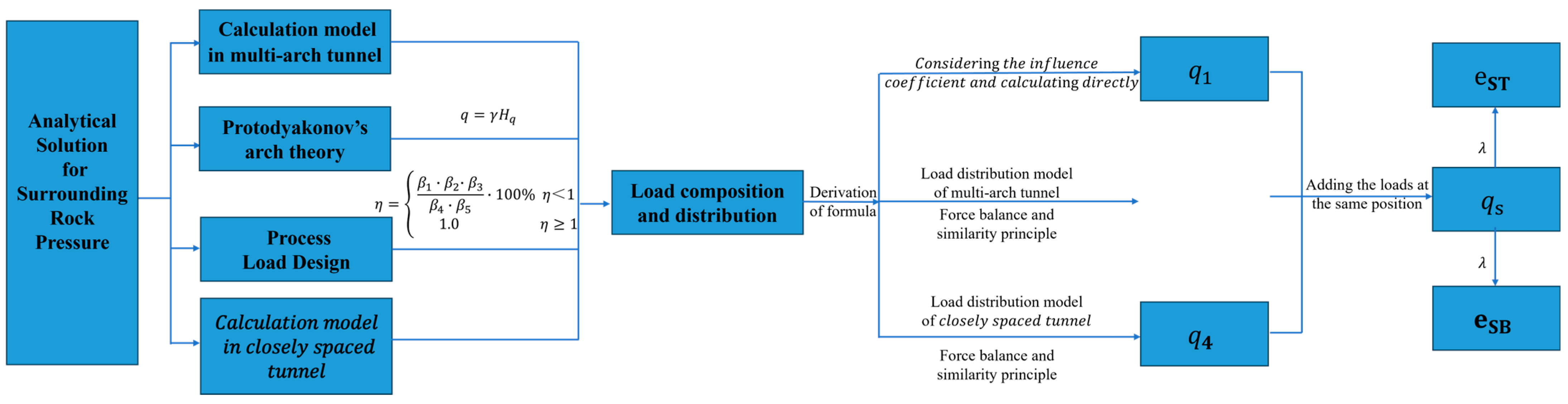
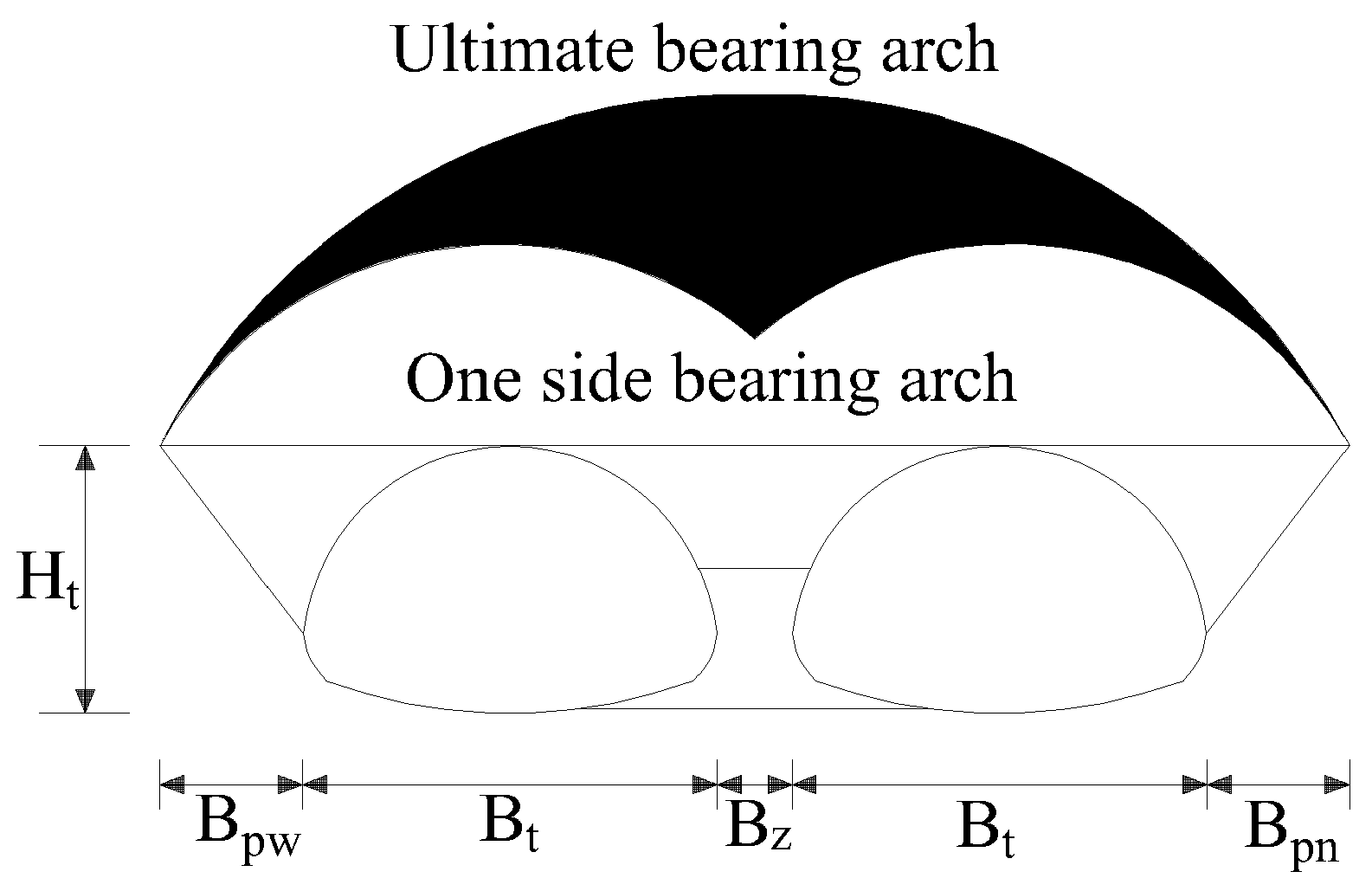
3.2. The Calculation Formula of Surrounding Rock Pressure
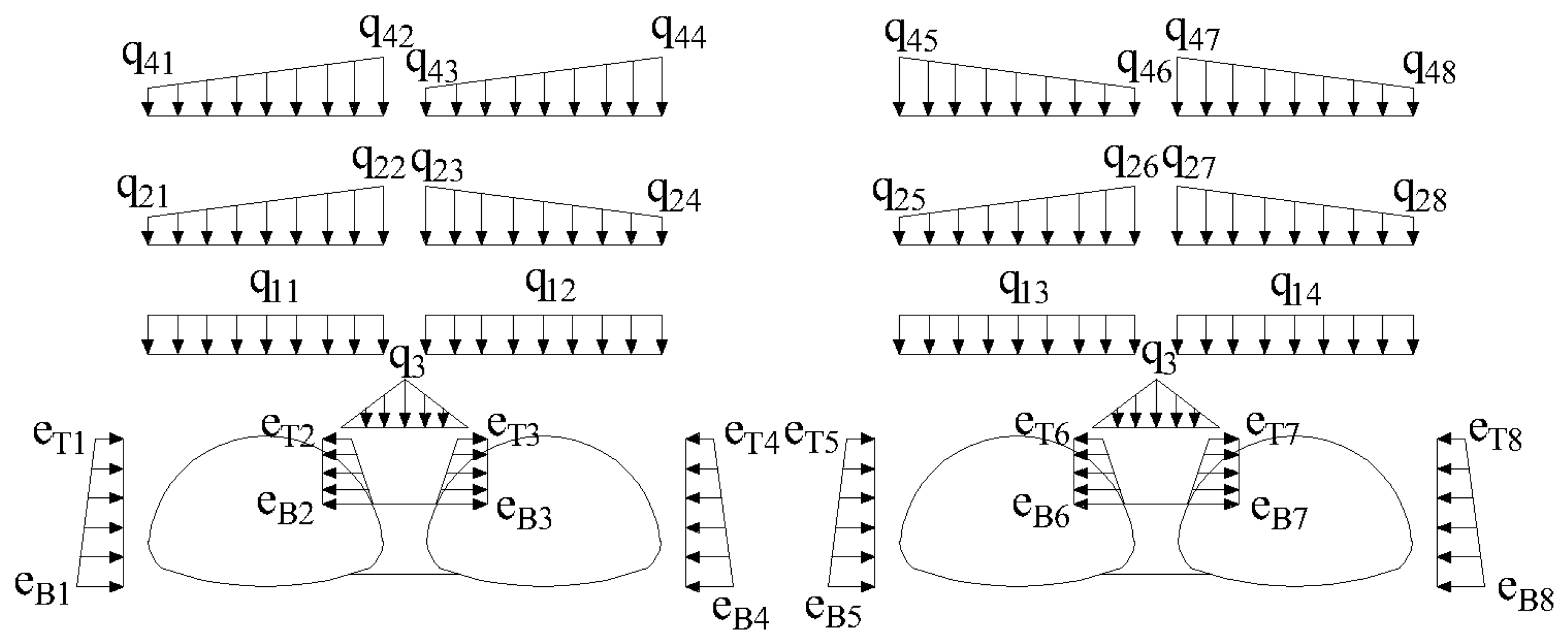
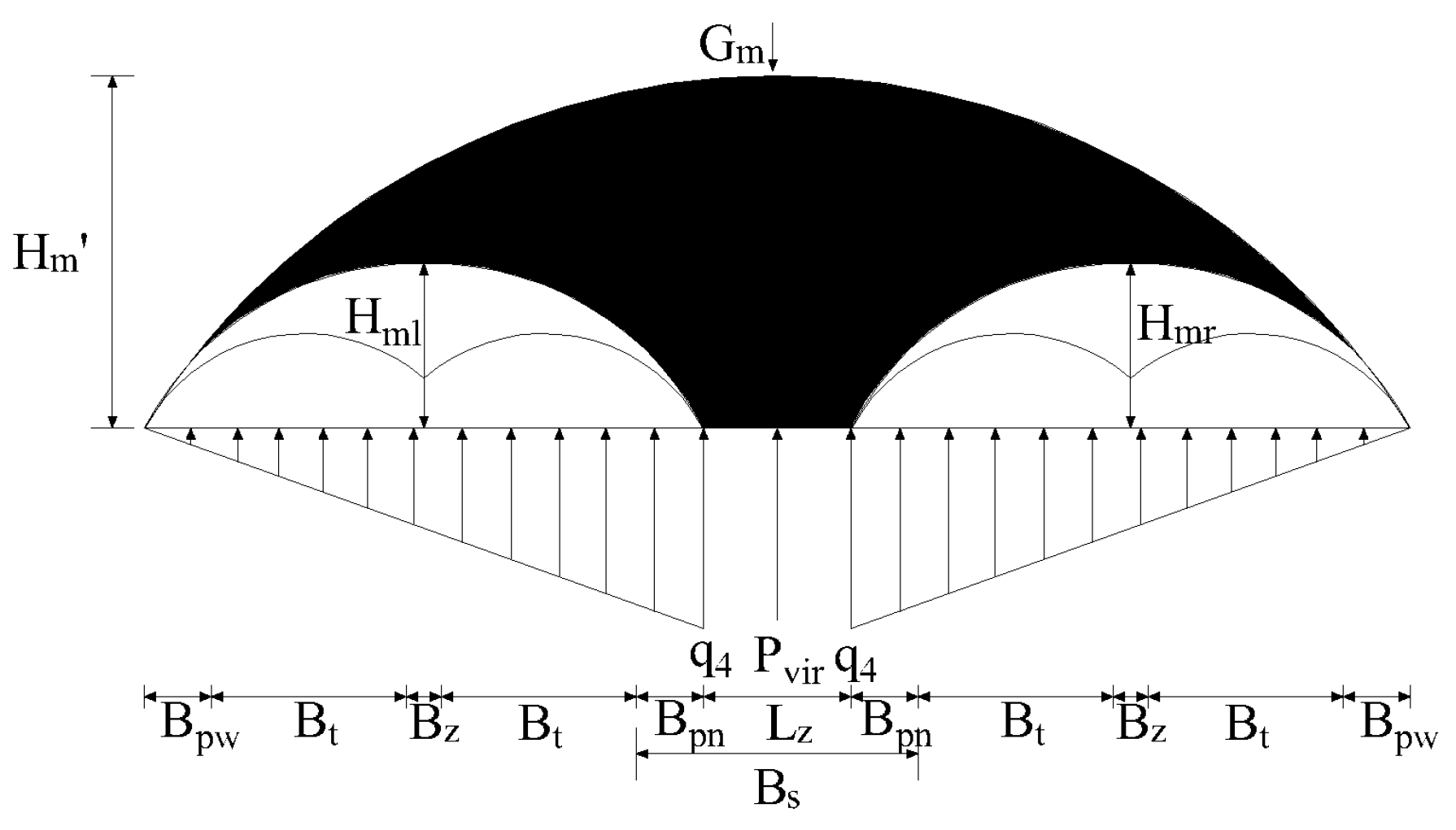
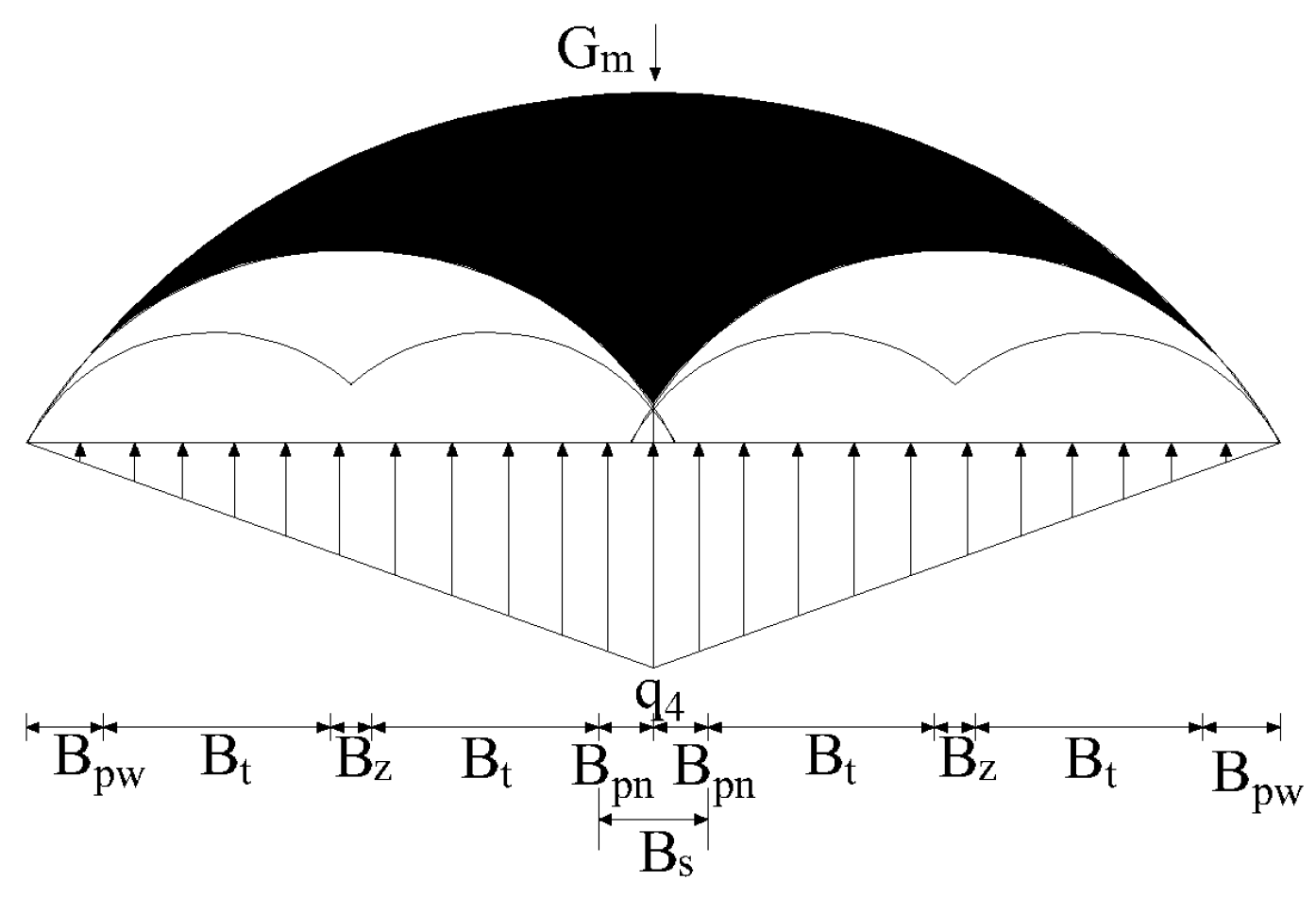
3.2.1. Load Distribution
3.2.2. Load Formula Derivation
3.2.3. Final Surrounding Rock Pressure
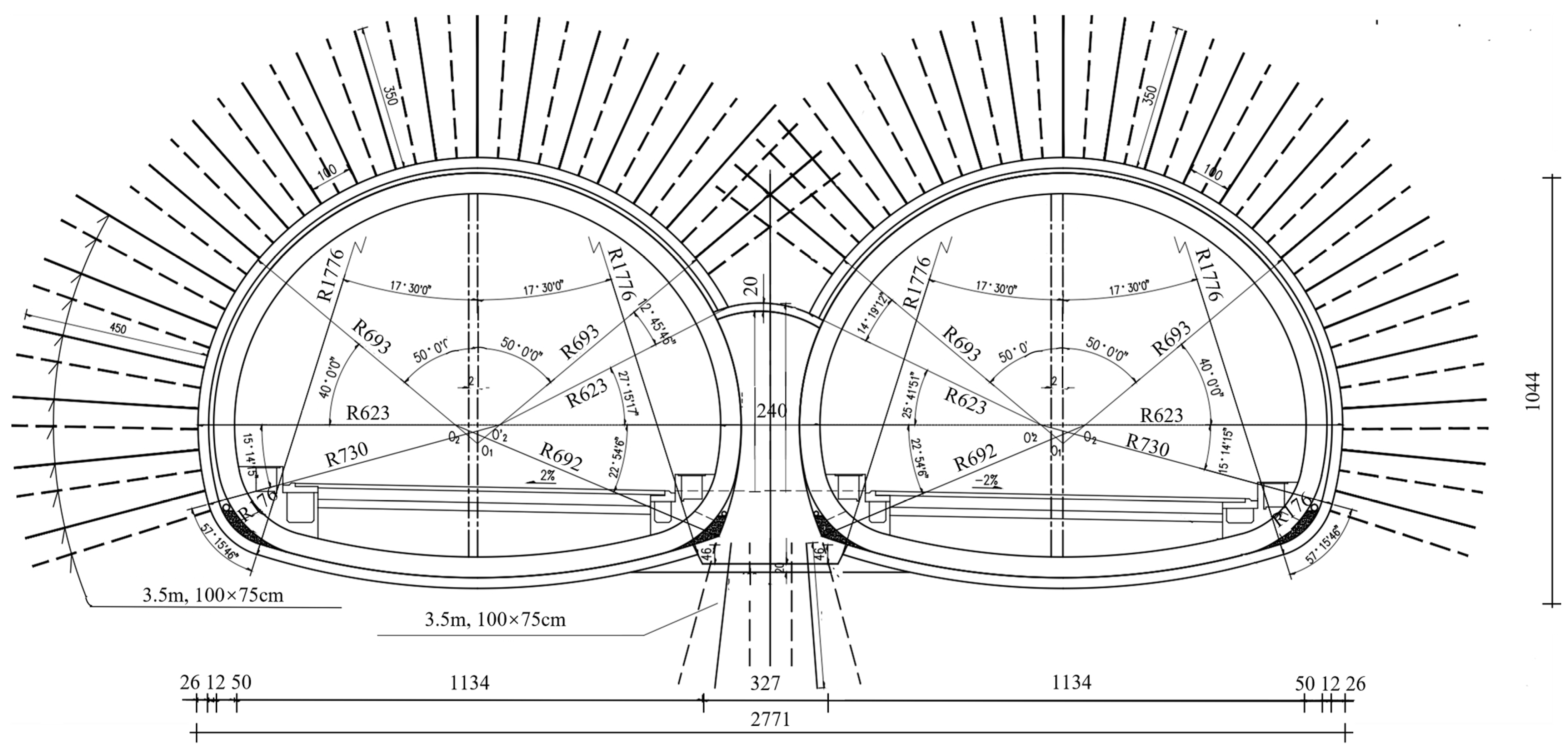
4. Result Verification
4.1. Calculation of Rock Pressure
4.2. Verification of Theoretical Formulas Based on the Width of Rock Pillars
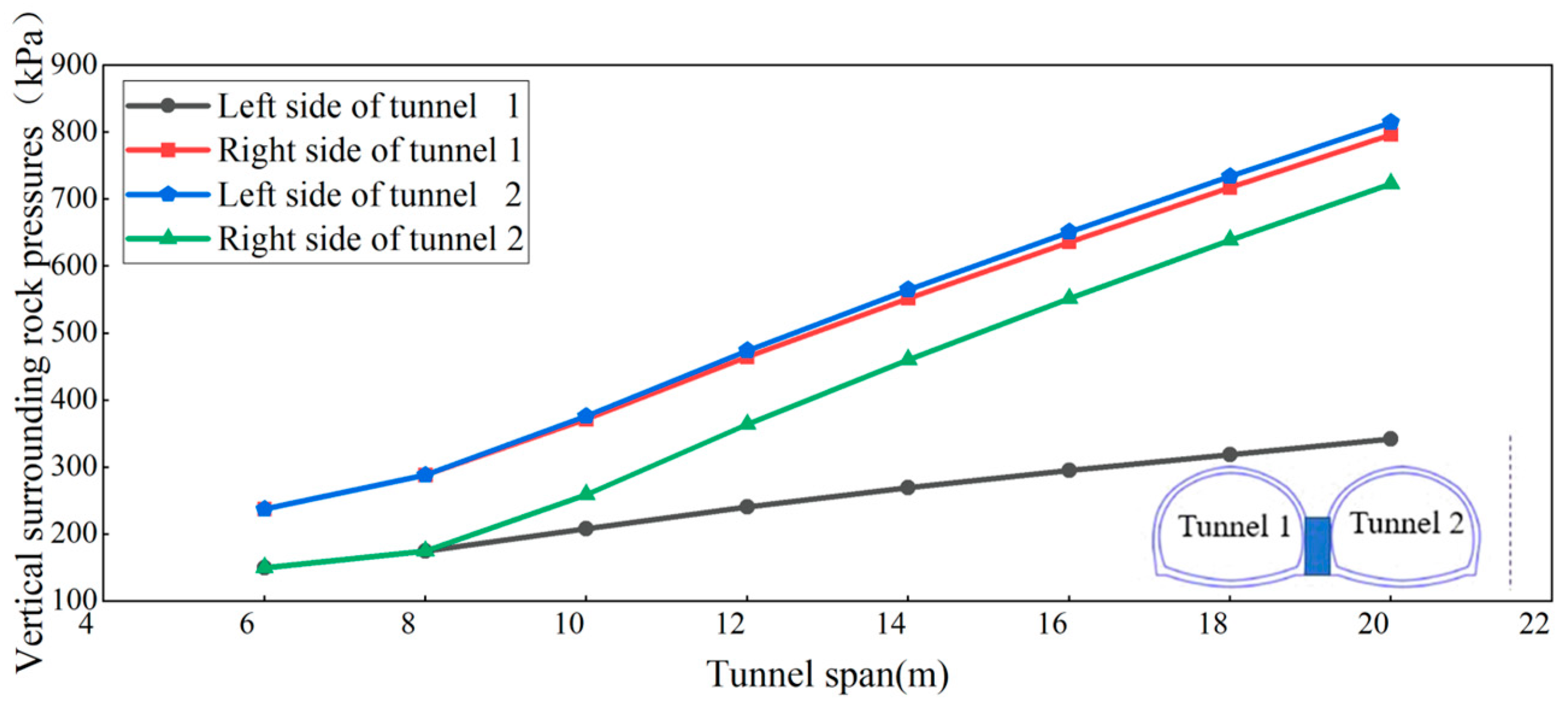
4.3. Verification of Theoretical Formulas Under Different Tunnel Excavation Spans
5. Analysis of Influencing Factors
5.1. Influence of Parameters of Middle Rock Pillar on Surrounding Rock Pressure
5.2. The Influence of Excavation Sequence on Surrounding Rock Pressure
5.3. Influence of Excavation Span on Surrounding Rock Pressure
5.4. Influence of Strength of Rock and Soil Mass at the Top of Middle Partition Wall on Surrounding Rock Pressure
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Indices | Implication | Unit |
|---|---|---|
| The vertical surrounding rock pressure | ||
| The basic surrounding rock pressure | ||
| The double hole additional surrounding rock pressure | ||
| The additional surrounding rock pressure in the left line double-hole multi-arch tunnel | ||
| The additional surrounding rock pressure in right line double-hole multi-arch tunnel | ||
| The maximum pressure of the loose earth above the middle partition wall | ||
| The compressive strength of the middle partition wall | ||
| the four holes’ additional surrounding rock pressure | ||
| The compressive strength of the unexcavated rock mass in the middle | ||
| The saturated uniaxial compressive strength of rock | ||
| The design compressive strength of the rock mass at the top of the middle partition wall | ||
| The compressive strength of the middle rock pillar | ||
| The supporting force of the unexcavated rock mass | ||
| The supporting force of the middle partition wall | ||
| The left line shadow rock weight force | ||
| The shadow rock weight force | ||
| The excavation height of the tunnel | ||
| The vertical height from the tunnel floor to the beginning of the fracture surface | ||
| The calculated height of the pressure of the loose surrounding rock at the top of the middle partition wall | ||
| The height of the middle partition wall | ||
| The vertical height of the balanced arch | ||
| The load height of the composite bearing arch of the left line | ||
| The load height of the composite bearing arch of the right line | ||
| The height of the four-hole composite arch | ||
| The height of the four-hole composite arch under extremely good condition | ||
| The excavation span of the tunnel | ||
| The width of the middle partition wall | ||
| The width of the middle pillar | ||
| The horizontal width of the balanced arch | ||
| The tunnel left line double hole composite bearing arch width | ||
| The tunnel right line double hole composite bearing arch width | ||
| The composite bearing arch width of the tunnel with four holes | ||
| The horizontal projection width of the outer fracture surface | ||
| The horizontal projection width of the inner fracture surface | ||
| The effective support width of the rock pillar | ||
| The weight of the surrounding rock | ||
| The fracture plane angle | ||
| The calculated friction angle | ° | |
| The angle between the fracture plane and the horizontal direction | ° | |
| The side pressure coefficient | ||
| The firmness coefficient of the surrounding rock | ||
| The process load influence coefficient | ||
| The additional load correction factor | ||
| The safety factor |
References
- Wu, B.; Lu, M.; Huang, W.; Lan, Y.; Wu, Y.; Huang, Z. A Case Study on the Construction Optimization Decision Scheme of Urban Subway Tunnel Based on the TOPSIS Method. KSCE J. Civ. Eng. 2020, 24, 3488–3500. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, X.; Zhang, Z.; Sun, W. 3D Discrete Element Method Modelling of Tunnel Construction Impact on an Adjacent Tunnel. KSCE J. Civ. Eng. 2020, 24, 657–669. [Google Scholar] [CrossRef]
- Tian, Z.; Sun, Y.; Zhao, Q.; Zhang, B.; Liu, W.; Zhang, X. Calculation method and evaluation of surrounding rock pressure of vertical shaft. Sci. Rep. 2024, 14, 7721. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; He, P.; Chen, Z.; Li, X. Study on a Surrounding Rock Pressure Calculation Method for Super-Large Section Highway Tunnels. Symmetry 2019, 11, 1133. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, J.; Yang, Y.; Wang, Z.; Xie, Y.; Qiu, J.; He, S.; Wang, X. Study on the Surrounding Rock Pressure Characteristics of Loess Tunnel Based on Statistical Analysis in China. Appl. Sci. 2022, 12, 6329. [Google Scholar] [CrossRef]
- Hu, J.; Xiao, J.; Yang, Z.; Xie, P.; Wen, H. Improved Protodyakonov’s Method of the Tunnel Surrounding Rock Pressure under the Seepage Condition of Weak Interlayer. Geofluids 2022, 2022, 1–14. [Google Scholar] [CrossRef]
- Yang, X.-L.; Jin, Q.-Y.; Ma, J.-Q. Pressure from surrounding rock of three shallow tunnels with large section and small spacing. J. Cent. South. Univ. 2012, 19, 2380–2385. [Google Scholar] [CrossRef]
- Hu, B.; Xiao, M.; Fu, X.; Yang, J.; Xu, C.; Wu, J.; Zhou, Y. FDEM numerical study of the influence law of geostress on state and pressure of tunnel surrounding rock. Front. Ecol. Evol. 2023, 11, 1237250. [Google Scholar] [CrossRef]
- Tong, J. General Formulas for Calculating Surrounding Rock Pressure of Tunnels and Underground Spaces. KSCE J. Civ. Eng. 2020, 24, 1348–1356. [Google Scholar] [CrossRef]
- Liu, J.; Xie, C.; Rao, J. Calculation Model and Influencing Factors of Surrounding Rock Loosening Pressure for Tunnel in Fold Zone. Adv. Civ. Eng. 2021, 2021, 1–15. [Google Scholar] [CrossRef]
- Yang, S.; Dai, R.; Ai, Z.; Li, X.; Zhang, C.; Huang, X. Analytical Solutions for the Mechanical Responses of Shallow Double-Arched Tunnel Subjected to Symmetric Loads. Adv. Civ. Eng. 2021, 2021, 1–33. [Google Scholar] [CrossRef]
- Li, R.; Zhang, D.; Fang, Q.; Liu, D.; Luo, J.; Fang, H. Mechanical responses of closely spaced large span triple tunnels. Tunn. Undergr. Space Technol. 2020, 105, 103574. [Google Scholar] [CrossRef]
- Cheng, X.; Liu, Y.; Liu, G.; Bu, Y. Study on Disturbance Characteristics of Surrounding Rock During Construction of Shallow Buried Bias Loess Tunnel with Small Clear Distance. Indian Geotech. J. 2024, 54, 2421–2442. [Google Scholar] [CrossRef]
- Tang, H.; Jiang, C.Y.; Deng, Q.; Bi, T.J.; Qin, Y.Q. A Method for Determining Surrounding Rock Load Borne by Antecedence Tunnel Lining of Shallowly Buried Double-arch Tunnel without Middle Drift. Rock Soil Mech. 2024, 45, 1170–1180. [Google Scholar] [CrossRef]
- Tang, H.; Jiang, C.; Deng, Q.; Bi, T.; Cha, Z. Calculation of Pressure on the Shallow-buried Double-arch Tunnel Without Middle Drift. KSCE J. Civ. Eng. 2022, 26, 4805–4814. [Google Scholar] [CrossRef]
- Gao, H.-J.; He, P.; Chen, Z. Calculation of Process Load of Deep-buried Asymmetric Multi-arch Tunnels. Chin. J. Geotech. Eng. 2020, 42, 1059–1066. [Google Scholar] [CrossRef]
- Li, P.; Wang, F.; Fan, L.; Wang, H.; Ma, G. Analytical scrutiny of loosening pressure on deep twin-tunnels in rock formations. Tunn. Undergr. Space Technol. 2019, 83, 373–380. [Google Scholar] [CrossRef]
- Wu, F.; He, C.; Kou, H.; Wang, B.; Meng, W.; Meng, H.; Guo, D. Discussion on Reasonable Clear Spacing of Twin-Tunnels in Weak Surrounding Rock: Analytical Solution and Numerical Analysis. KSCE J. Civ. Eng. 2022, 26, 2428–2442. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, D.; Li, R.; Chen, X.; Qi, W. Calculation Method for Surrounding Rock Pressure of Deeply Buried Triple-Arch Tunnel. Chin. J. Theor. Appl. Mech. 2024, 56, 3213–3226. [Google Scholar]
- JTG 3370.1-2018; Design Code for Highway Tunnels Volume 1 Civil Engineering. Ministry of Transport of the People’s Republic of China: Beijing, China, 2019.
- Bai, S.; Zhang, Y.; Fu, J.; Yang, X.; Yang, J. Study on Calculation Method for Surrounding Rock Pressure of Four-arch Tunnel. J. Highw. Transp. Res. Dev. 2023, 40, 163–171, 196. [Google Scholar] [CrossRef]
- Wu, X.; Tu, Z. Research of the Shape of Pressure Arch in Layered Rock Mass Based on the Protodyakonov’s Theory. In Proceedings of the 2017 7th International Conference on Manufacturing Science and Engineering (ICMSE 2017), Zhuhai, China, 11–12 March 2017. [Google Scholar]
- Gao, H.J.; He, P.; Chen, Z.; Li, X.Y. A Novel Calculation Method of Process Load for Extra-Large Section Tunnels. Symmetry 2019, 11, 1228. [Google Scholar] [CrossRef]
- Xie, C.; Tao, T.; Rao, J. Research Article Time-Varying Response Analysis of Surrounding Rock Construction Mechanics of a Double-Arch Tunnel without a Middle Pilot Tunnel and Suggestions for Tunnel Construction. Lithosphere 2022, 2022, 16. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X.; Song, D.; Wang, E.; He, Z.; Tan, R. Structural response of former tunnel in the construction of closely-spaced cross-river twin tunnels. Tunn. Undergr. Space Technol. 2024, 147, 105652. [Google Scholar] [CrossRef]
- Qi, W. Study on Surrounding Rock Pressure Calculation and Pressure Arch Effect in Triple-arch Tunnel. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2022. [Google Scholar]
- Jiang, C.; Tang, H.; Deng, Q.; He, Z.; Bi, T. Calculation Method of Surrounding Rock Pressure of Deeply Buried Double-arch Tunnel without Middle Drift. J. Cent. South Univ. (Sci. Technol.) 2023, 54, 1168–1177. [Google Scholar] [CrossRef]
- Qu, H. Study on Load Mode of Road Tunnel with Extra-large Cross-section and Low Flat-ratio and Its Application. Ph.D. Dissertation, Tongji University, Shanghai, China, 2007. [Google Scholar]
- Li, H.; Guo, X. Research on Calculation Metheods of Earth Pressure on Muti-arch Tunnel for Highway. Rock Soil Mech. 2009, 30, 3429–3434. [Google Scholar]
- Chen, S.L.; Lee, S.C.; Gui, M.W. Effects of rock pillar width on the excavation behavior of parallel tunnels. Tunn. Undergr. Space Technol. 2009, 24, 148–154. [Google Scholar] [CrossRef]
- Liu, J.; Guo, X. A Study on Calculation Method of Surrounding Rock Pressure About Deep-Buried Tunnel with Small Spacing. Highway 2009, 200–205. [Google Scholar]


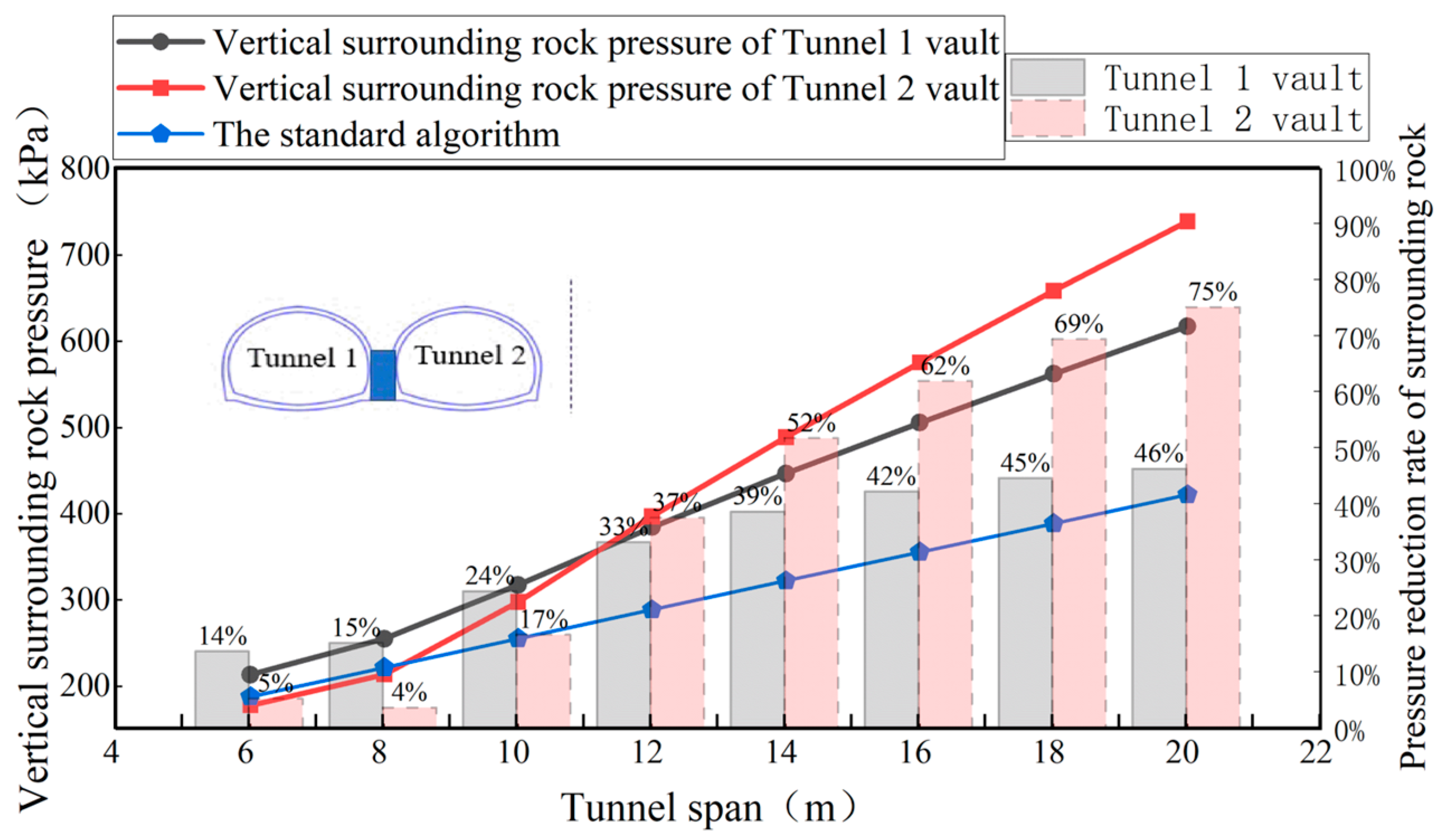
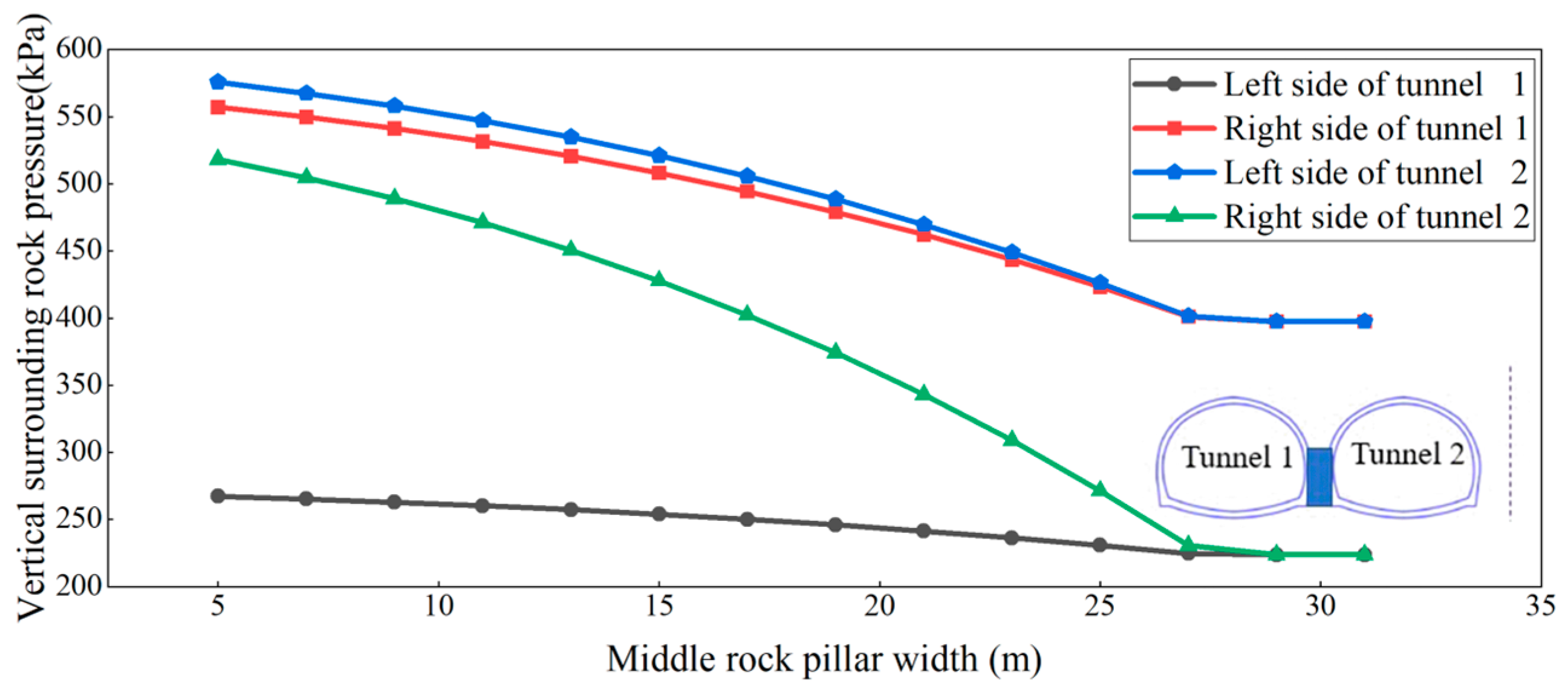
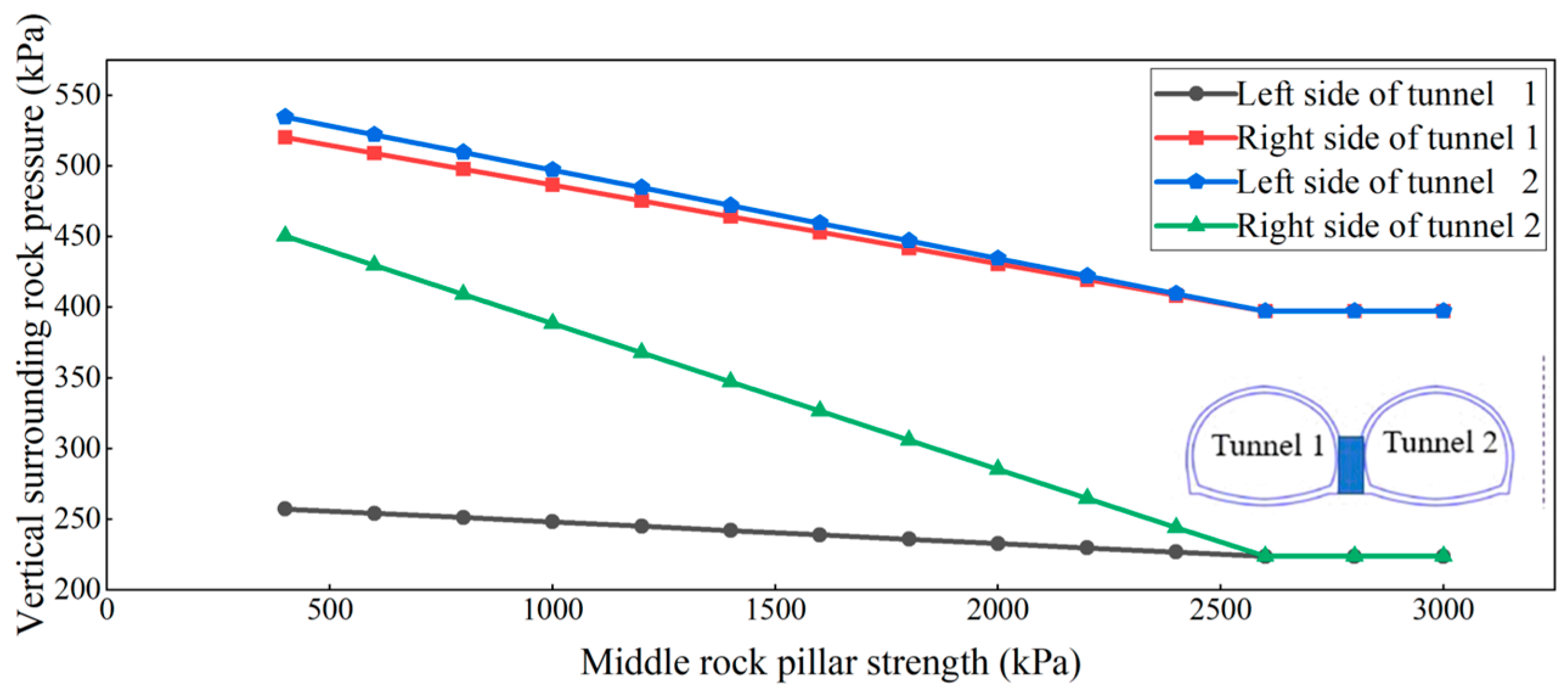
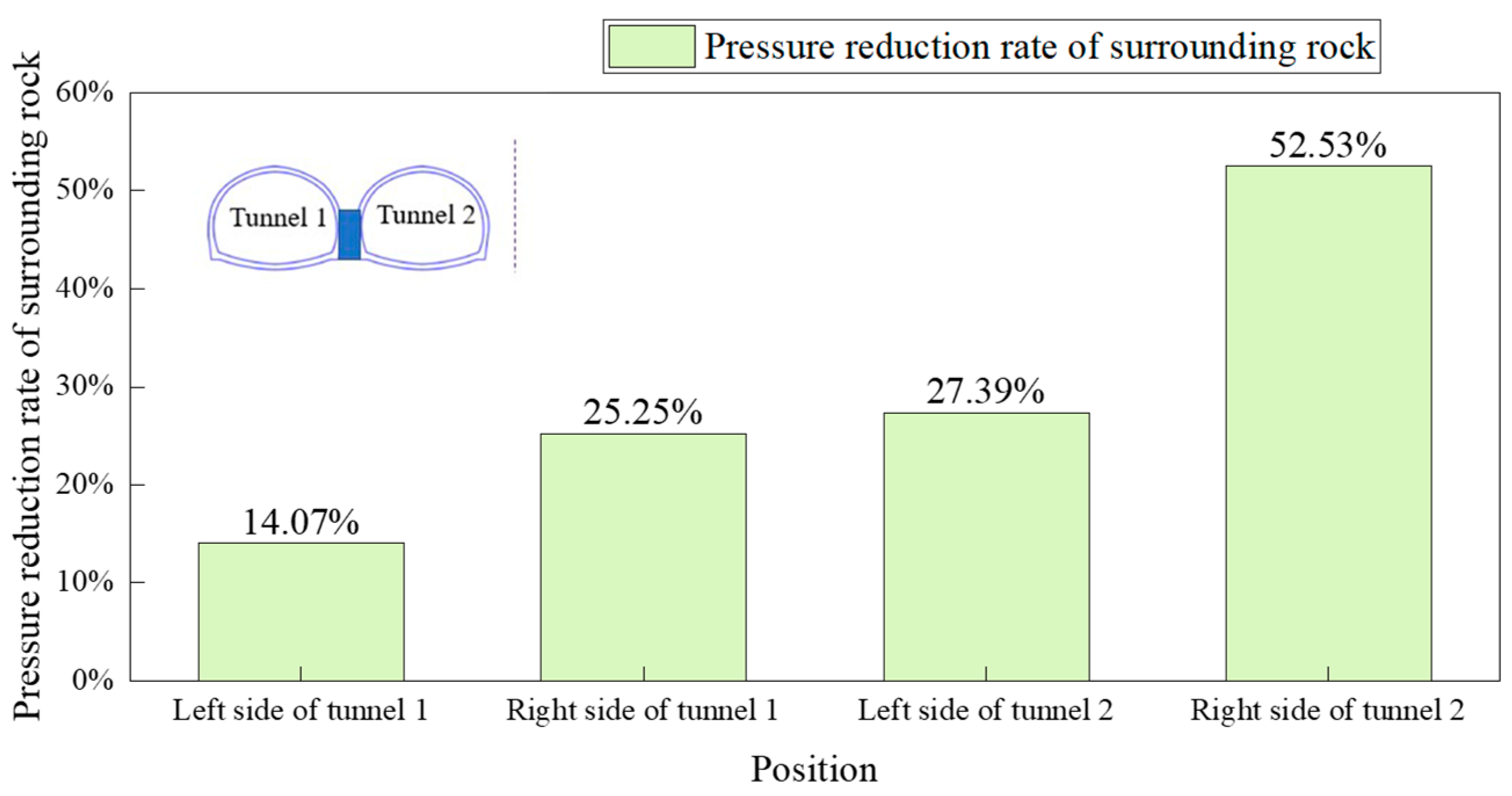


| Tunnel Span | 0–0.2B | 0.2B–0.4B | 0.4B–0.6B | 0.6B–0.8B | 0.8B–1.0B |
|---|---|---|---|---|---|
| 1.8 | 1.75 | 1.70–1.75 | 1.65–1.70 | 1.50–1.65 |
| Depth–Span Ratio | <0.6 | 0.6–1.0 | 1.0–1.2 | 1.2–1.6 | >1.6 |
|---|---|---|---|---|---|
| β2 | 1.5–1.2 | 1.2–1.0 | 1.0 | 0.9 | 0.8 |
| Inclusion Factor | 0 | |||
|---|---|---|---|---|
| β3 | 1.0 | 1.05 | 1.1 | 1.15 |
| Supporting Effect | Unsupported | Weak Support | Ordinary Support | Strong Support |
|---|---|---|---|---|
| β4 | 1.0 | 1.0–1.35 | 1.35 | 1.35–1.5 |
| Rock Grade | >III | IV | V | VI |
|---|---|---|---|---|
| β5 | 1.2 | 1.1 | 1.0 | 0.9 |
| Sequence 1 | Sequence 2 | Sequence 3 | Sequence 4 |
|---|---|---|---|
| 1→2→3→4 | 1→2→4→3 | 2→1→3→4 | 2→1→4→3 |
| Tunnel Span | Depth–Span Ratio | Inclusion Factor | Supporting Effect | Rock Grade | |
|---|---|---|---|---|---|
| Judging standard | 2 | 0.8 | 0 | Strong support | V |
| 1.8 | 1.1 | 1 | 1.5 | 1 | |
| 1.32 | |||||
| Tunnel Span | Depth–Span Ratio | Inclusion Factor | Supporting Effect | Rock Grade | |
|---|---|---|---|---|---|
| Judging standard | 18 | 0.8 | 0 | Strong support | V |
| 1.18 | 1.1 | 1 | 1.5 | 1 | |
| 0.87 < 1 | |||||
| 1 | 228.10 | 41.39 | 38 | 24.41 | 293.90 | 68.73 | 83.02 |
| 2 | 228.10 | 151.73 | 89.46 | 507.29 | 68.73 | 93.56 | |
| 3 | 172.80 | 151.73 | 38 | 99.87 | 462.40 | 72.19 | 85.86 |
| 4 | 172.80 | 41.39 | 164.93 | 379.13 | 72.19 | 97.65 | |
| 5 | 228.10 | 41.39 | 38 | 164.93 | 434.42 | 81.68 | 107.13 |
| 6 | 228.10 | 151.73 | 99.87 | 517.70 | 81.68 | 95.34 | |
| 7 | 172.80 | 151.73 | 38 | 89.46 | 451.99 | 59.24 | 84.07 |
| 8 | 172.80 | 41.39 | 24.41 | 238.60 | 59.24 | 73.54 |
| Sequence | ||||
|---|---|---|---|---|
| Sequence 1 (1→2→3→4) | ||||
| Sequence 2 (1→2→4→3) | ||||
| Sequence 3 (2→1→3→4) | ||||
| Sequence 4 (2→1→4→3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Shi, Q.; Wu, J.; Liu, D.; Wu, S. Analytical Solution for Surrounding Rock Pressure of Deep-Buried Four-Hole Closely Spaced Double-Arch Tunnel. Mathematics 2025, 13, 286. https://doi.org/10.3390/math13020286
Sun X, Shi Q, Wu J, Liu D, Wu S. Analytical Solution for Surrounding Rock Pressure of Deep-Buried Four-Hole Closely Spaced Double-Arch Tunnel. Mathematics. 2025; 13(2):286. https://doi.org/10.3390/math13020286
Chicago/Turabian StyleSun, Xianghao, Qi Shi, Jian Wu, Dunwen Liu, and Shan Wu. 2025. "Analytical Solution for Surrounding Rock Pressure of Deep-Buried Four-Hole Closely Spaced Double-Arch Tunnel" Mathematics 13, no. 2: 286. https://doi.org/10.3390/math13020286
APA StyleSun, X., Shi, Q., Wu, J., Liu, D., & Wu, S. (2025). Analytical Solution for Surrounding Rock Pressure of Deep-Buried Four-Hole Closely Spaced Double-Arch Tunnel. Mathematics, 13(2), 286. https://doi.org/10.3390/math13020286





